Abstract
The relatively stable lunar illumination may be used to realize radiometric calibration under low light. However, there is still an insufficient understanding of the accuracy of models and the influence of parameters when conducting research on low-light radiometric calibration. Therefore, this study explores the applicability of three atmospheric radiative transfer models under different nighttime conditions. The simulation accuracies of three nighttime atmospheric radiative transfer models (Night-SCIATRAN, Night-MODTRAN, and Night-6SV) were evaluated using the visible-infrared imaging radiometer suite day/night band (VIIRS/DNB) data. The results indicate that Night-MODTRAN has the highest simulation accuracy under DNB. The consistency between simulated top-of-atmosphere (TOA) radiance and DNB radiance is approximately 3.1%, and uncertainty is 2.5%. This study used Night-MODTRAN for parameter sensitivity analysis. The results indicate that for the lunar phase angle, aerosol optical depth, surface reflectance, lunar zenith angle, satellite zenith angle, and relative azimuth angle, the average change rates are 68%, 100%, 2561%, 75%, 20%, and 0%. This paper can help better understand the performance of models under different atmospheric and geographical conditions, as well as whether existing models can simulate the complex processes of atmospheric radiation.
1. Introduction
Radiometric calibration is the premise for the quantitative application of optical satellite data. However, after the payload is launched, it becomes challenging to achieve on-orbit radiometric calibration due to the complexity of the transmission link of the calibration reference on the satellite. Additionally, ground target measurement, which could be used as a reference for site calibration, is often influenced by uncertain factors such as scale effects, atmospheric conditions, and environmental changes [1,2,3,4]. At present, the accuracy issue of radiometric calibration for remote-sensing payloads remains an urgent problem that needs to be addressed. Although the application of traditional optical remote-sensing payload radiometric-calibration methods is relatively well-established, research on the radiometric calibration of low-light remote-sensing payloads is still challenging [5,6,7,8]. In recent years, there has been the successful launch of more and more satellites equipped with low-light imagers (such as LuoJia1-01, Fengyun-3E, and Sustainable Development Goals Science Satellite-1 (SDGSAT-1)). The application technology of low-light remote sensing has been developed rapidly, which has led to the increasing demand for low-light remote-sensing data. Therefore, it is essential to realize the radiometric calibration of low-light remote-sensing payloads.
Due to the ground light source being relatively stable, it is not influenced by the lunar radiation. Therefore, the active calibration method using ground light has been widely used [9,10]. Cao et al. [11] conducted a study using point sources such as fishing boats, bridges, and urban lights for low-light calibration. The results indicated a good consistent correlation between the estimated light power of bridge lights and the light power retrieved from satellite data. It also suggests designing specially created light sources to minimize uncertainty in low-light calibration. Because the sea surface is a dark background at night, the radiation of cross-sea bridge lights is relatively stable at night. Ma et al. [12] proposed a low-light calibration method based on bridge lights. The Hangzhou Bay Bridge and Donghai Bridge in China were selected as the calibration targets for VIIRS/DNB, with satellite observation data from August 2012 to July 2014 used. A comparison was made between simulated calculated TOA radiance and DNB radiance. The results revealed that the relative error of the low-light calibration method based on the Hangzhou Bay Bridge was −2.9% ± 9.3%, and the low-light calibration method based on the Donghai Bridge was −3.9% ±7.2%. Factors such as cloud scattering radiation, traffic signal lights, and vehicle headlamp radiation can easily influence the results during the simulation. Therefore, ground light source-active calibration methods require light sources with long-term stability and direct upward radiation emission capabilities. Hu et al. [13] conducted long-term monitoring of Dunhuang radiation correction field light sources, analyzed DNB imaging rules of target pixels under different observation geometric conditions, and developed a ground light source with stable radiation intensity and uniform directionality in all directions. However, these ground light sources are easily influenced by other light sources, and the type, position, and other factors of ground light sources are difficult to measure directly. Consequently, the on-orbit radiometric calibration of low-light remote-sensing payloads remains a significant challenge in need of resolution.
Recently, a method for the radiometric calibration of low-light remote-sensing payloads has been developed [14,15,16]. This method entails the selection of multiple low-phase and cloudless low-light remote-sensing images and through long-term sequence observations of uniformly stable targets on the surface. Following radiation transmission simulation calculations, the simulated values are compared with the observed values. Desert areas, due to their relatively stable atmospheric conditions and minimal time-based changes, are frequently utilized as vicarious calibration fields. For instance, Liao et al. [17] selected the Railroad Valley Playa (RVP) Desert in the United States as a vicarious calibration field, choosing 18 near-full-moon RVP observation values from March to October 2012. They used the MODTRAN model combined with the ROLO lunar irradiance model to simulate the TOA radiance at the top of the atmosphere, yielding an average deviation of −6.1% and an uncertainty of 8.9% in radiation error estimation. The albedo of ice and snow is relatively stable in the visible light band, making polar ice and snow coverage areas suitable for vicarious calibration. Qiu et al. [18] selected the Dome C area in Antarctica and the Greenland ice sheet area in the Arctic as vicarious calibration fields. The reflectance at the top of the atmosphere of the calibration area obtained by the lunar irradiance model (MT2009) showed good consistency with the corresponding product of Hyperion, with a radiometric calibration uncertainty of about 8%. Hu et al. [19] compared the difference between simulated TOA and actual observed radiance after a year of observations in the Dome C region of Antarctica and the RVP desert region of the United States. The results indicated average relative errors of −7.14% and −4.14%, respectively. Hu et al. [20] employed a low-light substitution calibration based on the Dunhuang radiation correction field. They analyzed 14 sets of DNB observation data from September 2012 to July 2014. By leveraging Ma et al.’s [21] refined atmospheric radiative transfer models, they obtained simulated TOA radiance values. When compared to actual DNB radiance, the relative error was found to be −6.2% ± 8.6%. Given that convective clouds lie above atmospheric aerosols and water vapor, their impact can be disregarded, thereby preventing inaccuracies in atmospheric radiative transfer models. Consequently, Ma et al. [21] introduced a low-light substitution calibration technique based on deep convective clouds. They selected six months of DNB data spanning August 2012 to January 2013. By integrating the MT2009 lunar irradiance model into the SCIATRAN model, they achieved radiative transfer to compute simulated albedos for target pixels. When comparing these simulated albedos with DNB observations under prevailing observational geometric conditions, the results indicated that the radiative uncertainty stemming from diurnal variations lies within ±10%. In summary, a lot of research has been developed on the radiation calibration of low-light satellites using the nighttime atmospheric radiative transfer model.
While these studies use the nighttime atmospheric radiative transfer model for low-light radiometric calibration, existing models have certain limitations. Firstly, basic research on point source radiation transfer is still underdeveloped in the context of ground light radiometric calibration methods. This lack of maturity hinders the effective application of the radiative transfer model in these studies [22]. Subsequently, in the study of low-light radiometric calibration methods, existing models are susceptible to discrepancies arising from surface properties and weather conditions, leading to significant inaccuracies in their predictions. Therefore, this paper studies the applicability of different atmospheric radiative transfer models at nighttime. This study employs lunar illumination as a radiation source to replace the existing atmospheric radiative transfer models. Then, the nighttime atmospheric radiative transfer model was constructed and compared with the VIIRS/DNB data. Furthermore, the influence of parameters, including lunar phase angle, aerosol optical depth, surface reflectance, lunar zenith angle, observation zenith angle, and relative azimuth angle, on nighttime radiative transfer simulations was meticulously analyzed. This study aims to elucidate the suitability of various radiative transfer models during nighttime, thereby facilitating informed decision making regarding model selection for diverse scenarios. Concurrently, it seeks to advance the development of high-precision nighttime atmospheric radiative transfer models, enhancing the precision of low-light radiometric calibration.
2. Materials and Methods
2.1. Research Region
China National High-Resolution Remote Sensing Integrated Calibration Field, also known as the Baotou Field, is situated in Bayannur City, within China’s Inner Mongolia Autonomous Region. Its central coordinates are 40.85° N and 109.62° E, and it is approximately 50 km from the Baotou urban area. The Baotou field has superior basic geographical conditions, flat regional terrain, and uniform surface reflection. The climate in the field is dry, with little rain in four seasons. The annual average rainfall is 320 mm and has good atmospheric visibility conditions [23]. It spans an area of 3.0 km2, with a central altitude of 1.27 km [24]. Furthermore, the Baotou Field has an automatic atmospheric parameter observation system, as depicted in Figure 1. This system comprises an automatic sun-tracking photometer, CIMEL CE318, and an automated weather station, which operates in a full-day observation mode to gather atmospheric and meteorological parameters routinely [25]. Consequently, the Baotou Field was selected for the nighttime radiative transfer simulation experiment.
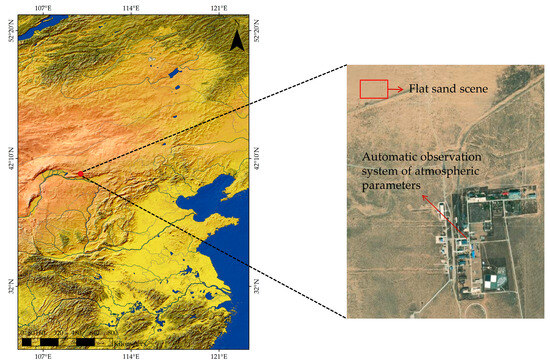
Figure 1.
The location of Baotou Field and automatic observation system.
2.2. Data Collection
2.2.1. Nighttime Light Data
The Suomi National Polar-orbiting Partnership (SNPP) is the first satellite of the National Polar-orbiting Environmental Satellite System (NPOESS) in the United States, and VIIRS, as the core payloads of this satellite, is a scanning radiometer with a side-looking scan width of about 3044 km and a revisit cycle of 12 h. There are 22 bands in VIIRS, including 5 high-resolution (I-band), 16 medium-resolution (M-band), and 1 DNB [26,27]. This study used two sets of SNPP data products: SVDNB and GDNBO products composed of 3072 × 4064 pixels in sensor data records (SDRs). Among them, the SVDNB product provides calibrated TOA radiance, and its quality flags for operational use; the GDNBO product includes latitude and longitude corresponding to the TOA radiance, lunar phase angle, satellite zenith angle, and other observation geometric information [28,29,30]. The spatial resolution of these data is 750 m, and they are published in HDF5 format. Figure 2 shows the spectral response function of the DNB used. DNB was obtained from https://www.avl.noaa.gov/, accessed on 16 April 2023 [31].
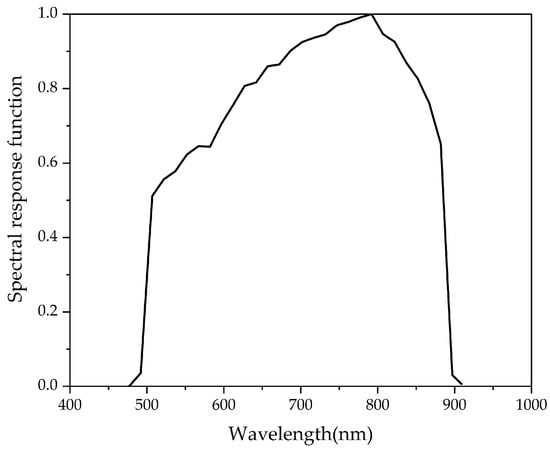
Figure 2.
DNB spectral response function.
It is essential to filter the VIIRS/DNB data from 2020 to 2022 to ensure accuracy in the final calibration results. The criteria for observation selection are as follows:
- (1)
- The research region is focused on the DNB pixel corresponding to the central location of the Baotou Field, extending outwards to a range of 10 km × 10 km.
- (2)
- The lunar zenith angle is less than 90°, meaning the moon is positioned above the horizon. This ensures that the lunar illumination can effectively illuminate the target pixel area.
- (3)
- The lunar phase angle is less than 120°, meaning more than two-thirds of the lunar phase is illuminated. This ensures an adequate downward illumination of the top of the atmosphere.
2.2.2. Surface Reflectance Data
This study utilizes the surface reflectance parameter product, part of the MODIS Level 3 Land Standard Product data. These data represent multi-angle reflectance data derived from the cumulative changes in the solar surface satellite’s relative position, as observed over a continuous 16-day period by orbital platforms (TERRA and AQUA). The product is presented as raster data with a spatial resolution of 500 m. In this study, the average surface reflectance of Band1, Band2, and Band4 is used instead of the surface reflectance at DNB.
2.2.3. Aerosol Optical Depth Data
Aerosol Robotic Network (AERONET) is a global aerosol observation network based on ground monitoring, providing long-term aerosol monitoring, and can provide near real-time aerosol information with an observation error of only 0.02. AERONET offers three different quality levels: level 1.0 (uncurated verified), level 1.5 (cloud-curated), and level 2.0 (strict quality assurance) [32]. This study uses the aerosol optical depth (AOD) of level 1.5 at the AOE_BaoTou site. Because the aerosol optical depth at 550 nm is missing in the AERONET measured data, it cannot be used as a parameter input into the atmospheric radiative transfer model [33,34]. Therefore, aerosol optical depth at 550 nm was calculated using Equation (1):
where τ0.44 and τ0.675 are the aerosol optical depth at wavelengths of 440 nm and 675 nm, and τ0.55 is the aerosol optical depth at 550 nm obtained by interpolation.
2.2.4. Lunar Irradiance Data
The MT2009 is a hyperspectral lunar irradiance model developed by Miller and Turner. It is used to calibrate with VIIRS/DNB data, realizing the quantitative application of nighttime remote-sensing data. The model encompasses a wavelength range from 0.2 μm to 2.8 μm, with a spectral resolution of 1 nm [35]. The irradiance calculated using this model is represented by Equation (2):
where Lm is the lunar reflected radiance, Ωm is the Earth-observed lunar solid angle, Rse is the average distance between the sun and Earth, Rsm is the average distance between the sun and moon, rm is the radius of the moon, re is the radius of the Earth, and Rme is the average distance between the Earth and moon. While f(θp, λ) is the lunar phase function, and its empirical expression is given by Equation (3):
where a and b are the fitting coefficients of lunar brightness variation with wavelength and phase angle, obtained from the measured data.
The solar irradiance utilized in MT2009 is derived from satellite-based measurement data of Solar Radiation and Climate Experiment (SORCE) [36]. Furthermore, the model fits the geometric relationship of sun–moon–Earth. It also provides the lunar phase angle, the mean distance between the sun and the moon, and the average distance between Earth and the moon at varying times. Figure 3 illustrates the lunar irradiance under different lunar phase angles, considering the average distance between the sun and the moon and the average distance between Earth and the moon.
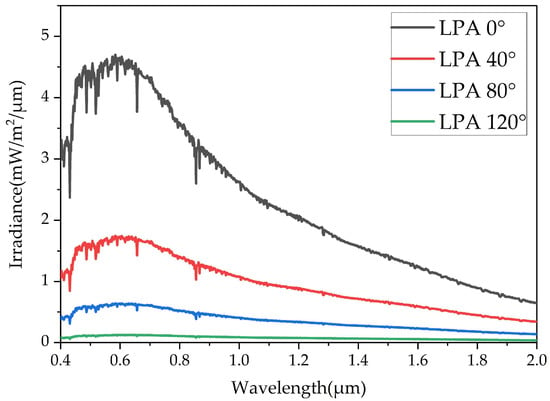
Figure 3.
Lunar irradiance simulated by MT2009 under different lunar phase angles.
This section presents the data used in this paper and the data processing. Table 1 describes the details of the datasets used in this paper.

Table 1.
Statistics of datasets.
2.3. Methods
Figure 4 shows the workflow of this study. It involves data collection and processing, model construction, model precision evaluation, and model sensitivity analysis.
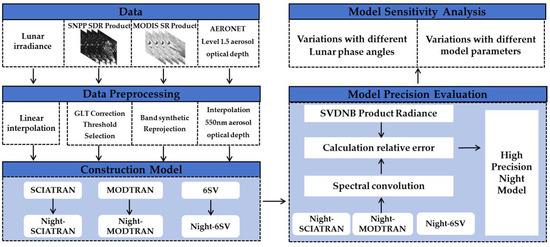
Figure 4.
Flow chart of this study.
- (1)
- Data collection and processing: This study used SNPP satellite data, surface reflectance data, aerosol optical depth data, lunar irradiance data, and DNB spectral response function. The SNPP satellite data were processed by Geographic Lookup Table (GLT) correction. The surface reflectance data are reprojected to the WGS84 coordinate system. The aerosol optical depth at 550 nm was obtained by interpolating aerosol data. The resolution of lunar irradiance data is converted into three formats: 1 nm, 0.5 nm, and 1 cm−1.
- (2)
- Model construction: This study analyzes the characteristics of lunar radiation for the MT2009 lunar irradiance model. The lunar irradiance is introduced into MODTRAN, SCIATRAN, and 6SV, and the lunar illumination is used as the radiation source of the atmospheric radiative transfer model.
- (3)
- Model precision evaluation: The radiance value of the SVDNB product was used as a benchmark to evaluate the accuracy of simulated values from three nighttime atmospheric radiation transfer models. Then, the accuracy of the nighttime atmospheric radiative transfer model is evaluated by calculating the average relative error.
- (4)
- Model sensitivity analysis: Utilizing the nighttime atmospheric radiative transfer model, calculated the sensitivity of different parameters to the TOA radiance, including lunar phases, aerosol optical depths, surface reflectances, lunar zenith angles, and observation zenith angles. Concurrently, the applicability of the atmospheric radiative transfer model under different conditions is further analyzed.
2.3.1. Principle of Atmospheric Radiative Transfer at Nighttime
Figure 5 is the path diagram of atmospheric radiative transfer at nighttime. As shown in Figure 5, the TOA lunar radiation undergoes atmospheric extinction before reaching the surface; after ground reflection, its radiance, along with that emitted by ground artificial lights and other sources, undergoes atmospheric effects and is received and recorded by satellite sensors [7,9]. At present, it is difficult to quantify the radiation of ground lights accurately, and related research on the ground light model is still underway. Therefore, to ensure the calculation’s accuracy, this paper chooses the area without ground lights. This area is located in the calibration site of Baotou, China, which is far from the city center, so ground lights will not affect it.
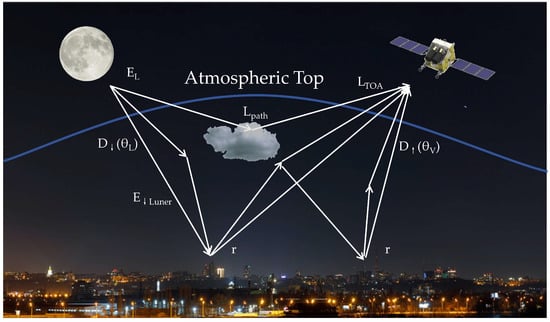
Figure 5.
Nighttime atmospheric radiation transmission process.
When the impact of atmospheric absorption is not taken into account, the downward irradiance of lunar illumination after atmospheric attenuation can be expressed as Equation (4):
where μL is the cosine of the lunar zenith angle, EL is the TOA lunar irradiance, is the downward transmission rate, and θL is the lunar zenith angle.
When lunar radiation reaches the surface, it undergoes reflection by the ground and absorption. The lunar radiation reflected by the ground will reach the atmosphere after being continuously scattered between the atmospheric boundary and the surface. Equations (5) and (6) are used to calculate this reflected lunar irradiance.
where a is the albedo of the atmospheric hemisphere, r is the ground reflectance, and L is the lunar irradiance the ground reflects.
When the lunar radiation reaches the surface, it will be reflected and absorbed by the ground. Lunar radiation reflected by the ground will eventually reach the atmosphere after continuous scattering between the atmospheric boundary and the surface. The radiance received by the sensor is expressed in Equation (7):
where LTOA is the TOA radiance, is the atmospheric uplink transmittance, θv is the satellite zenith angle, and Lpath is the path radiance.
2.3.2. Construction Process of Nighttime Atmospheric Radiative Transfer Models
This study used three atmospheric radiative transfer models: SCIATRAN, MODTRAN, and 6SV. Because 6SV model was used to simulate high spectral TOA reflectance over the entire visible and near-infrared spectral range. This facilitated the calibration of satellite’s low radiance using 6SV model [37]. The high-resolution model, SCIATRAN, has been used in low-light radiometric calibration studies at Dome C in Antarctica, the Railroad Valley Playa (RVP) desert region in the USA, and the Dunhuang radiometric correction field [19,20,38]. Meanwhile, the mid-resolution model, MODTRAN, operating in lunar mode, has been used to assess the accuracy of the in-orbit radiometric calibration of low-light satellites and to simulate lunar radiation transmission [39].
SCIATRAN is a high spectral-resolution model with a spectral range of 175–2400 nm and a spectral resolution of 0.24–0.5 nm. The SCIATRAN software package used in this study is version 4.6. MODTRAN is an enhanced version of LOWTRAN, covering the spectral range of 0–22,600 cm−1. It has a spectral resolution of 2 cm−1, making it a medium-resolution atmospheric radiation transfer model. The MODTRAN software package used in this study is version 5. 6SV is a vector model developed based on the 6S model. Researchers have considered the polarization characteristics of the atmosphere and surface and further enriched parameters such as scattering angle, wavelength node, aerosol vertical profile, etc. The 6SV software package used in this study is version 2.1. Then, the MT2009 was combined with SCIATRAN, MODTRAN, and 6SV, and these three modified atmospheric radiation transfer models will be employed to simulate the nighttime radiation transfer process.
Firstly, the solar spectrum files within the three atmospheric radiative transfer models must be substituted with lunar irradiance files from the MT2009 model. However, due to a discrepancy between the spectral resolution of the atmospheric radiative transfer model and that of the lunar irradiance file, it is necessary to obtain three distinct resolutions of lunar irradiance via interpolation processing to accommodate different atmospheric radiative transfer models. In this study, SCIATRAN has a spectral resolution of 0.5 nm, MODTRAN has a spectral resolution of 1 cm−1, and 6SV has a spectral resolution of 1 nm.
Secondly, it is also necessary to interpolate the DNB spectral response function files to facilitate the convolution of simulated TOA radiance with spectral response functions. This ensures a consistent resolution.
Ultimately, the simulated TOA radiance at different wavelengths must be convolved with that wavelength’s corresponding spectral response function. This process will yield the simulated TOA radiance at the DNB, as depicted in Equation (8):
where P is the simulation TOA radiance, P(λ) is the simulated radiance under different wavelengths, i is the band, λs(i) and λe(i) are the start and end wavelengths of the range of this band, and Si(λ) is the spectral response function of the corresponding band.
2.3.3. Parameter Settings of Nighttime Atmospheric Radiative Transfer Models
When using Night-SCIATRAN to simulate the TOA radiance, it is necessary to set the type of calculation results, radiation transmission mode, and other parameters in the model (Table 2).

Table 2.
The Night-SCIATRAN parameter setting.
When using Night-MODTRAN to simulate the TOA radiance, it is necessary to set the atmospheric model, geometric conditions, and other parameters in the model (Table 3).

Table 3.
The Night-MODTRAN parameter setting.
When using Night-6SV to simulate the TOA radiance, it is necessary to set the aerosol type, spectral conditions, and other parameters in the model (Table 4).

Table 4.
The Night-6SV parameter setting.
3. Results
3.1. Models Precision Evaluation
SVDNB products of the Baotou Field were collected from April to November each year between 2020 and 2022. Finally, 30 sets of nighttime data that fit the observation conditions were obtained (Table A1). Figure 6 shows the variation in simulated TOA and DNB radiance with observation time for different models. The average relative error and uncertainty of the observed data are calculated to quantitatively describe the relative error between the difference between DNB radiance and simulated TOA radiance. As can be seen from Figure 6, the average relative error and uncertainty of Night-SCIATRAN are −14.8% ± 8.2%, Night-6SV are 66.6% ± 8.8%, and Night-MODTRAN are 3.1% ± 2.5% (Table 5). Therefore, the Night-MODTRAN has the best accuracy among the three models in this experiment. The sources of errors and uncertainties in the results may be mainly caused by surface reflectance, aerosols, lunar zenith angle, etc.
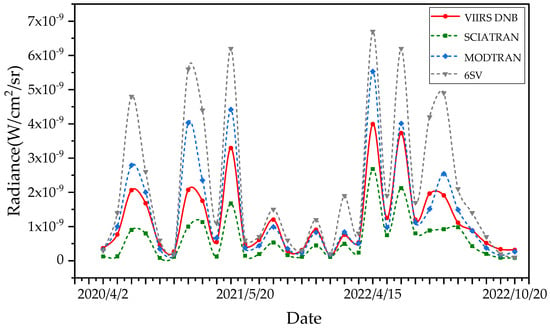
Figure 6.
Simulation results of TOA radiance and their comparison.

Table 5.
Accuracy evaluation of three nighttime radiative transfer models.
It is noted that the characteristics of the atmosphere and surface can introduce errors and uncertainties into the model. First of all, in the radiative transfer model, it is typically assumed that the surface exhibits homogeneous characteristics. However, upon closer examination, it becomes evident that the surface possesses distinct directional reflection properties [40]. Moreover, the data on surface reflectance show that it is coarse (spatial resolution of 500 m). This limitation is a detailed description of alterations in surface reflectance characteristics, particularly in regions by cities or vegetation-covered surfaces. Another possible source of error and uncertainties can be the inaccurate characterization of aerosol optical depth. Due to the current uneven distribution of AERONET sites, it is impossible to monitor on a large scale. And the diurnal variation in aerosols is large, and there will still be biased situations using aerosol daily average data [41]. Consequently, the overestimation of aerosol optical depth could cause the overestimation of simulated results and vice versa.
In addition, it can also be seen from Figure 6 that the TOA radiance simulated by Night-MODTRAN is closest to the DNB observation value, followed by the TOA radiance simulated by Night-SCIATRAN, while the difference between the TOA radiance simulated by Night-6SV and the DNB observation is the largest. Therefore, the results of this experiment show that the simulation results of Night-MODTRAN have the best accuracy and are suitable for nighttime radiative transfer simulations. Night-6SV has the worst accuracy and should be used carefully for nighttime radiative transfer simulations.
Correspondingly, after comparing the nighttime radiative transfer model of other scholars with the model of this study, it was found that the performance of Night-MODTRAN is better than that of other models (Table 6).

Table 6.
Statistics based on accuracy evaluation of nighttime radiative transfer model.
In this study, in order to further analyze the variability characteristics of the nighttime radiative transfer simulation, the error analysis of Night-MODTRAN is carried out by using the relative error (RE) and absolute error (AE), as shown in Equations (9) and (10).
Figure 7 shows the relative error distribution with respect to the lunar phase angle, and it can be seen that the relative error is relatively scattered in the longitudinal, basically varying within the range of −35% to 40%, which is within an acceptable error range [20,42]. The calculation results show that when the lunar phase angle is smaller, the simulated TOA radiance is usually greater than the DNB radiance. When the lunar phase angle is larger, the simulated TOA radiance is generally less than the DNB radiance.
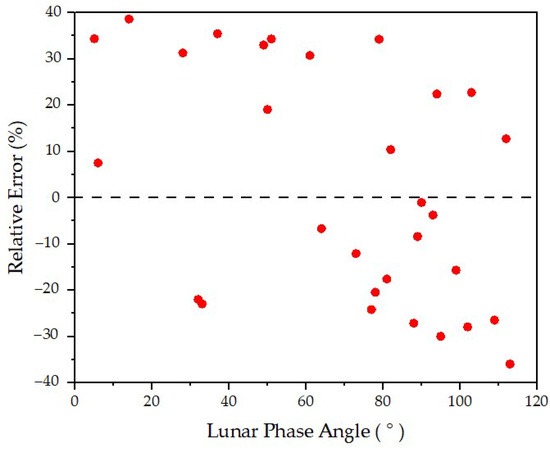
Figure 7.
The distribution of relative error with the lunar phase angle.
Figure 8 shows the distribution of absolute errors with the lunar phase angle. It can be seen that as the lunar phase angle increases, the absolute error between the simulated TOA radiance and the DNB radiance gradually decreases, and the absolute error value tends to be stable at the lunar phase angle of 90°. The results show that the absolute error can be ensured in the appropriate range when the lunar phase angle is near 90°.
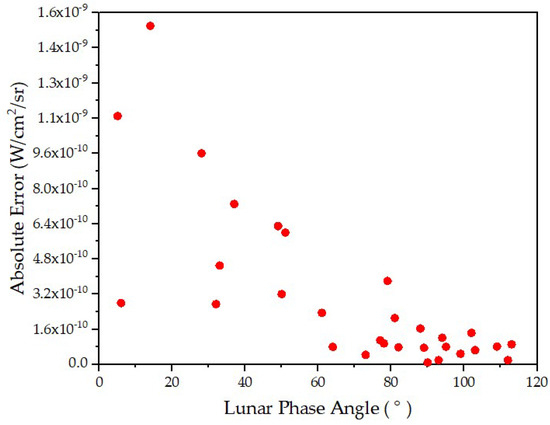
Figure 8.
The distribution of absolute error with the lunar phase angle.
3.2. Sensitivity Analysis
This section develops the sensitivity analysis of the parameters such as lunar phase angles, aerosol optical depths, surface reflectances, lunar zenith angles, satellite zenith angles, and relative azimuth angles. The sensitivity parameters are changed in a certain range while keeping the other parameters in Night-MODTRAN unchanged. Table 7 lists the sensitivity parameters’ specific reference value and input range.

Table 7.
Parameter settings.
Figure 9 illustrates the change trends of simulated TOA radiance with five parameters under four lunar phase angles. As can be seen from Figure 9, the simulated TOA radiance increases with the increase in aerosol optical depth and surface reflectance, and the average change rates are 100% and 2561%. The simulated TOA radiance decreases with the increase in the lunar phase angle, lunar zenith angle, and satellite zenith angle, and the average change rates are 68%, 75%, and 20%. However, there was no significant change with the increase in the relative azimuth angle.
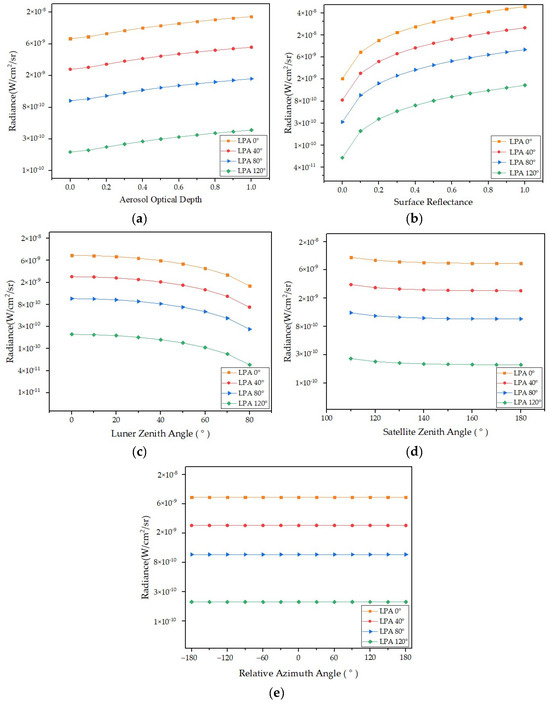
Figure 9.
The simulated TOA radiance change trends with different parameters under four lunar phase angles: (a) aerosol optical depth, (b) surface reflectance, (c) lunar zenith angle, (d) satellite zenith angle, and (e) relative azimuth angle.
When the average change rate is greater than 50%, the parameter is considered to be sensitive to the simulated TOA radiance [17,43]. Therefore, the results show that the simulated TOA radiance is sensitive to the changes in lunar phase angle, aerosol optical depth, surface reflectance, and lunar zenith angle. The simulated TOA radiance is not sensitive to the changes in the satellite zenith angle and relative azimuth angle.
4. Discussion
This study explores the applicability of atmospheric radiative transfer models under different nighttime conditions from two aspects: the model’s accuracy and the parameters’ sensitivity. Utilizing the VIIRS/DNB observation data as a radiation benchmark, the simulation accuracy of three nighttime atmospheric radiation transfer models was analyzed. The results indicate that Night-MODTRAN offers superior accuracy, with a relative error range of 3.1% ± 2.5%. This is followed by Night-SCIATRAN, which presents a relative error range of −14.8% ± 8.2%, and Night-6SV, which demonstrates the poorest accuracy with a relative error range of 66.6% ± 8.8%. An assessment of the relative error between simulated TOA radiance and DNB radiance indicates that this error ranges from −35% to 40%, and the simulated TOA radiance fluctuates greatly. The absolute error is larger when the lunar phase angle is less than 90°, with smaller lunar phase angles correlating to larger errors. However, the error fluctuation is not obvious when the lunar phase angle falls between 90° and 120°. It is advisable to select conditions with a smaller lunar phase angle and stronger lunar radiation when the error gap is not apparent, as this can avoid some image noise. Consequently, this study suggests that the radiative transfer simulation calculation methods for lunar phase angles proximate to 90° are most suitable for low-light remote-sensing payloads radiometric calibration.
The sensitivity of Night-MODTRAN was examined with respect to parameters such as lunar phase angle, aerosol optical depth, surface reflectance, lunar zenith angle, satellite zenith angle, and relative azimuth angle. The findings indicate that the TOA radiance is most sensitive to surface reflectance variations; the average change rate is 2561%. This can be attributed to the higher surface reflectance value resulting in a brighter surrounding environment, leading to increased reflected radiation received by the satellite sensor. Therefore, high-precision surface reflectance data must be provided when simulating the TOA radiance. However, the TOA radiance shows no sensitivity to the relative azimuth angle, and the average change rate is 0%. It may be that the TOA radiance is less influenced by the relative azimuth angle during the simulation process, ensuring a consistent size of lunar radiation [44,45].
Due to the influence of solar stray light on the lunar illumination and the impact of clouds on atmospheric radiation, the construction of nighttime atmospheric radiation transfer models will produce errors. Consequently, the DNB nighttime observation data of clear sky and cloudless in Baotou Field are obtained using visual identification methods. For satellite sensors with low spatial resolutions, such as AVHRR and MODIS, an approximate 10 km × 10 km area near the center of the research region is typically utilized as a substitute for the target site for calibration. Considering the spatial resolution of DNB to be 750 m, which is deemed low. This study selected satellite observation data from a 10 km × 10 km area near the center of the Baotou Field for analysis and processing.
The successful application of low-light detection data, from the inception of the Defense Meteorological Satellite Program–Operational Linescan System (DMSP/OLS) to VIIRS/DNB, is largely contingent upon the precise radiometric calibration of payload detection data [46]. Through the results of this study, a highly accurate nighttime radiative transfer model can be obtained, thereby achieving accurate radiometric calibration. And research studies have shown that an accurate nighttime radiative transfer model also plays an important role in the field of nighttime atmospheric parameter inversion [47]. It is noted that the VIIRS/DNB measurements of nighttime emission are mainly from the moon and ground lights. In future works, the contribution of ground lights should be quantified, and an atmospheric radiative transfer model for point sources on the ground should be established. This will be of great significance to improve the accuracy of the nighttime radiative transfer model.
5. Conclusions
This study constructs nighttime atmospheric radiative transfer models by integrating the MT2009 lunar irradiance model into the atmospheric radiative transfer model. The current state of different atmospheric radiative transfer models in nighttime simulations is analyzed using the VIIRS/DNB nighttime observation data. After experimental verification, three conclusions have been drawn.
- (1)
- In this study, the relative error range for Night-SCIATRAN is −14.8% ± 8.2%, that for Night-6SV is 66.6% ± 8.8%, and for Night-MODTRAN is 3.1% ± 2.5%. The results indicate that the simulation accuracy of Night-MODTRAN is optimal for nighttime radiative transfer simulations.
- (2)
- By calculating the relative error between simulated and DNB radiance, it has been found that when the lunar phase angle is smaller, the simulated TOA radiance is usually higher than the DNB radiance. Conversely, when the lunar phase angle is larger, the simulated TOA radiance is usually lower than the DNB radiance. The absolute error fluctuation tends to be stable near the lunar phase angle of 90°.
- (3)
- In this study, the simulated TOA radiance is sensitive to the changes in the lunar phase angle, aerosol optical depth, surface reflectance, and lunar zenith angle, and the average change rates are 68%, 100%, 2561%, and 75%. However, the simulated TOA radiance is not sensitive to the changes in satellite zenith angle and relative azimuth angle, and the average change rates are 20% and 0%.
In summary, the nighttime radiative transfer model is significant for the radiometric calibration of low-light satellite remote sensing. This study analyzed the applicability of three atmospheric radiative transfer models under different nighttime conditions. It provides an important reference for future research on the radiometric calibration methods of low-light remote-sensing payloads, as well as for understanding the radiative processes of the nighttime atmospheric system. Currently, the atmospheric radiative transfer model effectively captures the impact of the atmosphere on parallel light radiation transfer. Nonetheless, a substantial gap persists in fundamental theoretical research concerning radiation transfer from point sources within the atmosphere. Future research should focus on point light source radiative transfer models and the incorporation of ground lights into nighttime radiative transfer models. These will broaden the model’s application range and enhance its accuracy.
Author Contributions
Conceptualization, methodology, validation, formal analysis, and data curation, J.H. and W.Z.; writing—original draft preparation, J.H.; writing—review and editing, all authors; supervision, L.Z.; and funding acquisition, W.Z.; and project administration, S.L., X.G., T.Y. and Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
The Major Project of High-Resolution Earth Observation System, No. 30-Y60B01-9003-22/23 and No. 30-Y30F06-9003-20/22; North China Institute of Aerospace Engineering Foundation of Doctoral Research, BKY-2021-31; Science and Technology Research Projects of Higher Education Institutions in Hebei Province, ZD2021303; North China Institute of Aerospace Engineering’s University-level Innovation Project, No. YKY-2023-79.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://www.avl.class.noaa.gov/saa/products/catSearch.
Acknowledgments
The authors would like to thank S. Miller for making his lunar irradiance model publicly available. We also thank V. V. Rozanov for his assistance with radiative transfer simulation and SCIATRAN working group for making SCIATRAN publicly available. Finally, the authors would like to thank the anonymous reviewers for their constructive suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Table A1 shows that 30 sets of nighttime satellite data from 2020 and 2022 were used for the model’s precision evaluation in Section 3.1.

Table A1.
The 30 sets of nighttime satellite data used for the model’s precision evaluation.
Table A1.
The 30 sets of nighttime satellite data used for the model’s precision evaluation.
| NO. | Lunar Phase Angle | Aerosol Optical Depth | Surface Reflectance | Lunar Zenith Angle | Lunar Azimuth Angle | Satellite Zenith Angle | Satellite Azimuth Angle |
|---|---|---|---|---|---|---|---|
| 1 | 73° | 0.189 | 0.195 | 84.78° | −65.63° | 26.02° | −74.81° |
| 2 | 61° | 0.187 | 0.196 | 73.31° | −78.72° | 2.54° | 90.39° |
| 3 | 37° | 0.142 | 0.200 | 60.93° | 161.26° | 44.44° | 96.39° |
| 4 | 50° | 0.189 | 0.201 | 70.58° | 144.89° | 59.19° | 92.94° |
| 5 | 78° | 0.263 | 0.207 | 83.31° | −73.27° | 37.93° | 97.44° |
| 6 | 95° | 0.164 | 0.205 | 85.29° | 102.16° | 44.75° | 96.35° |
| 7 | 28° | 0.075 | 0.196 | 51.59° | −174.26° | 16.98° | −75.78° |
| 8 | 50° | 0.134 | 0.187 | 49.12° | 137.58° | 38.05° | 97.35° |
| 9 | 94° | 0.162 | 0.197 | 56.23° | 88.11° | 2.67° | 100.84° |
| 10 | 5° | 0.094 | 0.200 | 61.82° | −137.38° | 7.53° | −78.86° |
| 11 | 78° | 0.342 | 0.208 | 83.11° | −77.43° | 38.21° | 96.79° |
| 12 | 89° | 0.116 | 0.198 | 72.43° | 107.84° | 21.68° | 99.26° |
| 13 | 81° | 0.135 | 0.187 | 66.80° | 100.68° | 62.72° | 92.20° |
| 14 | 103° | 0.139 | 0.187 | 64.94° | 89.14° | 8.11° | −78.68° |
| 15 | 109° | 0.182 | 0.163 | 71.89° | 73.12° | 29.79° | 97.78° |
| 16 | 89° | 0.219 | 0.170 | 63.09° | 81.66° | 54.49° | 93.91° |
| 17 | 112° | 0.194 | 0.172 | 74.14° | 82.80° | 26.86° | −75.05° |
| 18 | 82° | 0.112 | 0.182 | 60.94° | 101.24° | 18.47° | −76.62° |
| 19 | 93° | 0.169 | 0.181 | 65.86° | 94.06° | 11.06° | 100.64° |
| 20 | 14° | 0.195 | 0.214 | 54.80° | −132.70° | 21.90° | 98.90° |
| 21 | 32° | 0.106 | 0.215 | 80.50° | −104.20° | 62.90° | −68.20° |
| 22 | 6° | 0.105 | 0.214 | 70.40° | −138.10° | 33.30° | −74.90° |
| 23 | 64° | 0.232 | 0.217 | 72.70° | 148.70° | 40.10° | −73.40° |
| 24 | 33° | 0.166 | 0.216 | 66.90° | 178.30° | 33.30° | −74.40° |
| 25 | 49° | 0.054 | 0.179 | 43.16° | 149.85° | 2.02° | 99.35° |
| 26 | 78° | 0.390 | 0.178 | 41.41° | 99.49° | 1.77° | 89.59° |
| 27 | 89° | 0.208 | 0.180 | 52.99° | 85.64° | 29.78° | 98.53° |
| 28 | 102° | 0.145 | 0.200 | 64.45° | 80.66° | 1.94° | 111.13° |
| 29 | 113° | 0.218 | 0.201 | 78.36° | 74.03° | 40.73° | 98.59° |
| 30 | 99° | 0.467 | 0.188 | 79.35° | 98.95° | 7.07° | −78.97° |
References
- Lyapustin, A.; Wang, Y.; Choi, M.; Xiong, X.; Angal, A.; Wu, A.; Doelling, D.R.; Bhatt, R.; Go, S.; Korkin, S.; et al. Calibration of the SNPP and NOAA 20 VIIRS sensors for continuity of the MODIS climate data records. Remote Sens. Environ. 2023, 295, 113717. [Google Scholar] [CrossRef]
- Cui, Z.; Ma, C.; Zhang, H.; Hu, Y.; Yan, L.; Dou, C.; Li, X.M. Vicarious Radiometric Calibration of the Multispectral Imager Onboard SDGSAT-1 over the Dunhuang Calibration Site, China. Remote Sens. 2023, 15, 2578. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, Y.; Zhang, L.; Wu, J.; Li, W.; Yan, J.; Jiang, X.; Yan, Z.; Zhao, J. On-Orbit Radiometric Calibration of Hyperspectral Sensors on Board Micro-Nano Satellite Constellation Based on RadCalNet Data. Remote Sens. 2022, 14, 4720. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, K.; Li, W.; Hu, X.; Li, P.; Bai, T. Vicarious Calibration of FengYun-3D MERSI-II at Railroad Valley Playa Site: A Case for Sensors with Large View Angles. Remote Sens. 2021, 13, 1347. [Google Scholar] [CrossRef]
- Che, H.; Zhang, X.; Chen, H.; Damiri, B.; Goloub, P.; Li, Z.; Zhang, X.; Wei, Y.; Zhou, H.; Dong, F. Instrument calibration and aerosol optical depth validation of the China Aerosol Remote Sensing Network. J. Geophys. Res. Atmos. 2009, 114, D03206. [Google Scholar] [CrossRef]
- Hu, X.; Liu, J.; Sun, L.; Rong, Z.; Li, Y.; Zhang, Y.; Zheng, Z.; Wu, R.; Zhang, L.; Gu, X. Characterization of CRCS Dunhuang test site and vicarious calibration utilization for Fengyun (FY) series sensors. Can. J. Remote Sens. 2014, 36, 566–582. [Google Scholar] [CrossRef]
- Min, M.; Deng, J.; Liu, C.; Guo, J.; Lu, N.; Hu, X.; Chen, L.; Zhang, P.; Lu, Q.; Wang, L. An investigation of the implications of lunar illumination spectral changes for Day/Night Band-based cloud property retrieval due to lunar phase transition. J. Geophys. Res. Atmos. 2017, 122, 9233–9244. [Google Scholar] [CrossRef]
- Qiu, S.; Shao, X.; Cao, C.Y.; Uprety, S.; Wang, W.H. Assessment of straylight correction performance for the VIIRS Day/Night Band using Dome-C and Greenland under lunar illumination. Int. J. Remote Sens. 2017, 38, 5880–5898. [Google Scholar] [CrossRef]
- Xi, S.; Changyong, C.; Sirish, U. Vicarious calibration of S-NPP/VIIRS day-night band. Proc. SPIE 2013, 8866, 88661S. [Google Scholar] [CrossRef]
- Zakharov, Y.N.; Popov, A.Y.; Tyurin, A.V. Semiconductor laser’s on-line coherence calibration and testing of frequency stability. Proc. SPIE 2008, 7008, 70081P. [Google Scholar] [CrossRef]
- Cao, C.; Bai, Y. Quantitative Analysis of VIIRS DNB Nightlight Point Source for Light Power Estimation and Stability Monitoring. Remote Sens. 2014, 6, 11915–11935. [Google Scholar] [CrossRef]
- Ma, S.; Yan, W.; Huang, Y.; Jiang, J.; Hu, S.; Wang, Y. Calibration Method of Low-Light Sensor Based on Bridge Lights. J. Atmos. Ocean. Technol. 2016, 33, 1123–1134. [Google Scholar] [CrossRef]
- Hu, S.; Ma, S.; Yan, W.; Lu, W.; Zhao, X. Feasibility of a specialized ground light source for night-time low-light calibration. Int. J. Remote Sens. 2018, 39, 2543–2559. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, J.; Weng, F.; Sun, N.; Anderson, K.; Liu, Q.; Kim, E.J. Developing Vicarious Calibration for Microwave Sounding Instruments Using Lunar Radiation. IEEE T. Geosci. Remote 2018, 56, 6723–6733. [Google Scholar] [CrossRef]
- Ryan, R.E.; Pagnutti, M.; Burch, K.; Leigh, L.; Ruggles, T.A.; Cao, C.; Aaron, D.; Blonski, S.; Helder, D.L. The Terra Vega Active Light Source: A First Step in a New Approach to Perform Nighttime Absolute Radiometric Calibrations and Early Results Calibrating the VIIRS DNB. Remote Sens. 2019, 11, 710. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.E.; Zhizhin, M.; Hsu, F.-C. Why VIIRS data are superior to DMSP for mapping nighttime lights. Proc. Asia-Pac. Adv. Netw. 2013, 35, 62. [Google Scholar] [CrossRef]
- Liao, L.B.; Weiss, S.; Mills, S.; Hauss, B. Suomi NPP VIIRS day-night band on-orbit performance. J. Geophys. Res. Atmos. 2013, 118, 12705–12718. [Google Scholar] [CrossRef]
- Qiu, S.; Shao, X.; Cao, C.; Uprety, S. Feasibility demonstration for calibrating Suomi-National Polar-Orbiting Partnership Visible Infrared Imaging Radiometer Suite day/night band using Dome C and Greenland under moon light. J. Appl. Remote Sens. 2016, 10, 16024. [Google Scholar] [CrossRef]
- Hu, S.; Ma, S.; Yan, W.; Huang, Y. Using two different targets for the calibration of S-NPP VIIRS day night band under lunar illumination. Proc. SPIE 2016, 10255, 102552O. [Google Scholar] [CrossRef]
- Hu, S. VIIRS Low-Light Channel Data Radiometric Calibration and Application Technology. Ph.D. Dissertation, National University of Defense Technology, Wuhan, China, 2019; pp. 27–38. [Google Scholar]
- Ma, S.; Yan, W.; Huang, Y.-X.; Ai, W.-H.; Zhao, X. Vicarious calibration of S-NPP/VIIRS day–night band using deep convective clouds. Remote Sens. Environ. 2015, 158, 42–55. [Google Scholar] [CrossRef]
- Li, X.; Elvidge, C.; Zhou, Y.; Cao, C.; Warner, T. Remote sensing of night-time light. Int. J. Remote Sens. 2017, 38, 5855–5859. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Liu, J.; Zhang, Z.; Gao, W. Enhancing research and application of urban rainwater harvesting and utilisation. Inn. Mong. Water Resour. 2007, 4, 120–121. [Google Scholar]
- Tang, H.; Xiao, C.; Shang, K.; Wu, T.; Li, Q. Radiometric Calibration of GF5-02 Advanced Hyperspectral Imager Based on RadCalNet Baotou Site. Remote Sens. 2023, 15, 2233. [Google Scholar] [CrossRef]
- Barreto, Á.; Cuevas, E.; Granados-Muñoz, M.-J.; Alados-Arboledas, L.; Romero, P.M.; Gröbner, J.; Kouremeti, N.; Almansa, A.F.; Stone, T.; Toledano, C.; et al. The new sun-sky-lunar Cimel CE318-T multiband photometer—A comprehensive performance evaluation. Atmos. Meas. Tech. 2016, 9, 631–654. [Google Scholar] [CrossRef]
- Hlaing, S.; Harmel, T.; Gilerson, A.; Foster, R.; Weidemann, A.; Arnone, R.; Wang, M.; Ahmed, S. Evaluation of the VIIRS ocean color monitoring performance in coastal regions. Remote Sens. Environ. 2013, 139, 398–414. [Google Scholar] [CrossRef]
- Wolfe, R.E.; Lin, G.; Nishihama, M.; Tewari, K.P.; Tilton, J.C.; Isaacman, A.R. Suomi NPP VIIRS prelaunch and on-orbit geometric calibration and characterization. J. Geophys. Res. Atmos. 2013, 118, 11508–11521. [Google Scholar] [CrossRef]
- Hu, S.; Ma, S.; Yan, W.; Jiang, J.; Huang, Y. A new multichannel threshold algorithm based on radiative transfer characteristics for detecting fog/low stratus using night-time NPP/VIIRS data. Int. J. Remote Sens. 2016, 38, 5919–5933. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, W.; Zhang, L.; Gu, X.; Yu, T. Estimation of Ground-Level PM2.5 Concentration at Night in Beijing-Tianjin-Hebei Region with NPP/VIIRS Day/Night Band. Remote Sens. 2023, 15, 825. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, W.; Chen, X.; Zhang, L.; Liu, Q. High Spatial Resolution Nighttime PM2.5 Datasets in the Beijing–Tianjin–Hebei Region from 2015 to 2021 Using VIIRS/DNB and Deep Learning Model. Remote Sens. 2023, 15, 4271. [Google Scholar] [CrossRef]
- Chen, H.; Xiong, X.; Sun, C.; Chen, X.; Chiang, K. Suomi-NPP VIIRS day-night band on-orbit calibration and performance. J. Appl. Remote Sens. 2017, 11, 036019. [Google Scholar] [CrossRef]
- He, Q.; Zhang, M.; Huang, B.; Tong, X. MODIS 3 km and 10 km aerosol optical depth for China: Evaluation and comparison. Atmos. Environ. 2017, 153, 150–162. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, H.; Zheng, F. Aerosol Optical Depth Retrieval over East Asia Using Himawari-8/AHI Data. Remote Sens. 2018, 10, 137. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, H.; Zhang, L. Assessment of Himawari-8 AHI Aerosol Optical Depth over Land. Remote Sens. 2019, 11, 1108. [Google Scholar] [CrossRef]
- Zeng, X.; Li, C. The Influence of Heterogeneity on Lunar Irradiance Based on Multiscale Analysis. Remote Sens. 2019, 11, 2696. [Google Scholar] [CrossRef]
- Mauceri, S.; Pilewskie, P.; Woods, T.; Béland, S.; Richard, E. Intercomparing Solar Spectral Irradiance from SORCE SIM. Earth Space Sci. 2020, 7, e2019EA001002. [Google Scholar] [CrossRef]
- Bassani, C.; Sterckx, S. Calibration of Satellite Low Radiance by AERONET-OC Products and 6SV Model. Remote Sens. 2021, 13, 781. [Google Scholar] [CrossRef]
- Mei, L.; Rozanov, V.; Rozanov, A.; Burrows, J.P. SCIATRAN software package (V4.6): Update and further development of aerosol, clouds, surface reflectance databases and models. Geosci. Model Dev. 2023, 16, 1511–1536. [Google Scholar] [CrossRef]
- Yakunin, M.A.; Yurchenko, A.V. MODTRAN5 simulations of responses from MODIS spectroradiometer channels. Tech. Phys. 2015, 60, 141–144. [Google Scholar] [CrossRef]
- Wang, J.; Zhou, M.; Xu, X.; Roudini, S.; Sander, S.P.; Pongetti, T.J.; Miller, S.D.; Reid, J.S.; Hyer, E.; Spurr, R. Development of a nighttime shortwave radiative transfer model for remote sensing of nocturnal aerosols and fires from VIIRS. Remote Sens. Environ. 2020, 241, 111727. [Google Scholar] [CrossRef]
- Okpalaonwuka, C.; Olusegun, C.F.; Olusola, A.; Ogunjo, S. Validation of MODIS AOD retrievals in West Africa: A comparison with AERONET observations. Air Qual. Atmos. Health 2023, 16, 2085–2094. [Google Scholar] [CrossRef]
- Li, J.; Qiu, S.; Zhang, Y.; Gao, C.; Qian, Y.; Liu, Y. Performance assessments of VIIRS DNB on-orbit radiometric calibration accuracy and stability on SNPP and NOAA-20. J. Infrared Millim. Waves 2021, 40, 809–819. [Google Scholar] [CrossRef]
- Min, M.; Zheng, J.; Zhang, P.; Hu, X.; Chen, L.; Li, X.; Huang, Y.; Zhu, L. A low-light radiative transfer model for satellite observations of moonlight and earth surface light at night. J. Quant. Spectrosc. Radiat. Transf. 2020, 247, 106954. [Google Scholar] [CrossRef]
- Feng, Q.; Yang, P.; Kattawar, G.W.; Hsu, C.N.; Tsay, S.-C.; Laszlo, I. Effects of particle nonsphericity and radiation polarization on retrieving dust properties from MODIS observations. J. Aerosol. Sci. 2009, 40, 776–789. [Google Scholar] [CrossRef]
- Stathopoulou, M.; Cartalis, C. Downscaling AVHRR land surface temperatures for improved surface urban heat island intensity estimation. Remote Sens. Environ. 2009, 113, 2592–2605. [Google Scholar] [CrossRef]
- Zhao, Y.; Qu, Z.; Zhang, Y.; Ao, Y.; Han, L.; Kang, S.; Sun, Y. Effects of human activity intensity on habitat quality based on nighttime light remote sensing: A case study of Northern Shaanxi, China. Sci. Total. Environ. 2022, 851 Pt 1, 158037. [Google Scholar] [CrossRef]
- Deng, J.; Qiu, S.; Zhang, Y.; Cui, H.; Li, K.; Cheng, H.; Liu, Z.; Dou, X.; Qian, Y. Estimating Nighttime PM2.5 Concentration in Beijing Based on NPP/VIIRS Day/Night Band. Remote Sens. 2023, 15, 349. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).