A Radar Echo Extrapolation Model Based on a Dual-Branch Encoder–Decoder and Spatiotemporal GRU

Abstract

Precipitation forecasting is an immensely significant aspect of meteorological prediction. Accurate weather predictions facilitate services in sectors such as transportation, agriculture, and tourism. In recent years, deep learning-based radar echo extrapolation techniques have found effective applications in precipitation forecasting. However, the ability of existing methods to extract and characterize complex spatiotemporal features from radar echo images remains insufficient, resulting in suboptimal forecasting accuracy. This paper proposes a novel extrapolation algorithm based on a dual-branch encoder–decoder and spatiotemporal Gated Recurrent Unit. In this model, the dual-branch encoder–decoder structure independently encodes radar echo images in the temporal and spatial domains, thereby avoiding interference between spatiotemporal information. Additionally, we introduce a Multi-Scale Channel Attention Module (MSCAM) to learn global and local feature information from each encoder layer, thereby enhancing focus on radar image details. Furthermore, we propose a Spatiotemporal Attention Gated Recurrent Unit (STAGRU) that integrates attention mechanisms to handle temporal evolution and spatial relationships within radar data, enabling the extraction of spatiotemporal information from a broader receptive field. Experimental results demonstrate the model’s ability to accurately predict morphological changes and motion trajectories of radar images on real radar datasets, exhibiting superior performance compared to existing models in terms of various evaluation metrics. This study effectively improves the accuracy of precipitation forecasting in radar echo images, provides technical support for the short-range forecasting of precipitation, and has good application prospects.

1. Introduction

Severe convective weather refers to intense convective movements occurring in the atmosphere, such as thunderstorms, tornadoes, and heavy rainfall. These weather phenomena can cause significant short-term, localized heavy rainfall, resulting in substantial economic and property losses. Precipitation nowcasting is a meteorological forecasting method that primarily focuses on providing timely and accurate predictions of rainfall intensity and extents for specific local areas within a short time frame, typically ranging from a few hours [1]. Accurate forecasting is crucial in various domains, including flood prevention, agriculture, aviation, and travel planning. Consequently, the acquisition of precise and rapid nowcasting has become a prominent research issue in meteorology [2,3].

Traditional precipitation forecasting primarily relies on the NWP approach [4,5], which utilizes physical equations and numerical methods to simulate atmospheric motion and predict weather conditions over a future time period. It considers factors such as atmospheric dynamics, thermodynamics, radiation transfer, and turbulence. However, NWP methods suffer from uncertainties, parameter errors, and significant computational costs associated with solving mathematical equations. In recent years, the radar echo extrapolation technique has been mainly used for precipitation forecasting tasks. The method is based on the extrapolation of radar echo data from historical observations, after which the rainfall in the forecast area is obtained through the Z-R relationship [6]. Currently, traditional radar echo extrapolation methods mainly include centroid tracking [7], cross-correlation [8], and optical flow [9]. Among them, the centroid tracking method is primarily suitable for tracking strong echoes and making short-term predictions. When radar echoes are scattered or exhibit merging and splitting phenomena, the accuracy of extrapolation forecasts is significantly affected [10,11,12]. The cross-correlation method assumes that the evolution of echoes is linear and tracks the echo regions based on the optimal correlation coefficients between neighboring temporal regions. However, it is challenging to accurately estimate the nonlinear evolution of radar echoes using this method. The optical flow method is a two-step calculation approach that first computes the optical flow field from consecutive radar images and then extrapolates the nearest precipitation field based on the optical flow field. However, the two-stage extrapolation approach employed by the optical flow method can lead to cumulative errors. Radar echo data, as a type of sequential image data, possess high spatiotemporal dimensions, lack obvious periodicity, and exhibit variable motion speed and shape changes. Therefore, the aforementioned three traditional methods have limitations in fully utilizing abundant historical observation data and are insufficient in obtaining satisfactory forecasting results.

With the rapid development in the field of computers, deep learning techniques are experiencing rapid development and have been successfully applied in various fields, including video prediction [13,14,15] and traffic forecasting [16,17,18], demonstrating outstanding performance. Deep learning methods can handle complex spatiotemporal relationships in order to adaptively learn the patterns of rainfall variability from a large number of previous radar echo sequences. As a result, more and more deep learning methods are being combined with radar echo extrapolation tasks [19,20], aiming to achieve more accurate predictions. First, some radar echo extrapolation algorithms based on recurrent neural networks (RNNs) have been employed for precipitation forecasting [21,22]. Shi et al. [23] first proposed the combination of Convolutional Neural Network (CNN) and Long Short-Term Memory (LSTM) networks, known as ConvLSTM, for precipitation prediction in the Hong Kong region. This network enables the better learning and modeling of spatiotemporal information. Subsequently, Shi et al. [24] introduced the TrajGRU model to address the local invariance issue within the convolutional structure of ConvLSTM. By incorporating the concept of optical flow into ConvGRU, this model learned non-rigid transformation patterns such as the rotation, scaling, appearance, and disappearance of radar images, enabling the tracking of rapidly changing radar evolution processes. Considering that ConvLSTM only focuses on temporal information while neglecting spatial information from different layers, Wang et al. [25] proposed PredRNN. They introduced a new parallel spatial memory unit in ConvLSTM to preserve spatial features from each layer. This enhancement allows for the better modeling of both temporal and spatial information in the prediction process. Furthermore, Wang et al. [26] continued their research and introduced PredRNN++, where the gradient highway unit was combined with causal LSTM to address the gradient vanishing problem. Additionally, several variant structures based on ConvLSTM and PredRNN have emerged, such as MIM [27], PredRANN [28], SAST-LSTM [29], and PrecipLSTM [30], among others. MIM [27] can model the non-smooth and nearly smooth characteristics of the spatiotemporal dynamics in the radar echo sequences, effectively improving the prediction accuracy. The PredRANN [28] model incorporates the Time Attention Module (TAM) and Layer Attention Module (LAM) into the prediction unit to retain representations of both temporal and spatial dimensions. TAM focuses on preserving more temporal information, while LAM focuses on preserving more spatial information. SAST-LSTM [29] captures the spatial and temporal global features of radar echo motion by introducing a self-attention mechanism and an additional memory mechanism to save the global spatiotemporal features into the original spatiotemporal LSTM (ST-LSTM). PrecipLSTM [30] combines the Spatial Localized Attention Memory (SLAM) module, which captures meteorological spatial relationships using a combination of local attention and memory mechanisms, and the Time Difference Memory (TDM) module, which captures meteorological temporal variables using differential techniques and memory mechanisms. These two modules are integrated with PredRNN to fully capture the spatiotemporal dependencies of radar data. These models have sought to improve the performance of radar echo extrapolation by incorporating different architectural modifications and enhancements. Meanwhile, some faster-trained fully convolutional networks [31] have been applied to weather forecasting [32,33]. Among them, the representative UNet [34] utilizes convolutional modules to learn the spatiotemporal variations in data. Kevin Trebing et al. [35] proposed the SmaAt-Unet model, which has a smaller number of parameters and better prediction performance by using depth-separable convolution and CBAM. Fernandez et al. [36] introduced a Broad-UNet that incorporates asymmetric parallel convolutions and an atrous spatial pyramid pooling (ASPP) component, enabling the model to extract multi-scale features for near-term forecasting. The aforementioned fully convolutional approaches aim to extract spatial features but overlook information at different temporal scales, thus limiting their ability to represent complex spatiotemporal nonlinear changes.

Although the aforementioned extrapolation methods for radar echoes have achieved some notable improvements, there is still significant room for improvement in predicting high-resolution radar echo images, far from reaching satisfactory levels. There are two main reasons for this: First, there is the issue of information loss during the feature extraction stage. Typically, to conserve resources, prediction models encode the images into low-dimensional features using an encoder and then input them into prediction units, which further extract temporal and spatial features. However, this process often leads to interference between temporal and spatial information, resulting in information loss. Second, most current improvement methods still rely on the complex and parameter-intensive LSTM structure, which leads to longer training cycles and gradient problems. Additionally, as the prediction time increases, the prediction model suffers from information forgetting, causing rapid decay in areas with high echo values during the prediction process.

To address the aforementioned issues, we propose a radar echo extrapolation model that combines dual-branch encoder–decoder and spatiotemporal gate recurrent units. First, we employ a dual-branch encoding–decoding structure to independently encode the input image in the temporal and spatial domains, avoiding unnecessary interactions between time and space. This significantly enhances the efficiency of the prediction unit in handling spatiotemporal features. Additionally, we introduce a Multi-Scale Channel Attention Module (MSCAM) embedded within the encoding–decoding structure to learn local and global contextual features of the encoded information, thereby enhancing the focus on image details. Furthermore, we devise a novel Spatiotemporal Attention Gate Recurrent Unit (STAGRU), comprising the spatiotemporal gate recurrent unit (STGRU) and the time attention module (TAM). The STGRU is an extension of the standard GRU, which is able to adaptively learn spatiotemporal features in sequence data using a gating mechanism. Compared to the ST-LSTM structure, STGRU is simpler and has fewer parameters. The TAM effectively expands the temporal receptive field of the prediction unit, thereby mitigating issues related to information loss during information propagation.

The contribution of our method can be summarized as follows:

1. We propose a two-branch coding and decoding structure that incorporates a multi-scale channel attention module for efficient multi-granularity feature extraction. The blurring problem of predicted images is effectively improved, and the detail is enhanced.

2. We propose a spatiotemporally gated recursive unit that combines the attention mechanism, which effectively improves the forgetting problem of the prediction unit during information transmission, better establishes long-term temporal dependence, and improves the prediction ability for high-echo regions.

3. By combining the above two methods, DE-STAGRU was constructed. Experiments showed that DE-STAGRU achieved state-of-the-art results on the CIKM 2017 dataset.

2. Data

This study utilized a publicly available dataset from CIKM 2017, consisting of Doppler weather radar echo maps observed in Shenzhen City for two consecutive years. The dataset was acquired using a Doppler meteorological radar, the horizontal resolution of the dataset is 0.01° (about 1 km), and the temporal resolution is 6 min. The dataset comprised 8000 sample sequences for training and 4000 sample sequences for testing. In addition, 2000 sample sequences were used as the validation set. We take into account that high echo values usually signify the occurrence of strong convective weather, while smaller echo values are rain-free weather or stray waves; we specifically chose 2473 sample sequences from the test set that contained strong echo values.

Each sample sequence in the dataset consisted of 15 consecutive CAPPI radar echo images. The original size of each echo image was 101 × 101, with each grid point representing a 1 km × 1 km area. For the ease of inputting the model during training, zero-padding was applied to the bottom right corner of the map, resulting in a new image size of 128 × 128. In this experiment, all models utilized the first five images as the input and predicted the subsequent 10 images. Therefore, our task involved predicting the next hour based on the historical observation data from the past half hour.

3. Methods

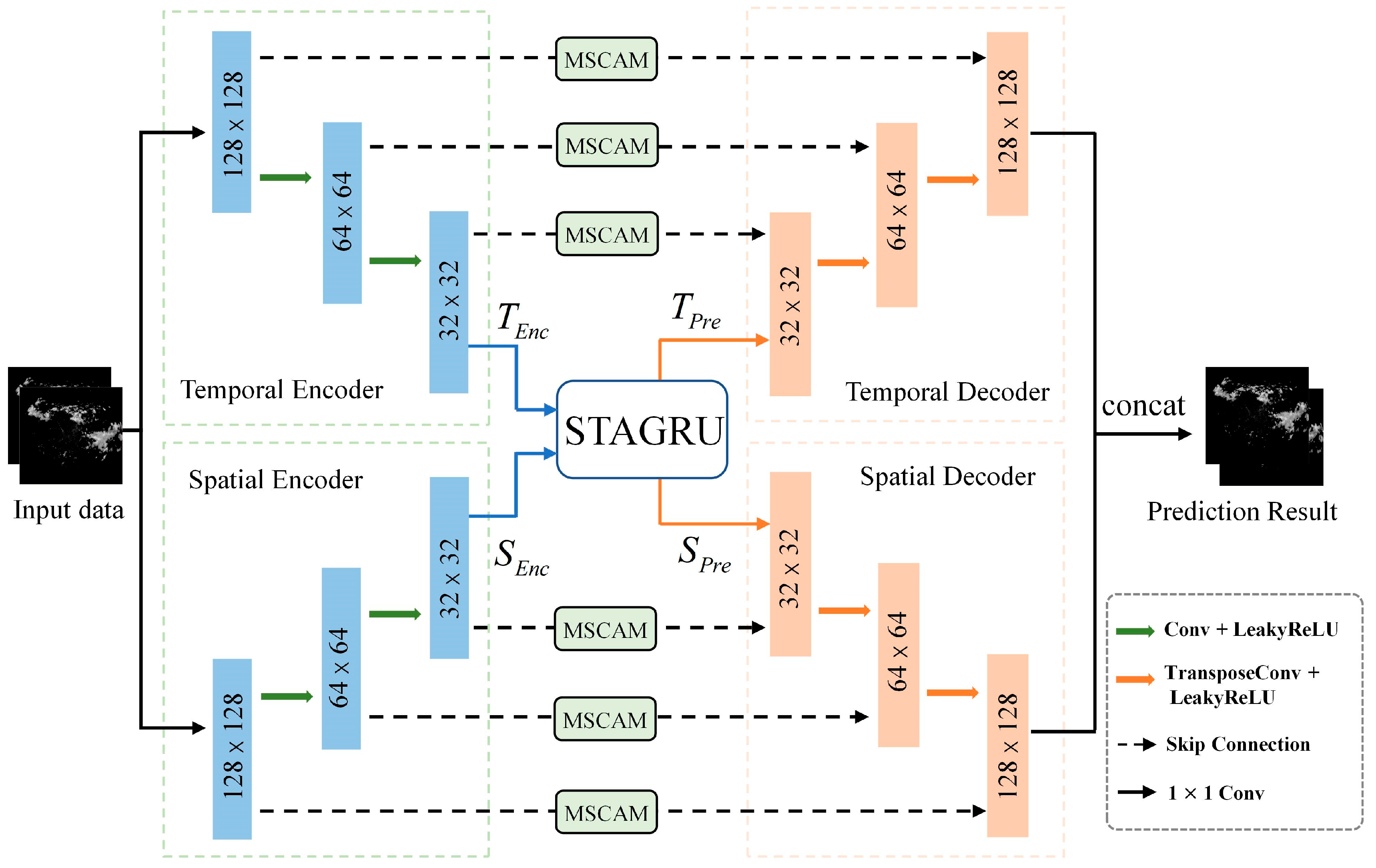
In this section, we will discuss the proposed DE-STAGRU model in detail. First, we will present the overall architecture of the proposed DE-STAGRU model. Subsequently, we will elaborate on the dual-branch encoder–decoder structure and the Spatiotemporal Attention Gated Recurrent Unit (STAGRU), explaining how the Multi-Scale Channel Attention Module is incorporated into our model. Figure 1 presents the proposed extrapolation architecture based on a dual-branch encoder–decoder and spatiotemporal GRU.

3.1. Overall Network

The proposed model comprises a Temporal Encoder (TE), a Spatial Encoder (SE), a Spatial Decoder (SD), a Temporal Decoder (TD), a Multi-Scale Channel Attention Module (MSCAM), and a Spatiotemporal Attention-Gated Recurrent Unit (STAGRU). The TE and SE are employed to extract intricate features from the radar images. MSCAM is positioned within skip connections to extract local and global contextual features from the encoded information. The Spatiotemporal Attention-Gated Recurrent Unit (STAGRU) is utilized to capture spatiotemporal relationships and long-term dependencies. TD and SD are used to output the image after reduction.

3.2. The Dual-Branch Encoder–Decoder Structure

The process of convective weather evolution is influenced by a variety of factors, such as dynamical factors such as wind fields and topography that affect the development of convection, as well as thermodynamic factors such as temperature, humidity, and pressure in the atmosphere. Therefore, the development process of convective weather is non-linear and irregular, and it is difficult to accurately predict the changes in weather radar echoes. This study adopts a spatiotemporal dual-branch encoder–decoder structure to separately encode temporal and spatial information. The advantage of this design lies in its ability to extract rich features from both encoders, thereby avoiding interference between spatiotemporal information within the prediction units. Information on the intensity, spatial distribution, and range of radar echoes is effectively extracted to better understand the evolution of convective processes from massive radar data.

The Encoders: As shown in the left half of Figure 1, the encoders consist of a temporal encoder and a spatial encoder. Each encoder consists of three consecutive modules, with each module primarily comprising a 3 × 3 convolutional layer, a LeakyReLU activation layer, and downsampling through convolution. With the progression of network layers, as the input passes through each encoding module, the spatial dimension of the original input is halved, allowing the feature maps to capture feature information at different scales.

The Decoders: As shown in the right half of Figure 1, the decoders consist of a temporal decoder and a spatial decoder. Starting from the output of the STGRU unit, the decoders comprise three consecutive modules, with each module primarily consisting of a 3 × 3 transpose convolutional layer and a LeakyReLU activation layer. Upsampling is performed through transpose convolution to gradually restore the output to its original size. Finally, the temporal decoder and spatial decoder information are fused to output the image.

Skip-Connection: The MSCAM is employed to further extract detailed features of each layer’s encoded information.

In order to extract fine-grained features from the encoded information and improve the model’s long-range dependency capability, we propose a multi-scale channel attention block. This block incorporates channel attention mechanisms to learn the importance weights for each channel. This enables the model to automatically focus on channels that contribute more significantly to important features. By enhancing the weights assigned to these important channels, MSCAM is able to better capture detailed information, as illustrated in Figure 2.

The Multi-Scale Channel Attention Module takes the encoded information as the input and extracts both local and global contextual features. The channel attention for local features, denoted as L(x), is obtained through point-wise convolution. On the other hand, the channel attention for global features, denoted as G(x), involves performing global average pooling (GAP) on the input, followed by point-wise convolution.

By performing element-wise addition to fuse the local and global features and then obtaining the attention weights by the Sigmoid function, the entire Multi-Scale Channel Attention Module can be represented as follows:

$$X^{\prime }=X\odot \sigma (L(X)+G(X))$$

(1)

3.3. STAGRU Module

Prediction models based on ConvRNNs suffer from the problem of forgetting during the information transfer process, i.e., it is difficult to effectively recall information about the convective evolution process learned at historical moments. Therefore, this information-forgetting problem can lead to the unsatisfactory accuracy of the prediction results. To further enhance the efficiency of the prediction unit in transforming spatiotemporal information and improve the issue of information loss during information propagation, we propose a spatial-temporal attention gated recurrent unit (STAGRU). In this section, we will elaborate on the functioning principles of the temporal attention module and the spatial-temporal gated attention recurrent unit (STAGRU).

3.3.1. Temporal Attention Module

The proposed temporal attention module, as illustrated in Figure 3, is described in this paper. First, the input $S_t^{l-1}$ is element-wise multiplied with the spatial states $S_{t-\tau :t-1}^{l-1}$ from multiple previous time steps. The resulting correlations are computed using the softmax function, yielding the relevance scores ${\alpha }_j$. By ${\alpha }_j$ assigning attention weights to the historical temporal states and performing an additive fusion, the candidate temporal attention information ${\tilde{T}}_{att}$ is obtained, as shown in Equation (2).

$$\begin{array}{l}{\alpha }_j=\mathrm{Softmax}(S_{t-\tau :t-1}^{l-1}\cdot S_t^{l-1})\\ {\tilde{T}}_{att}={\displaystyle \sum _{j=1}^{\tau }{\alpha }_j\cdot T_{t-j}^l}\end{array}$$

(2)

In particular, when l = 1, $S_t^{l-1}=S_{Enc}$ and $T_{t-1}^l=T_{Enc}$, where τ = 5 and “$\cdot$” denotes the dot product of the matrix. ${\tilde{T}}_{att}$ denotes long-term movement trend information.

To effectively integrate the long-term motion trend information ${\tilde{T}}_{att}$ and the short-term motion information $T_{t-1}^l$, a fusion gate $G_t$ is introduced to control the fusion rate between them, as shown in Equation (3).

$$\begin{array}{l}{G}_t=\sigma (W_g\ast T_{t-1}^l)\\ T_{att}=G_t\odot T_{t-1}^l+(1-G_t)\odot {\tilde{T}}_{att}\end{array}$$

(3)

Here, $W_g$ denotes the convolution operation, “⊙” represents the Hadamard product of matrices, and “σ” denotes the sigmoid activation function. Consequently, the attention information $T_{att}$ encompasses multiple historical temporal states, thereby possessing a broader temporal receptive field.

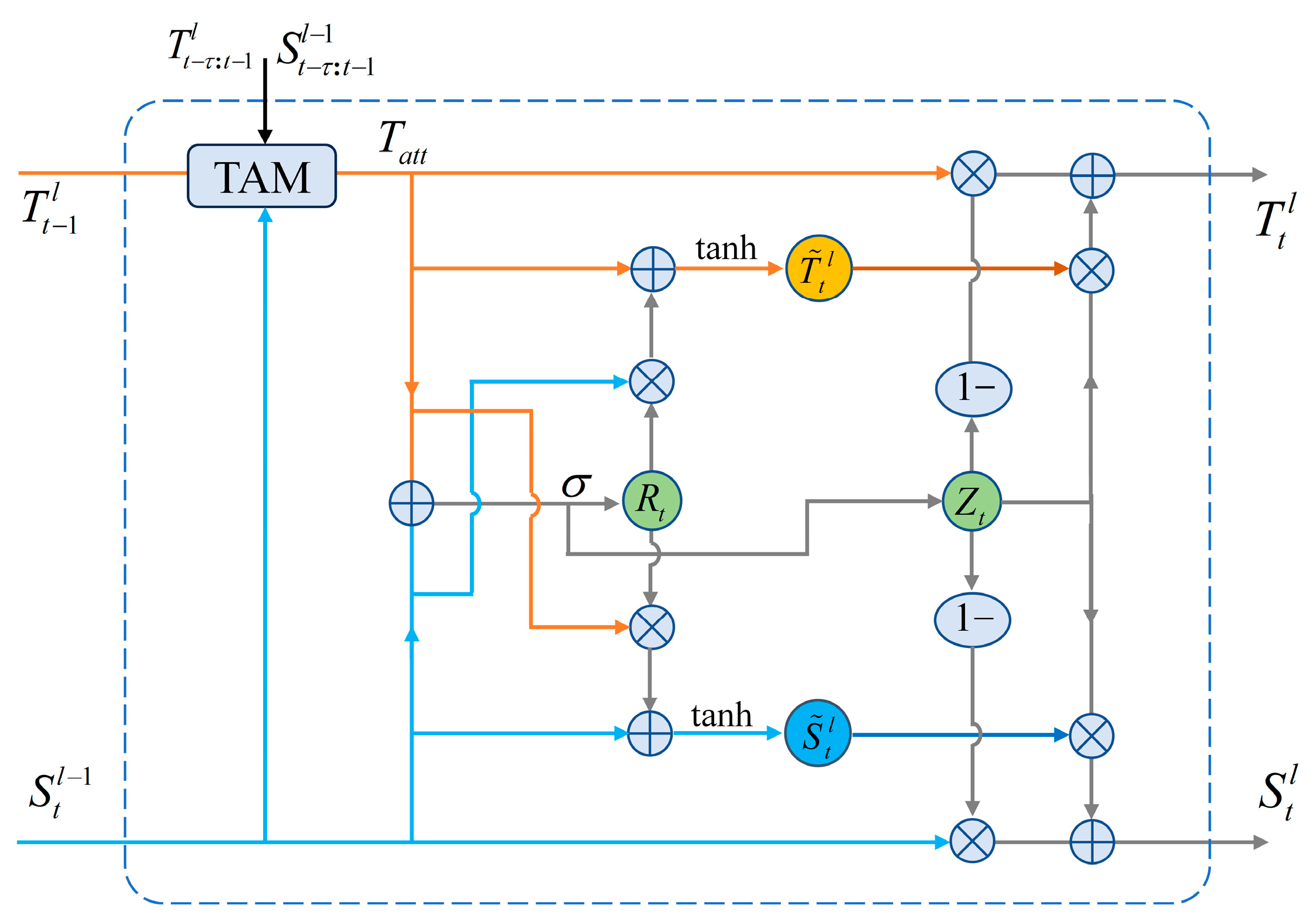
3.3.2. STAGRU

The STAGRU consists of the Time Attention Block and the STGRU, as depicted in Figure 4. The STAGRU prediction module can effectively predict the strength, morphology, and movement trend of the precipitation system through an efficient temporal and spatial state transformation mechanism. Among them, the time-attention module fuses multi-step time information to effectively improve the information-forgetting problem.

Each STAGRU encompasses two gating mechanisms, namely, the update gate $Z_t$ and reset gate $R_t$, as described in Equation (4).

$$\begin{array}{l}{Z}_t=\sigma (W_{sz}\ast S_t^{l-1}+W_{tz}\ast T_{att})\\ R_t=\sigma (W_{sr}\ast S_t^{l-1}+W_{tr}\ast T_{att})\end{array}$$

(4)

Among them, the update gate is responsible for updating the current state, while the reset gate is used to combine the current spatial and temporal states. The specific transformation is given by Equation (5).

$$\begin{array}{l}{\tilde{T}}_t^l=\tanh (W_{st}\ast T_{att}+R_t\odot (W_{tt}\ast S_t^{l-1}))\\ {\tilde{S}}_t^l=\tanh (W_{ts}\ast S_t^{l-1}+R_t\odot (W_{ss}\ast T_{att}))\\ T_t^l=(1-Z_t)\odot T_{att}+Z_t\odot {\tilde{T}}_t^l\\ S_t^l=(1-Z_t)\odot S_t^{l-1}+Z_t\odot {\tilde{S}}_t^l\end{array}$$

(5)

Here, ${\tilde{T}}_t^l$ represents the candidate temporal state, ${\tilde{S}}_t^l$ represents the candidate spatial state, W denotes the parameters of the convolution operation, and “⊙” is the Hadamard product.

To further extract more effective deep spatiotemporal features, it is common to stack four STAGRU units together to form an integrated extrapolation architecture, as illustrated in Figure 5. The horizontal direction carries temporal information, while the vertical direction carries spatial information. After passing through the fourth unit, both the temporal and spatial information are outputted and then decoded using the temporal decoder and spatial decoder, respectively.

4. Experiment

We conducted experiments based on extrapolated 0–1 h short-term forecasts. We evaluated the proposed DE-STAGRU algorithm on the CIKM 2017 dataset and compared it with several state-of-the-art models, namely, ConvLSTM, PredRNN, PredRNN++, MIM, and IDA-LATM, to validate its advancement in performance.

4.1. Implementation Details

In this section, all models were carried out on an NVIDIA A10 GPU. During the training process, all comparative models employed a common single encoding–decoding structure to encode radar images into low-dimensional features before feeding them into the prediction model. To ensure a fair comparison, all models utilized four prediction units with a channel size of 64 and a convolutional kernel size of 5 × 5. The Adam optimizer was employed for optimization with a learning rate of 0.0001. The batch size was set to four, and the models were trained for 80,000 iterations.

4.2. Evaluation Metrics

In order to validate the effectiveness of each model in precipitation forecasting, we conducted experiments to analyze and evaluate the results using both image quality assessment metrics and prediction accuracy indicators.

Image Quality Assessment Metrics: To validate the performance of our model in predicting image details, we employed the widely used Structural Similarity (SSIM) index [37] as an image quality assessment metric. SSIM is utilized to measure the degree of structural similarity between images, with a focus on brightness, contrast, and structure. A higher SSIM value indicates greater similarity between the two images. The formula for SSIM is provided in the following Equation (6):

$$SSIM(\mathrm{x},\mathrm{y})=\frac{(2{\mu }_x{\mu }_y+C_1)(2{\sigma }_{xy}+C_2)}{({\mu }_x^2+{\mu }_y^2+C_1)({\sigma }_x^2+{\sigma }_y^2+C_2)}$$

(6)

In the equation, x denotes the predicted image, and y denotes the real image. µ denotes the mean value of the image, σ represents the covariance of the image, and C₁ and C₂ are constants introduced to prevent computational errors caused by the division by zero.

Metrics for Forecast Accuracy: This study evaluates the results using two commonly employed indicators of predictive accuracy, namely, the Critical Success Index (CSI) and the Heidke Skill Score (HSS), which are widely utilized for assessing the precision of forecasting models.

To compute evaluation scores, the pixels in the image with a radar echo intensity greater than a specified threshold are set to 1, while those below the threshold are set to 0. For each corresponding position, if both the predicted value and the ground truth are 1, the total number of pixels of the same type is denoted as true positives (TP). If the predicted value is 1 and the ground truth is 0, the total number of pixels of the same type is denoted as false positives (FP). If both the predicted value and the ground truth are 0, the total number of pixels of the same type is denoted as true negatives (TN). If the predicted value is 0 and the ground truth is 1, the total number of pixels of the same type is denoted as false negatives (FN). Then, the following formulas are used to calculate the CSI and HSS scores for each model:

CSI (Critical Success Index) and HSS (Heidke Skill Score) scores are calculated based on the aforementioned definitions and the following formulas:

$$\begin{array}{l}CSI=\frac{TP}{TP+FN+FP}\\ HSS=\frac{2\times (TP\times TN-FN\times FP)}{(TP+FN)(\mathrm{F}\mathrm{N}+TN)+(TP+FP)(FP+TN)}\end{array}$$

(7)

4.3. Results and Analysis

We comprehensively assessed the predictive power of the algorithms by setting multiple thresholds and evaluating the performance of the algorithms using CSI, HSS, and SSIM metrics. The results in

Table 1. Comparison results on CIKM 2017 in terms of CSI, HSS, and SSIM. Bold denotes the best evaluated index among all models. ‘↑’ indicates that the larger the value, the better the effect.

Methods	CSI ↑				HSS ↑				SSIM ↑
	10	20	40	Avg	10	20	40	Avg
ConvLSTM	0.6678	0.4205	0.0401	0.3761	0.7103	0.5099	0.0605	0.4269	0.7488
PredRNN	0.6734	0.4295	0.0442	0.3824	0.7169	0.5209	0.0670	0.4349	0.7552
PredRNN++	0.6669	0.4292	0.0526	0.3829	0.7105	0.5192	0.0738	0.4345	0.7526
MIM	0.6706	0.4372	0.0454	0.3844	0.7157	0.5283	0.0701	0.4380	0.7534
IDA-LSTM	0.6780	0.4353	0.0521	0.3885	0.7201	0.5250	0.0785	0.4412	0.7557
DE-STAGRU	0.6806	0.4462	0.0577	0.3948	0.7238	0.5366	0.0882	0.4495	0.7578

provide an in-depth analysis of the relative performance of the algorithms and identify the best-performing algorithms based on the highlighted values.

From the table, it can be observed that the proposed DE-STAGRU model demonstrates improved CSI, HSS, and SSIM scores compared to previous models. The reason is that ConvLSTM only focuses on the temporal information propagated horizontally and ignores the spatial information propagated vertically between different cell layers. Compared with ConvLSTM, models such as PredRNN and PredRNN++ can focus on both temporal and spatial information, and PredRNN++ solves the problem of vanishing gradients. MIM simulates non-stationary and nearly stationary properties in spatiotemporal dynamics by using two cascaded self-updating memory modules. IDA-LSTM improves this problem by utilizing self-attentive modules, but some of the self-attentive modules only focus on themselves and cannot obtain historical information from more distant prediction units. Therefore, the above methods still lack the effective feature extraction capability to effectively model long-term spatiotemporal relationships. Considering the strong correlation between points with relatively higher dBZ values and heavy precipitation, achieving accurate predictions at higher thresholds (40 dBZ) is of significant importance. The proposed DE-STAGRU model outperforms the IDA-LSTM [38] method by 10.7% and the PredRNN++ method by 9.7% at the 40 dBZ threshold. Moreover, in terms of HSS scores, DE-STAGRU exhibits a 12.4% improvement over IDA-LSTM and a 19.5% improvement over PredRNN++. These results indicate an enhancement in the long-term dependency modeling capability of our proposed DE-STAGRU model, thereby improving the forecasting ability for areas with intense echo patterns. Additionally, the SSIM scores also demonstrate improvement compared to other models. Overall, the experimental results highlight the significant advancements achieved by the proposed DE-STAGRU model across all three accuracy metrics.

To better compare the quality of radar echo maps, we present an extrapolation example of a 60 min forecast using different methods in Figure 6. The color bars on the right side represent the echo intensities corresponding to the different colors. The red color in the color bar corresponds to regions with echo intensities greater than 40 dBZ. When the radar image contains red or darker-colored areas, it indicates that severe weather is occurring in the area. All models are extrapolating the first row’s subsequent ten images based on the first row’s initial five images.

In this example, the high-echo region in the lower left can be seen to be decaying and moving to the right. At the same time, the center-left position is evolving to generate a new high-echo region. During the prediction process, we observed minimal differences in the predicted results among the various models in the first three time steps, which closely matched the actual observed results. However, as the prediction time increased, from the figure, it can be seen that ConvLSTM can only roughly predict the contour of the newly evolved high-echo region, which is quite different from the actual. There is an underestimation of the high echo value in PredRNN, and the predicted location is also biased. The PredRNN++ and MIM models were able to approximate the locations of high-echo regions; the extrapolated images gradually became blurred, and the high-echo areas diminished. Only the IDA-LSTM and DE-STAGRU models were able to preserve a larger portion of the high-echo regions, with DE-STAGRU demonstrating the best performance.

Furthermore, from the ground truth sequence, it is evident that as time progresses, the intensity and location of high-echo regions change. The DE-STAGRU model demonstrates the ability to accurately predict these variations and maintains a higher level of detail in its predictions. This can be attributed to the dual-branch encoder–decoder of the DE-STAGRU model, which extracts multi-scale spatiotemporal features, reducing interference among the temporal and spatial information. Additionally, the Multi-Scale Channel Attention Module (MSCAM) employs global and local channel attention to aid in feature extraction, effectively addressing the issue of information loss and preserving more details during the prediction process. Moreover, in the Spatial-Temporal Attention Gated Recurrent Unit (STAGRU), the temporal and spatial states are independently transferred between different memory units, enabling the efficient modeling of temporal and spatial evolution between previous and future frames. The inclusion of a temporal attention module in STAGRU effectively expands the temporal receptive field of the prediction unit, significantly improving the predictive capability for high-echo regions. In contrast, other deep learning models fail to predict high-echo regions, and as the prediction time increases, their predictions gradually become blurred or even disappear. In the future, the incorporation of a priori knowledge into the short-range prediction of precipitation can be considered to further improve the prediction accuracy [39].

4.4. Ablation Study

In order to further observe the impact of different modules on the prediction results, we conducted an ablation study on the model proposed in this paper using the CIKM 2017 dataset. Based on the STGRU, we sequentially incorporated the Dual Encoding (DE) structure, the Multi-Scale Channel Attention Module (MSCAM), and the Temporal Attention Module (TAM) into the STGRU. We compared these variations with the STGRU and the final DE-STAGRU. The experimental results are shown in

Table 2. Comparison ablation study results on CIKM 2017 in terms of CSI, HSS, and SSIM. Bold denotes the best evaluated index among all models. ‘↑’ indicates that the larger the value, the better the effect.

Methods	CSI ↑				HSS ↑				SSIM ↑
	10	20	40	Avg	10	20	40	Avg
STGRU	0.6696	0.4230	0.0425	0.3784	0.7136	0.5116	0.0653	0.4302	0.7485
DESTGRU	0.6755	0.4302	0.0468	0.3842	0.7191	0.5208	0.0716	0.4372	0.7494
DESTGRU-MSCAM	0.6761	0.4379	0.0545	0.3895	0.7198	0.5278	0.0821	0.4432	0.7523
DESTGRU-TAM	0.6785	0.4345	0.0477	0.3869	0.7204	0.5227	0.0722	0.4384	0.7521
DE-STAGRU	0.6806	0.4462	0.0577	0.3948	0.7238	0.5366	0.0882	0.4495	0.7574

.

First, by incorporating the Dual Encoding (DE) structure into the STGRU, we formed the DESTGRU model, and the scores obtained at various thresholds indicate an improvement in performance. This demonstrates the effectiveness of the Dual Encoding structure. Furthermore, the MSCAM and TAM modules were separately added to the DESTGRU. From the data presented in the table, it can be observed that the performance of the DESTGRU with MSCAM and that of the DESTGRU with TAM both outperformed the DESTGRU and STGRU models. Thus, it can be seen that MSCAM and TAM play a positive role in improving prediction accuracy. The proposed standard DE-STAGRU yielded the best results, which can be attributed to the combined effect of the aforementioned Dual Encoding structure and the two new modules.

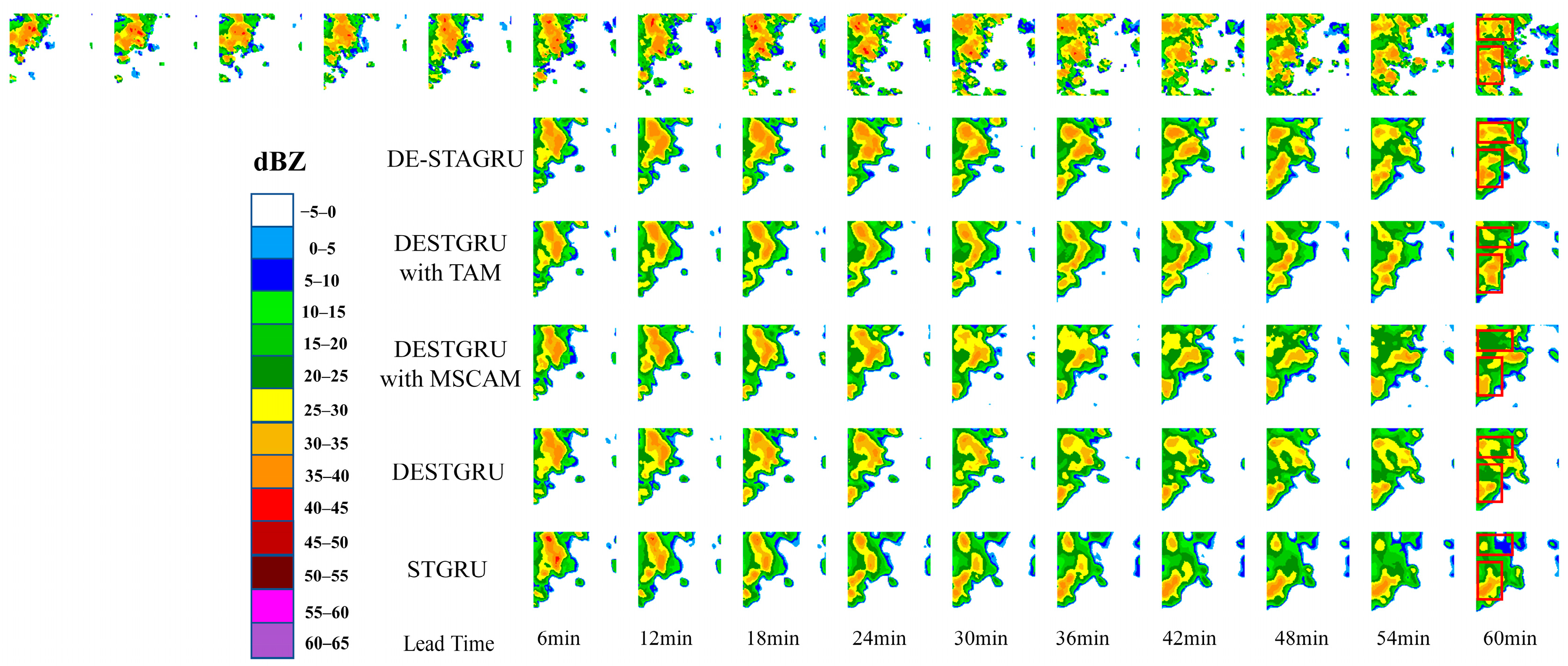
To visually compare the experimental results, we performed visualizations on a sample from the CIKM 2017 test dataset, as shown in Figure 7. From the figure, it can be observed that the extrapolation results of STGRU exhibit a gradually smooth trend, with some regions gradually disappearing. However, the DESTGRU model, which incorporates the dual-branch encoder–decoder structure, is capable of extracting more spatiotemporal features, leading to more accurate predictions of the locations of echo regions. The introduction of the MSCAM module in DESTGRU enables the extraction of local and global contextual features of the encoded representation, thus enhancing the level of detail in the predicted images. Additionally, the TAM module in DESTGRU expands the receptive field of the prediction units, resulting in more accurate predictions of high-echo regions. The standard DE-STAGRU model achieves the best forecasting performance, highlighting the effectiveness of incorporating MSCAM and TAM into the dual-branch encoder–decoder structure and the overall improvement in prediction accuracy.

5. Discussion

In this paper, we investigate a deep learning-based echo image extrapolation model for weather radar-based 0–1 h short-term precipitation proximity forecasting. Aiming at the current problem of the fuzzy distortion of radar echo extrapolation results over time, especially the underestimation problem in the high-echo region, we propose a novel DE-STAGRU model, which achieves a higher accuracy of radar echo extrapolation results by combining a two-branch codec structure and a gated-attention recurrent network. We conduct comparative experiments on the CIKM 2017 dataset with selected deep learning networks such as ConvLSTM, PredRNN, PredRNN++, MIM, and IDA-LSTM. In addition, we conducted ablation experiments to verify the effectiveness of the modules of the DE-STAGRU model. The experiments show that our method is more advantageous in terms of the clarity and detail of the extrapolated image, and the prediction ability of the high-echo region is also improved.

To address the problem of ambiguous prediction results, we found that existing methods have the disadvantage of insufficient feature extraction capability, such as ConvLSTM, which only focuses on temporal information and ignores the spatial information between different cell layers. Models such as PredRNN and PredRNN++ have been improved and upgraded in comparison to ConvLSTM, but they still have not obtained a good solution. In this paper, we propose a two-branch coding and decoding structure to extract features from the temporal and spatial domains, respectively, while the multi-scale channel attention module embedded in the structure helps the decoder better recall the encoder information. To address the problem of underestimating the prediction results in the high-echo region, there is information attenuation during the prediction process in existing methods, such as MIM and IDA-LSTM. Although IDA-LSTM uses self-attention modules to ameliorate the problem a bit, some self-attention modules focus only on themselves and cannot obtain historical information from more distant prediction units. In this paper, we propose a gated recurrent neural network incorporating a temporal attention mechanism that can obtain historical information from multiple time steps in the past from a wider perceptual domain, effectively improving the attenuation problem in information transfer and improving the prediction ability for high-echo regions.

However, despite the excellent performance of our DE-STAGRU model in the experiments, we also recognize that the training of DL models still requires a large amount of data, which may limit their generalizability in practical applications. In addition, we will explore how to incorporate other meteorologically related elements into our DE-STAGRU model to further improve the richness of the model and its prediction performance.

6. Conclusions

In this paper, we propose a DE-STAGRU model for the radar echo extrapolation task. In our approach, a two-branch encoder–decoder structure is used to extract spatial-temporal multiscale features from radar images, which avoids interference between temporal and spatial information and effectively improves the problem of ambiguity in prediction results. A gated recurrent network (STAGRU) incorporating an attention mechanism is used to capture the spatial-temporal evolutionary relationship, while the temporal attention module broadens the sensory field and effectively solves the problem of underestimating the high-echo region during the prediction process. By combining the two structures, it is possible to model the evolution of weather convective processes. We validated the performance of the model using the CIKM 2017 dataset. The results show that the model can effectively predict the evolution of convective processes and improve prediction accuracy.