Abstract
Hourly solar radiation (SR) forecasting is a vital stage in the efficient deployment of solar energy management systems. Single and hybrid machine learning (ML) models have been predominantly applied for precise hourly SR predictions based on the pattern recognition of historical heterogeneous weather data. However, the integration of ML models has not been fully investigated in terms of overcoming irregularities in weather data that may degrade the forecasting accuracy. This study investigated a strategy that highlights interactions that may exist between aggregated prediction values. In the first investigation stage, a comparative analysis was conducted utilizing three different ML models including support vector machine (SVM) regression, long short-term memory (LSTM), and multilayer artificial neural networks (MLANN) to provide insights into their relative strengths and weaknesses for SR forecasting. The comparison showed the proposed LSTM model had the greatest contribution to the overall prediction of six different SR profiles from numerous sites in Morocco. To validate the stability of the proposed LSTM, Taylor diagrams, violin plots, and Kruskal–Wallis (KW) tests were also utilized to determine the robustness of the model’s performance. Secondly, the analysis found coupling the models outputs with aggregation techniques can significantly improve the forecasting accuracy. Accordingly, a novel aggerated model that integrates the forecasting outputs of LSTM, SVM, MLANN with Sugeno λ-measure and Sugeno integral named (SLSM) was proposed. The proposed SLSM provides spatially and temporary interactions of information that are characterized by uncertainty, emphasizing the importance of the aggregation function in mitigating irregularities associated with SR data and achieving an hourly time scale forecasting accuracy with improvement of 11.7 W/m2.
1. Introduction
Solar radiation (SR), often noted because the energy emitted by the sun and reaching the Earth’s surface, plays an important role in various natural Earth processes, as noted by [1,2]. This type of energy finds applications in fields like hydrology, climate science, irrigation planning, and also the development of crop growth models, as demonstrated by the works of [3,4,5,6]. Moreover, radiation stands as a sustainable energy source, presenting a viable alternative to fossil fuels, as highlighted by [7,8,9,10].
Nonetheless, obtaining direct measurements of (SR) remains a challenge on a world scale, as acknowledged by [11,12,13]. Consequently, to handle this limitation, scientists have endeavored to predict radiation using various modeling approaches. Among these models, we will categorize them into three main types:
Empirical Relationships: These models are supported established empirical equations and relationships. Examples include the works of [14,15,16,17,18,19]. Artificial Intelligence (ANN)-Based Models: These models utilize ANN and machine learning (ML) techniques to estimate radiation. Examples include the research of [20,21,22,23,24]. Satellite-Based Models: These models depend upon satellite data and remote sensing technology to derive radiation estimates. They include the works of [25,26,27,28,29]. These diverse approaches offer various methods for estimating radiation, catering to different data availability, and modeling preferences.
Each of the models mentioned above has its own strengths and weaknesses. Therefore, when selecting a model for a study associated with radiation, several key factors acquire play, as noted by [2]. These factors include the desired level of accuracy, the desired spatial distribution of information, and therefore the availability of meteorological data. For instance, when considering satellite-based models, like the one discussed by [26], the continual data they supply, both in terms of spatial coverage and temporal resolution, can give researchers a highly accurate and spatially distributed view of radiation across an outsized geographical region at any given point in time. This could be particularly valuable in studies where comprehensive coverage and up-to-date information are essential. There is a big body of research on the ML approach for radiation forecasting. Notably, a considerable portion of those studies emerged after 2018. These recent investigations demonstrate a growing interest in several key areas:
Climate Change: Many of those studies have a pronounced target global climate change. This reflects the broader recognition of the importance of accurate radiation forecasting in understanding and mitigating the results of global climate change.
Deep Learning (DL): Researchers are increasingly exploring the potential of DL techniques for SR forecasting. Their architectures have shown promise in capturing complex patterns in radiation data.
New Machine Learning Models: Beyond traditional ML algorithms, like support vector machine (SVM) and extreme learning machine (ELM), newer and more advanced ML models are gaining attention. These models may offer improved accuracy and performance in SR forecasting.
Renewable Energy Development: The connection between radiation forecasting and also the development of renewable energy generation may be a significant area of interest. Accurate predictions of radiation are crucial for optimizing the efficiency of solar energy systems.
Several researchers have delved into modeling and forecasting radiation using various mathematical equations and ML approaches. Kumar et al. (2015) conducted a study comparing the performance of regression models with ANN models for SR prediction [30]. This research likely aimed to assess the effectiveness of ML techniques during this context [31]. This team employed a wavelet transform approach together with various ML techniques, including ANN, ELM, and radial basis function (RBF) networks, yet as their hybrid variations. This means an investigation into the potential benefits of mixing wavelet analysis with ML for SR modeling. Şahin (2013) involved a comparison between ANN-based methods and statistical methodologies to estimate radiation from satellite images [32]. This research could explore the benefits of using ANN in remote sensing applications. Polo et al. (2014) investigated the sensitivity of satellite-based approaches to calculate radiation concerning different aerosol input parameters and model choices [33]. This research likely aimed to grasp how varying factors affect the accuracy of satellite-derived radiation estimates. These studies collectively represent the varied approaches and methods employed by researchers to reinforce our understanding of radiation and its prediction using both traditional mathematical techniques and modern machine learning methods. In an investigation conducted by [34], various models for solar radiation (SR) estimation and forecasting were explored. Their research revealed that, among the models they assessed, the one modified by Gueymard from the Collares-Pereira and Rabl model demonstrated the very best level of accuracy in forecasting average hourly radiation. This means that, for his or her study, this specific model adaptation proved to be the foremost precise for predicting radiation under these specific circumstances. Belmahdi et al. (2023) provide five approaches for forecasting daily global solar radiation (GSR) in two Moroccan cities [35], Tetouan and Tangier; autoregressive integrated moving average (ARI-MA), autoregressive moving average (ARMA), feed forward back propagation neural networks (FFBP), hybrid ARIMA-FFBP, and hybrid ARMA-FFBP were selected to forecast the daily global radiation with different combinations of meteorological parameters, and the hybrid models improved accuracy and reduced errors in forecasting. The hybrid k-means and nonlinear autoregressive neural network models provide better hourly global solar radiation forecasting results than either method alone [36]. Machine learning techniques slightly improve hourly solar forecasting performance compared to linear autoregressive and scaled persistence models, with more pronounced improvements in unstable sky conditions [37].
Based on the literature available in the Web of Sciences database, more than 1000 research papers in the field of SR prediction with ML approaches were identified. These studies were analyzed bibliometrically using VOSviewer software (version1.6.20) [38,39]. Figure 1 shows the connection between keywords.
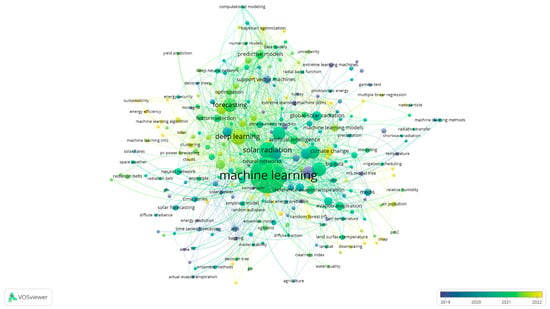
Figure 1.
Keywords of SR prediction studies with machine learning approach.
Figure 1 shows the intense use of ML approaches in SR predictions, solar energy, solar irradiation, renewable energy studies, and in recent years, especially that DL and remote sensing are among the topics researched by the authors.
SR is extensively researched worldwide, especially in sun-rich areas just like the Mediterranean and also the Mideast [40,41]. Unfortunately, many locations lack access to reliable observed radiation data because of the high costs related to acquiring, installing, and maintaining measurement devices. Challenges associated with calibrating radiation detection equipment further contribute to the present data gap [31]. Consequently, researchers commonly resort to numerous methods for estimating SR, including location-based, temperature-based, remote sensing-based, day and month-number-based, cloudiness-based, sunshine-based models, and hybrid models [42,43,44]. However, the complex relationships between independent and dependent variables often limit the accuracy of those models, especially in humid regions where inclemency significantly affects radiation [42].
The aim of this study is to investigate SR forecasting using long short-term memory, support vector machine regression, and multilayer artificial neural networks approaches. For SR estimation and to propose a novel aggerated model that integrates the forecasting outputs of LSTM, SVM, and MLANN with Sugeno λ-measure and Sugeno integral named (SLSM), 10 hydro-meteorological parameters and various reflectance values obtained by remote sensing techniques from 6 stations located in Morocco (Tantan, Fes, Agadir, Marrakech, Ouarzazate, and Tangier) were used as the main contributions to the present research, which are:
- (1)
- Combining information from remote sensing parameters and hydro-meteorological data to improve hourly SR forecast accuracy using input data from hourly timesteps.
- (2)
- Capturing a wider variety of environmental variables and incorporating spatial components into the study by using the reflectance data from remote sensing.
- (3)
- Long short-term memory (LSTM), support vector machine (SVM) regression, and multilayer artificial neural networks (MLANN) are being investigated as ML approaches to perform a comprehensive comparison of SR prediction models and provide valuable insights into their relative strengths and weaknesses.
- (4)
- Using various weather dataset profiles, and comparing different ML techniques to assess the stability of the offered approaches.
- (5)
- Evaluating the efficacy of the proposed methodologies under various geographical and meteorological variables to validate the generalizability and reliability of SR prediction.
- (6)
- Conducting statistical analysis using the Kruskal–Wallis test to see whether the forecasts and observations data points have the same underlying distributions.
- (7)
- Improving the forecasting accuracy by applying fuzzy measure of that combines the accurate prediction information of the three models.
2. Materials and Methods
2.1. Data Profiles
The sites are located in Morocco, North Africa, namely: Tantan, Fes, Agadir, Marrakech, Ouarzazate, and Tangier, as shown in Figure 2 and Table 1. The country encompasses a population of 37 million people and an expanse of 710,850 square kilometers. Northern and southern Morocco have very different climates. Both rainfall and temperature are greatly impacted by the Atlantic, Mediterranean Sea, and desert. The period from October to May sees the most rainfall. Southern and south-eastern dry and semi-arid regions have high temperatures. Average monthly temperatures range from 9.4 °C (December, January) to 26 °C (July, August). The wettest months are from October to April, and therefore the driest are from June to August [17]. Recently, the National Centre of Meteorology and the Moroccan Agency for Energy Efficiency (AMEE) worked together to form a replacement climatic zoning map for Morocco [45,46]. All the new climate zones in Morocco share the similar sun irradiation, height, and other key climatic characteristics. A key city is the indicator for every zone (Figure 2).
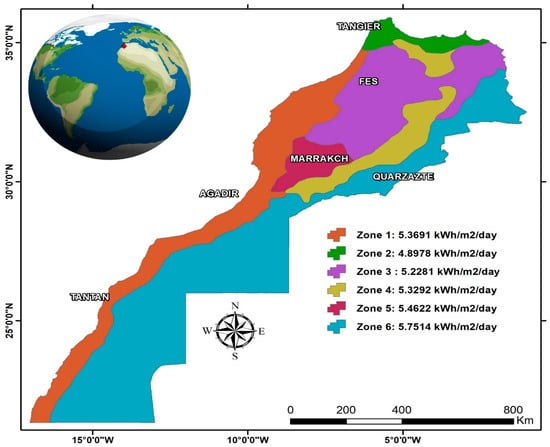
Figure 2.
Sites and SR zones modified from [17].

Table 1.
A table showing study area: Latitude, longitude, altitude, climate region, or climate type.
As can be seen, Table 1 distributes these sites from Morocco’s south to its north. Each site corresponds to a distinct climate zone, with variables such as latitude, longitude, altitude, and climate type.
2.2. Data Collection
The data employed in this study are sourced from SOLCAST, a poster enterprise [47,48,49] renowned for its solar irradiance estimation methods, leverages satellite technology to determine solar irradiance by effectively discerning cloud coverage. The combination of satellite data, clear sky models, and reanalysis data allows for a more accurate estimation of solar energy reaching the Earth’s surface, considering the impact of clouds [50]. Temporal granularity varies, encompassing basic hourly averages, as well as more finely grained options like 5-min, 10-min, 15-min, and 30-min intervals. For those requiring even more precise data, 1-min intervals may be obtained upon request. These datasets have been accessible since January 2007, with a seven-day delay, and may be accessed through the SOLCAST website. SOLCAST extends its data coverage globally, except for oceanic and polar regions. The spatial resolution of their data stands at a powerful 1 to 2 km [47,48,49].
The National Aeronautics and Space Administration (NASA) has been providing data at 0.5° spatial resolution worldwide since 1981 to support the renewable energy and agriculture sectors, and recently launched the Projection of Worldwide Energy Resources (POWER) project to produce long-term climate variables [51]. The user-friendly data access interface is the main focus of NASA POWER, and every dataset is available at four temporal levels: hourly, daily, monthly, and climatologically [52] Numerous studies are conducted to validate the performance of NASA POWER data in various locations around the world; i.e., Jordan [53], Iran [54], Africa [55], Brazil [56], Iraq [57], and Malaysia [58]. In northern Peninsular Malaysia, Bandira et al. (2022) reported that NASA POWER performed statistically satisfactorily for radiation and maximum and minimum temperatures, but less successfully for precipitation, wind speed, and mixing ratio [59]. Additionally, Rodrigues and Braga (2021) demonstrated that NASA POWER data are in good agreement with observed data, with a coefficient of determination (R2) more than 0.82 for radiation data [60]. However, only a few studies have evaluated NASA POWER within the tropics like in Morocco.
2.3. Morocco’s Solar Energy Potential
According to the Moroccan Agency for Solar Energy (MASEN), Morocco is known for its abundant solar energy, with an average of 5.3 kilowatt-hours per square meter of solar radiation annually. Sunshine durations vary across the country, ranging from approximately 2700 h per year in the northern regions to approximately 3500 h per year in the south [61]. Morocco has recently unveiled an ambitious plan for the development of integrated solar projects in combination with combined cycle units (Integrated Solar Energy Generation Project, Kingdom of Morocco. Available online at (www.one.org.ma, accessed on 14 October 2023) [62]. This initiative is expected to result in significant benefits, including the annual savings of 1 million tons of oil equivalent (Toe) and the reduction of 3.7 million tons of carbon dioxide (CO2) emissions. The primary objectives were to establish 2000 megawatts (MW) of solar capacity across five specific sites (Ouarzazate—500 MW, Ain Beni Mathar—400 MW, Foum Al Ouad—500 MW, Boujdour—100 MW, and Sebkhat Tah—500 MW) by the year 2020 [63] provides a brief overview of these sites, including their location, grid connection, water availability, and approximate coordinates. These projects were planned to utilize two main solar technologies, concentrated solar power (CSP) and photovoltaic (PV).
2.4. ALLSKY_SFC_SW_DWN
A parameter called ALLSKY_SFC_SW_DWN represents the entire amount of shortwave radiation that reaches the layer in all sky circumstances, including overcast and clear skies [64]. To comprehend the Earth’s energy balance, temperature, and other environmental processes, it measures the quantity of additional energy that enters the shortwave spectrum and reaches the planet’s surface. This metric is used in environmental research, climate modeling, and prediction. It is typically measured or calculated in measures such as watts per unit of measurement (W/m2) [65]. Because it offers vital information about the solar energy that reaches the surface under different sky conditions, the entire shortwave radiation received at the surface under all sky situations is incredibly essential. These data are essential for a fair number of applications, including environmental management, renewable energy planning, forecasting, and climate modeling [66,67].
3. Forecasting Models
The requirements of the specific application, the level of precision needed, and the resources available all influence the approach and instrument selection. To obtain extensive and precise data on shortwave radiation, a variety of techniques, such as satellite data collection and ground-based observations, are frequently utilized.
3.1. Long Short-Term Memory (LSTM)
Artificial neural networks that can learn from sequential input and forecast the future using historical data are known as recurrent neural networks (RNNs) [68]. However, when trained with back-propagation, RNNs suffer from vanishing or exploding gradients and forget long-term dependencies [69]. To solve this issue, the LSTM model—a variation on the RNN—was presented. Its hidden layers contain unique units known as memory cells, which have the ability to store and retrieve data for extended periods of time [70,71]. The architecture of the LSTM is displayed in Figure 3 [72]. The LSTM equations are as follows:
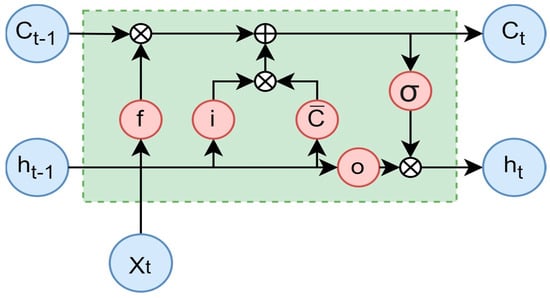
Figure 3.
The LSTM structure.
Three gates serve as the foundation for the LSTM equations: the input gate (it), the forget gate (ft), and the output gate (ot). The amount of information that enters, exits, and stays inside the memory cell is managed by these gates. The weights (Wi, Wf, Wo) and biases (bi, bf, bo) that link the gates to the input (xt) and the preceding hidden state (ht−1) are their parameters. Both the current state (Ct) and the prior state (Ct−1) of the memory cell exist. The current state and the output gate determine the cell’s output (ht).
3.2. Support Vector Machine (SVM)
Developed by Vapnik, the SVM is a class of machine learning techniques that can handle both classification and regression tasks [73]. Regression using SVMs is referred to in the literature as support vector regression (SVR) [74,75]. Finding a function that can roughly represent the relationship between the input x and the output y(x) is the aim of SVR. Figure 4 shows the SVR architecture.
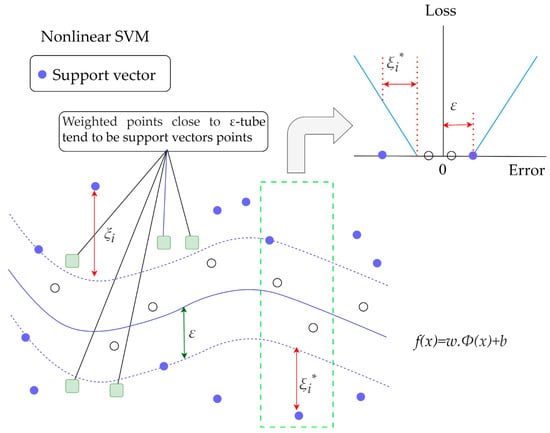
Figure 4.
Setting up the configuration for support vector regression.
In this study, the input vectors (x) are the historical SR values, while the output values (y) are the forecast values. The input–output data set for SVR is represented by (x,y), where x is the input vector and y is the output value. The function that SVR tries to estimate has the following form:
where ϕ is a nonlinear function, w is the weight vector and b is the deviation.
3.3. Multilayer Artificial Neural Networks (MLANN)
In hydraulic and hydrological engineering, artificial neural network modeling is a comparatively well-known and often utilized technique. It is essentially a “black box” technique that uses a particular collection of nonlinear basis functions to connect input and output data. Because artificial neural networks (ANNs) are nonlinear statistical techniques, they can be applied to solve issues that are not amenable to standard statistical and mathematical techniques [76,77,78]. Figure 5 displays the structure of the MLANN model.
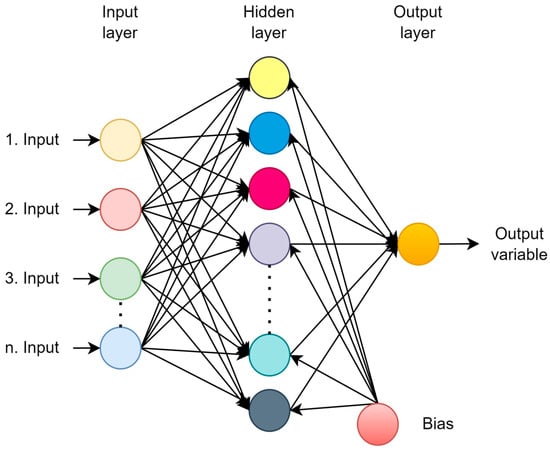
Figure 5.
The MLANN structure.
3.4. Aggregation Model Based on Sugeno λ-Measure and Sugeno Integral (SLSM)
Combining multiple forecasting models through aggregation can mitigate the variability in forecasting errors and improve the overall forecasting accuracy. In this context, Sugeno integral is implemented to amalgamate the different sources of information while reducing the level of uncertainty in the decision-making stage. The proposed Sugeno integral is applied to fuse the outputs of individual modes within a ML model designed for irradiance prediction. To achieve this, the Sugeno integral will be used as an aggregation operator to combine the output of each model as shown in Figure 6. This will enable the interaction between the forecasting outputs aggregated via a fuzzy measure. This aggregation function can identify the highest level of agreement within the different forecasting outcomes, making the most of the strengths of each individual model.
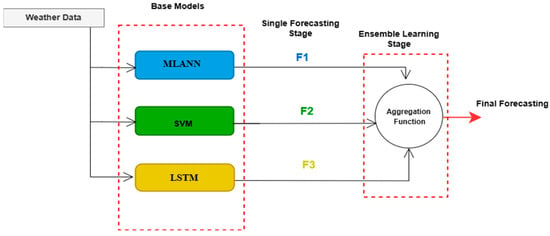
Figure 6.
The SLSM structure.
Sugeno λ-Measure
In this work, Sugeno λ-measure applies to measure the worth of each model accuracy.
X represents the proposed individual predictive model, so let where n = 3. The fuzzy measure is represented by the function for each and the possible combination of subsets of the universe of discourse . The properties of the aforementioned fuzzy measure are stated in as following [79]: , and represents the measures of an empty set and a combination of the all sets represents monotonicity property.
represents the possible subsets and the combined subsets.
represents the values of fuzzy measures where .
The process of obtaining the fuzzy measure starts with calculating Equestion (9) by arbitrarily selecting fuzzy densities that associated with each subset/model. This can be followed by calculating the combined subsets fuzzy measures Equation (8).
The Sugeno integral covers the ideas of weighted minimum and maximum, allowing for the evaluation of the importance of each model via the utilization of fuzzy measures. The fuzzy integral involves determining the highest level of similarity between the target and the predicted values.
f(x) is a function in the universe of discourse , and the Sugeno integral (S) of f:X → [0, 1] with respect to the fuzzy measure is represented by:
where is reorder the model accuracy. The information will be permuted where the high model accuracy has the most significant influence on the final model, gradually moving to less impact with the lowest model accuracy.
4. Metrics for Performance Evaluation of Models
This section explains the statistical metrics that were used to evaluate the models’ performance for SR prediction. The coefficient of determination (R2), root mean square error (RMSE), and mean absolute error (MAE) are the metrics [80]. These measures show how well the models fit the observed data, as well as how accurate and reliable their forecasts are. High R2 values near to 1, as well as low RMSE and MAE values, indicate high model performance. The metrics’ formulas are as follows:
The following symbols are used in the formulas for the statistical metrics: SRmeasured is the observed SR values from the data; SRpredicted is the predicted SR values from the models; is the mean of the observed SR values; n is the number of data points. To compare the models, this study also used a Taylor diagram and Violin plot [81]. These plots show the correlation, bias, and standard deviation of the models relative to the observations.
5. Modeling Development Procedure
5.1. Model Implementation
The proposed methodology follows these steps: (i) data collection; analysis and preprocessing of data, (ii) training network of neural networks. The latter involves the selection of architecture, training functions, training algorithms, and network hyperparameters, (iii) testing the trained network; and using the trained neural network for simulation and prediction [82]. In this study, three different models, LSTM, MLANN, and SVM, were used for SR forecasting. The proposed forecasting models were developed using MATLAB (R2021a), Statistics and Machine Learning Toolbox, and Deep Learning Toolbox. The models were run using a laptop computer with a 12th Generation Intel (R) Core (TM), i7-12700H, 2.30 GHz, 64 GB RAM, and a 6 GB graphics card. The data were collected from various meteorological parameters, including air temperature, cloud opacity, direct horizontal irradiance (DHI), direct normal irradiance (DNI), global horizontal irradiance (GHI), precipitable water, relative humidity, surface pressure, wind direction at 10 m, wind speed at 10 m, and daily albedo. The data for these parameters were provided hourly between 2013 and 2020 from NASA POWER and SOLCAST [49,52]. The dataset was divided into a training set comprising 80% of the data (57,253 data) and a test set with 20% of the data (14,313 data). Statistical information about the data is given in Table 2. The ultimate goal is to predict a critical parameter, ALLSKY_SFC_SW_DWN (all-sky surface shortwave downward irradiance), which plays a crucial role in solar energy system performance and planning.

Table 2.
Statistical information of data, W/m2.
5.2. Model Architecture
SR is estimated using input data from hourly timesteps and the prediction results are compared with the actual hourly data. The hyper parameters of the LSTM model are; ‘GradientThreshold’: 1, ‘InitialLearnRate’: 0.05, ‘Learn Rate Schedule’: ‘piecewise’, ‘Learn Rate Drop Period’: 125 and ‘Learn Rate Drop Factor’: 0.2. The proposed LSTM is implemented by MATLAB-written scripts, and trained using adaptive moment estimation (Adam) with 300 epochs and a maximum of 10 hidden layers are designed. The proposed SVM is designed by using Lagrangian multipliers and polynomial kernel function to find the optimal decision boundary. The polynomial Kernel function transforms the input data into a higher-dimensional spaces a way to enhance the forecasting decision capabilities and handle the high variability of the irradiance. The proposed MLANN is designed by adaptive learning rates to enhance the learning task during the training phase. Log-sigmoid transfer function and the Levenberg–Marquardt training algorithm were used in training the model. This is because this technique is more powerful than traditional gradient descent techniques [78]. Additionally, the data were normalized between 0.2 and 0.8, inspired by [83]. Single ML model flowchart diagram of the study is shown in Figure 7.
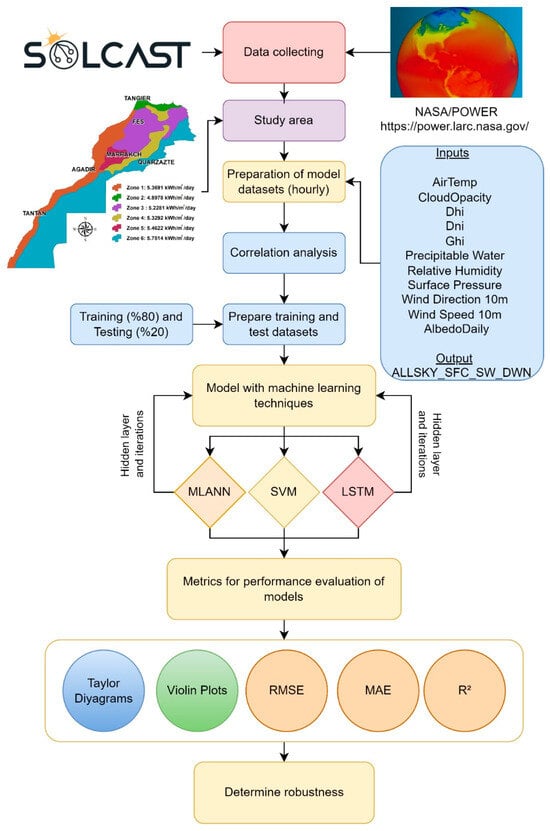
Figure 7.
Study flowchart diagram.
6. Results and Discussion
The performance of the three proposed models was evaluated by statistical indictors which are listed in this section. The RMSE and MAE values along with R2 are utilized for evaluating the designed models that belong to irradiance and meteorological data for different locations in Morocco. The results indicate that the LSTM model has good forecasting performance where errors measuring between predicted and actual values are generally small as shown in Table 3. For instance, LSTM model achieves RMSE values ranges between 25.38 W/m2 and 41.09 W/m2 for the data of the six sites. However, the proposed SVM and MLANN yield higher forecasting error with RMSE value ranges between 57.04 W/m2 to 70.10 W/m2, and 75.85 W/m2 to 80.64 W/m2, respectively, with the data of the same sites. Further, the mean values of LSTM model for the six sites were calculated and compared to those in the other two forecasting models. The comparison shows the LSTM’s superiority in predicting hourly irradiances. Comparing LSTM model to conventional ANN (i.e., MLANN) and ML techniques (i.e., SVM) in the solar irradiance forecasting showed the capability of LSTM model to learn from nonlinearity patterns in high variability irradiance data by capturing a long range of temporal sequence dependencies. Further, as shown in Table 3 and the scatter plots in Figure 8, Figure 9 and Figure 10, which are the results under all training and testing phases, the proposed LSTM model outperformed the SVM and MLANN, performing better generalization capability and less overfitting behavior, and accurately predicting irradiance data showing strong correlations between the predicted and actual data points.

Table 3.
Model results of the training and testing phase W/m2.
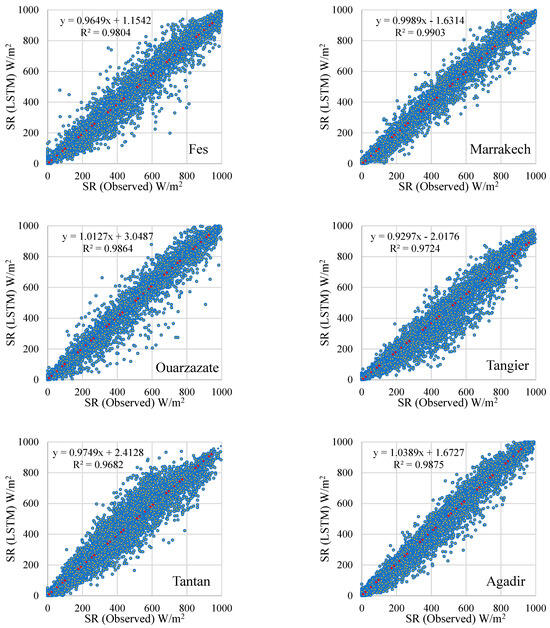
Figure 8.
Scatter plots of the LSTM model.
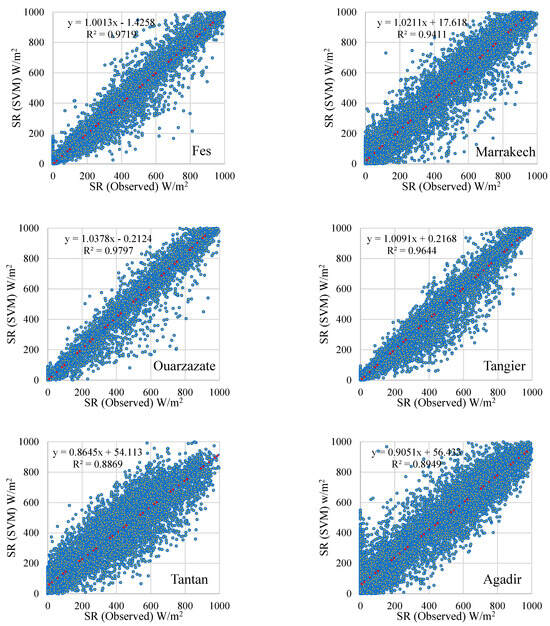
Figure 9.
Scatter plots of the SVM model.
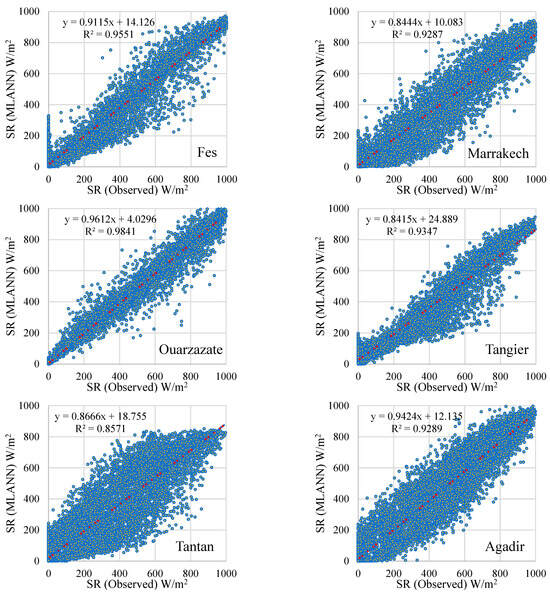
Figure 10.
Scatter plots of the MLANN model.
The findings regarding the performance evaluation of the models are included in Table 3 for all stations. The models used in the study are an example of the advancement of artificial intelligence techniques. The first ANN models were replaced by machine learning methods such as SVM, followed by deep learning methods such as LSTM architectures. When the results obtained are examined; considering the average values, the highest R2 values are in the LSTM model, followed by SVM and ANN. Similarly, RMSE and MAE values are compatible with this ranking. The scatter plots of the models are shown in Figure 8, Figure 9 and Figure 10.
As a way of validation, advanced statistical analyses were considered to the proposed LSTM by applying the violin plot, Taylor diagram, and Kruskal–Wallis (KW) test for predictive accuracy. As can be seen in the violin plot in Figure 11, the correspondence distribution of predicted data with actual data were examined. The comparison of predicted and actual data distributions showed that effectiveness of the proposed LSTM to mimic the peaks, valleys, and tails of the density curve of the actual data. The proposed LSTM model is also validated by the Taylor diagram in Figure 11 that represented the correlation between the predicted and actual data. Figure 11 showed a way of graphically summarizing how closely the patterns of the proposed LSTM predicted data (the blue cross sign) match the actual data (the red circle sign) with correlation confections of 98% to 99% for the six sites.
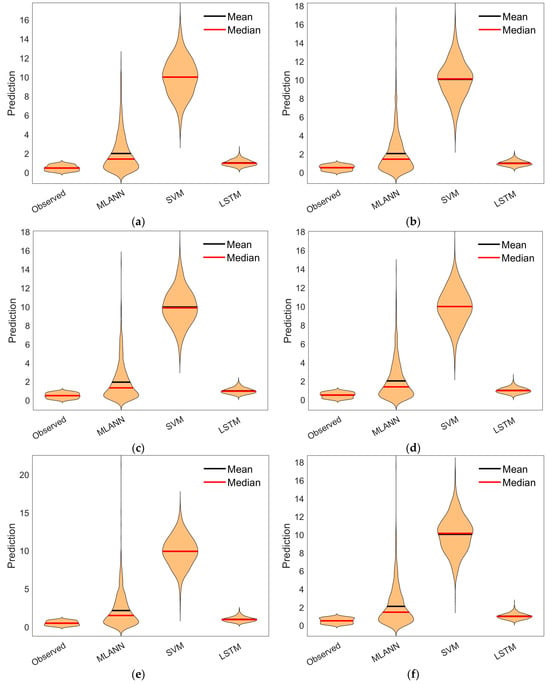
Figure 11.
Violin graphs; for Agadir (a), Fes (b), Marrakech (c), Ouarzazate (d), Tangier (e), and Tantan (f).
Violin diagrams are essentially based on the formal description of statistical quantities. In the study, normalization was made to see the change between shapes. From this perspective, the best fit to the observed data is observed in the LSTM model at all stations, while the average and median values are larger than the data observed in the SVM model. According to the correlation and RMSD relationship between the observation and models, the results were also examined using the Taylor diagram (Figure 12).
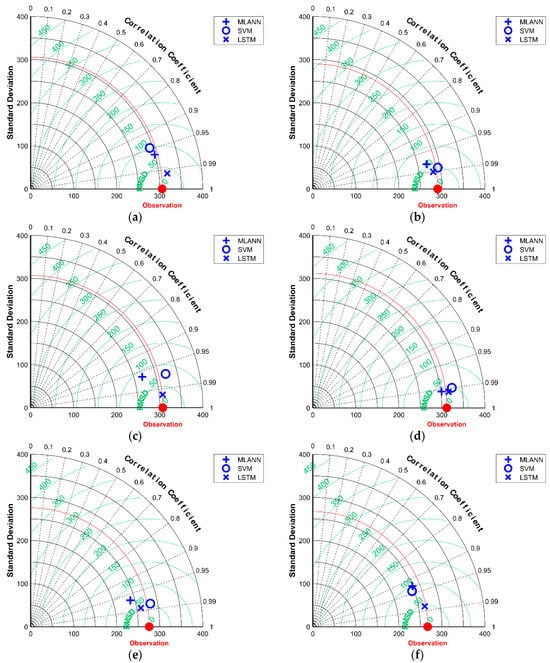
Figure 12.
Taylor diagrams; for Agadir (a), Fes (b), Marrakech (c), Ouarzazate (d), Tangier (e), and Tantan (f).
In Figure 12, Taylor diagrams are positioned at a point on the standard deviation axes according to correlation and RMSD values, and comparisons are made by taking into account the proximity of this point to the observed data. The graphs show that the models give very close results at the Fes, Ouarzazate, and Tangier stations, but LSTM is more successful than SVM and MLANN in terms of closeness to the data observed at other stations.
To further validate the model, the proposed LSTM was examined by statistical indicators to receive a proper evaluation of the model’s performance. The Kruskal–Wallis (KW) test is a nonparametric test that was employed to compare the distributions of the predicted and actual data, the work hypothesis was formulated as follows [84].
H0: the two distributions are different; H1: the two distributions are identical.
The statistic value is calculated as follows:
where C: the sample number, : the observation number in ith sample, : the ranks sum in ith sample, and : observations number.
As shown in Table 4, The KW test was performed at 95% confidence interval where the p-values indicate that H0 is significantly rejected, and distribution of the predicted and actual models is identical. Likewise, the p-values of the KW test indicate that we reject H0 and accept the alternative hypothesis for the six sites while showing the generalization capability of the proposed LSTM model.

Table 4.
KW test results for LSTM model.
The implementation of the proposed aggregation-based model (SLSM) developed with the fuzzy Sugeno integral-built MATLAB function. The obtained RMSE measures of the proposed SLSM are shown in Table 5 for the six different solar irradiance profiles. The RMSE values range between 16.09 W/m2 and 22.67 W/m2 for forecasting the highly fluctuating irradiance. Comparing the performance of the proposed SLSM with the proposed individual models for all sites, the proposed SLSM performed the best of all the models (e.g., LSTM, SVM, MLANN), achieving a high accuracy with an average RMSE of 20.16 W/m2.

Table 5.
The RMSE results for the SLSM model W/m2.
To visualize the performance of the four proposed prediction models, Figure 13 shows the comparison of the predicted SR obtained by the proposed models with the real measurements of SR for the six sites for January 2014. The results show that the SLSM performance is significantly stable and superior for the different SR profiles. Most of the night-time irradiance measurements were zero or ideally close to zero; however, errors may occur, which are associated with the noise or failure in the sensor readings. Dealing with errors caused by noise or sensor failures in night-time irradiance measurements requires careful analysis and appropriate techniques.
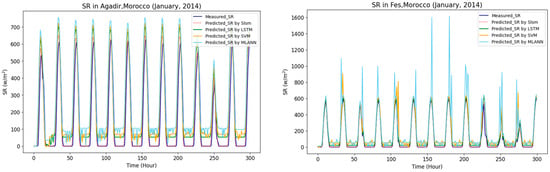
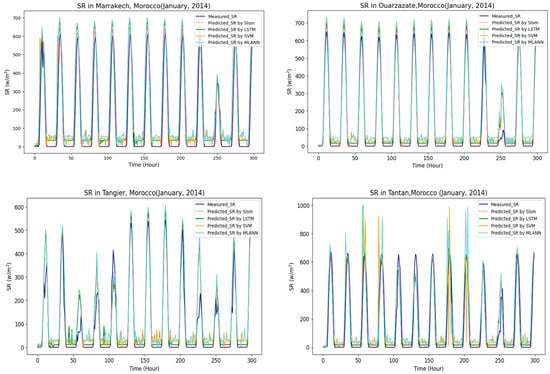
Figure 13.
The performance of the four proposed prediction models for the six sites, January 2014.
Additionally, the proposed model was further tested with data covering different months. The predicted hourly SR for the month of April 2016 is shown in Figure 14. The months of January and April can convey data and climate information for different seasons and cities in Morocco. The results showed that the proposed SLSM is superior compared to the other models. It also displayed good generalization and satiability capabilities when interaction with different data. This indicates that, in addition to aggerating data, SLSM also had a comprehension capture of the patterning within different data and lower prediction errors when faced with data from a variety of seasons. The proposed SLSM demonstrated an effective strategy for reliable forecasting by capturing the high variability and seasonality patterns in the irradiance dataset. The SLSM model’s superior performance is likely due to the idea of combining multiple forecasting models and aggregating the interaction between the predicted values of these individual models. This is also clearly shown when the model was validated by data across various seasons and exhibited lower prediction errors.
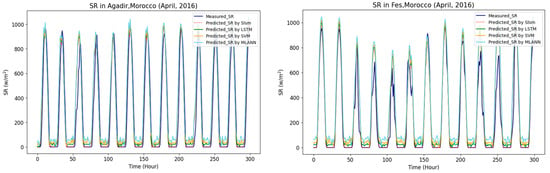
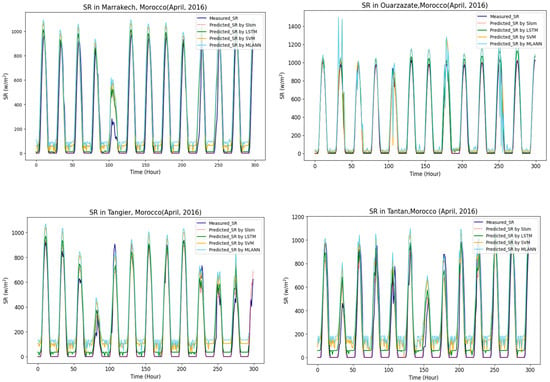
Figure 14.
The performance of the four proposed prediction models for the six sites, April 2016.
7. Conclusions
In this study, the SR estimation was carried out using LSTM, SVM, and MLANN approaches. For SR estimation, 10 hydro-meteorological parameters and various reflectance values obtained by remote sensing techniques from six stations in Morocco (Tantan, Fes, Agadir, Marrakesh, Ouarzazate, and Tangier) were used, and the main findings of the current research are as follows:
- The results were evaluated using the Taylor diagrams, violin plots, and the error criteria of RMSE, MAE, and R2, and it was determined that the method that best predicted the observed values was LSTM (mean, RMSE: 41.05, MAE: 21.99, R2: 0.98). SVM and ANN come after LSTM. While the advantage of the LSTM model is that it makes predictions with less error due to its integration with the learn-and-forget structure and optimization techniques. It is also more complex than other methods due to its structure consisting of hyper parameters.
- The robustness of the model’s performance was also assessed using Kruskal–Wallis (KW) tests, which were used to confirm the stability of the suggested LSTM. The KW test confirmed at 95% confidence level that the distribution of the predicted and actual models were the same.
- The investigation discovered that predicting accuracy can be greatly increased by connecting the model outputs with aggregation techniques. The hybrid model was used by integrating the prediction outputs of LSTM, SVM, and MLANN with the Sugeno λ-measure and the Sugeno integral named (SLSM). SLSM improved prediction accuracy with an improvement of 11.7 w/m2 in reducing irregularities associated with SR data.
- Finally, these results proved that the LSTM model is applicable, valid, and an alternative for SR prediction in Morocco, which has tropical and subtropical desert climate zones.
The six main limitations of this study can be listed as follows: (i) use of data obtained for six stations to represent Morocco, (ii) use of daily data from 2013 to 2020, (iii) use of correlation analysis in input selection, (iv) use of three different machine learning methods, (v) use of visual comparison criteria (Violin, Taylor) as well as performance metrics, and (vi) that KW testing was used to compare the distributions of predicted and actual data.
Author Contributions
Conceptualization, A.M. and V.D.; methodology, V.D., A.M. and N.O.; validation, A.M., N.O., O.O. and V.D.; visualization, O.O., V.D. and A.M.; resources, A.M., N.O., O.O. and V.D.; writing—original draft preparation, A.M., N.O., O.O., V.D. and T.W.; editing, A.M., N.O., O.O. and T.W.; funding acquisition, T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy considerations. Requests for access to the data will be considered and facilitated for further research purposes.
Acknowledgments
The authors would like to thank NASA POWER and SOLCAST and their employees for the data they provided.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, K.; Koike, T.; Ye, B. Improving Estimation of Hourly, Daily, and Monthly Solar Radiation by Importing Global Data Sets. Agric. For. Meteorol. 2006, 137, 43–55. [Google Scholar] [CrossRef]
- Jahani, B.; Dinpashoh, Y.; Raisi Nafchi, A. Evaluation and Development of Empirical Models for Estimating Daily Solar Radiation. Renew. Sustain. Energy Rev. 2017, 73, 878–891. [Google Scholar] [CrossRef]
- Asl, S.J.; Khorshiddoust, A.M.; Dinpashoh, Y.; Sarafrouzeh, F. Frequency Analysis of Climate Extreme Events in Zanjan, Iran. Stoch. Environ. Res. Risk Assess. 2013, 27, 1637–1650. [Google Scholar] [CrossRef]
- Jhajharia, D.; Kumar, R.; Dabral, P.P.; Singh, V.P.; Choudhary, R.R.; Dinpashoh, Y. Reference Evapotranspiration under Changing Climate over the Thar Desert in India. Meteorol. Appl. 2015, 22, 425–435. [Google Scholar] [CrossRef]
- Dinpashoh, Y.; Jahanbakhsh-Asl, S.; Rasouli, A.A.; Foroughi, M.; Singh, V.P. Impact of Climate Change on Potential Evapotranspiration (Case Study: West and NW of Iran). Theor. Appl. Climatol. 2019, 136, 185–201. [Google Scholar] [CrossRef]
- Jahani, B.; Mohammadi, A.S.; Albaji, M. Impact of Climate Change on Crop Water and Irrigation Requirement (Case Study: Eastern Dez Plain, Iran). Pol. J. Nat. Sci. 2016, 31, 151–167. [Google Scholar]
- Mohammadi, K.; Mostafaeipour, A.; Dinpashoh, Y.; Pouya, N. Electricity Generation and Energy Cost Estimation of Large-Scale Wind Turbines in Jarandagh, Iran. J. Energy 2014, 2014, 613681. [Google Scholar] [CrossRef]
- Demirhan, H.; Atilgan, Y.K. New Horizontal Global Solar Radiation Estimation Models for Turkey Based on Robust Coplot Supported Genetic Programming Technique. Energy Convers. Manag. 2015, 106, 1013–1023. [Google Scholar] [CrossRef]
- Şen, Z. Solar Energy Fundamentals and Modeling Techniques: Atmosphere, Environment, Climate Change and Renewable Energy; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–276. [Google Scholar] [CrossRef]
- Khare, V.; Nema, S.; Baredar, P. Solar–Wind Hybrid Renewable Energy System: A Review. Renew. Sustain. Energy Rev. 2016, 58, 23–33. [Google Scholar] [CrossRef]
- Liu, D.L.; Scott, B.J. Estimation of Solar Radiation in Australia from Rainfall and Temperature Observations. Agric. For. Meteorol. 2001, 106, 41–59. [Google Scholar] [CrossRef]
- Das, A.; Park, J.-K.; Park, J.-H. Estimation of Available Global Solar Radiation Using Sunshine Duration over South Korea. J. Atmos. Sol.-Terr. Phys. 2015, 134, 22–29. [Google Scholar] [CrossRef]
- Almorox, J. Estimating Global Solar Radiation from Common Meteorological Data in Aranjuez, Spain. Turk. J. Phys. 2011, 35, 53–64. [Google Scholar] [CrossRef]
- Angstrom, A. Solar and Terrestrial Radiation. Report to the International Commission for Solar Research on Actinometric Investigations of Solar and Atmospheric Radiation. Q. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Hossain, F.M.A.; Ali, M.K. Relation between Individual and Society. Open J. Soc. Sci. 2014, 02, 130–137. [Google Scholar] [CrossRef][Green Version]
- Hargreaves, G.H.; Asce, F.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Mendyl, A.; Mabasa, B.; Bouzghiba, H.; Weidinger, T. Calibration and Validation of Global Horizontal Irradiance Clear Sky Models against McClear Clear Sky Model in Morocco. Appl. Sci. 2023, 13, 320. [Google Scholar] [CrossRef]
- Mendyl, A.; Gandhi, A.; Musyimi, P.K.; Székely, B.; Weidinger, T. Comparative Analysis of Wind and Solar Energy Potential from Differnet Climate Regions, Case Studies of Morocco, India and Kenya. In Proceedings of the EGU22, the 24th EGU General Assembly, Vienna, Austria, 23–27 May 2022. [Google Scholar] [CrossRef]
- Chen, R.; Ersi, K.; Yang, J.; Lu, S.; Zhao, W. Validation of Five Global Radiation Models with Measured Daily Data in China. Energy Convers. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mohammadi, K.; Khorasanizadeh, H.; Yee, P.L.; Lee, M.; Petković, D.; Zalnezhad, E. Estimating the Diffuse Solar Radiation Using a Coupled Support Vector Machine–Wavelet Transform Model. Renew. Sustain. Energy Rev. 2016, 56, 428–435. [Google Scholar] [CrossRef]
- López, G.; Batlles, F.J.; Tovar-Pescador, J. Selection of Input Parameters to Model Direct Solar Irradiance by Using Artificial Neural Networks. Energy 2005, 30, 1675–1684. [Google Scholar] [CrossRef]
- Benghanem, M.; Mellit, A.; Alamri, S.N. ANN-Based Modelling and Estimation of Daily Global Solar Radiation Data: A Case Study. Energy Convers. Manag. 2009, 50, 1644–1655. [Google Scholar] [CrossRef]
- Mohandes, M.A. Modeling Global Solar Radiation Using Particle Swarm Optimization (PSO). Sol. Energy 2012, 86, 3137–3145. [Google Scholar] [CrossRef]
- Vakili, M.; Sabbagh-Yazdi, S.R.; Khosrojerdi, S.; Kalhor, K. Evaluating the Effect of Particulate Matter Pollution on Estimation of Daily Global Solar Radiation Using Artificial Neural Network Modeling Based on Meteorological Data. J. Clean. Prod. 2017, 141, 1275–1285. [Google Scholar] [CrossRef]
- Pinker, R.T.; Kustas, W.P.; Laszlo, I.; Moran, M.S.; Huete, A.R. Basin-Scale Solar Irradiance Estimates in Semiarid Regions Using GOES 7. Water Resour. Res. 1994, 30, 1375–1386. [Google Scholar] [CrossRef]
- Pinker, R.T.; Frouin, R.; Li, Z. A Review of Satellite Methods to Derive Surface Shortwave Irradiance. Remote Sens. Environ. 1995, 51, 108–124. [Google Scholar] [CrossRef]
- Pinker, R.T.; Zhang, B.; Dutton, E.G. Do Satellites Detect Trends in Surface Solar Radiation? Science 2005, 308, 850–854. [Google Scholar] [CrossRef] [PubMed]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL); 1 Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Posselt, R.; Mueller, R.W.; Stöckli, R.; Trentmann, J. Remote Sensing of Solar Surface Radiation for Climate Monitoring—The CM-SAF Retrieval in International Comparison. Remote Sens. Environ. 2012, 118, 186–198. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.K.; Sharma, J.D. Comparison of Regression and Artificial Neural Network Models for Estimation of Global Solar Radiations. Renew. Sustain. Energy Rev. 2015, 52, 1294–1299. [Google Scholar] [CrossRef]
- Kisi, O.; Alizamir, M.; Trajkovic, S.; Shiri, J.; Kim, S. Solar Radiation Estimation in Mediterranean Climate by Weather Variables Using a Novel Bayesian Model Averaging and Machine Learning Methods. Neural Process. Lett. 2020, 52, 2297–2318. [Google Scholar] [CrossRef]
- Şahin, M. Comparison of Modelling ANN and ELM to Estimate Solar Radiation over Turkey Using NOAA Satellite Data. Int. J. Remote Sens. 2013, 34, 7508–7533. [Google Scholar] [CrossRef]
- Polo, J.; Antonanzas-Torres, F.; Vindel, J.M.; Ramirez, L. Sensitivity of Satellite-Based Methods for Deriving Solar Radiation to Different Choice of Aerosol Input and Models. Renew. Energy 2014, 68, 785–792. [Google Scholar] [CrossRef]
- Ahmad, M.J.; Tiwari, G.N. Solar Radiation Models—A Review. Int. J. Energy Res. 2011, 35, 271–290. [Google Scholar] [CrossRef]
- Belmahdi, B.; Louzazni, M.; Marzband, M.; Bouardi, A. El Global Solar Radiation Forecasting Based on Hybrid Model with Combinations of Meteorological Parameters: Morocco Case Study. Forecasting 2023, 5, 172–195. [Google Scholar] [CrossRef]
- Benmouiza, K.; Cheknane, A. Forecasting Hourly Global Solar Radiation Using Hybrid K-Means and Nonlinear Autoregressive Neural Network Models. Energy Convers. Manag. 2013, 75, 561–569. [Google Scholar] [CrossRef]
- Lauret, P.; Voyant, C.; Soubdhan, T.; David, M.; Poggi, P. A Benchmarking of Machine Learning Techniques for Solar Radiation Forecasting in an Insular Context. Sol. Energy 2015, 112, 446–457. [Google Scholar] [CrossRef]
- VOSviewer. Welcome to VOSviewer. Available online: https://www.vosviewer.com/ (accessed on 12 December 2023).
- van Eck, N.J.; Waltman, L. Software Survey: VOSviewer, a Computer Program for Bibliometric Mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef] [PubMed]
- Yacef, R.; Mellit, A.; Belaid, S.; Şen, Z. New Combined Models for Estimating Daily Global Solar Radiation from Measured Air Temperature in Semi-Arid Climates: Application in Ghardaïa, Algeria. Energy Convers. Manag. 2014, 79, 606–615. [Google Scholar] [CrossRef]
- Bayram, S.; Çıtakoğlu, H. Modeling Monthly Reference Evapotranspiration Process in Turkey: Application of Machine Learning Methods. Environ. Monit. Assess. 2023, 195, 67. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Salazar, G.A.; Zhu, Z.; Gong, W. Solar Radiation Prediction Using Different Techniques: Model Evaluation and Comparison. Renew. Sustain. Energy Rev. 2016, 61, 384–397. [Google Scholar] [CrossRef]
- Ozoegwu, C.G. Artificial Neural Network Forecast of Monthly Mean Daily Global Solar Radiation of Selected Locations Based on Time Series and Month Number. J. Clean. Prod. 2019, 216, 1–13. [Google Scholar] [CrossRef]
- Guermoui, M.; Melgani, F.; Gairaa, K.; Mekhalfi, M.L. A Comprehensive Review of Hybrid Models for Solar Radiation Forecasting. J. Clean. Prod. 2020, 258, 120357. [Google Scholar] [CrossRef]
- Allouhi, A.; Kousksou, T.; Jamil, A.; El Rhafiki, T.; Mourad, Y.; Zeraouli, Y. Economic and Environmental Assessment of Solar Air-Conditioning Systems in Morocco. Renew. Sustain. Energy Rev. 2015, 50, 770–781. [Google Scholar] [CrossRef]
- Allouhi, A.; Jamil, A.; Kousksou, T.; El Rhafiki, T.; Mourad, Y.; Zeraouli, Y. Solar Domestic Heating Water Systems in Morocco: An Energy Analysis. Energy Convers. Manag. 2015, 92, 105–113. [Google Scholar] [CrossRef]
- Yang, D.; Bright, J.M. Worldwide Validation of 8 Satellite-Derived and Reanalysis Solar Radiation Products: A Preliminary Evaluation and Overall Metrics for Hourly Data over 27 Years. Sol. Energy 2020, 210, 3–19. [Google Scholar] [CrossRef]
- Bright, J.M. Solcast: Validation of a Satellite-Derived Solar Irradiance Dataset. Sol. Energy 2019, 189, 435–449. [Google Scholar] [CrossRef]
- SOLCAST|Solar Api and Solar Weather Forecasting Tool. Available online: https://solcast.com/ (accessed on 14 October 2023).
- Gueymard, C.A. REST2: High-Performance Solar Radiation Model for Cloudless-Sky Irradiance, Illuminance, and Photosynthetically Active Radiation—Validation with a Benchmark Dataset. Sol. Energy 2008, 82, 272–285. [Google Scholar] [CrossRef]
- Sparks, A. Nasapower: A NASA POWER Global Meteorology, Surface Solar Energy and Climatology Data Client for R. J. Open Source Softw. 2018, 3, 1035. [Google Scholar] [CrossRef]
- NASA/POWER. The POWER Project. Available online: https://power.larc.nasa.gov/ (accessed on 12 November 2023).
- Al-Kilani, M.R.; Rahbeh, M.; Al-Bakri, J.; Tadesse, T.; Knutson, C. Evaluation of Remotely Sensed Precipitation Estimates from the NASA POWER Project for Drought Detection Over Jordan. Earth Syst. Environ. 2021, 5, 561–573. [Google Scholar] [CrossRef]
- Kheyruri, Y.; Sharafati, A. Spatiotemporal Assessment of the NASA POWER Satellite Precipitation Product over Different Regions of Iran. Pure Appl. Geophys. 2022, 179, 3427–3439. [Google Scholar] [CrossRef]
- Jed, M.; Ihaddadene, N.; El Hacen Jed, M.; Ihaddadene, R.; El Bah, M. Validation of the Accuracy of NASA Solar Irradiation Data for Four African Regions. Int. J. Sustain. Dev. Plan. 2022, 17, 29–39. [Google Scholar] [CrossRef]
- Duarte, Y.C.N.; Sentelhas, P.C. NASA/POWER and Daily Gridded Weather Datasets—How Good They Are for Estimating Maize Yields in Brazil? Int. J. Biometeorol. 2020, 64, 319–329. [Google Scholar] [CrossRef] [PubMed]
- Kadhim Tayyeh, H.; Mohammed, R. Analysis of NASA POWER Reanalysis Products to Predict Temperature and Precipitation in Euphrates River Basin. J. Hydrol. 2023, 619, 129327. [Google Scholar] [CrossRef]
- Tan, M.L.; Armanuos, A.M.; Ahmadianfar, I.; Demir, V.; Heddam, S.; Al-Areeq, A.M.; Abba, S.I.; Halder, B.; Cagan Kilinc, H.; Yaseen, Z.M. Evaluation of NASA POWER and ERA5-Land for Estimating Tropical Precipitation and Temperature Extremes. J. Hydrol. 2023, 624, 129940. [Google Scholar] [CrossRef]
- Bandira, P.N.A.; Tan, M.L.; Teh, S.Y.; Samat, N.; Shaharudin, S.M.; Mahamud, M.A.; Tangang, F.; Juneng, L.; Chung, J.X.; Samsudin, M.S. Optimal Solar Farm Site Selection in the George Town Conurbation Using GIS-Based Multi-Criteria Decision Making (MCDM) and NASA POWER Data. Atmosphere 2022, 13, 2105. [Google Scholar] [CrossRef]
- Rodrigues, G.C.; Braga, R.P. Estimation of Daily Reference Evapotranspiration from NASA POWER Reanalysis Products in a Hot Summer Mediterranean Climate. Agronomy 2021, 11, 2077. [Google Scholar] [CrossRef]
- Azeroual, M.; Makrini, E.L.; El Moussaoui, H.; El Markhi, H. Renewable Energy Potential and Available Capacity for Wind and Solar Power in Morocco Towards 2030. J. Eng. Sci. Technol. Rev. 2018, 11, 189–198. [Google Scholar] [CrossRef]
- ONEE—Branche Eau. Available online: http://www.onep.ma/ (accessed on 14 October 2023).
- Richts, C. The Moroccan Solar Plan—A Comparative Analysis of CSP and PV Utilization until 2020; University of Kassel: Kassel, Germany, 2012; 113p, Available online: http://www.uni-kassel.de/eecs/fileadmin/datas/fb16/remena/theses/batch2 (accessed on 14 October 2023).
- Yu, Y.C.; Shi, J.; Wang, T.; Letu, H.; Zhao, C. All-Sky Total and Direct Surface Shortwave Downward Radiation (SWDR) Estimation from Satellite: Applications to MODIS and Himawari-8. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102380. [Google Scholar] [CrossRef]
- Kolsi, L.; Al-Dahidi, S.; Kamel, S.; Aich, W.; Boubaker, S.; Khedher, N.B. Prediction of Solar Energy Yield Based on Artificial Intelligence Techniques for the Ha’il Region, Saudi Arabia. Sustainability 2023, 15, 774. [Google Scholar] [CrossRef]
- Teklay, A.; Dile, Y.T.; Asfaw, D.H.; Bayabil, H.K.; Sisay, K. Impacts of Land Surface Model and Land Use Data on WRF Model Simulations of Rainfall and Temperature over Lake Tana Basin, Ethiopia. Heliyon 2019, 5, E02469. [Google Scholar] [CrossRef]
- El Khalki, E.M.; Tramblay, Y.; Amengual, A.; Homar, V.; Romero, R.; Saidi, M.E.M.; Alaou, M. Validation of the AROME, ALADIN and WRF Meteorological Models for Flood Forecasting in Morocco. Water 2020, 12, 437. [Google Scholar] [CrossRef]
- ArunKumar, K.E.; Kalaga, D.V.; Kumar, C.M.S.; Kawaji, M.; Brenza, T.M. Forecasting of COVID-19 Using Deep Layer Recurrent Neural Networks (RNNs) with Gated Recurrent Units (GRUs) and Long Short-Term Memory (LSTM) Cells. Chaos Solitons Fractals 2021, 146, 110861. [Google Scholar] [CrossRef] [PubMed]
- Canizo, M.; Triguero, I.; Conde, A.; Onieva, E. Multi-Head CNN–RNN for Multi-Time Series Anomaly Detection: An Industrial Case Study. Neurocomputing 2019, 363, 246–260. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, Long Short-Term Memory, Fully Connected Deep Neural Networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow Prediction Using an Integrated Methodology Based on Convolutional Neural Network and Long Short-Term Memory Networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef] [PubMed]
- Demir, M.E.; Çıtakoğlu, F. Design and Modeling of a Multigeneration System Driven by Waste Heat of a Marine Diesel Engine. Int. J. Hydrogen Energy 2022, 47, 40513–40530. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Smola, A.; Burges, C.; Drucker, H.; Golowich, S.; van Hemmen, L.; Muller, K.-R.M.M.; Schölkopf, B.S.; Vapnik, V. Regression Estimation with Support Vector Learning Machines; Physic Department, Technische Universität München: Munich, Germany, 1996; 78p. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial Neural Networks in Hydrology. II: Hydrologic Applications. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. IEEE Trans. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training Feedforward Networks with the Marquardt Algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Melin, P.; Mendoza, O.; Castillo, O. Face Recognition with an Improved Interval Type-2 Fuzzy Logic Sugeno Integral and Modular Neural Networks. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011, 41, 1001–1012. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of “goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Citakoglu, H.; Demir, V. Developing Numerical Equality to Regional Intensity–Duration–Frequency Curves Using Evolutionary Algorithms and Multi-Gene Genetic Programming. Acta Geophys. 2023, 71, 469–488. [Google Scholar] [CrossRef]
- Doğan, E.; Yüksel, İ.; Kişi, Ö. Estimation of Total Sediment Load Concentration Obtained by Experimental Study Using Artificial Neural Networks. Environ. Fluid Mech. 2007, 7, 271–288. [Google Scholar] [CrossRef]
- Kisi, O. Discussion of “Application of Neural Network and Adaptive Neuro-Fuzzy Inference Systems for River Flow Prediction”. Hydrol. Sci. J. 2010, 55, 1453–1454. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).