An Analysis for the Applicability of Global Precipitation Measurement Mission (GPM) IMERG Precipitation Data in Typhoons
Abstract
1. Introduction
2. Data and Methods
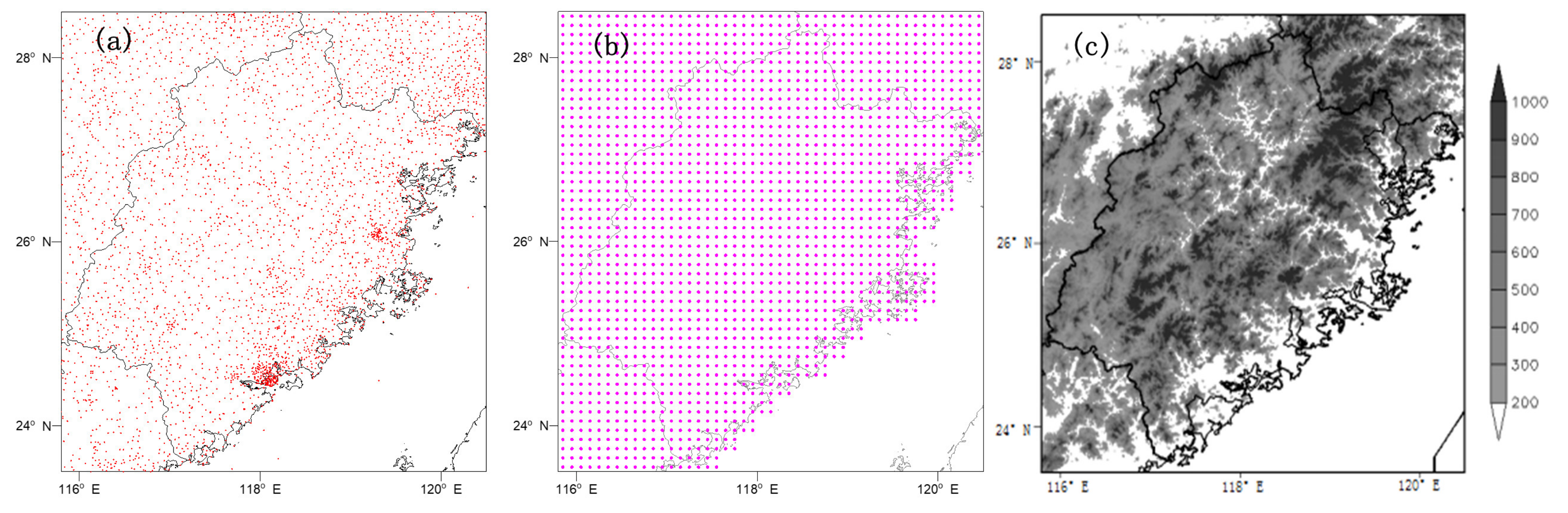
2.1. Data
2.2. Methods
3. Results and Discussion
3.1. Evaluation of the Satellite Precipitation Product on Different Time Scales
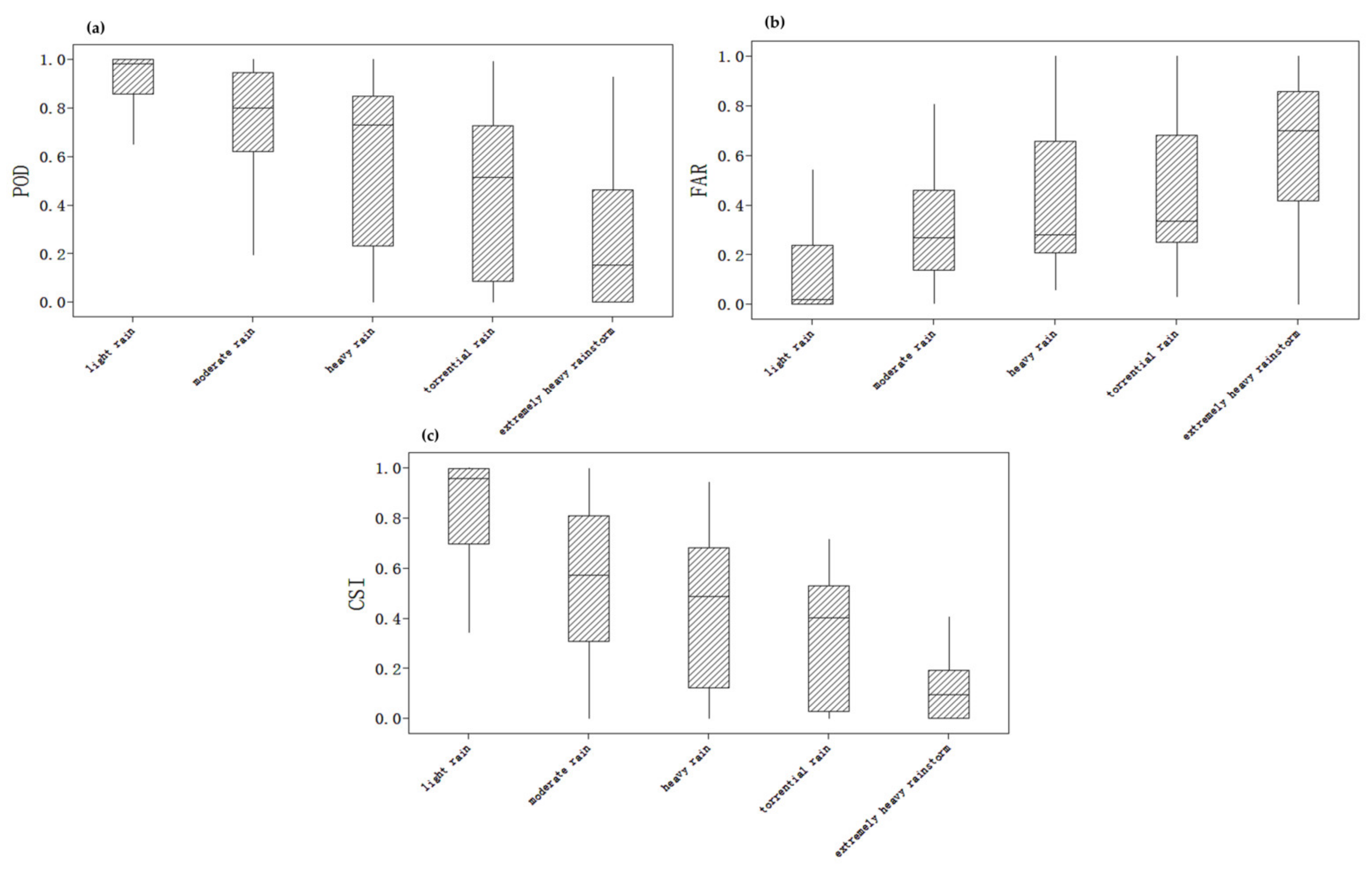
3.2. Evaluation of the Satellite Precipitation Product on Different Rainfall Intensity
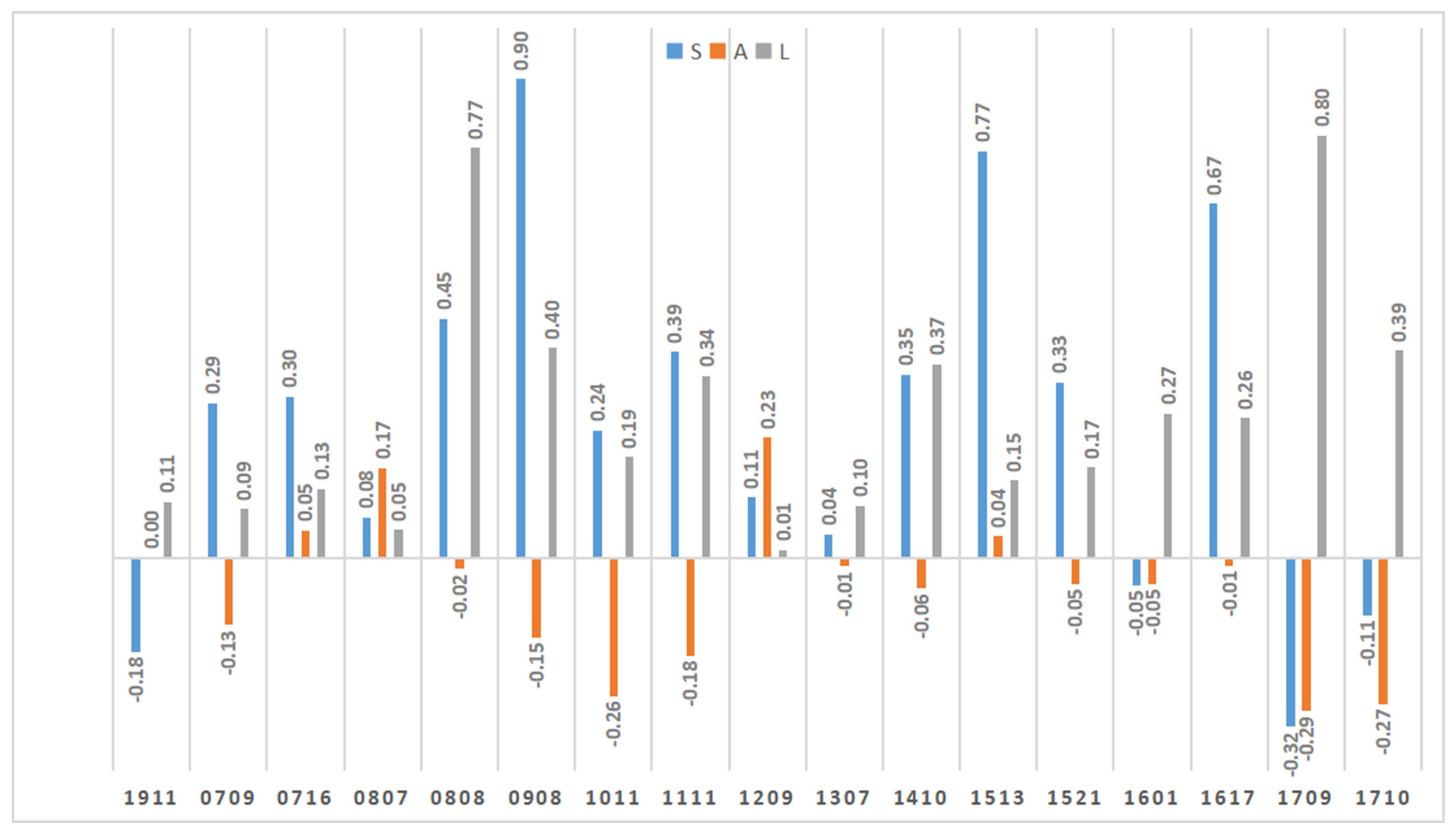
3.3. Spatial Assessment of Heavy Precipitation
3.3.1. Spatial Assessment of Process Heavy Precipitation
3.3.2. Spatial Assessment of Maximum Rainstorm Day
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Yang, B.; Stepanian, P. Comprehensive Evaluation of High-Resolution Satellite-Based Precipitation Products over China. Atmosphere 2016, 7, 6. [Google Scholar] [CrossRef]
- Wang, L.; Chen, R.; Song, Y. Research Review on Calculation Methods and Influential Factors on Areal Precipitation of Alpine Mountains. Plateau Meteorol. 2017, 36, 1546–1556. [Google Scholar]
- Groisman, P.Y.; Legates, D.R. Documenting and Detecting Long-Term Precipitation Trends: Where We Are and What Should Be Done. Clim. Change 1995, 31, 601–622. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, How Much of the Earth’s Surface Is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, Q.; Song, P.; Zhao, X.; Dou, C. Satellite retrieval of precipitation: An overview. Adv. Earth Sci. 2011, 26, 1162–1172. [Google Scholar]
- Liu, J.; Yin, Y.; Sun, X.; Ma, J.; Gao, Y. Multivariate statistical analysis of influence of underlying surface change on runoff. Water Resour. Prot. 2016, 32, 41–43. [Google Scholar]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early Assessment of Integrated Multi-Satellite Retrievals for Global Precipitation Measurement over China. Atmos. Res. 2016, 176, 121–133. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Hu, J.; Gebregiorgis, A.; Xue, X.; Zhang, X. Inter-Comparison of High-Resolution Satellite Precipitation Products over Central Asia. Remote Sens. 2015, 7, 7181–7211. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Amer. Meteor. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Jin, X.; Shao, H.; Zhang, C.; Yan, Y. The Applicability Evaluation of Three Satellite Products in Tianshan Mountains. J. Nat. Resour. 2016, 31, 2074–2085. [Google Scholar]
- Caracciolo, D.; Francipane, A.; Viola, F.; Noto, L.V.; Deidda, R. Performances of GPM Satellite Precipitation over the Two Major Mediterranean Islands. Atmos. Res. 2018, 213, 309–322. [Google Scholar] [CrossRef]
- Tang, G.; Wan, W.; Zeng, Z.; Guo, X.; Li, N.; Long, D.; Hong, Y. An Overview of the Global Precipition Measurement (GPM) Mission and It’s Latest Development. Remote Sens. Technol. Appl. 2015, 30, 607–615. [Google Scholar]
- Chen, F.; Li, X. Evaluation of IMERG and TRMM 3B43 Monthly Precipitation Products over Mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Li, N.; Tang, G.; Zhao, P.; Hong, Y.; Gou, Y.; Yang, K. Statistical Assessment and Hydrological Utility of the Latest Multi-Satellite Precipitation Analysis IMERG in Ganjiang River Basin. Atmos. Res. 2017, 183, 212–223. [Google Scholar] [CrossRef]
- Lu, M.; Wei, M. GPM Data Application Analysis of Vertical Structure of Typhoon ‘Mujigae’ Precipition. Remote Sens. Technol. Appl. 2017, 32, 904–912. [Google Scholar]
- Fang, M.; He, J.; Fu, Y.; Wang, D.; Zhu, M. Applicability Analysis of GPM Satellite Precipitation Data in Coastal Areas: A case in Sanya. Meteorlogical Sci. Technol. 2020, 48, 622–629. [Google Scholar]
- Yu, Z.; Ma, S.; Hu, X.; Yan, W. Analysis of Atmospheric Circulation, Cloud and Precipitation Characteristics of Typhoon ’Lekima’ based on Multi-source Data. J. Meteorol. Sci. 2020, 40, 41–52. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeor. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Li, J.; Hsu, K.-L.; AghaKouchak, A.; Sorooshian, S. Object-Based Assessment of Satellite Precipitation Products. Remote Sens. 2016, 8, 547. [Google Scholar] [CrossRef]
- Tan, J.; Petersen, W.A.; Tokay, A. A Novel Approach to Identify Sources of Errors in IMERG for GPM Ground Validation. J. Hydrometeorol. 2016, 17, 2477–2491. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Zeng, S.; Chen, X.; Wu, Z. Analysis of Soil and Water Loss in Fujian Province. Bull. Soil Water Conserv. 2017, 37, 169–175. [Google Scholar]
- Xu, D.; Zhou, J.; Lu, Y.; Pan, F. Evaluation on Applicability of TRMM Satellite Precipitation Product in the NuJiang River Basin. Res. Soil Water Conserv. 2019, 26, 240–244+251. [Google Scholar]
- Stunder, J.B. An Assessment of the Quality of Forecast Trajectories. J. Appl. Meteorol. 1996, 35, 1319–1331. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Kirstetter, P.-E.; Gourley, J.J.; Qi, Y.; Zhang, J.; Howard, K.; Hu, J.; Wang, J. Performance Evaluation of Radar and Satellite Rainfalls for Typhoon Morakot over Taiwan: Are Remote-Sensing Products Ready for Gauge Denial Scenario of Extreme Events? J. Hydrol. 2013, 506, 4–13. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Xu, C.-Y.; Yuan, L.; Yong, B.; Yan, S. Evaluating the Non-Stationary Relationship between Precipitation and Streamflow in Nine Major Basins of China during the Past 50 Years. J. Hydrol. 2011, 409, 81–93. [Google Scholar] [CrossRef]
- Wernli, H.; Paulat, M.; Hagen, M.; Frei, C. SAL—A Novel Quality Measure for the Verification of Quantitative Precipitation Forecasts. Mon. Weather Rev. 2008, 136, 4470–4487. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-Based Verification of Precipitation Forecasts. Part I: Methodology and Application to Mesoscale Rain Areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Yu, Y.; Bi, M.; Yan, Q.; Lin, H.; Feng, D.; Yu, F. Cause analysis and spatial test of milti-mode numerical prediction on regional rainstorms in Liaoning province. J. Meteorol. Envionment 2022, 38, 11–18. [Google Scholar]
- Yang, Y.; Tang, G.; Lei, X.; Hong, Y.; Yang, N. Verification and preliminary calibration on frontal rainstorm forecast of ECMWF model in Jiang Xi and near by areas. Meteorol. Disaster Reduct. Res. 2023, 46, 28–34. [Google Scholar]
- Yin, S.; Lin, X.; Yang, S. Characteristics of Rainstorm in Fujian Induced by Typhoon Passing through Taiwan Island. Trop. Cyclone Res. Rev. 2022, 11, 50–59. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, G.; Lei, X.; Hong, Y.; Yang, N. Can Satellite Precipitation Products Estimate Probable Maximum Precipitation: A Comparative Investigation with Gauge Data in the Dadu River Basin. Remote Sens. 2017, 10, 41. [Google Scholar] [CrossRef]





| Typhoon (Year) | Landfalling Time | Duration (h) | Landfalling Location | Landfalling Intensity (m/s) |
|---|---|---|---|---|
| Bailu (2019) | 23:00 UTC 24 August | 48 | Dongshan | 23 |
| Haitang (2017) | 19:00 UTC 30 July | 39 | Fuqing | 20 |
| Nesat (2017) | 22:00 UTC 29 July | 41 | Fuqing | 33 |
| Megi (2016) | 21:00 UTC 27 September | 80 | Quanzhou | 33 |
| Nepartak (2016) | 05:00 UTC 9 July | 62 | Quanzhou | 20 |
| Dujuan (2015) | 00:00 UTC 29 September | 55 | Putian | 28 |
| Soudelor (2015) | 14:00 UTC 8 August | 71 | Putian | 30 |
| Matmo (2014) | 07:00 UTC 23 July | 61 | Fuqing | 30 |
| Soulik (2013) | 08:00 UTC 13 July | 54 | Lianjiang | 30 |
| Saola (2012) | 23:00 UTC 2 August | 81 | Fuding | 25 |
| Nanmadol (2011) | 01:00 UTC 31 August | 125 | Huian | 18 |
| Fanapi (2010) | 23:00 UTC 19 September | 74 | Zhangpu | 35 |
| Morakot (2009) | 09:00 UTC 9 August | 69 | Xiapu | 33 |
| Fung-wong (2008) | 14:00 UTC 28 July | 81 | Fuqing | 33 |
| Kalmaegi (2008) | 10:00 UTC 18 July | 50 | Xiapu | 25 |
| Krosa (2007) | 07:00 UTC 7 October | 51 | Fuding | 33 |
| Sepat (2007) | 18:00 UTC 18 August | 71 | Huian | 33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, N.; Lin, X.; Guo, H. An Analysis for the Applicability of Global Precipitation Measurement Mission (GPM) IMERG Precipitation Data in Typhoons. Atmosphere 2023, 14, 1224. https://doi.org/10.3390/atmos14081224
Fan N, Lin X, Guo H. An Analysis for the Applicability of Global Precipitation Measurement Mission (GPM) IMERG Precipitation Data in Typhoons. Atmosphere. 2023; 14(8):1224. https://doi.org/10.3390/atmos14081224
Chicago/Turabian StyleFan, Nengzhu, Xiaohong Lin, and Hong Guo. 2023. "An Analysis for the Applicability of Global Precipitation Measurement Mission (GPM) IMERG Precipitation Data in Typhoons" Atmosphere 14, no. 8: 1224. https://doi.org/10.3390/atmos14081224
APA StyleFan, N., Lin, X., & Guo, H. (2023). An Analysis for the Applicability of Global Precipitation Measurement Mission (GPM) IMERG Precipitation Data in Typhoons. Atmosphere, 14(8), 1224. https://doi.org/10.3390/atmos14081224






