Assessment of NEX-GDDP-CMIP6 Downscale Data in Simulating Extreme Precipitation over the Huai River Basin
Abstract
:1. Introduction
2. Material and Methods
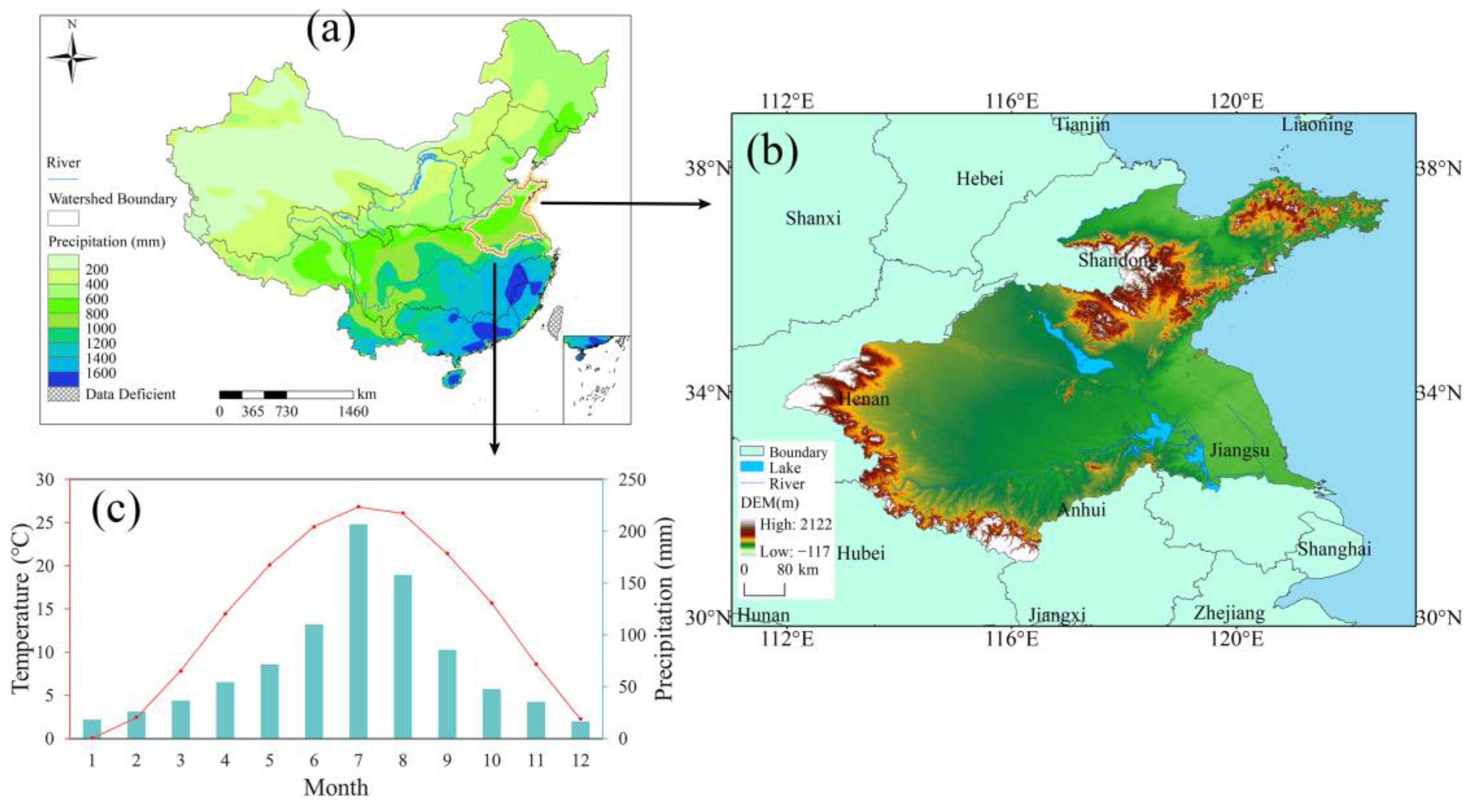
2.1. Study Area
2.2. Data
2.3. Methodology
2.3.1. Extreme Precipitation Indices
2.3.2. Methods for Trend Analysis and Significance Testing
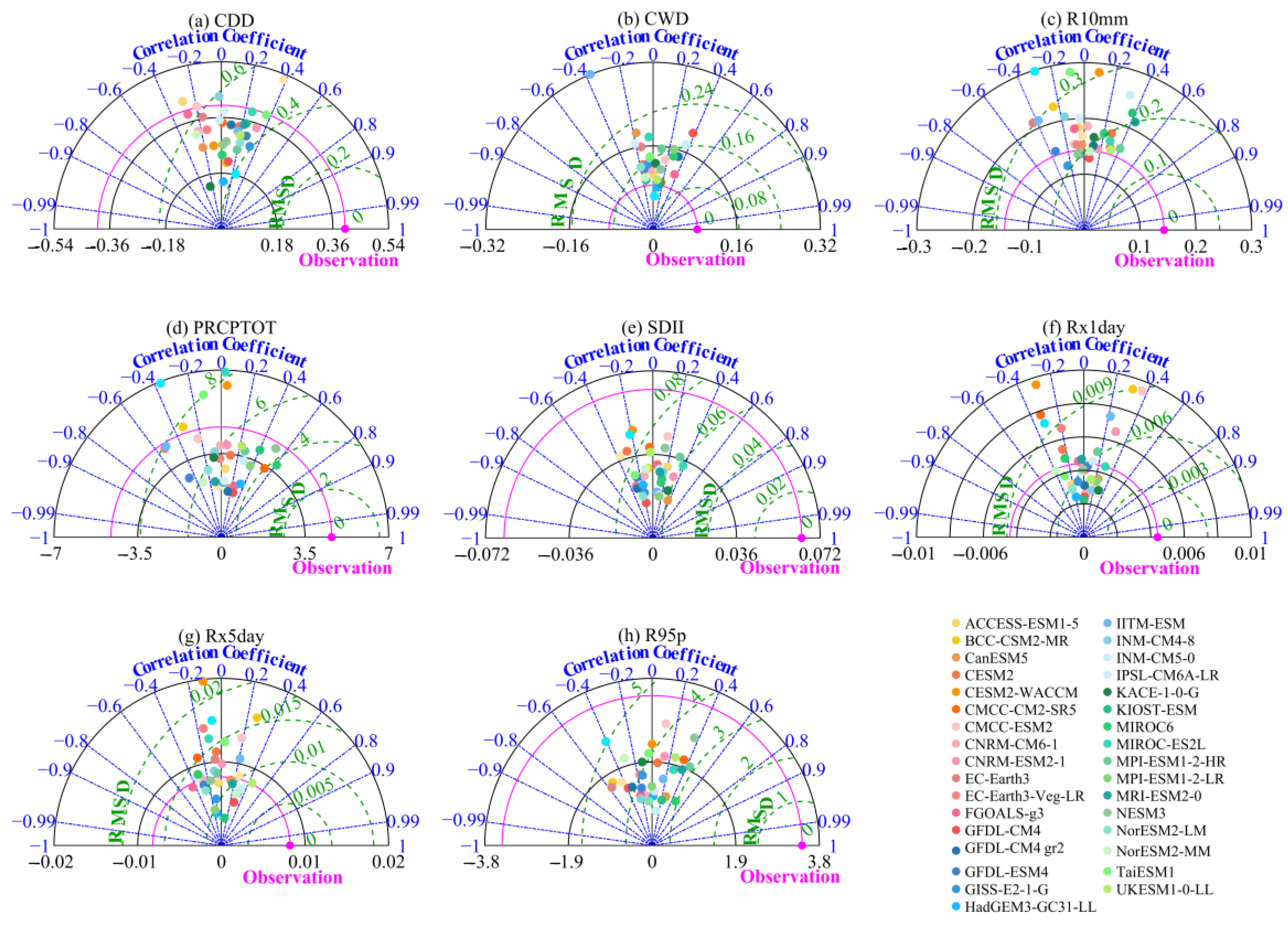
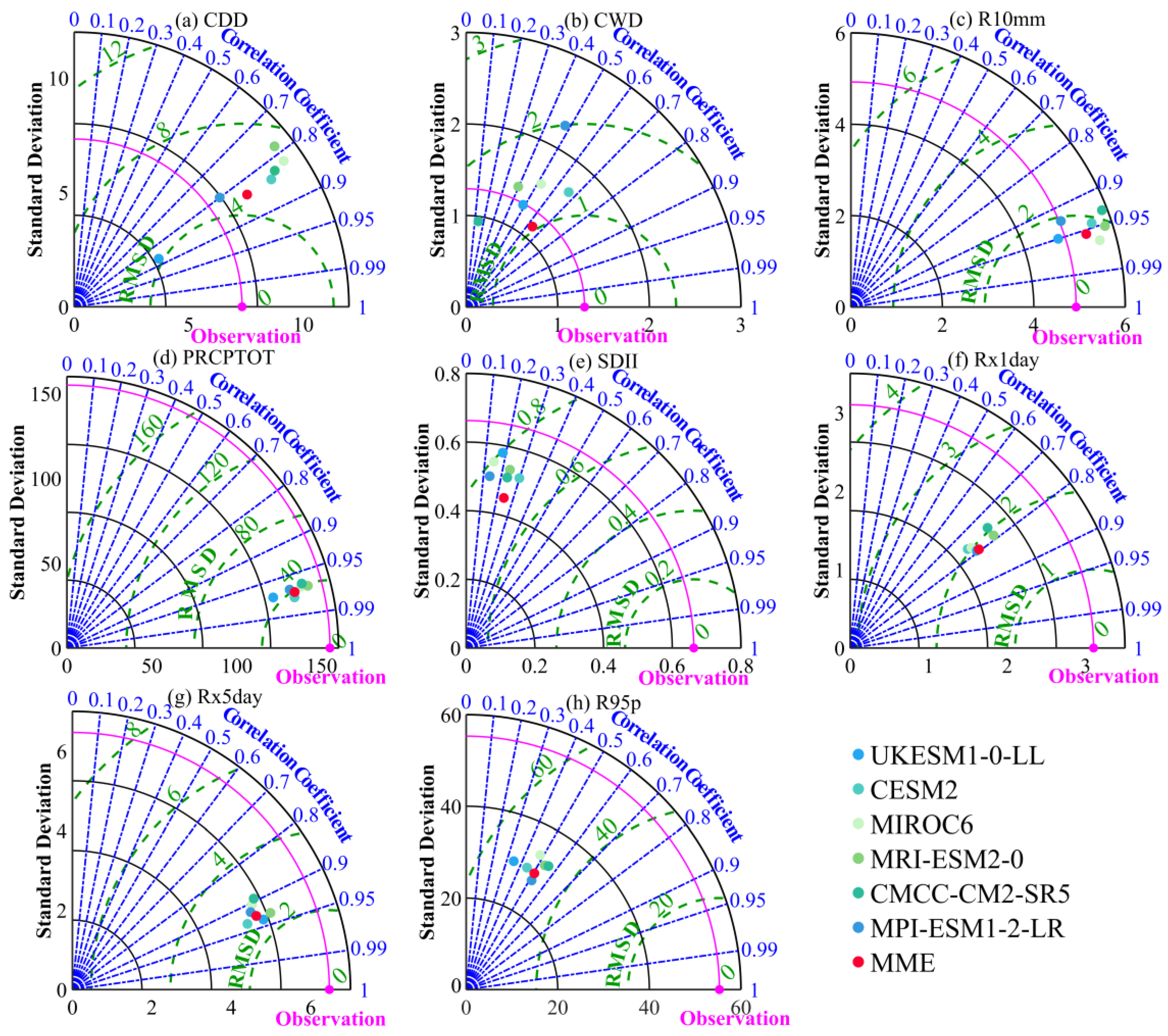
2.3.3. Taylor Diagram
2.3.4. TS
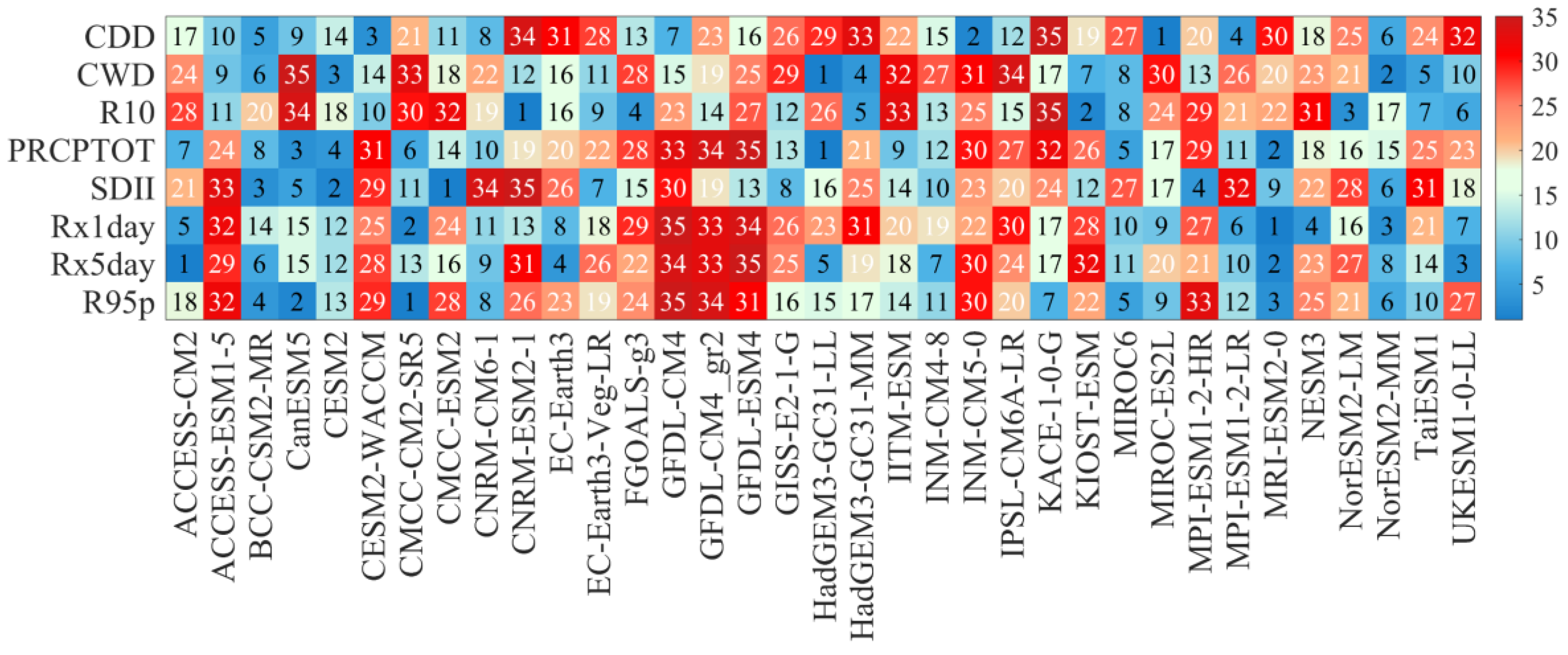
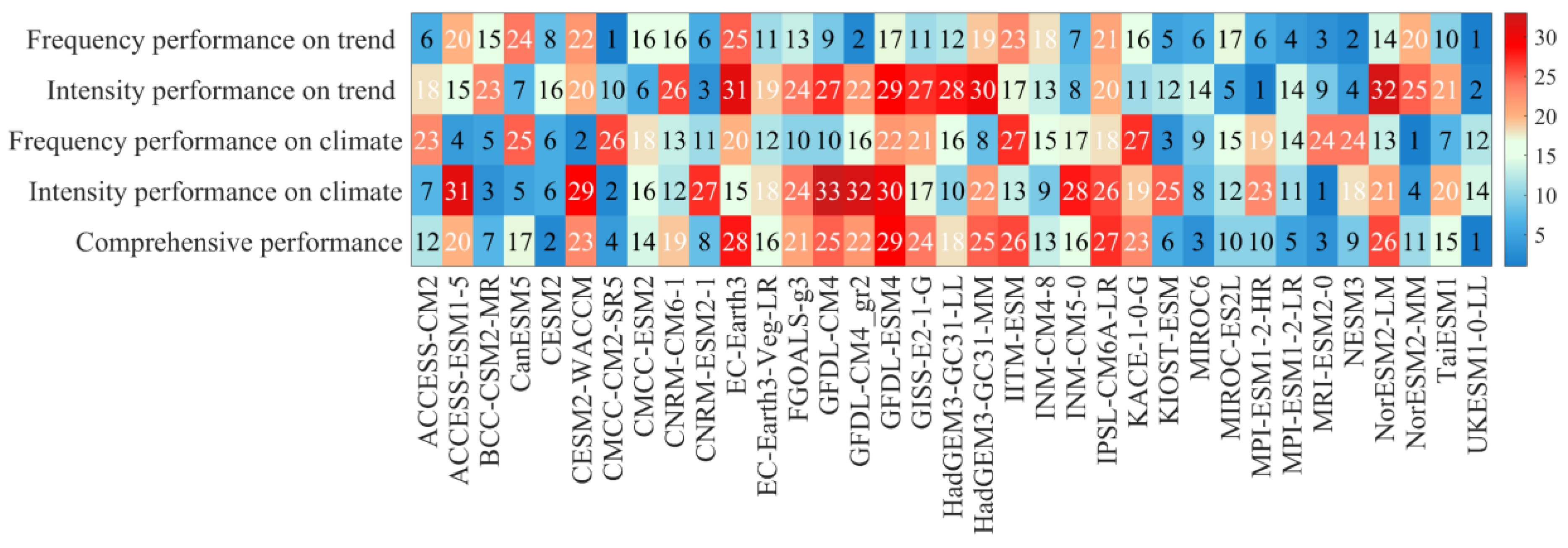
2.3.5. Mr (Modified rank) Scores
2.3.6. Weighted Average Formula
3. Results
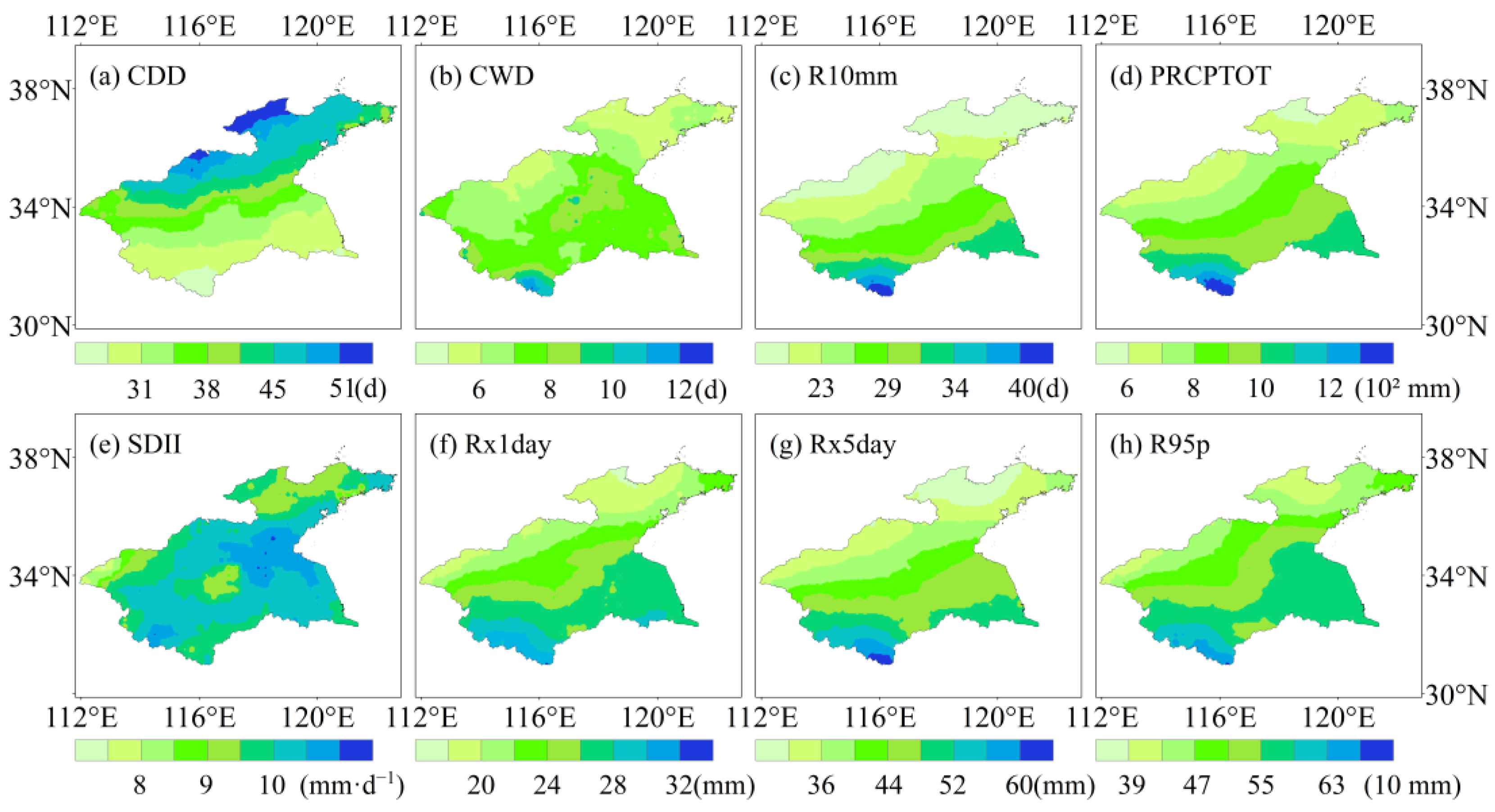
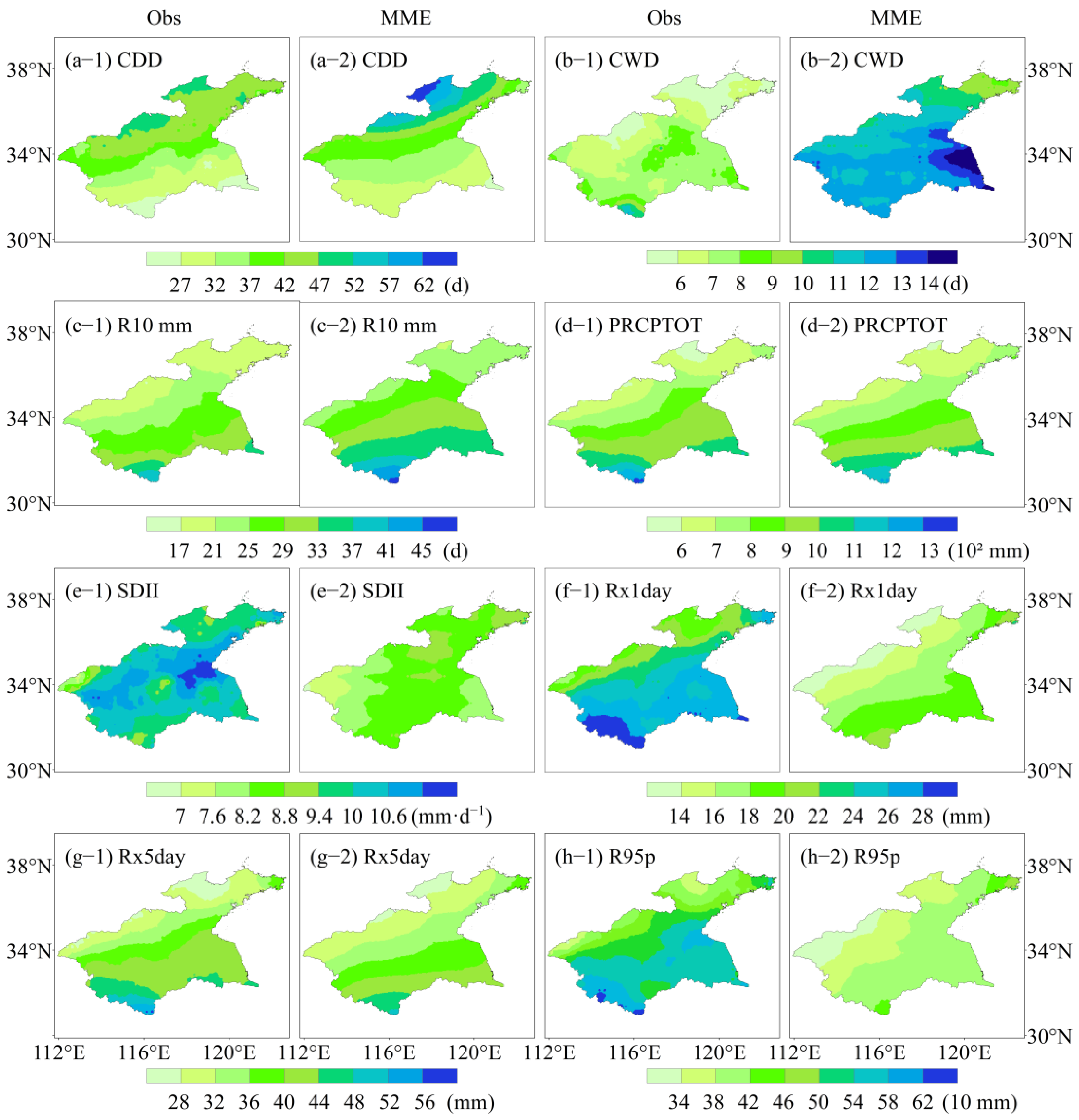
3.1. Characteristics of Extreme Precipitation Indices
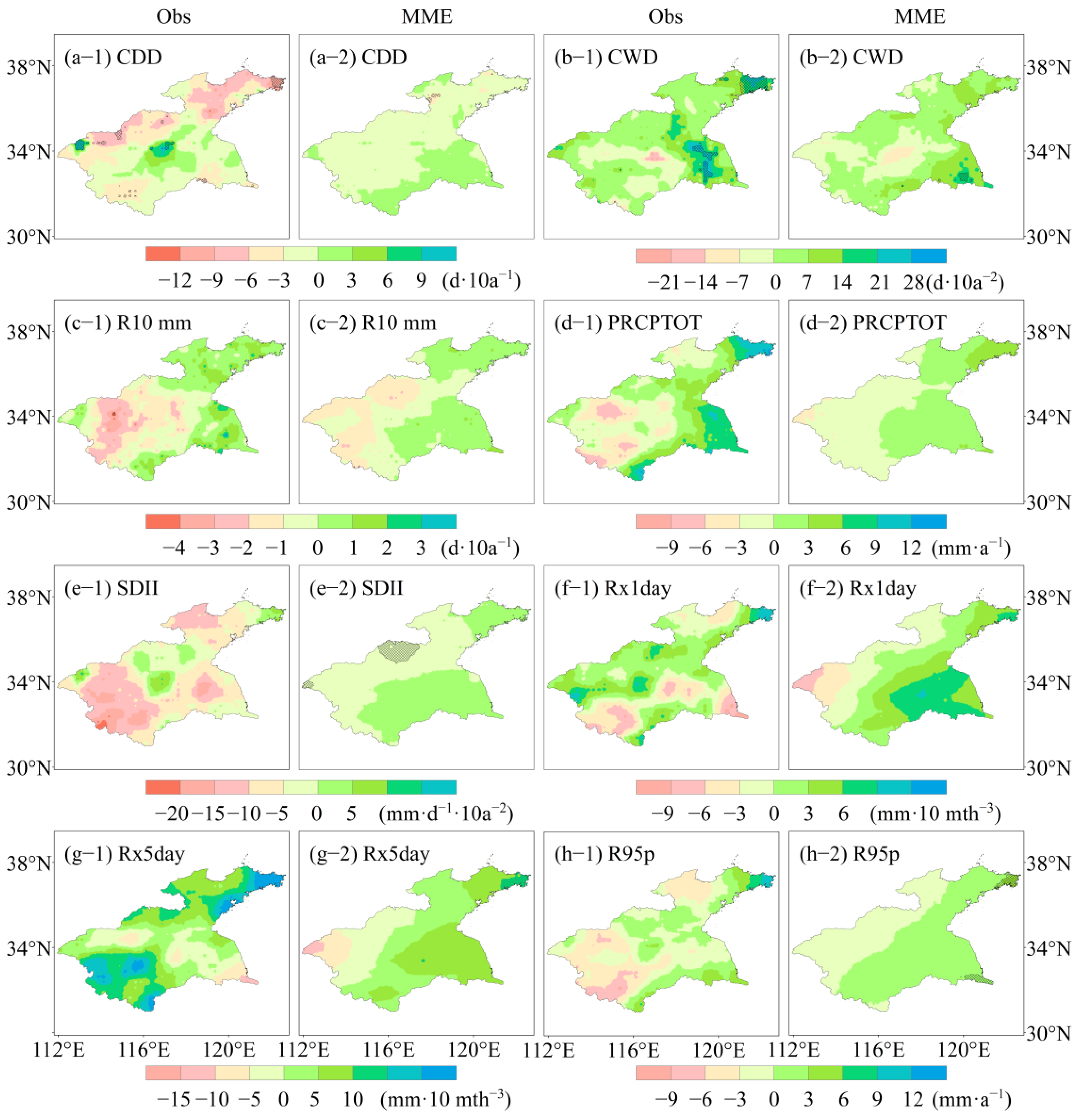
3.2. Assessment of Model Performance for Extreme Precipitation Indices
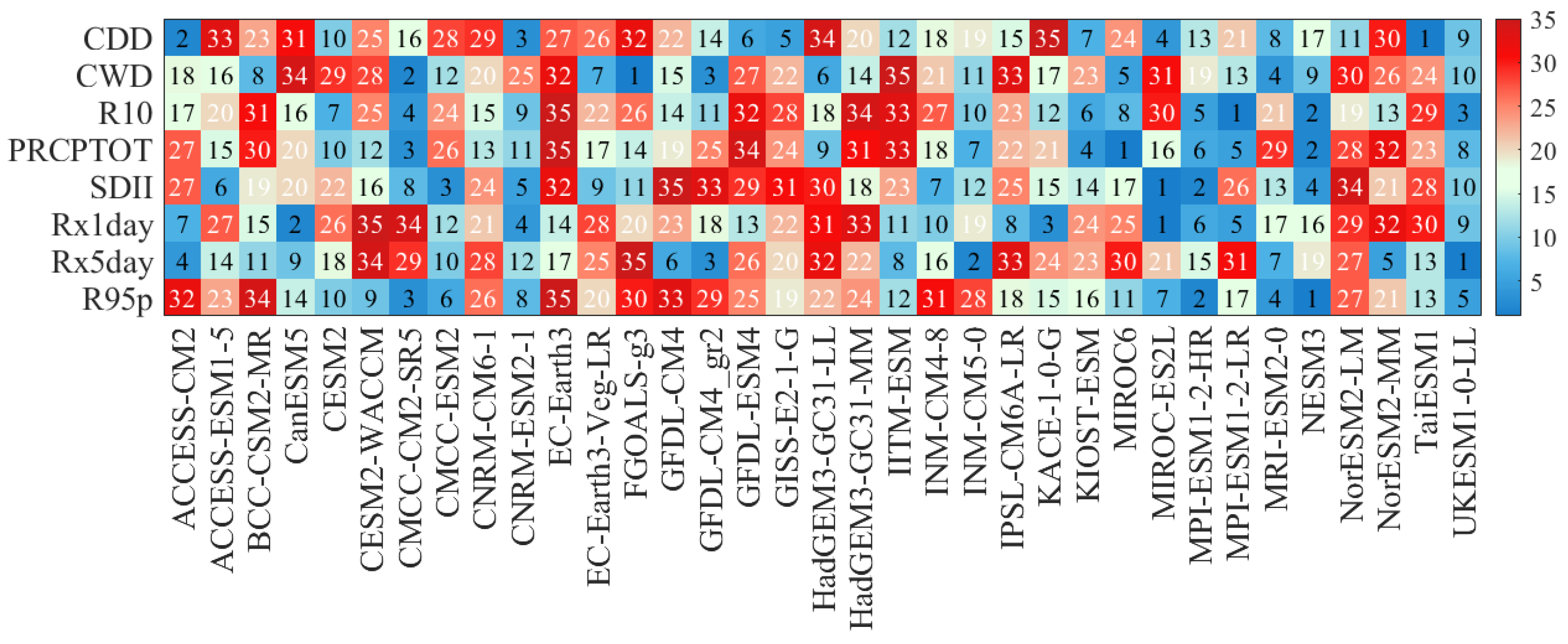
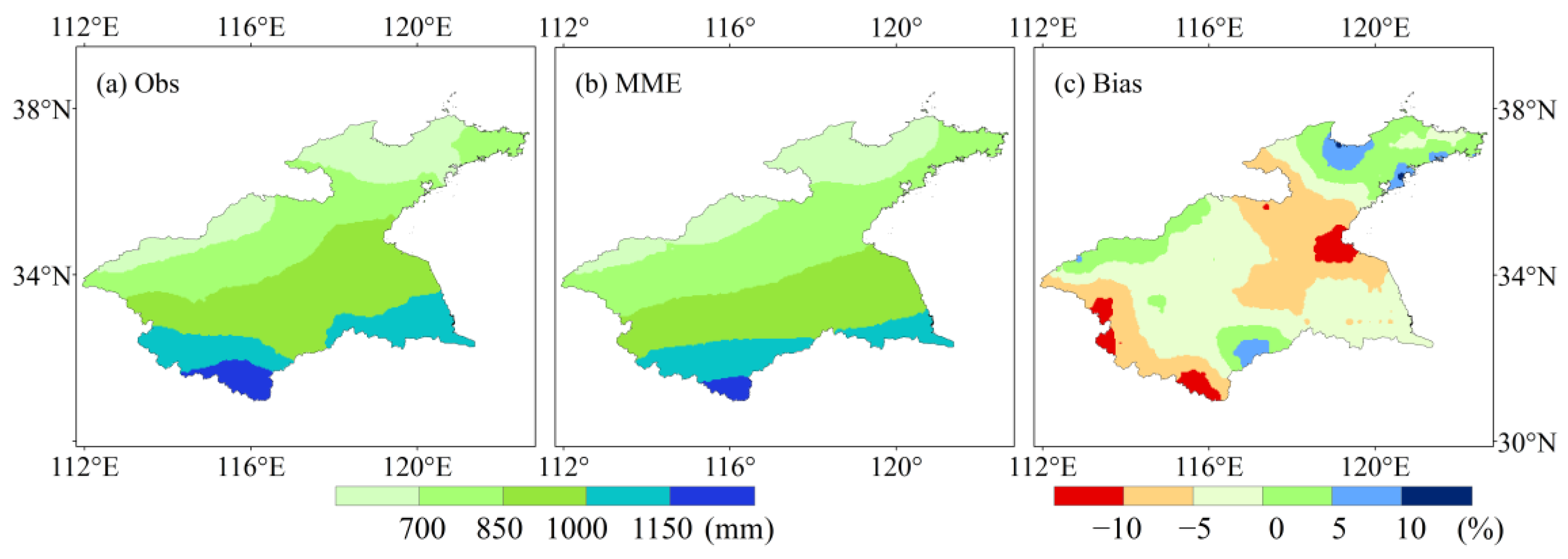
3.3. Assessment of Preferred Models
4. Discussion
5. Conclusions
- (1)
- The underlying topography and the spatial dynamics of extreme precipitation indices over the HRB are well related. Both frequency and intensity indices exhibit noticeable variations in regions with significant changes in the topography, which emphasizes the need for climate models to accurately replicate the complex spatial features linked to these indices.
- (2)
- The models’ capacity to replicate the trends of extreme precipitation requires further development. With a positive correlation with the observed field in 87% of the extreme precipitation indices, UKESM1-0-LL outperforms the other considered models, but still with a relatively weak connection. Since different models exhibit large differences in their capacity to represent both the trends and climatology of various indices, a great deal of uncertainty is introduced into the simulation of extreme precipitation indices. In comparison to their trend simulations, models perform better when modeling the climatological means, and they are better at simulating frequency indices than intensity indices. NorESM2-MM and MRI-ESM2-0, in particular, are excellent at simulating climatology. UKESM1-0-LL, CMCC-CM2-SR5, and MPI-ESM1-2-HR have relatively superior performance in terms of changing trends.
- (3)
- Based on their comparatively superior simulation abilities, the preferred models, UKESM1-0-LL, CESM2, MIROC6, MRI-ESM2-0, CMCC-CM2-SR5, and MPIESMI-2-LR, were ultimately chosen. Only a few of these models’ ensembles deviate from the observed data, primarily in the western mountains. Additionally, the contribution rate of the deviation varies very little between the eastern, central, and western regions. The models’ performances for frequency indices show strong agreement with the spatial pattern of the observed climate, and the negative correlations in the temporal patterns of intensity indices are significantly mitigated. To put it another way, the ensemble of selected models shows some degree of applicability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dessler, A.E.; Schoeberl, M.R.; Wang, T.; Davis, S.M.; Rosenlof, K.H. Stratospheric water vapor feedback. Proc. Natl. Acad. Sci. USA 2013, 110, 18087–18091. [Google Scholar] [CrossRef]
- Burke, C.; Stott, P.; Ciavarella, A.; Sun, Y. Attribution of Extreme Rainfall in Southeast China During May 2015. Bull. Am. Meteorol. Soc. 2016, 97, S92–S96. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J. Changes in climate extreme events in China associated with warming. Int. J. Climatol. 2015, 35, 2735–2751. [Google Scholar] [CrossRef]
- Huo, R.; Li, L.; Chen, H.; Xu, C.Y.; Chen, J.; Guo, S. Extreme Precipitation Changes in Europe from the Last Millennium to the End of the Twenty-First Century. J. Clim. 2021, 34, 567–588. [Google Scholar] [CrossRef]
- Shenoy, S.; Gorinevsky, D.; Trenberth, K.E.; Chu, S. Trends of extreme US weather events in the changing climate. Proc. Natl. Acad. Sci. USA 2022, 119, e2207536119. [Google Scholar] [CrossRef] [PubMed]
- IPCC. AR6 Climate Change 2021: The Physical Science Basis; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Jiang, T.; Su, B.; Huang, J.; Zhai, J.; Xia, J.; Tao, H.; Wang, Y.; Su, H.; Luo, Y.; Zhang, L.; et al. Each 0.5 °C of Warming Increases Annual Flood Losses in China by More than US$60 Billion. Bull. Am. Meteorol. Soc. 2020, 101, E1464–E1474. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, T. Increasing impacts from extreme precipitation on population over China with global warming. Sci. Bull. 2020, 65, 243–252. [Google Scholar] [CrossRef]
- Hirabayashi, Y.; Tanoue, M.; Sasaki, O.; Zhou, X.; Yamazaki, D. Global exposure to flooding from the new CMIP6 climate model projections. Sci. Rep. 2021, 11, 3740. [Google Scholar] [CrossRef]
- Cook, B.I.; Mankin, J.S.; Marvel, K.; Williams, A.P.; Smerdon, J.E.; Anchukaitis, K.J. Twenty-first century drought projections in the CMIP6 forcing scenarios. Earth's Future 2020, 8, e2019EF001461. [Google Scholar] [CrossRef]
- Wang, B.; Jin, C.; Liu, J. Understanding Future Change of Global Monsoons Projected by CMIP6 Models. J. Clim. 2020, 33, 6471–6489. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2015, 9, 1937–1958. [Google Scholar] [CrossRef]
- Zhou, T.J.; Zhou, L.W.; Chen, X.L. Commentary on the coupled model intercomparison project phase 6 (CMIP6). Adv. Clim. Chang. Res. 2019, 15, 445–456. (In Chinese) [Google Scholar]
- Chen, H.; Sun, J.; Lin, W.; Xu, H. Comparison of CMIP6 and CMIP5 models in simulating climate extremes. Sci. Bull. 2020, 65, 1415–1418. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Jiang, Z.; Li, L. Projection of climate extremes in China, an incremental exercise from CMIP5 to CMIP6. Sci. Bull. 2021, 66, 2528–2537. [Google Scholar] [CrossRef]
- Kim, Y.H.; Min, S.K.; Zhang, X.; Sillmann, J.; Sandstad, M. Evaluation of the CMIP6 multi-model ensemble for climate extreme indices. Weather Clim. Extrem. 2020, 29, 100269. [Google Scholar] [CrossRef]
- Li, Y.; Yan, D.; Peng, H.; Xiao, S. Evaluation of precipitation in CMIP6 over the Yangtze River Basin. Atmos. Res. 2020, 253, 105406. [Google Scholar] [CrossRef]
- Gu, X.; Ye, L.; Xin, Q.; Zhang, C.; Zeng, F.; Nerantzaki, S.D.; Papalexiou, S.M. Extreme Precipitation in China: A Review on Statistical Methods and Applications. Adv. Water Resour. 2022, 163, 104144. [Google Scholar] [CrossRef]
- Wu, G.; Li, J.; Zhou, T.; Lu, R.; Yu, Y.; Zhu, J.; Mu, M. CMIP. Adv. Earth Sci. 2006, 21, 1109. [Google Scholar]
- Kailin, Y.; Miao, Y.; Li, G.; Hong, L. Relationships Between Precipitation Anomaly in Meiyu Period in the Yangtze-Huaihe Region and Surface Sensible Heat Flux over East Asia. J. Arid Meteorol. 2019, 37, 771. [Google Scholar]
- Yin, Y.; Chen, H.; Zhai, P.; Xu, C.Y.; Ma, H. Characteristics of summer extreme precipitation in the Huai River basin and their relationship with East Asia summer monsoon during 1960–2014. Int. J. Climatol. 2019, 39, 1555–1570. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C. Extreme Rainfall (R20mm, RX5day) in Yangtze–Huai, China, in June–July 2016: The Role of ENSO and Anthropogenic Climate Change. Bull. Am. Meteorol. Soc. 2018, 99, S102–S106. [Google Scholar] [CrossRef]
- Chen, F.; Zheng, X.; Wen, H.; Yuan, Y. Microphysics of Convective and Stratiform Precipitation during the Summer Monsoon Season over the Yangtze–Huaihe River Valley, China. J. Hydrometeorol. 2022, 23, 239–252. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, B.; Yao, Y.; Zhang, X.; Wang, J.; Yu, F.; Li, J. Latitudinal differentiation and patterns of temperate and subtropical plants in the Qinling-Daba Mountains. J. Geogr. Sci. 2023, 33, 907–923. [Google Scholar] [CrossRef]
- Sun, Y.; Ding, Y. A projection of future changes in summer precipitation and monsoon in East Asia. Sci. China Earth Sci. 2010, 53, 284–300. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Y.; Li, T.; Ding, Y.; Hu, T. Future changes in East Asian summer monsoon circulation and precipitation under 1.5 to 5 C of warming. Earth's Future 2019, 7, 1391–1406. [Google Scholar]
- Li, X.; Fang, G.; Wei, J.; Arnault, J.; Laux, P.; Wen, X.; Kunstmann, H. Evaluation and projection of precipitation and temperature in a coastal climatic transitional zone in China based on CMIP6 GCMs. Clim. Dyn. 2023, 61, 1–23. [Google Scholar] [CrossRef]
- Mou, S.; Shi, P.; Qu, S.; Feng, Y.; Chen, C.; Dong, F. Projected regional responses of precipitation extremes and their joint probabilistic behaviors to climate change in the upper and middle reaches of Huaihe River Basin, China. Atmos. Res. 2020, 240, 104942. [Google Scholar] [CrossRef]
- Jin, H.; Chen, X.; Zhong, R.; Duan, K. Frequency analysis of extreme precipitation in different regions of the Huaihe River Basin. Int. J. Climatol. 2021, 42, 3517–3536. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Wang, Y.; Ju, Q.; Jin, J.; Bao, Z. Projecting Changes in Rainfall Extremes for the Huai River Basin in the Context of 1.5 °C and 2 °C Global Warming. Atmosphere 2022, 13, 1708. [Google Scholar] [CrossRef]
- Wu, Y.; Miao, C.; Duan, Q.; Shen, C.; Fan, X. Evaluation and projection of daily maximum and minimum temperatures over China using the high-resolution NEX-GDDP dataset. Clim. Dyn. 2020, 55, 2615–2629. [Google Scholar] [CrossRef]
- Thrasher, B.; Wang, W.; Michaelis, A.; Melton, F.; Lee, T.; Nemani, R. NASA Global Daily Downscaled Projections, CMIP6. Sci. Data 2022, 9, 262. [Google Scholar] [CrossRef]
- Chen, H.P.; Sun, J.Q.; Li, H.X. Future changes in precipitation extremes over China using the NEX-GDDP high-resolution daily downscaled data-set. Atmos. Ocean. Sci. Lett. 2017, 10, 403–410. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Q.; Ullah, S.; Chen, C.; Shen, L.; Liu, Z. Substantial increase in abrupt shifts between drought and flood events in China based on observations and model simulations. Sci. Total Environ. 2023, 876, 162822. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Zhang, T.; Yu, W.; Yang, S. Changes in concurrent precipitation and temperature extremes over the Asian monsoon region: Observation and projection. Environ. Res. Lett. 2023, 18, 044021. [Google Scholar] [CrossRef]
- Qin, Z.; Zhao, J.; Cheng, W.X.; Wang, J.; Su, H.L.; He, Y.L. Change of subtropical northern boundary in Qinling− Huaihe region in the context of climate change. Adv. Clim. Chang. Res. 2023, 19, 38–48. (In Chinese) [Google Scholar]
- Cao, Q.; Hao, Z.; Yuan, F.; Berndtsson, R.; Xu, S.; Gao, H.; Hao, J. On the predictability of daily rainfall during rainy season over the Huaihe River Basin. Water 2019, 11, 916. [Google Scholar] [CrossRef]
- Dai, C.; Qin, X.; Lu, W.; Huang, Y. Assessing adaptation measures on agricultural water productivity under climate change: A case study of Huai River Basin, China. Sci. Total Environ. 2020, 721, 137777. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.J. A gridded daily observation dataset over China region and comparison with the other datasets. Chin. J. Geophys. Chin. Ed. 2013, 56, 1102–1111. (In Chinese) [Google Scholar]
- Sun, B.; Wang, H. Enhanced connections between summer precipitation over the Three-River-Source region of China and the global climate system. Clim. Dyn. 2019, 52, 3471–3488. [Google Scholar] [CrossRef]
- Song, Z.; Xia, J.; She, D.; Li, L.; Hu, C.; Hong, S. Assessment of meteorological drought change in the 21st century based on CMIP6 multi-model ensemble projections over mainland China. J. Hydrol. 2021, 601, 126643. [Google Scholar] [CrossRef]
- Wood, A.W.; Maurer, E.P.; Kumar, A.; Lettenmaier, D.P. Long-range experimental hydrologic forecasting for the eastern United States. J. Geophys. Res. Atmos. 2002, 107, ACL 6-1–ACL 6-15. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic Implications of Dynamical and Statistical Approaches to Downscaling Climate Model Outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Bi, D.; Dix, M.; Marsland, S.; O’farrell, S.; Sullivan, A.; Bodman, R.; Law, R.; Harman, I.; Srbinovsky, J.; Rashid, H.A. Configuration and spin-up of ACCESS-CM2, the new generation Australian community climate and earth system simulator coupled model. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 225–251. [Google Scholar] [CrossRef]
- Ziehn, T.; Chamberlain, M.A.; Law, R.M.; Lenton, A.; Bodman, R.W.; Dix, M.; Stevens, L.; Wang, Y.P.; Srbinovsky, J. The Australian earth system model: : ACCESS-ESM1. 5. J. South. Hemisph. Earth Syst. Sci. 2020, 70, 193–214. [Google Scholar] [CrossRef]
- Wu, T.; Lu, Y.; Fang, Y.; Xin, X.; Li, L.; Li, W.; Jie, W.; Zhang, J.; Liu, Y.; Zhang, L. The Beijing Climate Center climate system model (BCC-CSM): The main progress from CMIP5 to CMIP6. Geosci. Model Dev. 2019, 12, 1573–1600. [Google Scholar] [CrossRef]
- Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S. The Canadian earth system model version 5 (CanESM5. 0.3). Geosci. Model Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef]
- Danabasoglu, G.; Lamarque, J.F.; Bacmeister, J.; Bailey, D.; DuVivier, A.; Edwards, J.; Emmons, L.; Fasullo, J.; Garcia, R.; Gettelman, A. The community earth system model version 2 (CESM2). J. Adv. Model. Earth Syst. 2020, 12, e2019MS001916. [Google Scholar] [CrossRef]
- Gettelman, A.; Mills, M.; Kinnison, D.; Garcia, R.; Smith, A.; Marsh, D.; Tilmes, S.; Vitt, F.; Bardeen, C.; McInerny, J. The whole atmosphere community climate model version 6 (WACCM6). J. Geophys. Res. Atmos. 2019, 124, 12380–12403. [Google Scholar] [CrossRef]
- Cherchi, A.; Fogli, P.G.; Lovato, T.; Peano, D.; Iovino, D.; Gualdi, S.; Masina, S.; Scoccimarro, E.; Materia, S.; Bellucci, A. Global mean climate and main patterns of variability in the CMCC-CM2 coupled model. J. Adv. Model. Earth Syst. 2019, 11, 185–209. [Google Scholar] [CrossRef]
- Lovato, T.; Peano, D.; Butenschön, M.; Materia, S.; Iovino, D.; Scoccimarro, E.; Fogli, P.; Cherchi, A.; Bellucci, A.; Gualdi, S. CMIP6 simulations with the CMCC Earth system model (CMCC-ESM2). J. Adv. Model. Earth Syst. 2022, 14, e2021MS002814. [Google Scholar] [CrossRef]
- Voldoire, A.; Saint-Martin, D.; Sénési, S.; Decharme, B.; Alias, A.; Chevallier, M.; Colin, J.; Guérémy, J.F.; Michou, M.; Moine, M.P. Evaluation of CMIP6 deck experiments with CNRM-CM6-1. J. Adv. Model. Earth Syst. 2019, 11, 2177–2213. [Google Scholar] [CrossRef]
- Séférian, R.; Nabat, P.; Michou, M.; Saint-Martin, D.; Voldoire, A.; Colin, J.; Decharme, B.; Delire, C.; Berthet, S.; Chevallier, M. Evaluation of CNRM Earth System Model, CNRM-ESM2-1: Role of Earth system processes in present-day and future climate. J. Adv. Model. Earth Syst. 2019, 11, 4182–4227. [Google Scholar] [CrossRef]
- Döscher, R.; Acosta, M.; Alessandri, A.; Anthoni, P.; Arneth, A.; Arsouze, T.; Bergmann, T.; Bernadello, R.; Bousetta, S.; Caron, L.P. The EC-earth3 Earth system model for the climate model intercomparison project 6. Geosci. Model Dev. Discuss. 2021, 15, 2973–3020. [Google Scholar] [CrossRef]
- Pu, Y.; Liu, H.; Yan, R.; Yang, H.; Xia, K.; Li, Y.; Dong, L.; Li, L.; Wang, H.; Nie, Y. CAS FGOALS-g3 model datasets for the CMIP6 scenario model intercomparison project (ScenarioMIP). Adv. Atmos. Sci. 2020, 37, 1081–1092. [Google Scholar] [CrossRef]
- Held, I.; Guo, H.; Adcroft, A.; Dunne, J.; Horowitz, L.; Krasting, J.; Shevliakova, E.; Winton, M.; Zhao, M.; Bushuk, M. Structure and performance of GFDL's CM4. 0 climate model. J. Adv. Model. Earth Syst. 2019, 11, 3691–3727. [Google Scholar] [CrossRef]
- Dunne, J.P.; Horowitz, L.; Adcroft, A.; Ginoux, P.; Held, I.; John, J.; Krasting, J.P.; Malyshev, S.; Naik, V.; Paulot, F. The GFDL Earth System Model version 4.1 (GFDL-ESM 4.1): Overall coupled model description and simulation characteristics. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002015. [Google Scholar] [CrossRef]
- Kelley, M.; Schmidt, G.A.; Nazarenko, L.S.; Bauer, S.E.; Ruedy, R.; Russell, G.L.; Ackerman, A.S.; Aleinov, I.; Bauer, M.; Bleck, R. GISS-E2. 1: Configurations and climatology. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002025. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.J.; Baker, A.; Blockley, E.W.; Calvert, D.; Coward, A.; Hewitt, H.T.; Jackson, L.C.; Kuhlbrodt, T.; Mathiot, P.; Roberts, C.D. Description of the resolution hierarchy of the global coupled HadGEM3-GC3. 1 model as used in CMIP6 HighResMIP experiments. Geosci. Model Dev. 2019, 12, 4999–5028. [Google Scholar] [CrossRef]
- Kuhlbrodt, T.; Jones, C.G.; Sellar, A.; Storkey, D.; Blockley, E.; Stringer, M.; Hill, R.; Graham, T.; Ridley, J.; Blaker, A. The low-resolution version of HadGEM3 GC3. 1: Development and evaluation for global climate. J. Adv. Model. Earth Syst. 2018, 10, 2865–2888. [Google Scholar]
- Küsters, R.; Tuengerthal, M.; Rausch, D. The IITM model: A simple and expressive model for universal composability. J. Cryptol. 2020, 33, 1461–1584. [Google Scholar] [CrossRef]
- Volodin, E.M.; Mortikov, E.V.; Kostrykin, S.V.; Galin, V.Y.; Lykossov, V.N.; Gritsun, A.S.; Diansky, N.A.; Gusev, A.V.; Iakovlev, N.G.; Shestakova, A.A. Simulation of the modern climate using the INM-CM48 climate model. Russ. J. Numer. Anal. Math. Model. 2018, 33, 367–374. [Google Scholar] [CrossRef]
- Volodin, E.; Gritsun, A. Simulation of observed climate changes in 1850–2014 with climate model INM-CM5. Earth Syst. Dyn. 2018, 9, 1235–1242. [Google Scholar] [CrossRef]
- Boucher, O.; Servonnat, J.; Albright, A.L.; Aumont, O.; Balkanski, Y.; Bastrikov, V.; Bekki, S.; Bonnet, R.; Bony, S.; Bopp, L. Presentation and evaluation of the IPSL-CM6A-LR climate model. J. Adv. Model. Earth Syst. 2020, 12, e2019MS002010. [Google Scholar] [CrossRef]
- Pak, G.; Noh, Y.; Lee, M.I.; Yeh, S.W.; Kim, D.; Kim, S.Y.; Lee, J.L.; Lee, H.J.; Hyun, S.H.; Lee, K.Y. Korea institute of ocean science and technology earth system model and its simulation characteristics. Ocean Sci. J. 2021, 56, 18–45. [Google Scholar] [CrossRef]
- Tatebe, H.; Ogura, T.; Nitta, T.; Komuro, Y.; Ogochi, K.; Takemura, T.; Sudo, K.; Sekiguchi, M.; Abe, M.; Saito, F. Description and basic evaluation of simulated mean state, internal variability, and climate sensitivity in MIROC6. Geosci. Model Dev. 2019, 12, 2727–2765. [Google Scholar] [CrossRef]
- Hajima, T.; Watanabe, M.; Yamamoto, A.; Tatebe, H.; Noguchi, M.A.; Abe, M.; Ohgaito, R.; Ito, A.; Yamazaki, D.; Okajima, H. Development of the MIROC-ES2L Earth system model and the evaluation of biogeochemical processes and feedbacks. Geosci. Model Dev. 2020, 13, 2197–2244. [Google Scholar] [CrossRef]
- Müller, W.A.; Jungclaus, J.H.; Mauritsen, T.; Baehr, J.; Bittner, M.; Budich, R.; Bunzel, F.; Esch, M.; Ghosh, R.; Haak, H. A higher-resolution version of the max planck institute earth system model (MPI-ESM1. 2-HR). J. Adv. Model. Earth Syst. 2018, 10, 1383–1413. [Google Scholar] [CrossRef]
- Mauritsen, T.; Bader, J.; Becker, T.; Behrens, J.; Bittner, M.; Brokopf, R.; Brovkin, V.; Claussen, M.; Crueger, T.; Esch, M. Developments in the MPI-M Earth System Model version 1.2 (MPI-ESM1. 2) and its response to increasing CO2. J. Adv. Model. Earth Syst. 2019, 11, 998–1038. [Google Scholar] [CrossRef]
- Yukimoto, S.; Kawai, H.; Koshiro, T.; Oshima, N.; Yoshida, K.; Urakawa, S.; Tsujino, H.; Deushi, M.; Tanaka, T.; Hosaka, M. The Meteorological Research Institute Earth System Model version 2.0, MRI-ESM2. 0: Description and basic evaluation of the physical component. J. Meteorol. Soc. Japan. Ser. II 2019, 97, 931–965. [Google Scholar] [CrossRef]
- Cao, J.; Wang, B.; Yang, Y.M.; Ma, L.; Li, J.; Sun, B.; Bao, Y.; He, J.; Zhou, X.; Wu, L. The NUIST Earth System Model (NESM) version 3: Description and preliminary evaluation. Geosci. Model Dev. 2018, 11, 2975–2993. [Google Scholar] [CrossRef]
- Seland, Ø.; Bentsen, M.; Olivié, D.; Toniazzo, T.; Gjermundsen, A.; Graff, L.S.; Debernard, J.B.; Gupta, A.K.; He, Y.C.; Kirkevåg, A. Overview of the Norwegian Earth System Model (NorESM2) and key climate response of CMIP6 DECK, historical, and scenario simulations. Geosci. Model Dev. 2020, 13, 6165–6200. [Google Scholar] [CrossRef]
- Wang, Y.C.; Hsu, H.H.; Chen, C.A.; Tseng, W.L.; Hsu, P.C.; Lin, C.W.; Chen, Y.L.; Jiang, L.C.; Lee, Y.C.; Liang, H.C. Performance of the Taiwan earth system model in simulating climate variability compared with observations and CMIP6 model simulations. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002353. [Google Scholar] [CrossRef]
- Sellar, A.A.; Walton, J.; Jones, C.G.; Wood, R.; Abraham, N.L.; Andrejczuk, M.; Andrews, M.B.; Andrews, T.; Archibald, A.T.; de Mora, L. Implementation of UK Earth system models for CMIP6. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001946. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Ohlson, J.A.; Kim, S. Linear valuation without OLS: The Theil-Sen estimation approach. Rev. Account. Stud. 2014, 20, 395–435. [Google Scholar] [CrossRef]
- Kendall, M.G.; Gibbons, J.D. Rank Correlation Methods, 5th ed.; Edward Arnold Press: London, UK, 1981. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- He, X.M.; Jiang, C.; Wang, J.; Wang, X.P. Comparison of CMIP6 and CMIP5 models performance in simulating temperature in Northeast China. Chin. J. Geophys. 2022, 65, 4194–4207. (In Chinese) [Google Scholar]
- Schuenemann, K.C.; Cassano, J.J. Changes in synoptic weather patterns and Greenland precipitation in the 20th and 21st centuries 1. Evaluation of late 20th century simulations from IPCC models. J. Geophys. Res. Atmos. 2009, 114, D20113. [Google Scholar] [CrossRef]
- Lu, R.; Zhu, Z.; Li, T.; Pan, X.; Jiang, Y.; Lu, Y. Objective Clustering of Spatial Patterns of Summer Extreme Precipitation Frequency over the Huaihe River Basin and Their Formation Mechanisms. Chin. J. Atmos. Sci. 2021, 45, 1415–1432. (In Chinese) [Google Scholar]
- Jin, H.; Chen, X.; Zhong, R.; Pan, Y.; Zhao, T.; Liu, Z.; Tu, X. Spatiotemporal distribution analysis of extreme precipitation in the Huaihe River Basin based on continuity. Nat. Hazards 2022, 114, 3627–3656. [Google Scholar] [CrossRef]
- Randall, D.A.; Wood, R.A.; Bony, S.; Colman, R.; Fichefet, T.; Fyfe, J.; Kattsov, V.; Pitman, A.; Shukla, J.; Srinivasan, J. Climate models and their evaluation. In Climate Change 2007: The Physical Science Basis; Contribution of Working Group I to the Fourth Assessment Report of the IPCC (FAR); Cambridge University Press: London, UK, 2007; pp. 589–662. [Google Scholar]
- Munday, C.; Washington, R. Systematic Climate Model Rainfall Biases over Southern Africa: Links to Moisture Circulation and Topography. J. Clim. 2018, 31, 7533–7548. [Google Scholar] [CrossRef]
- Zhong, S. Advances in the Study of the Influencing Mechanism and Forecast Methods for Orographic Precipitation. Plateau Meteorol. 2020, 39, 1122–1132. (In Chinese) [Google Scholar]
- Li, J.; Wang, A.; Guo, D.; Wang, D. Evaluation of extreme temperature indices over China in the NEX-GDDP simulated by high-resolution statistical downscaling models. Acta Meteorol. Sin. 2019, 77, 579–593. (In Chinese) [Google Scholar]
- Wang, Q.Z.; Liu, K.; Wang, M. Evaluation of extreme precipitation indices performance based on NEX-GDDP downscaling data over China. Adv. Clim. Chang. Res. 2022, 18, 31–43. (In Chinese) [Google Scholar]
- Tian, J.; Zhang, Z.; Ahmed, Z.; Zhang, L.; Jiang, T. Projections of precipitation over China based on CMIP6 models. Stoch. Environ. Res. Risk Assess. 2021, 35, 1–18. [Google Scholar] [CrossRef]
- Li, X.; Fang, G.; Wen, X.; Xu, M.; Zhang, Y. Characteristics analysis of drought at multiple spatiotemporal scale and assessment of CMIP6 performance over the Huaihe River Basin. J. Hydrol. Reg. Stud. 2022, 41, 101103. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Hubert, M. Anomaly detection by robust statistics. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1236. [Google Scholar] [CrossRef]



| Model Name | Intuition/Country | Horizontal Resolution (lon × lat) | |
|---|---|---|---|
| Grid | Degree | ||
| ACCESS-CM2 [44] | CSIRO-ARCCSS/Australia | 144 × 192 | 1.875° × 1.25° |
| ACCESS-ESM1-5 [45] | CSIRO/Australia | 192 × 145 | 1.875° × 1.25° |
| BCC-CSM2-MR [46] | BCC/China | 160 × 320 | 1.125° × 1.125° |
| CanESM5 [47] | CCCma/Canada | 64 × 128 | 2.812° × 2.77° |
| CESM2 [48] | NCAR/USA | 288 × 192 | 1.25° × 0.94° |
| CESM2-WACCM [49] | NCAR/USA | 288 × 192 | 1.25° × 0.94° |
| CMCC-CM2-SR5 [50] | CMCC/Italy | 288 × 192 | 1.25° × 0.9375° |
| CMCC-ESM2 [51] | CMCC/Italy | 288 × 192 | 1.25° × 0.94° |
| CNRM-CM6-1 [52] | CNRM-CERFACS/France | 64 × 128 | 1.406° × 1.406° |
| CNRM-ESM2-1 [53] | CNRM-CERFACS/France | 128 × 256 | 1.406° × 1.406° |
| EC-Earth3 [54] | EC-Earth-Consortium/EC-Earth consortium | 256 × 512 | 0.703° × 0.703° |
| EC-Earth3-Veg-LR [54] | EC-Earth-Consortium/EC-Earth consortium | 256 × 512 | 1.125° × 1.125° |
| FGOALS-g3 [55] | CAS/China | 180 × 80 | 2° × 2.025° |
| GFDL-CM4 [56] | NOAA-GFDL/USA | 288 × 180 | 1.25° × 1° |
| GFDL-CM4_gr2 [56] | NOAA-GFDL/USA | 90 × 144 | 4° × 1.25° |
| GFDL-ESM4 [57] | NOAA-GFDL/USA | 288 × 180 | 1.25° × 1° |
| GISS-E2-1-G [58] | NASA-GISS/USA | 144 × 90 | 2.5° × 2° |
| HadGEM3-GC31-LL [59] | MOHC, NERC/UK | 144 × 192 | 1.875° × 1.25° |
| HadGEM3-GC31-MM [60] | MOHC/UK | 324 × 432 | ~0.8° × 0.6° |
| IITM-ESM [61] | CCCR-IITM/India | 192 × 94 | 1.875° × 1.915° |
| INM-CM4-8 [62] | INM/Russia | 180 × 120 | 2° × 1.5° |
| INM-CM5-0 [63] | INM/Russia | 180 × 120 | 2° × 1.5° |
| IPSL-CM6A-LR [64] | IPSL/France | 144 × 143 | 2.5° × 1.259° |
| KACE-1-0-G [65] | NIMS-KMA/Republic of Korea | 144 × 192 | 1.875° × 1.25° |
| KIOST-ESM [65] | KIOST/Republic of Korea | 96 × 192 | 0.938° × 0.938° |
| MIROC6 [66] | MIROC/Japan | 256 × 128 | 1.403° × 1.403° |
| MIROC-ES2L [67] | MIROC/Japan | 256 × 128 | 1.403° × 1.403° |
| MPI-ESM1-2-HR [68] | MPI-M, DWD, DKRZ/Germany | 384 × 192 | 0.938° × 0.939° |
| MPI-ESM1-2-LR [69] | MPI-M, AWI, DKRZ, DWD/Germany | 192 × 96 | 1.9° × 1.9° |
| MRI-ESM2-0 [70] | MRI/Japan | 320 × 160 | 1.125° × 1.125° |
| NESM3 [71] | NUIST/China | 192 × 96 | 1.88° × 1.88° |
| NorESM2-LM [72] | NCC/Norway | 144 × 96 | 2.5° × 1.89° |
| NorESM2-MM [72] | NCC/Norway | 288 × 192 | 1.25° × 0.94° |
| TaiESM1 [73] | AS-RCEC/Taiwan, China | 288 × 192 | 1.25° × 0.94° |
| UKESM1-0-LL [74] | MOHC/UK | 144 × 192 | 1.875° × 1.25° |
| Index | Descriptive Name | Definition | Units | |
|---|---|---|---|---|
| Indexes for frequency | CDD | Consecutive dry days | Maximum number of consecutive dry days | d |
| CWD | Consecutive wet days | Maximum number of consecutive wet days | d | |
| R10 mm | Number of heavy precipitation days | Annual count of days when RR ≥ 10 mm | d | |
| Indexes for intensity | PRCPTOT | Wet day precipitation | Annual total precipitation from wet days | mm |
| SDII | Simple daily intensity index | Average precipitation on wet days | mm d−1 | |
| Rx1day | Maximum 1-day precipitation | Monthly maximum 1-day precipitation | mm | |
| Rx5day | Maximum consecutive 5-day precipitation | Monthly maximum consecutive 5-day precipitation | mm | |
| R95p | Very wet day precipitation | Annual total precipitation when RR > 95th percentile of 1961–2020 daily | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, F.; Wen, S.; Gao, M.; Zhu, A. Assessment of NEX-GDDP-CMIP6 Downscale Data in Simulating Extreme Precipitation over the Huai River Basin. Atmosphere 2023, 14, 1497. https://doi.org/10.3390/atmos14101497
Jiang F, Wen S, Gao M, Zhu A. Assessment of NEX-GDDP-CMIP6 Downscale Data in Simulating Extreme Precipitation over the Huai River Basin. Atmosphere. 2023; 14(10):1497. https://doi.org/10.3390/atmos14101497
Chicago/Turabian StyleJiang, Fushuang, Shanshan Wen, Miaoni Gao, and Aiping Zhu. 2023. "Assessment of NEX-GDDP-CMIP6 Downscale Data in Simulating Extreme Precipitation over the Huai River Basin" Atmosphere 14, no. 10: 1497. https://doi.org/10.3390/atmos14101497
APA StyleJiang, F., Wen, S., Gao, M., & Zhu, A. (2023). Assessment of NEX-GDDP-CMIP6 Downscale Data in Simulating Extreme Precipitation over the Huai River Basin. Atmosphere, 14(10), 1497. https://doi.org/10.3390/atmos14101497








