Abstract
Auroral events are the prominent manifestation of solar/stellar forcing on planetary atmospheres because they are closely related to the stellar energy deposition by and evolution of planetary atmospheres. A numerical kinetic Monte Carlo model was developed with the aim to calculate the steady-state energy distribution functions of suprathermal N(4S) atoms in the polar upper atmosphere formed due to the precipitation of high-energy auroral electrons in the N2-O2 atmospheres of rocky planets in solar and exosolar planetary systems. This model describes on the molecular level the collisions of suprathermal N(4S) atoms and atmospheric gas taking into account the stochastic nature of collisional scattering at high kinetic energies. It was found that the electron impact dissociation of N2 is an important source of suprathermal N atoms, significantly increasing the non-thermal production of nitric oxide in the auroral regions of the N2-O2 atmospheres of terrestrial-type planets.
1. Introduction
The nitric oxide concentration in the Earth’s upper atmosphere is known to be highly dependent on solar activity. It can be transported to the stratosphere by atmospheric circulation, where it is responsible for the destruction of ozone, consequently affecting stratospheric heating rates. This is one of the mechanisms by which solar variability has been suspected to drive the variability in the energetic budget of the Earth’s climate. Therefore, it is essential to know the physical and chemical processes leading to the production or to the destruction of nitric oxide in the atmospheric regions where NO is formed.
One of the possible mechanisms by which solar activity could impact Earth’s climate [1] is the variations in the nitric oxide concentration in the polar upper atmosphere (see, e.g., [2]). Odd nitrogen species, and especially NOx, are produced in the lower thermosphere and mesosphere through molecular dissociation and ionization of the ambient gas by the precipitating high-energy electrons. Because NOx are long-living species in the lower thermosphere and mesosphere, they remain for a long time in the atmosphere during the polar night, experiencing horizontal and vertical transport. The latter likely takes place in the polar vortex and may transport NO produced in the thermosphere down to low atmospheric layers where it destroys the ozone [2,3].
There is another problem of space physics concerning atmospheric NO production in dependence on solar/stellar activity. As it was pointed out in the recent paper [4], the detection of an N2-O2 atmosphere on an exoplanet orbiting in the habitable zone around a solar-type star could be a strong sign of the presence of a developed aerobic extraterrestrial biosphere. The idea of using NO as a potential biomarker is widely discussed (see, e.g., [5]), because its formation and loss processes strongly depend on the presence of molecular nitrogen and oxygen as the main components in terrestrial-type atmospheres. The possibility of observing nitric oxide on exoplanets was recently discussed [6], where it was indicated that under favorable conditions, nitric oxide can be detected in exoplanetary atmospheres using modern space missions such as the Spektr-UV (WSO-UV) space telescope [7]. To approach this problem, kinetic Monte Carlo and multi-component MHD models [8,9] were developed with the aim to describe the evolution and, especially, the concentrations of nitric oxide in the N2-O2 upper atmospheres of sub-Neptunes and super- and exo-Earths under the influence of UV radiation and stellar wind from the parent star.
As it was discussed in [9], two mechanisms have been identified from observations as sources of nitric oxide in the upper atmospheres of terrestrial-type planets: (a) the precipitation of auroral electrons (1–10 keV) at high latitudes results in N2 dissociation, which leads to the production of nitric oxide [10]; (b) the main source of NO at low latitudes is the absorption of solar soft X-rays accompanied by the formation of high-energy photoelectrons [11]. Space observations [12,13] show that the largest density of nitric oxide that occurs at 106–110 km is produced by 1–10 keV electrons precipitating into the auroral region (60–70° geomagnetic latitude). Moreover, the polar source of NO under disturbed solar events influences the nitric oxide distribution even at middle latitudes [11,13,14,15].
It is well known that the Monte Carlo models [16,17,18,19] of auroral electron precipitation are an efficient approach to study the auroral events. These models are based on the stochastic tracking of numerous modeling particles representing the precipitating high-energy electrons. In our recent study [9], such a stochastic model was used to investigate the high-energy electron impact dissociation of atmospheric N2 resulting in the formation of suprathermal nitrogen atoms.
In this paper, the kinetic Monte Carlo (KMC) model [8,20] is also used to investigate the kinetics and transport of suprathermal N atoms in the polar upper atmosphere and to calculate the steady-state energy distributions of suprathermal (hot) nitrogen atoms in the Earth’s polar atmosphere. It is important to point out that the calculations in our previous study’s [9] source functions of the suprathermal N atoms are used as an input to the KMC model. This procedure allows us to estimate the input of the suprathermal N fraction to the odd nitrogen chemistry in the N2-O2 atmospheres under the changing conditions of solar/stellar activity.
2. Materials and Methods
2.1. Suprathermal N Atom Formation Due to the Auroral Electron Precipitation and Odd Nitrogen Chemistry
The nitric oxide is formed and lost in a set of chemical reactions involving both main atmospheric species—N2 and O2. The so-called odd chemistry of nitrogen involves atomic nitrogen in the ground and metastable states, N(4S) and N(2D), respectively, and is described by a simple stiff set of chemical reactions in the upper layers of the Earth’s atmosphere (see, e.g., [21,22,23]). The nitric oxide is formed in chemical reactions with dissociation products of N2 with O2 and is lost in collisions with atomic nitrogen in the ground and metastable electronic states N(4S, 2D), reproducing N2 molecules.
Solar UV photons and electrons can dissociate molecular nitrogen, thereby producing atomic nitrogen:
with the kinetic energies E and E′ < E of an auroral electron before and after collision, and the nitrogen atoms in the ground N(4S) and N(2D,2P) metastable electronic states. The atomic nitrogen then reacts with molecular oxygen to produce nitric oxide:
e(E) + N2(X1Σ+g)→e(E′) + N(4S) + N(4S,2D,2P),
N(2D) + O2→NO + O
N(4S) + O2→NO + O
Below 130 km, reaction (2) mainly produces NO during the day, being much less efficient at night. Above 130 km, reaction (3) is the main source of NO during the day and the main source during the night under 130 km [13,24].
Nitric oxide is mainly destroyed by the photon flux in the extreme ultraviolet, which dissociates NO according to [13]
and by collisions with N(4S) through
NO + hν→N + O,
NO + N(4S) →N2 + O.
This is one of the reasons why NO is much less abundant in the dayside thermosphere in comparison with the polar nighttime atmosphere.
The polar source of nitric oxide and, especially, non-thermal channels of its production should be considered in more detail because of the well-established connection between energetic precipitations and climate [2,3] showing that the effects (direct and indirect) of solar/stellar forcing persist in the Earth’s upper atmosphere down to the stratosphere.
Observations of ultraviolet and infrared NO emissions (see, e.g., [12,25,26]) in the planetary atmospheres are usually obtained using space instruments. With the rising astrobiological interest to molecular NO as a possible atmospheric biomarker [5], the possibility of NO observations should be clearly estimated [6] using more sophisticated models of nitric oxide formation and loss in the upper atmospheres of terrestrial-type exoplanets. In our previous models of the odd nitrogen chemistry in the Earth’s upper atmosphere [21,22,23,27], for the first time, the input of suprathermal nitrogen atoms to the chemistry of odd nitrogen was taken into account, but the polar sources and transport of hot N atoms were not considered. In this paper, we extend the KMC approach to the polar regions of the Earth and terrestrial-type (exo)planets partially based on the satellite data that slightly improved our understanding of odd nitrogen chemistry [13,14,15,24,26,28].
2.2. The Kinetic Monte Carlo Model for Suprathermal N Atom Kinetics and Transport in the Planetary Atmosphere
The distribution of auroral electrons by kinetic energy, calculated with the KMC model [9], could be used to estimate the source function
of atomic nitrogen in the ground and metastable excited states [10,12,14] formed in the electron impact dissociation of molecular nitrogen N2. In formula (6), function qNh(h) is the production rate of suprathermal N(4S) atoms in reaction (1) at height h, and fNh(h,E) is the normalized-to-unity distribution function of the fresh N(4S) atoms by kinetic energy at height h. As it follows from laboratory studies (see, e.g., [29]), the following molecular data are needed to calculate the source function (6):
QNh(h, E) = qNh(h) × fNh(h,E)
- (a)
- The differential and total cross-sections dependent on the collision energy for reaction (1);
- (b)
- The energy distribution function of fresh nitrogen atoms formed in reaction (1);
- (c)
- The branching ratios describing the probabilities to form N atoms in the ground and electron excited states.
The suprathermal nitrogen atoms lose their excess kinetic energy in collisions with other atmospheric particles and move in the transition region between the thermosphere and exosphere [20,27], and their steady-state distribution is a solution of the Boltzmann kinetic equation with source function (6):
where fNh(r,v) and fM(r,v) are the distribution functions by velocities v for hot nitrogen atoms and for components of the surrounding atmospheric gas at space point r, respectively.
The left-hand part of (7) describes the transport of suprathermal nitrogen atoms in the atmospheric region under study under the influence of the planetary gravitational field s. In the right-hand part, the collision terms Jmt for elastic and inelastic scattering of hot nitrogen atoms in collisions with the surrounding atmospheric gas are written in the standard form [20,27]. It is assumed that the atmospheric gas is characterized by the local Maxwell velocity distribution function.
The KMC method is an effective tool for studying complex kinetic systems in the stochastic approximation, and its general algorithmic implementation was recently reviewed in detail in [20].
Formally, it is usually accepted that hot particles are those with kinetic energies an order of magnitude larger than the mean thermal energy of the surrounding atmospheric gas. Since the temperature in the polar upper atmosphere of the Earth varies, depending on the level of solar activity—within 300–1600 K [30]—we can consider the hot atoms as those with kinetic energies above ~0.1 eV. Because, in this study, we are primarily interested in calculating the population by suprathermal N atoms in the polar Earth’s upper atmosphere and its input to the non-thermal NO production, the lower bound of the energy of suprathermal atoms in the model is set at 0.3 eV corresponding to the energy barrier of reaction (3).
The same as in the study [9], the atmospheric region between the altitudes of 80 and 700 km is considered. Its lower boundary is placed in the relatively dense lower thermosphere, where hot particles quickly and locally lose their excess kinetic energy in collisions with thermal molecules of nitrogen and oxygen. The upper boundary is placed above the exobase (~500–600 km), where the gas flow becomes collisionless. The area under study is divided into cells with a height grid varying below the local mean free path. In each cell, atmospheric gas is represented by model particles with given concentrations and temperatures. Model particles are born in every cell determined by the source function (6) of hot nitrogen atoms formed in the dissociation collisions (1). A detailed description of the stochastic procedures for modeling the local statistics of collisions and transport of hot particles in the planetary upper atmosphere can be found in [20]. Since the KMC model simulates the real atmospheric gas at the molecular level, detailed statistics on the distribution functions of hot N atoms by the velocity (kinetic energy) in the polar Earth’s atmosphere are accumulated in the KMC model runs.
3. Results
The different auroral precipitation conditions correspond to the different levels of solar activity (see, e.g., [31]). We studied the impact of different precipitation conditions for three distinct cases. The first case mentioned later in the text as Case A represents the conditions when a faint aurora becomes visible with the naked eye, with a mean kinetic energy of E0 = 1 keV for precipitating electrons. Two other considered cases, Case B and Case C, correspond to the visible auroral events and are characterized by the harder energy spectra of precipitating auroral electrons with mean kinetic energies of E0 = 2 keV and 5 keV, respectively, and are related to the more disturbed conditions of solar activity. The neutral atmosphere remains the same in all three cases (Ap = 6, f10.7 = 180) in order to distinguish the effect of precipitating electrons only. The distribution function of auroral electrons by kinetic energy was taken as the Maxwellian function with a characteristic energy of Em = E0/2, and an isotropic pitch-angle distribution for precipitating auroral electrons at the upper boundary was used [32]. The energy flux Q0 = 1.0 erg cm−2 s−1 of precipitating electrons was taken as the same for all cases at the upper boundary in the model polar atmosphere. The magnetic field geometry, i.e., magnetic line convergence in Earth’s polar regions, was taken into account as in the model [9,18] by the conservation of the second adiabatic invariant.
The altitude distributions of the main neutral species—O2, N2, O, and N—and their temperature were adopted with the MSISE90 empirical model [30] and are shown in Figure 1. The model atmosphere was calculated for 29 December 1975 at midnight local time. The latitude and longitude were taken as equal to 70° and 0°, respectively. The solar and geomagnetic conditions were at a high level corresponding to F10.7 = 180 and Ap = 6.
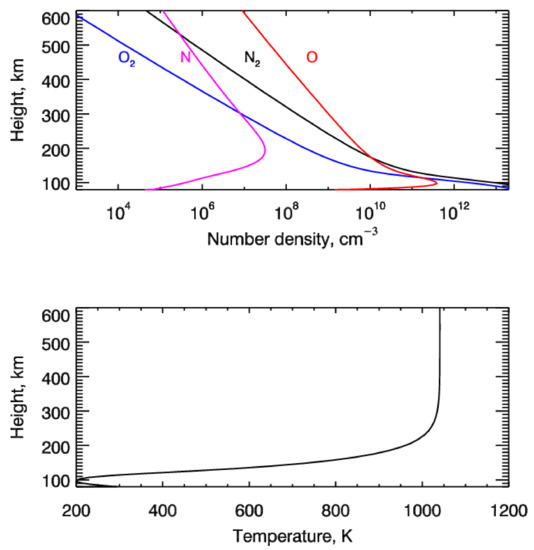
Figure 1.
Height profiles of the number densities of O2, N2, O, and N (top panel), and temperature (bottom panel) calculated with the MSISE90 model [30].
3.1. Distribution of the Suprathermal N(4S) Atoms in the Polar Upper Atmosphere
The main output of the developed KMC model is the steady-state energy distribution functions (EDFs) of suprathermal N atoms in the region under study. The thermalization rate of hot nitrogen atoms is determined by the collisional cross-sections with the ambient neutral atmosphere. A key aspect of this model is the stochastic treatment of the scattering angle distribution in elastic and inelastic collisions of suprathermal N(4S) atoms with ambient atmospheric gas (see, e.g., [20]). The results of the detailed calculations of cross-sections for elastic and inelastic collisions between suprathermal nitrogen and atomic nitrogen [33], and molecular nitrogen [34,35,36] were adopted. To take into account the scattering angle distribution, we used the calculated differential cross-sections for N–N2 [34].
As an example, in Figure 2, the energy distribution functions (EDFs) of the suprathermal N(4S) atoms with kinetic energies higher than the energy barrier of 0.3 eV for reaction (3) are shown at heights of 102.5, 113.0, and 125 km in the Earth’s polar atmosphere. Calculations were conducted for the considered Cases A, B, and C of the precipitating fluxes of auroral electrons with mean energies of E0 = 1, 2, and 5 keV. Selected heights correspond to the maximum production of fresh suprathermal N(4S) atoms due to the auroral electron precipitation. Local Maxwellian distributions by energy for thermal atmospheric N atoms at given heights were calculated with the temperature and number density of thermal N atoms (see Figure 1) and are shown by dashed lines in Figure 2. From Figure 2, it is clearly seen that at low altitudes, the suprathermal N EDFs strongly differ from the local Maxwellian functions for kinetic energies higher than 0.3 eV. The presence of non-thermal tails in suprathermal N atom EDFs is extremely important for calculations of their possible input to the odd nitrogen chemistry through reaction (3), which has an energy barrier of ~0.3 eV.
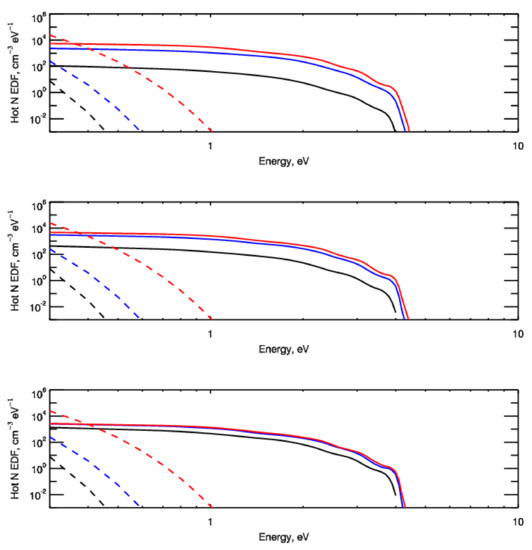
Figure 2.
The energy distribution functions (EDFs) of the suprathermal N(4S) atoms at the heights of 102.5 (black lines), 113.0 (blue lines), and 125 km (red lines) in the Earth’s polar atmosphere. Calculations were conducted for the considered Cases A (upper panel), B (middle panel), and C (bottom panel) of the precipitating fluxes of auroral electrons. Dashed lines correspond to the local Maxwellian distributions of atmospheric N with the parameters calculated by the MSISE90 empirical atmospheric model (see Figure 1).
Knowing the steady-state EDFs of the suprathermal N atoms at each height allows us to calculate their height profiles of hot nitrogen in the polar atmosphere of the Earth. In Figure 3, the calculated height profiles of the number density (upper panel), bulk velocity (middle panel), and mean kinetic energy (bottom panel) of the suprathermal N(4S) atoms in the polar atmosphere of the Earth are demonstrated. These atoms were formed due to the influx of auroral electrons with an energy flux of Q0 = 1 erg cm−2 s−1. As it was described above, the auroral electrons at the upper boundary were represented by a Maxwellian distribution by kinetic energy with the mean kinetic energies corresponding to the considered Cases A, B, and C of the auroral electron precipitation.
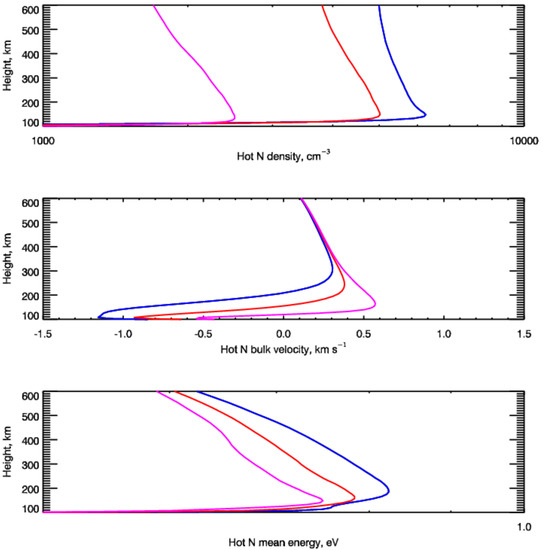
Figure 3.
Height distributions of the number density (upper panel), bulk velocity (middle panel), and mean kinetic energy (bottom panel) of the suprathermal N(4S) atoms in the polar atmosphere of the Earth. The blue lines correspond to Case A (E0 = 1 keV), red lines to Case B (E0 = 2 keV), and magenta lines to Case C (E0 = 5 keV).
It is seen that the peaks of height profiles of suprathermal N atoms in the polar atmosphere directly correspond to the peaks of the energy deposition by the precipitating auroral electrons (see, e.g., [9]). Also, it could be seen that the number densities of hot N atoms with kinetic energies higher than 0.3 eV are much lower than the number density of the ambient neutral atmosphere (see, e.g., the number densities of the main atmospheric species shown in the top panel of Figure 1). But the mean kinetic energy of hot N atoms is a few times higher than the thermal energy of the ambient atmospheric gas shown by the black line in the bottom panel of Figure 1. Therefore, such energetic N(4S) atoms could be considered as an additional source of nitric oxide in the polar Earth’s thermosphere.
3.2. Non-Thermal NO Production Due to the Auroral Electron Precipitation
Reactions (2) and (3) are the main processes in odd nitrogen atmospheric chemistry [27,37]. Because of an energy barrier of about 0.3 eV, reaction (3) proceeds slow at gas temperatures in the lower thermosphere. Thus, only energetic N(4S) atoms react with O2 at temperatures of the ambient atmosphere. The non-equilibrium energy distribution functions of the nitrogen atoms have been widely investigated for the mid- and low latitude of Earth’s atmosphere [19,23,27,35,38] where it had been established that a significant population of hot nitrogen atoms is created. But, in all of these studies, the transport of suprathermal N atoms in the planetary upper atmosphere was not taken into account.
Reaction (3) was extensively studied in both experimental (see, e.g., [39]) and theoretical (see, e.g., [40,41,42,43]) investigations. In the paper [44], the following value of 1.45 × 10−16T1.6 × e−2894/T cm3 molecule−1 s−1 at temperatures of 300–5000 K of the rate coefficient for reaction (3) was provided as an approximation of the experimental measurements and theoretical calculations. Calculations [23,35,38] have shown that reaction (3) dominates NO production at altitudes above 120 km and the reaction between atomic nitrogen in the metastable state N(2D) and O2 molecules dominates at lower altitudes. As it was mentioned above in all these studies, the transport of suprathermal N(4S) was not taken into account. This effect could be important for auroral regions of the terrestrial planets [9,14,15].
To estimate the input of the suprathermal N(4S) atoms into the non-thermal NO production in the polar regions of the Earth’s upper atmosphere, we extended the standard set of odd nitrogen chemistry, consisting of reactions (2), (3) and (5), by the additional reaction:
Nh(4S) + O2→NO + O.
This additional reaction takes into account the existence of nitrogen atoms of non-thermal origin with kinetic energies above 0.3 eV in the terrestrial upper atmosphere. In the case of polar regions, the main source is the dissociation (1) by the precipitating auroral electrons (see, e.g., [9]). Based on the calculated steady-state EDFs functions for the impact N2 dissociation by auroral electrons, we calculated the differential frequency for the additional reaction (8):
where v(E) is the relative velocity of interacting particles in (8) and is the energy-dependent cross-section for reaction (8) for which the results of theoretical calculations [41,42] were used.
Results of our calculations are given in Figure 4 for the different levels of solar activity, i.e., Cases A, B, and C. The height profiles of the calculated reaction (8) frequency are shown by black lines in Figure 4. To compare with non-thermal NO production, the reaction frequencies for thermal NO production in reactions (2) and (3) are also shown by red and blue lines, respectively. These frequencies were calculated for atmospheric atomic nitrogen using the following rate coefficients: K3 = 1.45 × 10−16T1.6 × e−2894/T cm3 molecule−1 s−1 [44] for reaction (3); and K2 = 6 × 10−12 cm3 molecule−1 s−1 [45] for reaction (2).
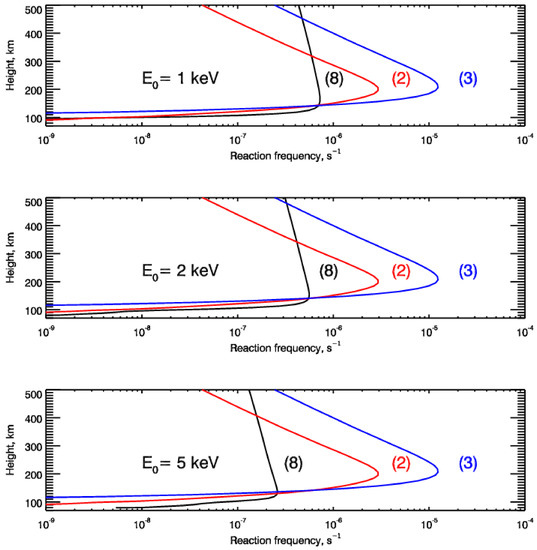
Figure 4.
Height profiles of non-thermal reaction frequency calculated with steady-state EDFs of the suprathermal N(4S) atoms for the considered Cases A (upper panel), B (middle panel), and C (bottom panel) of the auroral electron precipitation are shown by black lines. For comparison, in all panels, the frequencies for thermal NO production in reactions (2) and (3) are also shown by red and blue lines, respectively.
The comparison of the reaction frequencies responsible for the non-thermal and thermal NO production in the Earth’s polar atmosphere shows that the non-thermal frequency (8) has a different dependence on height comparing to the thermal frequencies (2) and (3) dependent on height. Because both thermal (reactions (2), (3), and (5)) and non-thermal (reactions (2), (3), (5), and (8)) models of odd nitrogen chemistry in the polar atmosphere are the stiff chemical systems (see, e.g., [20]), the addition of reaction (8), which is responsible for non-thermal NO production, can strongly change the solution of such a chemical system.
To summarize, in the upper panel of Figure 5, the height profiles of the non-thermal NO production in the reaction Nh(4S) + O2→NO + O are shown. These values are the frequencies of reaction (8) (black lines in Figure 4) multiplied by the local number densities of molecular oxygen. The non-thermal reaction frequencies were calculated with the steady-state EDFs of the suprathermal N(4S) atoms for the considered Cases A, B, and C of the precipitating auroral electrons with the energy flux of Q0 = 1 erg cm−2 s−1. The curves in the bottom panel represent the height profiles of the calculated production rates of fresh suprathermal N(4S) atoms formed in the N2 dissociation using the KMC model [9].
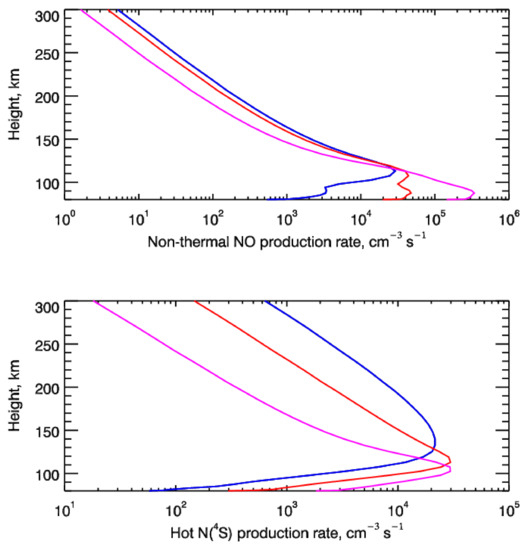
Figure 5.
(upper panel) Height profiles of the non-thermal NO production rate through the reaction Nh(4S) + O2→NO + O. These values were calculated with the steady-state EDFs of the suprathermal N(4S) atoms for the considered Cases A (blue line), B (red line), and C (magenta line) of the auroral electron precipitation. (bottom panel) The production rates of fresh suprathermal N(4S) atoms formed in the N2 dissociation by the precipitating auroral electrons for the same considered cases. The blue lines correspond to Case A (E0 = 1 keV), red lines to Case B (E0 = 2 keV), and magenta lines to Case C (E0 = 5 keV).
From the calculations presented in Figure 2, Figure 3, Figure 4 and Figure 5, it is seen that electron impact dissociation of N2 is an important source of suprathermal N atoms in the auroral regions of the N2-O2 atmospheres of terrestrial-type planets. Moreover, calculations of the steady-state energy distributions for suprathermal N(4S) atoms allowed us to estimate the possible input of hot N atoms into the non-thermal production of nitric oxide. To do this, we calculated the coupled set of reactions (2), (3), (5), and (8), in which the input of suprathermal N atoms was taken into account through reaction (8). The outputs of these calculations were the estimates of the NO density in the auroral atmosphere of the Earth. For this, the steady-state one-dimensional mass continuity equation was solved including vertical transport (due to the eddy and molecular diffusion) and neglecting horizontal transport (see, e.g., [46,47,48]). To remind the reader, the reaction rates used in these calculations were the following: K3 = 1.45 × 10−16 T1.6 × e−2894/T cm3 molecule−1 s−1 ([44], as discussed above); K2 = 6 × 10−12 cm3 molecule−1 s−1 [45]; and K5 = 3.4 × 10−12 cm3 molecule−1 s−1 [49]. The neutral atmosphere and temperature distribution were calculated from MSISE90 reference model [30] with the input parameters described above. The boundary conditions were the following: at the lowest altitude, the minimum of NO density was assumed, and at the highest altitude, there was supposedly no upward flux [46]. Thus, the described steady-state problem had the form of the Sturm–Liouville problem and was solved by the three-point elimination method [50]. It should be noted that, as it was mentioned above, calculations using the described model for Cases A–C were made with the assumption that the neutral atmosphere remains the same. The ratio of N(2D) and N(4S) production rates was also assumed the same for all cases. However, the concentration of NO can be strongly dependent on this ratio [27]. These assumptions as well as the stationary problem statement are rough but appropriate for our modeled estimates of thermal and non-thermal NO production in the Earth’s polar atmosphere under the different levels of solar activity.
Results of calculations of non-thermal production of NO in the polar regions of the Earth’s upper atmosphere are presented in the top panel of Figure 6. In this figure, the height profiles of the NO number density calculated in the odd nitrogen chemistry model without (black line) and with (color lines) taking into account the input of the suprathermal N(4S) atoms through reaction (8) are shown. The height profiles of NO number density were calculated for the considered Cases A, B, and C of the precipitating auroral electrons with an energy flux of Q0 = 1 erg cm−2 s−1. The bottom panel represents the height profiles of NO column densities and its color palette is the same as the top one. Figure 6 evidently shows that the input of suprathermal N(4S) atoms to the non-thermal production of NO is important because the auroral electron precipitation caused by the disturbed solar conditions results in the significant increase in NO abundance in the polar regions of the Earth’s atmosphere. It is seen that the peak values of NO number density (top panel of Figure 6) and NO column density (bottom panel of Figure 6) increase by a factor of a few times:
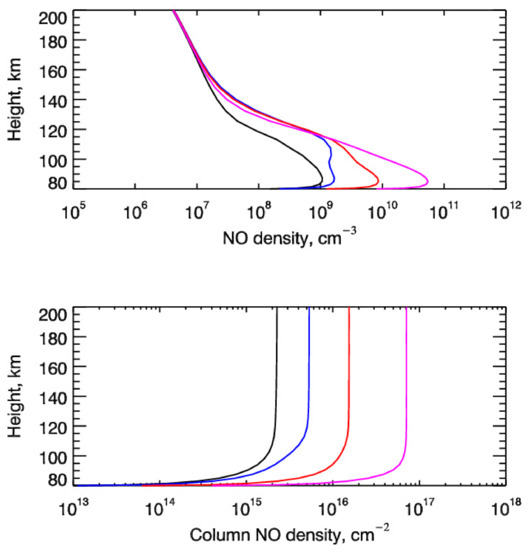
Figure 6.
(upper panel) Height profiles of the NO number density calculated in the odd nitrogen chemistry model without (black line) and with taking into account the input of the suprathermal N(4S) atoms through the reaction Nh(4S) + O2→NO + O. Height profiles of NO number density were calculated for the considered Cases A (E0 = 1 keV, blue lines), B (E0 = 2 keV, red lines), and C (E0 = 5 keV, magenta lines) of the auroral electron precipitation. (bottom panel) Height profiles of NO column densities calculated in the odd nitrogen chemistry model without (black line) and with taking into account the input of the suprathermal N(4S) atoms. The color palette is the same as at the top one.
- Peak NO number densities in low thermosphere heights between 80 and 110 km—no hot N(4S) atom input—1.1 × 108 cm−3 at h = 85 km; with hot N(4S) atom input—Case A—3.5 × 109 cm−3 between h = 85 and h = 105 km; Case B—9.0 × 109 cm−3 at h = 85 km; and Case C—5.7 × 1010 cm−3 at h = 85 km.
- Column NO densities—no hot N(4S) atom input—2.5 × 1015 cm−2; Case A—8.4 × 1015 cm−2; Case B—1.7 × 1016 cm−2; and Case C—7.9 × 1016 cm−2.
Therefore, it is necessary to conclude that non-thermal NO production should be taken into account in the aeronomic models of odd nitrogen chemistry in the polar atmosphere of the Earth and atmospheres of terrestrial-type exoplanets. Moreover, the presented results correspond to the calculations with the model inputs of precipitating fluxes of auroral electrons—Maxwellian distributions by energy with mean kinetic energies of 1, 2, and 5 keV and an energy flux of 1 erg cm−2 s−1. Under disturbed conditions of solar/stellar activity, the precipitating fluxes of auroral electrons could be characterized by much higher values of both mean kinetic energy (E0) and energy flux (Q0) (see, e.g., [31,51]), resulting in the higher values of the non-thermal NO production.
4. Discussion
A numerical kinetic Monte Carlo model was used to calculate the steady-state energy distribution functions of the suprathermal N(4S) atoms in the polar upper atmosphere formed due to the precipitation of high-energy auroral electrons into the N2-O2 atmospheres of the rocky planets in the solar and exosolar planetary systems. This model describes on a molecular level the collisions of the hot N(4S) atoms and atmospheric gas taking into account the stochastic nature of collisional scattering at suprathermal kinetic energies. It was found that the electron impact dissociation of N2 is an important source of suprathermal N atoms that increases significantly the non-thermal production of nitric oxide in the auroral regions. As it was estimated, when suprathermal nitrogen atoms are taken into account, the NO column density can potentially increase by a factor of 3, 7, and 32 at mean kinetic energies of E0 = 1, 2, and 5 keV for precipitating electrons, respectively, compared with the case when hot N(4S) atoms are not supplied to the input.
The consequences of the excess NO production during the auroral events in the polar atmosphere are twofold.
First, it is necessary to keep in mind that auroral electron precipitation is a sporadic event in the Earth’s polar atmosphere [31]. Therefore, the calculated non-thermal NO production caused by the auroral electron precipitation is also a sporadic input into the odd nitrogen chemistry in the polar regions. Nevertheless, the disturbed solar activity conditions are widely and often observed and usually are accompanied by auroral electron precipitation in the polar lower thermosphere. Such events as was shown in this paper could result in the significant increase in NO column density by the non-thermal source of nitric oxide. Further, the downward transport of NO by polar vortex to the mesosphere and stratosphere should be taken into account in the prognosis of climate change due to the solar forcing.
Second, the presented study of non-thermal NO production caused by the auroral electron precipitation results in the further understanding of the input of the hot fraction to the odd nitrogen chemistry in the N2-O2 atmospheres of terrestrial-type exoplanets. This problem is very important for estimating the possibility of the space observations of potential atmospheric biomarkers such as NO (for example, the γ-bands of this molecule, 205–248 nm) [5,6]. If terrestrial exoplanets located close-in to the host star are considered, then auroral electron precipitation can be much more powerful than on Earth, which, in turn, will increase non-thermal NO production and significantly improve the detectability of nitric oxide in the atmospheres of these planets. At the same time, the N2-O2 atmospheres of such close-in exoplanets can be resistant to high-XUV fluxes from the host star [52]. In addition, the lack of an exoplanet’s own magnetic field and the presence of only an induced one can also be a reason for high electron fluxes and, as a result, a sufficiently high production of NO to detect this molecule. Therefore, we will continue our studies of the non-thermal NO production in the N2-O2 atmospheres of hot sub-Neptunes and exo-Earths orbiting in the potential habitable zones of their host stars. The developed kinetic Monte Carlo models [8,9] will be used to calculate the distribution of nitric oxide formed by both thermal and non-thermal sources in the upper atmosphere of the terrestrial-type exoplanet depending on the stellar activity and to assess the possibility of observing nitric oxide as a potential atmospheric biomarker.
Author Contributions
V.S., conceptualization, numerical modeling, writing—review and editing; D.B., data analysis, writing—review and editing; G.T., data analysis, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
We acknowledge the financial support of the Russian Science Foundation, grant # 22-12-00364.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All necessary data are contained in this paper.
Acknowledgments
The authors are grateful to the reviewers and Editor of the Special Issue for useful comments. The authors are also grateful to A. G. Zhilkin for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Wit, T.D.; Ermolli, I.; Haberreiter, M.; Kambezidis, H.; Lam, M.M.; Lilensten, J.; Matthes, K.; Mironova, I.; Schmidt, H.; Seppälä, A.; et al. (Eds.) Earth’s Climate Response to a Changing Sun; EDP Science: Les Ulis, France, 2015. [Google Scholar] [CrossRef]
- Seppälä, A.; Funke, B.; Verronen, P. Impact of energetic particle precipitation on atmospheric chemistry and climate. In Earth’s Climate Response to a Changing Sun; EDP Science: Les Ulis, France, 2015; pp. 267–272. [Google Scholar] [CrossRef]
- Rozanov, E.V.; Calisto, M.; Egorova, T.A.; Peter, T.; Schmutz, W.K. Influence of the precipitating energetic particles on atmospheric chemistry and climate. Survays Geophys. 2012, 33, 483–501. [Google Scholar] [CrossRef]
- Lammer, H.; Sproß, L.; Grenfell, J.L.; Scherf, M.; Fossati, L.; Lendl, M.; Cubillos, P.E. The Role of N2 as a Geo-Biosignature for the Detection and Characterization of Earth-like Habitats. Astrobiology 2019, 19, 927–950. [Google Scholar] [CrossRef] [PubMed]
- Sproß, L.; Scherf, M.; Shematovich, V.I.; Bisikalo, D.V.; Lammer, H. Life is the Only Reason for the Existence of N2-O2-Dominated Atmospheres. Astron. Rep. 2021, 65, 275–296. [Google Scholar] [CrossRef]
- Tsurikov, G.N.; Bisikalo, D.V. On the Possibility of Observing Nitric Oxide on Terrestrial Exoplanets Using the WSO-UV Observatory. Astron. Rep. 2023, 67, 125–143. [Google Scholar] [CrossRef]
- Boyarchuk, A.A.; Shustov, B.M.; Savanov, I.S.; Sachkov, M.E.; Bisikalo, D.V.; Mashonkina, L.I.; Wiebe, D.Z.; Shematovich, V.I.; Shchekinov, Y.A.; Ryabchikova, T.A.; et al. Scientific problems addressed by the Spektr-UV space project (world space Observatory—Ultraviolet). Astron. Rep. 2016, 60, 1–42. [Google Scholar] [CrossRef]
- Bisikalo, D.V.; Shematovich, V.I.; Kaygorodov, P.V.; Zhilkin, A.G. Extended envelopes of hot Jupiters. Phys. Uspiekhy 2021, 64, 747–800. [Google Scholar] [CrossRef]
- Bisikalo, D.; Shematovich, V.; Hubert, B. The Kinetic Monte Carlo Model of the Auroral Electron Precipitation into N2-O2 Planetary Atmospheres. Universe 2022, 8, 437. [Google Scholar] [CrossRef]
- Gérard, J.C.; Barth, C.A. High-latitude nitric oxide in the lower thermosphere. J. Geophys. Res. 1977, 82, 674–680. [Google Scholar] [CrossRef]
- Barth, C.A.; Bailey, S.C.; Solomon, S.C. Solar–terrestrial coupling: Solar soft x-rays and thermospheric nitric oxide. Geophys. Res. Lett. 1999, 26, 1251–1254. [Google Scholar] [CrossRef]
- Barth, C.A.; Baker, D.N.; Mankoff, K.D.; Bailey, S.M. The northern auroral region as observed in nitric oxide. Geophys. Res. Lett. 2001, 28, 1463–1466. [Google Scholar] [CrossRef]
- Barth, C.A.; Mankoff, K.D.; Bailey, S.M.; Solomon, S.C. Global observations of nitric oxide in the thermosphere. J. Geophys. Res. 2003, 108, 1027–1038. [Google Scholar] [CrossRef]
- Dothe, H.; Duff, J.W.; Sharma, R.H.; Wheeler, N.B.; Wise, J.O. A model of odd nitrogen in the aurorally dosed nighttime terrestrial thermosphere. J. Geophys. Res. 2002, 107, 1071. [Google Scholar] [CrossRef]
- Sætre, C.; Barth, C.A.; Stadsnes, J. Thermospheric nitric oxide at higher latitudes: Model calculations with auroral energy input. J. Geophys. Res. 2007, 112, A08306. [Google Scholar] [CrossRef]
- Solomon, S.C. Auroral particle transport using Monte Carlo and hybrid methods. J. Geophys. Res. 2001, 106, 107–116. [Google Scholar] [CrossRef]
- Solomon, S.C. Global modeling of thermospheric airglow in the far ultraviolet. J. Geophys. Res. Space Phys. 2017, 122, 7834–7848. [Google Scholar] [CrossRef]
- Shematovich, V.I.; Bisikalo, D.V.; Gérard, J.C.; Cox, C.; Bougher, S.W.; Leblanc, F. Monte Carlo model of electron transport for the calculation of Mars dayglow emissions. J. Geophys. Res. 2008, 113, E02011. [Google Scholar] [CrossRef]
- Gérard, J.C.; Hubert, B.; Shematovich, V.I.; Bisikalo, D.V.; Gladstone, G.R. The Venus ultraviolet oxygen dayglow and aurora: Model comparison with observations. Planet. Space Sci. 2008, 56, 542–552. [Google Scholar] [CrossRef]
- Shematovich, V.I. Suprathermal particles in astrochemistry. Russ. Chem. Rev. 2019, 88, 1013–1045. [Google Scholar] [CrossRef]
- Shematovich, V.I.; Bisikalo, D.V.; Gérard, J.-C. Non-thermal nitrogen atoms in the earth’s thermosphere. I—Kinetics of hot N(4S). Geophys. Res. Lett. 1991, 18, 1691–1693. [Google Scholar] [CrossRef]
- Gérard, J.-C.; Shematovich, V.I.; Bisikalo, D.V. Non-thermal nitrogen atoms in the earth’s thermosphere. II—A source of nitric oxide. Geophys. Res. Lett. 1991, 18, 1695–1697. [Google Scholar]
- Gérard, J.C.; Shematovich, V.I.; Bisikalo, D.V.; Duff, J.W. An updated model of the hot nitrogen atom kinetics and thermospheric nitric oxide. J. Geophys. Res. 1997, 102, 285–292. [Google Scholar] [CrossRef]
- Bermejo-Pantaleón, D.; Funke, B.; López-Puertas, M.; García-Comas, M.; Stiller, G.P.; Von Clarmann, T.; Linden, A.; Grabowski, U.; Höpfner, M.; Kiefer, M.; et al. Global observations of thermospheric temperature and nitric oxide from MIPAS spectra at 5.3 μm. J. Geophys. Res. Space Phys. 2011, 116, A10313. [Google Scholar] [CrossRef]
- Hubert, B.; Gérard, J.-C.; Shematovich, V.I.; Bisikalo, D.V. High rotational excitation of NO infrared thermospheric airglow: A signature of superthermal nitrogen atoms? Geophys. Res. Lett. 1996, 23, 2215–2218. [Google Scholar] [CrossRef]
- Venkataramani, K.; Yonker, J.D.; Bailey, S.M. Contribution of chemical processes to infrared emissions from nitric oxide in the thermosphere. J. Geophys. Res. Space Phys. 2016, 121, 2450–2461. [Google Scholar] [CrossRef]
- Shematovich, V.I.; Bisikalo, D.V.; Gérard, J.-C. The thermospheric odd nitrogen photochemistry: Role of non-thermal N(4S) atoms. Ann. Geophys. 1992, 10, 792–801. [Google Scholar]
- Duff, J.W.; Dothe, H.; Sharma, R.H. A first-principles model of spectrally resolved 5.3 micron nitric oxide emission from aurorally dosed nighttime high-altitude terrestrial thermosphere. Geophys. Res. Lett. 2005, 32, L17108. [Google Scholar] [CrossRef]
- Cosby, P.C. Electron-impact dissociation of nitrogen. J. Chem. Phys. 1993, 98, 9544–9553. [Google Scholar] [CrossRef]
- Hedin, A.E. Extension of the MSIS thermosphere model into the middle and lower atmosphere. J. Geophys. Res. 1991, 96, 1159–1172. [Google Scholar] [CrossRef]
- Akasofu, S.-I. Exploring the Secrets of the Aurora; Astrophysics and Space Science Library; Springer: Berlin, Germany, 2007; Volume 346. [Google Scholar]
- Decker, D.T.; Kozelov, B.V.; Basu, B.; Jasperse, J.R.; Ivanov, V.E. Collisional degradation of the proton-H atom fluxes in the atmosphere: A comparison of theoretical techniques. J. Geophys.Res. 1996, 101, 26947–26960. [Google Scholar] [CrossRef]
- Kharchenko, V.; Balakrishnan, N.; Dalgarno, A. Thermalization of fast nitrogen atoms in elastic and inelastic collisions with molecules of atmospheric gases. J. Ofatmospheric Sol.-Terr. Phys. 1998, 60, 95–106. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kharchenko, V.; Dalgarno, A. Quantum mechanical and semiclassical studies of N + N2 collisions and their application to thermalization of fast N atoms. J. Chem. Phys. 1998, 108, 943–949. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Sergueeva, E.; Kharchenko, V.; Dalgarno, A. Kinetics and thermalization of hot N(4S) atoms in the upper atmosphere. J. Geophys. Res. 2000, 105, 18549–18555. [Google Scholar] [CrossRef]
- Nakayama, T.; Takahashi, K.; Matsumi, Y. Thermalization cross sections of suprathermal N(4S) atoms in collisions with atmospheric molecules. Geophys. Res. Lett. 2005, 32, L24803. [Google Scholar] [CrossRef]
- Solomon, S. The possible effect of translationally excited nitrogen atoms on lower thermospheric odd nitrogen. Planet. Space Sci. 1983, 31, 135–144. [Google Scholar] [CrossRef]
- Dothe, H.; Sharma, R.H.; Duff, J.W. On the steady-state assumption for the energy distribution function of the nonthermal N(4S) atoms and the efficiency of NO production by these atoms in the terrestrial thermosphere. Geophys. Res. Lett. 1997, 24, 3233–3236. [Google Scholar] [CrossRef]
- Caledonia, G.E.; Krech, R.H.; Oakes, D.B.; Lipson, S.J.; Blumberg, W.A.M. Products of the reaction of 8 km/s N (4S) and O2. J. Geophys. Res. 2000, 105, 12833–12837. [Google Scholar] [CrossRef]
- Duff, J.W.; Sharma, R.D. Quasiclassical trajectory study of the N (4S) + NO(2II)→N2(X1Σ+g) + O(3P) reaction rate coefficient. Geophys. Res. Lett. 1996, 23, 2777–2780. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Dalgarno, A. Rate coefficients for NO formation in energetic N+O2 collisions. Chem. Phys. Lett. 1999, 302, 485–488. [Google Scholar] [CrossRef]
- Sultanov, R.A.; Balakrishnan, N. Quantum mechanical investigations of the N(4S)+O2(X 3Σg-)-->NO(X 2Π)+O(3P) reaction. J. Chem. Phys. 2006, 124, 124321. [Google Scholar] [CrossRef]
- Esposito, F.; Armenise, I. Reactive, Inelastic, and Dissociation Processes in Collisions of Atomic Nitrogen with Molecular Oxygen. J. Phys. Chem. A 2021, 125, 3953–3964. [Google Scholar] [CrossRef]
- Sayos, R.; Oliva, C.; Gonzalez, M. New analyticalsurfaces and theoretical rate constants for the N(4S)+O2 reaction. J. Chem. Phys. 2002, 117, 670–678. [Google Scholar] [CrossRef]
- Lin, C.I.; Kaufman, F. Reactions of metastable nitrogen atoms. J. Chem. Phys. 1971, 55, 3760. [Google Scholar] [CrossRef]
- Bailey, S.M.; Barth, C.A.; Solomon, S.C. A model of nitric oxide in the lower thermosphere. J. Geophys. Res. 2002, 107, 1205. [Google Scholar] [CrossRef]
- Cleary, D.D. Daytime High-Latitude Rocket Observations of the NO γ, δ, ε bands. J. Geophys. Res. 1986, 91, 11337–11344. [Google Scholar] [CrossRef]
- Colegrove, F.D.; Hanson, W.B.; Johnson, F.S. Eddy diffusion and oxygen transport in the lower thermosphere. J. Geophys. Res. 1965, 70, 4931–4941. [Google Scholar] [CrossRef]
- Lee, J.H.; Michael, J.V.; Payne, W.A.; Stief, L.J. Absolute rate of the reaction of N(4S) with NO from 196–400 K with DF–RF and FP–RF techniques. J. Chem. Phys. 1978, 69, 3069–3076. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Nikolaev, E.S. Numerical Methods for Grid Equations: Volume I Direct Methods; Birkhäuser: Basel, Switzerland, 1989. [Google Scholar]
- Vidotto, A.A. The evolution of the solar wind. Living Rev. Sol. Phys. 2021, 18, 3. [Google Scholar] [CrossRef]
- Nakayama, A.; Ikoma, M.; Terada, N. Survival of Terrestrial N2–O2 Atmospheres in Violent XUV Environments through Efficient Atomic Line Radiative Cooling. Astrophys. J. 2022, 937, 72. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).