Computerized Ionospheric Tomography Based on the ADS-B System
Abstract
1. Introduction
2. Materials and Methods
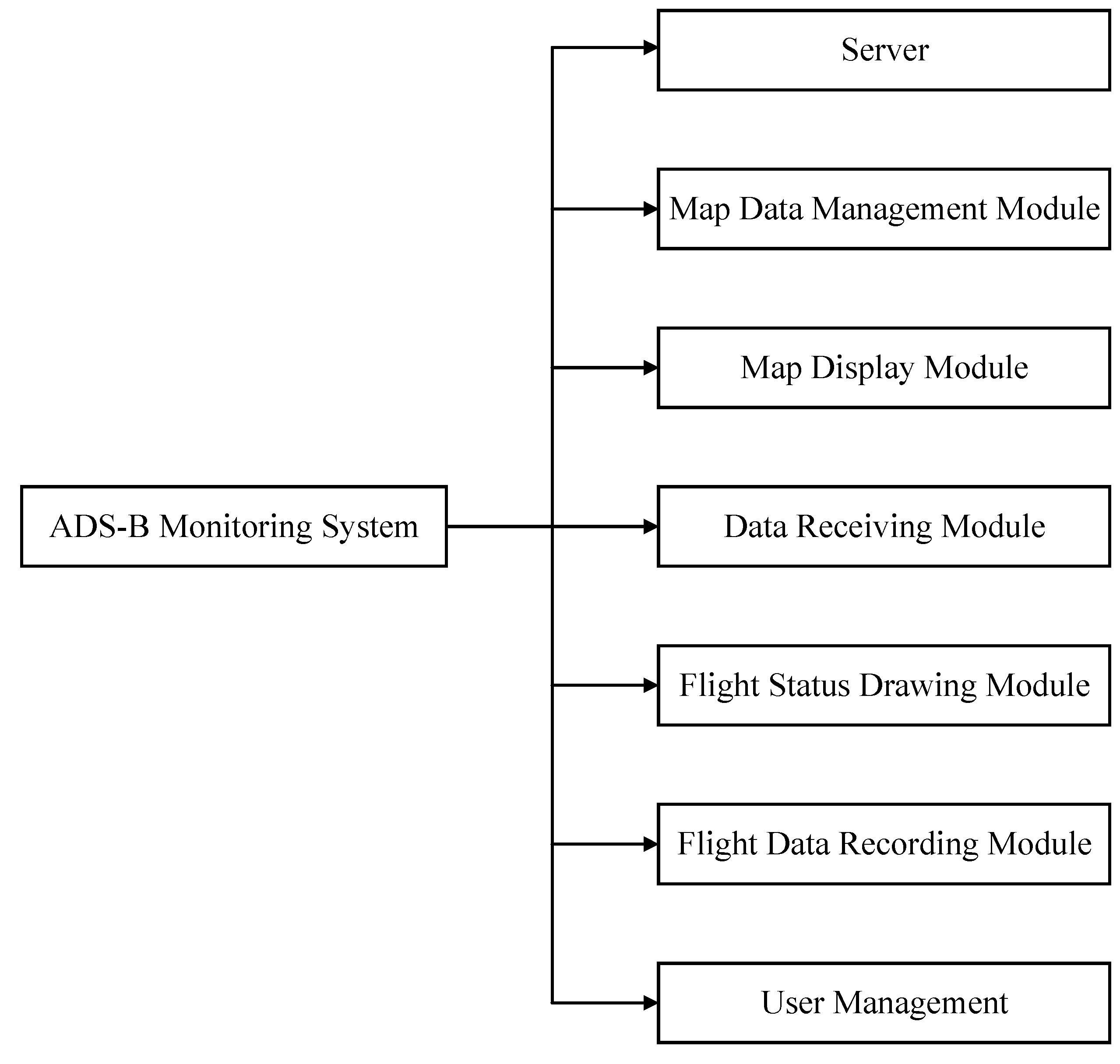
2.1. ADS-B Signal
2.2. Ionospheric Computerized Tomography
2.2.1. IRI Model
2.2.2. Multiplicative Algebra Reconstruction
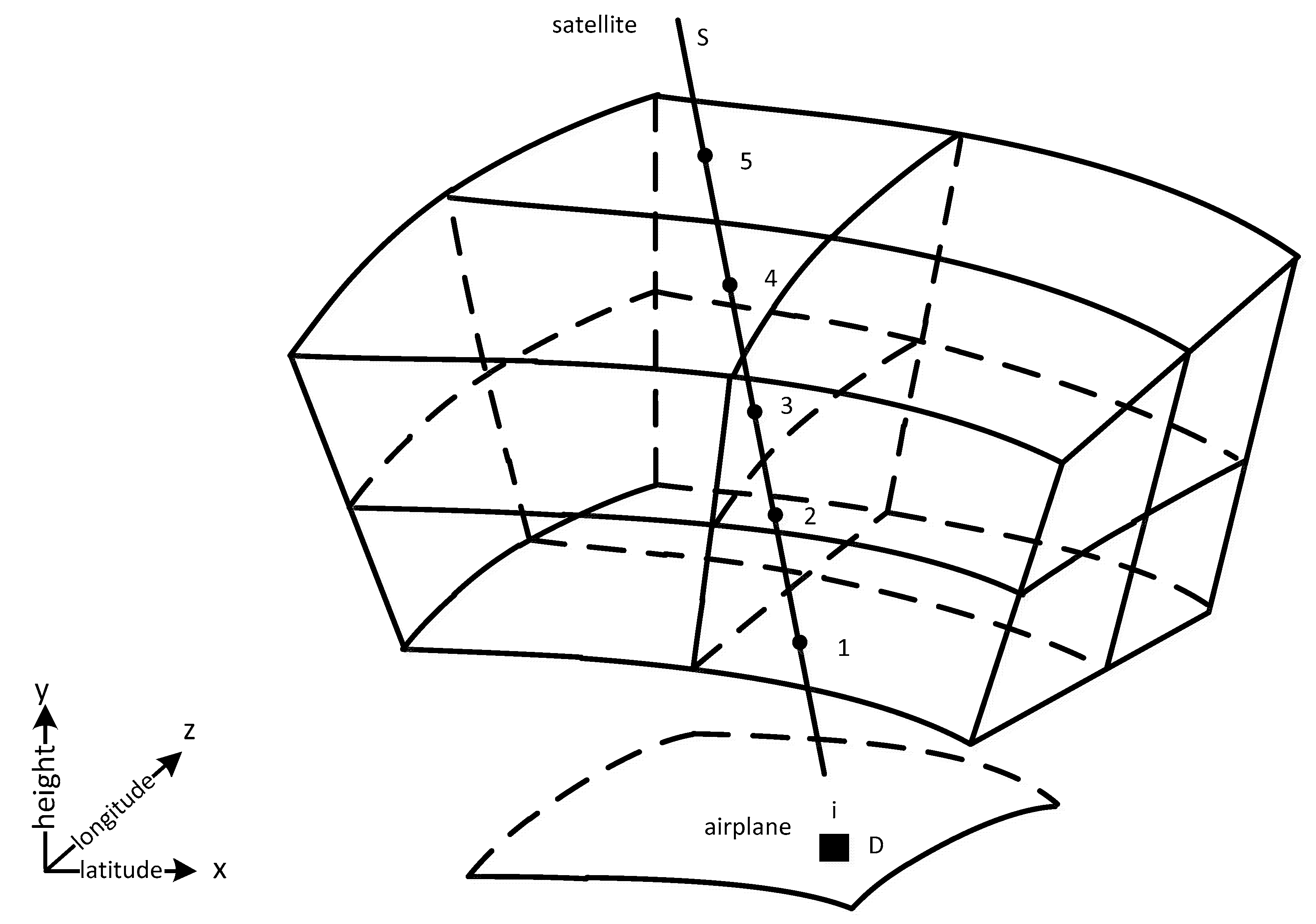
2.2.3. Establishment of Chromatographic Equation
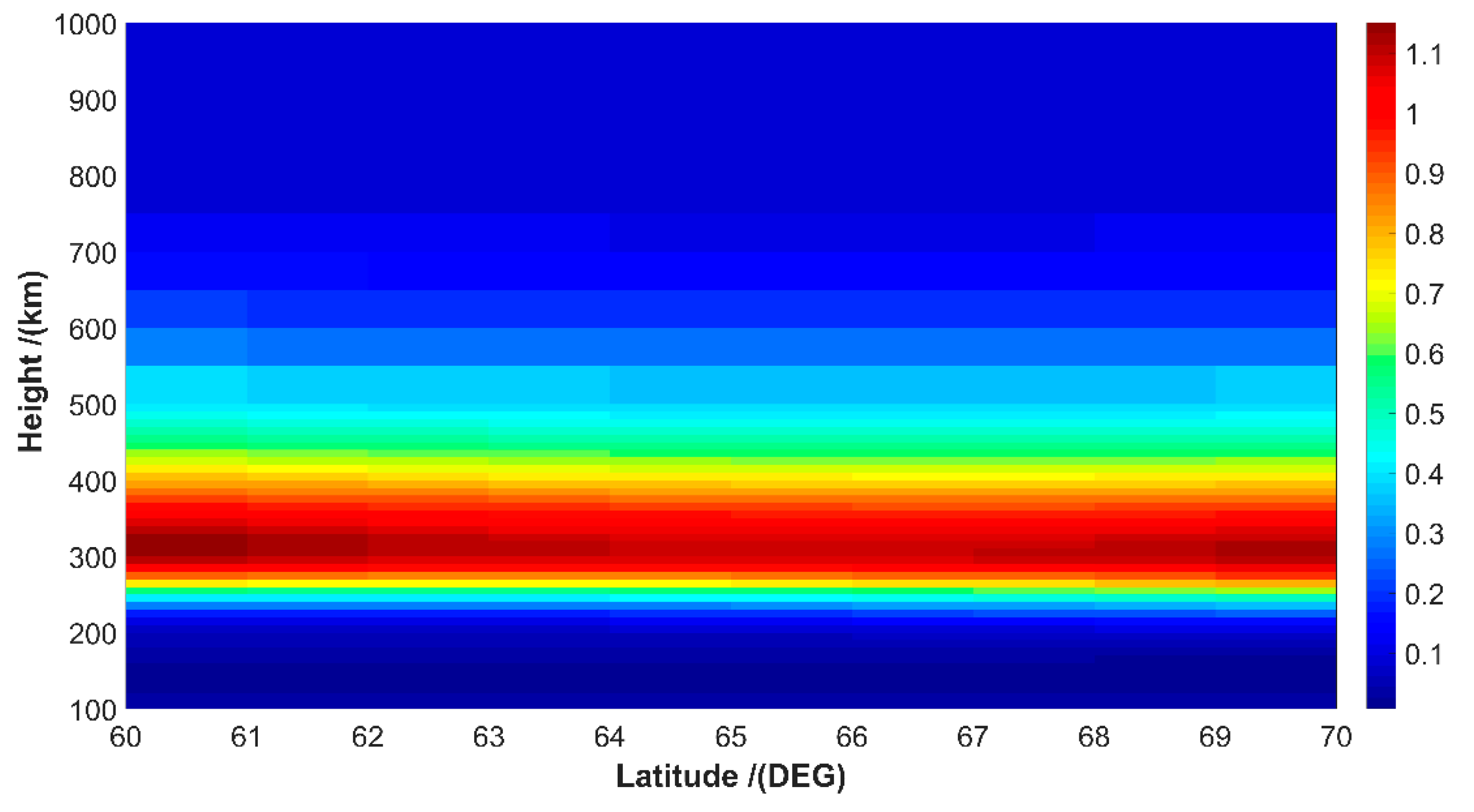
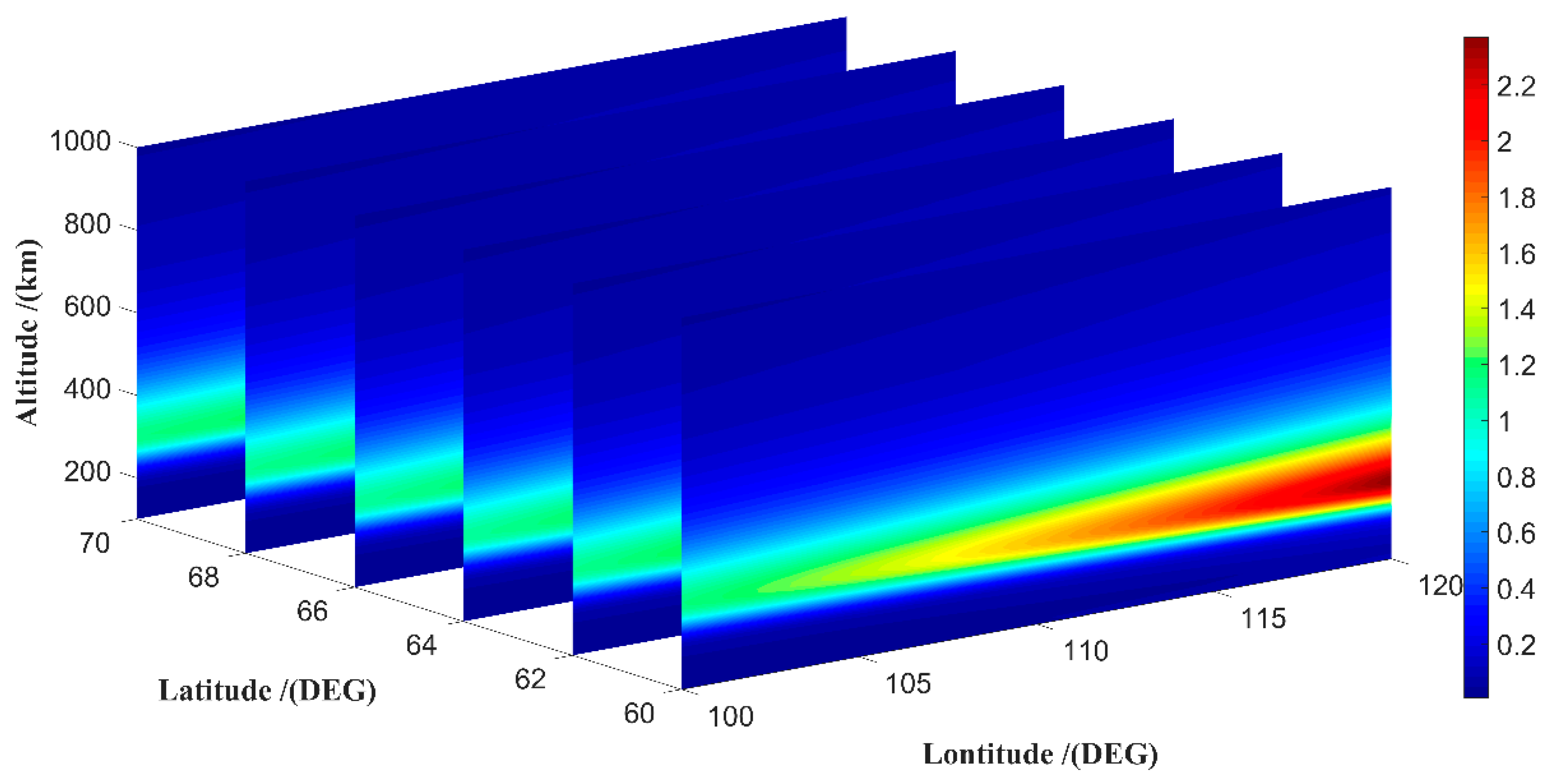
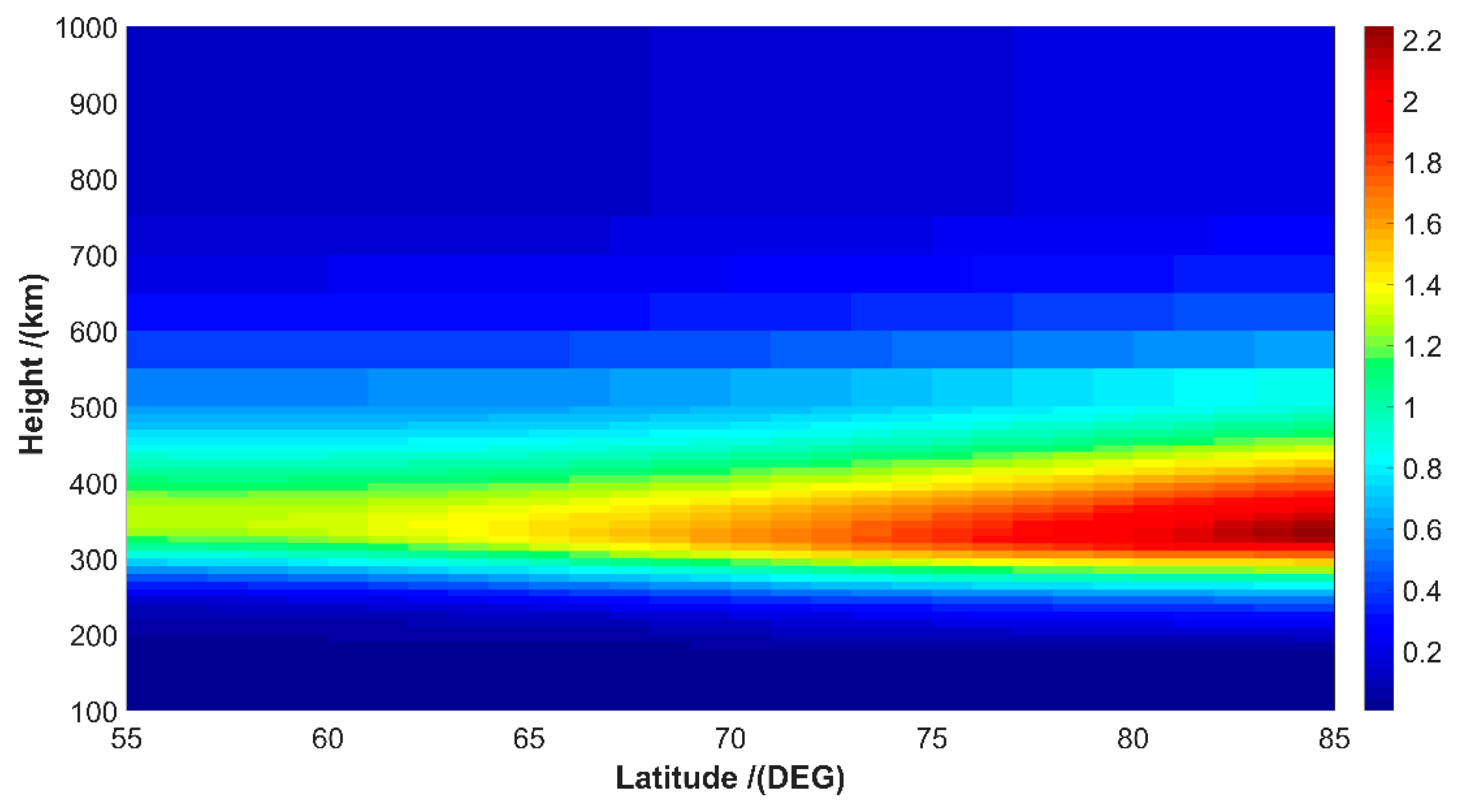
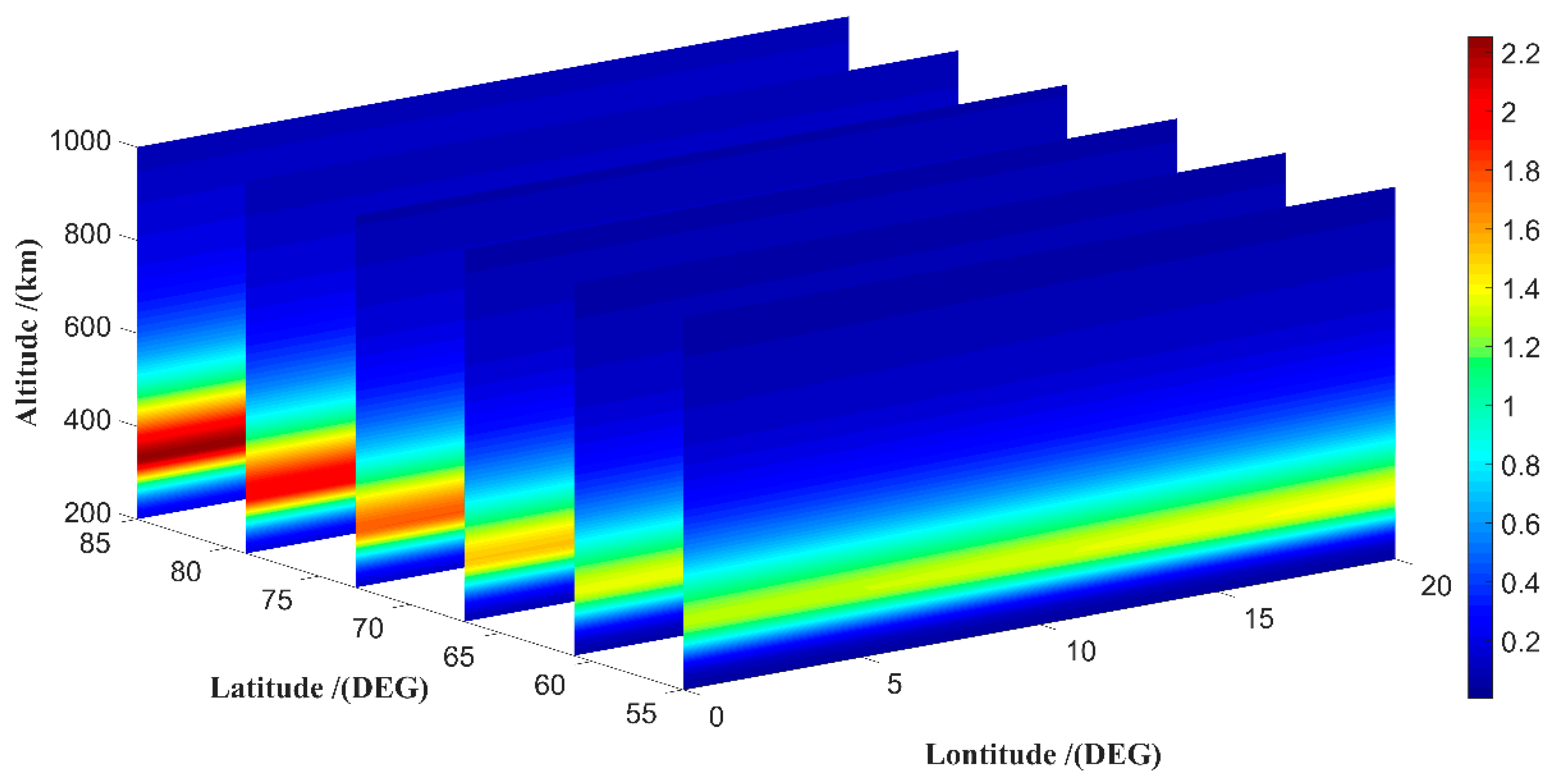
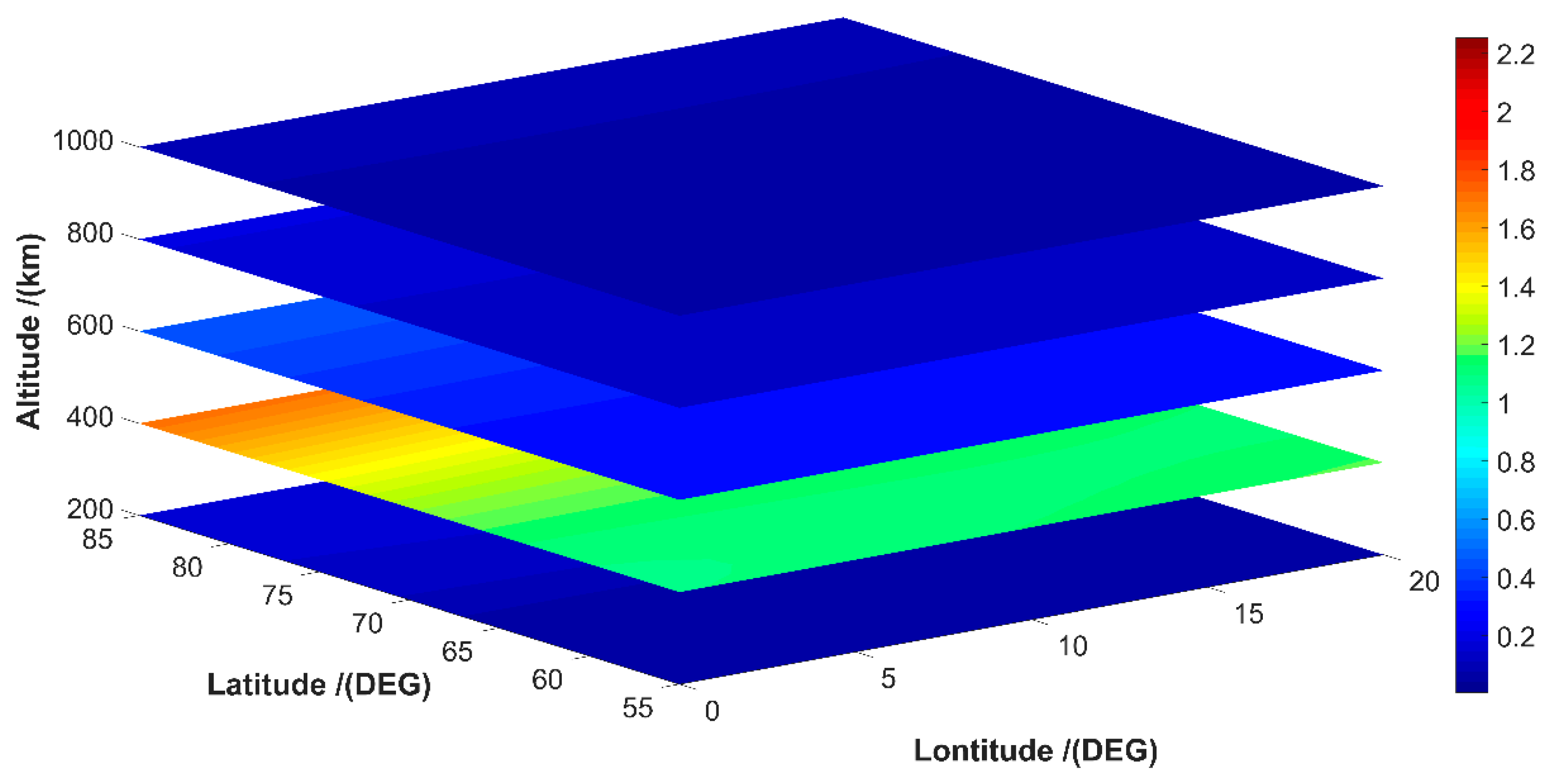
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pryse, S.E. Radio Tomography: A New Experimental Technique. Surv. Geophys. 2003, 24, 1–38. [Google Scholar] [CrossRef]
- Aarons, J. Global Morphology of Ionospheric Scintillations. Proc. IEEE 1982, 70, 360–378. [Google Scholar] [CrossRef]
- Alexander, P.; de la Torre, A.; Hierro, R.; Llamedo, P. Assessment of precision in ionospheric electron density profiles retrieved by GPS radio occultations. Adv. Space Res. 2014, 54, 2249–2258. [Google Scholar] [CrossRef]
- Huang, L.; Wang, J.; Jiang, Y.; Huang, J.; Chen, Z.; Zhao, K. A preliminary study of the single crest phenomenon in total electron content (TEC) in the equatorial anomaly region around 120°E longitude between 1999 and 2012. Adv. Space Res. 2014, 54, 2200–2207. [Google Scholar] [CrossRef]
- Brunini, C.; Azpilicueta, F.J. Accuracy assessment of the GPS-based slant total electron content. J. Geodesy 2009, 83, 773–785. [Google Scholar] [CrossRef]
- Sayyed, M.I.; Akman, F.; Geçibesler, I.H.; Tekin, H.O. Measurement of mass attenuation coefficients, effective atomic numbers, and electron densities for different parts of medicinal aromatic plants in low-energy region. Nucl. Sci. Tech. 2018, 29, 144. [Google Scholar] [CrossRef]
- Brandi, F.; Gizzi, L.A. Optical diagnostics for density measurement in high-quality laser-plasma electron accelerators. High Power Laser Sci. Eng. 2019, 7, 40–50. [Google Scholar] [CrossRef]
- Inada, Y.; Aono, K.; Ono, R.; Kumada, A.; Hidaka, K.; Maeyama, M. Two-dimensional electron density measurement of pulsed positive primary streamer discharge in atmospheric-pressure air. J. Phys. D Appl. Phys. 2017, 50, 174005. [Google Scholar] [CrossRef]
- Van Der Pryt, R.; Vincent, R. A Simulation of Reflected ADS-B Signals over the North Atlantic for a Spaceborne Receiver. Positioning 2016, 07, 51–62. [Google Scholar] [CrossRef]
- Cushley, A. Ionospheric Tomography Using Faraday Rotation of Automatic Dependent Surveillance Broadcast (UHF) Signals. Master’s Thesis, Royal Military College of Canada, Kingston, ON, USA, 2013. [Google Scholar]
- Cushley, A.C.; Noël, J.-M. Ionospheric tomography using ADS-B signals. Radio Sci. 2014, 49, 549–563. [Google Scholar] [CrossRef]
- Cushley, A.C.; Kabin, K.; Noël, J.-M. Faraday rotation of Automatic Dependent Surveillance-Broadcst (ADS-B) signals as a method of ionospheric characterization. Radio Sci. 2017, 52, 1293–1300. [Google Scholar] [CrossRef]
- Cushley, A.C.; Noel, J.-M. Ionospheric sounding and tomography using Automatic Identification System (AIS) and other signals of opportunity. Radio Sci. 2020, 55, e2019RS006872. [Google Scholar] [CrossRef]
- Wright, J.W. Ionogram inversion for a tilted ionosphere. Radio Sci. 1990, 25, 1175–1182. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, Y.; Skone, S. A study of smoothed TEC precision inferred from GPS measurements. Earth Planets Space 2005, 57, 999–1007. [Google Scholar] [CrossRef]
- Abdulaziz, A.; Yaro, A.S.; Adam, A.A.; Kabir, M.T.; Salau, H.B. Optimum Receiver for Decoding Automatic Dependent Surveillance Broadcast (ADS-B) Signals. Am. J. Signal Process. 2015, 5, 23–31. [Google Scholar] [CrossRef]
- Zeitlin, A.D.; Strain, R.C. Augmenting ADS-B with Traffic Information Service-Broadcast. IEEE Aerosp. Electron. Syst. Mag. 2003, 18, 13–18. [Google Scholar] [CrossRef]
- Zhang, Z. Optimization Performance Analysis of 1090ES ADS-B Signal Separation Algorithm based on PCA and ICA. Int. J. Perform. Eng. 2018, 14, 741–750. [Google Scholar] [CrossRef]
- Francis, R.; Vincent, R.; Noël, J.; Tremblay, P.; Desjardins, D.; Cushley, A.; Wallace, M. The Flying Laboratory for the Observation of ADS-B Signals. Int. J. Navig. Obs. 2011, 2011, 973656. [Google Scholar] [CrossRef]
- Xu, J.S.; Zou, Y.H.; Ma, S.Y. Time-dependent 3-D Computerized Ionospheric Tomography with Ground-Based GPS Network and Occultation Observations. Chin. J. Geophys. 2005, 48, 835–844. [Google Scholar] [CrossRef]
- Zhou, C.; Lei, Y.; Li, B.; An, J.; Zhu, P.; Jiang, C.; Zhao, Z.; Zhang, Y.; Ni, B.; Wang, Z.; et al. Comparisons of ionospheric electron density distributions reconstructed by GPS computerized tomography, backscatter ionograms, and vertical ionograms. J. Geophys. Res. Space Phys. 2015, 120, 11–32, 47. [Google Scholar] [CrossRef]
- Bilitza, D.; Brown, S.A.; Wang, M.Y.; Souza, J.R.; Roddy, P.A. Measurements and IRI model predictions during the recent solar minimum. J. Atmos. Sol.-Terr. Phy. 2012, 86, 99–106. [Google Scholar] [CrossRef]
- Adeniyi, J.O. Experimental equatorial ionospheric profiles and IRI model profiles. J. Atmos. Sol.-Terr. Phys. 1997, 59, 1205–1208. [Google Scholar] [CrossRef]
- Kimura, I.; Tsunehara, K.; Hikuma, A.; Su, Y.Z.; Kasahara, Y.; Oya, H. Global electron density distribution in the plasmasphere deduced from Akebono wave data and the IRI model. J. Atmos. Sol.-Terr. Phy. 1997, 59, 1569–1586. [Google Scholar] [CrossRef]
- Wen, D.; Wang, Y.; Norman, R. A new two-step algorithm for ionospheric tomography solution. Gps Solut. 2012, 16, 89–94. [Google Scholar] [CrossRef]
- Wen, D.; Liu, S. A new ionospheric tomographic algorithm—Constrained multiplicative algebraic reconstruction technique (CMART). J. Earth Syst. Sci. 2010, 119, 489–496. [Google Scholar] [CrossRef]
- Fougere, P.F. Ionospheric radio tomography using maximum entropy 1. Theory and simulation studies. Radio Sci. 1995, 30, 429–444. [Google Scholar] [CrossRef]
- Buresova, D.; Nava, B.; Galkin, I.; Angling, M.; Stankov, S.M.; Coisson, P. Data ingestion and assimilation in ionospheric models. Ann. Geophys. 2009, 52, 235–253. [Google Scholar] [CrossRef]
- Das, S.K.; Shukla, A.K. Two-dimensional ionospheric tomography over the low-latitude Indian region: An intercomparison of ART and MART algorithms. Radio Sci. 2011, 46, 1–13. [Google Scholar] [CrossRef]
- Wen, D.; Liu, S.; Tang, P. Tomographic reconstruction of ionospheric electron density based on constrained algebraic reconstruction technique. Gps Solut. 2010, 14, 375–380. [Google Scholar] [CrossRef]
- Gritti, F.; Guiochon, G. Fundamental chromatographic equations designed for columns packed with very fine particles and operated at very high pressures. J. Chromatogr. A 2008, 1206, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Krankowski, A.; Zakharenkova, I.; Krypiak-Gregorczyk, A.; Shagimuratov, I.I.; Wielgosz, P. Ionospheric electron density observed by FORMOSAT-3/COSMIC over the European region and validated by ionosonde data. J. Geod. 2011, 85, 949–964. [Google Scholar] [CrossRef]
- Wen, D.; Yuan, Y.; Ou, J. Monitoring the three-dimensional ionospheric electron density distribution using GPS observations over China. J. Earth Syst. Sci. 2007, 116, 235–244. [Google Scholar] [CrossRef]
- Le, H.; Han, T.; Li, Q.; Liu, L.; Chen, Y.; Zhang, H. A new global ionospheric electron density model based on grid modeling method. Space Weather 2022, 20, e2021SW002992. [Google Scholar] [CrossRef]
- Zhao, J.; Tang, Q.; Zhou, C.; Zhao, Z.; Wei, F. Three-dimensional ionospheric tomography based on compressed sensing. GPS Solut. 2023, 27, 90. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Yuan, Z.; Zhu, Q.; Wang, H.; Sun, F.; Zhu, J.; Liu, Y.; Zhou, C. Computerized Ionospheric Tomography Based on the ADS-B System. Atmosphere 2023, 14, 1091. https://doi.org/10.3390/atmos14071091
Dong X, Yuan Z, Zhu Q, Wang H, Sun F, Zhu J, Liu Y, Zhou C. Computerized Ionospheric Tomography Based on the ADS-B System. Atmosphere. 2023; 14(7):1091. https://doi.org/10.3390/atmos14071091
Chicago/Turabian StyleDong, Xiang, Zhigang Yuan, Qinglin Zhu, Haining Wang, Fang Sun, Jiawei Zhu, Yi Liu, and Chen Zhou. 2023. "Computerized Ionospheric Tomography Based on the ADS-B System" Atmosphere 14, no. 7: 1091. https://doi.org/10.3390/atmos14071091
APA StyleDong, X., Yuan, Z., Zhu, Q., Wang, H., Sun, F., Zhu, J., Liu, Y., & Zhou, C. (2023). Computerized Ionospheric Tomography Based on the ADS-B System. Atmosphere, 14(7), 1091. https://doi.org/10.3390/atmos14071091







