Abstract
Energetic electron precipitation (EEP) into the atmosphere are considered to play an important role in the natural forcing of the ozone variability and dynamics of the middle atmosphere during magnetospheric and geomagnetic disturbances. Energetic electrons from the radiation belt spill out into the atmosphere during geomagnetic disturbances and cause additional ionization rates in the polar middle atmosphere. These rates of induced atmospheric ionization lead to the formation of radicals in ion-molecular reactions at the heights of the mesosphere with the formation of reactive compounds of odd nitrogen groups NO and odd hydrogen groups HO. These compounds are involved in catalytic reactions that destroy ozone. The percentage of ozone destruction can depend not only intensity of EEP but also on season where it happens. In this work, we study mesospheric ozone depletion depending on seasons and precipitating energetic electrons with energies from keV up to relativistic energies about 1 MeV, based on the NOAA POES satellites observations in 2003. For estimation ozone deplation we use a one-dimensional radiative-convective model with ion chemistry. As one of the main results, we show that, despite the intensity of EEP-induced ionization rates, polar mesospheric ozone cannot be destroyed by EEP in summer in the presence of UV radiation. In winter time, the maximum ozone depletion, at altitude of about 80 km, can reach up to 80% during strong geomagnetic disturbances. In fall and spring, the maximum ozone depletion is less intense and can reach 20% during strong geomagnetic disturbances. Linear relation of EEP induced maximum mesospheric ozone depletion depending on geomagnetic disturbances and seasons have been obtained.
1. Introduction
The precipitating electrons of the radiation belt are considered to play an important role in the natural forcing of the middle atmosphere.
Precipitated electrons collide with molecules of air and induce increasing atmospheric ionization rates (formation of ion pairs per second) [1,2] and references therein. Ionization rates play a key role in production of reactive odd nitrogen (NO = N + NO + NO and NO = NO + NO + 2NO + HNO), e.g., [3,4] and odd hydrogen (HO = H + OH + HO), e.g., [5,6] in the atmosphere. HO production by energetic electron precipitation (EEP) occurs only below about 90 km altitude where enough water vapor is available and NO production by auroral electrons and energetic electrons accelerates mostly about 110–100 km altitude [4,7]. Finally energetic electron precipitation via production of ion pairs impacts middle atmosphere chemistry, dynamics and leads to ozone depletion, e.g., [1,4,8,9,10,11,12].
Ozone depletion in the polar mesosphere about 60–80 km is a reason by enhanced HO and NO concentrations that involves known catalytical ozone destruction cycles, e.g., [9,10,12,13]. The maximum ozone depletion in the polar mesosphere is the most pronounced at altitudes about 79 km and can exceed up to 90% for days, e.g., [10,11]. Such ozone depletion under EEP is comparable to the ozone destruction after one of the most powerful solar energetic particle (SEP) event of January 2005 [14].
Ozone depletion stands upon on intensity of energetic particle precipitation through the inducing atmospheric ionization rates, which in case of EEP strongly depend on geomagnetic activity. In this article, we propose a study of this relationship. As a parameter characterizing geomagnetic disturbance, we chose the planetary index of geomagnetic disturbance Kp, dividing EEP events into three groups according to the magnitude of geomagnetic activity.
On the other hand, the depletion of the ozone layer also depends on solar radiation and, therefore, on the season. It is known that the reactions involved in ozone depletion in the summer and winter polar regions are basically different [8]. The investigation of ozone depletion under moderate SEP that takes place during a polar night season lead to a large amount of ozone destruction that can be explained to formation of HO and NO in the polar cap atmosphere and lead to more ozone destruction [15]. Some studies of ozone variability under SEP, show that ozone quickly recovers after SEP event end in the presence of solar radiation, whereas over the dark area the ozone demonstratesl depletion, without recovery [16,17]. In the paper we explore not only summer and winter (as periods of maximum and minimum influence of solar radiation), but also intermediate seasons.
In this paper, we study the mesosphere ozone depletion as a function of the season and the precipitation of energetic electrons with energies from keV to relativistic energies of about 1 MeV based on the NOAA POES satellite observations in 2003. To estimate ozone depletion, we use a one-dimensional radiative-convective model with ion chemistry [18].
2. Materials and Methods
2.1. Energetic Electron Presipitation during Geomagnetic Disturbances
Near-Earth satellites, such as the Polar-orbiting Operational Environmental Satellites (POES) registre precipitating electrons at altitude about 820 km, e.g., [19,20]. The Medium Energy Proton and Electron Detectors (MEPED) instrument on board the NOAA POES spacecraft has two identical electron telescopes with solid-state detectors and measures electrons in several energy channels. Vertical telescope measures precipitating electrons, while the horizontal telescopes track particles trapped in the Van Allan radiation belts [19]. In our study we use data from the MEPED vertical electron telescope to estimate electron precipitation in high-latitude regions, where the EEP increase significantly during the period of geomagnetic disturbances. The EEP data were taken from the MEPED in three electron energy channels E1, E2, and E3 with electron energies >30, >100, and >300 keV, respectively [19]. In addition, we use the P6 proton channel (>6900 keV), which is contaminated electrons with energies above 800 keV, while the P5 proton channel (2500–6900 keV) is free of electrons. This means that in the absence particles in the P5 channel, the P6 channel registers electrons with energies above 800 keV [20].
Energetic electron precipitation into atmosphere leads to induce ionization rates of the atmosphere. The ionization rates of the atmosphere are the key parameter that uses in one-dimensional radiative-convective model with ion chemistry to estimate ozone destruction and climate change under energetic particle forcing. In this study we compute the ionization rates (ion pairs g s ) as follows: , where is a spectral distribution (cm s sr keV) of precipitating electrons at the top of atmosphere, and and are the minimum and maximum energies of electrons in a flux. The calculation of the yield function is discussed in the recent paper [21]. The power-law integral energy spectra are fitted MEPED POES satellite EEP flux mesurements.
In 2003 there were three satellites (NOAA POES 15, 16, and 17) in near-Earth space, separated by 100 degree in longitude. Based on a comparison of the results of EEP measurements on balloons [22,23] and onboard POES satellites in 2003, we propose a criterion that makes it possible to constantly monitor EEP ionization at stratospheric heights of the atmosphere using observations on POES satellites [24]. The criterion [24] reads that P6 channel reading more or equal 100 pfu with zero P5 gives us information about EEP that can be observed at stratospheric heights of the atmosphere. It should be noted that criterion [24] does not work during the injection of solar energetic particles or in other words during SEP events, because proton channel P5 registers protons at this time.
For our study the results of all three POES satellites (NOAA POES 15, 16, and 17) that met the specified conditions were averaged over a day. We use 16-s. MEPED measurement results that meet the following conditions: measurement geographic latitude of foot-of-field-line 60–70, geographic longitude of foot-of-field-line 0–360, McIlwain parameter 4–8. All SEP events as well as a period that includes the major solar particle event on the end of October 2003 known as the “Halloween storm” were excluded, because channel P5 registers not electrons during these time intervals and we take only those days when the electron precipitation was observed for at least 320 s.
EEP is strongly depend on geomagnetic disturbances, although this relationship is complex. This relationship includes many processes that the supply and accumulation of energy in the magnetosphere from the solar wind, the development of various waves, and the interaction of waves with particles. As a result, both the acceleration of electrons and their entry into the loss cone lead to precipitation of energetic electrons into the Earth’s atmosphere.
The strength of geomagnetic disturbances or geomagnetic storms is usually determined using various geomagnetic indices like as AE, Kp and Dst etc. In our study we devided EEP on different levels of geomagnetic disturbances based on Kp index. Kp index is a planetary index characterizing the global disturbances of the Earth’s magnetic field in a three-hour time interval. For our study, we chose levels of geomagnetic activity as (1)—strong geomagnetic disturbances where Kp · 10 ⩾ 50, (2)—a moderate geomagnetic environment with a Kp · 10 index is Kp · 10 < 50 and (3)—quiet conditions , where Kp · 10 < 30.
According to our EEP selection we have for quiet geomagnetic conditions -16 EEP events, for moderate geomagnetic conditions -155 EEP events and or high geomagnetic conditions -114 EEP events.
Figure 1 shows ionization rate profiles variablity during 2003 devided by various levels of geomagnetic activity. At Figure 1 blue lines present altitude profiles of atmospheric ionization for all events. In addition, the figure shows the mean ionization rate profile for all events (solid black line) and that within , and (red, orange and yellow lines respectively). One can see that the maximum ionization rates for almost all events are at the upper boundary of the mesosphere, at an altitude of about 90 km. As expected, the means within groups , and correlate as follows: mean () > mean () > mean (). Based on this result, we expect to find perturbations in the studied chemistry in the same ratio.
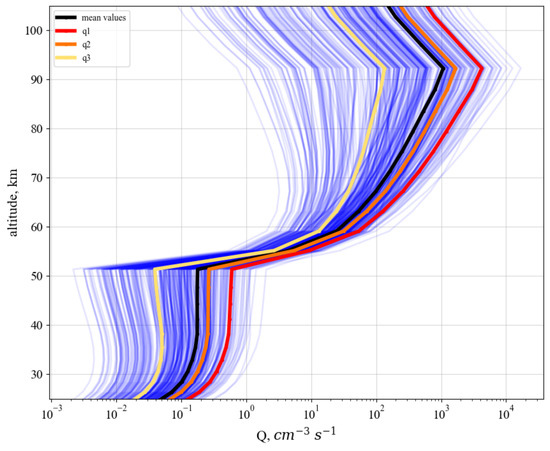
Figure 1.
Blue lines—variability of ionization rate profiles during 2003. Black line—mean values of ionization rates for 2003. Red line—mean values of ionization rates for high geomagnetic conditions (Kp·10 ⩾ 50). Orange line—mean values of ionization rates for moderate geomagnetic conditions ( Kp·10 < 50 ). Yellow line—mean values of ionization rates for quiet geomagnetic conditions (Kp·10 < 30).
2.2. One-Dimensional Radiative-Convective Photochemical Model with Ion Chemistry
In this study we applied the discussed EEP induced ionization rates during two hours (8–10 UT) into one-dimensional radiative-convective photochemical model with interactive neutral and ion chemistry. The reason for choosing this time interval is dictated by the circumstances of the observation of EEP precipitation by balloon observations over selected regions [24] and the model time step. In the one-dimensional radiative-convective photochemical model the complete ion chemistry scheme while modeling for studying processes in the stratosphere and upper mesosphere is used [18]. An ionic–photochemical block of the 1D-model is the main block with consideration for 30 positively charged ions, 12 negative ions and 29 neutrally charged gases. The model runs also include the ionization by solar radiation in the Lyman- line (121.6 nm) and the ionization in the UV region 102.7–111.8 nm. And in addition the ionization by EEP was included as described in the Section 2.1.
Since the complete ion chemistry applied on top of standard parameterization, including more than 100 reactions of ion chemistry [4], we can receive results in nitric chemical family NO and in odd hydrogen family HO, that includes HO = H + OH + HO. The NO chemical family includes NO = NO + NO + 2NO + HNO.
One-dimensional radiative-convective photochemical model with ion chemistry also includes the main catalytic reactions with NO that lead to the destruction of ozone: NO + O = NO + O and NO + O = NO + O⇒ O + O = 2O. And catalytic reactions with odd hydrogen HO that is also an effective catalyst for the destruction of O, especially in the mesosphere: OH + O = HO + O and HO + O = OH + O⇒ O + O = 2O.
2.3. Superposed Epoch Analysis
As it was mentioned above we separated the EEP events of 2003 in three groups based on their association with high geomagnetic disturbances , moderate geomagnetic environment and quiet conditions . We conducted superposed epoch analysis method within each group separately to obtain averaged information on how the magnitudes of geomagnetic activity and ozone depletion in the upper mesosphere are related. For all three datasets ozone losses during events chosen superposed on each other. The zero epoch is the midnight - the time where simulations with one-dimensional radiative-convective photochemical model with ion chemistry is started. Since the ionization rates for all selected events was applied in between 8 and 10 AM, the effects are observed since these time points. Note that the ionization from the impact of the EEP is applied for 2 h within each event. The effect within each event can last for several days.
2.4. Seasonal Partition Description
The paper also presents the results of considering seasonal dependence (as level of the UV variability) of ozone depletion according to the ionization rate for 2003.
Solar radiation is an important factor for formation of the OH radicals, which leads to the formation of oxygen atoms. The oxygen atoms in the excited state are generated only in the presence of UV solar radiation due to the processes: O + 175.9 nm) → O (D) + O and O + 310 nm) → O + O (D). In its turn mechanism of NO formation includes oxygen atoms in the excited state: NO + O(D) → NO + NO [17]. Therefore, in the absence of solar radiation, the formation of NO is impossible, and this means that ozone is less prone to depletion. As soon catalytic reactions ozone depletion with NO needs NO formation. From the other side near the polar night boundary with absent of UV, photolysis of water vapor decreases thus reducing the amount of HO in the atmosphere, which, in turn, decreases the effect of HO catalytic cycles on O loss [15]. Based on the above mechanisms of NO and HO formation with and without UV, it should be noted that the ozone content in the mesosphere should be persistent in winter when UV is absent.
This mean the present or absent of solar radiation is one of the important factor that can control ozone depletion induced by EEP ionization rates. Mesospheric ozone is more stable during the polar night and highly dependent on UV radiation during the summer with less dependence during the intermediate seasons.
Figure 2 is a representation for the seasons chosen. We chose four intervals for 2003, which were assigned to the winter, spring, summer and fall periods. The division was made relative to the days of the solstices and equinoxes. The numbers in the figure are corresponding days of the year (DOY).
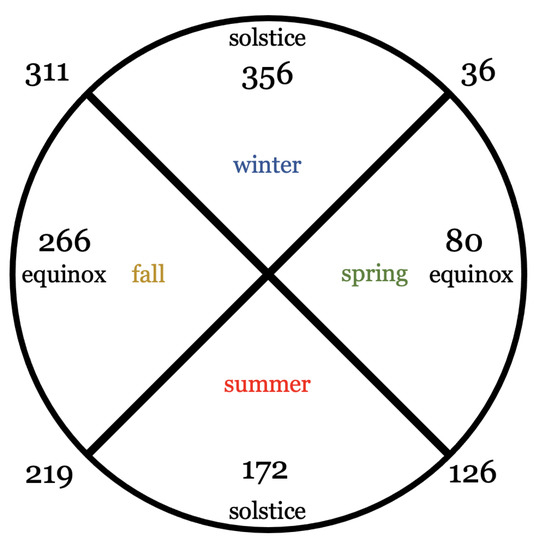
Figure 2.
Seasonal partition. The spring period is for DOY in 36-126, the summer period is for DOY in 126–219, the fall period is for DOY in 219–311; the remaining interval is associated with winter period.
Thus, the chosen time intervals are located almost symmetrically with respect to the chosen separation time points (equinoxes and solstices).
3. Results
3.1. EEP Ozone Depletion and Geomagnetic Disturbances
The EEP ionization rates were implemented into the one-dimensional radiative-convective model with ion chemistry, taking into account the duration and levels of the geomagnetic disturbance and its effects over seasons.
In Figure 3 three panels represent the results of applying the superposed epoch analysis method for elements of the HO family described earlier, in the levels of geomagnetic activity , and from top to bottom panels. The result agrees with the theoretical concepts: changes in HO have a very short duration due to the low lifetime, and the values are within the limits allowed for the mesosphere. In addition, the fact about the strength of the effects of events is confirmed: the maximum change for was 12 ppb, for —10.5 ppb, for —2.8 ppb at altitude about 80 km. Discovered a little drift of maximum response of HO from at 75 km to at 85 km.
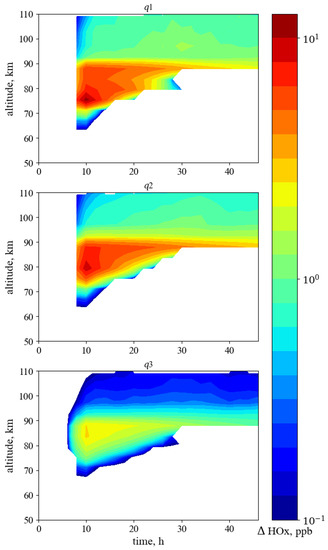
Figure 3.
Results of superposed epoch analysis method for elements of the HO for the levels of geomagnetic activity , and . The white color represents values of HO less than 0.1 ppb.
It is notable that the increased amount of HO remains increased for much more than few hours after ionization was applied for various levels of geomagnetic activitye , and . In our results we observe the enhancement of ozone loss by odd nitrogen modifiers [13]: the NO (which includes the NO) increasing leads to increase of HO and decrease of O. The root cause is the increasing in NO. Figure 4 demonstrates that the cause is respected.
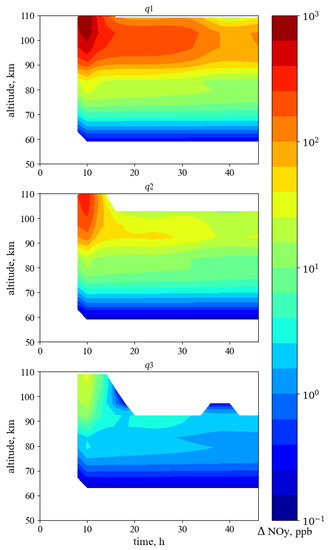
Figure 4.
Results of superposed epoch analysis method elements of the NO for the levels of geomagnetic activity , and . The white color represents values of NO less than 0.1 ppb.
Figure 4 shows the changes in NO for the superposed epoch analysis method within groups , and in the same sequence as for HO. The maximum values of NO remain at the same altitude around 105 km. The maximum values are 1050 ppb for , 350 ppb for and 30 ppb for .
And therefore, since the increasing leading to increase in HO, remains, both HO and NO gain indicates that the ozone is depleting.
Figure 5 shows the results of superposed epoch analysis method of ozone simulation for described levels of geomagnetic activity , and . The maximum ozone depletion up to 36% was obtained at altitude of about 80 km for geomagnetic disturbances which characterized Kp·10 ⩾ 50. At about the same altitude range ozone depletion has place for , and geomagnetic disturbances. The depletion of the ozone layer reaches 36% for , up to 21% for and up to about 5% for .
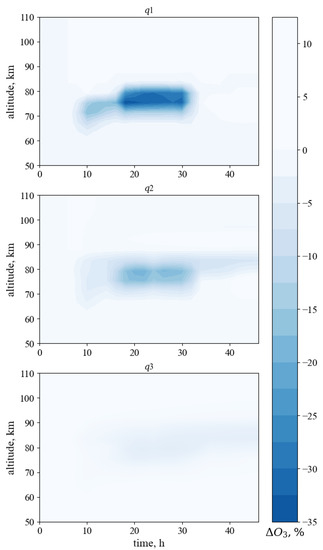
Figure 5.
Results of superposed epoch analysis method of ozone simulation for the levels of geomagnetic activity , and .
The deep analysis of the EEP induced maximum of ozone depletion (during various levels of geomagnetic disturbances) at the altitude of 79 km shown in Figure 6. Let us consider the red line, i.e., high geomagnetic disturbance level (the set) only, since the following analysis can be applied to both and easily. We see that during night time ozone accumulates (by 0 h, the midnight) reaching values of ∼1 ppm. During daytime ozone depletes (by 12 h). But during next night (18–24 h) ozone mixing ratio is not restored to that of one day before the event. In total, approximately 0.25 ppm of ozone is depleted with the impact of EEP, which is 36% loss. The same analysis represented for both and levels which leads to up to 21% and up to about 5% of ozone maximum decreases. The recovering of ozone layer after EEP is observed only on the second days after the EEP event.
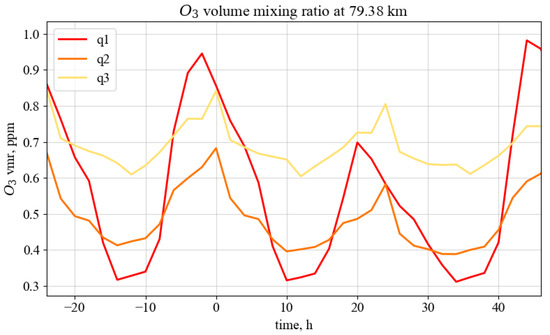
Figure 6.
Ozone volume mixing ratios for (red line), (orange line) and (yellow line) sets. The shown time interval starts one day before the day of appliance of ionization rates and ends one day after that (i.e., the 0–24 h is the day of the EEP event).
3.2. EEP Ozone Depletion and Seasons
Figure 7 shows EEP-driven mesospheric ozone depletion (in %) during time intervals described in the Section 2.4, see Figure 2. The magnitude of the ozone depletion O and corresponding ionization rate Q are chosen at the altitude of 79 km, because at this altitude level, according to Figure 5, the depletion peaks.
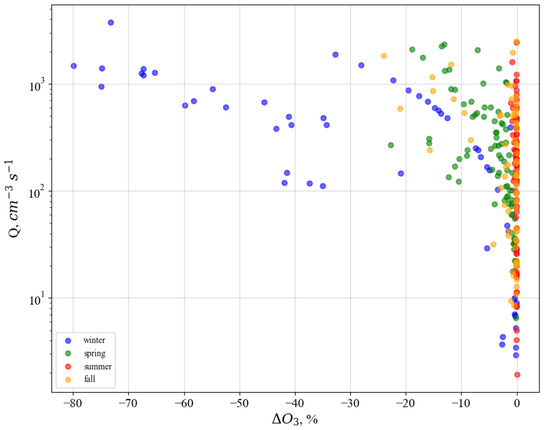
Figure 7.
EEP forcing ozone response during various seasons. The ozone depletion O and corresponding ionization rate Q are chosen at the altitude of 79 km.
Here one can see, that in spite of intensity of EEP induced ionization rates, the mesospheric ozone would be mostly destroyed during winter period. During winter, EEP ozone destruction can reach up to 80% in mesosphere during strong geomagnetic disturbances with ionization rates ∼10 ion pairs cm s at about 80 km. EEP ozone depletion during spring and fall periods is more or less the same, reaching a maximum of about . In the presence of UV effects of EEP on ozone depletion will be neglectable. In summer time, EEP does not induce ozone depletion in spite of increasing ionization rates under geomagnetic disturbances. It is clearly seen that an increase in ionization rates in winter, spring, and autumn leads to a decrease in the ozone content in the mesospheric layer by about 80 km. This means, see Figure 7, that linear dependences of ozone depletion on the ionization rate and time of year have been obtained.
4. Summary and Conclusions
In this work, we study mesospheric ozone depletion induced by energetic electron precipitation (EEP) in dependence on seasons and levels of geomagnetic disturbances.
As EEP events we selected days of precipitating energetic electrons with energies from keV up to relativistic energies about 1 MeV, based on the NOAA POES satellites observations in 2003. For estimation EEP spectra we used the MEPED POES in three electron energy channels and P6 proton channel which is contaminated electrons with energies above 800 keV, while the P5 proton channel is free of electrons. All SEP events were excluded, because channel P5 registers not electrons during these time intervals and we take only those days when the electron precipitation was observed for at least 320 s [24]. Here we show that moderate to strong geomagnetic disturbances lead to EEP-induced ionization rates with a maximum production of ions in the form of 10 ion pairs cm s per altitude of about 80 km of northern polar hemisphere ( 4–8).
For estimation EEP ozone depletion we use a one-dimensional radiative-convective photochemical model with ion chemistry. The model simulations was applied to the region of polar mesosphere about 60–70 N where we have local time and seasons that explained into the paper. We found that the EEP induced depletion of the mesospheric ozone has maximum depletion at altitude about 80 km and reaches up to 36% during strong geomagnetic disturbances with Kp·10 ⩾ 50, up to 21% for moderate geomagnetic disturbances with Kp·10 < 50 and up to about 5% for quiet geomagnetic conditions, where Kp·10 < 30. During strong geomagnetic disturbances mesospheric ozone will be recovered on the second day after precipitating energetic electrons.
Despite the intensity of the EEP-induced ionization rates, mesospheric ozone content cannot be destroyed under EEP during summer time in the present UV. In winter time, the maximum ozone depletion, at altitude of about 80 km, can reach up to 80% during strong geomagnetic disturbances. In fall and spring, the maximum ozone depletion is less intense and can reach 20% during strong geomagnetic disturbances. Linear dependences of EEP induced ozone depletion depending on geomagnetic disturbances and seasons have been obtained.
In this work we also trace the results of both direct (associated with HO increase), e.g., [10] and indirect (associated with NO increase) [13] processes that lead to ozone loss in upper mesosphere.
In conclusion, it can be said that ozone is stable in winter without the presence of UV, and if EEP takes place during the polar winter night season, EEP will produce a large amount of HO and NO, it means that EEP will lead to more ozone depletion comparable to the polar fall, spring or summer with the presence of UV. The presence of UV radiation dampens the effect of EEP on the formation of HO and NO and results in less ozone depletion during polar autumn, spring or summer. The higher the UV, the less ozone depletion occurs during EEP, regardless of the levels of geomagnetic disturbances. Here we show the existence of linear dependences of EEP-induced maximum ozone depletion on geomagnetic disturbances and seasons.
Author Contributions
Conceptualization, I.M. and E.R.; validation, D.G. and I.M.; investigation, D.G. and I.M.; data curation, I.M. and D.G.; writing—original draft preparation, I.M.; writing—review and editing, D.G. and E.R. All authors have read and agreed to the published version of the manuscript.
Funding
Investigation ozone depletion induced by EEP in various seasons and geomagnetic disturbances was done by the Project RSF No. 22-62-00048 in the frame of the task “Atmospheric effects of precipitation of energetic electrons from the outer radiation belt: Part II”. The treatment of one-dimensional radiative-convective photochemical model with ion chemistry for present investigation was done in the “Laboratory for the study of the ozone layer and the upper atmosphere” with the support of the Ministry of Science and Higher Education of the Russian Federation under agreement 075-15-2021-583.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
NOAA POES data: https://www.ngdc.noaa.gov/stp/satellite/poes/index.html (last accessed on 20 June 2023). Geomagnetic indices: https://omniweb.gsfc.nasa.gov/cgi/nx1.cgi (last accessed on 20 June 2023). All data from the investigation is available upon request from I.M. and D.G.
Acknowledgments
We are grateful to the reviewers for their careful reading of our manuscript and for their comments that helped to improve our article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mironova, I.A.; Aplin, K.L.; Arnold, F.; Bazilevskaya, G.A.; Harrison, R.G.; Krivolutsky, A.A.; Nicoll, K.A.; Rozanov, E.V.; Turunen, E.; Usoskin, I.G. Energetic Particle Influence on the Earth’s Atmosphere. Space Sci. Rev. 2015, 194, 1–96. [Google Scholar] [CrossRef]
- Artamonov, A.; Mironova, I.; Kovaltsov, G.; Mishev, A.; Plotnikov, E.; Konstantinova, N. Calculation of atmospheric ionization induced by relativistic electrons with non-vertical precipitation: Update of model CRAC:EPII. Adv. Space Res. 2017, 59, 2295–2300. [Google Scholar] [CrossRef]
- Porter, H.S.; Jackman, C.H.; Green, A.E.S. Efficiencies for production of atomic nitrogen and oxygen by relativistic proton impact in air. J. Chem. Phys. 1976, 65, 154–167. [Google Scholar] [CrossRef]
- Sinnhuber, M.; Nieder, H.; Wieters, N. Energetic Particle Precipitation and the Chemistry of the Mesosphere/Lower Thermosphere. Surv. Geophys. 2012, 33, 1281–1334. [Google Scholar] [CrossRef]
- Mironova, I.; Karagodin-Doyennel, A.; Rozanov, E. The effect of Forbush decreases on the polar-night HOx concentration affecting stratospheric ozone. Front. Earth Sci. 2021, 8, 669. [Google Scholar] [CrossRef]
- Solomon, S.; Rusch, D.W.; Gerard, J.C.; Reid, G.C.; Crutzen, P.J. The effect of particle precipitation events on the neutral and ion chemistry of the middle atmosphere: II. Odd hydrogen. Planet. Space Sci 1981, 29, 885–893. [Google Scholar] [CrossRef]
- Barth, C.A. Nitric oxide in the lower thermosphere. Planet. Space Sci. 1992, 40, 315–336. [Google Scholar] [CrossRef]
- Brasseur, G.P.; Solomon, S. Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Rozanov, E.; Calisto, M.; Egorova, T.; Peter, T.; Schmutz, W. Influence of the Precipitating Energetic Particles on Atmospheric Chemistry and Climate. Surv. Geophys. 2012, 33, 483–501. [Google Scholar] [CrossRef]
- Andersson, M.E.; Verronen, P.T.; Rodger, C.J.; Clilverd, M.A.; Seppälä, A. Missing driver in the Sun–Earth connection from energetic electron precipitation impacts mesospheric ozone. Nat. Commun. 2014, 5, 5197. [Google Scholar] [CrossRef]
- Mironova, I.; Sinnhuber, M.; Bazilevskaya, G.; Clilverd, M.; Funke, B.; Makhmutov, V.; Rozanov, E.; Santee, M.L.; Sukhodolov, T.; Ulich, T. Exceptional middle latitude electron precipitation detected by balloon observations: Implications for atmospheric composition. Atmos. Chem. Phys. 2022, 22, 6703–6716. [Google Scholar] [CrossRef]
- Grankin, D.; Mironova, I.; Bazilevskaya, G.; Rozanov, E.; Egorova, T. Atmospheric Response to EEP during Geomagnetic Disturbances. Atmosphere 2023, 14, 273. [Google Scholar] [CrossRef]
- Verronen, P.T.; Lehmann, R. Enhancement of odd nitrogen modifies mesospheric ozone chemistry during polar winter. Geophys. Res. Lett. 2015, 42, 10445–10452. [Google Scholar] [CrossRef]
- Jackman, C.H.; Marsh, D.R.; Vitt, F.M.; Roble, R.G.; Randall, C.E.; Bernath, P.F.; Funke, B.; López-Puertas, M.; Versick, S.; Stiller, G.P.; et al. Northern Hemisphere atmospheric influence of the solar proton events and ground level enhancement in January 2005. Atmos. Chem. Phys. 2011, 11, 6153–6166. [Google Scholar] [CrossRef]
- Seppälä, A.; Verronen, P.T.; Sofieva, V.F.; Tamminen, J.; Kyrölä, E.; Rodger, C.J.; Clilverd, M.A. Destruction of the tertiary ozone maximum during a solar proton event. Geophys. Res. Lett. 2006, 33, L07804. [Google Scholar] [CrossRef]
- Ondrášková, A.; Krivolutsky, A.; Kukoleva, A.; Vyushkova, T.; Kuminov, A.; Zakharov, G. Response of the lower ionosphere to solar proton event on July 14, 2000. Model simulations over both poles. J. Atmos. -Sol.-Terr. Phys. 2008, 70, 539–545. [Google Scholar] [CrossRef]
- Krivolutsky, A.A.; V’yushkova, T.Y.; Cherepanova, L.A.; Kukoleva, A.A.; Repnev, A.I.; Banin, M.V. The three-dimensional photochemical model CHARM. Incorporation of solar activity. Geomagn. Aeron. 2015, 55, 59–88. [Google Scholar] [CrossRef]
- Ozolin, Y.E.; Karol’, I.L.; Rozanov, E.V.; Egorova, T.A. A model of the impact of solar proton events on the ionic and gaseous composition of the mesosphere. Izv. Atmos. Ocean. Phys. 2009, 45, 737–750. [Google Scholar] [CrossRef]
- Rodger, C.J.; Clilverd, M.A.; Green, J.C.; Lam, M.M. Use of POES SEM-2 observations to examine radiation belt dynamics and energetic electron precipitation into the atmosphere. J. Geophys. Res. (Space Phys.) 2010, 115, A04202. [Google Scholar] [CrossRef]
- Yahnin, A.G.; Yahnina, T.A.; Raita, T.; Manninen, J. Ground pulsation magnetometer observations conjugated with relativistic electron precipitation. J. Geophys. Res. (Space Phys.) 2017, 122, 9169–9182. [Google Scholar] [CrossRef]
- Mironova, I.; Kovaltsov, G.; Mishev, A.; Artamonov, A. Ionization in the Earth’s Atmosphere Due to Isotropic Energetic Electron Precipitation: Ion Production and Primary Electron Spectra. Remote Sens. 2021, 13, 4161. [Google Scholar] [CrossRef]
- Bazilevskaya, G.A.; Kalinin, M.S.; Krainev, M.B.; Makhmutov, V.S.; Svirzhevskaya, A.K.; Svirzhevsky, N.S.; Stozhkov, Y.I.; Philippov, M.V.; Balabin, Y.V.; Gvozdevsky, B.B. Precipitation of magnetospheric electrons into the Earth’s atmosphere and the electrons of the outer radiation belt. Bull. Russ. Acad. Sci. Phys. 2017, 81, 215–218. [Google Scholar] [CrossRef]
- Bazilevskaya, G.A.; Dyusembekova, A.S.; Kalinin, M.S.; Krainev, M.B.; Makhmutov, V.S.; Svirzhevskaya, A.K.; Svirzhevsky, N.S.; Stozhkov, Y.I.; Tulekov, E.A. Comparison of the Results on Precipitation of High-Energy Electrons in the Stratosphere and on Satellites. Cosm. Res. 2021, 59, 24–29. [Google Scholar] [CrossRef]
- Mironova, I.; Bazilevskaya, G.; Makhmutov, V.; Mironov, A.; Bobrov, N. Energetic Electron Precipitation via Satellite and Balloon Observations: Their Role in Atmospheric Ionization. Remote Sens. 2023, 15, 3291. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).