Improvement of SAMI2 with Comprehensive Photochemistry at Mid-Latitudes and a Preliminary Comparison with Ionosonde Data
Abstract
1. Introduction
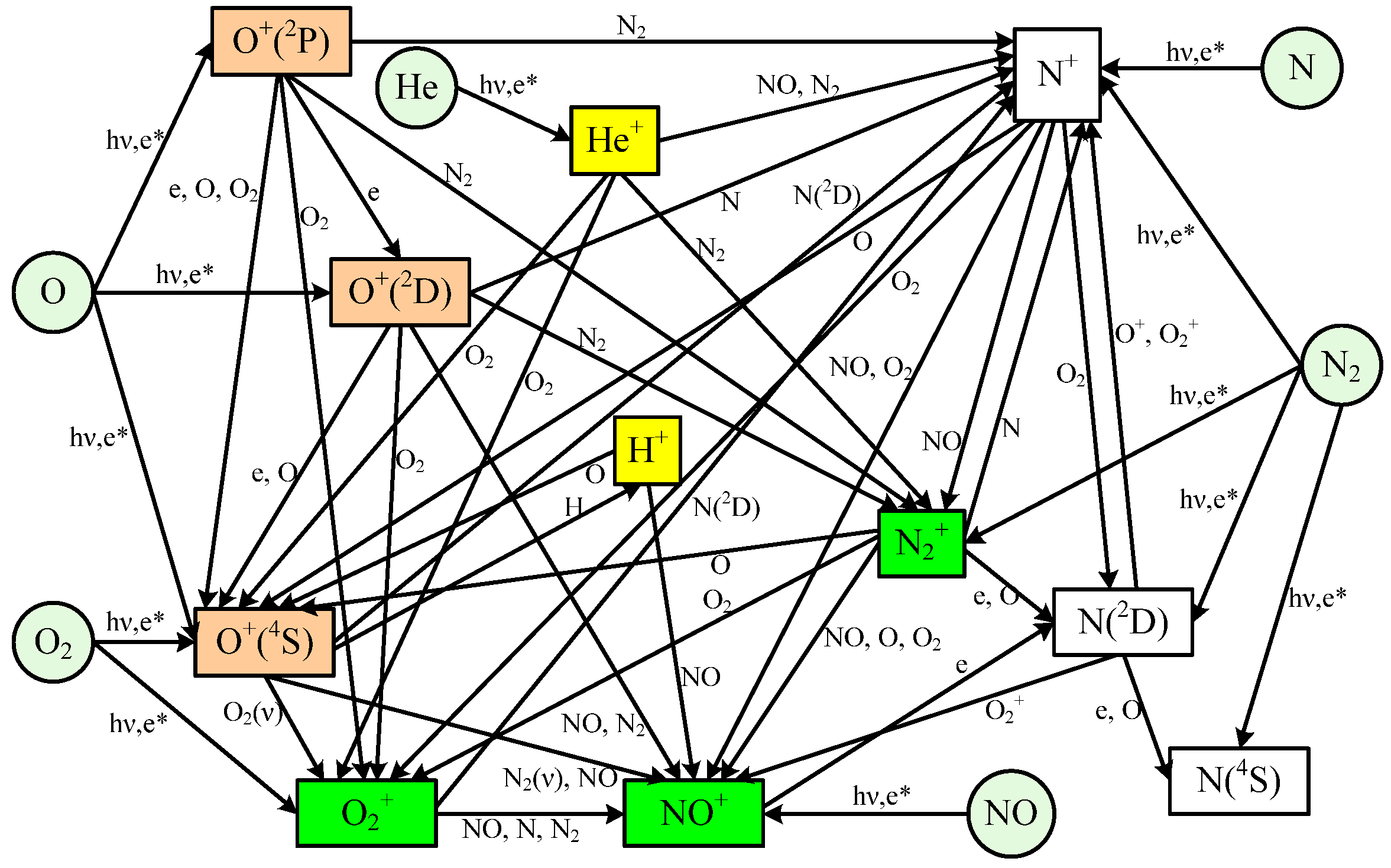
2. Photochemical Scheme
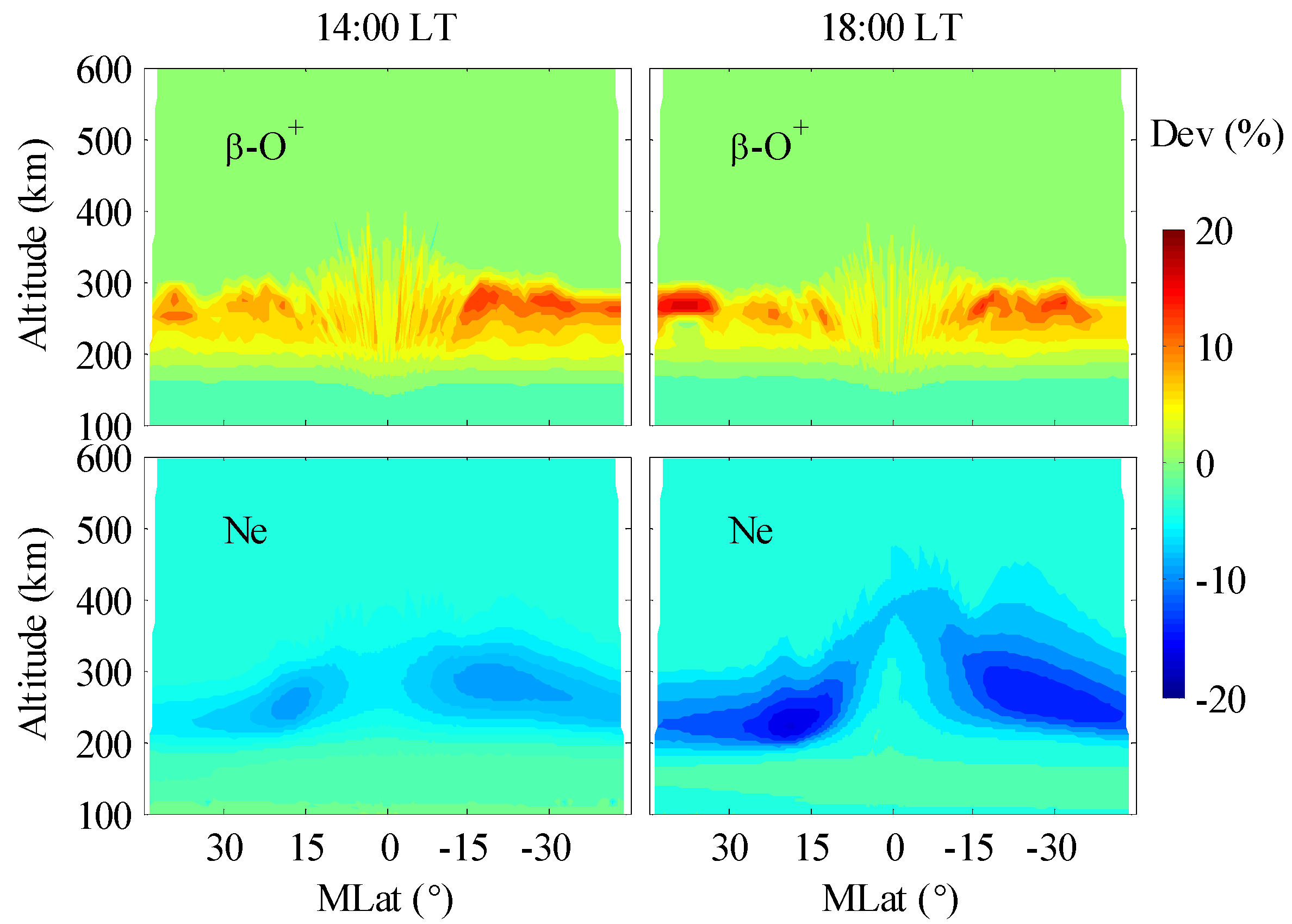
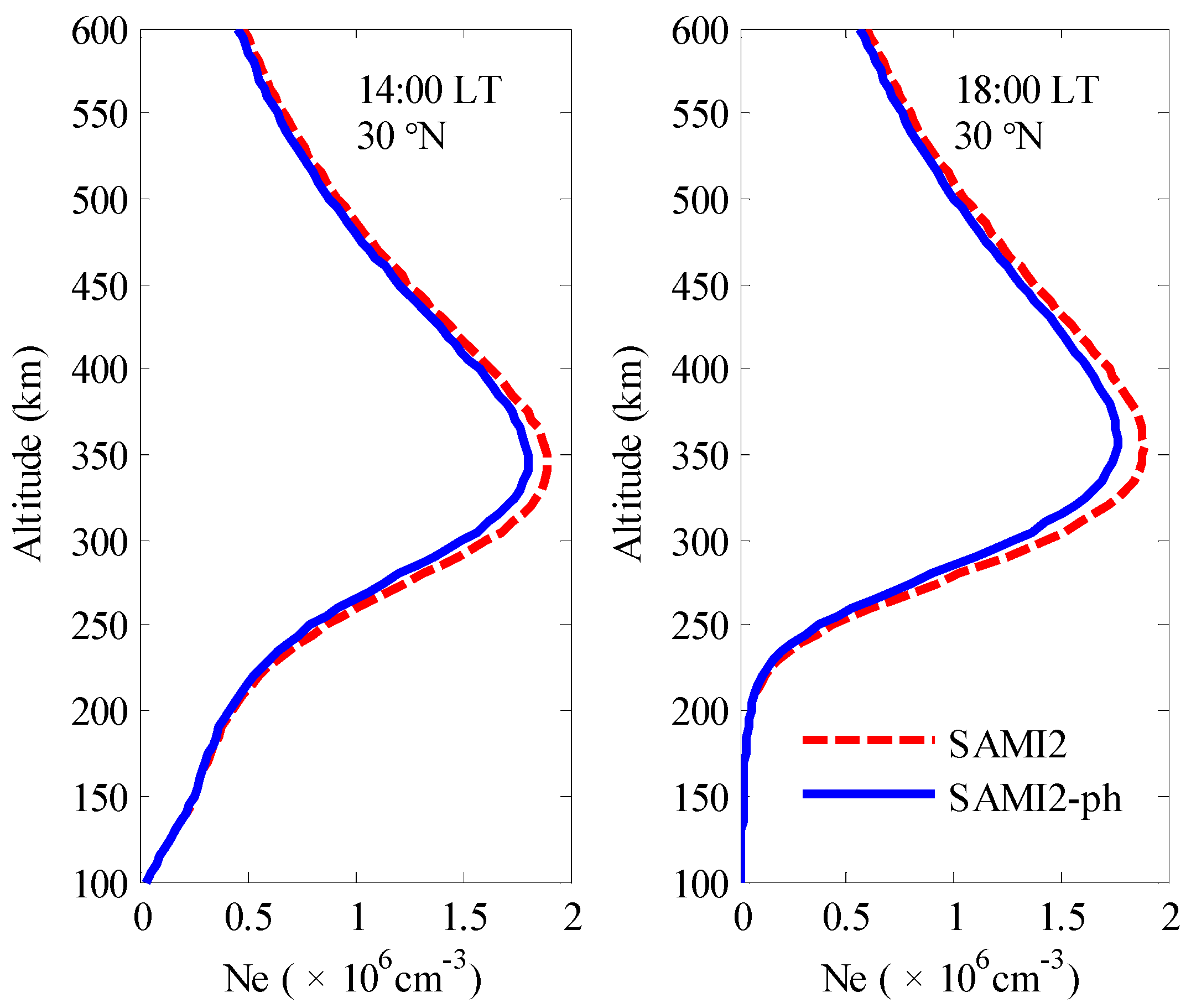
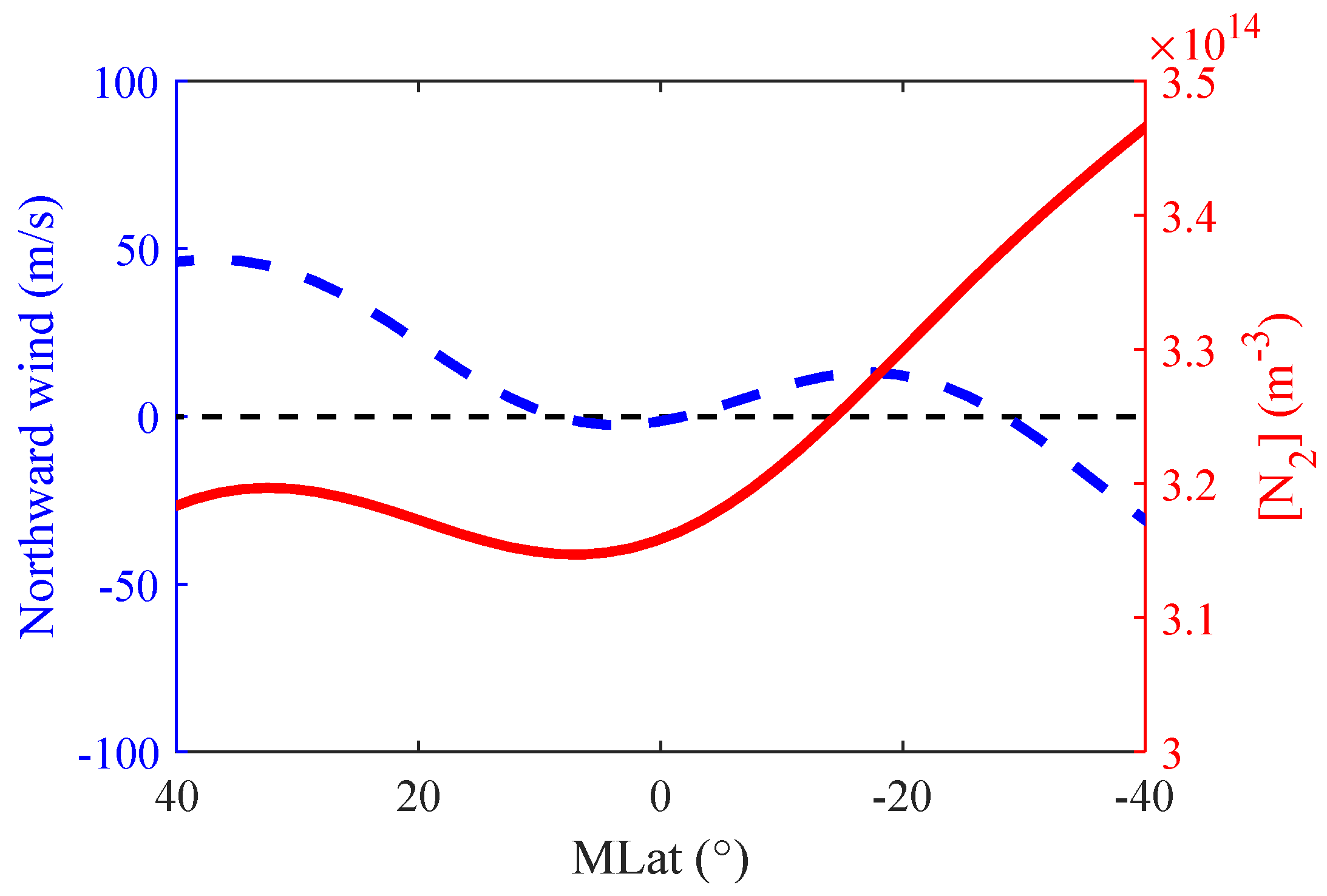
3. Influence of the Photochemical Scheme
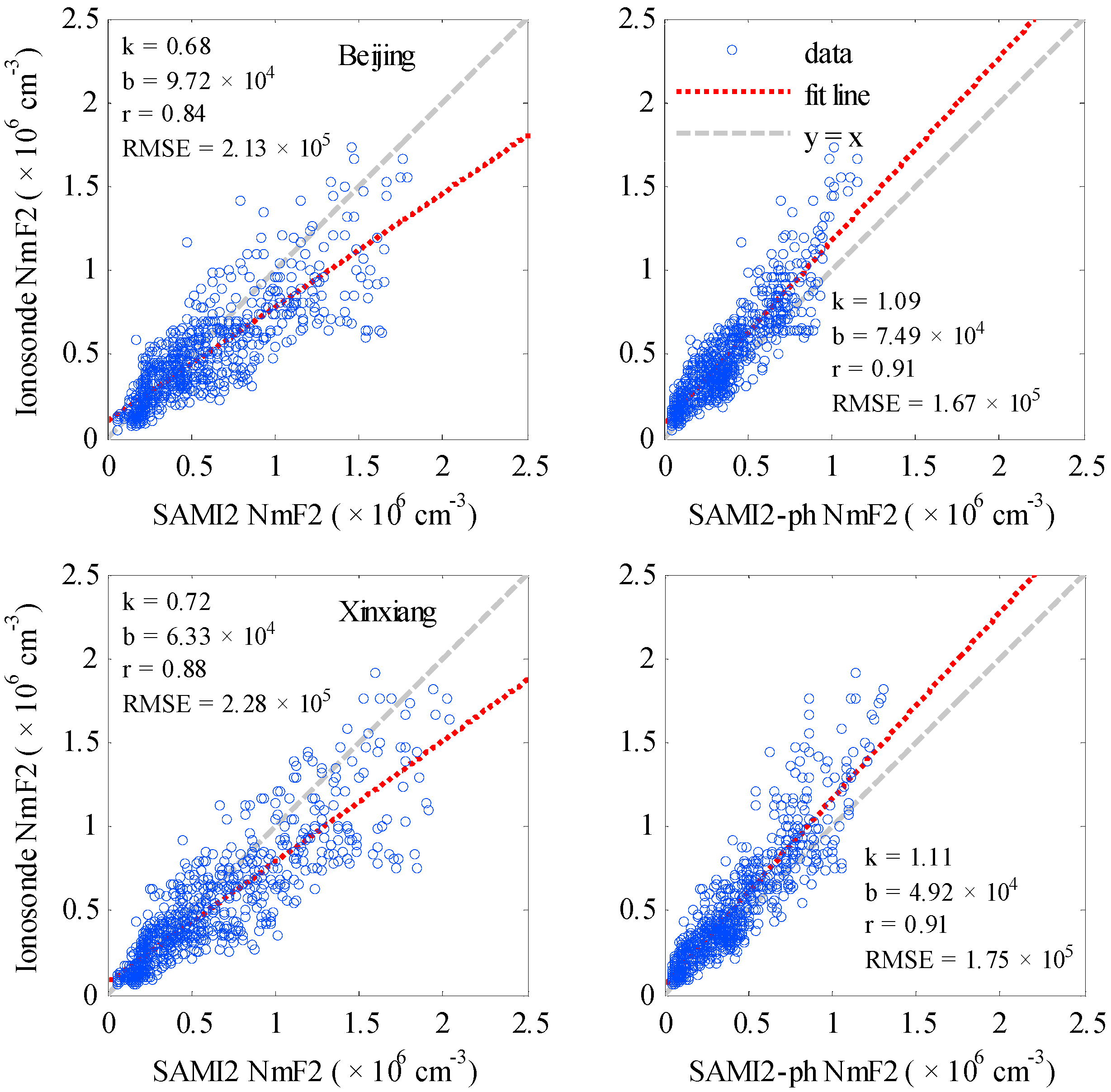
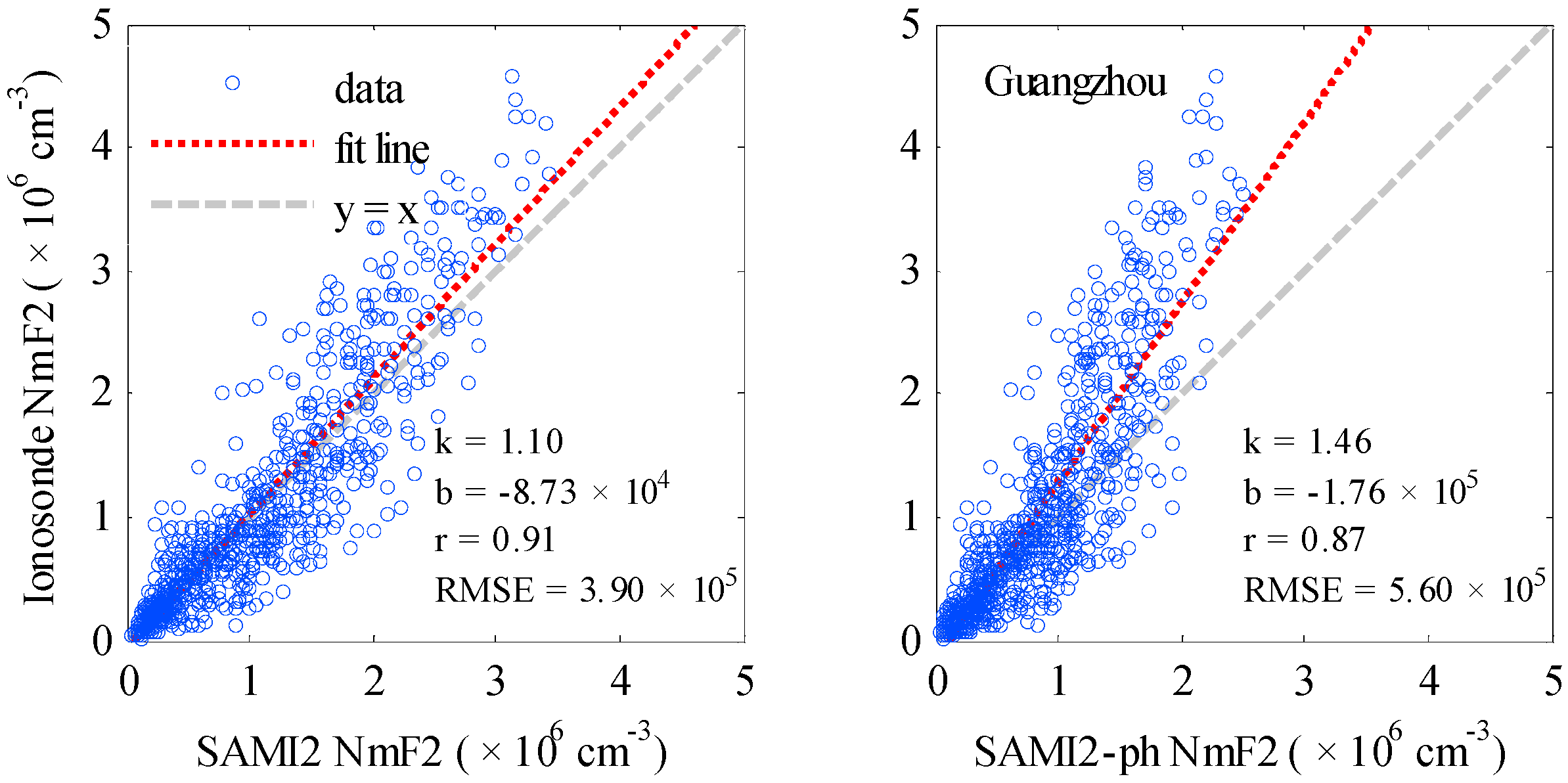
4. Comparison with Ionosonde Data
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Reaction | Rate (m−3s−1 or s−1) | Reference |
|---|---|---|
| O+ + N2(ν) → NO+ + N | k′10 = 1.533 × 10−18–5.92 × 10−19(Ti/300) + 8.60 × 10−20(Ti/300)2 300 K ≤ Ti ≤ 1700 K k′10 = 2.73 × 10−18–1.155 × 10−18(Ti/300) + 1.483 × 10−19(Ti/300)2 1700 K ≤ Ti ≤ 6000 K k′11 = k′10; k′12 = 38 k′10; k′13 = 85 k′10; k′14 = 220 k′10; k′15 = 270 k′10; [N2(0)] = [N2] (1 − exp(−3353/Tν)); [N2(ν)] = [N2(0)] exp(−3353ν/Tν); [N2] = ∑ [N2(ν)] k1 = ∑ k′1ν [N2(ν)] /[N2] | [31] |
| O+ + O2(ν) → O2+ + O | k2 = 1.7 × 10−17(300/Tn)0.77 + 8.54 × 10−17 exp(−3467/Tn) | [32] |
| O+ + H → H+ + O | k3 = 6.4 × 10−16 | [41] |
| O+ + NO → NO+ + O | k4 = 7.0 × 10−19(300/Ti)−0.87 | [42] |
| O+ + N(2D) → N+ + O | k5 = 1.3 × 10−16 | [43,44] |
| O+ + e → O | k6 = 4.43 × 10−18(300/Te)0.7 | [6] |
| O2+ + NO → NO+ + O2 | k7 = 4.5 × 10−16 | [45] |
| O2+ + N → NO+ + O | k8 = 1.2 × 10−16 | [46] |
| O2+ + N2 → NO+ + NO | k9 = 5.0 × 10−22 | [3] |
| O2+ + N(2D) → N+ + O2 | k10 = 8.65 × 10−17 | [47] |
| O2+ + e → O + O | k11 = 2.0 × 10−13(300/Te)0.70 Te < 1200 K k11 = 1.6 × 10−13(300/Te)0.55 Te ≥ 1200 K | [48] |
| NO+ + e → N + O | k12 = 0.2 k′ k′ = 4.2 × 10−13(300/Te)0.85 | [20] |
| N2+ + O → NO+ + N | k13 = 1.4 × 10−16(300/Ti)0.44 Ti ≤ 1500 K | [49] |
| N2+ + O → O+ + N2 | k14 = 9.8 × 10−18(300/Ti)0.23 Ti ≤ 1500 K | [50] |
| N2+ + O2 → O2+ + N2 | k15 = 5.1 × 10−17(300/Ti)1.16 Ti ≤ 1000 K k15 = 1.26 × 10−17(1000/Ti)−0.67 Ti > 1000 K | [51] |
| N2+ + O2 → NO+ + NO | k16 = 1.0 × 10−20 | [6] |
| N2+ + NO → NO+ + N2 | k17 = 3.3 × 10−16 | [51] |
| N2+ + N → N+ + N2 | k18 = 1.0 × 10−17 | [52] |
| N2+ + e → N + N | k19 = 0.1 k′ k′ = 1.75 × 10−13(300/Te)0.39 | [20] |
| H+ + O → O+ + H | k20 = 2.2 × 10−17 Ti0.5 | [53] |
| H+ + NO → NO+ + H | k21 = 1.9 × 10−15 | [54] |
| H+ + e → H | k22 = 4.43 × 10−18(300/Te)0.7 | [6] |
| He+ + N2 → N2+ + He | k23 = 6.4 × 10−16 | [54] |
| He+ + N2 → N+ + N + He | k24 = 9.6 × 10−16 | [54] |
| He+ + O2 → O+ + O + He | k25 = 1.1 × 10−15 | [54] |
| He+ + O2 → O2+ + O | k26 = 2.0 × 10−16 | [6] |
| He+ + NO → N+ + He + O | k27 = 1.25 × 10−15 | [54] |
| He+ + e → He | k28 = 4.43 × 10−18(300/Te)0.7 | [6] |
| N+ + O → O+ + N | k29 = 2.2 × 10−18 | [43,44] |
| N+ + NO → NO+ + N | k30 = 2.0 × 10−17 | [6] |
| N+ + NO → N2+ + O | k31 = 8.33 × 10−17(300/Ti)0.24 | [55] |
| N+ + O2 → O2+ + N | k32 = 3.1 × 10−16 | [56] |
| N+ + O2 → NO+ + O | k33 = 2.6 × 10−16 | [56] |
| N+ + e → N | k34 = 4.43 × 10−18(300/Te)0.7 | [6] |
| O+(2D) + N2 → N2+ + O | k35 = 1.5 × 10−16(Ti/300)0.5 | [57] |
| O+(2D) + N2 → NO+ + N | k36 = 2.5 × 10−17 | [57] |
| O+(2D) + O2 → O2+ + O | k37 = 1.3 × 10−16(Ti/300)0.5 | [7] |
| O+(2D) + N → N+ + O | k38 = 1.5 × 10−16 | [58] |
| O+(2D) + NO → NO+ + O | k39 = 1.2 × 10−15 | [59] |
| O+(2D) + O → O+(4S) + O | k40 = 1.0 × 10−16 | [60] |
| O+(2D) + e → O+(4S) + e | k41 = 4.0 × 10−14(300/Te)0.5 | [7] |
| O+(2P) + N2 → N2+ + O | k42 = 2.0 × 10−16(Ti/300)0.5 | [7,57] |
| O+(2P) + N2 → N+ + NO | k43 = 1.0 × 10−17 | [61] |
| O+(2P)+O2 → O2++O | k44 = 1.3 × 10−16 | [59] |
| O+(2P) + O2 → O+(4S) + O2 | k45 = 1.3 × 10−16 | [59] |
| O+(2P) + O → O+(4S) + O | k46 = 4.0 × 10−16 | [62] |
| O+(2P) + e → O+(4S) + e | k47 = 2.5 × 10−14(300/Te)0.5 | [63] |
| O+(2P) + e → O+(2D) + e | k48 = 7.0 × 10−14(300/Te)0.5 | [63] |
| O+(2P) → O+(4S) + hv | k49 = 0.0833 s−1 | [64] |
| O+(2P) → O+(2D) + hv | k50 = 0.277 s−1 | [64] |
| NO+ + e → N(2D) + O | k51 = 0.8 k′ k′ = 4.2 × 10−13(300/Te)0.85 | [20] |
| N2+ + e → N(2D) + N | k52 = 0.9 k′ k′ = 1.8 × 10−13(300/Te)0.39 | [20] |
| N2+ + O → N(2D) + NO+ | k53 = 1.4 × 10−16(300/TR)0.44 TR ≤ 1500 K k53 = 5.2 × 10−17(TR/300)0.2 TR > 1500 K TR = (Ti + Tn)/2 | [20] |
| N+ + O2 → N(2D) + O2+ | k54 = 0.15 k′ k′ = 5.5 × 10−16(Ti/300)0.45 Ti ≤ 1000 K k′ = 9.5 × 10−16 Ti > 1000 K | [47,65] |
| N(2D) → N(4S) + hv | k55 = 1.06 × 10−5 s−1 | [20] |
| N(2D) + e → N(4S) + e | k56 = 5.0 × 10−16(Te/300)0.5 | [66] |
| N(2D) + O → N(4S) + O | k57 = 7.0 × 10−19 | [67] |
| N(2D) + O2+ → NO+ + O | k58 = 1.8 × 10−16 | [68] |
| N(2D) + NO → N2 + O | k59 = 7 × 10−17 | [20] |
| N(2D) + O2 → NO + O | k60 = 6 × 10−18 | [69] |
References
- Richards, P.G. Reexamination of ionospheric photochemistry. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Richards, P.G.; Torr, D.G. Seasonal, diurnal, and solar cyclical variations of the limiting H+ flux in the Earth’s topside ionosphere. J. Geophys. Res. 1985, 90, 5261–5268. [Google Scholar] [CrossRef]
- Schunk, R.W. A mathematical model of the middle and high latitude ionosphere. Pure Appl. Geophys. 1988, 127, 255–303. [Google Scholar] [CrossRef]
- Bailey, G.J.; Sellek, R. A mathematical model of the Earth’s plasmasphere and its applications in a study of He+ at L = 3. Ann. Geophys. 1990, 8, 171–190. [Google Scholar]
- Anderson, D.N.; Decker, D.T.; Valladares, C.E. Global Theoretical Ionospheric Model (GTIM). In Solar-Terrestrial Energy Program: Handbook of Ionospheric Models; Schunk, R.W., Allen, J.H., Eds.; Utah State University: Logan, UT, USA, 1996; pp. 133–152. [Google Scholar]
- Huba, J.D.; Joyce, G.; Fedder, J.A. Sami2 is Another Model of the Ionosphere (SAMI2): A new low-latitude ionosphere model. J. Geophys. Res. 2000, 105, 23035–23053. [Google Scholar] [CrossRef]
- Pavlov, A.V. New method in computer simulations of electron and ion densities and temperatures in the plasmasphere and low-latitude ionosphere. Ann. Geophys. 2003, 21, 1601–1628. [Google Scholar] [CrossRef]
- Yue, X.A.; Wan, W.X.; Liu, L.B.; Le, H.J.; Chen, Y.D.; Yu, T. Development of a middle and low latitude theoretical ionospheric model and an observation system data assimilation experiment. Chin. Sci. Bull. 2008, 53, 94–101. [Google Scholar] [CrossRef]
- Namgaladze, A.A.; Korenkov, Y.N.; Klimenko, V.V.; Karpov, I.V.; Bessarab, F.S.; Surotkin, V.A.; Glushchenko, T.A.; Naumova, N.M. Global model of the thermosphere-ionosphere-protonsphere system. Pure Appl. Geophys. 1988, 127, 219–254. [Google Scholar] [CrossRef]
- Roble, R.G.; Ridley, E.C.; Richmond, A.D.; Dickinson, R.E. A coupled thermosphere/ionosphere general circulation model. Geophys. Res. Lett. 1988, 15, 1325–1328. [Google Scholar] [CrossRef]
- Fuller-Rowell, T.J.; Codrescu, M.V.; Rishbeth, H.; Moffett, R.J.; Quegan, S. On the seasonal response of the thermosphere and ionosphere to geomagnetic storms. J. Geophys. Res. 1996, 101, 2343–2353. [Google Scholar] [CrossRef]
- Ridley, A.J.; Deng, Y.; Tóth, G. The global ionosphere-thermosphere model. J. Atmos. Sol.-Terr. Phys. 2006, 68, 839–864. [Google Scholar] [CrossRef]
- Huba, J.D.; Joyce, G. Global modeling of equatorial plasma bubbles. Geophys. Res. Lett. 2010, 37, L17104. [Google Scholar] [CrossRef]
- Huba, J.D.; Krall, J. Modeling the plasmasphere with SAMI3. Geophys. Res. Lett. 2013, 40, 6–10. [Google Scholar] [CrossRef]
- Huba, J.D.; Maute, A.; Crowley, G. SAMI3_ICON: Model of the ionosphere/plasmasphere system. Space Sci. Rev. 2017, 212, 731–742. [Google Scholar] [CrossRef] [PubMed]
- Krall, J.; Huba, J.D.; Nossa, E.; Aponte, N.; Drob, D.P. SAMI3 simulations of ionospheric metallic layers at Arecibo. J. Geophys. Res. Space Phys. 2020, 125, e2019JA027297. [Google Scholar] [CrossRef]
- Richards, P.G.; Meier, R.R.; Wilkinson, P.J. On the consistency of satellite measurements of thermospheric composition and solar EUV irradiance with Australian ionosonde electron density data. J. Geophys. Res. 2010, 115, A10309. [Google Scholar] [CrossRef]
- Millward, G.H.; Müller-Wodarg, I.C.F.; Aylward, A.D.; Fuller-Rowell, T.J.; Richmond, A.D.; Moffett, R.J. An investigation into the influence of tidal forcing on F region equatorial vertical ion drift using a global ionosphere-thermosphere model with coupled electrodynamics. J. Geophys. Res. 2001, 106, 24733–24744. [Google Scholar] [CrossRef]
- Maruyama, N.; Sun, Y.Y.; Richards, P.G.; Middlecoff, J.; Fang, T.W.; Fuller-Rowell, T.J.; Akmaev, R.A.; Liu, J.Y.; Valladares, C. A new source of the midlatitude ionospheric peak density structure revealed by a new Ionosphere-Plasmasphere model. Geophys. Res. Lett. 2016, 43, 2429–2435. [Google Scholar] [CrossRef]
- Roble, R.G.; Ridley, E.C. A thermosphere-ionosphere-mesosphere-electrodynamics general circulation model (TIME-GCM): Equinox solar cycle minimum simulations (30–500 km). Geophys. Res. Lett. 1994, 21, 417–420. [Google Scholar] [CrossRef]
- Rishbeth, H.; Garriott, O.K. Introduction to Ionospheric Physics; Academic Press: New York, NY, USA; London, UK, 1969. [Google Scholar]
- Pavlov, A.V. Ion chemistry of the ionosphere at E- and F-region altitudes: A review. Surv. Geophys. 2012, 33, 1133–1172. [Google Scholar] [CrossRef]
- Rao, S.S.; Sharma, S.; Pandey, R. SAMI2 model results for the quiet time low latitude ionosphere over India. Adv. Space Res. 2018, 61, 2031–2039. [Google Scholar] [CrossRef]
- Oh, S.-J.; Kil, H.; Kim, W.-T.; Paxton, L.J.; Kim, Y.H. The role of the vertical E×B drift for the formation of the longitudinal plasma density structure in the low-latitude F region. Ann. Geophys. 2008, 26, 2061–2067. [Google Scholar] [CrossRef][Green Version]
- Richards, P.G.; Woods, T.N.; Peterson, W.K. HEUVAC: A new high resolution solar EUV proxy model. Adv. Space Res. 2006, 37, 315–322. [Google Scholar] [CrossRef]
- Richards, P.G.; Torr, D.G. Ratios of photoelectron to EUV ionization rates for aeronomic studies. J. Geophys. Res. 1988, 93, 4060–4066. [Google Scholar] [CrossRef]
- Titheridge, J.E. Model results for the ionospheric E region: Solar and seasonal changes. Ann. Geophys. 1997, 15, 63–78. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere. Earth Space Sci. 2015, 2, 301–319. [Google Scholar] [CrossRef]
- Prölss, G.W.; Werner, S. Vibrationally excited nitrogen and oxygen and the origin of negative ionospheric storms. J. Geophys. Res. 2002, 107, 1016–1621. [Google Scholar] [CrossRef]
- Pavlov, A.V.; Buonsanto, M.J. Using steady state vibrational temperatures to model effects of N2* on calculations of electron densities. J. Geophys. Res. 1996, 101, 26941–26945. [Google Scholar] [CrossRef]
- Pavlov, A.V. The role of vibrationally excited nitrogen in the ionosphere. Pure Appl. Geophys. 1988, 127, 529–544. [Google Scholar] [CrossRef]
- Hierl, P.M.; Dotan, I.; Seeley, J.V.; Van Doren, J.M.; Morris, R.A.; Viggiano, A.A. Rate constants for the reactions of O+ with N2 and O2 as a function of temperature (300-1800 K). J. Chem. Phys. 1997, 106, 3540–3544. [Google Scholar] [CrossRef]
- Lin, C.H.; Liu, J.Y.; Fang, T.W.; Chang, P.Y.; Tsai, H.F.; Chen, C.H.; Hsiao, C.C. Motions of the equatorial ionization anomaly crests imaged by FORMOSAT-3/COSMIC. Geophys. Res. Lett. 2007, 34, L19101. [Google Scholar] [CrossRef]
- Huang, L.F.; Huang, J.; Wang, J.S.; Jiang, Y.; Deng, B.C.; Zhao, K.; Lin, G.G. Analysis of the north–south asymmetry of the equatorial ionization anomaly around 110 °E longitude. J. Atmos. Sol.-Terr. Phys. 2013, 102, 354–361. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Fang, T.W.; Anderson, D.; Fuller-Rowell, T.; Akmaev, R.; Codrescu, M.; Millward, G.; Sojka, J.; Scherliess, L.; Eccles, V.; Retterer, J.; et al. Comparative studies of theoretical models in the equatorial ionosphere. Model. Ionos.-Thermosphere Syst. 2013, 201, 133–144. [Google Scholar]
- Gowtam, V.S.; Tulasi Ram, S.; Reinisch, B.; Prajapati, A. A new artificial neural network-based global three-dimensional ionospheric model (ANNIM-3D) using long-term ionospheric observations: Preliminary results. J. Geophys. Res. Space Phys. 2019, 124, 4639–4657. [Google Scholar] [CrossRef]
- Santos, Â.M.; Brum, C.G.M.; Batista, I.S.; Sobral, J.H.A.; Abdu, M.A.; Souza, J.R.; de Jesus, R.; Manoharan, P.K.; Terra, P. Ionospheric Variability over the Brazilian Equatorial Region during the Minima Solar Cycles 1996 and 2009: Comparison between Observational Data and the IRI Model. Atmosphere 2023, 14, 87. [Google Scholar] [CrossRef]
- Piggott, W.R.; Rawer, K. URSI Handbook of Ionogram Interpretation and Reduction; National Oceanic and Atmospheric Administration: Boulder, CO, USA, 1978. [Google Scholar]
- Fejer, B.G. Low Latitude Ionospheric Electrodynamics. Space Sci. Rev. 2011, 158, 145–166. [Google Scholar] [CrossRef]
- Anicich, V.G. Evaluated bimolecular ion-molecule gas phase kinetics of positive-ions for use in modeling planetary-atmospheres, cometary comae, and interstellar clouds. J. Phys. Chem. Ref. Data 1993, 22, 1469–1569. [Google Scholar] [CrossRef]
- Dotan, I.; Hierl, P.M.; Morris, R.A.; Viggiano, A.A. Rate constants for the reactions of N+ and N2+ with O2 as a function of temperature (300–1800 K). Int. J. Mass Spectrom. Ion Process. 1997, 167–168, 223–230. [Google Scholar] [CrossRef]
- Constantinides, E.R.; Black, J.H.; Dalgarno, A.; Hoffman, J.H. The photochemistry of N+ ions. Geophys. Res. Lett. 1979, 6, 569–572. [Google Scholar] [CrossRef]
- Bates, D.R. Theoretical considerations regarding some inelastic atomic collision processes of interest in aeronomy: Deactivation and charge transfer. Planet. Space Sci. 1989, 37, 363–368. [Google Scholar] [CrossRef]
- Midey, A.J.; Viggiano, A.A. Rate constants for the reaction of O2+ with NO from 300 to 1400 K. J. Chem. Phys. 1999, 110, 10746–10748. [Google Scholar] [CrossRef]
- Fehsenfeld, F.C. The reaction of O+ with atomic nitrogen and NO+, H2O and NO+ with atomic oxygen. Planet. Space Sci. 1977, 25, 195–196. [Google Scholar] [CrossRef]
- O´Keefe, A.; Mauclaire, G.; Parent, D.; Bowers, M.T. Product energy disposal in the reaction of N+(3P) with O2(X3∑). J. Chem. Phys. 1986, 84, 215–219. [Google Scholar] [CrossRef]
- Torr, D.G.; Torr, M.R.; Walker, J.C.G.; Nier, A.O.; Brace, L.H.; Briton, H.C. Recombination of the O2+ in the ionosphere. J. Geophys. Res. 1976, 81, 5578–5580. [Google Scholar] [CrossRef]
- Torr, M.R.; Torr, D.G. Chemistry of the thermosphere and ionosphere. J. Atmos. Sol. Terr. Phys. 1979, 41, 797–839. [Google Scholar] [CrossRef]
- McFarland, M.; Albritton, D.L.; Fehsenfeld, F.C.; Ferguson, E.E.; Schmeltekopf, A.L. Energy dependence and branching ration of the N2+ + O reaction. J. Geophys. Res. 1974, 79, 2925–2926. [Google Scholar] [CrossRef]
- Scott, G.B.L.; Fairley, D.A.; Milligan, D.B.; Freeman, C.G.; McEwan, M.J. Gas phase reactions of some positive ions with atomic and molecular oxygen and nitric oxide at 300 K. J. Phys. Chem. A 1999, 103, 7470–7473. [Google Scholar] [CrossRef]
- Ferguson, E.E. Rate constants of thermal energy binary ion-molecule reactions of aeronomic interest. At. Data Nucl. Data Tables 1973, 12, 159–178. [Google Scholar] [CrossRef]
- Raitt, W.J.; Schunk, R.W.; Banks, P.M. A comparison of the temperature and density structure in high and low speed thermal proton flows. Planet. Space Sci. 1975, 23, 1103–1117. [Google Scholar] [CrossRef]
- Schunk, R.W.; Nagy, A.F. Ionospheres of the Terrestrial Planets. Rev. Geophys. Space Phys. 1980, 18, 813–852. [Google Scholar] [CrossRef]
- Fahey, D.W.; Dotan, I.; Fehsenfeld, F.C.; Albritton, D.L.; Viehland, L.A. Energy dependence of the rate constant of the reaction N++NO at collision energies 0.04 to 2.5 eV. J. Chem. Phys. 1981, 74, 3320–3323. [Google Scholar] [CrossRef]
- Diloy, P.-Y.; Robineau, A.; Lilensten, J.; Blelly, P.L.; Fontanari, J. A numerical model of the ionosphere, including the E-region above EISCAT. Ann. Geophys. 1996, 14, 191–200. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.L.; Flesch, G.D.; Ng, C.Y. A state-selected study of the ion-molecule reactions O+ (4S, 2D, 2P) + N2. J. Chem. Phys. 1997, 106, 1373–1381. [Google Scholar] [CrossRef]
- Dalgarno, A.A.E. Reaction Rate Data; Rep AFGL-TR 790067; Air Force Geophys Lab: Bedford, MA, USA, 1979. [Google Scholar]
- Glosik, J.; Rakshit, A.B.; Twiddy, N.D.; Adams, N.G.; Smith, D. Measurement of the rates of the reaction on ground and metastable excited states of O2+, NO+ and O+ with atmospheric gases at thermal energy. J. Phys. B At. Mol. Opt. Phys. 1978, 11, 3365–3379. [Google Scholar] [CrossRef]
- Fox, J.L.; Dalgarno, A. The vibrational distribution of N2+ in the terrestrial ionosphere. J. Geophys. Res. 1985, 90, 7557–7567. [Google Scholar] [CrossRef]
- Rees, M.H. Physics and Chemistry of the Upper Atmosphere; Cambridge University Press: New York, NY, USA, 1989. [Google Scholar]
- Chang, T.; Torr, D.G.; Richards, P.G.; Solomon, S.C. Reevaluation of the O+(2P) reaction rate coefficients derived from atmosphere explorer-C observations. J. Geophys. Res. 1993, 98, 15589–15597. [Google Scholar] [CrossRef]
- McLaughlin, B.M.; Bell, K.L. Electron-impact excitation of the fine-structure levels (1s22s22p34S03/2, 2D05/2,3/2, 2P03/2,1/2) of singly ionized atomic oxygen. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 4317–4329. [Google Scholar] [CrossRef]
- Kaufman, V.; Sugar, J. Forbidden lines in ns2npk ground configuration and ns np excited configurations of Beryllium through Molybdenum atoms and ions. J. Phys. Chem. Ref. Data 1986, 15, 321–426. [Google Scholar] [CrossRef]
- Dotan, I.; Viggiano, A.A. Rate constants for the reaction of O+ with NO as a function of temperature (300–1400 K). J. Chem. Phys. 1999, 110, 4730–4733. [Google Scholar] [CrossRef]
- Frederick, J.E.; Rusch, D.W. On the chemistry of metastable atomic nitrogen in the F region deduced from simultaneous satellite measurement of the 5200 Å airglow and atmospheric composition. J. Geophys. Res. 1977, 82, 3509–3517. [Google Scholar] [CrossRef]
- Richards, P.G.; Torr, D.G.; Torr, M.R. Photodissociation of N2: A significant source of thermospheric atomic nitrogen. J. Geophys. Res. 1981, 86, 1495–1498. [Google Scholar] [CrossRef]
- Goldan, P.D.; Schmeltekopf, A.L.; Fehsenfeld, F.C.; Schiff, H.I.; Ferguson, E.E. Thermal energy ion-neutral reaction rates. II. Some reactions of ionospheric interest. J. Chem. Phys. 1966, 44, 4095. [Google Scholar] [CrossRef]
- Lin, C.L.; Kaufman, F. Reactions of metastable nitrogen atoms. J. Chem. Phys. 1971, 55, 3760–3770. [Google Scholar] [CrossRef]
| Date | Daily Ap | F107d | F107_81 |
|---|---|---|---|
| 20 March 2009 | 4 | 68.2 | 69.1 |
| 19 June 2009 | 2 | 69.2 | 71.2 |
| 24 September 2009 | 1 | 75.0 | 71.0 |
| 21 December 2009 | 3 | 80.0 | 75.6 |
| 21 March 2010 | 1 | 84.1 | 80.7 |
| 21 June 2010 | 4 | 74.3 | 77.3 |
| 22 September 2010 | 2 | 85.4 | 80.9 |
| 19 December 2010 | 2 | 78.3 | 81.2 |
| 19 March 2011 | 4 | 88.0 | 109.3 |
| 21 June 2011 | 9 | 98.2 | 97.0 |
| 25 September 2011 | 4 | 169.8 | 130.6 |
| 25 December 2011 | 3 | 139.6 | 133.0 |
| 10 June 2012 | 5 | 132.3 | 131.5 |
| 23 September 2012 | 0 | 134.4 | 119.2 |
| 20 December 2012 | 8 | 110.4 | 117.8 |
| 11 March 2013 | 5 | 118.2 | 110.7 |
| 20 June 2013 | 11 | 130.5 | 120.5 |
| 23 September 2013 | 4 | 108.5 | 119.7 |
| 22 December 2013 | 1 | 133.4 | 148.0 |
| 19 March 2014 | 4 | 147.9 | 151.4 |
| 17 June 2014 | 8 | 118.0 | 132.6 |
| 6 October 2014 | 6 | 129.9 | 147.3 |
| 4 June 2015 | 2 | 121.4 | 125.0 |
| 28 September 2015 | 3 | 124.5 | 106.0 |
| 24 March 2016 | 6 | 86.0 | 92.8 |
| 20 June 2016 | 4 | 87.1 | 89.7 |
| 23 September 2016 | 3 | 86.1 | 86.6 |
| 17 December 2016 | 5 | 69.8 | 74.8 |
| 20 March 2017 | 1 | 72.1 | 77.3 |
| 28 June 2017 | 3 | 74.5 | 78.3 |
| 23 September 2017 | 4 | 81.7 | 84.4 |
| 23 December 2017 | 5 | 73.7 | 69.3 |
| 13 March 2018 | 3 | 67.7 | 69.2 |
| 22 June 2018 | 3 | 83.0 | 73.5 |
| 20 September 2018 | 1 | 67.2 | 69.4 |
| 21 December 2018 | 4 | 68.8 | 68.3 |
| 22 March 2019 | 1 | 81.8 | 71.1 |
| 18 June 2019 | 3 | 69.2 | 70.6 |
| 23 September 2019 | 3 | 66.6 | 68.0 |
| 23 December 2019 | 3 | 70.2 | 69.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Xu, T.; Sun, S.; Zhu, M.; Deng, Z.; Xu, Z. Improvement of SAMI2 with Comprehensive Photochemistry at Mid-Latitudes and a Preliminary Comparison with Ionosonde Data. Atmosphere 2024, 15, 67. https://doi.org/10.3390/atmos15010067
Hu Y, Xu T, Sun S, Zhu M, Deng Z, Xu Z. Improvement of SAMI2 with Comprehensive Photochemistry at Mid-Latitudes and a Preliminary Comparison with Ionosonde Data. Atmosphere. 2024; 15(1):67. https://doi.org/10.3390/atmos15010067
Chicago/Turabian StyleHu, Yanli, Tong Xu, Shuji Sun, Mengyan Zhu, Zhongxin Deng, and Zhengwen Xu. 2024. "Improvement of SAMI2 with Comprehensive Photochemistry at Mid-Latitudes and a Preliminary Comparison with Ionosonde Data" Atmosphere 15, no. 1: 67. https://doi.org/10.3390/atmos15010067
APA StyleHu, Y., Xu, T., Sun, S., Zhu, M., Deng, Z., & Xu, Z. (2024). Improvement of SAMI2 with Comprehensive Photochemistry at Mid-Latitudes and a Preliminary Comparison with Ionosonde Data. Atmosphere, 15(1), 67. https://doi.org/10.3390/atmos15010067





