Abstract
Most of the current, popular approaches to monitoring real driving NOx emissions are based on direct measurement. However, due to the uncertainty of sensor-based measurements, such methods cannot always be used to accurately screen out the malfunctions of an emission control system. In this paper, a random forest (RF) model which extracts information from on-board diagnostics (OBD) data streams transmitted by a remote emission management vehicle terminal (REMVT) is proposed to provide a specific emission method for the online screening of high NOx emissions. First, two particular forms of modeling, random forest and logistic regression (LR), are laid out as representatives of nonparametric models and specified linear models. These two models were trained, validated and compared using OBD data collected from three China-VI heavy-duty diesel vehicles (HDDVs). The results show that as a data-driven, highly adaptive and robust learning method, the RF model can more accurately identify an abnormal emission state. Finally, a further validation was conducted, in which another China-VI HDDV was tested in two typical states, including a fault state and a normal state. The results indicated that the RF model could clearly distinguish the out-of-control emission condition from the normal operation state. The outcome of this research verifies the feasibility of using a machine learning model to process remote OBD data on HD vehicles and to identify high emissions in the case of an in-use fleet. On this basis, more sophisticated combined models and multi-stage models could be developed.
1. Introduction
Globally, diesel emissions, particularly those from heavy-duty vehicles, have crucial source effects on local air quality. In China, as reported by the Ministry of Ecology & Environment, more than 80% and 90% of annual vehicle-related NOx and PM emissions are attributed to heavy-duty diesel vehicles [1]. Although electrification and hybridization can effectively eliminate diesel emissions, concerns regarding the range, payload, and security of these applications have confined the use of such vehicles to mainly urban contexts. In the short term, heavy-duty diesel vehicles are deemed irreplaceable in road transportation; hence, curbing diesel emissions during real driving is still a high priority.
As an alternative to laboratory tests, the enforcement of real-world measurement requirements using the Portable Emission Measurement System (PEMS) through both the Euro-VI and China-VI regulations has largely secured the lower-pollution operation of new diesel vehicles, but given the high cost and limited availability of PEMS testing, PEMS will never be the panacea for the current large population of in-service vehicles, especially for developing economic entities. New techniques for enrolling as many in-service vehicles as possible are required to better monitor and curb diesel emissions [2].
On-board diagnostics (OBD) was first proposed to monitor vehicle performance based on sensor feedback. This idea has greatly improved the control of vehicle emissions beyond the scope of type approval. However, although OBD can identify emission-related faults and warn the driver by illuminating the malfunction indication light (MIL) on the dashboard, the main limitation of OBD is that it can only help to eliminate these high emissions if the driver fixes the vehicle in a timely manner.
Uploading key OBD data to a terminal, which is known as the remote emission management vehicle terminal (REMVT), allows the environmental authorities to be aware of the emission performance of any vehicle almost as quickly as its driver [3]. Such a strategy, which was first widely mandated through the heavy-duty China-VI regulation, could significantly strengthen the supervision of manufacturers’ compliance and drivers’ duties. However, the enormous scale of OBD data uploaded by millions of vehicles in a second-by-second manner poses a new challenge. New models are needed to accurately identify high emitters among the in-service vehicle fleet.
Previous studies have developed some mathematical models to compare the emission factors derived from real-time OBD data with the regulation limits. Zhang et al. calculated fuel consumption with a carbon balance method based on CO, CO2 and THC data measured by PEMS and recorded the OBD fuel consumption data using the REMVT, and analyzed the accuracy and factors influencing the latter [4]. Zhang et al. tested eight HDDVs, which included the retrofitting by PEMS of in-use China-IV/V HDDVs and China-VI HDDVs on road, in order to examine the reliability of remote OBD NOx concentrations, showing good agreement between the remote data and PEMS results, with an average relative error of approximately 15% [5]. Combining remote data and vehicle sales data, Wang et al. estimated NOx emission reductions after the implementation of China-VI standards [6].
Most of the high emission identification methods proposed thus far rely on a NOx sensor downstream of a selective catalytic reduction (SCR) system. This sensor-based algorithm is theoretically applicable, but in practice, the accuracy and stability of commercialized NOx sensors are far less reliable than those of laboratory and PEMS analyzers when carrying out high-precision quantifiable measurements. For example, almost all sensors are sensitive to aspects of ambient environments, including temperature, humidity and atmospheric pressure. Measurements of NOx concentration may drift and introduce uncertainty into calculated emission results [7,8,9,10,11].
To remedy this drawback, in this study, a machine learning model using engine operating features closely correlated with NOx emissions as criteria for the detection of high-emitters was designed, trained and validated with remote OBD data, at a volume of approximately 90,000 data points obtained from four China-VI-compliant heavy-duty vehicles.
2. OBD Resource
2.1. Test Vehicle and Route Information
OBD data from four different models of HDDV were selected as the research sample. V1 and V4 were 18-ton trucks, V2 was a 4.5-ton pickup truck, and V3 was a 19-seat bus. The basic parameters and key configurations of the test vehicles are shown in Table 1.

Table 1.
Test vehicles and emission control devices.
The vehicles V1–V3 were tested on road, according to the PEMS procedure [2], and the obtained data were used for the model training and cross-validation.
Many studies have shown that SCR systems can significantly reduce NOx emissions [12,13,14]. To further validate the capability of the model to identify high emissions, a pair of road tests, which consisted of a fault state test and a normal state test, were conducted on vehicle V4 for a comparative analysis. The test route and driving style were entirely determined by the vehicle owner’s choice. As for the fault state test, the urea injection of the test vehicle was halted by artificially removing the front temperature sensor of the SCR, resulting in abnormal NOx emissions. In the latter half of the test, the emission control monitoring system repaired the fault through self-diagnosis and brought the uncontrolled emissions back to a compliant level. The data of vehicle V4 in the fault state and normal state are denoted as samples S4-a and S4-b, respectively.
Detailed information on the test routes is summarized in Table 2. The mileage represents the total distance of travel, which is divided into three segments: urban, rural and motorway, according to the on-road speed (below 55 km/h is referred to as urban, between 55 km/h and 75 km/h as rural, and above 75 km/h as motorway). The duration proportions within the three segments, along with the corresponding average speeds, are also displayed.

Table 2.
Test route composition (urban, rural, motorway) *.
2.2. Test Equipment
The REMVT was provided by the manufacturer of the test vehicles. It is capable of sending and receiving OBD data via a wireless network. The transmitted data include important information about the vehicle’s instantaneous operating condition, along with the environmental temperature, humidity, atmospheric pressure, exhaust flow, GPS data and NOx concentrations. The system topology diagram is shown in Figure 1.
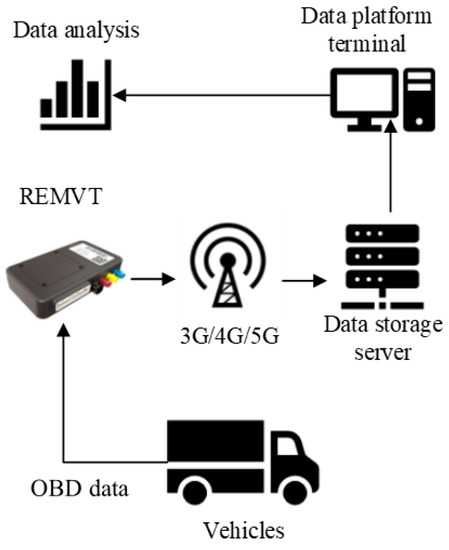
Figure 1.
System topology diagram.
3. Data Process and Methodology
After the collection, preprocessing and aggregation of the original OBD data, two models were constructed, analyzed and evaluated. The whole investigation procedure is illustrated in Figure 2.
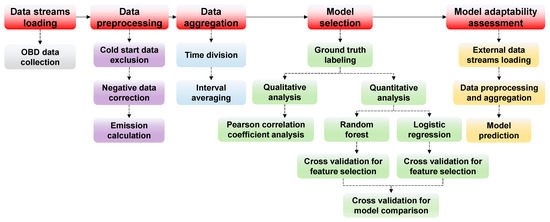
Figure 2.
Investigation procedure.
The OBD data volumes, recorded in seconds, are displayed in Table 3. Each single item has 19 attributes. The four vehicles have a total volume of approximately 90,000 remote data points, which were used to support the establishment of the model.

Table 3.
Single-item volume and total volume of OBD data.
3.1. Data Preprocessing
To exclude unrepresentative data and calculate the emission results, data preprocessing is required.
The original 1 Hz data streams acquired from the REMVT are preprocessed as follows:
- Cold-start data exclusion: Remove cold-start data with engine coolant temperatures less than 70 °C.
- Negative data correction: In the case of the actual torque percentage being less than the frictional torque percentage due to occasional, random fluctuations of the sensors, set both percentages to zero. Set negative readings of the NOx concentration (also caused by sensor drift) to zero.
- Emission calculation: Sequentially calculate the instantaneous torque, engine work, NOx emissions and specific NOx emissions from the calibrated data.
The instantaneous NOx emissions and instantaneous work are calculated according to Annex C A.5.2.3 and L.2.5.2 of the HD China-VI Emissions standard [2]. The instantaneous specific NOx emissions are obtained from the ratio of the emissions and work.
3.2. Data Aggregation
In this method, after data preprocessing, samples S1–S3 are used to train the models. Based on engineering experience, some channels are reprocessed to make it easier for the model to identify the internal relationship between non-emission features and emission features. From each sample, we extract 13-channel panel data, constituting 12 channels of emission-related features, denoted as , and a channel of the specific NOx emissions, denoted as . Here, stands for the time index measured in seconds, and stands for the total length of the effective time span. The information on the channels is displayed in Table 4.

Table 4.
Information on the channels.
To smooth out the data and reduce the follow-up computation load, the time span is divided into intervals of 1 min (60 s), and the mean of and for the th interval is calculated as
Here, are taken as predictors of the instantaneous emission state. This “divide and average” strategy is a type of data aggregation which has been widely applied in statistical process control tasks [15]. It has earned its popularity due to the following advantages:
- Enhancing independence within the data: After data aggregation, there is far less correlation between the one-minute samples, which better fits the basic assumptions of most current machine learning methodologies.
- Removing the burden of inefficient computation from the model: Through data aggregation, redundant information in the original sequence is greatly compressed, and the number of one-minute samples requires far fewer computing resources for the model training and validation.
- Improving the normality of the data distribution: According to the central limit theorem, the aggregated data approach a normal distribution regardless of the skewness and kurtosis of the distribution of the original sequence, which benefits the robustness of the model inference.
- Reducing the influence of outliers: The potential outliers that emerge due to the uncertainty of the indications are smoothed out by averaging, which further ensures the robustness of the model training.
When the above workflow is finished, the aggregated samples of the three data sets S1–S3 are merged, being denoted as and , for further utilization.
There are other statistical methods for data aggregation which may have a better performance in some situations. We chose two typical ones, namely, the 50% quantile and 90% quantile, for comparison in the construction of the predictor matrix . These were used in the same way as in the aforementioned procedure, the only change being the substitution of the mean operation in Equation (2) into the corresponding quantiles.
3.3. Ground Truth Labeling
To explore the correlation between the features and NOx emissions, the rows of the panel which represent information about each interval are divided into two categories, normal and abnormal, and benchmarked according to the specific NOx emissions. Then, we set the PEMS NOx limit of China-VI, 0.69 g/kWh, as the threshold [2]. Specifically, a binary label at the th interval is defined as
In other words, is taken as the ground truth of the normal/abnormal state. (Here, ground truth means information that is acknowledged to be true, demonstrated by empirical evidence such as direct observation and measurements. The term is originally borrowed from meteorology, in which “ground truth” refers to information obtained on the ground during the occurrence of a weather event [16].) Thus, the problem is converted into a supervised classification task, with each row of as a vector of predictors and the corresponding class of the sample as the response. This allows us to harness a variety of powerful and extensively studied classifiers through machine learning. Traditional detection methods implemented through direct measurements coupled with a well-trained classifier on the basis of emission-related features can be expected to substantially outperform state-of-the-art emission-monitoring systems. In the training of a classifier, the data from the NOx sensor are still used, but only in the ground truth labeling, which means that as long as the identification of the category is correct, the precise NOx emission values will not be included in the model. Thus, for the classification model, a lower requirement of accuracy is needed for sensor-based emission measurements. Since the model investigates the mechanisms of high emissions through their relationships with the engine’s operating features, it is expected to confirm the alarms provided by direct NOx monitoring, as well as the indications of abnormal operating conditions that direct monitoring fails to detect. Meanwhile, it is noteworthy that there are only 41 samples with the label in the total of 528 samples, which indicates that the total sample should be considered to be highly class-imbalanced.
3.4. Correlation Coefficient Analysis
Since there are numerous classification models in the literature on statistics and machine learning, including linear and nonlinear and parametric and nonparametric, it is important to choose one that fits the cause-and-effect mechanism of NOx emissions, with the selected features, to the greatest possible extent. To gain insight into the associations between variables as a guide for model selection, Pearson correlation coefficients between the features themselves and between the features and NOx-specific emissions are calculated based on the panel .
Figure 3 exhibits a heatmap of the correlation matrix for the considered channels. The channels are clustered in the figure based on their correlation coefficients, from which it is revealed that many features are highly correlated, especially the engine fuel rate, engine torque, mass air flow rate and exhaust volume flow rate. Most of the variables are positively correlated, with the commanded exhaust gas recirculation as an exception. The exhaust gas recirculation system returns part of the exhaust gas from the engine to the intake manifold, from which it then reenters the cylinder along with fresh air. Due to the large amount of CO2 contained in the exhaust gas, the maximum combustion temperature of the mixture in the cylinder decreases, thereby reducing the amount of NOx generated. From Figure 3, it can be seen that the feature that has the most significant correlation with the NOx-specific emissions is the engine torque, but the correlation is still far from sufficient to interpret the variation in the NOx emissions. This suggests that a multivariate model is required for the prediction of the emission condition. Some of the features show weak correlations with the specific NOx emissions, such as the engine speed. These features cannot be simply excluded from the modeling, due to the limited ability of the Pearson correlation coefficient to capture potential complicated nonlinear relationships between the variables, the existence of which will be further verified in the following sections.
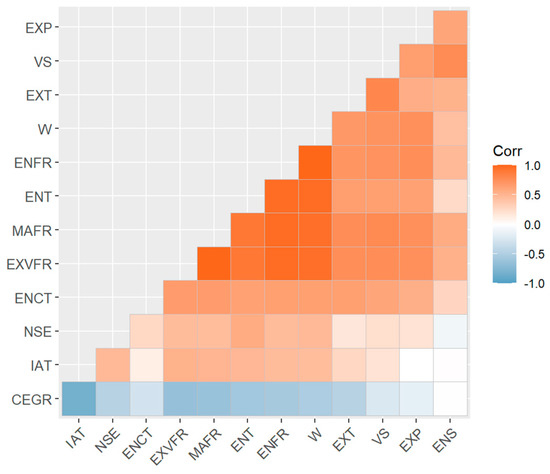
Figure 3.
Heatmap of the channel correlation matrix.
Of course, a linear model, or any parametric model of a given form, will carry the risk of model misspecification. Moreover, the aforementioned collinearity of the features is a non-negligible factor in modeling which may lead to overfitting [17]. Therefore, it is preferable to perform a feature selection step before the training, and cross-validation should be applied to guarantee an objective assessment of the generalization performance of the model [18,19]. To sum up, a data-driven, highly adaptive nonparametric multivariate model subjected to corresponding feature selection before and cross-validation after training is the starting point for our model design.
3.5. Modeling and Evaluation Design
3.5.1. Random Forest
Following the results obtained by correlation coefficient analysis, we chose random forest (RF) to model the classification task. Other nonlinear learning models, such as gradient boosting decision tree, support vector machine and neural network, also have appreciable flexibility, but this comes at the cost of more computational complexity and the need for more tuning work.
First proposed by Breiman [20], the random forest model is built upon classification and regression trees (CART) [21]. It constructs a collection of trees from bootstrap sample sets (bootstrap is a type of resampling method which involves repeatedly sampling observations with replacements from the data set to construct multiple sample sets with differences [22]). For every split of nodes in the generation process of an individual tree, a subset of features are randomly drawn as candidates, and the best feature and the corresponding best split point are chosen to maximize the improvement of the model fit [23]. For a classification task, the class of a new sample is predicted by a majority vote by the trees. The bootstrap method for generating sample sets combined with randomly selected features for node splitting provides the trees with great diversity, enabling them to capture more information on the training data, while retaining low correlation with each other; this eventually leads to an effective variance reduction achieved through voting. Using this strategy, random forest turns the notorious instability of a single tree, which easily leads to overfitting, into a kind of benefit, hence ensuring the robustness of the classification. In addition, the random forest model is also simple to train and tune, with the number of trees, the number of candidate features for each split and the minimum size of the terminal nodes as the only hyperparameters; a vast body of empirical studies have shown that the generalization performance of random forest is seldom affected by the particular choice of these hyperparameters. As an illustration, a single tree is trained using a bootstrap sample of the panel (as seen in Figure 4). In the case of random forest, a number of bootstrap trees are generated to form a committee, each casting a vote for the predicted class.
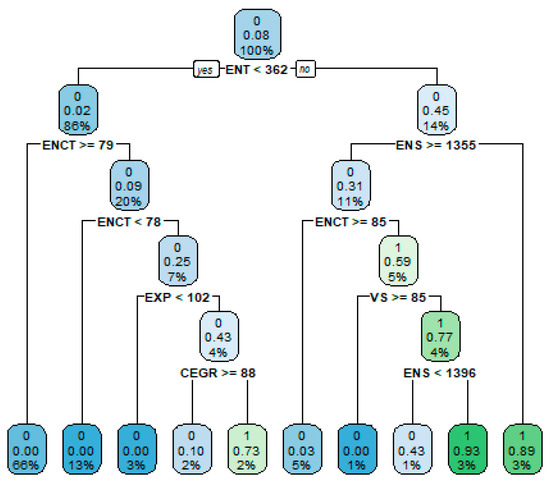
Figure 4.
CART generated by a bootstrap sample.
As discussed in the correlation coefficient analysis, the predictors are not equally relevant, with non-negligible collinearity. The generalization performance of a prediction model can often be improved by learning the importance of each predictor and only choosing the ones with substantial influence for modeling. To this end, a backward feature selection step tailored to random forest is added before training. The method is based on function “rfe” in the R package “caret”, a sketch of which is given below. At first, the random forest is trained with all 12 of the features, and 10-fold cross-validation is used to calculate the average prediction accuracy [23]. After this, the features are ranked in terms of importance based on their contributions to the overall enhancement of node purity at each split across all the trees. Then, with the feature of the lowest importance removed, the model is retrained and validated in the same way, through 10-fold cross-validation, and the average prediction accuracy together with the importance of the remained features is recorded again. The previous procedure is repeated a preset number of times, as determined by the user. Among the obtained models, the one with the highest prediction accuracy determines the features included in the final model. Considering the randomness of the above workflow (due to the generation process of the forest and the sample division in cross-validation), we repeat the procedure ten times and record the frequency with which each feature is selected to render the results more stable. The features with a frequency of no less than 0.5 are included in the final model.
After feature selection, 10-fold cross-validation is applied again to test the performance of the model. To control the randomness of the sampling, the ten folds of samples are drawn based on a stratified design. To be more specific, in each fold, the samples are drawn in proportion to the sample sizes of S1–S3. During training, a modification of the basic model is applied to provide better control for the false discovery rate (FDR) [24]. For the classification of a sample, an estimate of posterior probability , denoted as , is provided instead of a definite class label. The probability is estimated by the proportion of trees for which the sample falls into a terminal node labeled as class 1. A threshold is needed for the final dichotomy: If , is predicted to be 1; otherwise, is predicted to be 0. For the determination of , an additional hyperparameter is introduced. Denoting and as the numbers of normal/abnormal samples misclassified as class 1/0 in the training set, a loss function l is defined as
where is obtained by minimizing the above loss function. The hyperparameter is tuned to attain optimal FDR control for the validation set, which can equally be described as best improving the precision, as mentioned in the following sections.
For the prediction of samples in a validation set, there are four possible cases: equals 0 and is predicted as 0; equals 0 but is predicted to be 1; equals 1 and is predicted as 1; and equals 1 but is predicted to be 0. These four cases are recorded as true negative, false positive, true positive and false negative. We denote , , and as numbers of the four cases in the validation set, and as the summation of the four numbers. To measure the performance of the model, four indicators are used:
Total accuracy = : the ratio of correct classifications across all the test samples;
Null accuracy = : the ratio of correct classifications across all the test samples of class 0, which can also be taken as an estimate of , where is the probability of a type-I error (also known as the significance level) in the hypothesis testing ;
Recall = : the ratio of correct classifications across all the test samples of class 1, which can also be taken as an estimate of the power in the above hypothesis testing;
Precision =: the ratio of correct classifications across all the test samples predicted as class 1, which implies that improving the precision is equivalent to controlling the FDR.
The last two indicators are selected to better evaluate the effectiveness of the model in making its prediction, especially in consideration of the imbalanced characteristics of the sample. The trade-off between the two indicators should be considered because for the same learning model, an increase in the recall will trigger a decrease in the precision in a cause-and-effect manner. For the sake of our monitoring task, priority is given to precision, whereas a better recall rate is preferred when the precision is roughly the same.
To obtain more stable results, the 10-fold cross-validation is repeated ten times, through which the averages of the four indicators are obtained for the final comparison.
3.5.2. Logistic Regression
To further confirm the superiority of the nonlinear, more data-driven random forest classifier in the screening of out-of-control emission conditions, logistic regression (LR) is used as a benchmark. Logistic regression, introduced by Cox [25], is an ad hoc generalized linear model for classification. Through logit transformation, the posterior probability is modeled via a linear function in , as follows:
Although simple, the model often provides an interpretable view of how the features affect the response through the vector of the regression coefficients , and for prediction purposes, it can sometimes outperform more sophisticated nonlinear models, especially when the signal-to-noise ratio of the training data is low.
The components of are normalized in advance before training to eliminate the influence of the discrepancy of magnitudes, a problem which does not affect the training of the RF model. The subsequent procedures of training and validation are maintained in parallel with the above subsection to ensure a fair comparison.
For feature selection, the following minimization of the negative log-likelihood function with a penalty is solved to obtain the estimate of the regression coefficients :
The penalty aims to induce with sparsity, and only features with non-zero regression coefficients are considered to have a significant impact on the response. A number of penalty functions have been designed to make this conception work. One can mention, for example, the least absolute shrinkage and selection operator (LASSO) [26,27,28], the smoothly clipped absolute deviation (SCAD) [29], the adaptive LASSO [30,31], the grouped LASSO [32], the Dantzig selector [33], bridge regression [34] and the elastic net [35,36]. In this study, the penalty is chosen to be SCAD, which is reputed for its oracle property: under certain regular conditions, as the number of samples approaches infinity, the estimator only has non-zero values based on the true support of and is root-n-consistent [29]. The optimization of (6) is computed using the function “cv.ncvreg” in the R package “ncvreg”, the core of which is the coordinate descent algorithm [37]. The hyperparameter in the penalty function is tuned by 10-fold cross-validation to achieve the best prediction accuracy as a default. Again, to achieve better stability, we repeat the procedure ten times and record the frequency of each feature to obtain a non-zero weight in the estimate. The features with a frequency of no less than 0.5 are retained in the final model.
The model testing step is exactly the same as that used for random forest, with the same method for determining the threshold , the same four indicators for assessing the performance of the model, and ten 10-fold cross-validations for ensuring more stable results.
4. Results and Discussions
4.1. Model Comparison through Cross-Validation
Our comparisons of the two types of modeling, preprocessed using three patterns of data aggregation, are summarized in Table 5 and Table 6. Table 5 displays the frequency with which features were selected in the feature selection step. In the final modeling and validation step, only features with a selection rate of no less than 0.5 are retained. The results imply that the important features selected by the two different models vary, from which we can glean that the interpretability of the features with regard to the response is highly dependent on the mechanism of the specific model. Table 6 reveals the effectiveness of the prediction in more detail through the four indicators. For both models, the mean operation for data aggregation shows the overall best performance, with the 50% quantile following closely, and the 90% quantile being the least effective. This is in line with our previous research, in which it was shown that the 90% quantile resulted in significant uncertainty and could not be taken as a stable representative of NOx emissions [38]. For all the three modes of data aggregation, random forest outperforms logistic regression, which confirms our hypothesis that the relationship of NOx emissions with OBD features is strongly nonlinear. With higher precision, random forest also maintains the recall rate at an acceptable level (67.2% and 48.5%, respectively, for the mean mode). As a nonparametric and highly adaptive learning model, random forest captures further details of the nonlinear relation and is more robust to the high correlation between OBD features, which still exists after feature selection. At the same time, as with all other prevailing machine learning methods, the two models are still premature in treating the class imbalance problem, which is the main obstacle preventing the acquisition of higher precision and recall rates.

Table 5.
Frequency of features selected.

Table 6.
Model evaluation.
4.2. Trials for More Precision
Focusing on the random forest model with the preprocessing of the mean mode, some tests and analyses were conducted to better enhance its precision.
Concerning the class imbalance issue, oversampling was applied to the abnormal class to render the sample sizes of the two classes in a ratio of 1:1 [39]. Trained by the artificially modified sample, the performance in cross-validation showed no particular advantage. Although there was some increase in the recall rate, the precision decreased significantly, which indicates that in such an extremely imbalanced case (with the true normal–abnormal ratio being over 10:1), oversampling is not a substantive solution to the problem.
From the above study, it can be inferred that there is a limitation on the present 12 features preventing greater precision in the one-minute classification task. However, it should be kept in mind that the ultimate goal of the system is to screen out any out-of-control emissions through OBD data which are derived in sequence. A typical requirement of vehicle manufacturers is that they upload a new batch of information every 10 min. Observing the time series of the specific NOx emissions based on the one-minute interval average, as displayed in Figure 5, it can be seen that the abnormal points are concentrated in only a few time periods, and the state has time continuity. From this discovery, it can be determined whether an alarm should be set off based on the number of positive signals given by the classifier within the 10 min window, through which the impact of a single false discovery can be reduced. Furthermore, combined with the traditional supervision method based on the direct measurement of NOx emissions, the whole system is expected to better serve the real-time online monitoring of emissions.

Figure 5.
Time series of specific NOx emissions (based on one-minute interval average). The horizontal dotted line indicates the threshold value of 0.69 g/kWh.
5. Model Adaptability Assessment Using External Data
In this part of the study, the validation tests of V4 were conducted, and the results were analyzed to better illustrate the adaptability of the proposed monitoring model. The samples S4-a and S4-b, with respect to the fault state and normal state, were preprocessed and aggregated following the same rules as those used for S1–S3, and the emission states of the one-minute intervals were predicted by the random forest classifier retrained with , namely, the full sample of S1–S3 after aggregation and labeling. The CEGR feature was removed during training due to the lack of corresponding channel information in the OBD data of V4.
To simulate real online monitoring scenarios, the two predicted state sequences of S4-a and S4-b were further divided into windows in 10 min increments, with the number of alarms or, in other words, the number of one-minute states, predicted as abnormal by the classifier being recorded per window. Meanwhile, the specific NOx emissions per window were calculated using the ratio of cumulative NOx emissions and cumulative engine work during the corresponding 10 min period. In practical use, the above two processing sequences, which represent the learning model and the specific method, are instantly calculated and transmitted in parallel for real-time monitoring.
Figure 6 and Figure 7 plot the line charts of the two monitoring sequences of S4-a and S4-b. As seen in Figure 6, at the beginning of the route (corresponding to the first six windows), the specific emissions of the abnormal case, S4-a, are apparently higher compared to the normal case, S4-b. Afterwards, the specific emissions of S4-a return to a level comparable with S4-b due to the fault substitution strategy set by the manufacturer. This setup allows the vehicle OBD system to activate alternative strategies so as to control the emission level when a fault is detected. The variations in the lines in Figure 7 show many similarities with those in Figure 6, and most of the alarms occur around the local maxima of the specific emissions. These results indicate that the learning model successfully grasps the fluctuations in the emission process. Half of the windows show at least two signals during the uncontrolled stage in S4-a, with a peak value of three signals, while in contrast, there is only one window of two signals within the same period in S4-b. This demonstrates that the model can effectively distinguish the out-of-control emission condition of S4-a from the normal operation case.
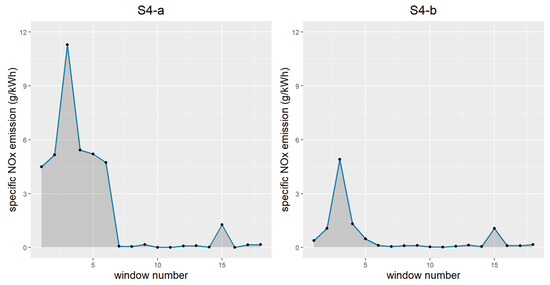
Figure 6.
Sequence of specific NOx emissions per 10 min (left/right for the abnormal/normal case).
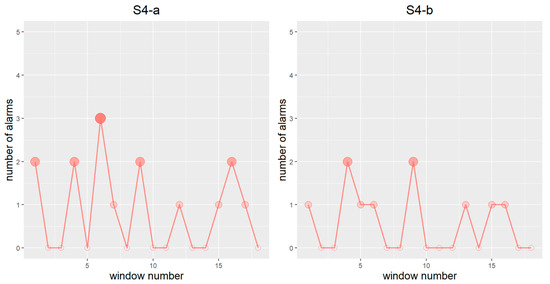
Figure 7.
Sequence of the number of alarms obtained per 10 min by the random forest classifier (left/right for the abnormal/normal case).
Nevertheless, the learning model fails to completely capture the high emissions at the beginning of the route, especially in the case of S4-a. This shortcoming may be ascribed to two aspects. On the one hand, due to the insufficiency of the training sample, the model cannot yet fully capture the general rule necessary to discriminate between normal and abnormal emissions, and the prediction accuracy is expected to be further improved with the increase in the training sample size. On the other hand, the mechanism of simulated faults may, to some extent, be different from the given cause of high emissions in actual working conditions. It should be remembered that the result of cross-validation is only meaningful if the test data are derived from the same distribution as the training data. Therefore, to obtain more reliable results in the context of heterogeneity, we recommend first clustering the vehicles to be monitored according to the vehicle models, road conditions and potential faults, and using a learning model trained on data with the same attributes.
6. Conclusion and Recommendations
In this paper, a random forest classification model using engine operating features other than NOx signals as the criteria for in-service high-emission diesel vehicle identification was proposed, trained and validated using remote OBD data collected from four China-VI diesel vehicles. The validation results confirm the feasibility of the method. This RF-based approach has better credibility than NOx signal-oriented methods because a multi-factor assessment tends to be more stable and reliable.
Compared to a straight-forward comparison between NOx readings and the regulative limits, this RF-based machine learning model is more effective in recognizing high emissions induced by cheating. A good example is the artificially lifted thermo-couple upstream of the SCR in this paper, which according to OBD logic will not be treated as a malfunction; hence, the environmental authorities will not be alerted of the occurrence of high NOx emissions. By contrast, for the RF-based algorithm, such a case is not difficult to identify, because the judgement is not dependent on any sole parameter.
Several extensions of the present work would be of practical interest. First, the ground truth labeled according to the calculated value of specific NOx emissions is not always reliable. A more comprehensive definition of an abnormal state could not only improve the reliability of the classifier but also render it more independent of the specific emission method, which will improve FDR control in combined testing [40,41]. Second, after data aggregation, the sample is taken as independent and identically distributed for modeling, but in reality, interdependence still exists along the time axis. An autoregressive model of NOx emissions could be employed and further boosted with a machine learning model trained on residuals [42]. Alternatively, in a more direct approach, NOx emissions with time lags could be added as additional features of our proposed classifier. The actual effects of these modifications should be examined carefully, as they may instead lead to a greater risk of overfitting. Third, the same kind of modeling could be applied and validated for the monitoring of emissions of other key pollutants, such as particulate matter. Fourth, recent research on the random forest model has expanded its functions to include treatment effect estimation, which has enabled the possibility of cause inference rather than the prediction of high emissions alone [43]. This indicates that the potential of the RF model is not limited to monitoring, but also encompasses the quality and design improvement of core components for vehicle manufacturers. Last but not least, in real applications, a large amount of OBD data are often monitored simultaneously by the environmental authorities and manufacturers. The latest computational technologies such as parallel computing and distributed computing can effectively save time in model updating and validation [44]. In our view, the study of remote monitoring with the aid of machine learning is an exciting and promising area for future research.
Author Contributions
Conceptualization, Y.G. and P.H.; methodology, Y.G. and P.H.; software, Y.G.; validation, Y.G.; formal analysis, P.H. and Y.L.; investigation, Y.G., T.L. and P.H.; resources, T.L.; data curation, Y.G. and T.L.; writing—original draft preparation, Y.G. and T.L.; writing—review and editing, P.H.; visualization, Y.G., T.L. and P.H.; supervision, S.S., W.L., M.H. and L.X.; project administration, P.H. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Young Scientists Fund, Natural Science Foundation of Tianjin City (18JCQNJC70100).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- MEE (Ministry of Ecology and Environment P.R. China). China Mobile Source Environmental Management Annual Report (2022). 2021. Available online: https://www.vecc.org.cn/dbfile.svl?n=/u/cms/jdchbw/202212/09170954wf3x.pdf (accessed on 22 February 2023).
- MEE (Ministry of Ecology and Environment P.R. China); SAMR (State Administration for Market Regulation). Limits and Measurement Methods for Emissions from Diesel Fuelled Heavy-Duty Vehicles (CHINA VI); China Environmental Science Press: Beijing, China, 2018.
- Sun, Y.; Guo, Y.; Wang, C. Research on Data Consistency of Remote Emission Management Vehicle Terminals for Heavy-Duty Vehicles. Small Intern. Combust. Engine Veh. Technol. 2019, 48, 1–6. [Google Scholar]
- Zhang, X.; Li, J.; Yang, Z.; Xie, Z.; Li, T. Accuracy Analysis of Carbon Emissions Measurement of Heavy Heavy-Duty Diesel Vehicles Based on Remote Data. China Environ. Sci. 2022, 42, 4565–4570. [Google Scholar]
- Zhang, S.; Zhao, P.; He, L.; Yang, Y.; Liu, B.; He, W.; Cheng, Y.; Liu, Y.; Liu, S.; Hu, Q. On-Board Monitoring (OBM) for Heavy-Duty Vehicle Emissions in China: Regulations, Early-Stage Evaluation and Policy Recommendations. Sci. Total Environ. 2020, 731, 139045. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, R.; Yin, H.; Wang, Y.; Wang, H.; He, C.; Liang, J.; He, D.; Yin, H.; He, K. Assessing Heavy-Duty Vehicles (HDVs) on-Road NOx Emission in China from on-Board Diagnostics (OBD) Remote Report Data. Sci. Total Environ. 2022, 846, 157209. [Google Scholar] [CrossRef]
- Mera, Z.; Fonseca, N.; Casanova, J.; López, J.-M. Influence of Exhaust Gas Temperature and Air-Fuel Ratio on NOx Aftertreatment Performance of Five Large Passenger Cars. Atmos. Environ. 2021, 244, 117878. [Google Scholar] [CrossRef]
- Giechaskiel, B.; Clairotte, M.; Valverde-Morales, V.; Bonnel, P.; Kregar, Z.; Franco, V.; Dilara, P. Framework for the Assessment of PEMS (Portable Emissions Measurement Systems) Uncertainty. Environ. Res. 2018, 166, 251–260. [Google Scholar] [CrossRef]
- Feist, M.D.; Sharp, C.A.; Spears, M.W. Determination of PEMS Measurement Allowances for Gaseous Emissions Regulated Under the Heavy-Duty Diesel Engine In-Use Testing Program: Part 1—Project Overview and PEMS Evaluation Procedures. SAE Int. J. Fuels Lubr. 2009, 2, 435–454. [Google Scholar] [CrossRef]
- Buckingham, J.P.; Mason, R.L.; Spears, M.W. Determination of PEMS Measurement Allowances for Gaseous Emissions Regulated Under the Heavy-Duty Diesel Engine In-Use Testing Program: Part 2—Statistical Modeling and Simulation Approach. SAE Int. J. Fuels Lubr. 2009, 2, 422–434. [Google Scholar] [CrossRef]
- Sharp, C.A.; Feist, M.D.; Laroo, C.A.; Spears, M.W. Determination of PEMS Measurement Allowances for Gaseous Emissions Regulated Under the Heavy-Duty Diesel Engine In-Use Testing Program: Part 3—Results and Validation. SAE Int. J. Fuels Lubr. 2009, 2, 407–421. [Google Scholar] [CrossRef]
- Su, S.; Ge, Y.; Zhang, Y. NOx Emission from Diesel Vehicle with SCR System Failure Characterized Using Portable Emissions Measurement Systems. Energies 2021, 14, 3989. [Google Scholar] [CrossRef]
- Yao, Q.; Yoon, S.; Tan, Y.; Liu, L.; Herner, J.; Scora, G.; Russell, R.; Zhu, H.; Durbin, T. Development of an Engine Power Binning Method for Characterizing PM2. 5 and NOx Emissions for Off-Road Construction Equipment with DPF and SCR. Atmosphere 2022, 13, 975. [Google Scholar] [CrossRef]
- Valverde, V.; Giechaskiel, B. Assessment of Gaseous and Particulate Emissions of a Euro 6d-Temp Diesel Vehicle Driven> 1300 Km Including Six Diesel Particulate Filter Regenerations. Atmosphere 2020, 11, 645. [Google Scholar] [CrossRef]
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2020; ISBN 1119723094. [Google Scholar]
- Lemoigne, Y.; Caner, A. Molecular Imaging: Computer Reconstruction and Practice; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; ISBN 1402087527. [Google Scholar]
- Cawley, G.C.; Talbot, N.L.C. On Over-Fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Allen, D.M. The Relationship between Variable Selection and Data Agumentation and a Method for Prediction. Technometrics 1974, 16, 125–127. [Google Scholar] [CrossRef]
- Stone, M. Cross-validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Ser. B 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: London, UK, 2017; ISBN 1315139472. [Google Scholar]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994; ISBN 0412042312. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 27, pp. 83–85. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Cox, D.R. The Regression Analysis of Binary Sequences. J. R. Stat. Soc. Ser. B 1958, 20, 215–232. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Zhao, P.; Yu, B. On Model Selection Consistency of Lasso. J. Mach. Learn. Res. 2006, 7, 2541–2563. [Google Scholar]
- Meinshausen, N.; Bühlmann, P. High-Dimensional Graphs and Variable Selection with the Lasso. Ann. Stat. 2006, 34, 1436–1462. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Zou, H. The Adaptive Lasso and Its Oracle Properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Zhang, H.H.; Lu, W. Adaptive Lasso for Cox’s Proportional Hazards Model. Biometrika 2007, 94, 691–703. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model Selection and Estimation in Regression with Grouped Variables. J. R. Stat. Soc. Ser. B 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Candes, E.; Tao, T. The Dantzig Selector: Statistical Estimation When p Is Much Larger than N. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar]
- Huang, J.; Horowitz, J.L.; Ma, S. Asymptotic Properties of Bridge Estimators in Sparse High-Dimensional Regression Models. Ann. Stat. 2008, 36, 587–613. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and Variable Selection via the Elastic Net. J. R. Stat. Soc. Ser. B 2005, 67, 301–320. [Google Scholar] [CrossRef]
- Zou, H.; Zhang, H.H. On the Adaptive Elastic-Net with a Diverging Number of Parameters. Ann. Stat. 2009, 37, 1733. [Google Scholar] [CrossRef]
- Breheny, P.; Huang, J. Coordinate Descent Algorithms for Nonconvex Penalized Regression, with Applications to Biological Feature Selection. Ann. Appl. Stat. 2011, 5, 232–253. [Google Scholar] [CrossRef]
- Su, S.; Ge, Y.; Hou, P.; Wang, X.; Wang, Y.; Lyu, T.; Luo, W.; Lai, Y.; Ge, Y.; Lyu, L. China VI Heavy-Duty Moving Average Window (MAW) Method: Quantitative Analysis of the Problem, Causes, and Impacts Based on the Real Driving Data. Energy 2021, 225, 120295. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Lebovitz, S.; Levina, N.; Lifshitz-Assaf, H. Is AI Ground Truth Really ‘True’? The Dangers of Training and Evaluating AI Tools Based on Experts’ Know-What. Manag. Inf. Syst. Q. 2021, 45, 1501–1525. [Google Scholar] [CrossRef]
- Dumitrache, A.; Aroyo, L.; Welty, C. Crowdsourcing Ground Truth for Medical Relation Extraction. ACM Trans. Interact. Intell. Syst. 2017, 8, 1–20. [Google Scholar] [CrossRef]
- Almeida, C.; Fan, J.; Freire, G.; Tang, F. Can a Machine Correct Option Pricing Models? J. Bus. Econ. Stat. 2022, 1–12. [Google Scholar] [CrossRef]
- Athey, S.; Tibshirani, J.; Wager, S. Generalized Random Forests. Ann. Stat. 2019, 47, 1148–1178. [Google Scholar] [CrossRef]
- Tan, X.; Chang, C.; Zhou, L.; Tang, L. A Tree-Based Model Averaging Approach for Personalized Treatment Effect Estimation from Heterogeneous Data Sources. In Proceedings of the International Conference on Machine Learning (PMLR), Baltimore, MD, USA, 17–23 July 2022; pp. 21013–21036. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).