Towards Space Deployment of the NDSA Concept for Tropospheric Water Vapour Measurements
Abstract
1. Introduction
2. Briefings of the NDSA Concept and Instrument Prototype
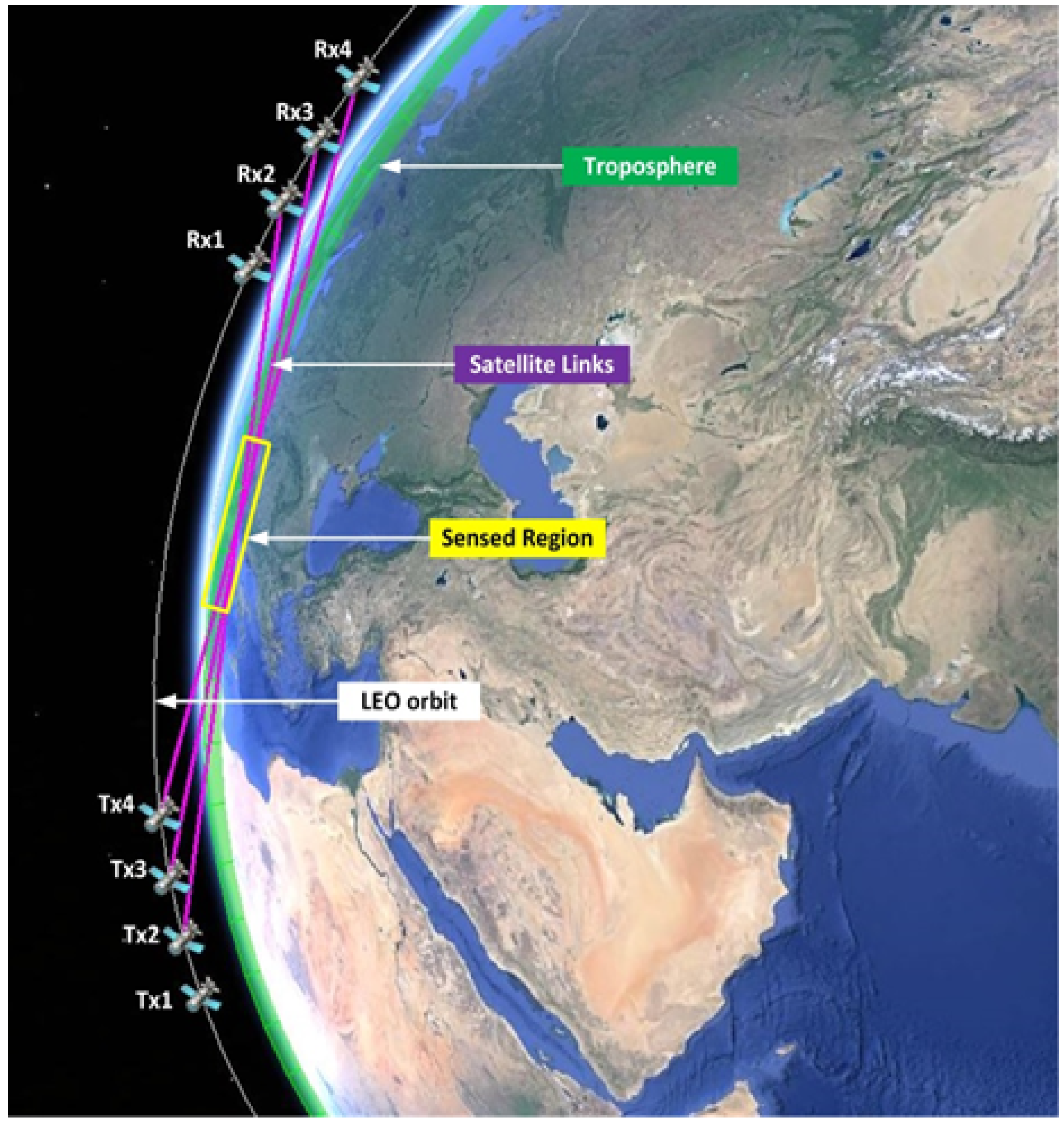
2.1. NDSA Concept
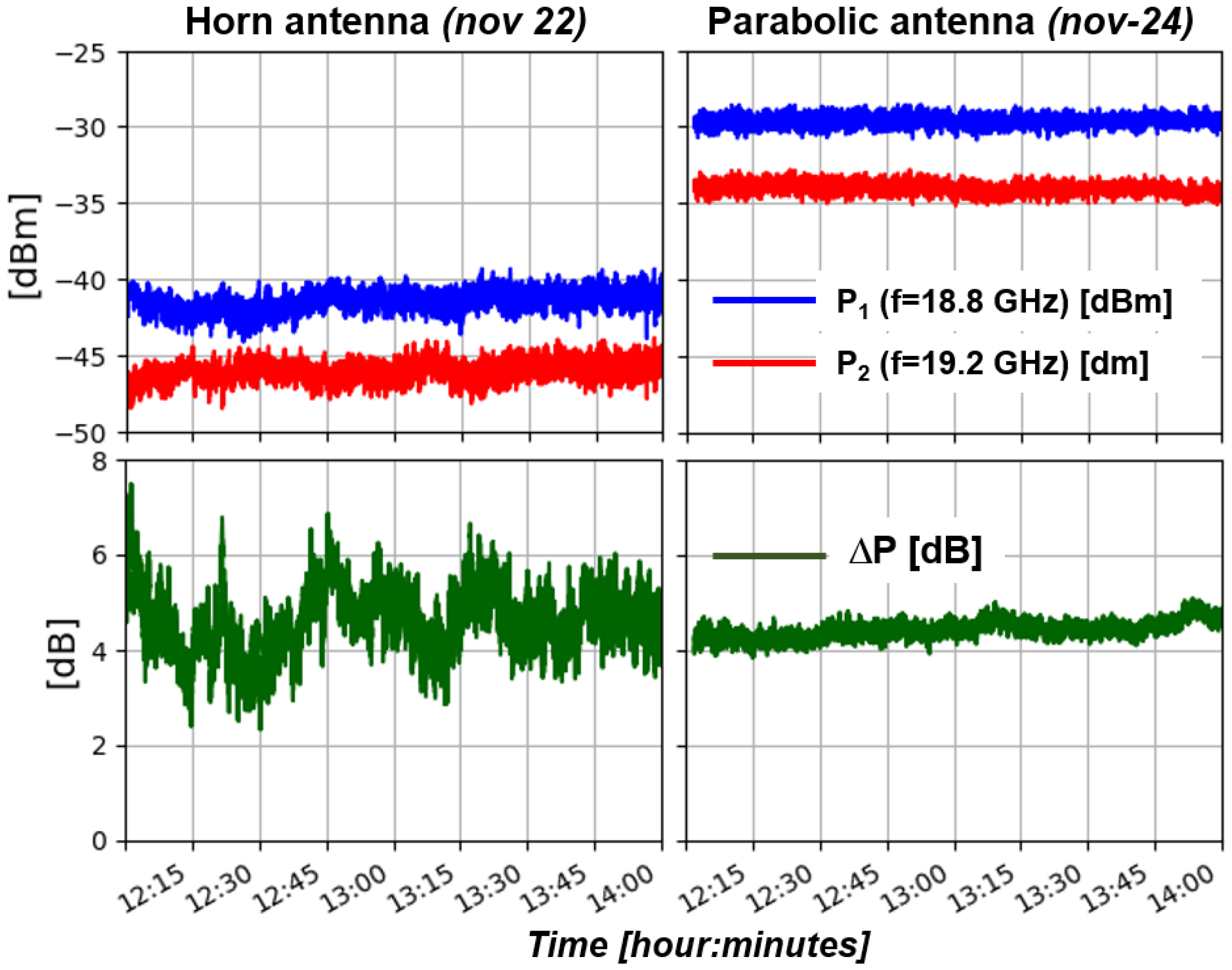
2.2. Instrument Prototype
3. NDSA Methods for Tropospheric Water Vapour Retrievals and Applications
3.1. Least Squares Inversion Method
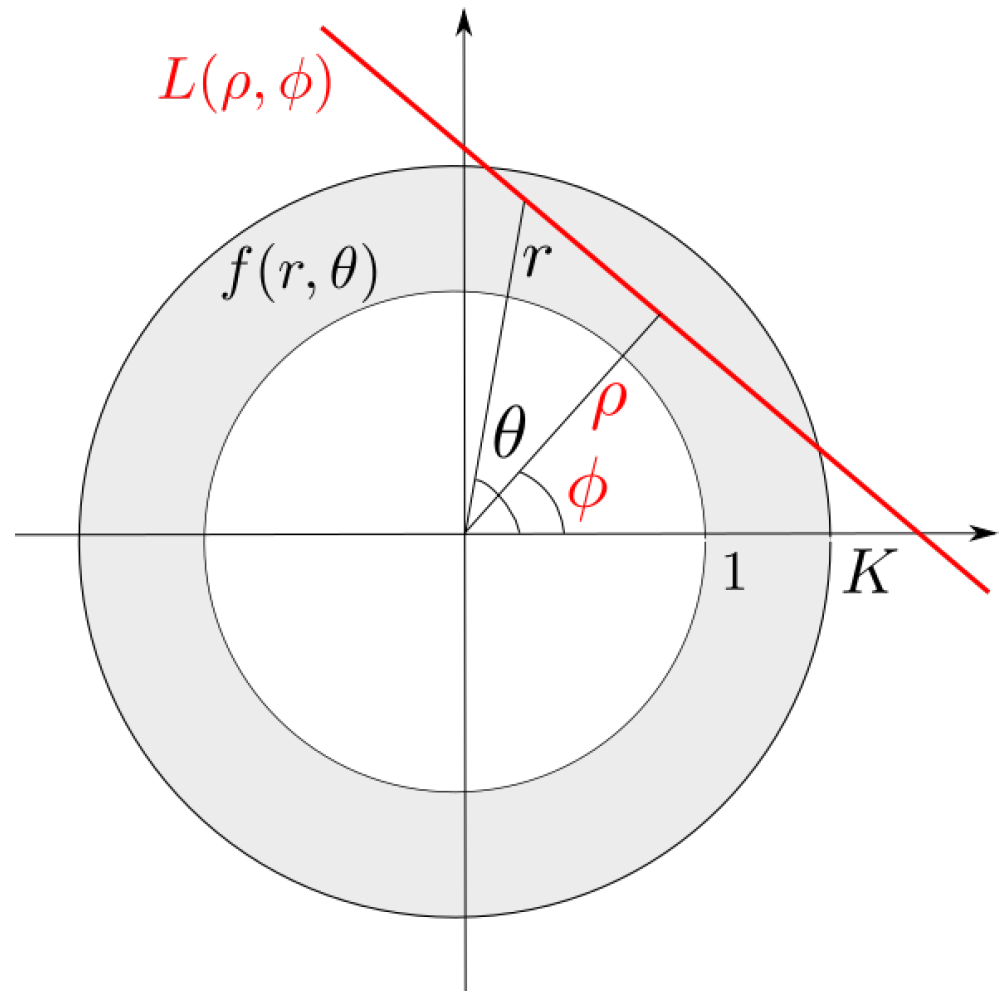
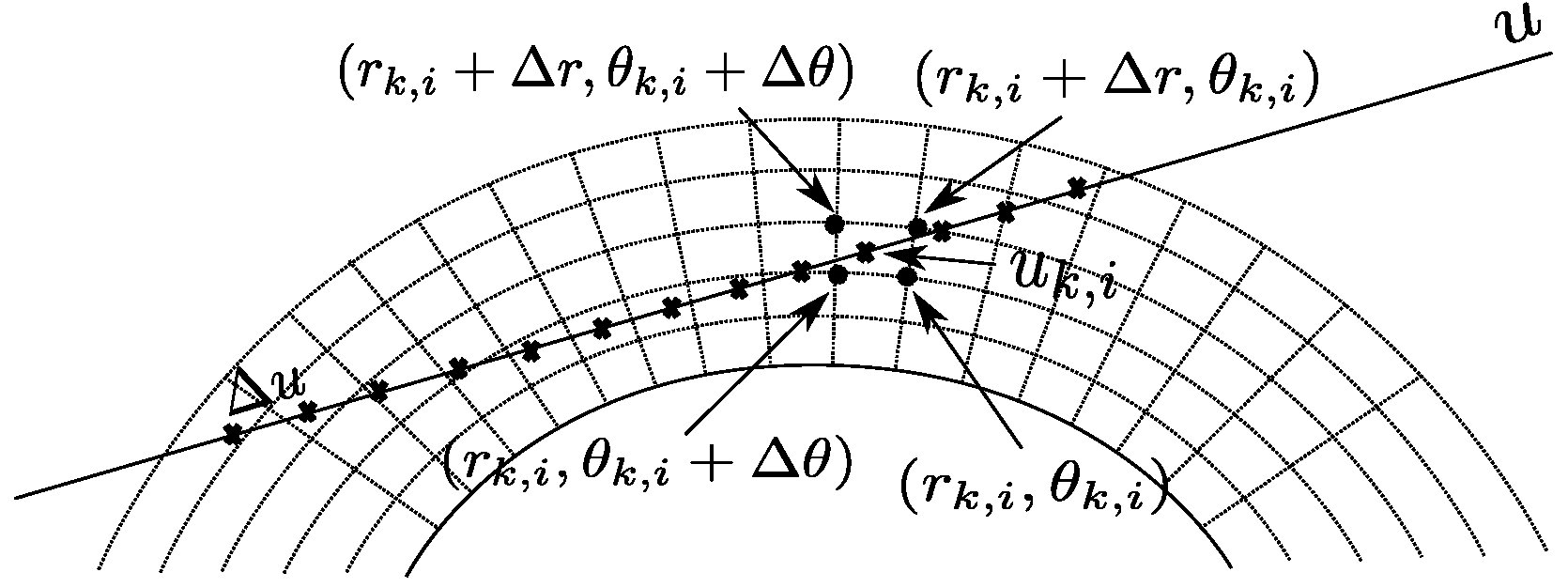
3.2. Exterior Reconstruction Method
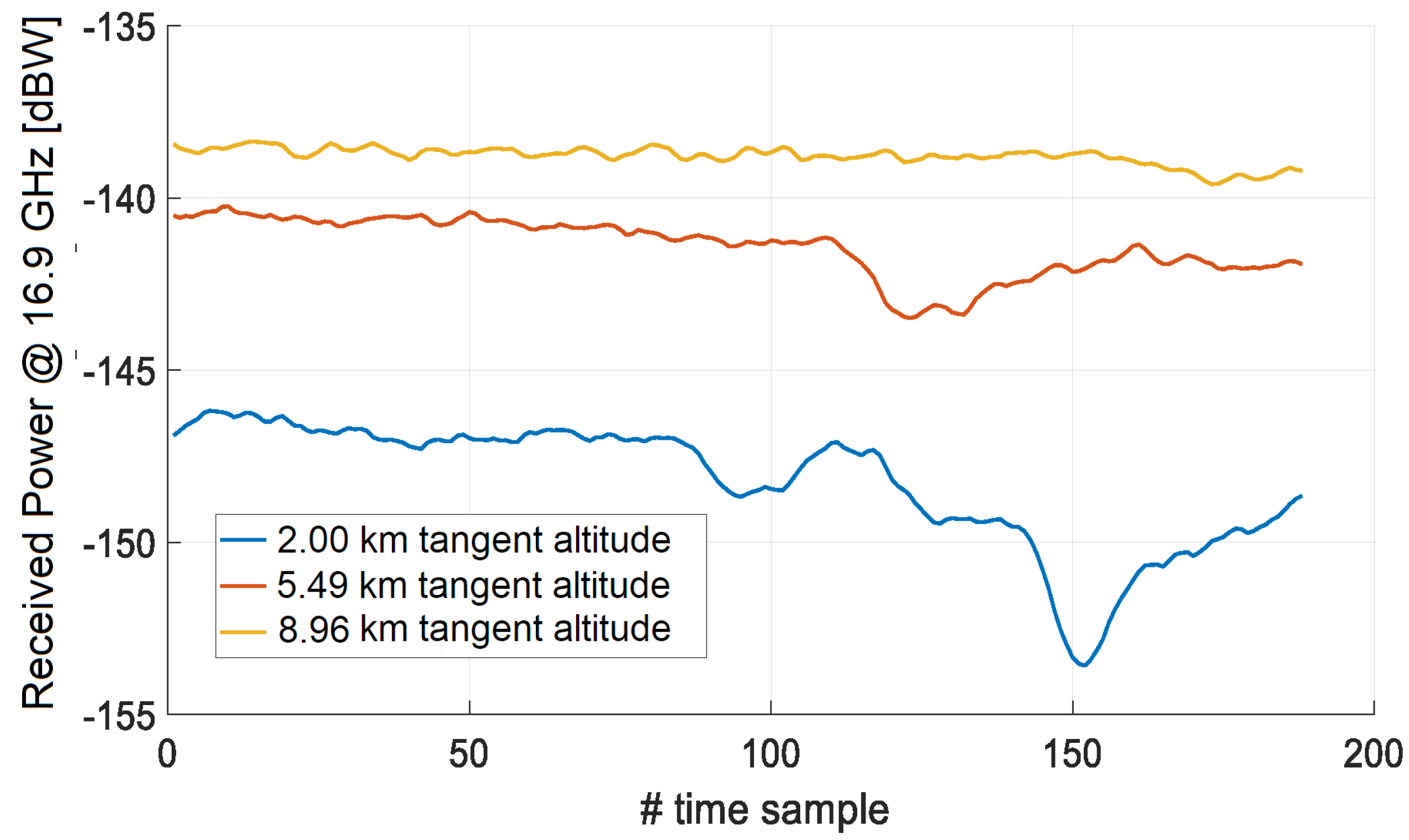
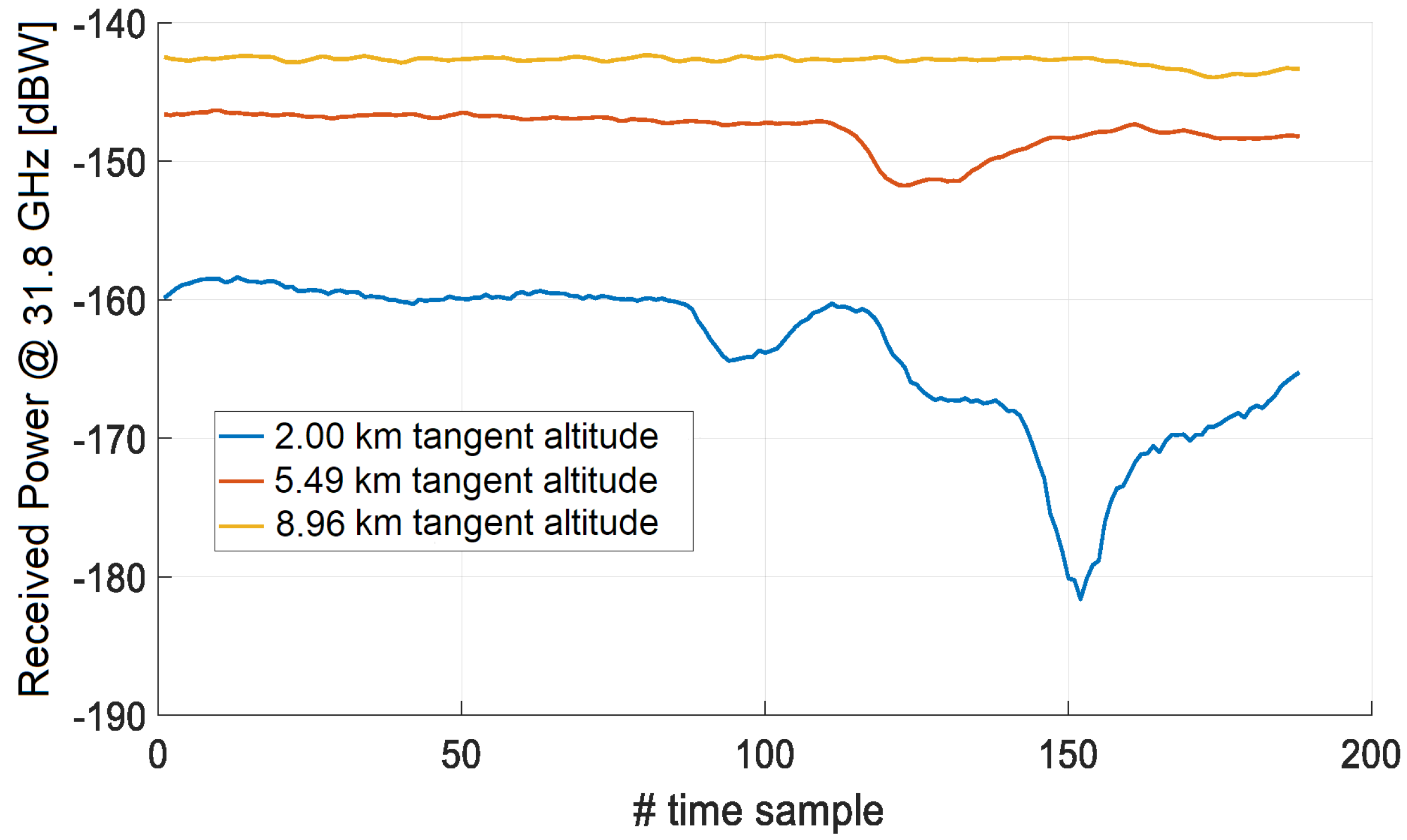
3.3. Applications
- Ideal transmission and acquisition conditions (absence of thermal noise and scintillation effects);
- One Tx satellite and five Rx satellites on the same circular orbit;
- Polar orbit with a satellite altitude equal to 273 km;
- Constant angular speed with a revolution period of 90 min;
- Integration time at the receiver = 1 s.
4. Other Related Considerations for NDSA Retrieval and Space Deployment
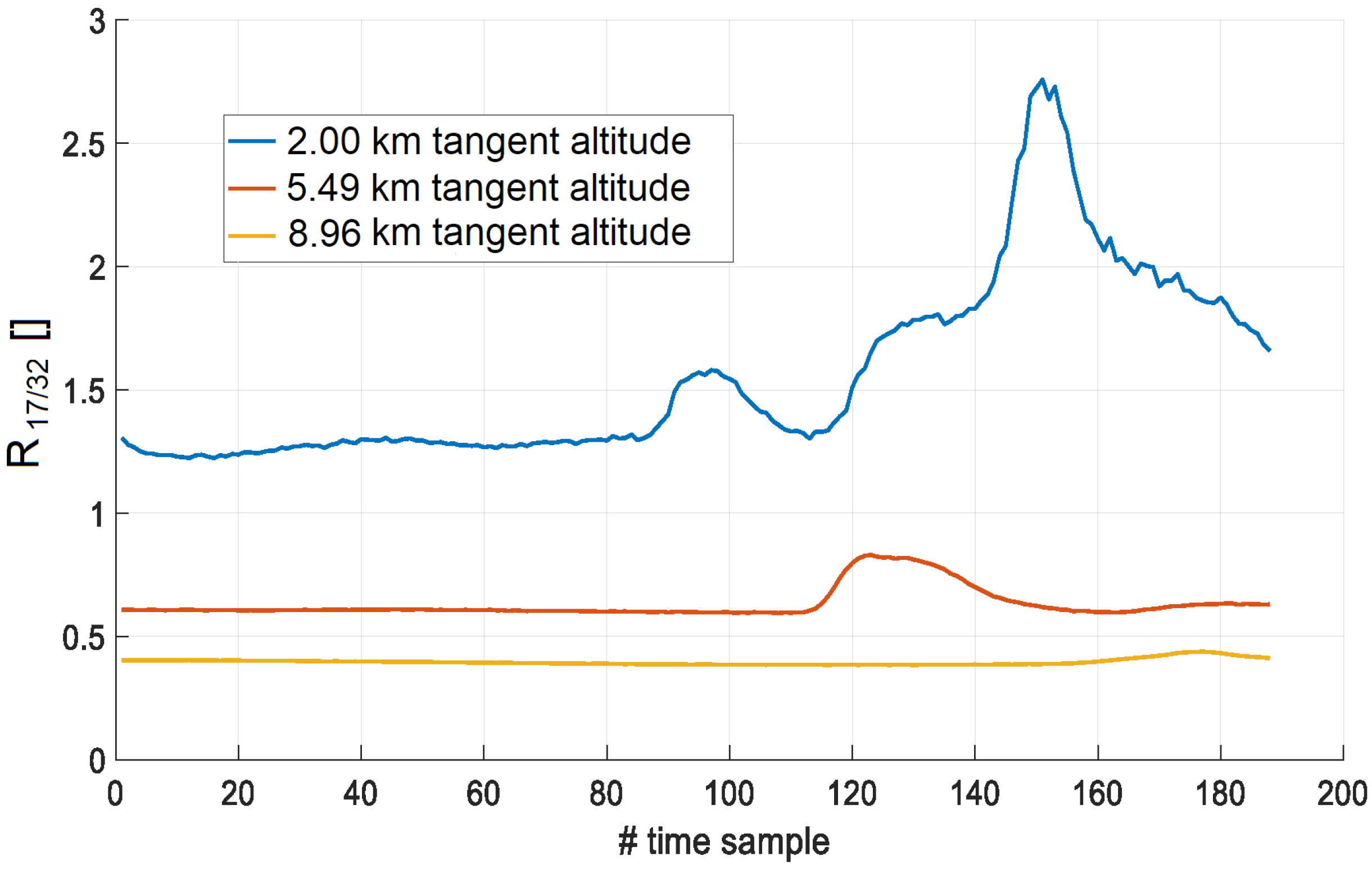
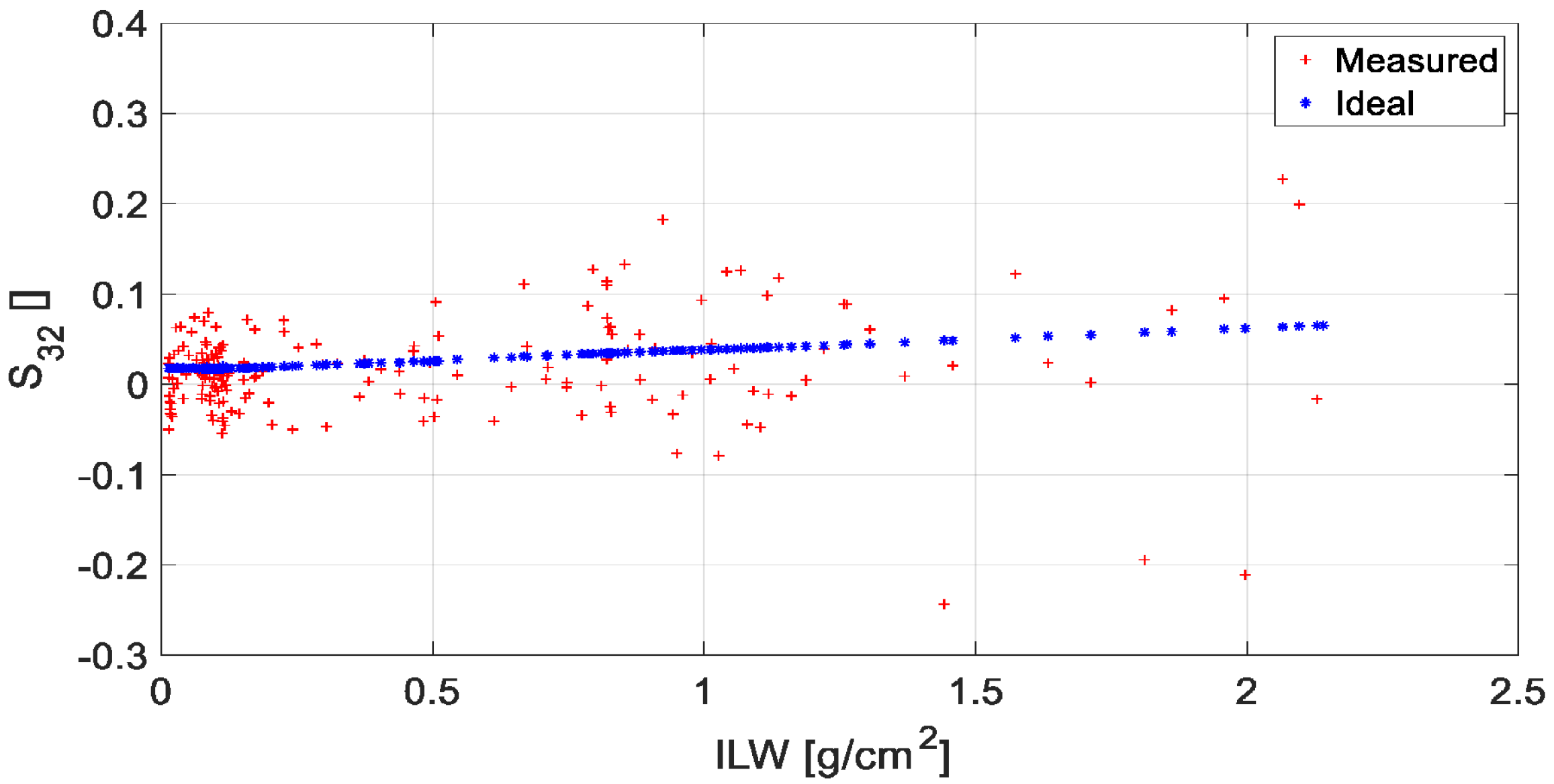
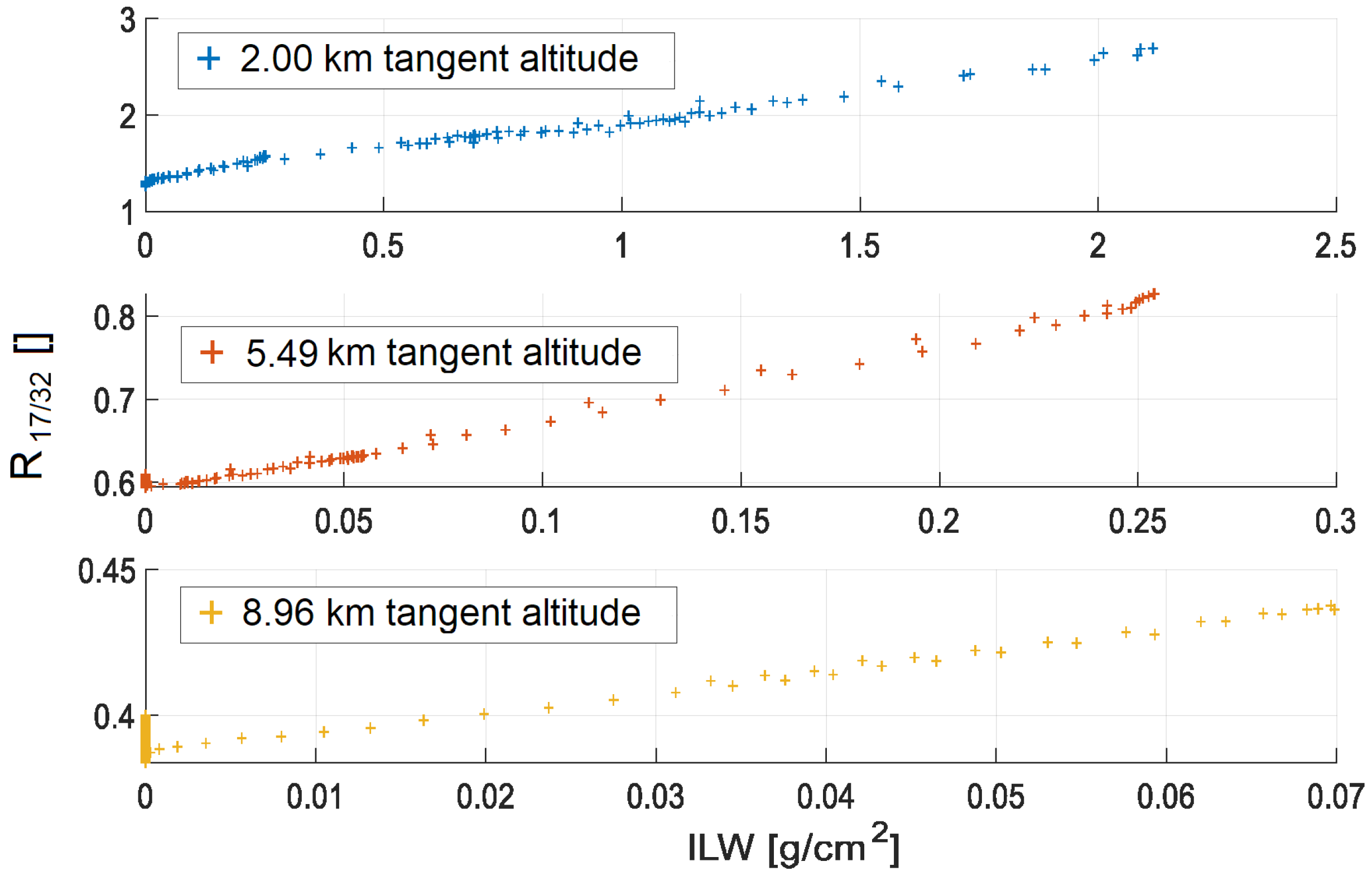
4.1. Correction of Tropospheric Liquid Water Contents on WV Retrievals
- Satellites co-orbiting on a circular polar orbit at constant angular speed, having a revolution period of approximately 90 min;
- Earth radius: 6378 km;
- Satellite orbit radius: 6651 km (273 km altitude);
- Integration time at the receiver: Ts = 0.5 s;
- Transmitted power: 3 dBW for each tone;
- Frequencies for power measurement: 16.9, 17.1, 18.9, 19.1, 20.9, 21.1, 31.8, and 32.2 GHz;
- Tx and Rx antenna gains: 26.4 dB;
- System noise equivalent temperature: 25.3 dBK.
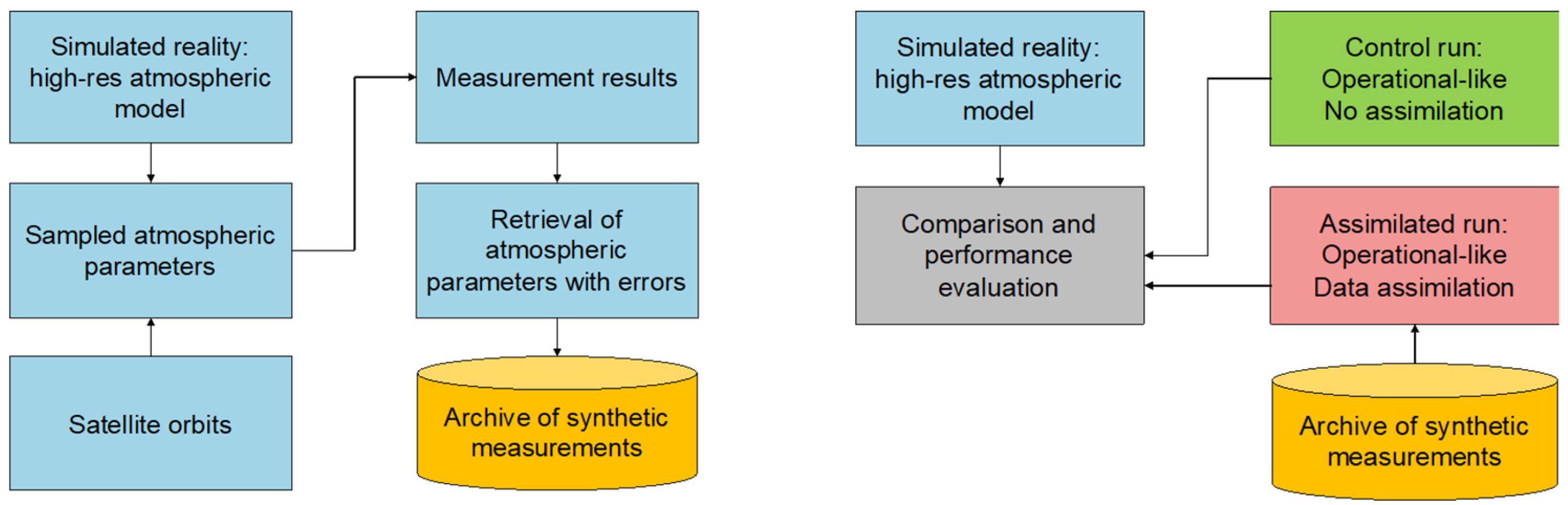
4.2. Mission and Payload Concept Demonstration
4.3. Assimilation Impact Assessment of WV Products from NDSA Measurements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACE+ | Atmosphere and Climate Explorer |
| ACTLIMB | Active limb sounding of planetary atmospheres |
| ALMETLEO | Alternative Measurements Techniques for LEO-LEO Radio Occultation |
| ANISAP | Analysis of NDSA technique for Inter-Satellite Atmospheric Profiling |
| ARW | Advanced Research WRF |
| ASI | Agenzia Spaziale Italiana |
| ASSIM | Assimilation |
| COTS | Commercial Off-The-Shelf |
| CTRL | Control |
| ESA | European Space Agency |
| FPGA | Field Programmable Gate Array |
| GNSS | Global Navigation Satellite systems |
| IFS | Integrated Forecasting System |
| ILW | Integrated Liquid Water |
| IWV | Integrated Water Vapour |
| LEO | Low Earth Orbit |
| LW | Liquid Water |
| NDSA | Normalised Differential Spectral Attenuation |
| NWP | Numerical Weather Prediction |
| OSSE | Observing System Simulation Experiment |
| PLL | Phase-Locked Loop |
| RAAN | Right Ascension of the Ascending Node |
| RO | Radio Occultation |
| RSSI | Receiver Signal Strength Indication |
| SATCROSS | SATelliti CoROtanti per la Stima del vapore acqueo in tropoSfera |
| SDR | Software-Defined Radio |
| SWAMM | Sounding Water Vapour by Attenuation Microwave Measurements |
| TA | Tangent Altitude |
| VR | Virtual Reality |
| WRF | Weather Research and Forecasting Model |
| WV | Water Vapour |
Appendix A
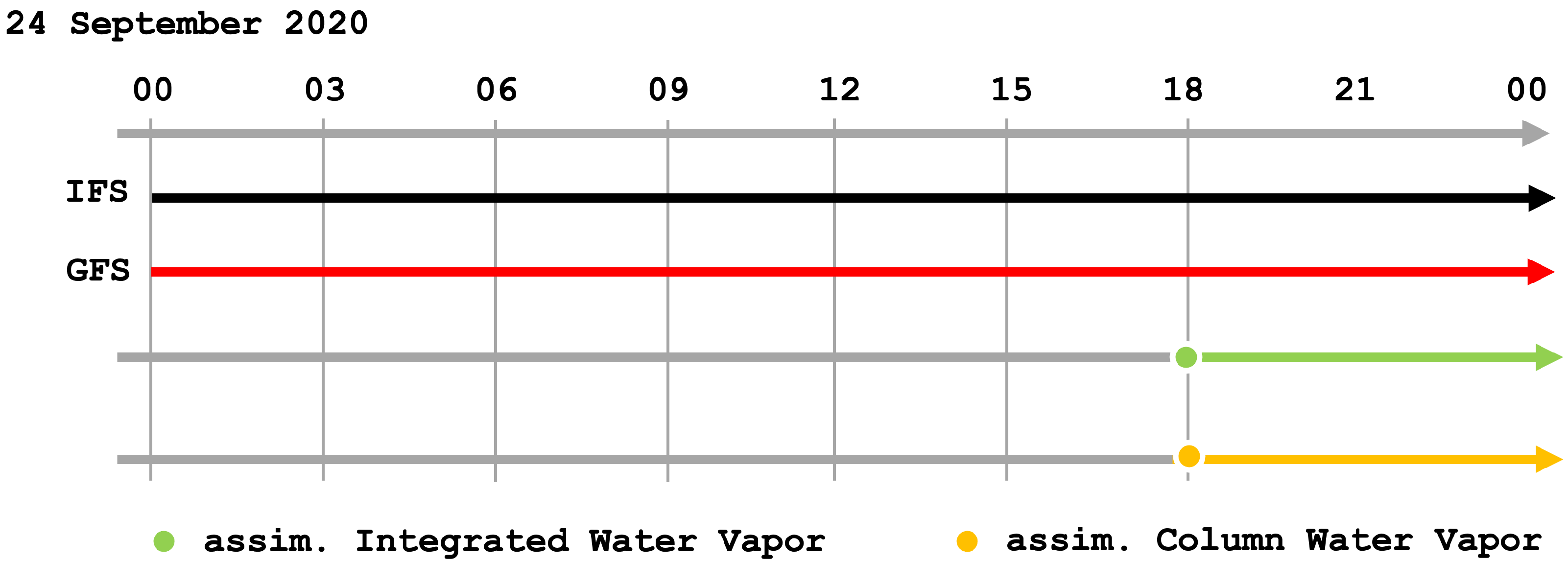
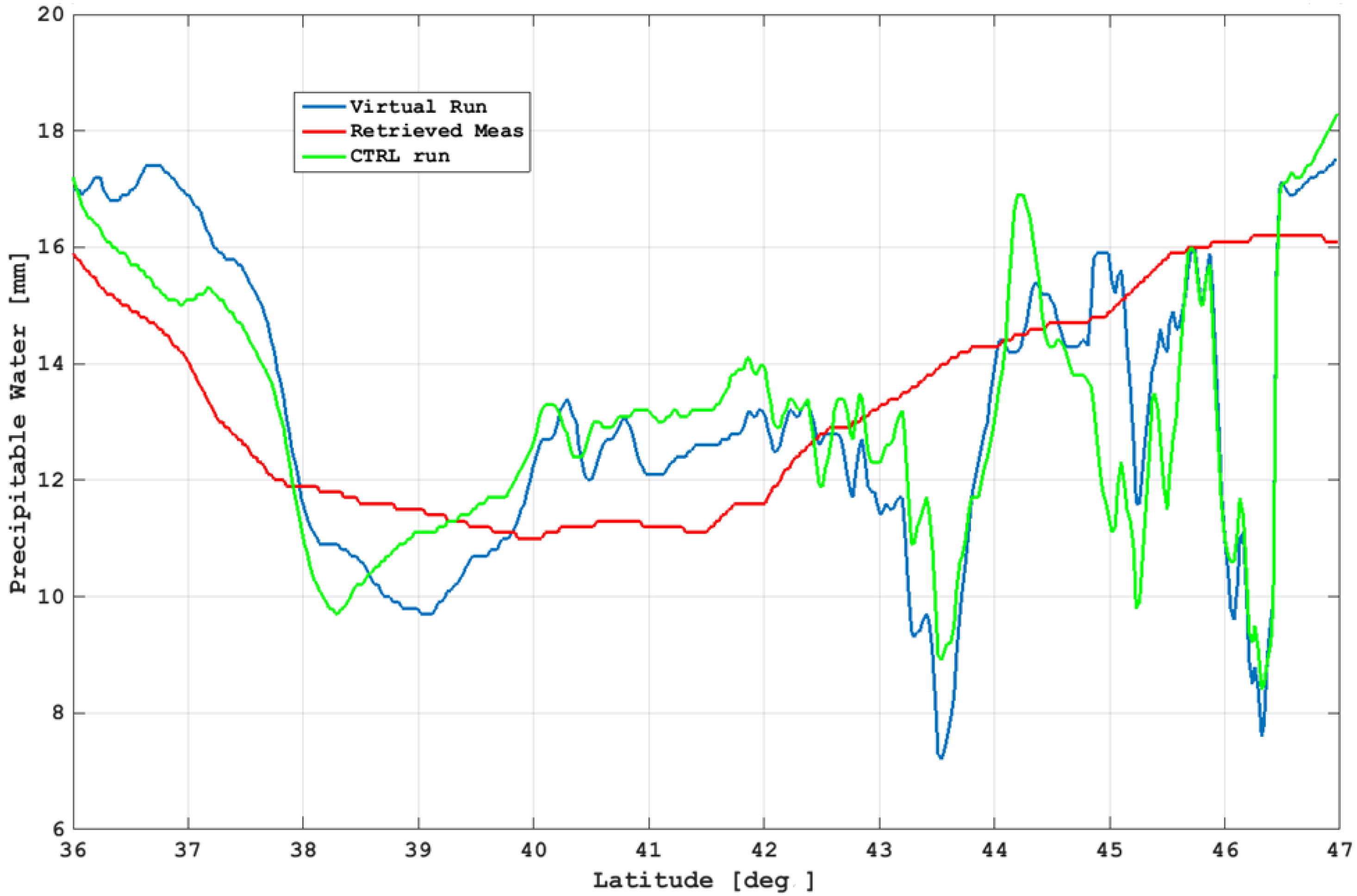
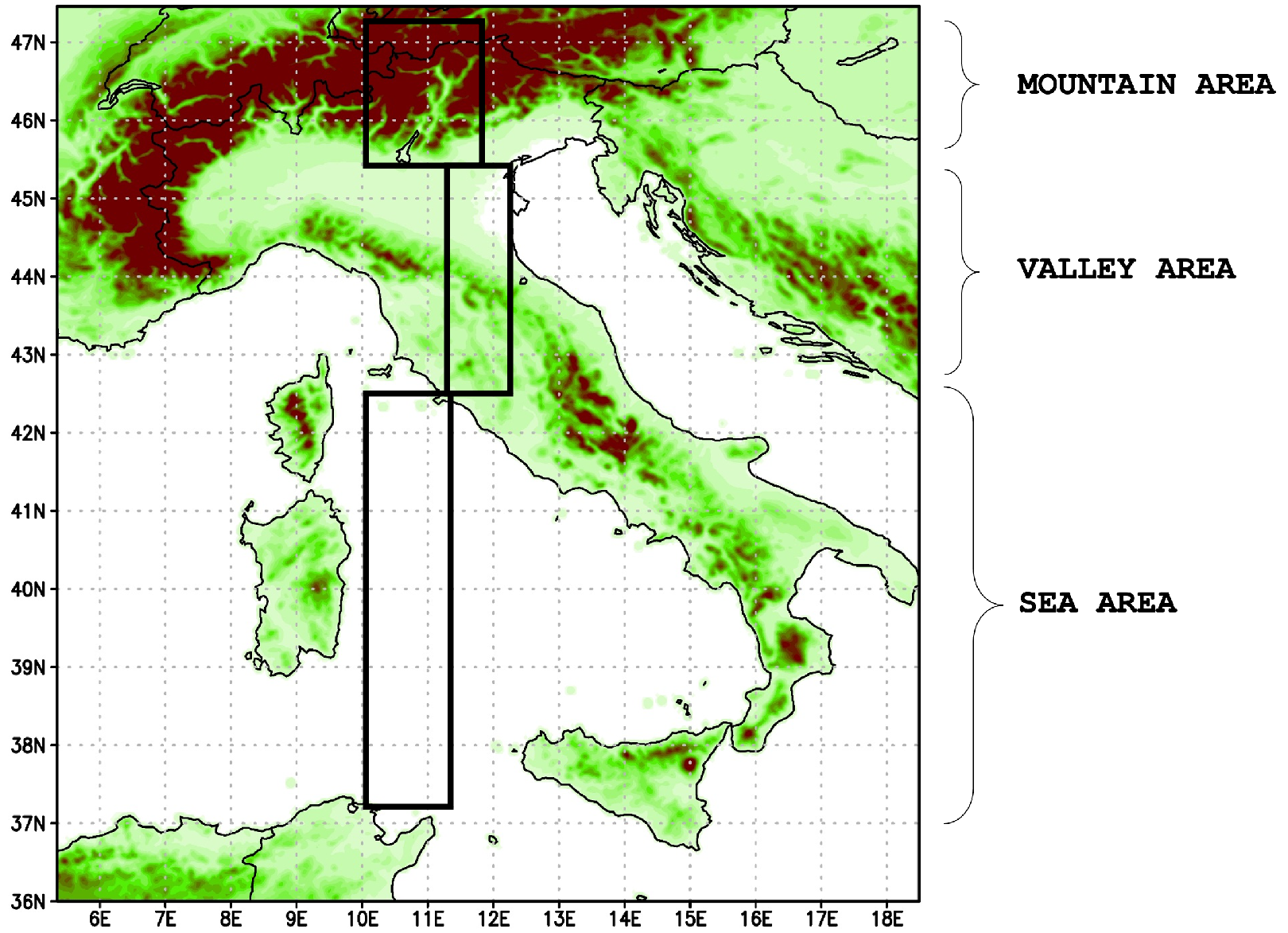
| Temperature 2 m | |||||||
|---|---|---|---|---|---|---|---|
| Hour | AREA | Assim(Int)-VR | Assim(Prof)-VR | CTRL-VR | |||
| RMSE | BIAS | RMSE | BIAS | RMSE | BIAS | ||
| 18 | Sea | 0.4 | −0.4 | 0.4 | −0.4 | 0.4 | −0.4 |
| Valley | 0.9 | −0.3 | 0.9 | −0.3 | 1.1 | −0.6 | |
| Mountain | 0.9 | −0.3 | 0.9 | −0.3 | 1.0 | −0.4 | |
| 21 | Sea | 0.5 | −0.3 | 0.5 | −0.4 | 0.5 | −0.3 |
| Valley | 1.0 | 0.1 | 1.3 | 0.4 | 0.8 | −0.2 | |
| Mountain | 0.9 | 0.0 | 1.1 | 0.3 | 0.9 | −0.1 | |
| 00 | Sea | 0.5 | −0.4 | 0.5 | −0.4 | 0.5 | −0.4 |
| Valley | 1.1 | −0.2 | 1.1 | 0.2 | 0.7 | 0.0 | |
| Mountain | 1.0 | −0.1 | 1.0 | 0.2 | 0.9 | −0.1 | |
| Relative Humidity | |||||||
|---|---|---|---|---|---|---|---|
| Hour | AREA | Assim(Int)-VR | Assim(Prof)-VR | CTRL-VR | |||
| RMSE | BIAS | RMSE | BIAS | RMSE | BIAS | ||
| 18 | Sea | 4.9 | 0.9 | 4.9 | 0.9 | 4.8 | 0.9 |
| Valley | 7.0 | 1.4 | 7.0 | 1.4 | 7.6 | 1.3 | |
| Mountain | 7.1 | −0.9 | 7.1 | −0.9 | 7.3 | −0.3 | |
| 21 | Sea | 6.5 | 0.1 | 6.2 | 0.0 | 6.1 | 0.7 |
| Valley | 6.4 | −3.6 | 8.4 | −5.4 | 6.5 | −1.5 | |
| Mountain | 6.0 | −1.8 | 7.1 | −2.4 | 6.7 | −0.8 | |
| 00 | Sea | 5.9 | 0.9 | 5.9 | 0.0 | 5.8 | 1.1 |
| Valley | 10.1 | −6.6 | 7.2 | −5.7 | 4.5 | −3.1 | |
| Mountain | 7.6 | −2.4 | 7.3 | −2.4 | 6.0 | −1.1 | |
| Cumulated Precipitation | |||||||
|---|---|---|---|---|---|---|---|
| Hour | AREA | Assim(Int)-VR | Assim(Prof)-VR | CTRL-VR | |||
| RMSE | BIAS | RMSE | BIAS | RMSE | BIAS | ||
| 18UTC +3 h | Sea | 0.1 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 |
| Valley | 5.9 | −1.1 | 4.5 | −1.8 | 4.4 | −1.2 | |
| Mountain | 10.4 | 0.8 | 10.1 | 0.3 | 10.8 | 0.5 | |
| 18UTC +6 h | Sea | 0.1 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 |
| Valley | 5.5 | −0.5 | 3.8 | −1.0 | 4.1 | −0.7 | |
| Mountain | 7.8 | 0.7 | 7.0 | 0.1 | 9.0 | 0.7 | |
- Overall, the assimilation after the first 3 h provides improved or in-line results in terms of BIAS and RMSE, primarily for the T2m variable for the three selected areas, and to a lesser extent for the RH variable, probably due to its high space-time variability.
- After 6 h from assimilation, however, the values returned line up or tend to be even worse than the CTRL ones for the three areas. This is probably due to the effects of assimilation beginning to dissolve quickly as time goes by, while the model tends to readjust itself according to its own dynamics and to the boundary conditions that prevail more often and faster in a relatively small simulation domain, as ours is.
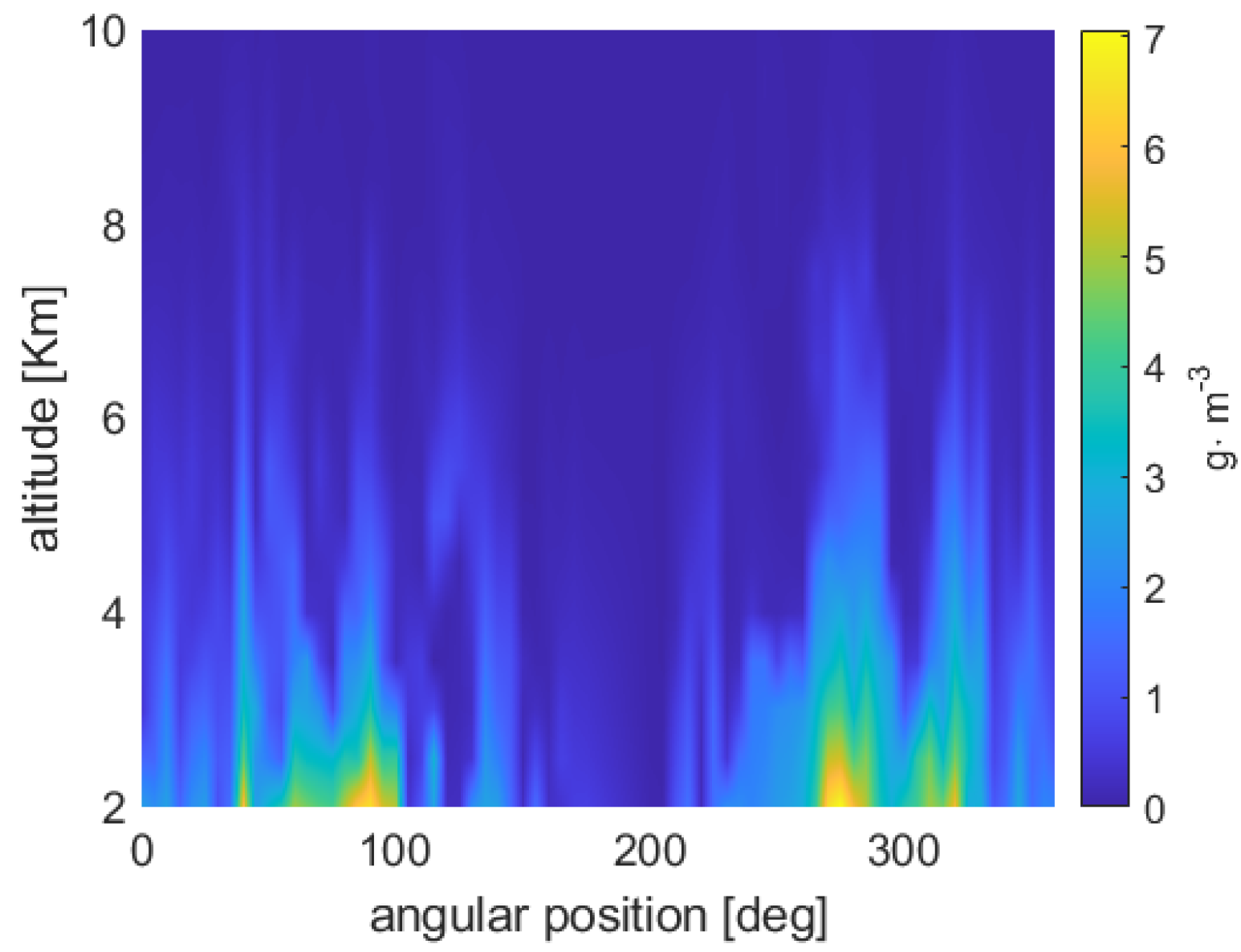
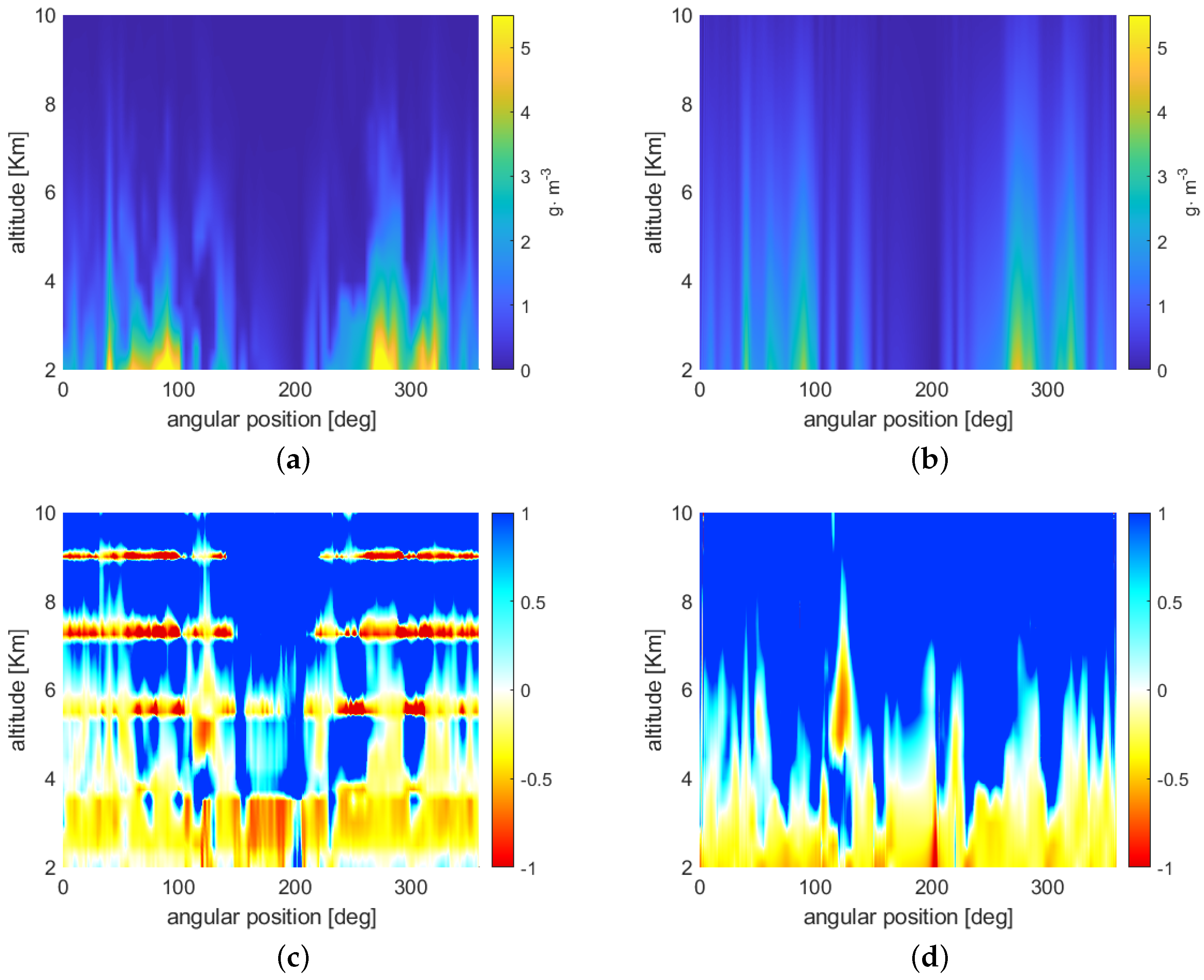
- Regarding precipitation, the assimilation (in both cases) provides an improvement for the Mountain region, and slightly for the Sea in the first 3 h after assimilation. The Valley area is generally the most problematic, probably because it is less homogeneous, consisting of a mix of plains and Apennine reliefs. After 6 h, the benefits of assimilation still persist in terms of the lesser RMSE and BIAS, especially for the Mountain area. As shown in Figure A2, on average, over the mountainous areas, the values of NDSA measurements are higher than those of VR and CTRL, and this probably forces the model towards wetter atmospheric conditions and then towards greater probabilities of precipitation. Anyway, precipitation is a complex phenomenon that depends on several factors, such as temperature profiles, vertical instabilities and induced dynamics, advection, etc., so that deeper analyses are necessary to interpret such results.
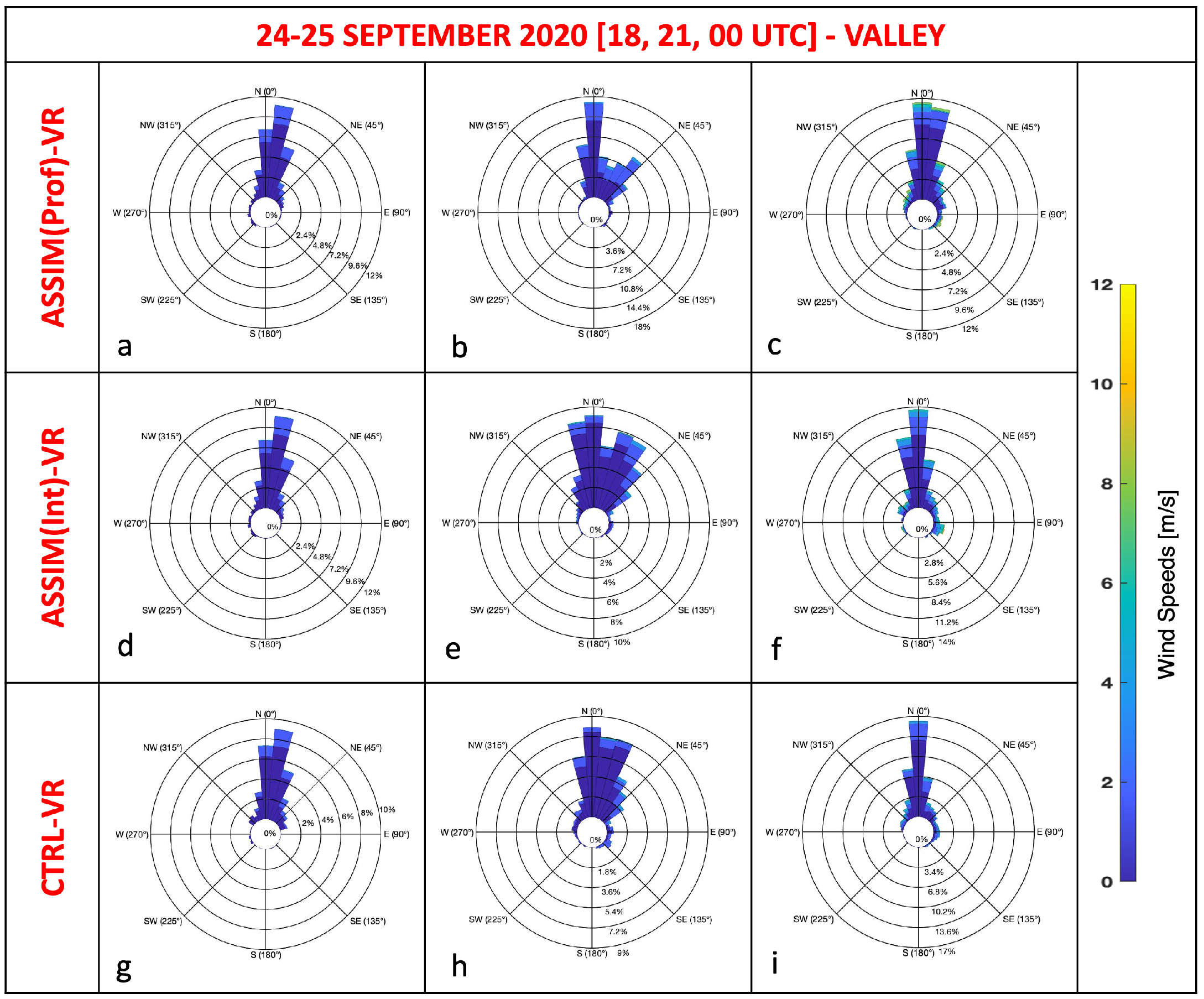
- In general, the differences in intensity are comparable between the CTRL run and the two ASSIM ones in the first 3 h, then they slightly tend to worsen as time goes by, especially for the ASSIM with WV vertical profiles.
- Regarding the direction, the distribution of values in the ASSIM is quite in line with the CTRL, which already provides good results compared to VR in the first hours, with negligible improvement possibilities. A slight worsening occurs in terms of a broadening of the distribution of the direction as the hours pass since the assimilation.
References
- Li, X.; Dick, G.; Lu, C.; Ge, M.; Nilsson, T.; Ning, T.; Wickert, J.; Schuh, H. Multi-GNSS meteorology: Real-time retrieving of atmospheric water Vapor from BeiDou, Galileo, GLONASS, and GPS observations. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6385–6393. [Google Scholar] [CrossRef]
- Negusini, M.; Petkov, B.H.; Sarti, P.; Tomasi, C. Ground-based water vapor retrieval in Antarctica: An assessment. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2935–2948. [Google Scholar] [CrossRef]
- Tang, A.; Kim, Y.; Xu, Y.; Virbila, G.; Reck, T.; Chang, M.C.F. Evaluation of 28 nm CMOS receivers at 183 GHz for space-borne atmospheric remote sensing. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 100–102. [Google Scholar] [CrossRef]
- Weaver, D.; Strong, K.; Schneider, M.; Rowe, P.; Sioris, C.; Walker, K.A.; Mariani, Z.; Uttal, T.; McElroy, C.T.; Vömel, H.; et al. Intercomparison of atmospheric water vapour measurements at a Canadian High Arctic site. Atmos. Meas. Tech. 2017, 10, 2851–2880. [Google Scholar] [CrossRef]
- Borger, C.; Schneider, M.; Ertl, B.; Hase, F.; García, O.E.; Sommer, M.; Höpfner, M.; Tjemkes, S.A.; Calbet, X. Evaluation of MUSICA MetOp/IASI tropospheric water vapour profiles by theoretical error assessments and comparisons to GRUAN Vaisala RS92 measurements. Atmos. Meas. Tech. 2017, 11, 4981–5006. [Google Scholar] [CrossRef]
- Stevens, B.; Bony, S. What Are Climate Models Missing. Science 2013, 340, 1053–1054. [Google Scholar] [CrossRef]
- Mattis, I.; Ansmann, A.; Althausen, D.; Jaenisch, V.; Wandinger, U.; Mueller, D.; Arshinov, Y.; Bobrovnikov, S.; Serikov, I. Relative-humidity profiling in the atmosphere with a Raman lidar. Appl. Opt. 2002, 41, 6451–6462. [Google Scholar] [CrossRef] [PubMed]
- Löhnert, U.; Turner, D.; Crewell, S. Ground-based temperature and humidity profiling using spectral infrared and microwave observations. Part I: Simulated retrieval performance in clear-sky conditions. J. Appl. Meteorol. Climatol. 2009, 48, 1017–1032. [Google Scholar] [CrossRef]
- Wong, M.; Jin, X.; Liu, Z.; Nichol, J.; Ye, S.; Jiang, P.; Chan, P. Geostationary satellite observation of precipitable water vapor using an Empirical Orthogonal Function (EOF) based reconstruction technique over Eastern China. Remote Sens. 2015, 7, 5879–5900. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the global position system. J. Geophys. Res. 1997, 102, 23439–23465. [Google Scholar] [CrossRef]
- Rohm, W. The ground GNSS tomography—Unconstrained approach. Adv. Space Res. 2013, 51, 501–513. [Google Scholar] [CrossRef]
- Perler, D.; Perler, F. 4D GPS water vapor tomography: New parameterized approaches. J. Geod. 2011, 85, 539–550. [Google Scholar] [CrossRef]
- Miranda, P.; Mateus, P. A new unconstrained approach to GNSS atmospheric water vapor tomography. Geophys. Res. Lett. 2021, 48, 1–10. [Google Scholar] [CrossRef]
- Millán, L.; Roy, R.; Lebsock, M. Assessment of global total column water vapor sounding using a spaceborne differential absorption radar. Atmos. Meas. Tech. 2020, 13, 5193–5205. [Google Scholar] [CrossRef]
- ESA Water Vapour Climate Change Initiative, User Requirements Document. 2021. Available online: https://climate.esa.int/en/projects/water-vapour/key-documents/ (accessed on 17 February 2023).
- Cuccoli, F.; Facheris, L. Normalized differential spectral attenuation (NDSA): A novel approach to estimate atmospheric water vapor along a LEO-LEO satellite link in the Ku/K bands. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1493–1503. [Google Scholar] [CrossRef]
- Facheris, L.; Cuccoli, F. Global ECMWF analysis data for estimating the water vapor content between two LEO satellites through NDSA measurements. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1546–1554. [Google Scholar] [CrossRef]
- Facheris, L.; Cuccoli, F. Alternative Measurement Techniques for LEO-LEO Radio Occultation; Final Report ESA-ESTEC Study Contract No. 17831/03/NL/FF; European Space Research and Technology Centre: Noordwijk, The Netherlands, 2004. [Google Scholar]
- Rocken, C.; Anthes, R.; Exner, M.; Hunt, D.; Sokolovskiy, S.; Ware, R.; Gorbunov, M.; Schreiner, W.; Feng, D.; Herman, B.; et al. Study of the Performance Envelope of Active Limb Sounding of Planetary Atmospheres; Final Report ESA-ESTEC Study Contract 21507/08/NL/HE; University of Graz: Graz, Austria, 2010. [Google Scholar]
- Facheris, L. Analysis of Normalised Differential Spectral Attenuation (NDSA) Technique for Inter-Satellite Atmospheric Profiling; Final Report of the ESA–ESTEC Study Contract No. 4000104831; European Space Research and Technology Centre: Noordwijk, The Netherlands, 2013. [Google Scholar]
- Facheris, L.; Cuccoli, F. and Argenti, F. Normalized differential spectral attenuation (NDSA) measurements between two LEO satellites: Performance and analysis in the Ku/K bands. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2345–2356. [Google Scholar] [CrossRef]
- Martini, E.; Freni, A.; Facheris, L.; Cuccoli, F. Impact of tropospheric scintillation in the Ku/K bands on the communications between two LEO satellites in a radio occultation geometry. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2063–2071. [Google Scholar] [CrossRef]
- Lapini, A.; Cuccoli, F.; Argenti, F.; Facheris, L. The Normalized Differential Spectral Sensitivity Approach Applied to the Retrieval of Tropospheric Water Vapor Fields Using a Constellation of Corotating LEO Satellites. IEEE Trans. Geosci. Remote Sens. 2016, 54, 135–152. [Google Scholar] [CrossRef]
- Montomoli, F.; Macelloni, G.; Facheris, L.; Cuccoli, F.; Del Bianco, S.; Gai, M.; Cortesi, U.; Di Natale, G.; Toccafondi, A.; Puggelli, F.; et al. Integrated Water Vapor Estimation Through Microwave Propagation Measurements: First Experiment on a Ground-to-Ground Radio Link. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Kirchengast, G.; Hoeg, P. The ACE+ Mission: An Atmosphere and Climate Explorer based on GPS, GALILEO, and LEO-LEO Radio Occultation. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg,Germany, 2004; pp. 201–220. [Google Scholar] [CrossRef]
- Mazzinghi, A.; Cuccoli, F.; Argenti, F.; Feta, A.; Facheris, L. Tomographic Inversion Methods for Retrieving the Tropospheric Water Vapor Content Based on the NDSA Measurement Approach. Remote Sens. 2022, 14, 414. [Google Scholar] [CrossRef]
- Hanke, M.; Hansen, P. Regularization methods for large-scale problems. Surv. Math. Ind. 1993, 3, 253–315. [Google Scholar]
- Cormack, A.M. Representation of a Function by Its Line Integrals, with Some Radiological Applications. J. Appl. Phys. 1963, 34, 2722–2727. [Google Scholar] [CrossRef]
- Cormack, A.M. Representation of a Function by Its Line Integrals, with Some Radiological Applications. II. J. Appl. Phys. 1964, 35, 2908–2913. [Google Scholar] [CrossRef]
- Cormack, A.M. The Radon Transform on a Family of Curves in the Plane. Proc. Am. Math. Soc. 1981, 83, 325–330. [Google Scholar] [CrossRef]
- Perry, R. On reconstructing a function on the exterior of a disk from its Radon transform. J. Math. Anal. Appl. 1977, 59, 324–341. [Google Scholar] [CrossRef]
- Quinto, E.T. Singular value decompositions and inversion methods for the exterior Radon transform and a spherical transform. J. Math. Anal. Appl. 1983, 95, 437–448. [Google Scholar] [CrossRef]
- Quinto, E.T. Tomographic reconstructions from incomplete data-numerical inversion of the exterior Radon transform. Inverse Probl. 1988, 4, 867–876. [Google Scholar] [CrossRef]
- Quinto, E.T. Exterior and limited-angle tomography in non-destructive evaluation. Inverse Probl. 1998, 14, 339–353. [Google Scholar] [CrossRef]
- Facheris, L.; Cuccoli, F.; Martini, E. Tropospheric IWV profiles estimation through multifrequency signal attenuation measurements between two counter-rotating LEO satellites: Performance analysis. In Remote Sensing of Clouds and the Atmosphere XVIII; and Optics in Atmospheric Propagation and Adaptive Systems XVI; SPIE: Bellingham, WA, USA, 2013; Volume 8890. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Wang, W.; Zhiquan, L.; Berner, J.; Powers, J.; Duda, M. A Description of the Advanced Research WRF Model; Version 4; Technical Report, No. NCAR/TN-556+STR; UCAR: Boulder, CO, USA, 2019. [Google Scholar]
- Klemp, J.B.; Skamarock, W.C.; Dudhia, J. Conservative Split-Explicit Time Integration Methods for the Compressible Nonhydrostatic Equations. Mon. Weather Rev. 2007, 135, 2897–2913. [Google Scholar] [CrossRef]
- Chen, S.; Dudhia, J. Annual Report: WRF Physics; Technical Report 38; Air Force Weather Agency: Bellevue, NE, USA, 2000. [Google Scholar] [CrossRef]
- Lynch, P. The Dolph-Chebyshev Window: A Simple Optimal Filter. Mon. Weather Rev. 1997, 125, 655–660. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Facheris, L.; Antonini, A.; Argenti, F.; Barbara, F.; Cortesi, U.; Cuccoli, F.; Del Bianco, S.; Dogo, F.; Feta, A.; Gai, M.; et al. Towards Space Deployment of the NDSA Concept for Tropospheric Water Vapour Measurements. Atmosphere 2023, 14, 550. https://doi.org/10.3390/atmos14030550
Facheris L, Antonini A, Argenti F, Barbara F, Cortesi U, Cuccoli F, Del Bianco S, Dogo F, Feta A, Gai M, et al. Towards Space Deployment of the NDSA Concept for Tropospheric Water Vapour Measurements. Atmosphere. 2023; 14(3):550. https://doi.org/10.3390/atmos14030550
Chicago/Turabian StyleFacheris, Luca, Andrea Antonini, Fabrizio Argenti, Flavio Barbara, Ugo Cortesi, Fabrizio Cuccoli, Samuele Del Bianco, Federico Dogo, Arjan Feta, Marco Gai, and et al. 2023. "Towards Space Deployment of the NDSA Concept for Tropospheric Water Vapour Measurements" Atmosphere 14, no. 3: 550. https://doi.org/10.3390/atmos14030550
APA StyleFacheris, L., Antonini, A., Argenti, F., Barbara, F., Cortesi, U., Cuccoli, F., Del Bianco, S., Dogo, F., Feta, A., Gai, M., Gregorio, A., Macelloni, G., Mazzinghi, A., Melani, S., Montomoli, F., Ortolani, A., Rovai, L., Severin, L., & Scopa, T. (2023). Towards Space Deployment of the NDSA Concept for Tropospheric Water Vapour Measurements. Atmosphere, 14(3), 550. https://doi.org/10.3390/atmos14030550












