Forecasting Maximum Mechanism Temperature in Advanced Technology Microwave Sounder (ATMS) Data Using a Long Short-Term Memory (LSTM) Neural Network
Abstract
1. Introduction
- No attempts to predict increases in mechanism temperature using any method;
- Transition to the ATMS’ safe mode operations is controlled only by whether current observations exceed a threshold value and not guided by any attempted forecasts.
2. Long Short-Term Memory (LSTM) Method and Its Application for Predicting Maximum Mechanism Temperature
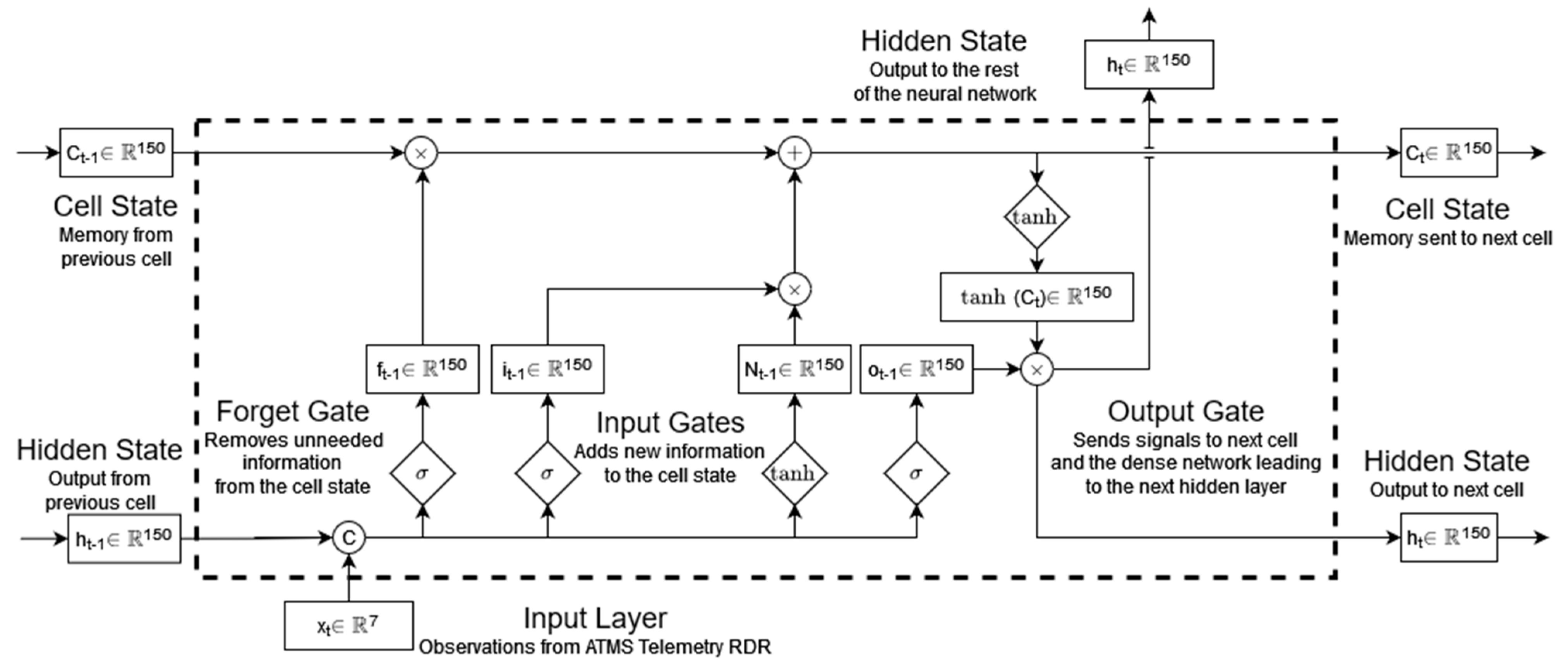
2.1. An Introduction to Long Short-Term Memory (LSTM) Networks
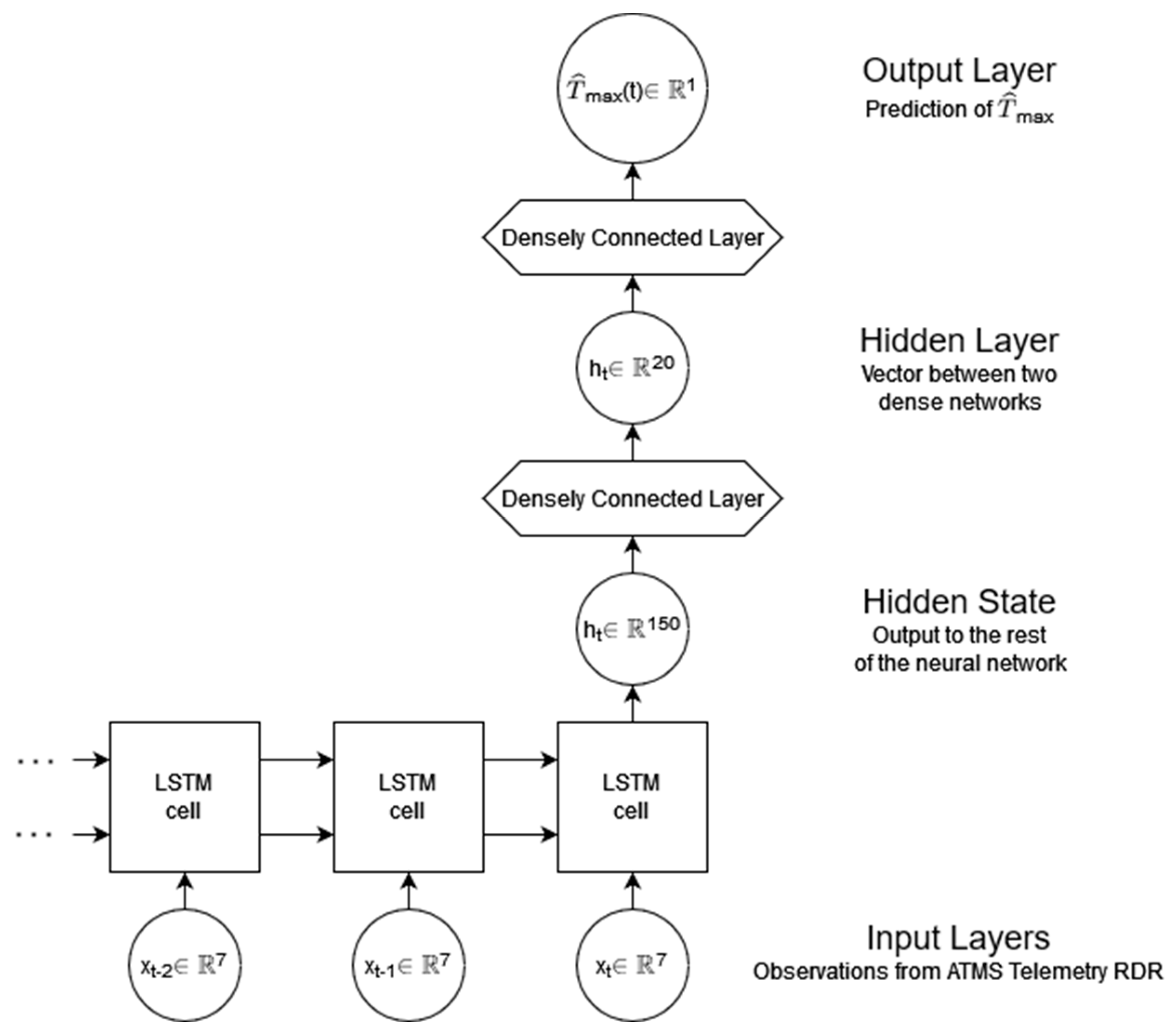
2.2. LSTM Design for Forecasting Local Mechanism Temperature Maxima
3. Prediction of ATMS Maximum Mechanism Temperature Using LSTM
3.1. Acquisition of datasets for Testing and Training and Determination of the Optimal Duration for Predicting Maximum Mechanism Temperature
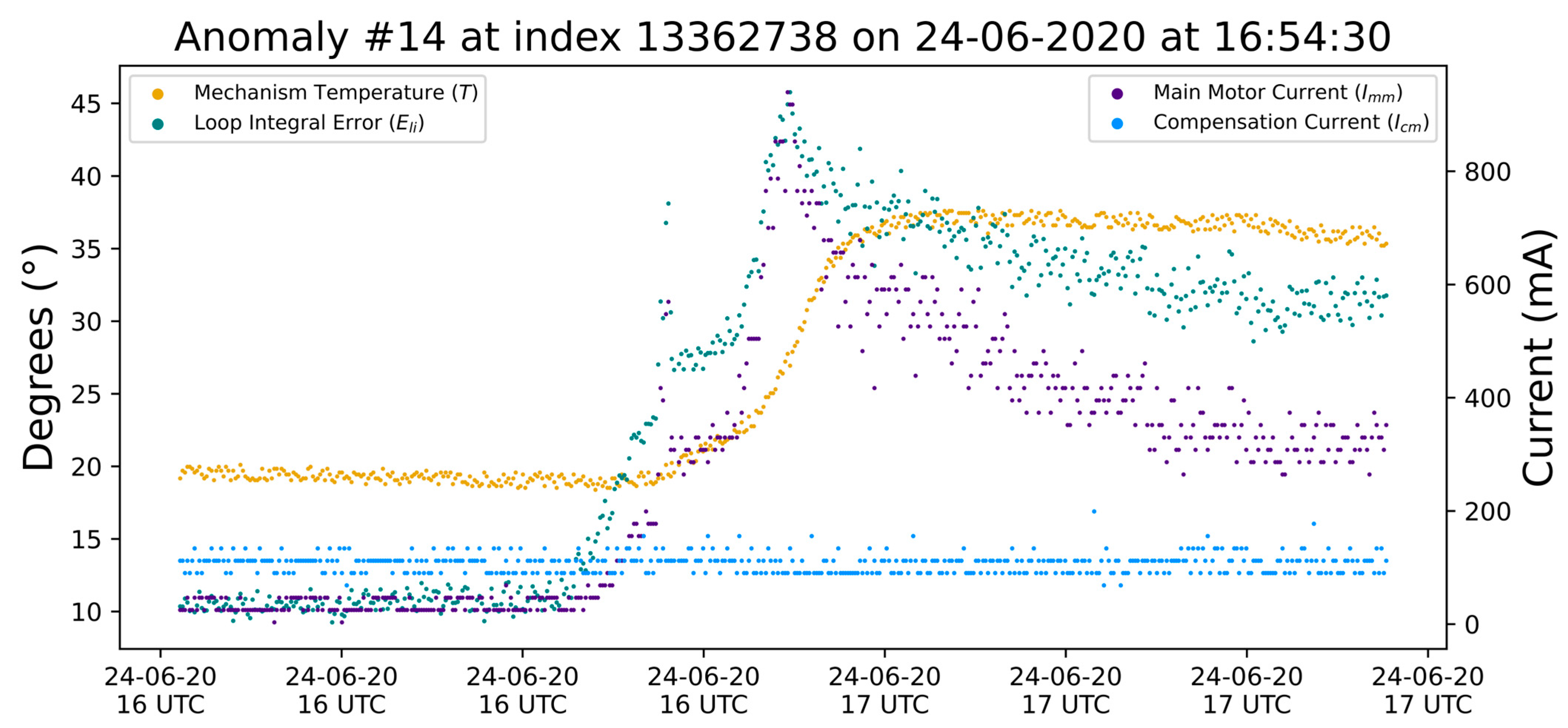
3.2. Case Studies
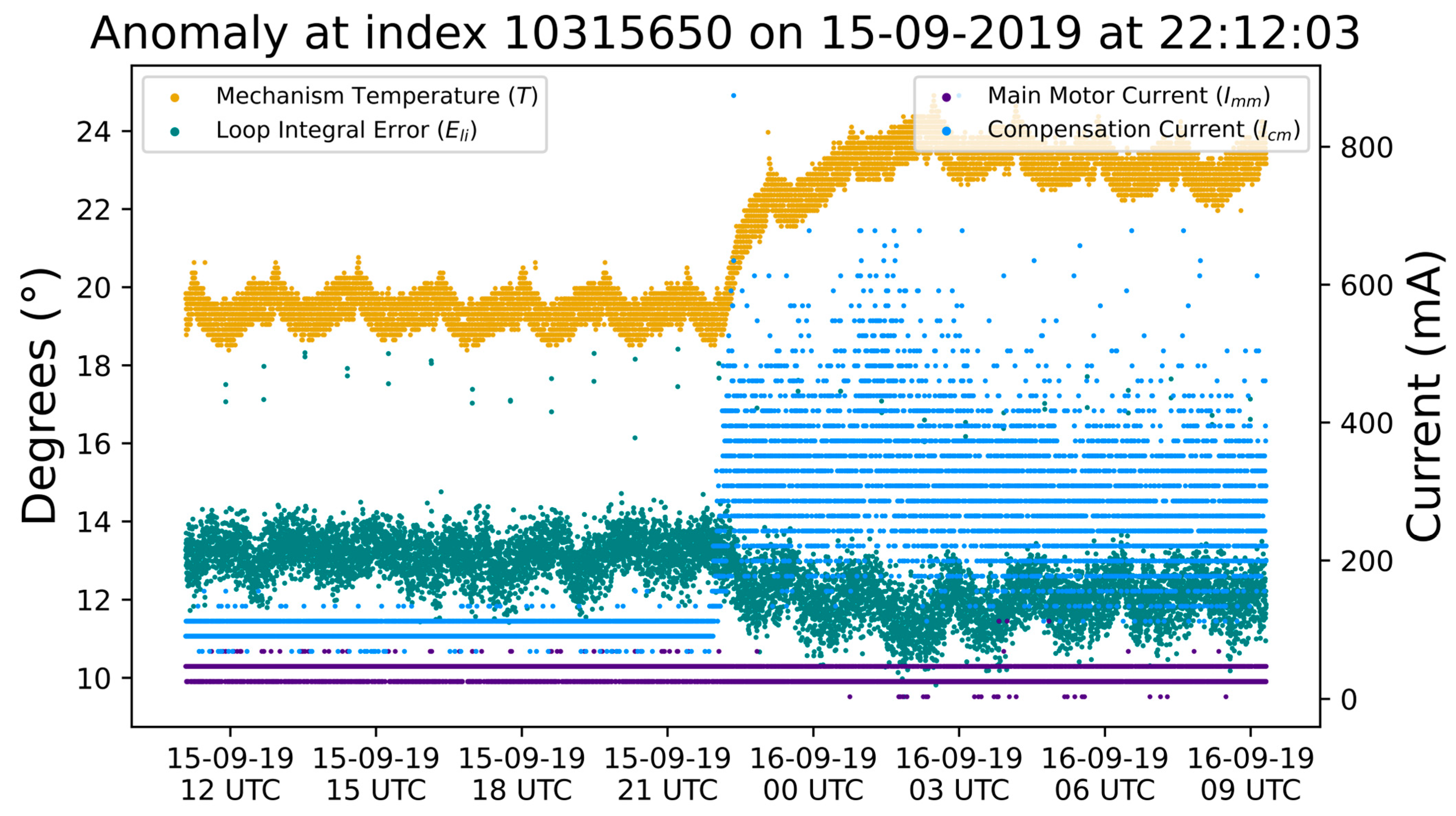
3.3. Discussion for Small Anomalous Events
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, B.; Kireev, S.V. A New Methodology on Noise Equivalent Differential Temperature Calculation for On-Orbit Advanced Microwave Sounding Unit-A Instrument. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8554–8567. [Google Scholar] [CrossRef]
- Sun, N.; Iacovazzi, R.A.; Yan, B.; Liu, Q. Evaluation of Advanced Technology Microwave Sounder (ATMS) Science Data Long-Term Trending through Intersatellite Comparisons. In Proceedings of the AMS, New Orleans, LA, USE, 15 January 2021. [Google Scholar]
- Huang, J.; Yan, B.; Sun, N. Monitoring of the Cross-Calibration Biases Between the S-NPP and NOAA-20 VIIRS Sensor Data Records Using Goes Advanced Baseline Imager as a Transfer. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6393–6396. [Google Scholar]
- Liang, D.; Yan, B.; Sun, N.; Flynn, L.; Pan, C.; Beck, T. Lifetime Performance Assessment of SNPP OMPS Nadir MAPPER SDR Data Using Simultaneous Nadir Overpass Collocated Observations with Gome-2. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 6258–6261. [Google Scholar]
- Yan, B.; Porter, W.; Chen, J.; Sun, N.; Kireev, S.; Zou, C.; Zhou, L. Re-Characterize Noise Performance for on-Orbit Advanced Technology Microwave Sounder on Snpp-NOAA-20 and Advanced Microwave Sounding Unit—A on Metop-a/B/C Satellites. In Proceedings of the AMS, 2019 Joint Satellite Conference, Boston, MA, USA, 28 September–4 October 2019. [Google Scholar]
- Porter, W.; Yan, B.; Iturbide-Sanchez, F.; Wang, L.; Tremblay, D.; Chen, Y.; Liang, X.; Jin, X.; Sun, N. Re-Assessing Lifetime Geolocation Performance of CrIS Aboard Suomi-NPP with ICVS. In Proceedings of the AMS Joint Satellite Conference, Boston, MA, USA, 2 October 2019. [Google Scholar]
- Yan, B.; Chen, J.; Porter, W.; Kireev, S.; Sun, N.; Zou, C.; Zhou, L. Accurately Quantifying NEDT Performance for In-Orbit AMSU-A and ATMS Instruments by Using a Newly Developed Algorithm. In Proceedings of the American Geophysical Union, Fall Meeting 2019, Boston, MA, USA, 9–13 December 2019. [Google Scholar]
- Weng, F.; Gottshall, E.; Zhou, L.; Layns, A.L. Advanced Technology Microwave Sounder (ATMS) SDR Radiometric Calibration Algorithm Theoretical Basic Document (ATBD); Joint Polar Satellite System (JPSS); Center for Satellite Applications and Research: College Park, MD, USA, 2013. [Google Scholar]
- Iturbide-Sanchez, F.; Vicente, G.; Zhou, L.; Layns, A.L. Cross Track Infrared Sounder (CrIS) Sensor Data Records (SDR) Algorithm Theoretical Basis Document (ATBD) for Full Spectral Resolution; Joint Polar Satellite System (JPSS); Center for Satellite Applications and Research: College Park, MD, USA, 2018. [Google Scholar]
- Baker, N.; Kilcoyne, H. VIIRS Radiometric Calibration Algorithm Theoretical Basis Document (ATBD); Joint Polar Satellite System (JPSS); Goddard Spaceflight Center: Greenbelt, MD, USA, 2017. [Google Scholar]
- Godin, R.; Gottshall, E. OMPS Nadir Profile Ozone Algorithm Theoretical Basis Document (ATBD); Joint Polar Satellite System (JPSS); JPSS Ground Project Configuration Management Office: Greenbelt, MD, USA, 2014.
- Godin, R.; Gottshall, E. OMPS NADIR Total Column Ozone Algorithm Theoretical Basis Document (ATBD); Joint Polar Satellite System (JPSS); JPSS Ground Project Configuration Management Office: Greenbelt, MD, USA, 2014.
- AMSU-A System Operation and Maintenance Manual for METSAT/METOP; NAS5-32314; NGES: Linthicum Heights, MD, USA, 2010; pp. 105–109.
- Sun, N.; Yan, B.; Jin, X.; Liang, D.; Huang, J.; Porter, W.; Liu, Q.; Chen, Y.; Kireev, S.; Sanchez, F.; et al. An Integrated Calibration/Validation System Long-Term (LT) Monitoring System Applicable for Lifetime Performance and Science Data Quality Assessments of Suomi-NPP, NOAA-20, and Legacy POES Instruments. J. Atmsophere 2023. [Google Scholar]
- Yan, B.; Sun, N.; Jin, X.; Liang, D.; Huang, J.; Porter, W.; Iacovazzi, R.; Wang, L.; Liu, Q.; Wu, X.; et al. Long-Term Inter-Sensor Radiance Difference Stability Assessments Applicable for SNPP, NOAA-20 and Several Other Satellite Instruments within NOAA ICVS. J. Remote Sens. 2023. [Google Scholar]
- Xue, T.; Xu, J.; Guan, Z.; Chen, H.-C.; Chiu, L.S.; Shao, M. An Assessment of the Impact of ATMS and CrIS Data Assimilation on Precipitation Prediction over the Tibetan Plateau. Atmos. Meas. Tech. 2017, 10, 2517–2531. [Google Scholar] [CrossRef]
- Zhu, Y.; Gayno, G.; Delst, P.; Liu, E.; Sun, R.; Han, J.; Derber, J.; Yang, F.; Purser, R.; Su, X.; et al. Further Development in the All-Sky Microwave Radiance Assimilation and Expansion to ATMS in the GSI at NCEP. In Proceedings of the 21st International TOVS Study Conference, Darmstadt, Germany, 2 February 2018. [Google Scholar]
- Zou, X.; Weng, F.; Zhang, B.; Lin, L.; Qin, Z.; Tallapragada, V. Impacts of Assimilation of ATMS Data in HWRF on Track and Intensity Forecasts of 2012 Four Landfall Hurricanes. J. Geophys. Res. Atmos. 2013, 118, 11558–11576. [Google Scholar] [CrossRef]
- Kelly, G.; Thépaut, J.-N. Evaluation of the Impact of the Space Component of the Global Observing System through Observing System Experiments. ECMWF Newsl. 2007, 113, 16–28. [Google Scholar] [CrossRef]
- Boukabara, S.-A.; Garrett, K.; Chen, W.; Iturbide-Sanchez, F.; Grassotti, C.; Kongoli, C.; Chen, R.; Liu, Q.; Yan, B.; Weng, F.; et al. MiRS: An All-Weather 1DVAR Satellite Data Assimilation and Retrieval System. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3249–3272. [Google Scholar] [CrossRef]
- Boukabara, S.-A.; Garrett, K.; Grassotti, C.; Iturbide-Sanchez, F.; Chen, W.; Jiang, Z.; Clough, S.A.; Zhan, X.; Liang, P.; Liu, Q.; et al. A Physical Approach for a Simultaneous Retrieval of Sounding, Surface, Hydrometeor, and Cryospheric Parameters from SNPP/ATMS: A physical algorithm for ATMS EDRS. J. Geophys. Res. Atmos. 2013, 118, 12600–12619. [Google Scholar] [CrossRef]
- Ferraro, R.; Meng, H.; Zavodsky, B.; Kusselson, S.; Kann, D.; Guyer, B.; Jacobs, A.; Perfater, S.; Folmer, M.; Dong, J.; et al. Snowfall Rates from Satellite Data Help Weather Forecasters. Eos 2018, 99. [Google Scholar] [CrossRef]
- Meng, H.; Dong, J.; Ferraro, R.; Yan, B.; Zhao, L.; Kongoli, C.; Wang, N.-Y.; Zavodsky, B. A 1DVAR-Based Snowfall Rate Retrieval Algorithm for Passive Microwave Radiometers: Microwave Snowfall Rate Algorithm. J. Geophys. Res. Atmos. 2017, 122, 6520–6540. [Google Scholar] [CrossRef]
- Tian, X.; Zou, X. ATMS- and AMSU-A-derived Hurricane Warm Core Structures Using a Modified Retrieval Algorithm. J. Geophys. Res. Atmos. 2016, 121, 12630–12646. [Google Scholar] [CrossRef]
- You, Y.; Wang, N.-Y.; Ferraro, R.; Meyers, P. A Prototype Precipitation Retrieval Algorithm over Land for ATMS. J. Hydrometeorol. 2016, 17, 1601–1621. [Google Scholar] [CrossRef]
- Zhu, T.; Zhang, D.-L.; Weng, F. Impact of the Advanced Microwave Sounding Unit Measurements on Hurricane Prediction. Mon. Wea. Rev. 2002, 130, 2416–2432. [Google Scholar] [CrossRef]
- Zhu, T.; Weng, F. Hurricane Sandy Warm-Core Structure Observed from Advanced Technology Microwave Sounder: ATMS-derived tropical cyclone warm cores. Geophys. Res. Lett. 2013, 40, 3325–3330. [Google Scholar] [CrossRef]
- Yan, B.; Liang, D.; Porter, W.; Huang, J.; Sun, N.; Zhou, L.; Zhu, T.; Goldberg, M.; Zhang, D.; Liu, Q. Gap Filling of Advanced Technology Microwave Sounder Data as Applied to Hurricane Warm Core Animations. Earth Space Sci. 2020, 7, e2019EA000961. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Q.; Yan, B.; Sun, N. A Deep Learning Trained Clear-Sky Mask Algorithm for VIIRS Radiometric Bias Assessment. Remote Sens. 2020, 12, 78. [Google Scholar] [CrossRef]
- Porter, W.; Yan, B.; Sun, N.; Liang, X.; Zhou, L. A ML-Based S-NPP ATMS Lifetime Performance Assessment Algorithm with ICVS: Preliminary Results; ATMS: College Park, MD, USA, 2019. [Google Scholar]
- Allmon, C.; Putnam, D. Design of the ATMS Scan Drive Mechanism. In Proceedings of the The 38th Aerospace Mechanisms Symposium, Williamsburg, VA, USA, 18 May 2006; pp. 197–207. [Google Scholar]
- Ruff, L.; Kauffmann, J.R.; Vandermeulen, R.A.; Montavon, G.; Samek, W.; Kloft, M.; Dietterich, T.G.; Muller, K.-R. A Unifying Review of Deep and Shallow Anomaly Detection. Proc. IEEE 2021, 109, 756–795. [Google Scholar] [CrossRef]
- Xiang, G.; Lin, R. Robust Anomaly Detection for Multivariate Data of Spacecraft Through Recurrent Neural Networks and Extreme Value Theory. IEEE Access 2021, 9, 167447–167457. [Google Scholar] [CrossRef]
- Yu, J.; Song, Y.; Tang, D.; Han, D.; Dai, J. Telemetry Data-Based Spacecraft Anomaly Detection With Spatial–Temporal Generative Adversarial Networks. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Naik, K.; Holmgren, A.; Kenworthy, J. Using Machine Learning to Automatically Detect Anomalous Spacecraft Behavior from Telemetry Data. In Proceedings of the 2020 IEEE Aerospace Conference, IEEE, Big Sky, MT, USA, 7–14 March 2020; pp. 1–14. [Google Scholar]
- Tariq, S.; Lee, S.; Shin, Y.; Lee, M.S.; Jung, O.; Chung, D.; Woo, S.S. Detecting Anomalies in Space Using Multivariate Convolutional LSTM with Mixtures of Probabilistic PCA. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, ACM, Anchorage, AK, USA, 25 July 2019; pp. 2123–2133. [Google Scholar]
- Smagulova, K.; James, A.P. Overview of Long Short-Term Memory Neural Networks. In Deep Learning Classifiers with Memristive Networks; James, A.P., Ed.; Springer International Publishing: Cham, Switzerland, 2020; Volume 14, pp. 139–153. ISBN 978-3-030-14522-4. [Google Scholar]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting Spacecraft Anomalies Using LSTMs and Nonparametric Dynamic Thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Association for Computing Machinery, New York, NY, USA, 19 July 2018; pp. 387–395. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Rossum, G. Python Tutorial; CWI (Centre for Mathematics and Computer Science): Amsterdam, The Netherlands, 1995. [Google Scholar]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Chollet, F. Others Keras: The Python Deep Learning Library; Astrophysics Source Code Library. Available online: https://keras.io2018 (accessed on 5 May 2022).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]


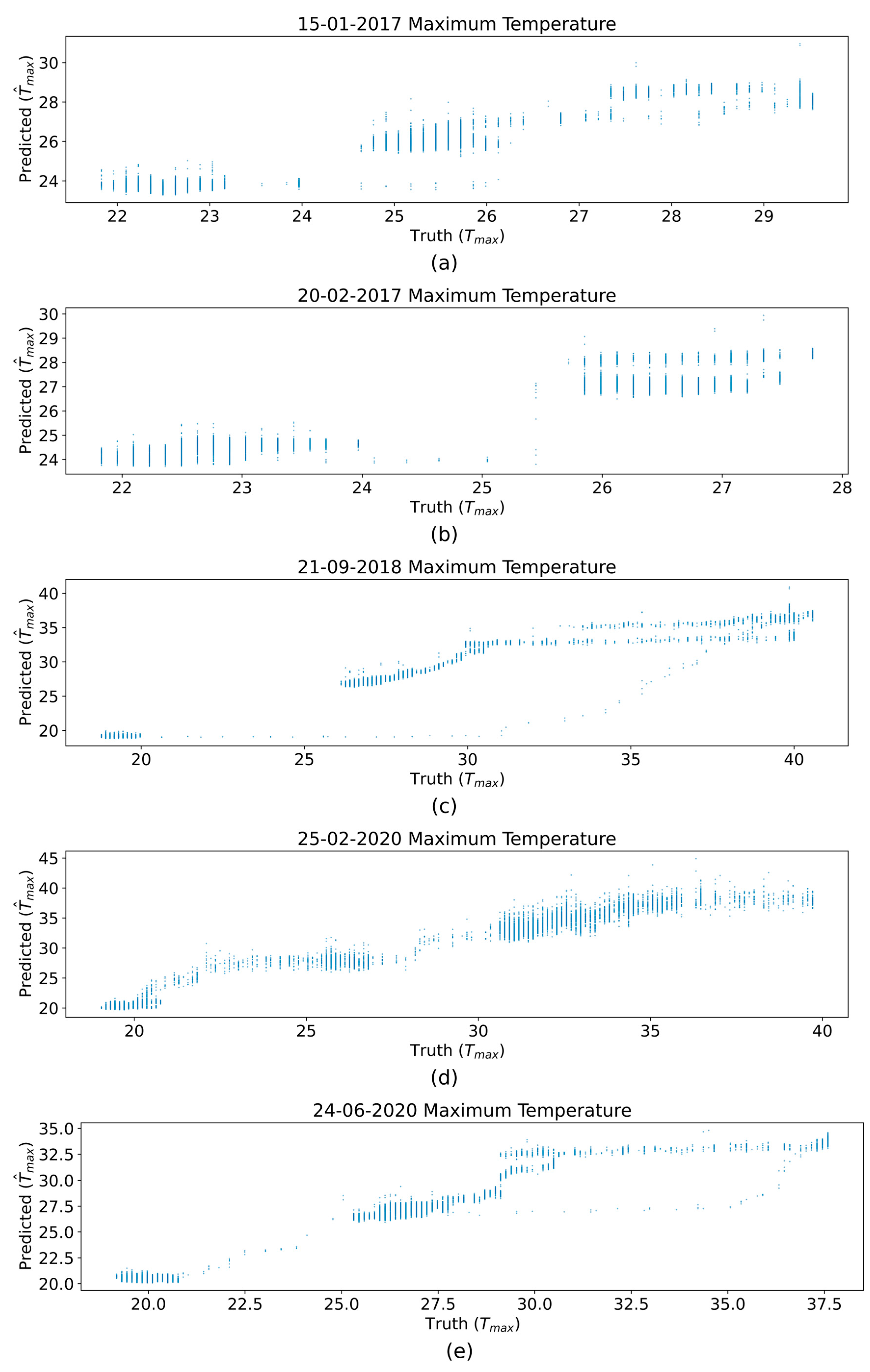

| Date | N | Avg MAE (°C) | Avg RMSE (°C) |
|---|---|---|---|
| 15 January 2017 (Testing Data) | 89 | 1.00 | 1.09 |
| 20 February 2017 (Testing Data) | 89 | 1.11 | 1.26 |
| 21 September 2018 (Testing Data) | 89 | 0.68 | 1.33 |
| 25 February 2020 (Testing Data) | 89 | 1.07 | 1.37 |
| 24 June 2020 (Testing Data) | 89 | 0.86 | 1.13 |
| 18 November 2021 (Training Data) | 89 | 0.63 | 1.16 |
| Whole Series | 89 | 0.80 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Porter, W.D.; Yan, B.; Sun, N. Forecasting Maximum Mechanism Temperature in Advanced Technology Microwave Sounder (ATMS) Data Using a Long Short-Term Memory (LSTM) Neural Network. Atmosphere 2023, 14, 503. https://doi.org/10.3390/atmos14030503
Porter WD, Yan B, Sun N. Forecasting Maximum Mechanism Temperature in Advanced Technology Microwave Sounder (ATMS) Data Using a Long Short-Term Memory (LSTM) Neural Network. Atmosphere. 2023; 14(3):503. https://doi.org/10.3390/atmos14030503
Chicago/Turabian StylePorter, Warren Dean, Banghua Yan, and Ninghai Sun. 2023. "Forecasting Maximum Mechanism Temperature in Advanced Technology Microwave Sounder (ATMS) Data Using a Long Short-Term Memory (LSTM) Neural Network" Atmosphere 14, no. 3: 503. https://doi.org/10.3390/atmos14030503
APA StylePorter, W. D., Yan, B., & Sun, N. (2023). Forecasting Maximum Mechanism Temperature in Advanced Technology Microwave Sounder (ATMS) Data Using a Long Short-Term Memory (LSTM) Neural Network. Atmosphere, 14(3), 503. https://doi.org/10.3390/atmos14030503







