Design and Experiments of a Naturally-Ventilated Radiation Shield for Ground Temperature Measurement
Abstract
1. Introduction
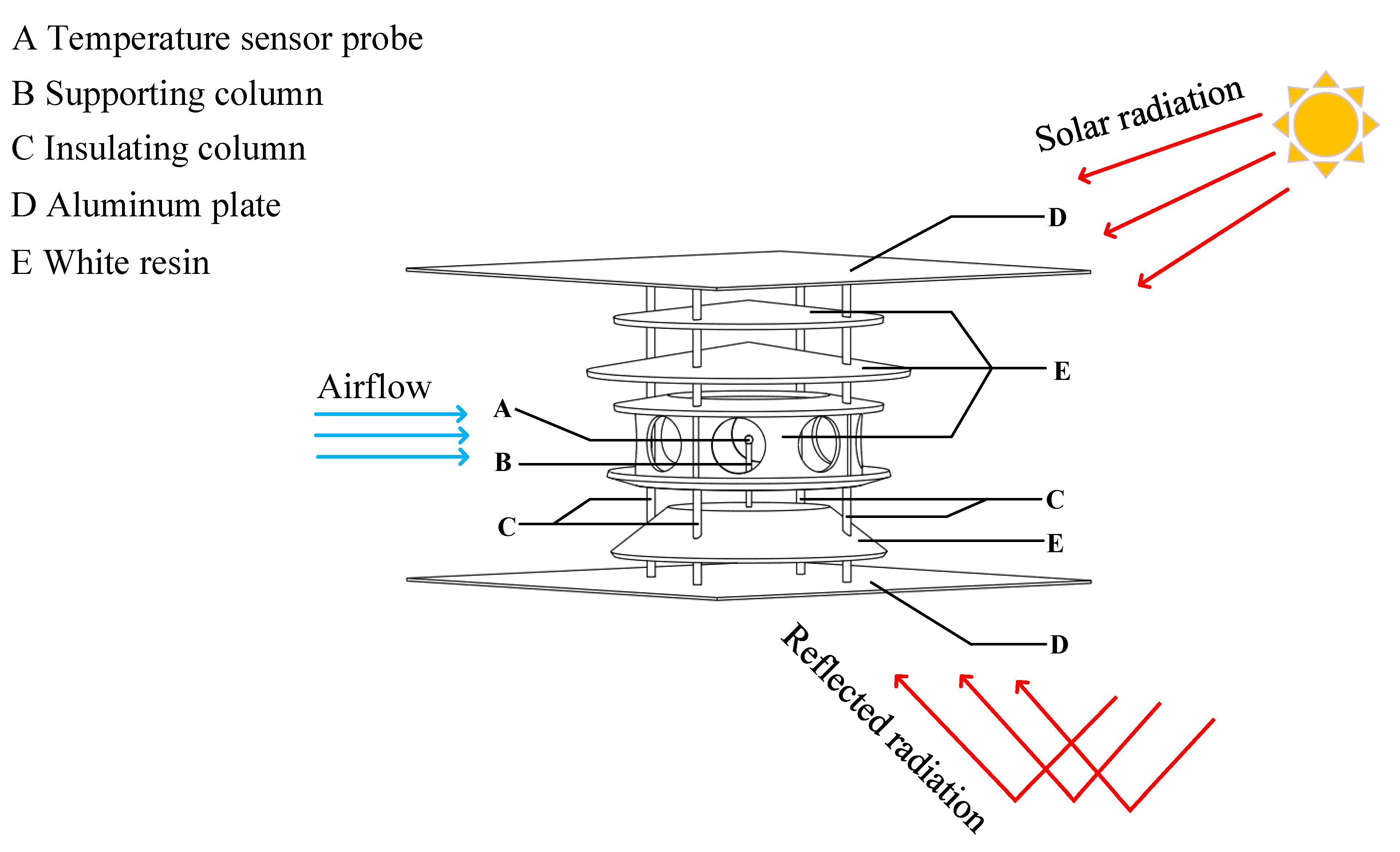
2. Design of the Radiation Shield
2.1. Model Construction of the Temperature Sensor
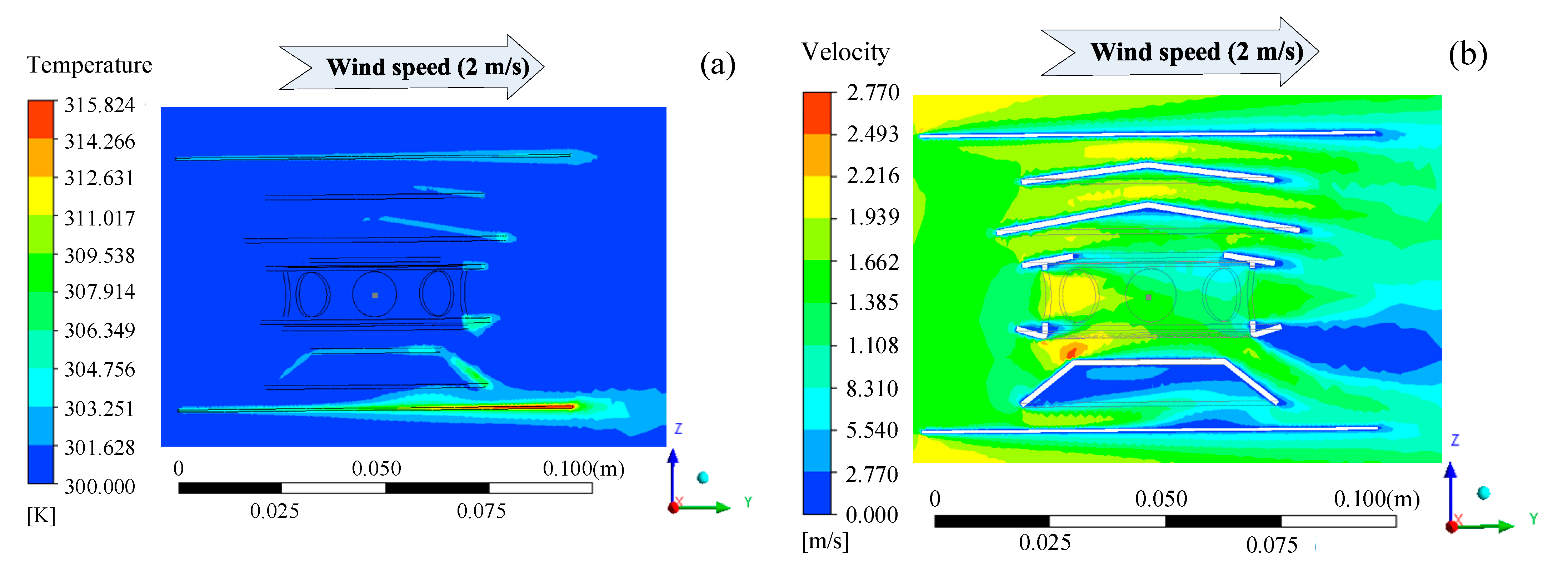
2.2. CFD Simulation and Result Analysis
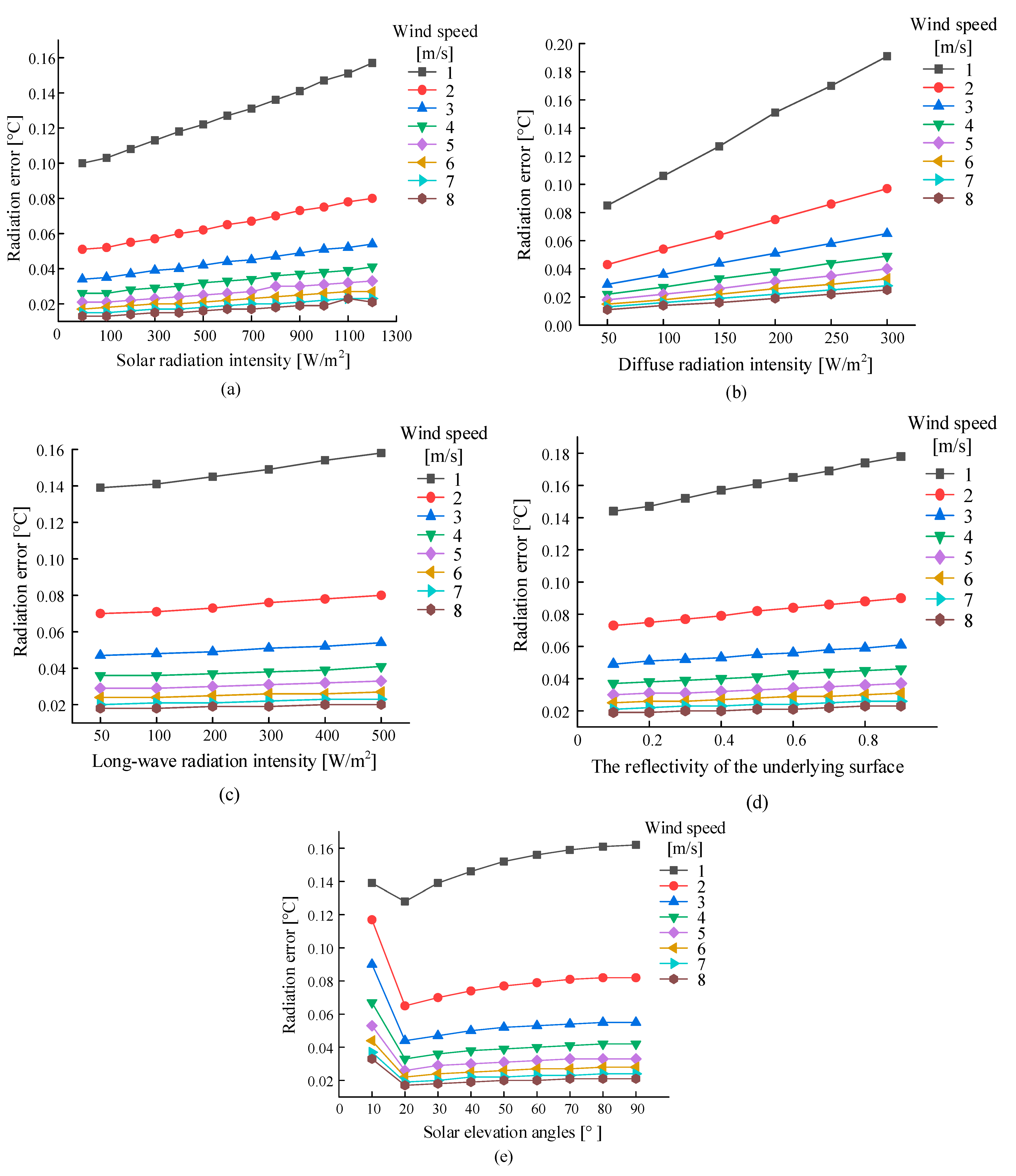
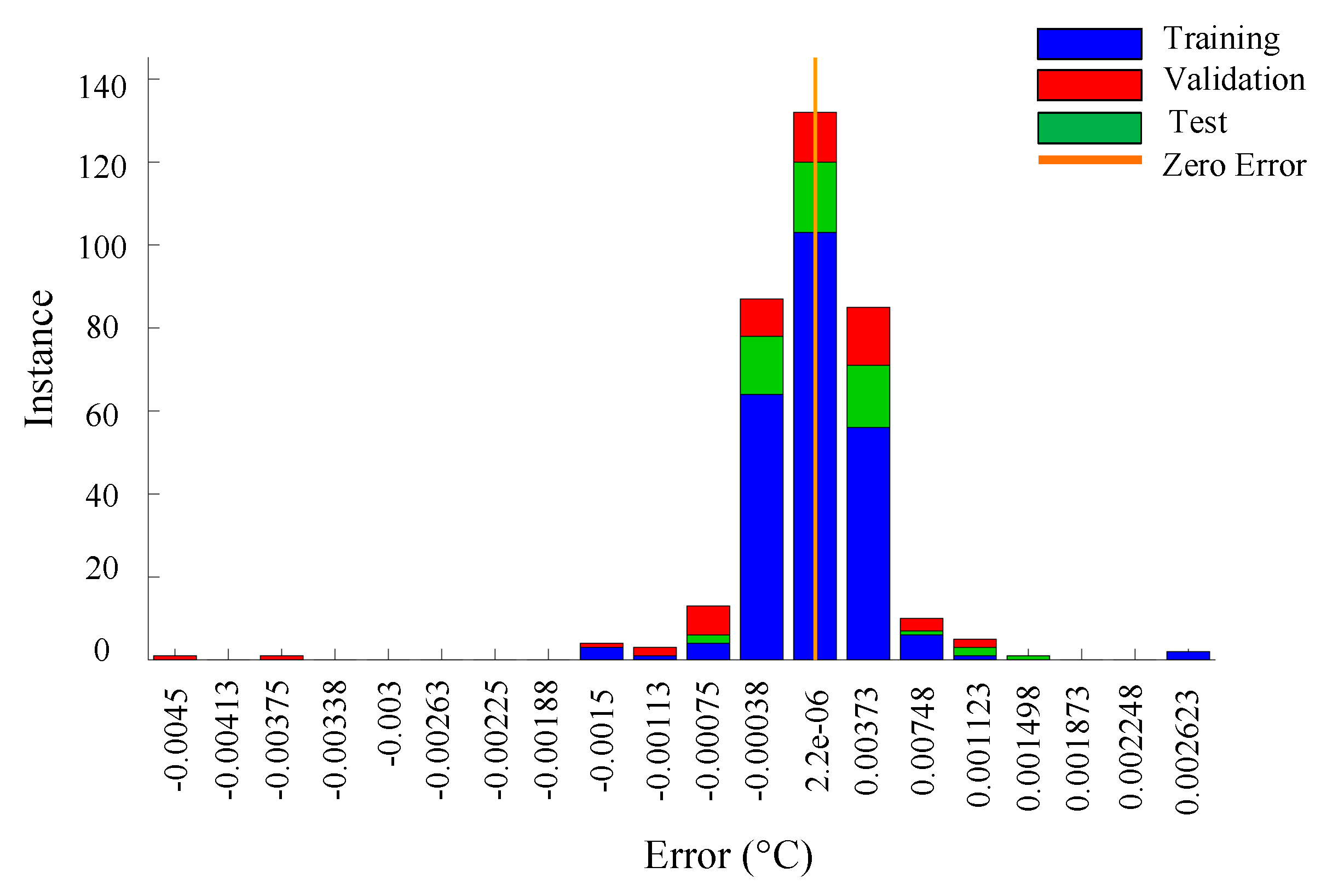
2.3. Radiation Error Correction
3. Observation Experiment and Result Analysis
4. Conclusions and Future Work
- (1)
- The natural radiation shield was designed with two aluminum plates, eight vents, and a multi-layer structure which is able to resist direct solar radiation, reflected radiation, and upwelling long-wave radiation better than a traditional shield while ensuring that the temperature sensor probe can work effectively.
- (2)
- The natural ventilation radiation shield proposed in this paper is simpler and lighter in structure compared with the traditional radiation shield, and the radiation error can be reduced to 0.1.
- (3)
- Using a BP neural network algorithm to establish the error correction equation, the error can be reduced again after the correction of the temperature data inside the radiation shield proposed in this paper. When the wind speed is greater than 1.5 m/s, the error can be reduced to within ±0.1 °C.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fyfe, J.C.; Gillett, N.P.; Zwiers, F.W. Overestimated global warming over the past 20 years. Nat. Clim. Chang. 2013, 3, 767–769. [Google Scholar] [CrossRef]
- Stott, P.; Good, P.; Jones, G.; Gillett, N.; Hawkins, E. The upper end of climate model temperature projections is inconsistent with past warming. Environ. Res. Lett. 2013, 8, 014024. [Google Scholar] [CrossRef]
- Gleisner, H.; Thejll, P.; Christiansen, B.; Nielsen, J.K. Recent global warming hiatus dominated by low-latitude temperature trends in surface and troposphere data. Geophys. Res. Lett. 2015, 42, 510–517. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Lopez-Moreno, J.I.; Correa, K.; Avalos, G.; Bazo, J.; Azorin-Molina, C.; Dominguez-Castro, F.; Kenawy, A.E.; Gimeno, L.; Nieto, R. Recent changes in monthly surface air temperature over Peru, 1964–2014. Int. J. Climatol. 2018, 38, 283–306. [Google Scholar] [CrossRef]
- Zhang, P.; Ren, G.; Qin, Y.; Zhai, Y.; Zhai, T.; Tysa, S.K.; Xue, X.; Yang, G.; Sun, X. Urbanization Effects on Estimates of Global Trends in Mean and Extreme Air Temperature. J. Clim. 2021, 34, 1923–1945. [Google Scholar] [CrossRef]
- Jiang, S.; Du, J.; Wei, Z. Impacts of Continuously Increasing Urbanisation Ratios on Warming Rates and Temperature Extremes Observed Over the Beijing Area. J. Geophys. Res.-Atmos. 2021, 126, e2021JD034536. [Google Scholar] [CrossRef]
- Ross-Pinnock, D.; Maropoulos, P.G. Review of industrial temperature measurement technologies and research priorities for the thermal characterisation of the factories of the future. Proc. Inst. Mech. Eng. Part B-J. Eng. Manuf. 2016, 230, 793–806. [Google Scholar] [CrossRef]
- Schweiger, H.G.; Multerer, M.; Gores, H.J. Fast multichannel precision thermometer. IEEE Trans. Instrum. Meas. 2007, 56, 2002–2009. [Google Scholar] [CrossRef]
- Silva, A.G.; Torres, M.C. Proposing an effective and inexpensive tool to detect urban surface temperature changes associated with urbanisation processes in small cities. Build. Environ. 2021, 192, 107634. [Google Scholar] [CrossRef]
- Erell, E.; Leal, V.; Maldonado, E. Measurement of air temperature in the presence of a large radiant flux: An assessment of passively ventilated thermometer screens. Bound.-Layer Meteorol. 2005, 114, 205–231. [Google Scholar] [CrossRef]
- Lopardo, G.; Bertiglia, F.; Curci, S.; Roggero, G.; Merlone, A. Comparative analysis of the influence of solar radiation screen ageing on temperature measurements by means of weather stations. Int. J. Climatol. 2014, 34, 1297–1310. [Google Scholar] [CrossRef]
- Lin, X.; Hubbard, K.G.; Baker, C.B. Surface air temperature records biased by snow-covered surface. Int. J. Climatol. 2005, 25, 1223–1236. [Google Scholar] [CrossRef]
- Mackiewicz, M.C. A new approach to quantifying soil temperature responses to changing air temperature and snow cover. Polar Sci. 2012, 6, 226–236. [Google Scholar] [CrossRef]
- Nakamura, R.; Mahrt, L. Air temperature measurement errors in naturally ventilated radiation shields. J. Atmos. Ocean. Technol. 2005, 22, 1046–1058. [Google Scholar] [CrossRef]
- Cheng, X.; Su, D.; Li, D.; Chen, L.; Xu, W.; Yang, M.; Li, Y.; Yue, Z.; Wang, Z. An improved method for correction of air temperature measured using different radiation shields. Adv. Atmos. Sci. 2014, 31, 1460–1468. [Google Scholar] [CrossRef]
- Lee, S.W.; Park, E.U.; Choi, B.I.; Kim, J.C.; Woo, S.B.; Park, S.; Yang, S.G.; Kim, Y.G. Dual temperature sensors with different emissivities in radiosondes for the compensation of solar irradiation effects with varying air pressure. Meteorol. Appl. 2018, 25, 49–55. [Google Scholar] [CrossRef]
- Kurzeja, R. Accurate Temperature Measurements in a Naturally-Aspirated Radiation Shield. Bound.-Layer Meteorol. 2010, 134, 181–193. [Google Scholar] [CrossRef]
- Huang, Y.; Coggon, M.M.; Zhao, R.; Lignell, H.; Bauer, M.U.; Flagan, R.C.; Seinfeld, J.H. The Caltech Photooxidation Flow Tube reactor: Design, fluid dynamics and characterisation. Atmos. Meas. Tech. 2017, 10, 839–867. [Google Scholar] [CrossRef]
- Kumar, P.; Singh, S.K.; Ngae, P.; Feiz, A.A.; Turbelin, G. Assessment of a CFD model for short-range plume dispersion: Applications to the Fusion Field Trial 2007 (FFT-07) diffusion experiment. Atmos. Res. 2017, 197, 84–93. [Google Scholar] [CrossRef]
- Qian, Y.; Han, Z.; Zhan, J.H.; Liu, X.; Xu, G. Comparative evaluation of heat conduction and radiation models for CFD simulation of heat transfer in packed beds. Int. J. Heat Mass Transf. 2018, 127, 573–584. [Google Scholar] [CrossRef]
- Yang, J.; Deng, X.; Liu, Q.; Ding, R. Design and experimental study of an effective, low-cost, naturally ventilated radiation shield for monitoring surface air temperature. Meteorol. Atmos. Phys. 2021, 133, 349–357. [Google Scholar] [CrossRef]
- Thomas, C.K.; Smoot, A.R. An Effective, Economic, Aspirated Radiation Shield for Air Temperature Observations and Its Spatial Gradients. J. Atmos. Ocean. Technol. 2013, 30, 526–537. [Google Scholar] [CrossRef]
- Villa, D.L. Institutional heat wave analysis by building energy modeling fleet and meter data. Energy Build. 2021, 237, 110774. [Google Scholar] [CrossRef]




| Material | Density (kg·m −3) | Heat Capacity (J·kg −1·K −1) | Thermal Conductivity (W·m −1·K −1) | Reflectivity |
|---|---|---|---|---|
| Aluminum | 2719 | 871 | 202.4 | 90% |
| White resin | 110 | 1591 | 0.2 | 20% |
| Copper | 9 | 381 | 387.6 | 60% |
| Environmental Factors | S (W/m2) | L (W/m2) | D (W/m2) | R | V (m/s) | A (°) |
|---|---|---|---|---|---|---|
| Range | 100–1300 | 50–500 | 50–300 | 0.1–0.9 | 1–8 | 10–90 |
| Default value | 1000 | 300 | 200 | 0.2 | 2 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; Jin, W.; Yang, J.; Zhu, H.; Dai, W. Design and Experiments of a Naturally-Ventilated Radiation Shield for Ground Temperature Measurement. Atmosphere 2023, 14, 523. https://doi.org/10.3390/atmos14030523
Liu Q, Jin W, Yang J, Zhu H, Dai W. Design and Experiments of a Naturally-Ventilated Radiation Shield for Ground Temperature Measurement. Atmosphere. 2023; 14(3):523. https://doi.org/10.3390/atmos14030523
Chicago/Turabian StyleLiu, Qingquan, Wei Jin, Jie Yang, Huanan Zhu, and Wei Dai. 2023. "Design and Experiments of a Naturally-Ventilated Radiation Shield for Ground Temperature Measurement" Atmosphere 14, no. 3: 523. https://doi.org/10.3390/atmos14030523
APA StyleLiu, Q., Jin, W., Yang, J., Zhu, H., & Dai, W. (2023). Design and Experiments of a Naturally-Ventilated Radiation Shield for Ground Temperature Measurement. Atmosphere, 14(3), 523. https://doi.org/10.3390/atmos14030523





