Calibration of the Ångström–Prescott Model for Accurately Estimating Solar Radiation Spatial Distribution in Areas with Few Global Solar Radiation Stations: A Case Study of the China Tropical Zone
Abstract
1. Introduction
2. Materials and Methods
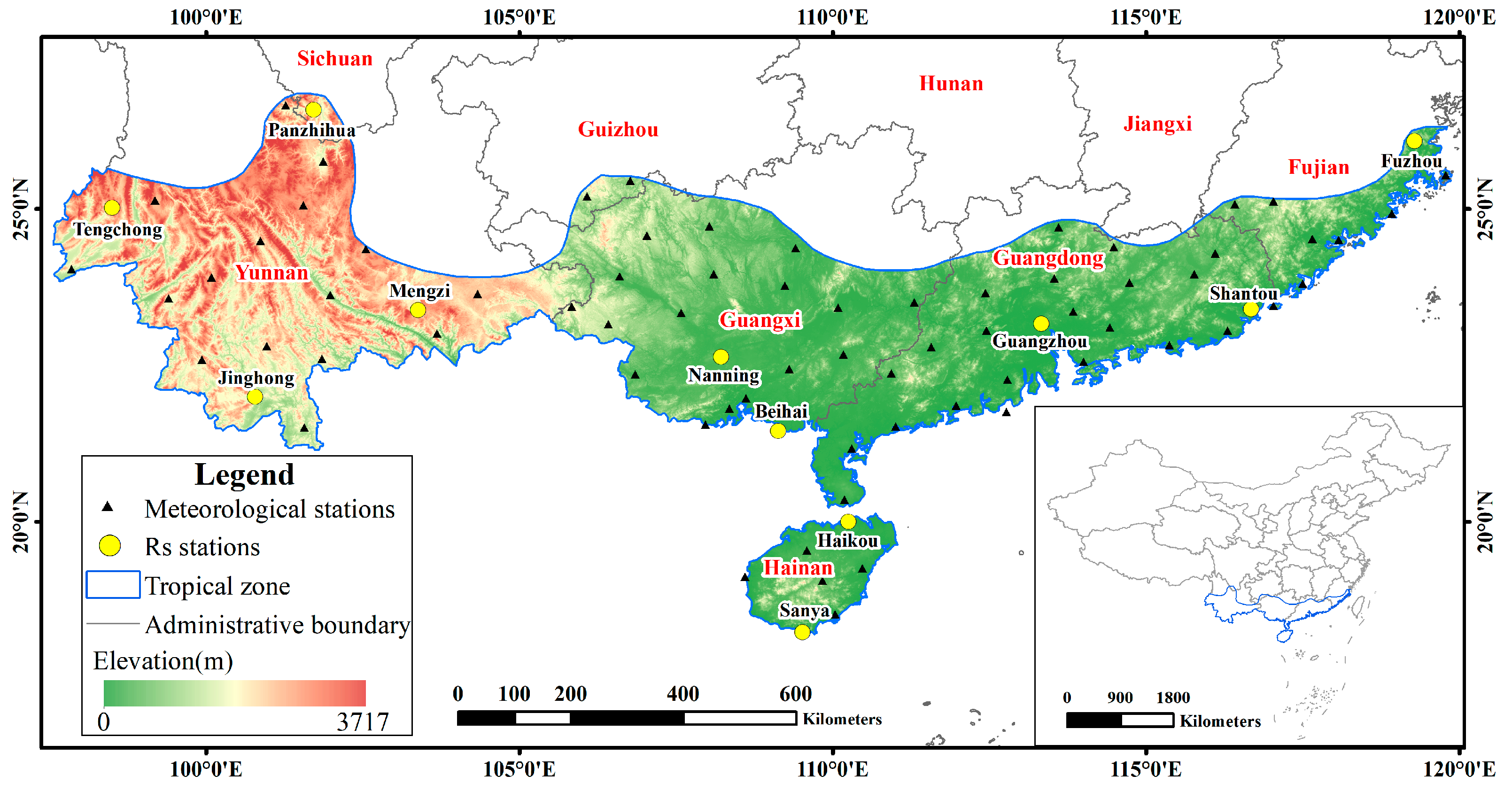
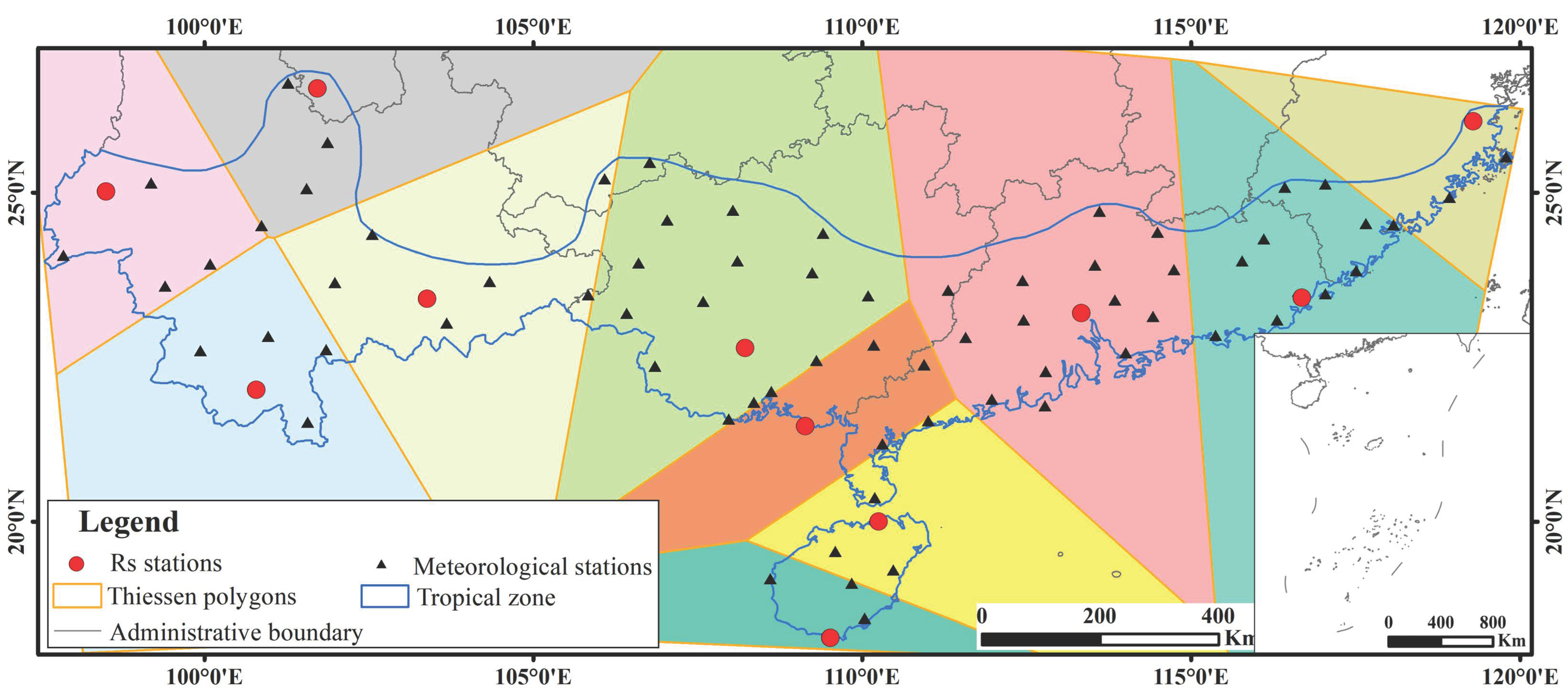
2.1. Study Area
2.2. Dataset
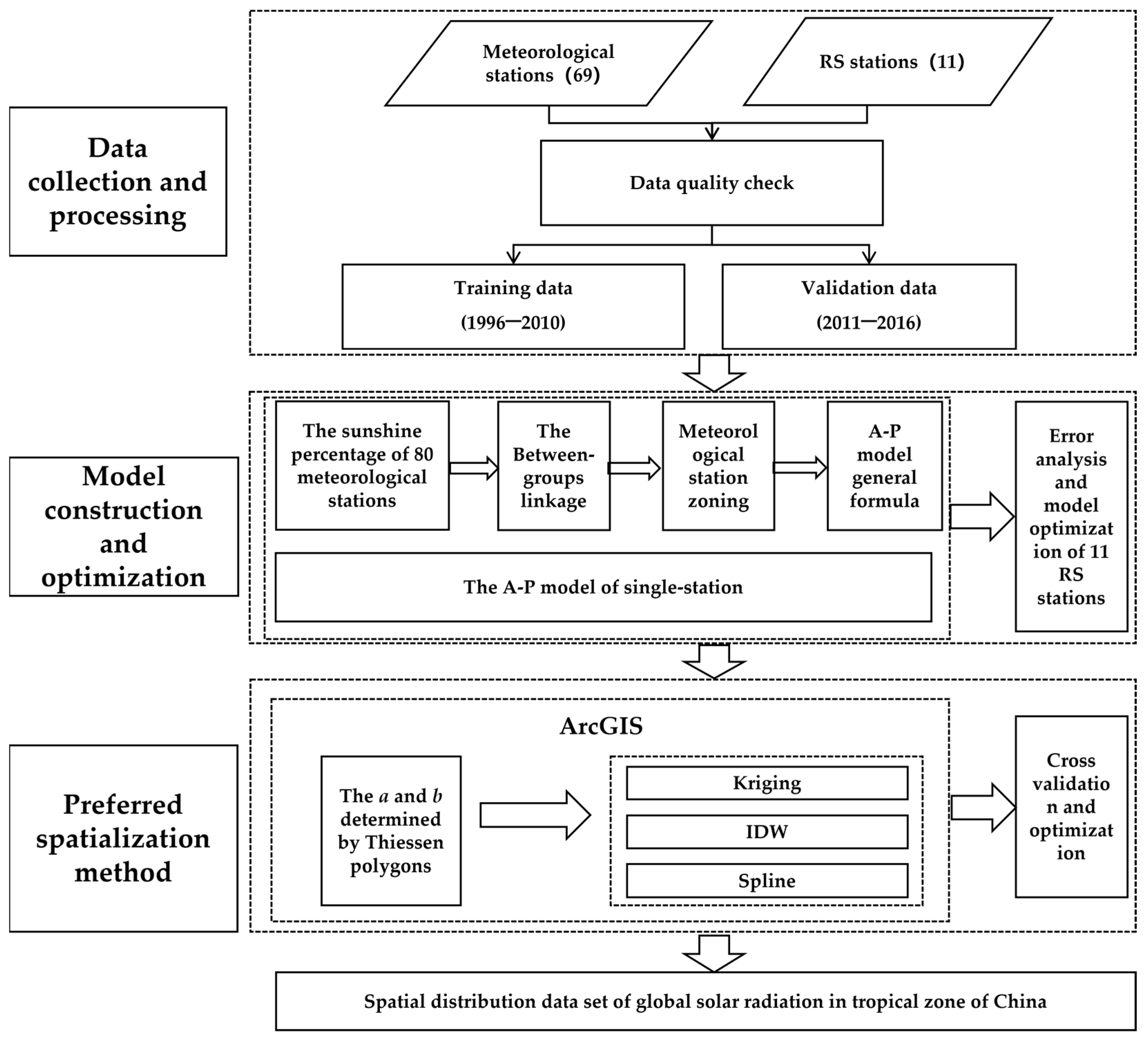
2.3. Methods
2.3.1. Estimation of the Global Solar Radiation under the A–P Model
2.3.2. The Between-Groups Linkage
2.3.3. Thiessen Polygons
2.3.4. Spatial Interpolation
2.3.5. Statistical Evaluation
3. Results and Discussion
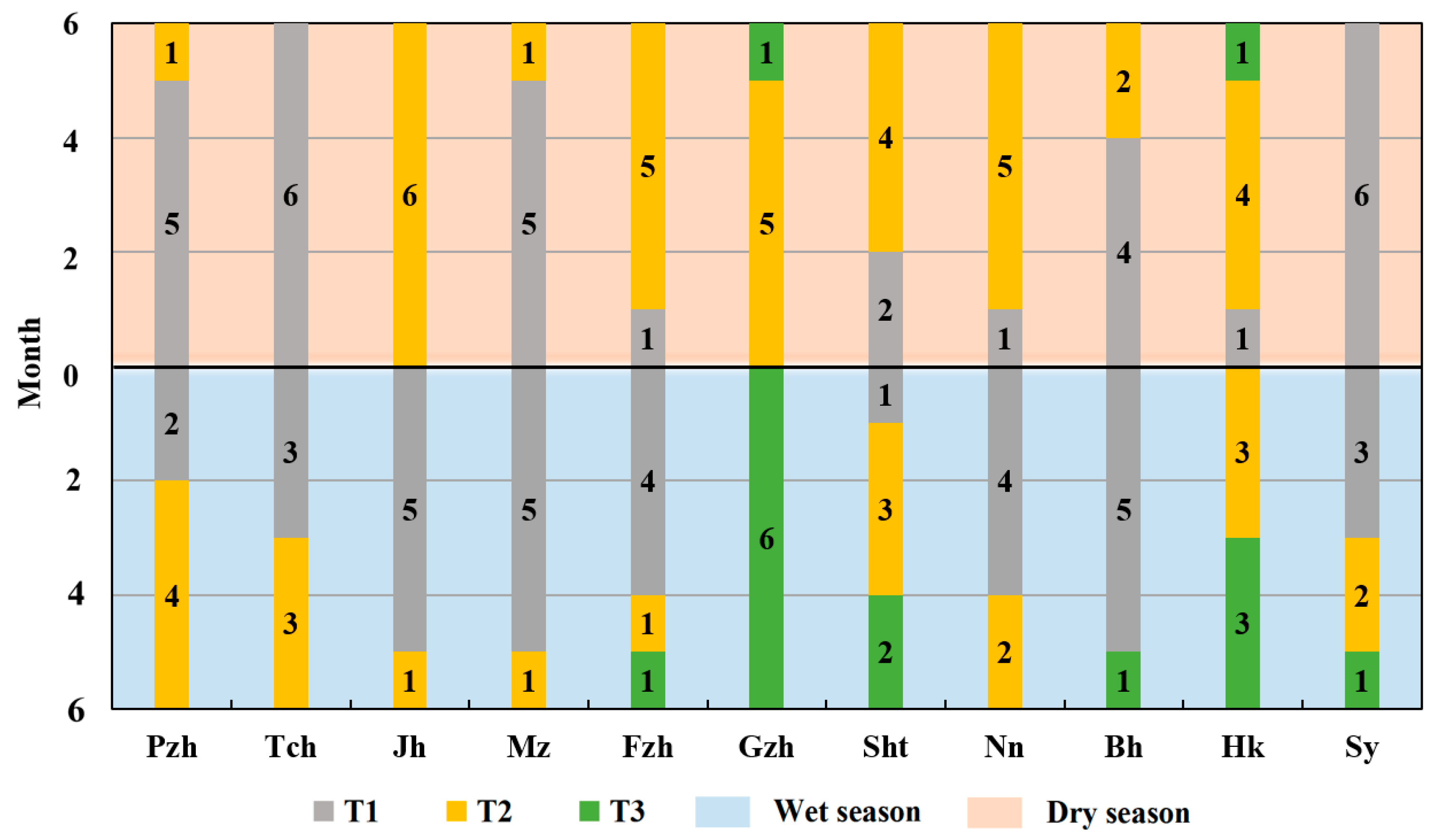
3.1. Result of the Between-Groups Linkage
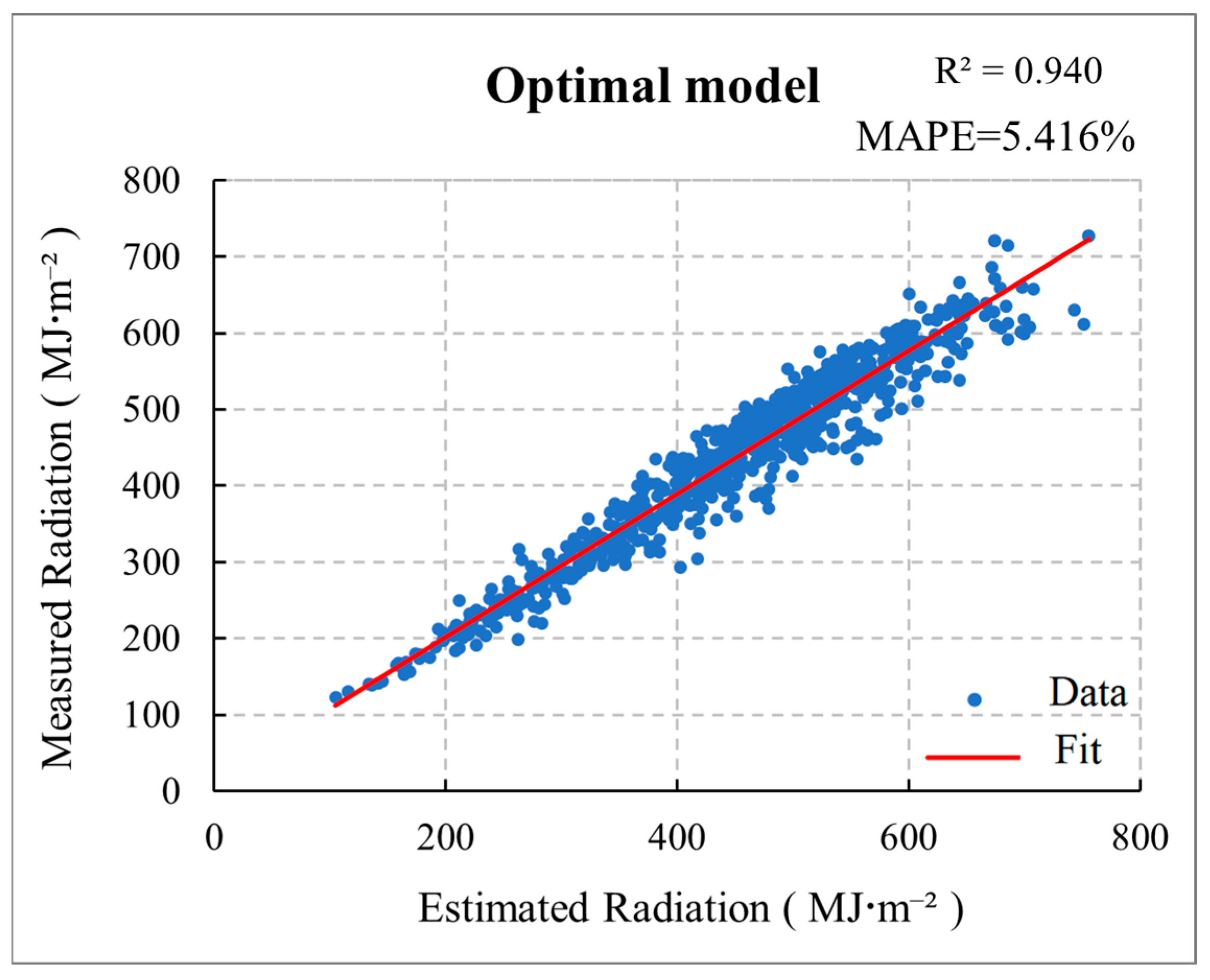
3.2. Error Analysis and Coefficient a and b Optimization of the A–P Model
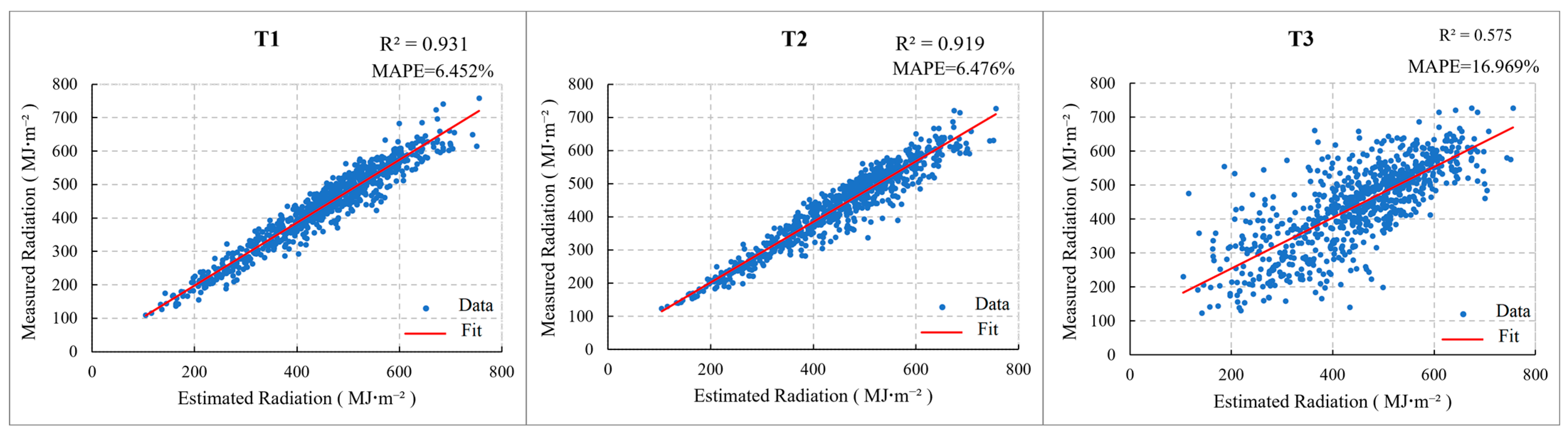
3.2.1. The Whole Year (January–December)
3.2.2. The Dry Season (November–April)
3.2.3. The Wet Season (May–October)
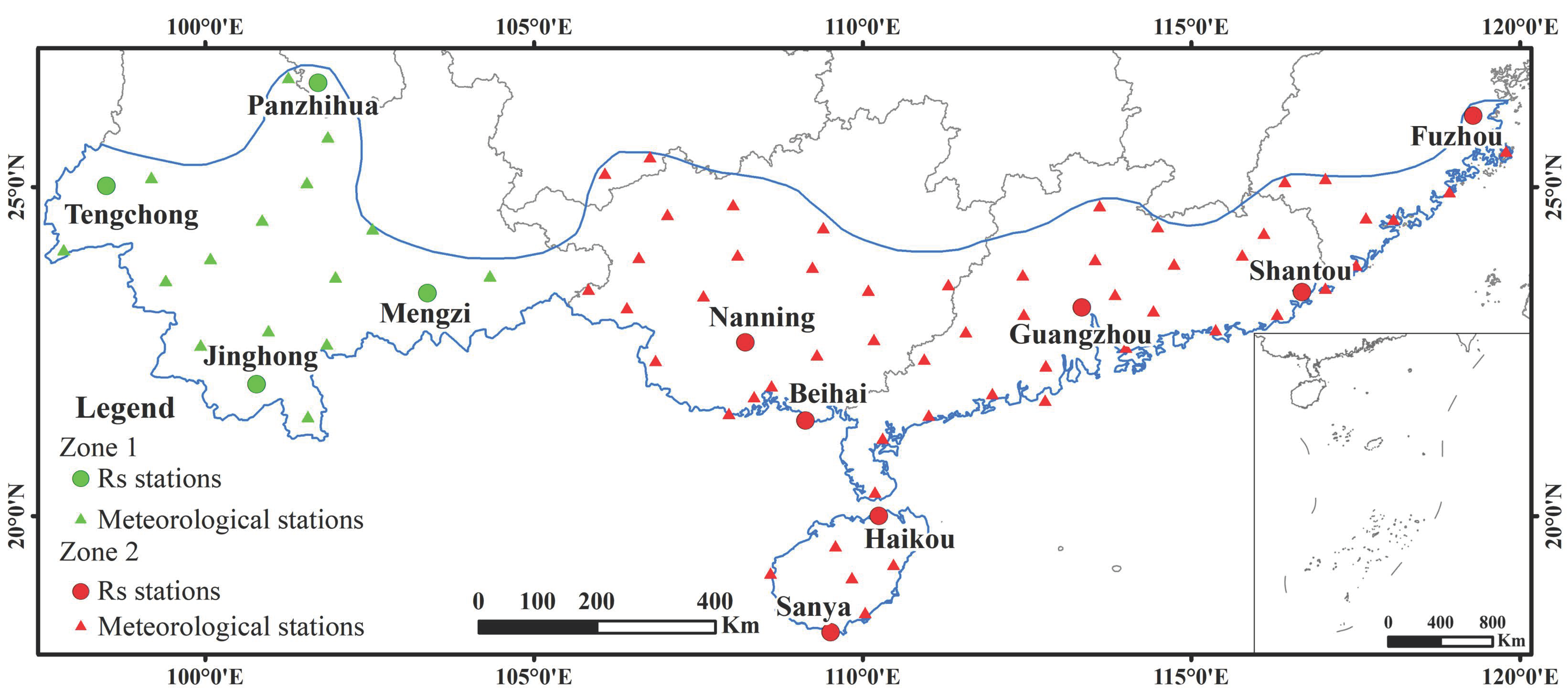
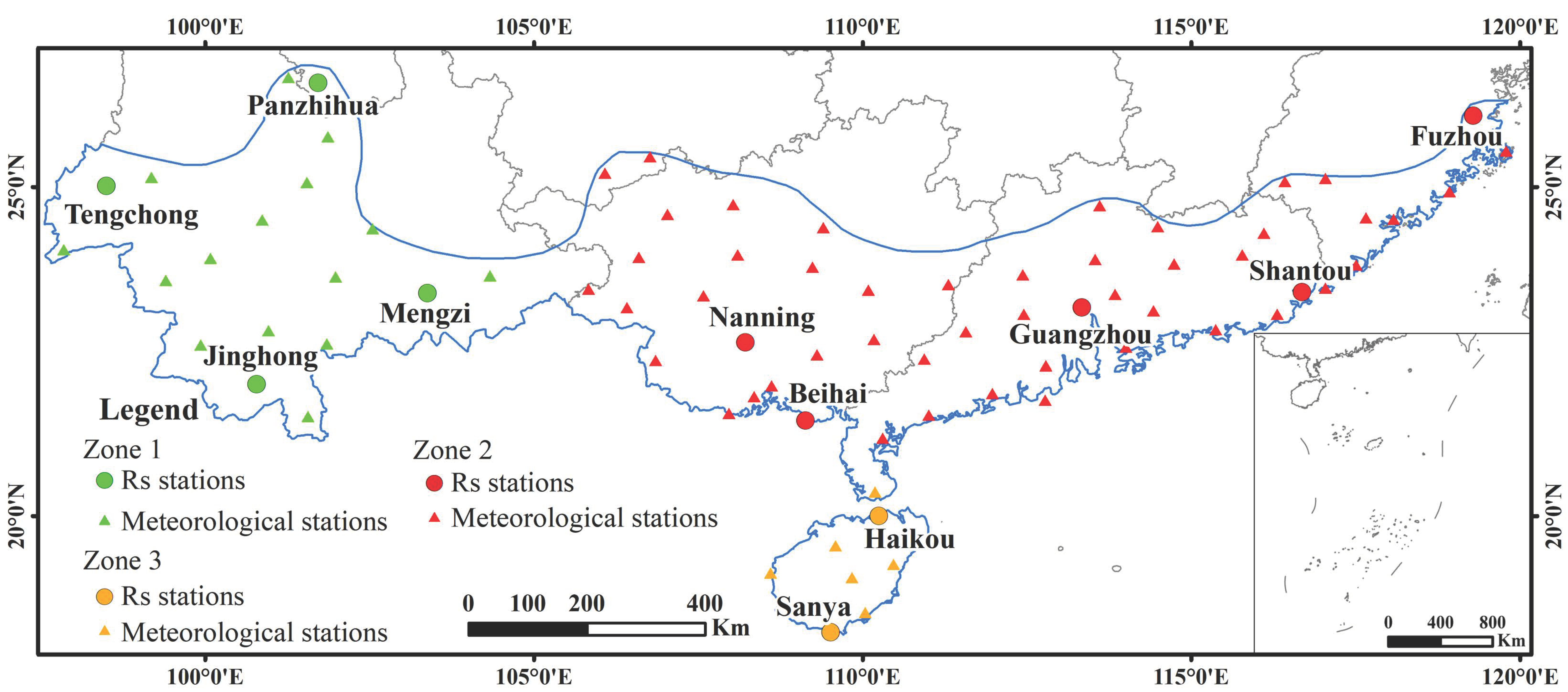
3.3. Result of Global Solar Radiation Zoning by the Thiessen Polygons
3.4. Verification of Spatial Interpolation Accuracy
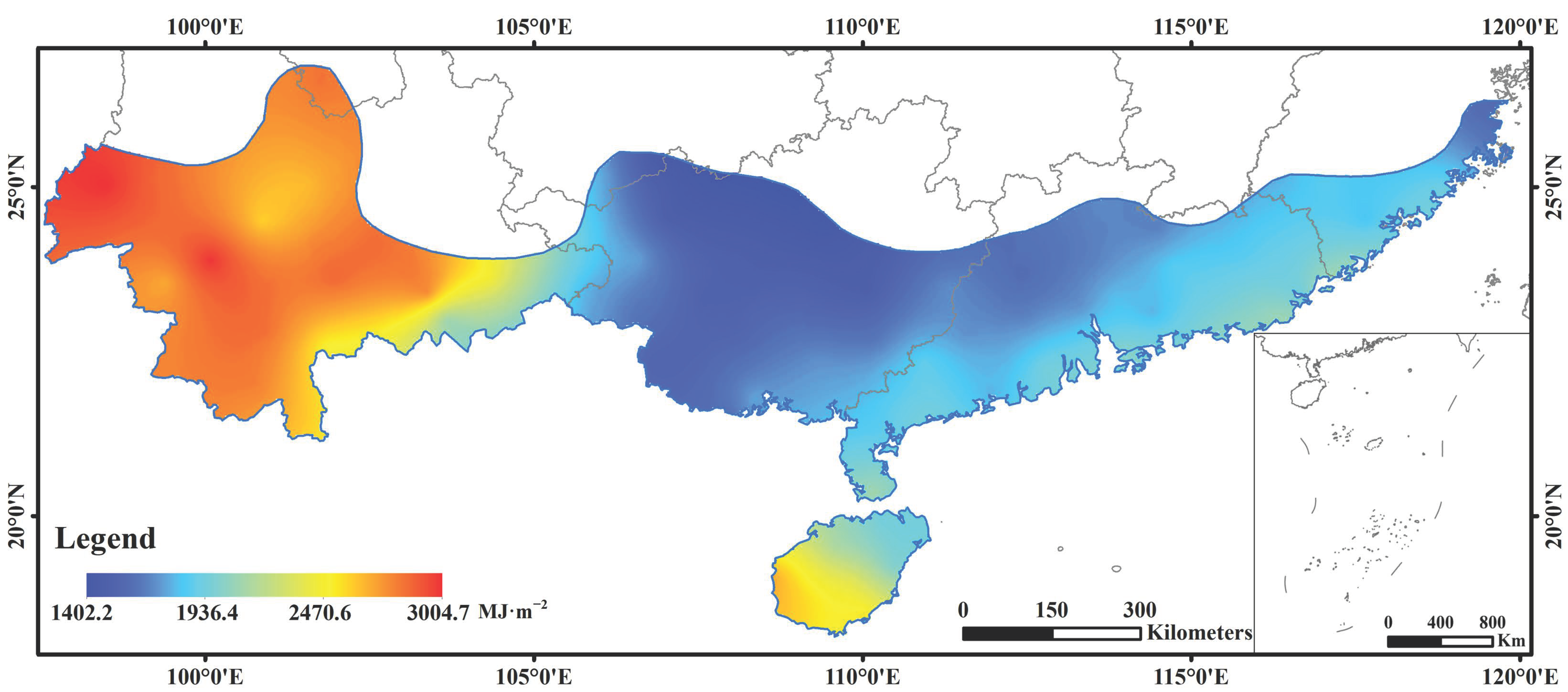
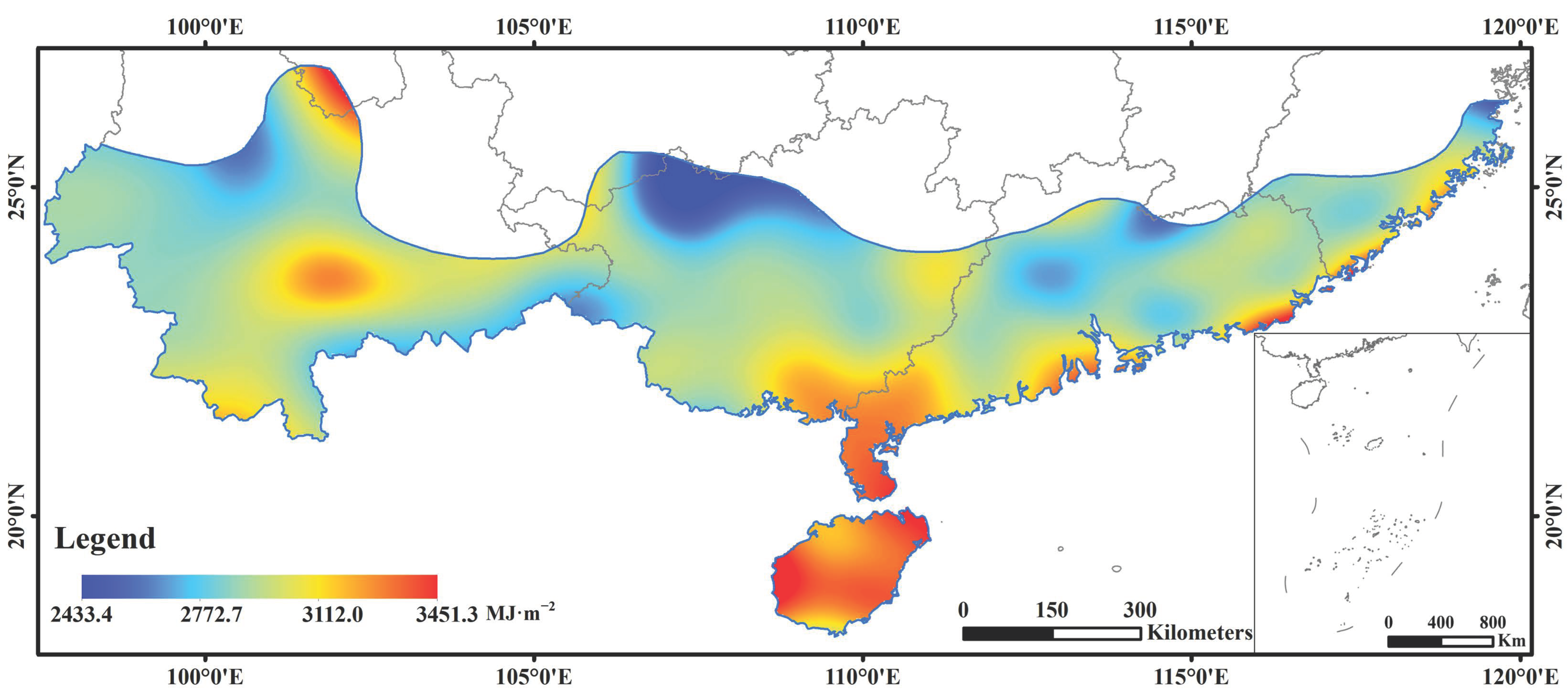
3.4.1. The Average Annual Global Solar Radiation during the Whole Year (January–December)
3.4.2. The Average Annual Global Solar Radiation during the Dry Season (November–April)
3.4.3. The Average Annual Global Solar Radiation during the Wet Season (May–October)
4. Conclusions
- (1)
- Based on the between-groups linkage of sunshine percentage, this study divided the meteorological stations into zones. Stations within the same zone were used for the regression coefficient calculation, which effectively increased the amount of regression sample data. This method could effectively compensate for the simulation accuracy of the regression coefficients in most months when the simulation accuracy of a single station was poor. After parameter optimization, the accuracy of the average annual global solar radiation simulation for each station during the dry and wet seasons and the whole year could be improved by 8.1%, 4.4%, and 5.3%, respectively. In addition, due to the increase in the sample number at specific stations, the multi-station simulation accuracy was lower than that of the single station.
- (2)
- To effectively apply the regression coefficients to non-solar radiation meteorological stations, this study used the property of the Thiessen polygons in which the distance between any point inside the polygon and the control point is the shortest. Based on this, the tropical zone of China was divided into 11 zones, and the stations in the same zone used the same a and b of the A–P model. Through validating the spatial interpolation results of solar radiation for the whole year, the dry season, and the wet season, the optimal methods for the spatial interpolation of solar radiation for the whole year were IDW, and those for the dry and wet seasons were Kriging and Spline, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
Appendix A
| Province | Station | Latitude (°N) | Longitude (°E) | Altitude (m) |
|---|---|---|---|---|
| Fujian | Shanghang | 25.05 | 116.42 | 198.00 |
| Fujian | Longyan | 25.05 | 117.02 | 376.00 |
| Fujian | Pingtan | 25.52 | 119.78 | 32.40 |
| Fujian | Zhangzhou | 24.50 | 117.65 | 28.90 |
| Fujian | Dongshan | 23.78 | 117.50 | 53.30 |
| Fujian | Xiamen | 24.48 | 118.07 | 139.40 |
| Fujian | Chongwu | 24.90 | 118.92 | 21.80 |
| Fujian | Fuzhou | 26.08 | 119.28 | 84.00 |
| Guangdong | Xuwen | 20.33 | 110.18 | 56.20 |
| Guangdong | Shaoguan | 24.67 | 113.60 | 121.30 |
| Guangdong | Fogang | 23.88 | 113.52 | 97.20 |
| Guangdong | Lianping | 24.37 | 114.48 | 215.20 |
| Guangdong | Meixian | 24.28 | 116.07 | 116.00 |
| Guangdong | Guangning | 23.63 | 112.42 | 92.70 |
| Guangdong | Gaoyao | 22.98 | 112.48 | 60.00 |
| Guangdong | Heyuan | 23.80 | 114.73 | 71.10 |
| Guangdong | Zengcheng | 23.33 | 113.83 | 30.80 |
| Guangdong | Huiyang | 23.07 | 114.37 | 108.50 |
| Guangdong | Wuhua | 23.92 | 115.75 | 135.90 |
| Guangdong | Huilai | 22.98 | 116.30 | 42.00 |
| Guangdong | Nanao | 23.43 | 117.03 | 8.00 |
| Guangdong | Xinyi | 22.35 | 110.93 | 141.40 |
| Guangdong | Luoding | 22.72 | 111.60 | 60.00 |
| Guangdong | Taishan | 22.25 | 112.78 | 33.10 |
| Guangdong | Shenzhen | 22.53 | 114.00 | 63.00 |
| Guangdong | Shanwei | 22.80 | 115.37 | 17.30 |
| Guangdong | Zhanjiang | 21.15 | 110.30 | 53.40 |
| Guangdong | Yangjiang | 21.85 | 111.98 | 90.30 |
| Guangdong | Dianbai | 21.55 | 110.98 | 31.80 |
| Guangdong | Shangchuan Island | 21.73 | 112.77 | 21.90 |
| Guangdong | Shantou | 23.38 | 116.68 | 2.30 |
| Guangdong | Guangzhou | 23.22 | 113.48 | 70.70 |
| Guangxi | Fengshan | 24.55 | 107.03 | 509.40 |
| Guangxi | Hechi | 24.70 | 108.03 | 260.20 |
| Guangxi | Duan | 23.93 | 108.10 | 170.80 |
| Guangxi | Liuzhou | 24.35 | 109.40 | 96.80 |
| Guangxi | Napo | 23.42 | 105.83 | 794.10 |
| Guangxi | Baise | 23.90 | 106.60 | 174.70 |
| Guangxi | Jingxi | 23.13 | 106.42 | 739.90 |
| Guangxi | Pingguo | 23.32 | 107.58 | 108.80 |
| Guangxi | Laibin | 23.45 | 109.08 | 96.70 |
| Guangxi | Guiping | 23.40 | 110.08 | 42.50 |
| Guangxi | Wuzhou | 23.48 | 111.30 | 114.80 |
| Guangxi | Longzhou | 22.33 | 106.85 | 128.80 |
| Guangxi | Lingshan | 22.42 | 109.30 | 66.60 |
| Guangxi | Yulin | 22.67 | 110.12 | 121.60 |
| Guangxi | Fangcheng | 21.78 | 108.35 | 32.40 |
| Guangxi | Qinzhou | 21.98 | 108.60 | 49.20 |
| Guangxi | Dongxing | 21.57 | 107.95 | 56.80 |
| Guangxi | Beihai | 21.45 | 109.13 | 12.80 |
| Guangxi | Nanning | 22.63 | 108.22 | 121.60 |
| Guizhou | Wangmo | 25.18 | 106.08 | 566.80 |
| Guizhou | Luodian | 25.43 | 106.77 | 440.30 |
| Hainan | Dongfang | 19.10 | 108.62 | 7.60 |
| Hainan | Danzhou | 19.52 | 109.58 | 169.00 |
| Hainan | Qiongzhong | 19.03 | 109.83 | 250.90 |
| Hainan | Qionghai | 19.23 | 110.47 | 24.00 |
| Hainan | Lingshui | 18.55 | 110.03 | 35.20 |
| Hainan | Sanya | 18.22 | 109.58 | 419.40 |
| Hainan | Haikou | 20.00 | 110.25 | 63.50 |
| Sichuan | Panzhihua | 26.57 | 101.72 | 1224.80 |
| Yunnan | Huaping | 26.63 | 101.27 | 1230.80 |
| Yunnan | Baoshan | 25.12 | 99.18 | 1652.20 |
| Yunnan | Yuanmou | 25.73 | 101.87 | 1120.60 |
| Yunnan | Chuxiong | 25.03 | 101.55 | 1824.10 |
| Yunnan | Ruili | 24.00 | 97.85 | 762.90 |
| Yunnan | Jingdong | 24.47 | 100.87 | 1162.30 |
| Yunnan | Yuxi | 24.33 | 102.55 | 1716.90 |
| Yunnan | Gengma | 23.55 | 99.40 | 1104.90 |
| Yunnan | Lincang | 23.88 | 100.08 | 1502.40 |
| Yunnan | Lancang | 22.57 | 99.93 | 1054.80 |
| Yunnan | Simao | 22.78 | 100.97 | 1302.10 |
| Yunnan | Yuanjiang | 23.60 | 101.98 | 400.90 |
| Yunnan | Mengla | 21.47 | 101.57 | 633.40 |
| Yunnan | Jiangcheng | 22.58 | 101.85 | 1120.50 |
| Yunnan | Yanshan | 23.62 | 104.33 | 1561.10 |
| Yunnan | Pingbian | 22.98 | 103.68 | 1414.10 |
| Yunnan | Mengzi | 23.45 | 103.33 | 1313.60 |
| Yunnan | Jinghong | 22.00 | 100.78 | 582.00 |
| Yunnan | Tengchong | 24.98 | 98.50 | 1695.90 |
References
- Zhou, Y.; Liu, Y.; Wang, D.; Liu, X.; Wang, Y. A review on global solar radiation prediction with machine learning models in a comprehensive perspective. Energy Convers. Manag. 2021, 235, 113960. [Google Scholar] [CrossRef]
- Fan, J.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluating the effect of air pollution on global and diffuse solar radiation prediction using support vector machine modeling based on sunshine duration and air temperature. Renew. Sustain. Energy Rev. 2018, 94, 732–747. [Google Scholar] [CrossRef]
- Lan, K.; Wang, L.; Zhou, Y.; Zhang, Z.; Fang, S.; Cao, P. The applicability of sunshine-based global solar radiation models modified with meteorological factors for different climate zones of China. Front. Energy Res. 2023, 10, 2296-598X. [Google Scholar] [CrossRef]
- Ramesh, D.; Chandrasekaran, M.; Soundararajan, R.P.; Subramanian, P.P.; Palled, V.; Kumar, D.P. Solar-Powered Plant Protection Equipment: Perspective and Prospects. Energies 2022, 15, 7379. [Google Scholar] [CrossRef]
- Gångström, A. Solar and terrestrial radiation. Report to the international commission for solar research on actinometric investigations of sola and atmospheric radiation. Q. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Besharat, F.; Dehghan, A.A.; Faghih, A.R. Empirical models for estimating global solar radiation: A review and case study. Renew. Sustain. Energy Rev. 2013, 21, 798–821. [Google Scholar] [CrossRef]
- Bawonda, F.I.; Adefarati, T. Evaluation of solar energy potential in six geopolitical regions of Nigeria using analytical and sim-ulation techniques. Energy Convers. Manag. 2023, 290, 117193. [Google Scholar] [CrossRef]
- Bird, R.E.; Hulstrom, R.L. Simplified Clear Sky Model for Direct and Diffuse Insolation on Horizontal Surfaces; Technical Report Solar Energy Research Institute; Solar Energy Research Institute: Golden, CO, USA, 1981. [Google Scholar] [CrossRef]
- Maxwell, E. METSTAT—The solar radiation model used in the production of the National Solar Radiation Data Base (NSRDB). Sol. Energy 1998, 62, 263–279. [Google Scholar] [CrossRef]
- Aradpour, S.; Deng, Z. Remote sensing algorithm for retrieving global-scale sea surface solar irradiance. Environ. Monit. Assess. 2023, 195, 1–19. [Google Scholar] [CrossRef]
- Nematchoua, M.K.; Orosa, J.A.; Afaifia, M. Prediction of daily global solar radiation and air temperature using six machine learning algorithms; a case of 27 European countries. Ecol. Inform. 2022, 69, 101643. [Google Scholar] [CrossRef]
- Zhao, S.; Wu, L.; Xiang, Y.; Dong, J.; Li, Z.; Liu, X.; Tang, Z.; Wang, H.; Wang, X.; An, J.; et al. Coupling meteorological stations data and satellite data for prediction of global solar radiation with machine learning models. Renew. Energy 2022, 198, 1049–1064. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M.; Allen, R.G.; Pereira, L.S.; Martin, S. Crop Evapotranspiration: Guidelines for Com-puting Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 56, p. D05109. [Google Scholar]
- Paulescu, M.; Stefu, N.; Calinoiu, D.; Paulescu, E.; Pop, N.; Boata, R.; Mares, O. Ångström–Prescott equation: Physical basis, empirical models and sensitivity analysis. Renew. Sustain. Energy Rev. 2016, 62, 495–506. [Google Scholar] [CrossRef]
- Li, M.-F.; Guo, P.-T.; Dai, S.; Luo, H.; Liu, E.; Li, Y. Empirical estimation of daily global solar radiation with contrasting seasons of rain and drought characterize over tropical China. J. Clean. Prod. 2020, 266, 121915. [Google Scholar] [CrossRef]
- Mohammadi, B.; Moazenzadeh, R. Performance Analysis of Daily Global Solar Radiation Models in Peru by Regression Analysis. Atmosphere 2021, 12, 389. [Google Scholar] [CrossRef]
- Manzano, A.; Martín, M.; Valero, F.; Armenta, C. A single method to estimate the daily global solar radiation from monthly data. Atmos. Res. 2015, 166, 70–82. [Google Scholar] [CrossRef]
- Zhao, N.; Zeng, X.; Han, S. Solar radiation estimation using sunshine hour and air pollution index in China. Energy Convers. Manag. 2013, 76, 846–851. [Google Scholar] [CrossRef]
- Chen, J.L.; Wen, Z.; Lv, M.; Yi, X.; Wu, S.; He, L. A General Empirical Model for Estimation of Solar Radiation in Yangtze River Basin. Appl. Ecol. Environ. Res. 2018, 16, 1471–1482. [Google Scholar] [CrossRef]
- Jia, D.; Yang, L.; Lv, T.; Liu, W.; Gao, X.; Zhou, J. Evaluation of machine learning models for predicting daily global and diffuse solar radiation under different weather/pollution conditions. Renew. Energy 2022, 187, 896–906. [Google Scholar] [CrossRef]
- Ali, M.A.; Elsayed, A.; Elkabani, I.; Akrami, M.; Youssef, M.E.; Hassan, G.E. Optimizing Artificial Neural Networks for the Accurate Prediction of Global Solar Radiation: A Performance Comparison with Conventional Methods. Energies 2023, 16, 6165. [Google Scholar] [CrossRef]
- Guermoui, M.; Benkaciali, S.; Gairaa, K.; Bouchouicha, K.; Boulmaiz, T.; Boland, J.W. A novel ensemble learning approach for hourly global solar radiation forecasting. Neural Comput. Appl. 2021, 34, 2983–3005. [Google Scholar] [CrossRef]
- Narvaez, G.; Giraldo, L.F.; Bressan, M.; Pantoja, A. Machine learning for site-adaptation and solar radiation forecasting. Renew. Energy 2021, 167, 333–342. [Google Scholar] [CrossRef]
- Stefu, N.; Paulescu, M.; Blaga, R.; Calinoiu, D.; Pop, N.; Boata, R.; Paulescu, E. A theoretical framework for Ångström equation. Its virtues and liabilities in solar energy estimation. Energy Convers. Manag. 2016, 112, 236–245. [Google Scholar] [CrossRef]
- Morf, H. Regression by Integration Demonstr. on Ångström-Prescott-type relations. Renew. Energy 2018, 127, 713–723. [Google Scholar] [CrossRef]
- Prieto, J.-I.; García, D. Modified temperature-based global solar radiation models for estimation in regions with scarce experimental data. Energy Convers. Manag. 2022, 268, 115950. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Zhong, X.; Zhang, W.; Porter, J.R.; Liu, W. Assessing models for parameters of the Ångström–Prescott formula in China. Appl. Energy 2012, 96, 327–338. [Google Scholar] [CrossRef]
- He, Q.H.; Xie, Y. Research on the Climatological Calculation Method of Solar Radiation in China. J. Nat. Resour. 2010, 9, 411–420. [Google Scholar] [CrossRef]
- Liu, J.; Pan, T.; Chen, D.; Zhou, X.; Yu, Q.; Flerchinger, G.N.; Liu, D.L.; Zou, X.; Linderholm, H.W.; Du, J.; et al. An Improved Ångström-Type Model for Estimating Solar Radiation over the Tibetan Plateau. Energies 2017, 10, 892. [Google Scholar] [CrossRef]
- Liu, X.; Mei, X.; Li, Y.; Zhang, Y.; Wang, Q.; Jensen, J.R.; Porter, J.R. Calibration of the Ångström–Prescott coefficients (a, b) under different time scales and their impacts in estimating global solar radiation in the Yellow River basin. Agric. For. Meteorol. 2009, 149, 697–710. [Google Scholar] [CrossRef]
- Xiong, Y.L.; Zhou, Y.J. Temporal-spatial distribution of surface total solar radiation and meteorological influencing factors over Sichuan area. Acta Energiae Solaris Sin. 2020, 41, 162–171. [Google Scholar]
- Xia, X.; Pan, Y.; Zhu, X.; Zhang, J. Monthly calibration and optimization of Ångström-Prescott equation coefficients for comprehensive agricultural divisions in China. J. Geogr. Sci. 2021, 31, 997–1014. [Google Scholar] [CrossRef]
- Dai, S.P.; Li, H.L.; Liu, H.Q.; Liu, E.P. Review on the regionalization of tropical zone in China. Guangdong Agric. Sci. 2012, 23, 205–208. [Google Scholar] [CrossRef]
- China Meteorological Administration. Assessment Method for Solar Energy Resource: QX/T 89—2018; The Standard Press of China: Beijing, China, 2018. [Google Scholar]
- Park, J.-K.; Das, A.; Park, J.-H. A new approach to estimate the spatial distribution of solar radiation using topographic factor and sunshine duration in South Korea. Energy Convers. Manag. 2015, 101, 30–39. [Google Scholar] [CrossRef]

| Province | Station | Abbrev | Latitude (°N) | Longitude (°E) | Altitude (m) |
|---|---|---|---|---|---|
| Yunnan | Tengchong | Tch | 24.98 | 98.50 | 1695.90 |
| Jinghong | Jh | 22.00 | 100.78 | 582.00 | |
| Mengzi | Mz | 23.45 | 103.33 | 1313.60 | |
| Sichuan | Panzhihua | Pzh | 26.57 | 101.72 | 1224.80 |
| Guangxi | Nanning | Nn | 22.63 | 108.22 | 121.60 |
| Beihai | Bh | 21.45 | 109.13 | 12.80 | |
| Guangdong | Guangzhou | Gzh | 23.22 | 113.48 | 70.70 |
| Shantou | Sht | 23.38 | 116.68 | 2.30 | |
| Fujian | Fuzhou | Fzh | 26.08 | 119.28 | 84.00 |
| Hainan | Haikou | Hk | 20.00 | 110.25 | 63.50 |
| Sanya | Sy | 18.22 | 109.58 | 419.40 |
| Station Abbrev | Pzh | Tch | Jh | Mz | Fzh | Gzh | Sht | Nn | Bh | Hk | Sy | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | a | b | a | b | a | b | a | b | a | b | a | b | a | b | a | b | a | b | a | b | |
| Jan | 0.282 | 0.363 | −0.033 | 0.841 | 0.214 | 0.495 | 0.164 | 0.618 | 0.15 | 0.628 | 0.15 | 0.628 | 0.15 | 0.628 | 0.15 | 0.628 | 0.15 | 0.628 | 0.15 | 0.628 | 0.224 | 0.52 |
| Feb | 0.195 | 0.506 | 0.206 | 0.513 | 0.195 | 0.506 | 0.074 | 0.736 | 0.15 | 0.613 | 0.15 | 0.613 | 0.162 | 0.567 | 0.145 | 0.63 | 0.175 | 0.563 | 0.15 | 0.613 | 0.24 | 0.467 |
| Mar | −0.008 | 0.738 | 0.227 | 0.43 | 0.25 | 0.39 | 0.306 | 0.332 | 0.143 | 0.626 | 0.143 | 0.626 | 0.163 | 0.562 | 0.143 | 0.626 | 0.188 | 0.476 | 0.19 | 0.512 | 0.372 | 0.156 |
| Apr | 0.188 | 0.482 | 0.282 | 0.32 | 0.276 | 0.352 | 0.287 | 0.37 | 0.212 | 0.423 | 0.156 | 0.612 | 0.171 | 0.562 | 0.171 | 0.562 | 0.186 | 0.54 | 0.225 | 0.456 | 0.316 | 0.304 |
| May | 0.231 | 0.451 | 0.231 | 0.451 | 0.248 | 0.424 | 0.225 | 0.513 | 0.194 | 0.529 | 0.18 | 0.564 | 0.21 | 0.479 | 0.194 | 0.529 | 0.131 | 0.671 | 0.317 | 0.303 | 0.424 | 0.136 |
| Jun | 0.285 | 0.327 | 0.3 | 0.19 | 0.324 | 0.257 | 0.285 | 0.327 | 0.226 | 0.457 | 0.197 | 0.505 | 0.204 | 0.496 | 0.204 | 0.496 | 0.213 | 0.493 | 0.204 | 0.496 | 0.319 | 0.293 |
| Jul | 0.261 | 0.389 | 0.261 | 0.389 | 0.261 | 0.389 | 0.252 | 0.5 | 0.263 | 0.408 | 0.194 | 0.507 | 0.195 | 0.509 | 0.234 | 0.442 | 0.181 | 0.553 | 0.195 | 0.509 | 0.271 | 0.373 |
| Aug | 0.2 | 0.5 | 0.309 | 0.253 | 0.284 | 0.357 | 0.31 | 0.302 | 0.261 | 0.412 | 0.201 | 0.499 | 0.199 | 0.505 | 0.242 | 0.448 | 0.146 | 0.624 | 0.199 | 0.505 | 0.199 | 0.505 |
| Sep | 0.187 | 0.532 | 0.278 | 0.376 | 0.326 | 0.283 | 0.276 | 0.416 | 0.236 | 0.43 | 0.21 | 0.486 | 0.21 | 0.486 | 0.21 | 0.517 | 0.172 | 0.579 | 0.243 | 0.401 | 0.263 | 0.356 |
| Oct | 0.253 | 0.432 | 0.261 | 0.435 | 0.259 | 0.432 | 0.274 | 0.419 | 0.213 | 0.49 | 0.213 | 0.49 | 0.213 | 0.49 | 0.229 | 0.487 | 0.213 | 0.49 | 0.214 | 0.474 | 0.213 | 0.487 |
| Nov | 0.154 | 0.544 | 0.239 | 0.48 | 0.213 | 0.505 | 0.08 | 0.793 | 0.202 | 0.511 | 0.202 | 0.511 | 0.202 | 0.511 | 0.202 | 0.511 | 0.214 | 0.508 | 0.202 | 0.511 | 0.287 | 0.389 |
| Dec | 0.000441 | 0.759 | 0.129 | 0.642 | 0.224 | 0.488 | 0.224 | 0.488 | 0.191 | 0.526 | 0.191 | 0.526 | 0.191 | 0.526 | 0.191 | 0.526 | 0.191 | 0.526 | 0.191 | 0.526 | 0.209 | 0.538 |
| R² | 0.953 | 0.864 | 0.897 | 0.857 | 0.951 | 0.971 | 0.98 | 0.981 | 0.938 | 0.934 | 0.839 | |||||||||||
| Error Analysis | Agricultural Comprehensive Area of China [32] | The Tropical Zone of China |
|---|---|---|
| R² | 0.71 | 0.94 |
| MAPE (%) | 8.64 | 5.42 |
| RMSE (MJ·m−2) | 79.99 | 33.20 |
| MAE (MJ·m−2) | 38.12 | 24.33 |
| MBE (MJ·m−2) | −10.67 | 14.15 |
| Interpolation Method | Error Analysis | The Whole Year | The Dry Season | The Wet Season |
|---|---|---|---|---|
| Kriging | RMSE (MJ·m−2) | 407.90 | 187.11 | 202.94 |
| MAE (MJ·m−2) | 309.61 | 132.61 | 150.97 | |
| MBE (MJ·m−2) | 203.52 | 87.89 | 93.45 | |
| R² | 0.72 | 0.92 | 0.44 | |
| IDW | RMSE (MJ·m−2) | 377.71 | 234.62 | 196.29 |
| MAE (MJ·m−2) | 293.42 | 169.51 | 143.98 | |
| MBE (MJ·m−2) | 189.13 | 111.77 | 77.36 | |
| R² | 0.77 | 0.87 | 0.43 | |
| Spline | RMSE (MJ·m−2) | 413.57 | 189.50 | 173.09 |
| MAE (MJ·m−2) | 334.77 | 142.17 | 133.80 | |
| MBE (MJ·m−2) | 61.60 | 19.27 | 42.35 | |
| R² | 0.63 | 0.89 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Yi, X.; Li, M.-F.; Dai, S.; Li, H.; Luo, H.; Zheng, Q.; Hu, Y. Calibration of the Ångström–Prescott Model for Accurately Estimating Solar Radiation Spatial Distribution in Areas with Few Global Solar Radiation Stations: A Case Study of the China Tropical Zone. Atmosphere 2023, 14, 1825. https://doi.org/10.3390/atmos14121825
Yu X, Yi X, Li M-F, Dai S, Li H, Luo H, Zheng Q, Hu Y. Calibration of the Ångström–Prescott Model for Accurately Estimating Solar Radiation Spatial Distribution in Areas with Few Global Solar Radiation Stations: A Case Study of the China Tropical Zone. Atmosphere. 2023; 14(12):1825. https://doi.org/10.3390/atmos14121825
Chicago/Turabian StyleYu, Xuan, Xia Yi, Mao-Fen Li, Shengpei Dai, Hailiang Li, Hongxia Luo, Qian Zheng, and Yingying Hu. 2023. "Calibration of the Ångström–Prescott Model for Accurately Estimating Solar Radiation Spatial Distribution in Areas with Few Global Solar Radiation Stations: A Case Study of the China Tropical Zone" Atmosphere 14, no. 12: 1825. https://doi.org/10.3390/atmos14121825
APA StyleYu, X., Yi, X., Li, M.-F., Dai, S., Li, H., Luo, H., Zheng, Q., & Hu, Y. (2023). Calibration of the Ångström–Prescott Model for Accurately Estimating Solar Radiation Spatial Distribution in Areas with Few Global Solar Radiation Stations: A Case Study of the China Tropical Zone. Atmosphere, 14(12), 1825. https://doi.org/10.3390/atmos14121825







