Numerical Simulation of Heat Transfer of Porous Rock Layers in Cold Sandy Regions
Abstract
:1. Introduction
2. Physical and Numerical Model
2.1. Governing Equations
2.1.1. Porous Media Zone
2.1.2. Soil Layer Zone
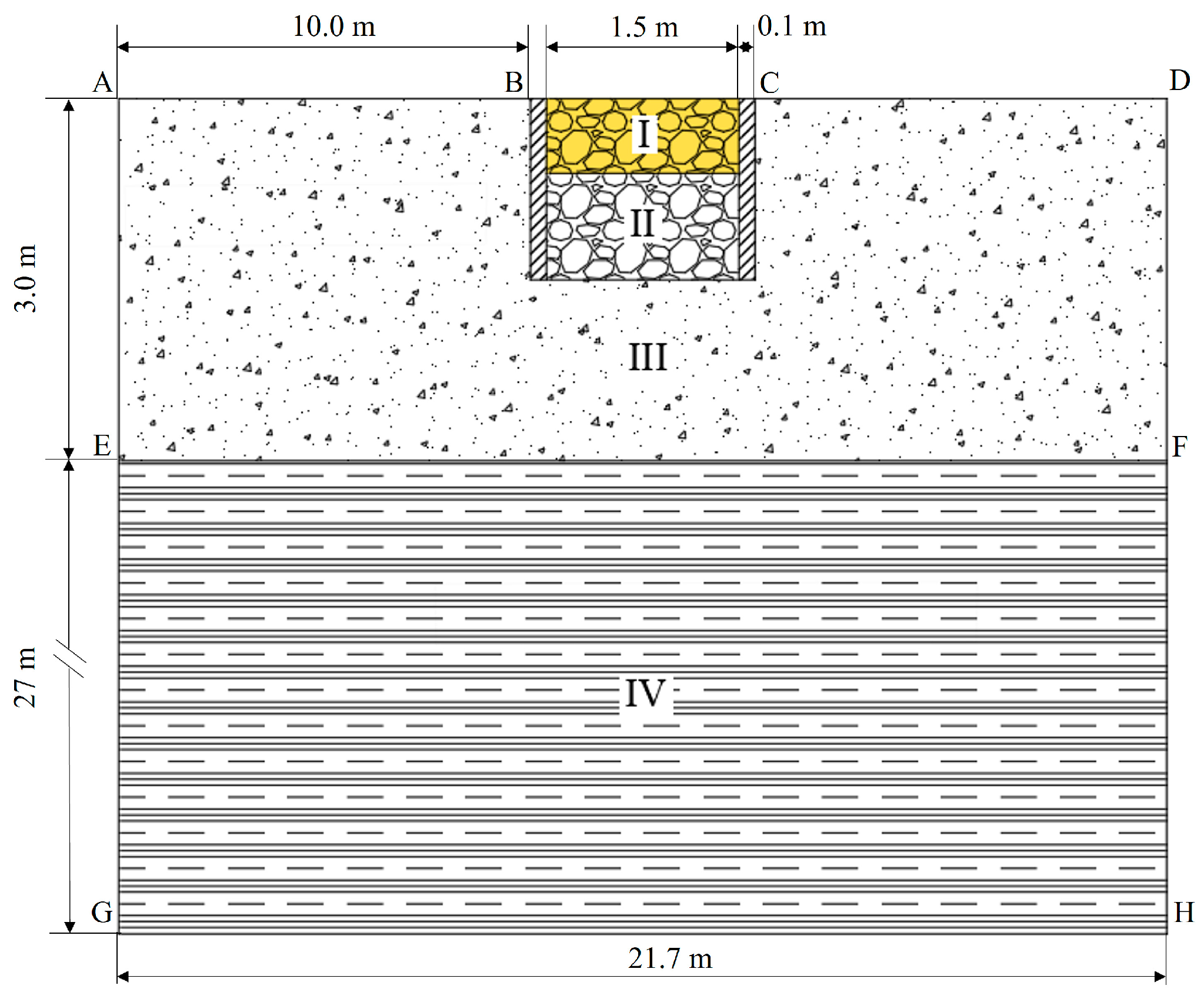
2.2. Physical Model and Parameters
2.3. Temperature Boundary Condition
2.4. Modeling Sequence and Calculation Cases
3. Results
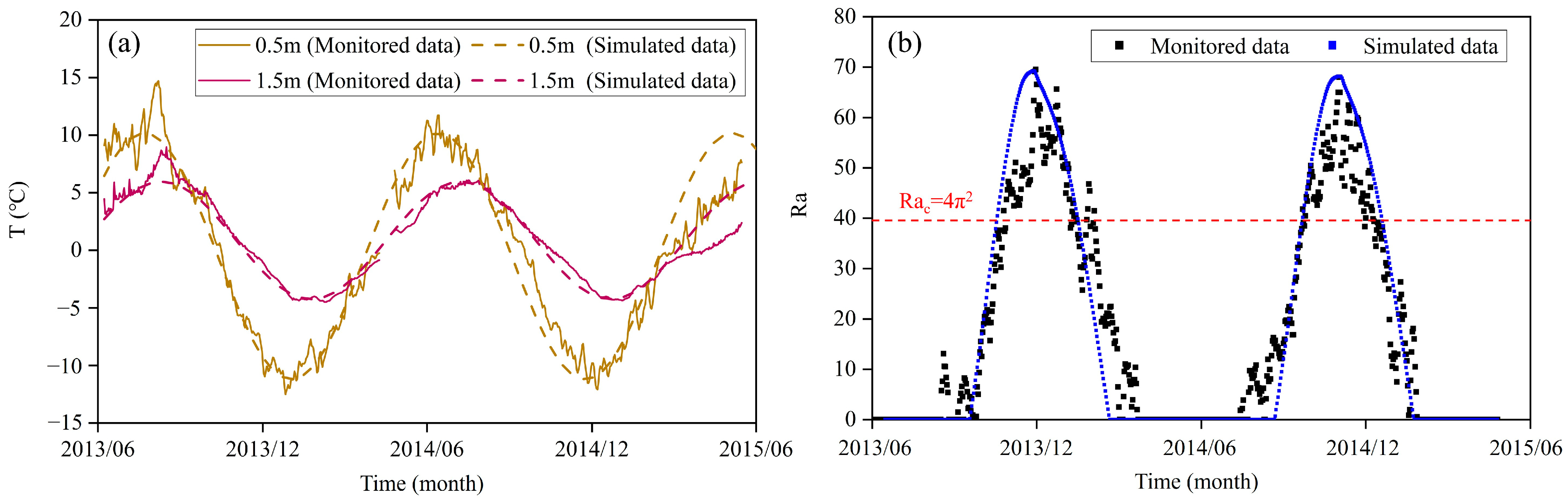
3.1. Modeling Validation
3.2. Natural Convection Characteristics in the Closed PRL
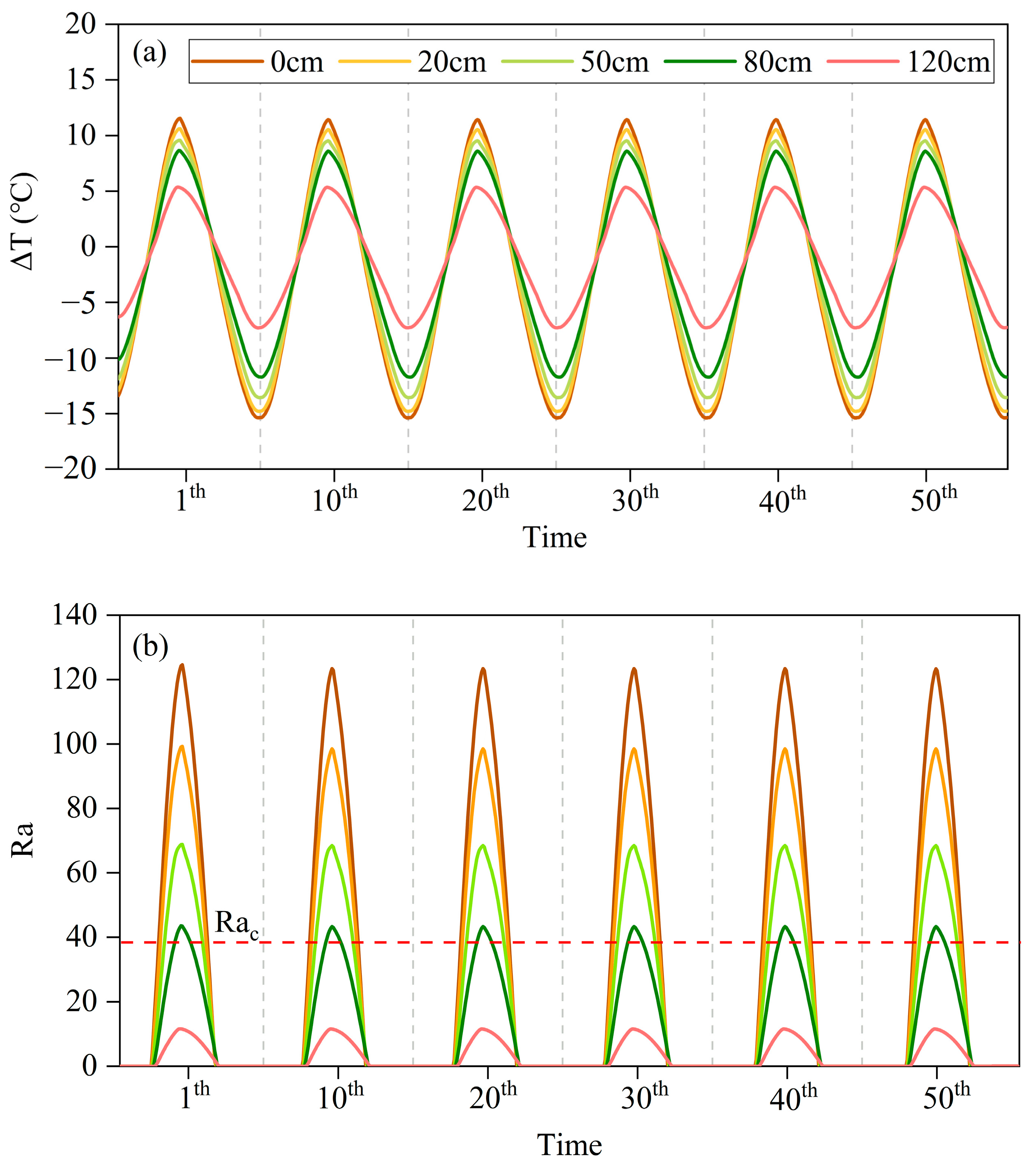
3.2.1. Impact of Sand Filling on the Convection Characteristics of the PRL
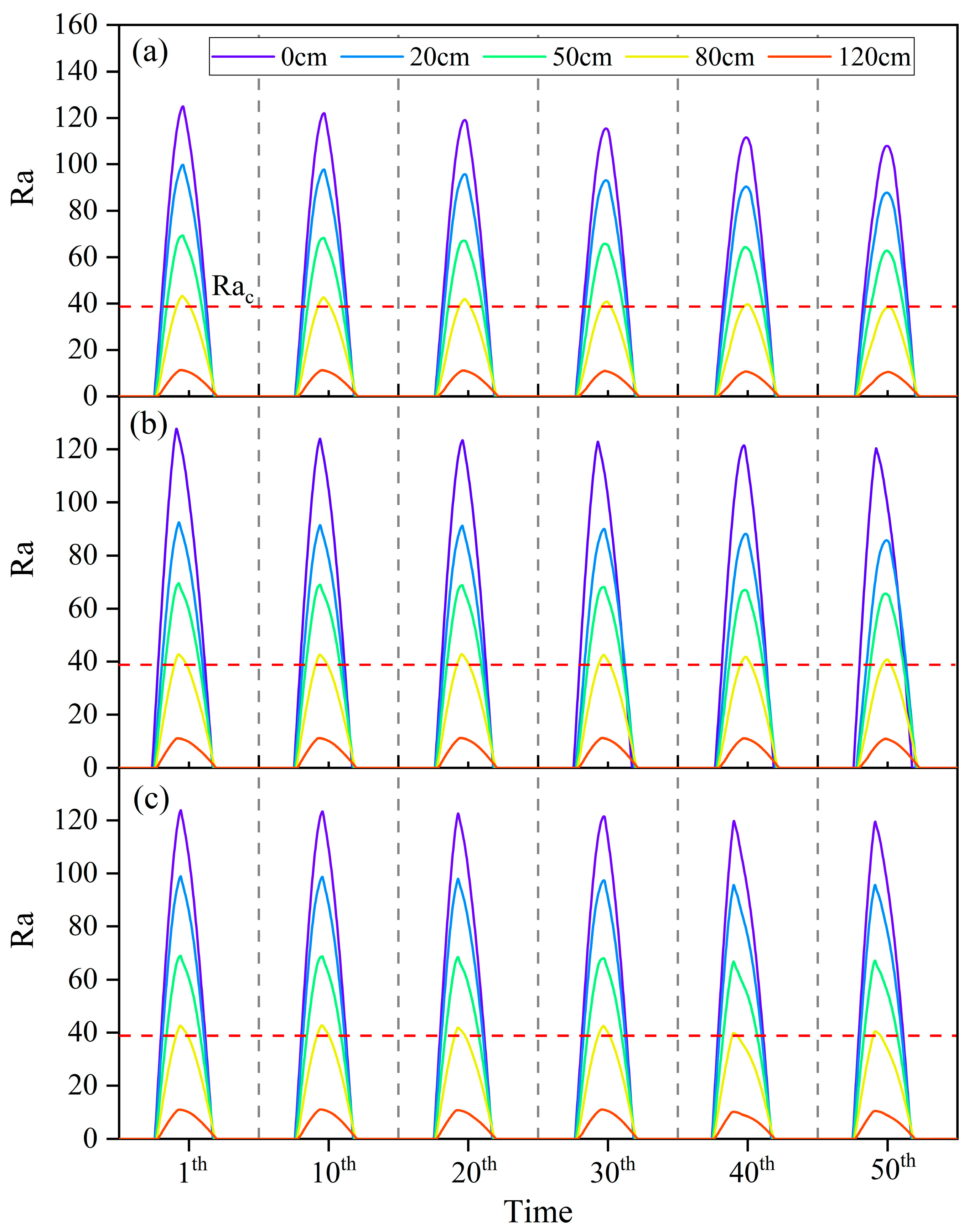
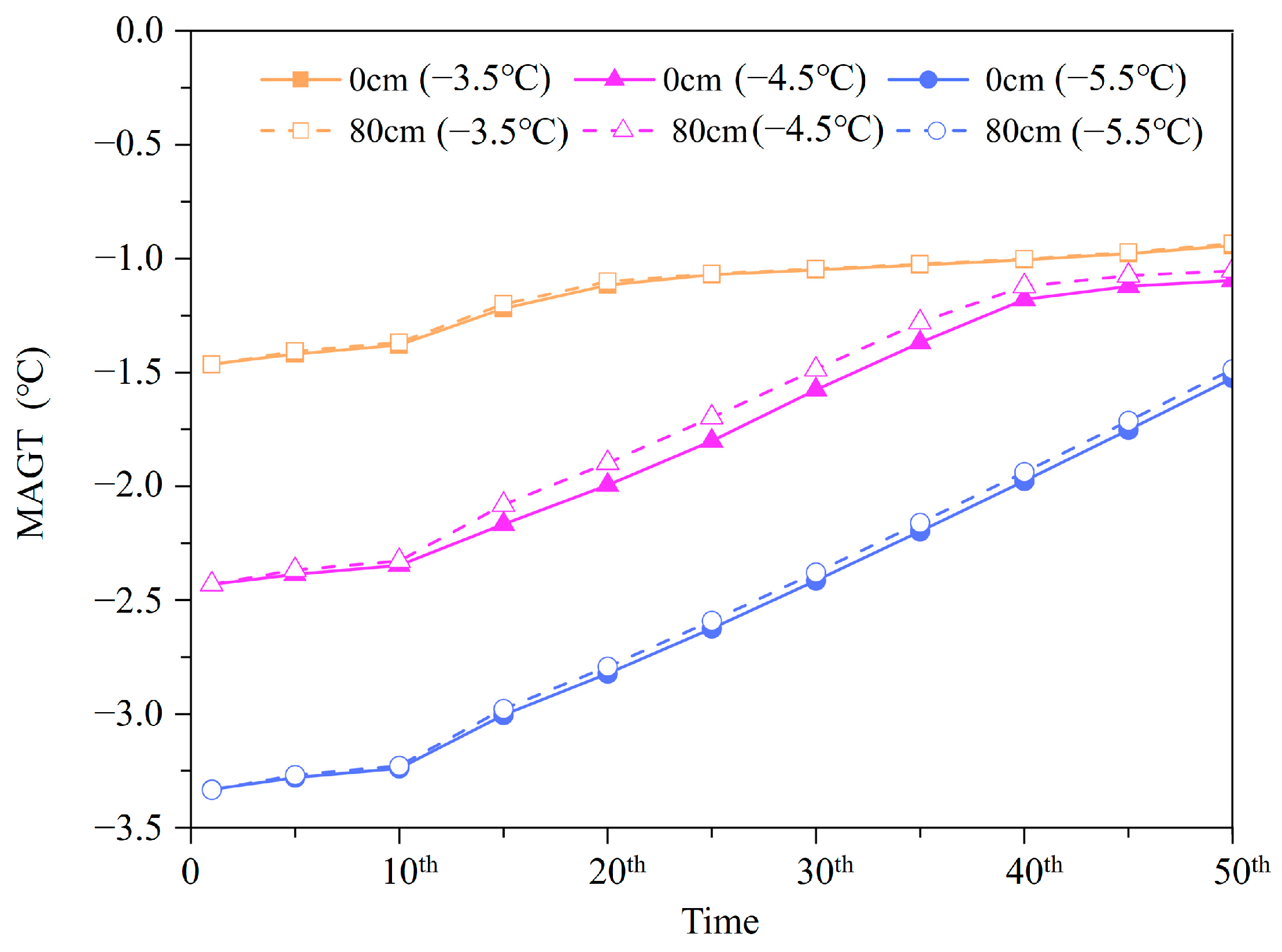
3.2.2. Comprehensive Impact of Climate Warming and Sand Filling on the Convection Characteristics of the Closed PRL
3.3. Permafrost Thermal Regime Beneath the PRL
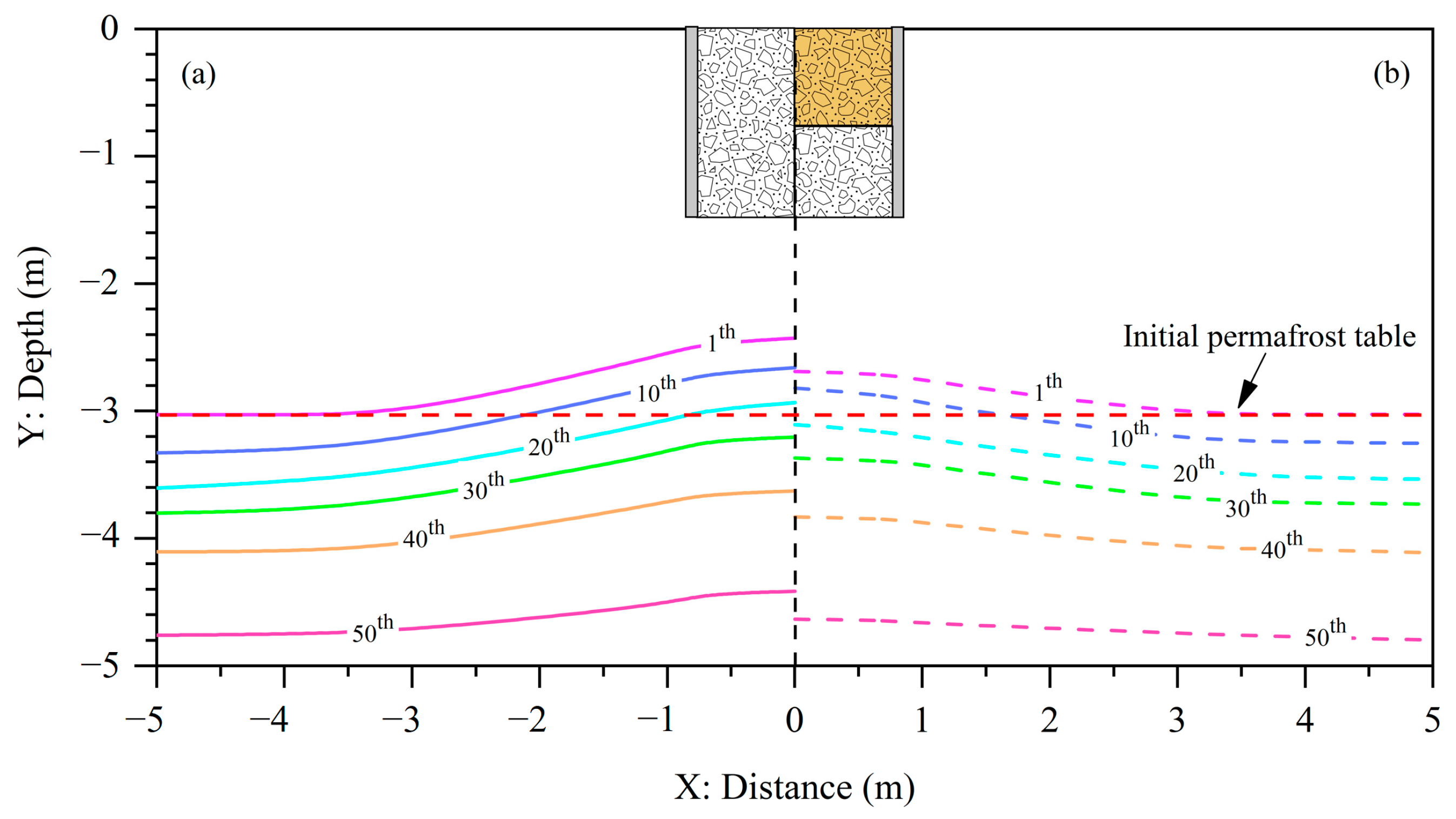
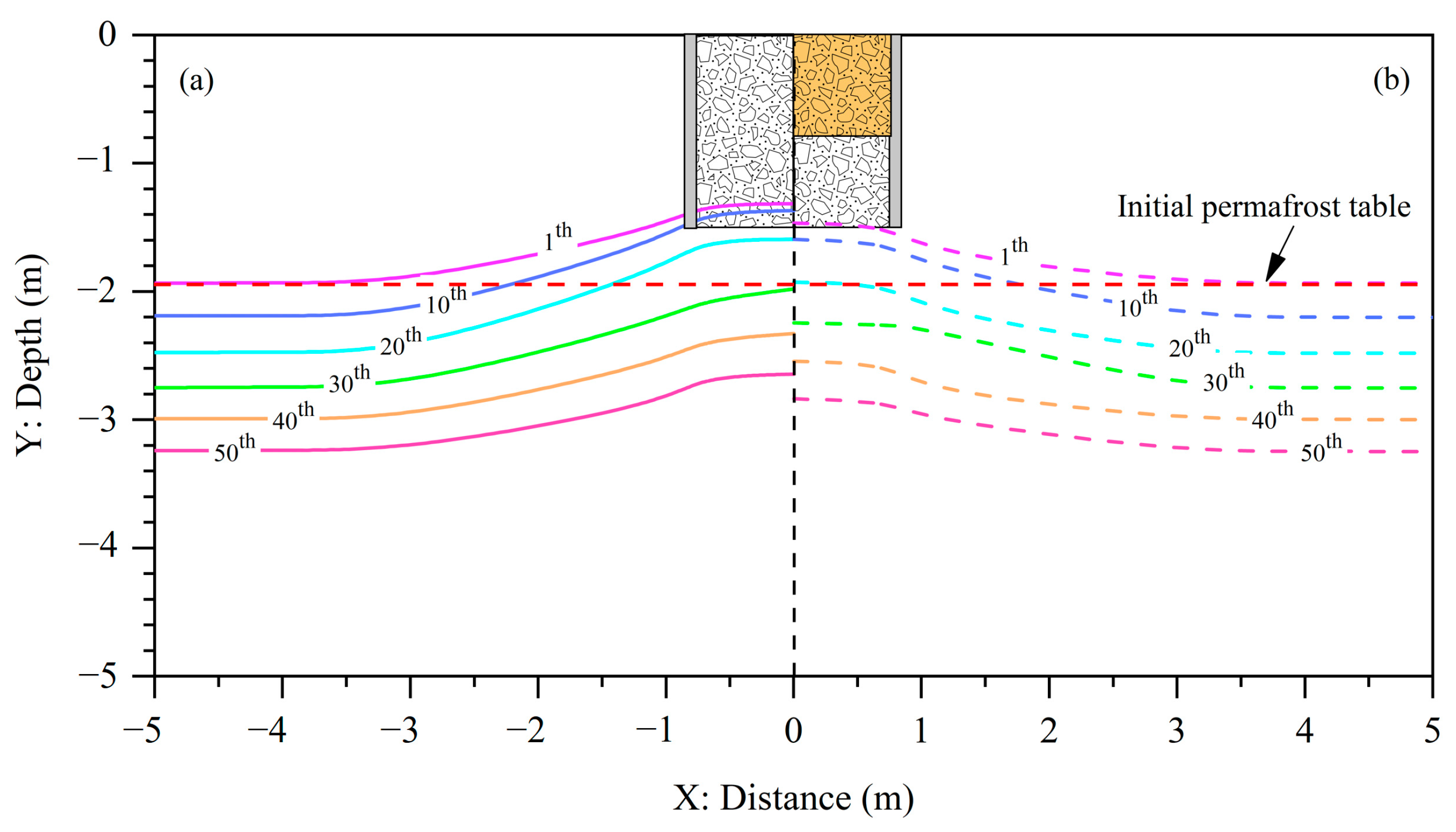
3.3.1. Variation in the Permafrost Table
3.3.2. Variation in Heat Flux of the Shallow Soil Layer Beneath the PRL
3.3.3. Thermal Changes in the Deep Soil
4. Discussion
5. Conclusions
- (1)
- The accuracy of the numerical model was verified using field tests. Natural convection within the closed PRL occurred only in cold seasons, and the convection strength was related to the effective convection height of the rock layer. As the thickness of sand filling increased, the Tac allowing natural convection to occur increased, and the Ra number decreased, which caused the weakening of the duration and intensity of natural convection.
- (2)
- Under a warming scenario of 0.052 °C·a−1, the cooling performance of a PRL can offset the adverse impacts of climate warming and raise the permafrost table during the first 20 years of operation. However, the cooling performance of the PRL diminishes with the increase in the operation year, and the underlying permafrost continues to degrade over the next several decades.
- (3)
- A closed PRL is more suitable for cooling measures of the subgrade in permafrost regions with colder MAATs. In the context of climate change and sand damage, the cooling effect of a PRL on the permafrost can no longer meet the long-term requirements.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Biskaborn, B.; Smith, S.; Noetzli, J. Permafrost is warming at a global scale. Nat. Commun. 2019, 10, 264. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Zou, D.; Hu, G.; Wu, T.; Du, E.; Liu, G.; Xiao, Y.; Li, R.; Pang, Q.; Qiao, Y.; et al. A synthesis dataset of permafrost thermal state for the Qinghai–Tibet (Xizang) Plateau, China. Earth Syst. Sci. Data 2021, 13, 4207–4218. [Google Scholar] [CrossRef]
- Cheng, G. A roadbed cooling approach for the construction of Qinghai–Tibet Railway. Cold Reg. Sci. Technol. 2005, 42, 169–176. [Google Scholar] [CrossRef]
- Malenfant-Lepage, J.; Doré, G.; Fortier, D.; Murchison, P. Thermal performance of the permafrost protection techniques at Beaver Creek experimental road site, Yukon, Canada. In Proceedings of the 10th International Conference on Permafrost, Salekhard, Russia, 25–29 June 2012; pp. 261–266. [Google Scholar]
- Dong, Y.; Pei, W.; Liu, G.; Jin, L.; Chen, D. In-situ experimental and numerical investigation on the cooling effect of a multi-lane embankment with combined crushed-rock interlayer and ventilated ducts in permafrost regions. Cold Reg. Sci. Technol. 2014, 104, 97–105. [Google Scholar] [CrossRef]
- Darrow, M.; Jensen, D. Modeling the performance of an air convection embankment (ACE) with thermal berm over ice-rich permafrost, Lost Chicken Creek, Alaska. Cold Reg. Sci. Technol. 2016, 130, 43–58. [Google Scholar] [CrossRef]
- Ma, Q.; Luo, X.; Gao, J.; Sun, W.; Li, Y.; Lan, T. Numerical evaluation for cooling performance of a composite measure on expressway embankment with shady and sunny slopes in permafrost regions. Energy 2022, 244, 123194. [Google Scholar] [CrossRef]
- Xie, S.; Qu, J.; Lai, Y.; Xu, X.; Pang, Y. Key evidence of the role of desertification in protecting the underlying permafrost in the Qinghai–Tibet Plateau. Sci. Rep. 2015, 5, 15152. [Google Scholar] [CrossRef]
- Xie, S.; Qu, J.; Zhang, K.; Mu, Y.; Xu, X.; Pang, Y.; Wang, T. Hydrothermal variation and its influence on the desertified ground surface of Qinghai–Tibet Plateau. Appl. Therm. Eng. 2018, 131, 201–208. [Google Scholar] [CrossRef]
- Lan, T.; Luo, X.; Ma, Q.; Jiang, W.; Xia, H. Desertification Caused by Embankment Construction in Permafrost Environment on the Qinghai-Tibetan Plateau. Arab. J. Sci. Eng. 2023, 48, 583–599. [Google Scholar] [CrossRef]
- Doré, G.; Niu, F.; Brooks, H. Adaptation methods for transportation infrastructure built on degrading permafrost. Permafr. Periglac. Process. 2016, 27, 352–364. [Google Scholar] [CrossRef]
- Luo, J.; Niu, F.; Liu, M.; Lin, Z.; Yin, G. Field experimental study on long-term cooling and deformation characteristics of crushed-rock revetment embankment at the Qinghai-Tibet Railway. Appl. Therm. Eng. 2018, 139, 256–263. [Google Scholar] [CrossRef]
- Han, F.; Yu, W.; Ma, L.; Yi, X.; Zhang, X. Heat transfer and cold energy capacity properties of crushed-rock layer in cold sandy regions. Int. J. Therm. Sci. 2023, 189, 108286. [Google Scholar] [CrossRef]
- Sun, B.; Yang, L.; Liu, Q.; Wang, W.; Xu, X. Experimental study on cooling enhancement of crushed rock layer with perforated ventilation pipe under air-tight top surface. Cold Reg. Sci. Technol. 2011, 68, 150–161. [Google Scholar] [CrossRef]
- Zhang, M.; Lai, Y.; Zhang, J.; Sun, Z. Numerical study on cooling characteristics of two-phase closed thermosyphon embankment in permafrost regions. Cold Reg. Sci. Technol. 2011, 65, 203–210. [Google Scholar] [CrossRef]
- Yu, W.; Liu, W.; Chen, L.; Yi, X.; Han, F.; Hu, D. Evaluation of cooling effects of crushed rock under sand-filling and climate warming scenarios on the Tibet Plateau. Appl. Therm. Eng. 2016, 92, 130–136. [Google Scholar] [CrossRef]
- Chen, L.; Lai, Y.; Fortier, D.; Harris, S. Impacts of snow cover on the pattern and velocity of air flow in air convection embankments of sub-Arctic regions. Renew. Energy 2022, 199, 1033–1046. [Google Scholar] [CrossRef]
- Yang, X.; Ji, Z.; Zhang, P.; Qi, J. Model test and numerical simulation on the development of artificially freezing wall in sandy layers considering water seepage. Transp. Geotech. 2019, 21, 100293. [Google Scholar] [CrossRef]
- Li, M.; Ma, Q.; Luo, X.; Jiang, H.; Li, Y. The coupled moisture-heat process of a water-conveyance tunnel constructed by artificial ground freezing method. Cold Reg. Sci. Technol. 2021, 182, 103197. [Google Scholar] [CrossRef]
- Wicky, J.; Hauck, C. Numerical modelling of convective heat transport by air flow in permafrost talus slopes. Cryosphere 2017, 11, 1311–1325. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, X.; Li, S.; Wu, D.; Pei, W.; Lai, Y. Evaluating the cooling performance of crushed-rock interlayer embankments with unperforated and perforated ventilation ducts in permafrost regions. Energy 2015, 93, 874–881. [Google Scholar] [CrossRef]
- Goering, D. Passively cooled railway embankments for use in permafrost areas. J. Cold Reg. Eng. 2003, 17, 119–133. [Google Scholar] [CrossRef]
- Wu, Q.; Lu, Z.; Zhang, T.; Ma, W. Analysis of cooling effect of crushed rock-based embankment of the Qinghai-Xizang Railway. Cold Reg. Sci. Technol. 2008, 53, 271–282. [Google Scholar] [CrossRef]
- Xie, S.; Qu, J.; Xu, X.; Pang, Y. Interactions between freeze–thaw actions, wind erosion desertification, and permafrost in the Qinghai–Tibet Plateau. Nat. Hazards. 2017, 85, 829–850. [Google Scholar] [CrossRef]
- Athith, T.; Trilok, G.; Jadhav, P.; Gnanasekaran, N. Heat transfer optimization using genetic algorithm and artificial neural network in a heat exchanger with partially filled different high porosity metal foam. Mater. Today Proc. 2022, 51, 1642–1648. [Google Scholar] [CrossRef]
- Jadhav, P.; Trilok, G.; Gnanasekaran, N.; Mobedi, M. Performance score based multi-objective optimization for thermal design of partially filled high porosity metal foam pipes under forced convection. Int. J. Heat Mass Tran. 2022, 182, 121911. [Google Scholar] [CrossRef]
- Zhang, M.; Lai, Y.; Niu, F.; He, S. A numerical model of the coupled heat transfer for duct-ventilated embankment under wind action in cold regions and its application. Cold Reg. Sci. Technol. 2006, 45, 103–113. [Google Scholar] [CrossRef]
- Li, S.; Zhan, H.; Lai, Y.; Sun, Z.; Pei, W. The coupled moisture-heat process of permafrost around a thermokarst pond in Qinghai-Tibet Plateau under global warming. J. Geophys. Res. Earth Surf. 2014, 119, 836–853. [Google Scholar] [CrossRef]
- Lai, Y.; Zhang, L.; Zhang, S.; Mi, L. Cooling effect of ripped-stone embankments on Qing-Tibet railway under climatic warming. Chin. Sci. Bull. 2003, 48, 598–604. [Google Scholar] [CrossRef]
- Tao, W.Q. Numerical Heat Transfer, 2nd ed.; Xi’an Jiaotong University Press: Xi’an, China, 2004; pp. 6–14. [Google Scholar]
- Ren, X.; Niu, F.; Yu, Q.; Yin, G. Research progress of soil thermal conductivity and its predictive models. Cold Reg. Sci. Technol. 2024, 217, 104027. [Google Scholar] [CrossRef]
- Lu, Y.; Yu, W.; Hu, D.; Liu, W. Experimental Study on the Thermal Conductivity of Aeolian Sand from the Tibetan Plateau. Cold Reg. Sci. Technol. 2018, 146, 1–8. [Google Scholar] [CrossRef]
- Wen, Z.; Ma, W.; Feng, W.; Deng, Y.; Wang, D.; Fan, Z.; Zhou, C. Experimental study on unfrozen water content and soil matric potential of Qinghai-Tibetan silty clay. Environ. Earth Sci. 2012, 66, 1467–1476. [Google Scholar] [CrossRef]
- Tsilingiris, P.T. Thermophysical and transport properties of humid air at temperature range between 0 and 100 °C. Energy Convers. Manag. 2008, 49, 1098–1110. [Google Scholar] [CrossRef]
- Lunardini, V. Theory of n-factors and correlation of data, Proceedings of the Third International Conference on Permafrost. Natl. Res. Counc. Can. Ott. 1978, 1, 40–46. [Google Scholar]
- Williams, T.; Pomeroy, J.; Janowicz, J.; Carey, S.; Rasouli, K.; Quinton, W. A radiative–conductive–convective approach to calculate thaw season ground surface temperatures for modelling frost table dynamics. Hydrol. Process. 2015, 29, 3954–3965. [Google Scholar] [CrossRef]
- Hou, Y.; Wu, Q.; Wang, K.; Ye, Z. Numerical evaluation for protecting and reinforcing effect of a new designed crushed rock revetment on Qinghaie–Tibet Railway. Renew. Energ. 2020, 156, 645–654. [Google Scholar] [CrossRef]
- Qin, D.; Ding, Y.; Wang, S. A study of environment change and its impacts in western China. Earth Sci. Front. 2002, 9, 321–328. [Google Scholar]
- Zhang, M.; Min, K.; Wu, Q.; Zhang, J.; Harbor, J. A new method to determine the upper boundary condition for a permafrost thermal model: An example from the Qinghai-Tibet Plateau. Permafr. Periglac. Process. 2012, 23, 301–311. [Google Scholar] [CrossRef]
- Hidalgo, A.; Tello, L. Modeling and Numerical Simulation of the Thermal Interaction between Vegetation Cover and Soil. Mathematics 2022, 10, 338. [Google Scholar] [CrossRef]
- Liu, C.; Chong, X.; Qi, C.; Yao, Z.; Wei, Y.; Zhang, J.; Li, Y. Numerical investigation of thermal parameter characteristics of the airfield runway adherent layer in permafrost region of Northeast China. Case Stud. Therm. Eng. 2022, 33, 101985. [Google Scholar] [CrossRef]



| Lithology | Thermal Conductivity (W·m−1·°C−1) | Volumetric Heat Capacity (J·kg−1·°C−1) | Latent Heat (J·m−3) | ||
|---|---|---|---|---|---|
| Frozen | Unfrozen | Frozen | Unfrozen | ||
| Porous rock layer | 0.442 | 0.442 | 1.016 × 106 | 1.016 × 106 | 0 |
| Sand-filled porous rock layer | 1.188 | 1.188 | 1.446 × 106 | 1.446 × 106 | 0 |
| Gravel soil | 2.720 | 1.870 | 1.864 × 106 | 2.401 × 106 | 2.338 × 107 |
| Weathered mudstone | 1.844 | 1.474 | 2.122 × 106 | 2.413 × 106 | 3.811 × 107 |
| Thermal insulation board | 0.029 | 0.029 | 2.406 × 105 | 2.406 × 105 | 0 |
| Physical Domain | cp (J·kg−1·°C−1) | λa (W·m−1·°C−1) | ρ (kg·m−3) | μ (kg·m−1·s−1) |
|---|---|---|---|---|
| Air | 1.004 × 103 | 0.02 | 0.641 | 1.75 × 10−5 |
| Case | MAAT (°C) | Climate Change | Sand-Filling Thickness (cm) |
|---|---|---|---|
| Case 1 | −3.5 | Warm | 0, 20, 50, 80, 120 |
| Case 2 | −4.5 | Warm | 0, 20, 50, 80, 120 |
| Case 3 | −5.5 | Warm | 0, 20, 50, 80, 120 |
| Case 4 | −3.5 | Unwarm | 0, 20, 50, 80, 120 |
| Time | Cases | 0 cm | 20 cm | 50 cm | 80 cm |
|---|---|---|---|---|---|
| 1a | ΔTac (°C) | 3.50 | 4.49 | 5.50 | 7.92 |
| Natural convection period | 11/1−2/28 | 11/7−2/25 | 11/6−2/16 | 12/13−1/13 | |
| Maximum Ra number | 124.59 | 99.33 | 68.85 | 43.56 | |
| 30a | ΔTac (°C) | 3.47 | 4.47 | 5.48 | 7.90 |
| Natural convection period | 11/1−2/28 | 11/7−2/22 | 11/16−2/13 | 12/13−1/13 | |
| Maximum Ra number | 123.37 | 98.55 | 68.52 | 43.33 | |
| 50a | ΔTac (°C) | 3.92 | 4.44 | 5.58 | 7.98 |
| Natural convection period | 11/7−2/30 | 11/11−2/26 | 11/21−2/17 | 11/22−2/27 | |
| Maximum Ra number | 121.99 | 98.75 | 68.18 | 44.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, K.; Huang, Y.; Han, F.; Yang, Q.; Yu, W.; Cheng, L.; Cao, H. Numerical Simulation of Heat Transfer of Porous Rock Layers in Cold Sandy Regions. Atmosphere 2023, 14, 1812. https://doi.org/10.3390/atmos14121812
Qiu K, Huang Y, Han F, Yang Q, Yu W, Cheng L, Cao H. Numerical Simulation of Heat Transfer of Porous Rock Layers in Cold Sandy Regions. Atmosphere. 2023; 14(12):1812. https://doi.org/10.3390/atmos14121812
Chicago/Turabian StyleQiu, Kaichi, Yong Huang, Fenglei Han, Qiuju Yang, Wenbing Yu, Lu Cheng, and Hang Cao. 2023. "Numerical Simulation of Heat Transfer of Porous Rock Layers in Cold Sandy Regions" Atmosphere 14, no. 12: 1812. https://doi.org/10.3390/atmos14121812
APA StyleQiu, K., Huang, Y., Han, F., Yang, Q., Yu, W., Cheng, L., & Cao, H. (2023). Numerical Simulation of Heat Transfer of Porous Rock Layers in Cold Sandy Regions. Atmosphere, 14(12), 1812. https://doi.org/10.3390/atmos14121812








