A Numerical Simulation Study of Secondary Ice Productions in a Squall Line Case
Abstract
:1. Introduction
2. Case and Methods
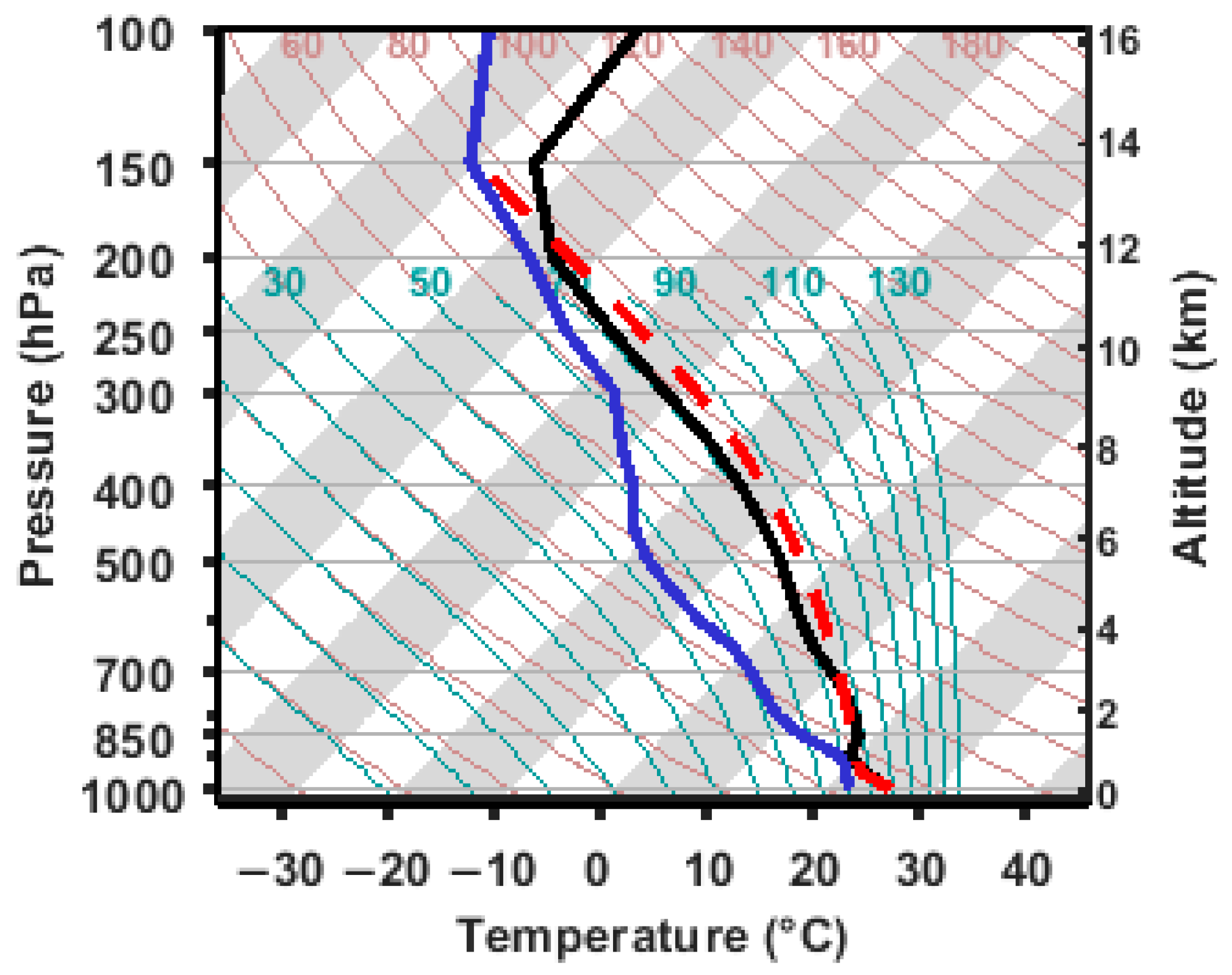
2.1. Observation Data
2.2. Overview of the Case
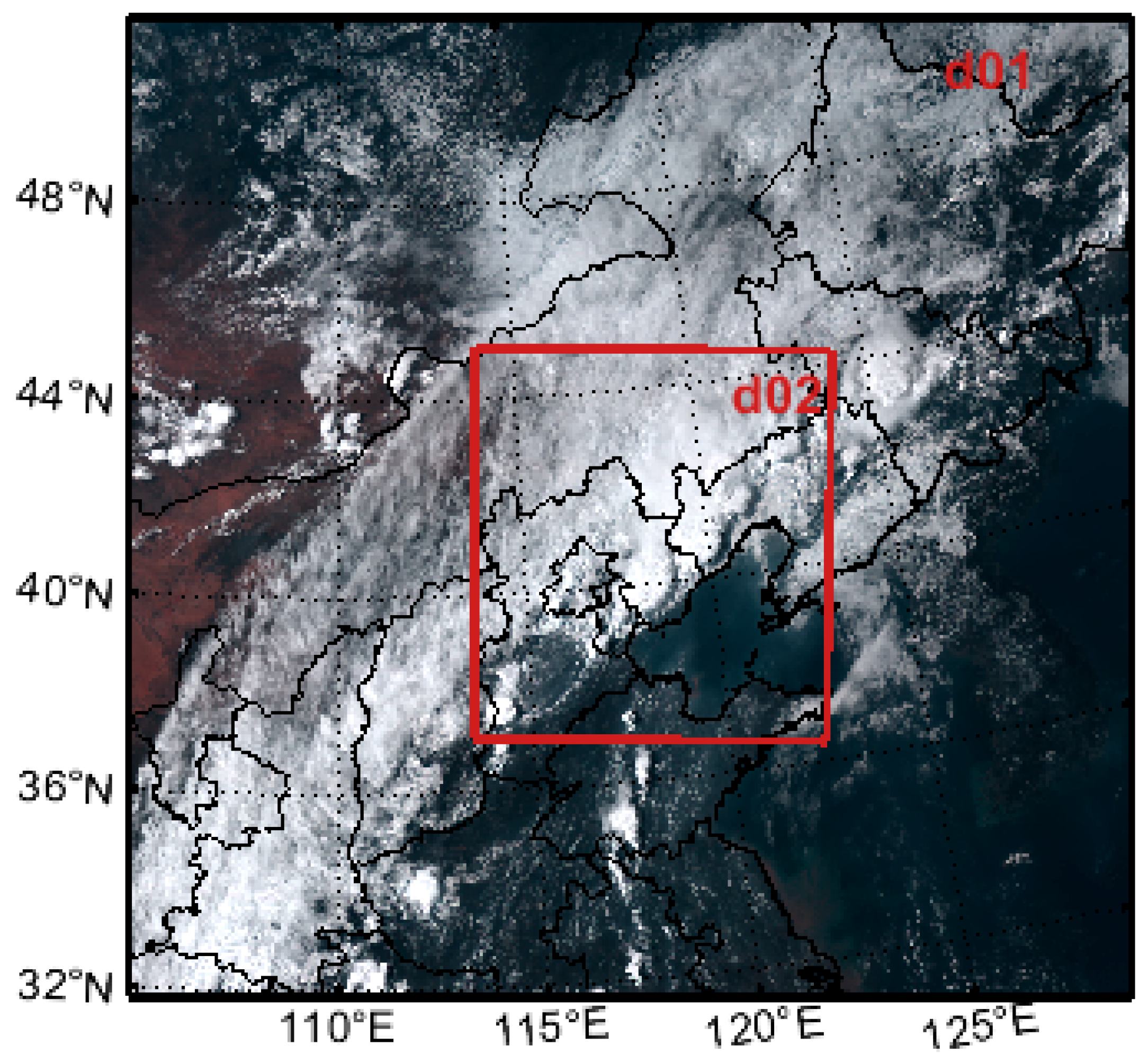
2.3. Model Setup
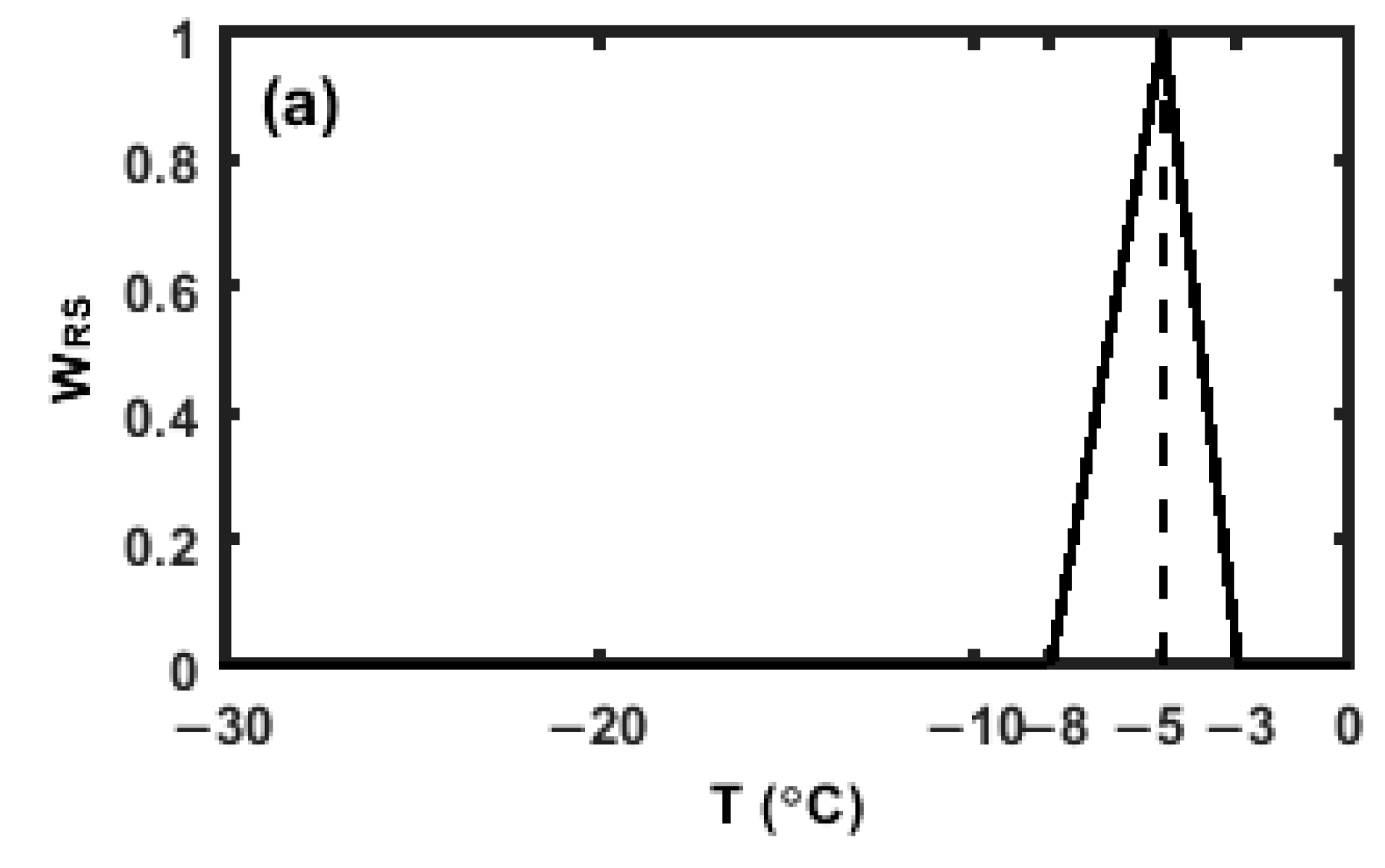
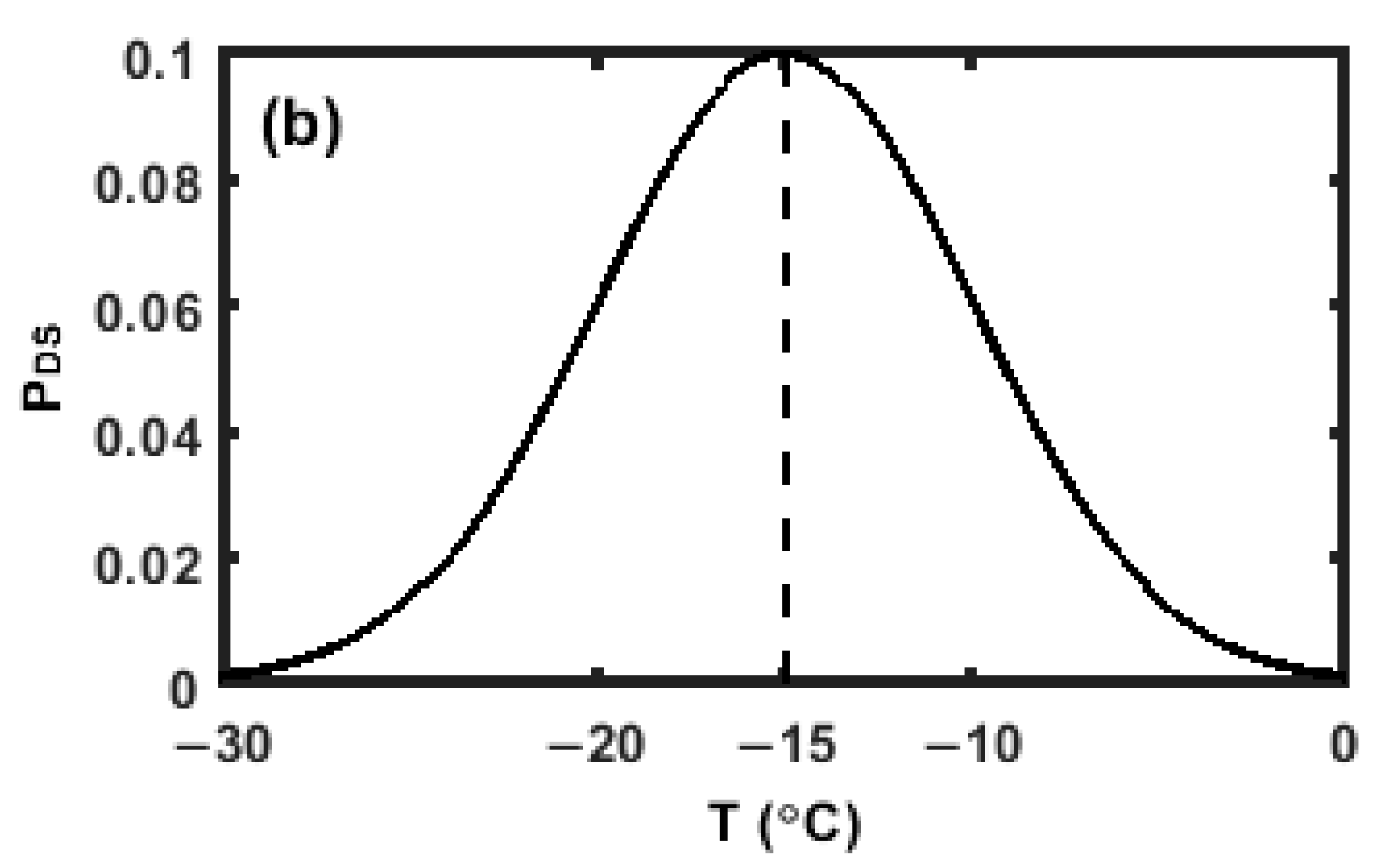
2.4. Parameterizations of SIPs
3. Comparisons between the Observations and Simulations
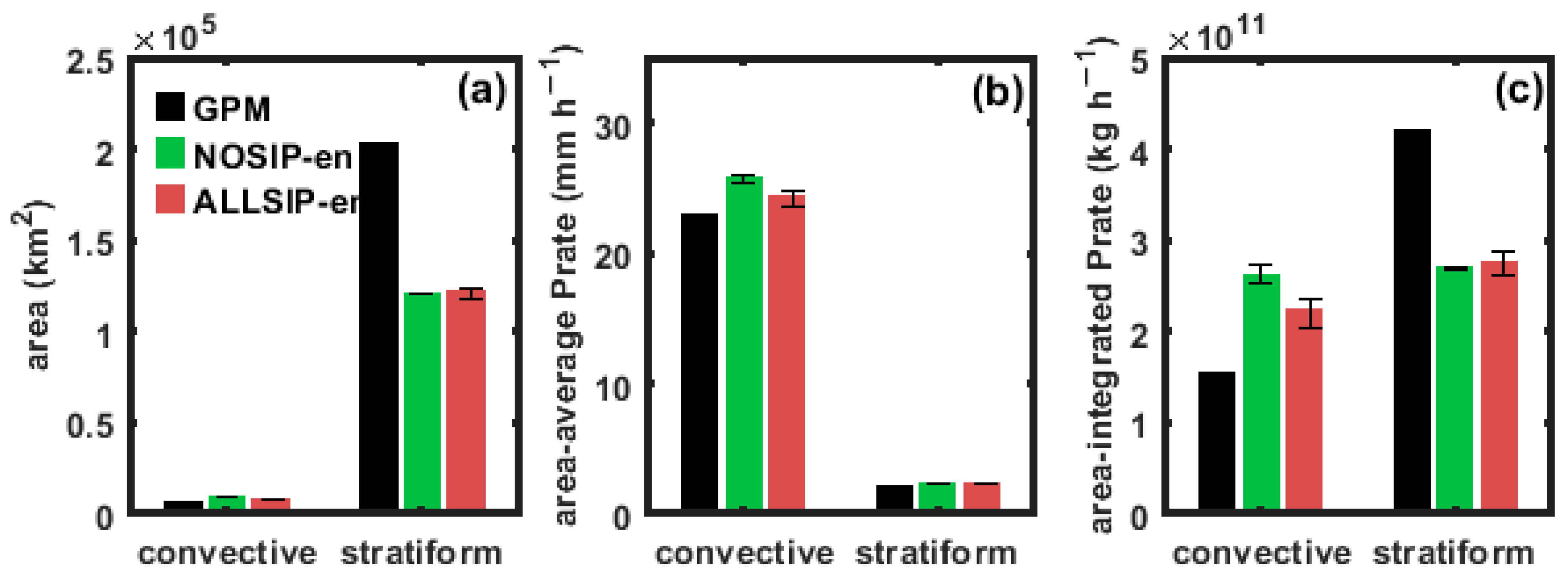
3.1. Comparison of Precipitation between Observations and Simulations
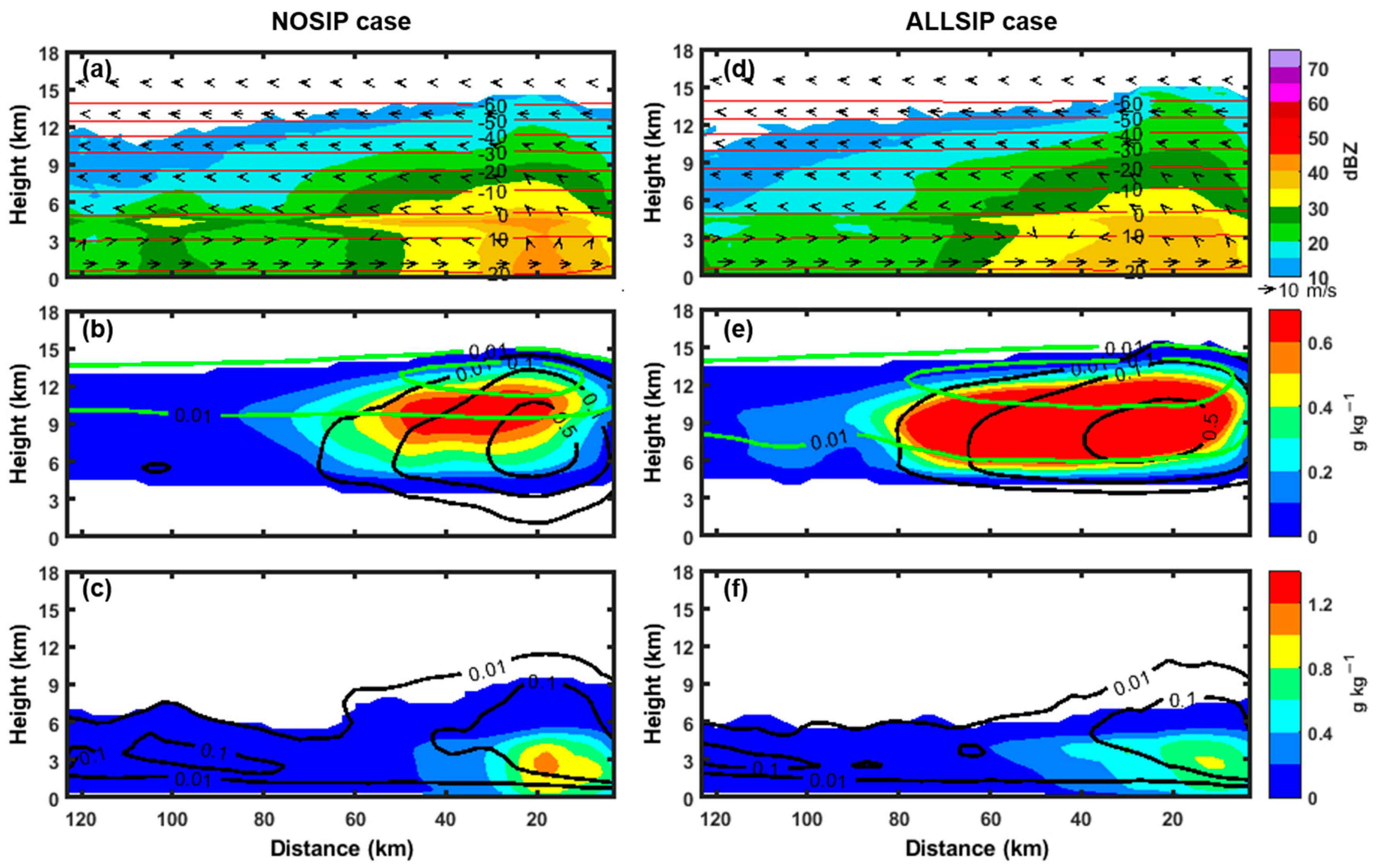
3.2. Comparison of Radar Reflectivity between Observations and Simulations
3.3. Model Uncertainty
4. Microphysical Properties and Feedback
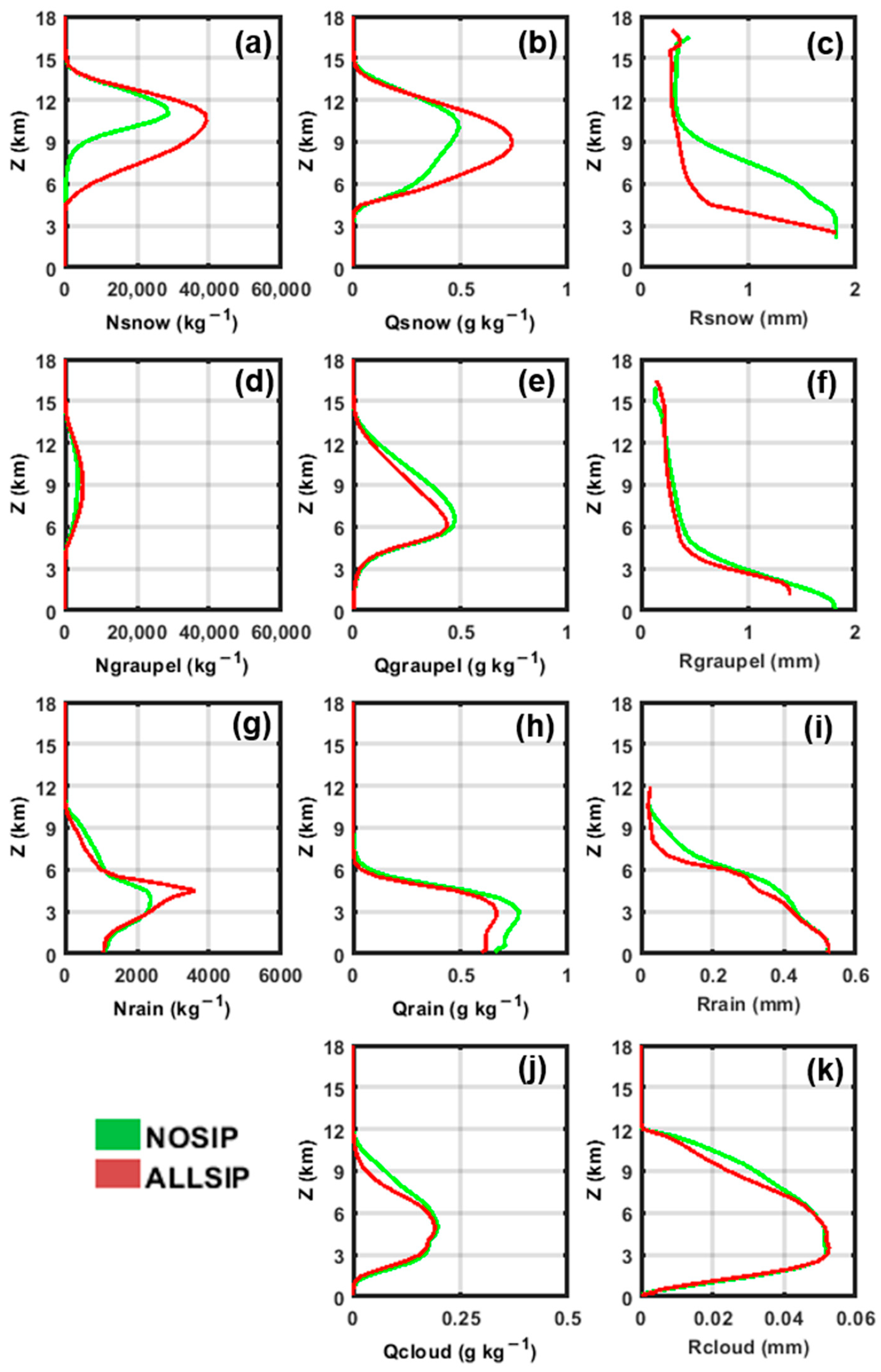
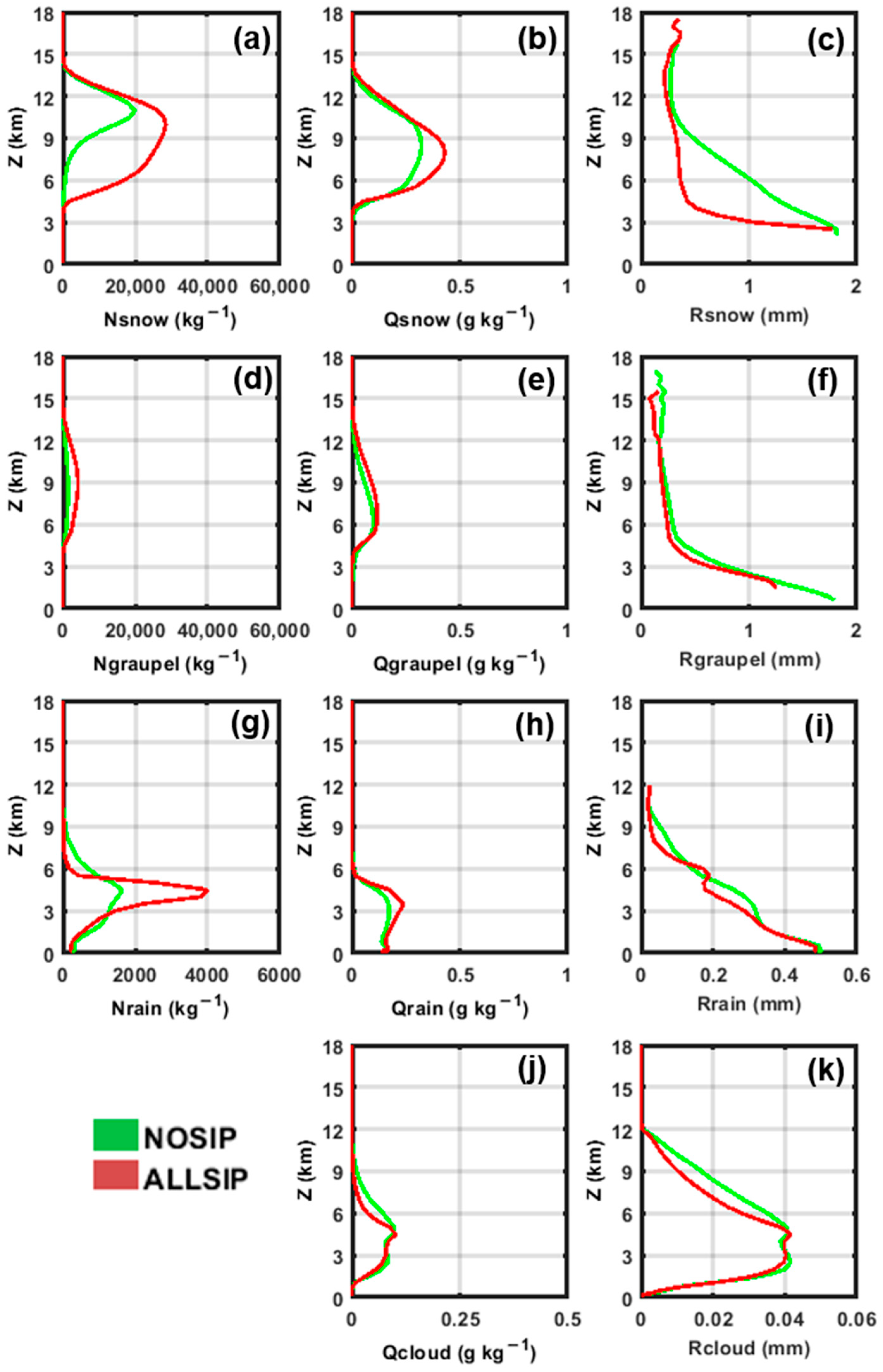
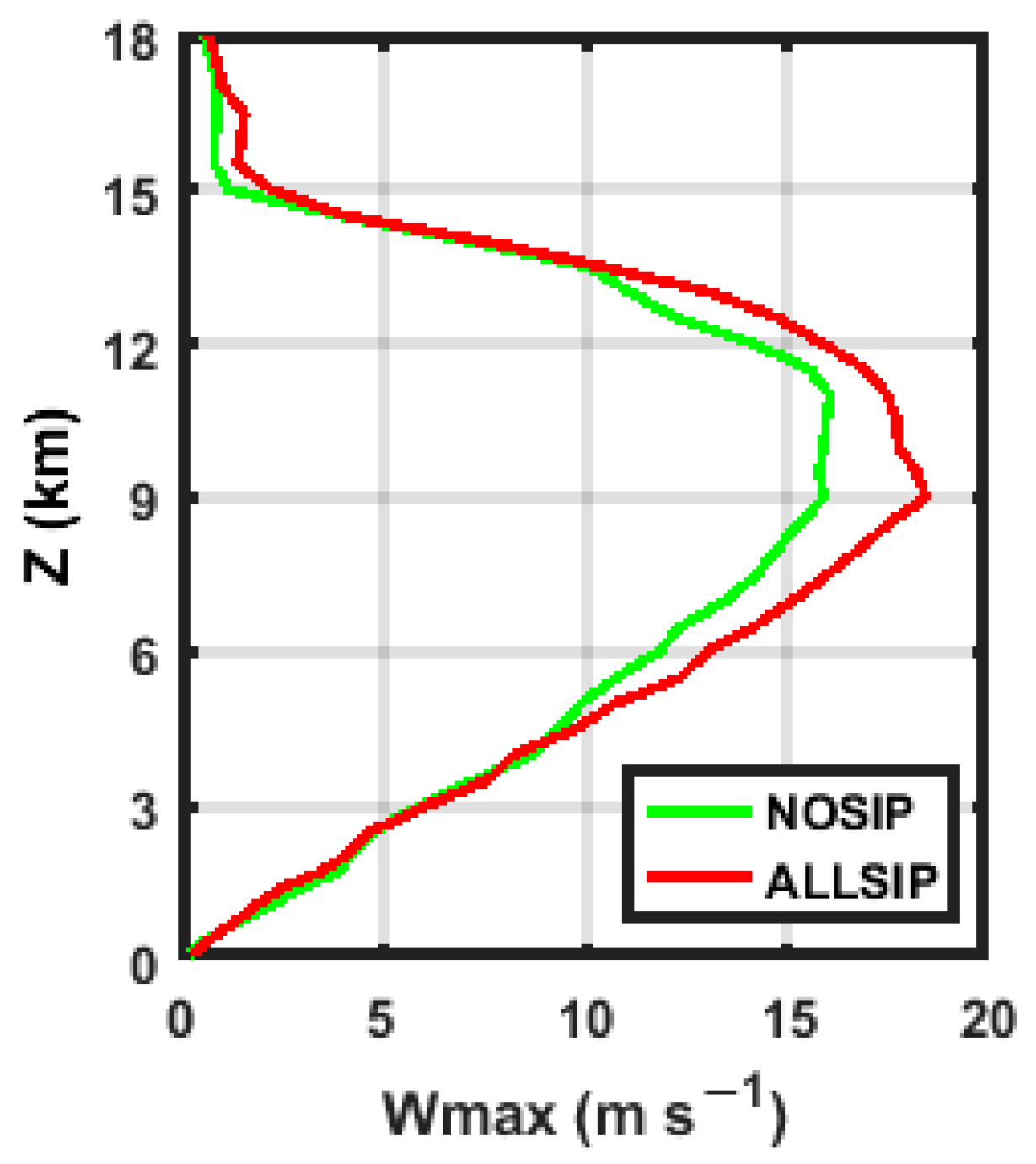
4.1. General Features of the Simulated Cases
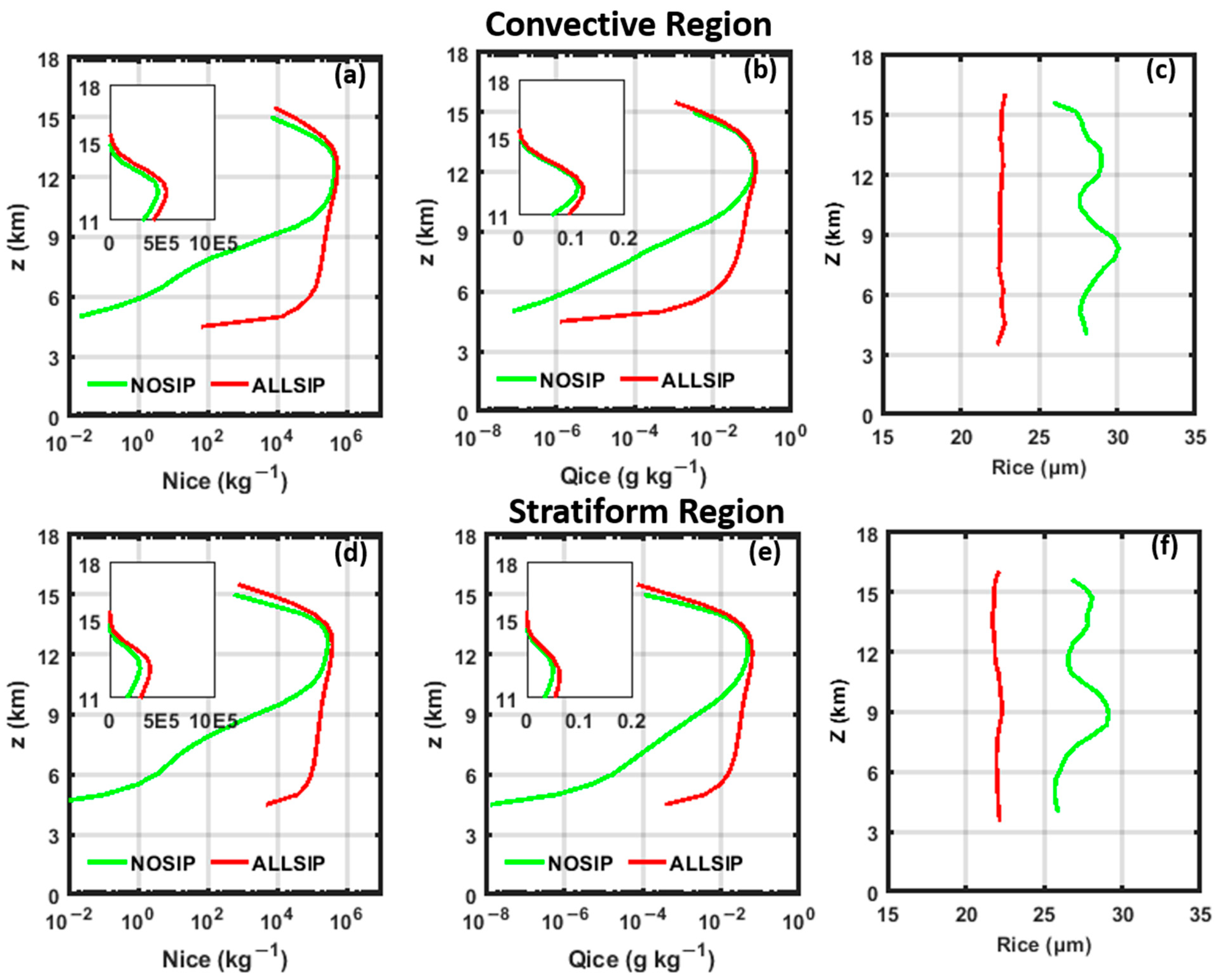
4.2. Ice Crystal Properties
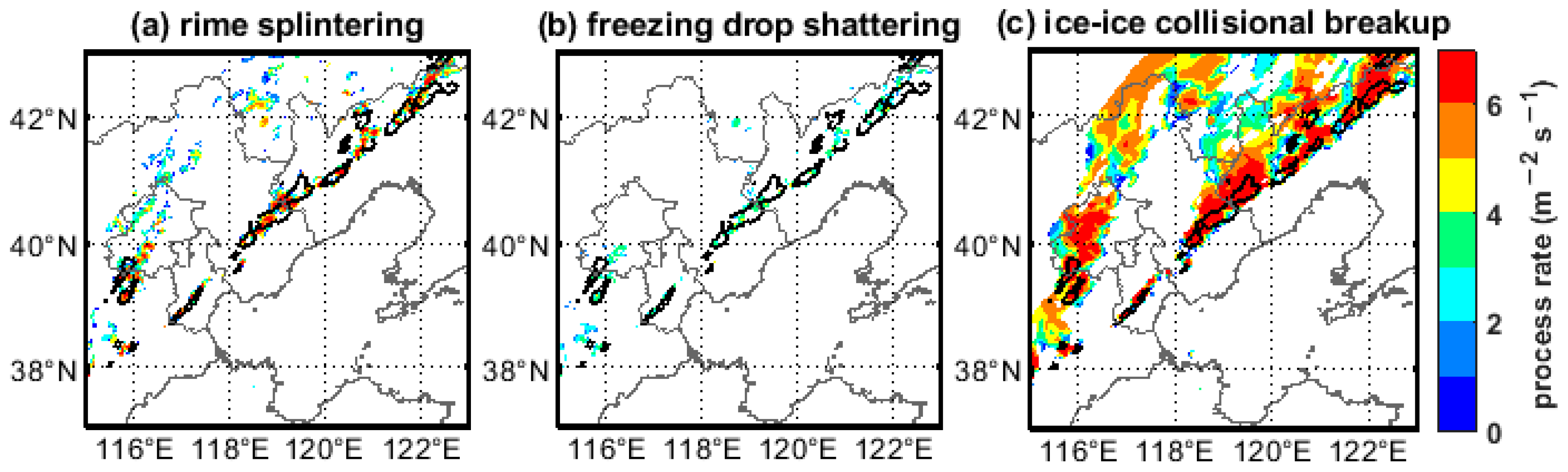
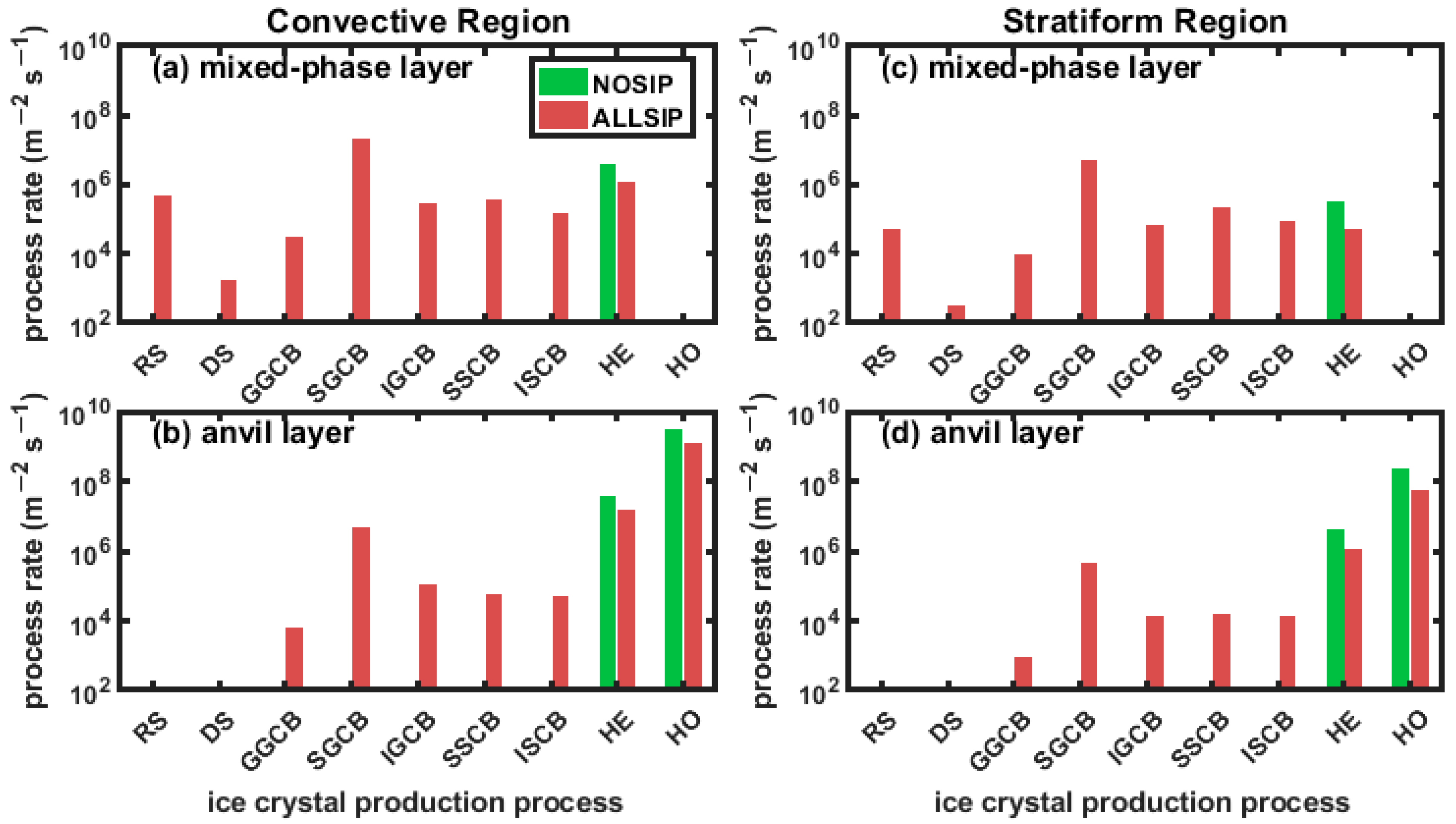
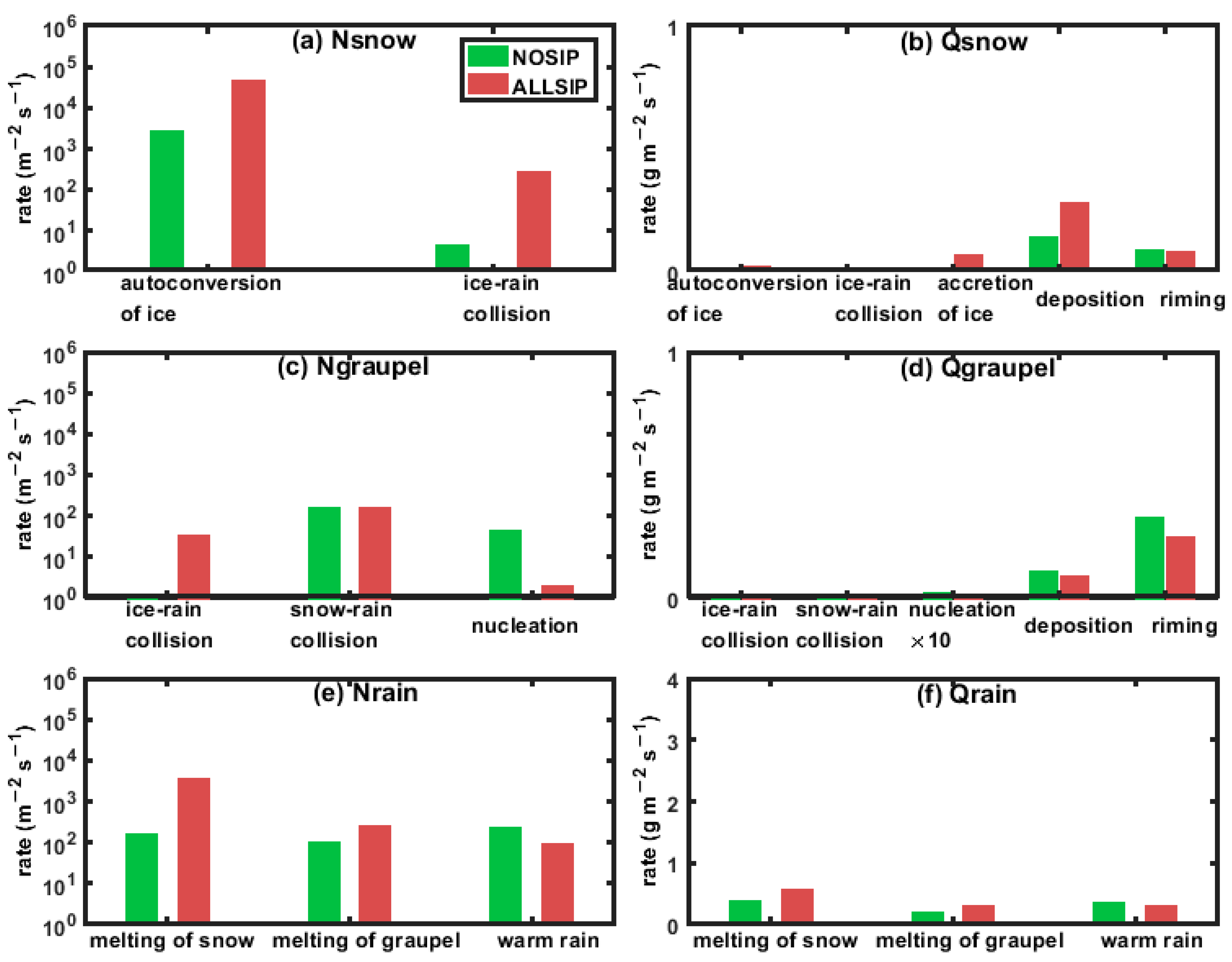
4.3. Secondary and Primary Ice Production Rates
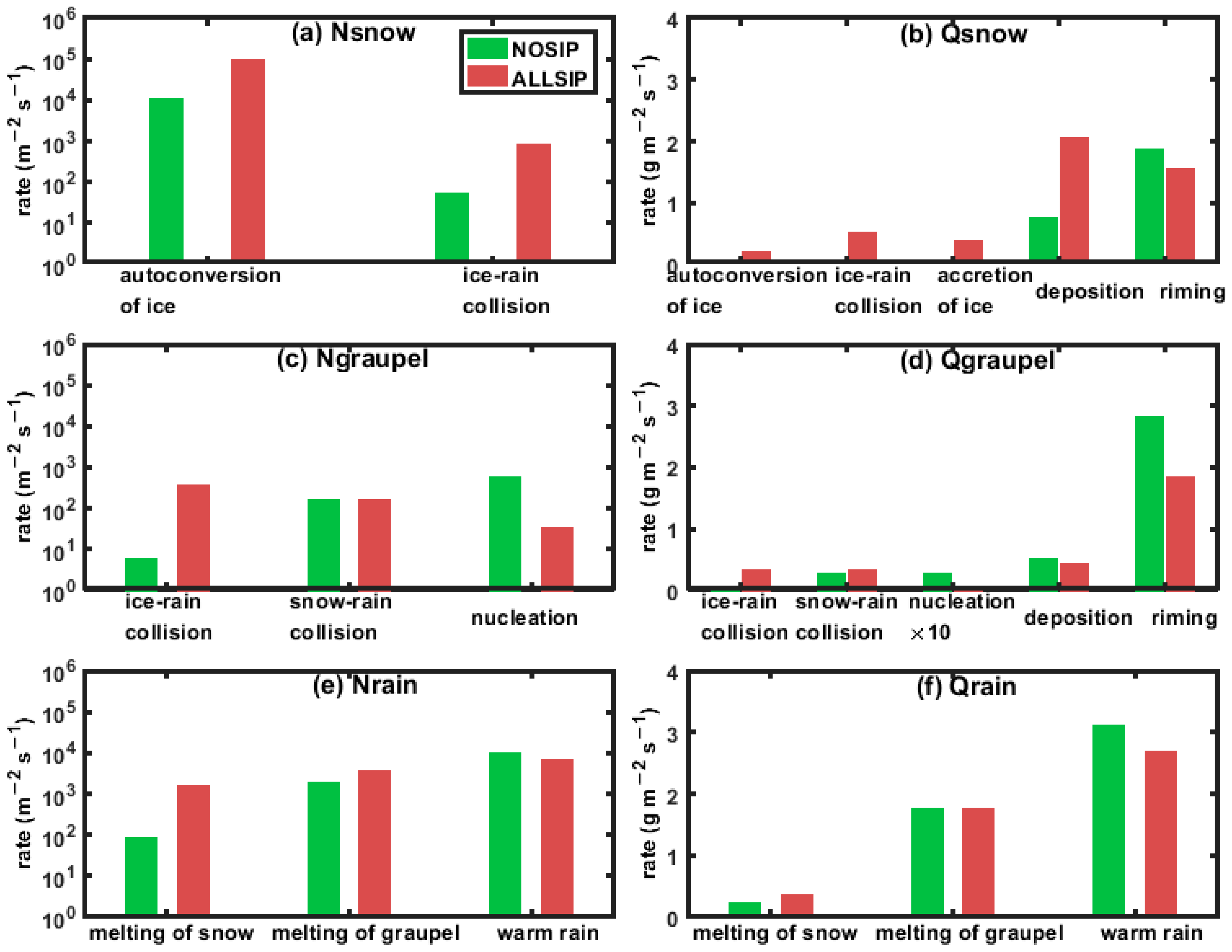
4.4. SIP-Related Microphysical Feedbacks in the Convective Region
4.5. SIP-Related Microphysical Feedbacks in the Stratiform Region
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clark, P.D.; Choularton, T.W.; Brown, P.R.A.; Field, P.R.; Illingworth, A.J.; Hogan, R.J. Numerical modelling of mixed-phase frontal clouds observed during the CWVC project. Q. J. R. Meteorol. Soc. 2005, 131, 1677–1693. [Google Scholar] [CrossRef]
- Crosier, J.; Choularton, T.W.; Westbrook, C.D.; Blyth, A.M.; Bower, K.N.; Connolly, P.J.; Dearden, C.; Gallagher, M.W.; Cui, Z.; Nicol, J.C. Microphysical Properties of Cold Frontal Rainbands. Q. J. R. Meteorol. Soc. 2013, 140, 1257–1268. [Google Scholar] [CrossRef]
- Field, P.R.; Lawson, R.P.; Brown, P.R.A.; Lloyd, G.; Westbrook, C.; Moisseev, D.; Miltenberger, A.; Nenes, A.; Blyth, A.; Choularton, T.; et al. Chapter 7. Secondary Ice Production-current state of the science and recommendations for the future. Meteorol. Monogr. 2017, 58, 7.1–7.20. [Google Scholar] [CrossRef]
- Finlon, J.A.; Rauber, R.M.; Wu, W.; Zaremba, T.J.; McFarquhar, G.M.; Nesbitt, S.W.; Schnaiter, M.; Järvinen, E.; Waitz, F.; Hill, T.C.J.; et al. Structure of an Atmospheric River Over Australia and the Southern Ocean: II. Microphysical Evolution. J. Geophys. Res. Atmos. 2020, 125, e2020JD032514. [Google Scholar] [CrossRef]
- Hobbs, P.V.; Rangno, A.L. Ice Particle Concentrations in Clouds. J. Atmos. Sci. 1985, 42, 2523–2549. [Google Scholar] [CrossRef]
- Ladino, L.A.; Korolev, A.; Heckman, I.; Wolde, M.; Fridlind, A.M.; Ackerman, A.S. On the role of ice-nucleating aerosol in the formation of ice particles in tropical mesoscale convective systems. Geophys. Res. Lett. 2017, 44, 1574–1582. [Google Scholar] [CrossRef] [PubMed]
- Lasher-Trapp, S.; Leon, D.C.; DeMott, P.J.; Villanueva-Birriel, C.M.; Johnson, A.V.; Moser, D.H.; Tully, C.S.; Wu, W. A Multisensor Investigation of Rime Splintering in Tropical Maritime Cumuli. J. Atmos. Sci. 2016, 73, 2547–2564. [Google Scholar] [CrossRef]
- Hallett, J.; Mossop, S.C. Production of Secondary Ice Particles During Riming Process. Nature 1974, 249, 26–28. [Google Scholar] [CrossRef]
- Langham, E.J.; Mason, B.J. The heterogeneous and homogeneous nucleation of supercooled water. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1958, 247, 493–504. [Google Scholar]
- Takahashi, T.; Nagao, Y.; Kushiyama, Y. Possible High Ice Particle Production during Graupel–Graupel Collisions. J. Atmos. Sci. 1995, 52, 4523–4527. [Google Scholar] [CrossRef]
- Vardiman, L. The Generation of Secondary Ice Particles in Clouds by Crystal–Crystal Collision. J. Atmos. Sci. 1978, 35, 2168–2180. [Google Scholar] [CrossRef]
- Bacon, N.J.; Swanson, B.D.; Baker, M.B.; Davis, E.J. Breakup of levitated frost particles. J. Geophys. Res. Atmos. 1998, 103, 13763–13775. [Google Scholar] [CrossRef]
- Oraltay, R.; Hallett, J. Evaporation and melting of ice crystals: A laboratory study. Atmos. Res. 1989, 24, 169–189. [Google Scholar] [CrossRef]
- Dye, J.E.; Hobbs, P.V. Influence of environmental parameters on freezing and fragmentation of suspended water drops. J. Atmos. Sci. 1968, 25, 82–96. [Google Scholar] [CrossRef]
- King, W.D.; Fletcher, N.H. Thermal Shock as an Ice Multiplication Mechanism. Part I. Theory. J. Atmos. Sci. 1976, 33, 85–96. [Google Scholar] [CrossRef]
- Baker, B.A. On the Nucleation of Ice in Highly Supersaturated Regions of Clouds. J. Atmos. Sci. 1991, 48, 1904–1907. [Google Scholar] [CrossRef]
- Korolev, A.; Leisner, T. Review of experimental studies of secondary ice production. Atmos. Meas. Tech. 2020, 20, 11767–11797. [Google Scholar] [CrossRef]
- Heymsfield, A.; Willis, P. Cloud Conditions Favoring Secondary Ice Particle Production in Tropical Maritime Convection. J. Atmos. Sci. 2014, 71, 4500–4526. [Google Scholar] [CrossRef]
- Korolev, A.; Heckman, I.; Wolde, M.; Ackerman, A.S.; Fridlind, A.M.; Ladino, L.A.; Lawson, R.P.; Milbrandt, J.; Williams, E. A new look at the environmental conditions favorable to secondary ice production. Atmos. Meas. Tech. 2020, 20, 1391–1429. [Google Scholar] [CrossRef]
- Phillips VTJBlyth, A.M.; Brown, P.R.A.; Choularton, T.W.; Latham, J. The glaciation of a cumulus cloud over New Mexico. Q. J. R. Meteorol. Soc. 2001, 127, 1513–1534. [Google Scholar] [CrossRef]
- Lawson, R.P.; Woods, S.; Morrison, H. The Microphysics of Ice and Precipitation Development in Tropical Cumulus Clouds. J. Atmos. Sci. 2015, 72, 2429–2445. [Google Scholar] [CrossRef]
- Phillips, V.T.J.; Patade, S.; Gutierrez, J.; Bansemer, A. Secondary Ice Production by Fragmentation of Freezing Drops: Formulation and Theory. J. Atmos. Sci. 2018, 75, 3031–3070. [Google Scholar] [CrossRef]
- Hoarau, T.; Pinty, J.-P.; Barthe, C. A representation of the collisional ice break-up process in the two-moment microphysics LIMA v1.0 scheme of Meso-NH. Geosci. Model Dev. 2018, 11, 4269–4289. [Google Scholar] [CrossRef]
- Phillips, V.T.J.; Yano, J.-I.; Khain, A. Ice Multiplication by Breakup in Ice–Ice Collisions. Part I: Theoretical Formulation. J. Atmos. Sci. 2017, 74, 1705–1719. [Google Scholar]
- Sullivan, S.C.; Barthlott, C.; Crosier, J.; Zhukov, I.; Nenes, A.; Hoose, C. The effect of secondary ice production parameterization on the simulation of a cold frontal rainband. Atmos. Meas. Tech. 2018, 18, 16461–16480. [Google Scholar] [CrossRef]
- Blyth, A.M.; Latham, J. Development of ice and precipitation in New Mexican summertime cumulus clouds. Q. J. R. Meteorol. Soc. 1993, 119, 91–120. [Google Scholar] [CrossRef]
- Huang, Y.; Blyth, A.M.; Brown, P.R.A.; Choularton, T.W.; Connolly, P.; Gadian, A.M.; Jones, H.; Latham, J.; Cui, Z.; Carslaw, K. The development of ice in a cumulus cloud over southwest England. New J. Phys. 2008, 10, 105021. [Google Scholar] [CrossRef]
- Lasher-Trapp, S.; Scott, E.L.; Järvinen, E.; Schnaiter, M.; Waitz, F.; DeMott, P.J.; McCluskey, C.S.; Hill, T.C.J. Observations and Modeling of Rime Splintering in Southern Ocean Cumuli. J. Geophys. Res. Atmos. 2021, 126, e2021JD035479. [Google Scholar] [CrossRef]
- Crosier, J.; Bower, K.N.; Choularton, T.W.; Westbrook, C.D.; Connolly, P.J.; Cui, Z.Q.; Crawford, I.P.; Capes, G.L.; Coe, H.; Dorsey, J.R.; et al. Observations of ice multiplication in a weakly convective cell embedded in supercooled mid-level stratus. Atmos. Meas. Tech. 2011, 11, 257–273. [Google Scholar] [CrossRef]
- Hogan, R.J.; Field, P.R.; Illingworth, A.J.; Cotton, R.J.; Choularton, T.W. Properties of embedded convection in warm-frontal mixed-phase cloud from aircraft and polarimetric radar. Q. J. R. Meteorol. Soc. 2002, 128, 451–476. [Google Scholar] [CrossRef]
- Hou, T.; Lei, H.; He, Y.; Yang, J.; Zhao, Z.; Hu, Z. Aircraft Measurements of the Microphysical Properties of Stratiform Clouds with Embedded Convection. Adv. Atmos. Sci. 2021, 38, 966–982. [Google Scholar] [CrossRef]
- Qu, Y.; Khain, A.; Vaughan, P.; Eyal, I.; Shpund, J.S.; Patade, S.; Chen, B. The Role of Ice Splintering on Microphysics of Deep Convective Clouds Forming Under Different Aerosol Conditions: Simulations Using the Model With Spectral Biwithcrophysics. J. Geophys. Res. Atmos. 2020, 125, e2019JD031312. [Google Scholar] [CrossRef]
- Qu, Z.; Korolev, A.; Milbrandt, J.A.; Heckman, I.; Huang, Y.; McFarquhar, G.M.; Morrison, H.; Wolde, M.; Nguyen, C. The impacts of secondary ice production on microphysics and dynamics in tropical convection. Atmos. Meas. Tech. 2022, 22, 12287–12310. [Google Scholar] [CrossRef]
- Aleksić, N.M.; Farley, R.; Orville, H. A numerical cloud model study of the Hallett-Mossop ice multiplication process in strong convection. Atmos. Res. 1989, 23, 1–30. [Google Scholar] [CrossRef]
- Phillips, V.T.J.; Choularton, T.W.; Blyth, A.M.; Latham, J. The influence of aerosol concentrations on the glaciation and precipitation of a cumulus cloud. Q. J. R. Meteorol. Soc. 2002, 128, 951–971. [Google Scholar] [CrossRef]
- Keinert, A.; Spannagel, D.; Leisner, T.; Kiselev, A. Secondary Ice Production upon Freezing of Freely Falling Drizzle Droplets. J. Atmos. Sci. 2020, 77, 2959–2967. [Google Scholar] [CrossRef]
- Lauber, A.; Kiselev, A.; Pander, T.; Handmann, P.; Leisner, T. Secondary Ice Formation during Freezing of Levitated Droplets. J. Atmos. Sci. 2018, 75, 2815–2826. [Google Scholar] [CrossRef]
- Wildeman, S.; Sterl, S.; Sun, C.; Lohse, D. Fast Dynamics of Water Droplets Freezing from the Outside In. Phys. Rev. Lett. 2017, 118, 084101. [Google Scholar] [CrossRef]
- Lawson, R.P.; Gurganus, C.; Woods, S.; Bruintjes, R. Aircraft Observations of Cumulus Microphysics Ranging from the Tropics to Midlatitudes: Implications for a “New” Secondary Ice Process. J. Atmos. Sci. 2017, 74, 2899–2920. [Google Scholar] [CrossRef]
- Rangno, A.L. Fragmentation of Freezing Drops in Shallow Maritime Frontal Clouds. J. Atmos. Sci. 2008, 65, 1455–1466. [Google Scholar] [CrossRef]
- Schwarzenboeck, A.; Shcherbakov, V.; Lefevre, R.; Gayet, J.-F.; Pointin, Y.; Duroure, C. Indications for stellar-crystal fragmentation in Arctic clouds. Atmos. Res. 2009, 92, 220–228. [Google Scholar] [CrossRef]
- Phillips, V.T.J.; Yano, J.-I.; Formenton, M.; Ilotoviz, E.; Kanawade, V.; Kudzotsa, I.; Sun, J.; Bansemer, A.; Detwiler, A.G.; Kahin, A.; et al. Ice Multiplication by Breakup in Ice–Ice Collisions. Part II: Numerical Simulations. J. Atmos. Sci. 2017, 74, 2789–2811. [Google Scholar]
- Dedekind, Z.; Lauber, A.; Ferrachat, S.; Lohmann, U. Sensitivity of precipitation formation to secondary ice production in winter orographic mixed-phase clouds. Atmos. Meas. Tech. 2021, 21, 15115–15134. [Google Scholar] [CrossRef]
- Georgakaki, P.; Sotiropoulou, G.; Vignon, É.; Billault-Roux, A.-C.; Berne, A.; Nenes, A. Secondary ice production processes in wintertime alpine mixed-phase clouds. Atmos. Meas. Tech. 2022, 22, 1965–1988. [Google Scholar] [CrossRef]
- Sotiropoulou, G.; Vignon, É.; Young, G.; Morrison, H.; O’Shea, S.J.; Lachlan-Cope, T.; Berne, A.; Nenes, A. Secondary ice production in summer clouds over the Antarctic coast: An underappreciated process in atmospheric models. Atmos. Meas. Tech. 2021, 21, 755–771. [Google Scholar] [CrossRef]
- Morrison, H.; Curry, J.A.; Khvorostyanov, V.I. A New Double-Moment Microphysics Parameterization for Application in Cloud and Climate Models. Part I: Description. J. Atmos. Sci. 2005, 62, 1665–1677. [Google Scholar] [CrossRef]
- Sotiropoulou, G.; Sullivan, S.; Savre, J.; Lloyd, G.; Lachlan-Cope, T.; Ekman, A.M.L.; Nenes, A. The impact of secondary ice production on Arctic stratocumulus. Atmospheric Meas. Tech. 2020, 20, 1301–1316. [Google Scholar] [CrossRef]
- Sullivan, S.C.; Hoose, C.; Kiselev, A.; Leisner, T.; Nenes, A. Initiation of secondary ice production in clouds. Atmos. Meas. Tech. 2018, 18, 1593–1610. [Google Scholar] [CrossRef]
- Connolly, P.J.; Choularton, T.W.; Gallagher, M.; Bower, K.N. Cloud-resolving simulations of intense tropicalHector thunderstorms: Implications for aerosol–cloud interactions. Q. J. R. Meteorol. Soc. 2006, 132, 3079–3106. [Google Scholar] [CrossRef]
- Crawford, I.; Bower, K.N.; Choularton, T.W.; Dearden, C.; Crosier, J.; Westbrook, C.; Capes, G.; Coe, H.; Connolly, P.J.; Dorsey, J.R.; et al. Ice formation and development in aged, wintertime cumulus over the UK: Observations and modelling. Atmos. Meas. Tech. 2012, 12, 4963–4985. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal Analysis of TRMM-Based Satellite Precipitation Products for Land Data Assimilation Applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Version 4; NCAR Tech; Note NCAR/TN-556+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2019; 145p. [Google Scholar]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of Cloud Microphysics on the Development of Trailing Stratiform Precipitation in a Simulated Squall Line: Comparison of One- and Two-Moment Schemes. Mon. Weather. Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Passarelli, R.E. An Approximate Analytical Model of the Vapor Deposition and Aggregation Growth of Snowflakes. J. Atmos. Sci. 1978, 35, 118–124. [Google Scholar] [CrossRef]
- Verlinde, J.; Flatau, P.J.; Cotton, W.R. Analytical Solutions to the Collection Growth Equation: Comparison with Approximate Methods and Application to Cloud Microphysics Parameterization Schemes. J. Atmos. Sci. 1990, 47, 2871–2880. [Google Scholar] [CrossRef]
- Ikawa, M.; Saito, K. Description of a nonhydrostatic model developed at the forecast research department of the MRI. Meteorol. Res. Institude Tech. Rep. 1991, 28, 238. [Google Scholar]
- Reisner, J.; Rasmussen, R.M.; Bruintjes, R.T. Explicit forecasting of supercooled liquid water in winter storms using the MM5 mesoscale model. Q. J. R. Meteorol. Soc. 1998, 124, 1071–1107. [Google Scholar] [CrossRef]
- Churchill, D.D.; Houze, R.A., Jr. Development and Structure of Winter Monsoon Cloud Clusters On 10 December 1978. J. Atmos. Sci. 1984, 41, 933–960. [Google Scholar] [CrossRef]
- Fan, J.; Han, B.; Varble, A.; Morrison, H.; North, K.; Kollias, P.; Chen, B.; Dong, X.; Giangrande, S.E.; Khain, A.; et al. Cloud-resolving model intercomparison of an MC3E squall line case: Part I—Convective updrafts. J. Geophys. Res. Atmos. 2017, 122, 9351–9378. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Fan, J.; Zhang, G.J.; Xu, K.-M.; Ghan, S.J. Improving representation of convective transport for scale-aware parameterization: 2. Analysis of cloud-resolving model simulations. J. Geophys. Res. Atmos. 2015, 120, 3510–3532. [Google Scholar] [CrossRef]
- Han, B.; Fan, J.; Varble, A. Cloud-Resolving Model Intercomparison of an MC3E Squall Line Case: Part II. Stratiform Precipitation Properties. J. Geophys. Res. Atmos. 2019, 124, 1090–1117. [Google Scholar] [CrossRef]
- Shpund, J.; Khain, A.; Lynn, B.; Fan, J.; Han, B.; Ryzhkov, A.; Snyder, J.; Dudhia, J.; Gill, D. Simulating a Mesoscale Convective System Using WRF With a New Spectral Bin Microphysics: 1: Hail vs Graupel. J. Geophys. Res. Atmos. 2019, 124, 14072–14101. [Google Scholar] [CrossRef]
- Shahi, N.K.; Polcher, J.; Bastin, S.; Pennel, R.; Fita, L. Assessment of the spatio-temporal variability of the added value on precipitation of convection-permitting simulation over the Iberian Peninsula using the RegIPSL regional earth system model. Clim. Dyn. 2022, 59, 471–498. [Google Scholar] [CrossRef]
- Stoelinga, M.T. Simulated Equivalent Reflectivity Factor as Currently Formulated in RIP: Description and Possible Improvements. White Paper, 2005; 5p. [Google Scholar]
- Korolev, A. Limitations of the Wegener–Bergeron–Findeisen Mechanism in the Evolution of Mixed-Phase Clouds. J. Atmos. Sci. 2007, 64, 3372–3375. [Google Scholar] [CrossRef]
- Varble, A.; Zipser, E.J.; Fridlind, A.M.; Zhu, P.; Ackerman, A.S.; Chaboureau, J.P.; Collis, S.; Fan, J.; Hill, A.; Shipway, B. Evaluation of cloud-resolving and limited area model intercomparison simulations using TWP-ICE observations: 1. Deep convective updraft properties. J. Geophys. Res. Atmos. 2014, 119, 13891–13918. [Google Scholar] [CrossRef]
- Varble, A.; Zipser, E.J.; Fridlind, A.M.; Zhu, P. Evaluation of cloud-resolving and limited area model intercomparison simulations using TWP-ICE observations: 2. Precipitation microphysics. J. Geophys. Res. Atmos. 2014, 119, 13919–13945. [Google Scholar] [CrossRef]
- Fan, J.; Leung, L.R.; Rosenfeld, D.; Chen, Q.; Li, Z.; Zhang, J.; Yan, H. Microphysical effects determine macrophysical response for aerosol impacts on deep convective clouds. Proc. Natl. Acad. Sci. USA 2013, 110, E4581–E4590. [Google Scholar] [CrossRef] [PubMed]
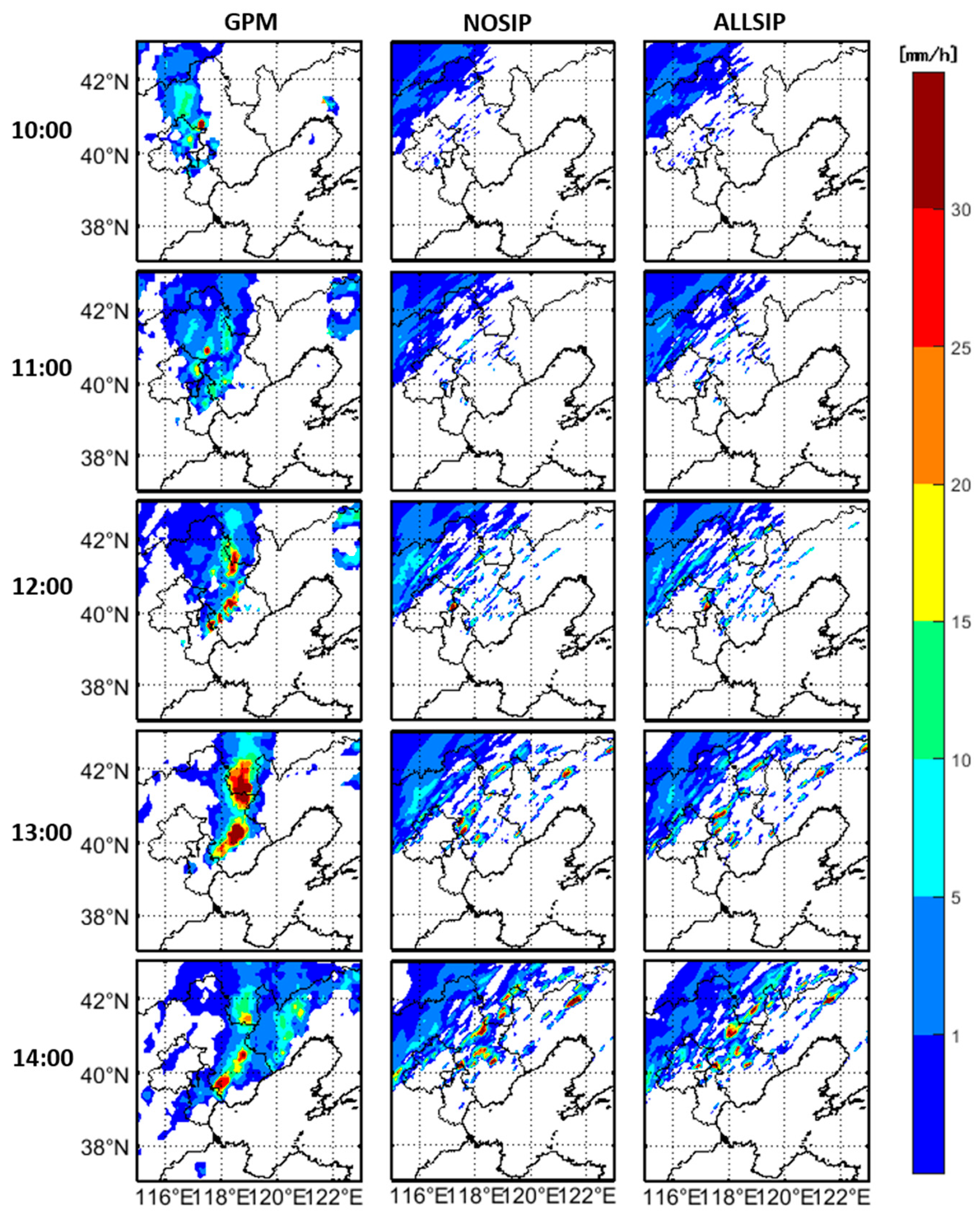
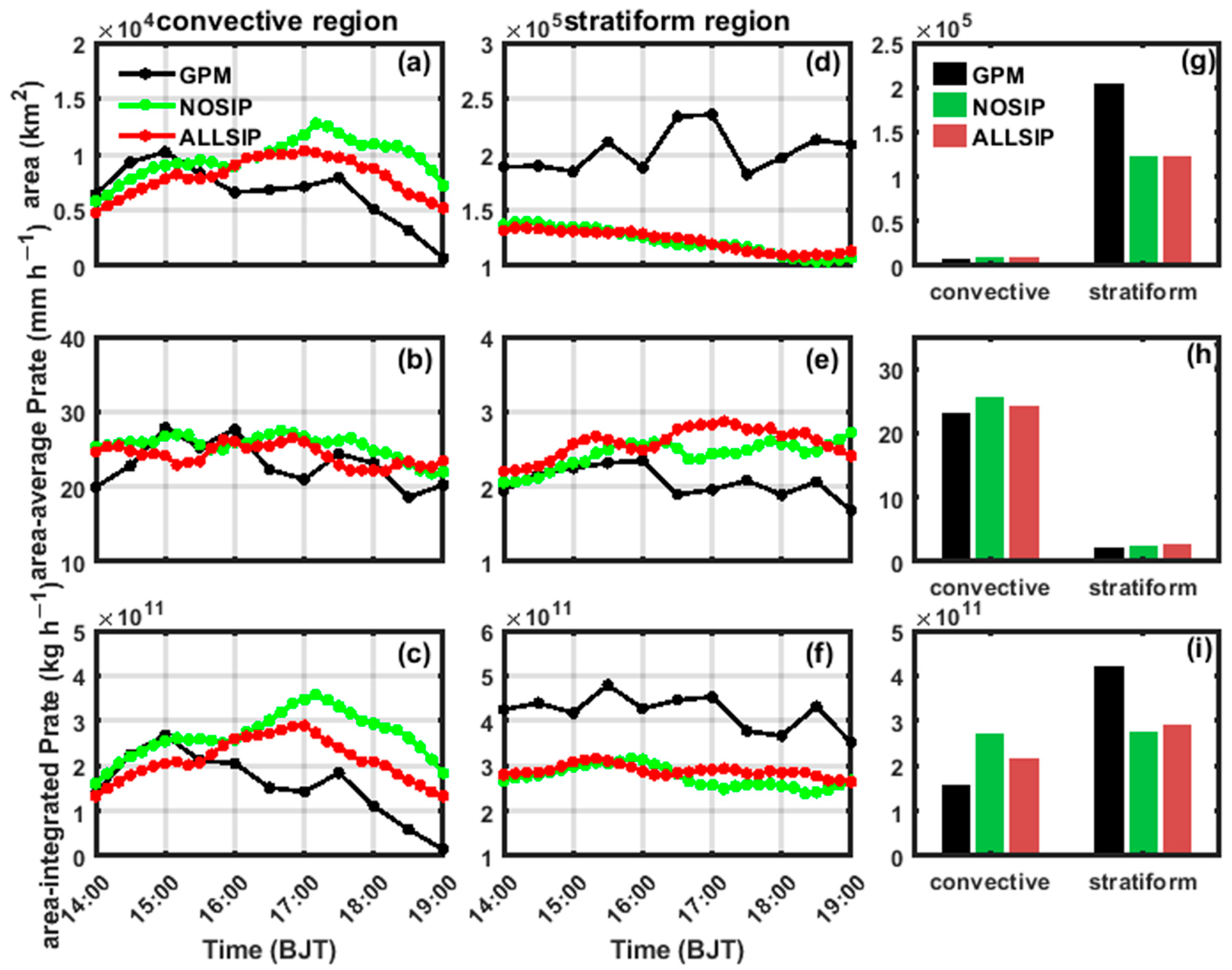
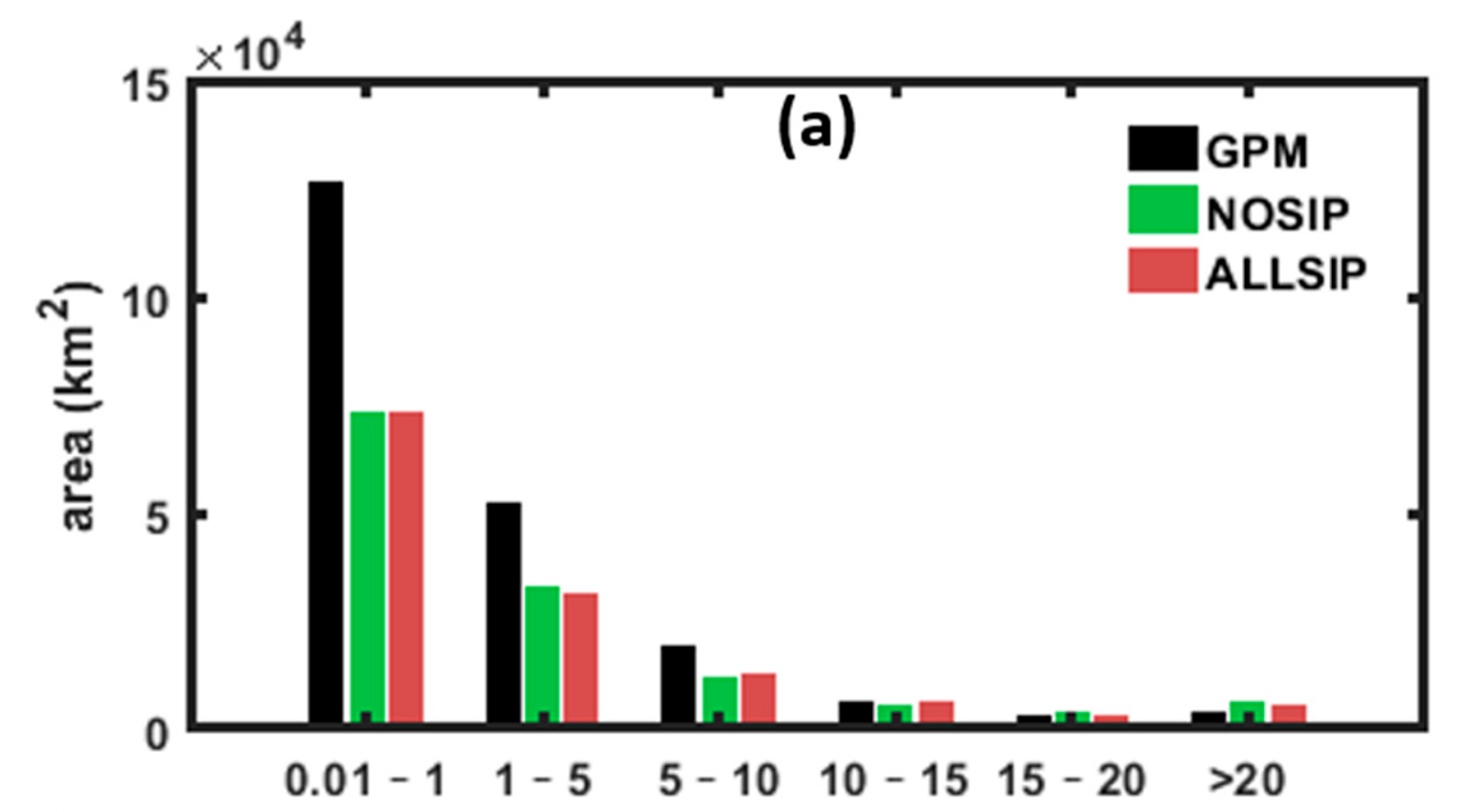
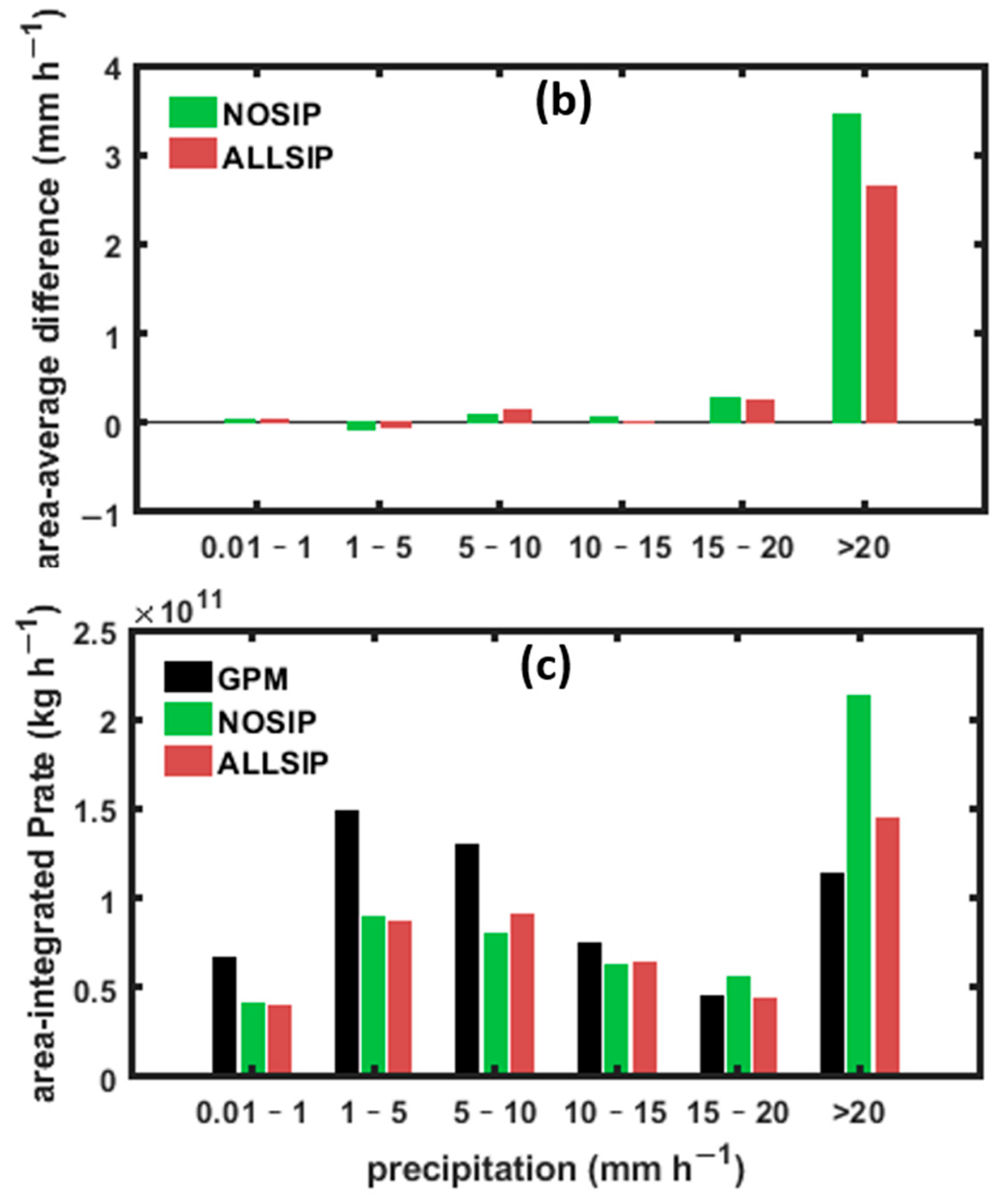
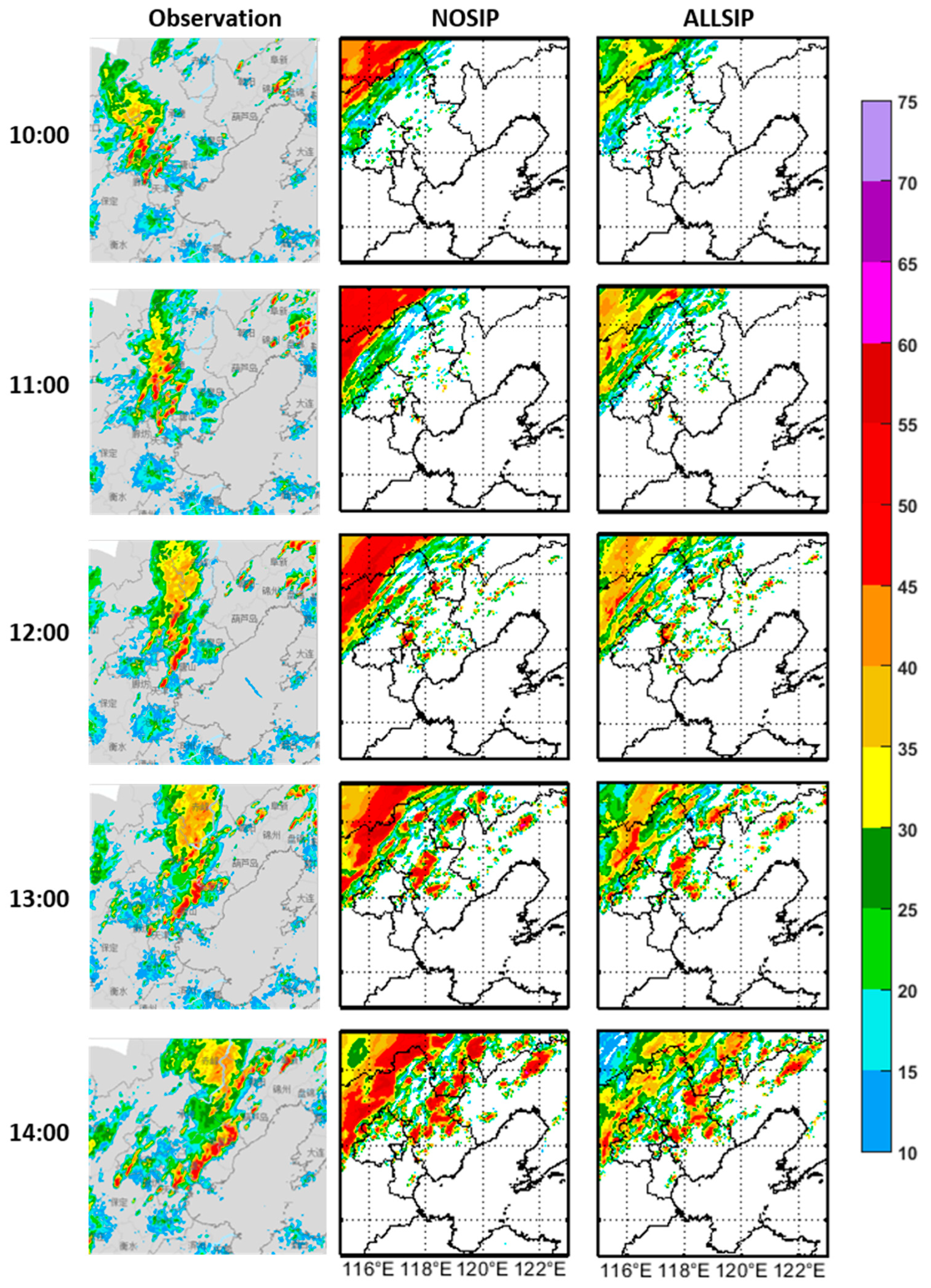
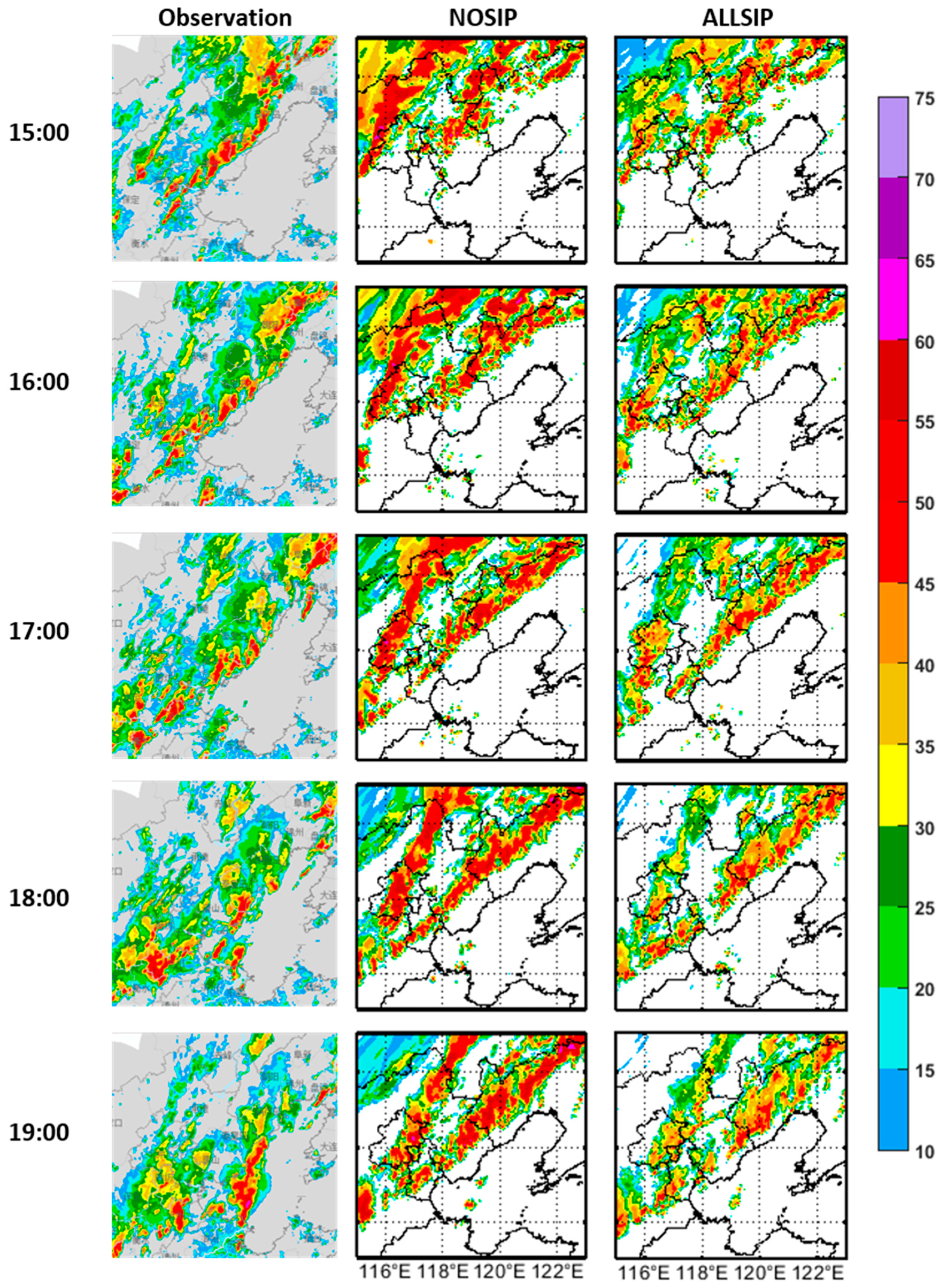

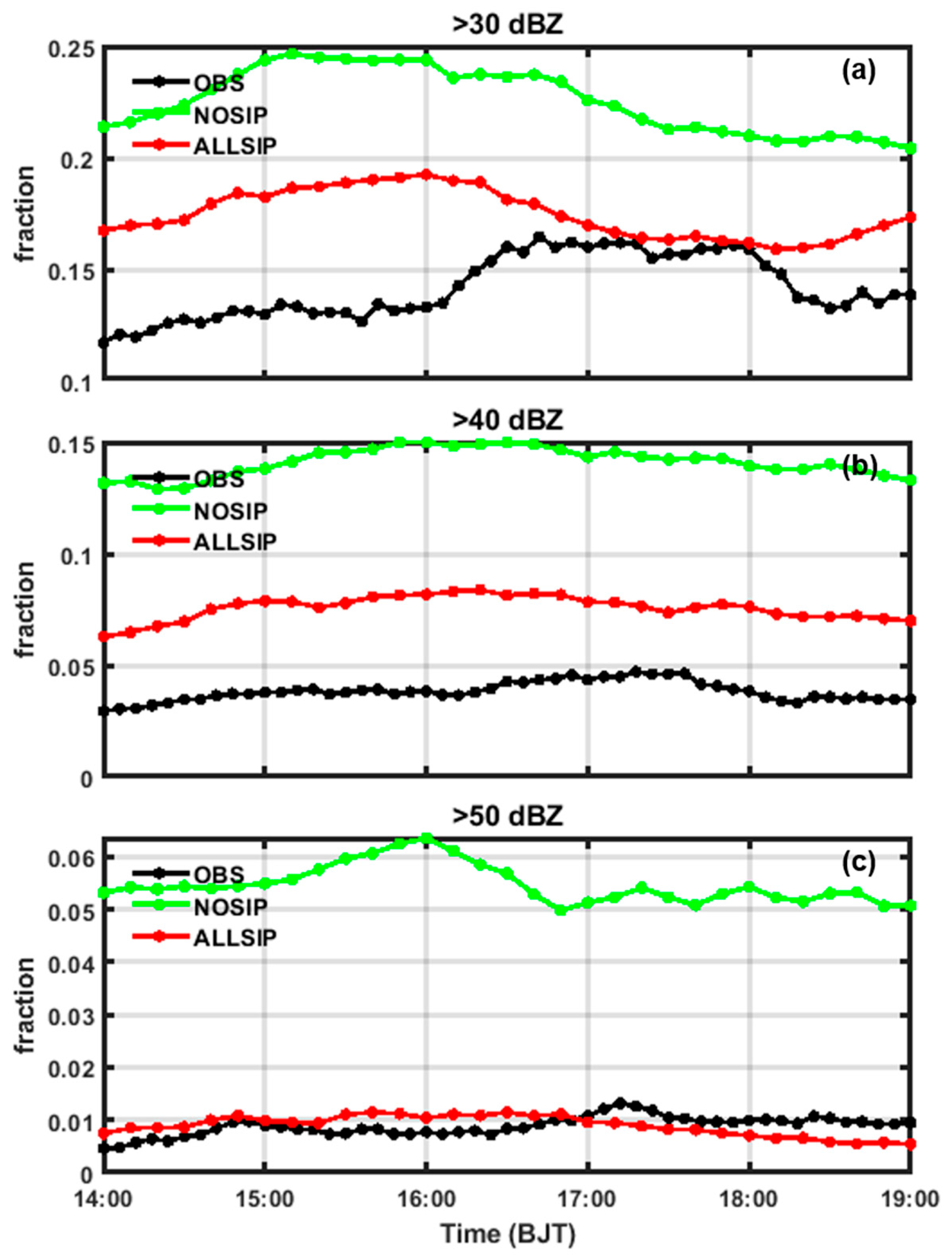

| Parameters | Domain 1 | Domain 2 |
|---|---|---|
| Grid size (km) | 9 | 3 |
| Vertical resolution | σ-z terrain tracking coordinates; 50 layers; model top: 10 hPa; | |
| Output time (min) | 60 | 10 |
| Microphysical scheme | Morrison | Morrison |
| Cumulus parameterization scheme | Kain–Fritsch | None |
| Boundary layer scheme | Yonsei University | Yonsei University |
| Longwave radiation scheme | RRTM | RRTM |
| Shortwave radiation scheme | Dudhia | Dudhia |
| Case | Secondary Ice Productions (SIPs) |
|---|---|
| NOSIP | No SIPs |
| ALLSIP | Including all the three SIPs |
| RS | Only including rime splintering |
| DS | Only including freezing drop-shattering |
| CB | Only including ice-ice collisional breakup |
| Collision Type in this Study | |||
|---|---|---|---|
| Graupel-Graupel | Type I in Phillips et al. [24] | Format in Passarelli [61], but with parameters of graupel instead of snow | Format in Verlinde et al. [62], but with parameters of graupel instead of snow |
| Snow-Graupel | Type II in Phillips et al. [24] | Format in Ikawa and Saito [63] | Format in Ikawa and Saito [63] |
| Ice crystal-Graupel | Type II in Phillips et al. [24] | Format in Reisner [64], but with parameters of graupel instead of raindrop | \ |
| Snow-Snow | Type III in Phillips et al. [24] | Format in Passarelli [61], which is already concluded in default Morrison scheme | Format in Verlinde et al. [62] |
| Ice crystal-Snow | Type III in Phillips et al. [24] | Format in Reisner [64], but with parameters of snow instead of raindrop | \ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Han, X.; Chen, Y.; Li, S.; Xue, H. A Numerical Simulation Study of Secondary Ice Productions in a Squall Line Case. Atmosphere 2023, 14, 1752. https://doi.org/10.3390/atmos14121752
Gao J, Han X, Chen Y, Li S, Xue H. A Numerical Simulation Study of Secondary Ice Productions in a Squall Line Case. Atmosphere. 2023; 14(12):1752. https://doi.org/10.3390/atmos14121752
Chicago/Turabian StyleGao, Jie, Xuqing Han, Yichen Chen, Shuangxu Li, and Huiwen Xue. 2023. "A Numerical Simulation Study of Secondary Ice Productions in a Squall Line Case" Atmosphere 14, no. 12: 1752. https://doi.org/10.3390/atmos14121752
APA StyleGao, J., Han, X., Chen, Y., Li, S., & Xue, H. (2023). A Numerical Simulation Study of Secondary Ice Productions in a Squall Line Case. Atmosphere, 14(12), 1752. https://doi.org/10.3390/atmos14121752






