Santa Ana Winds: Multifractal Measures and Singularity Spectrum
Abstract
:1. Introduction
2. Study Area
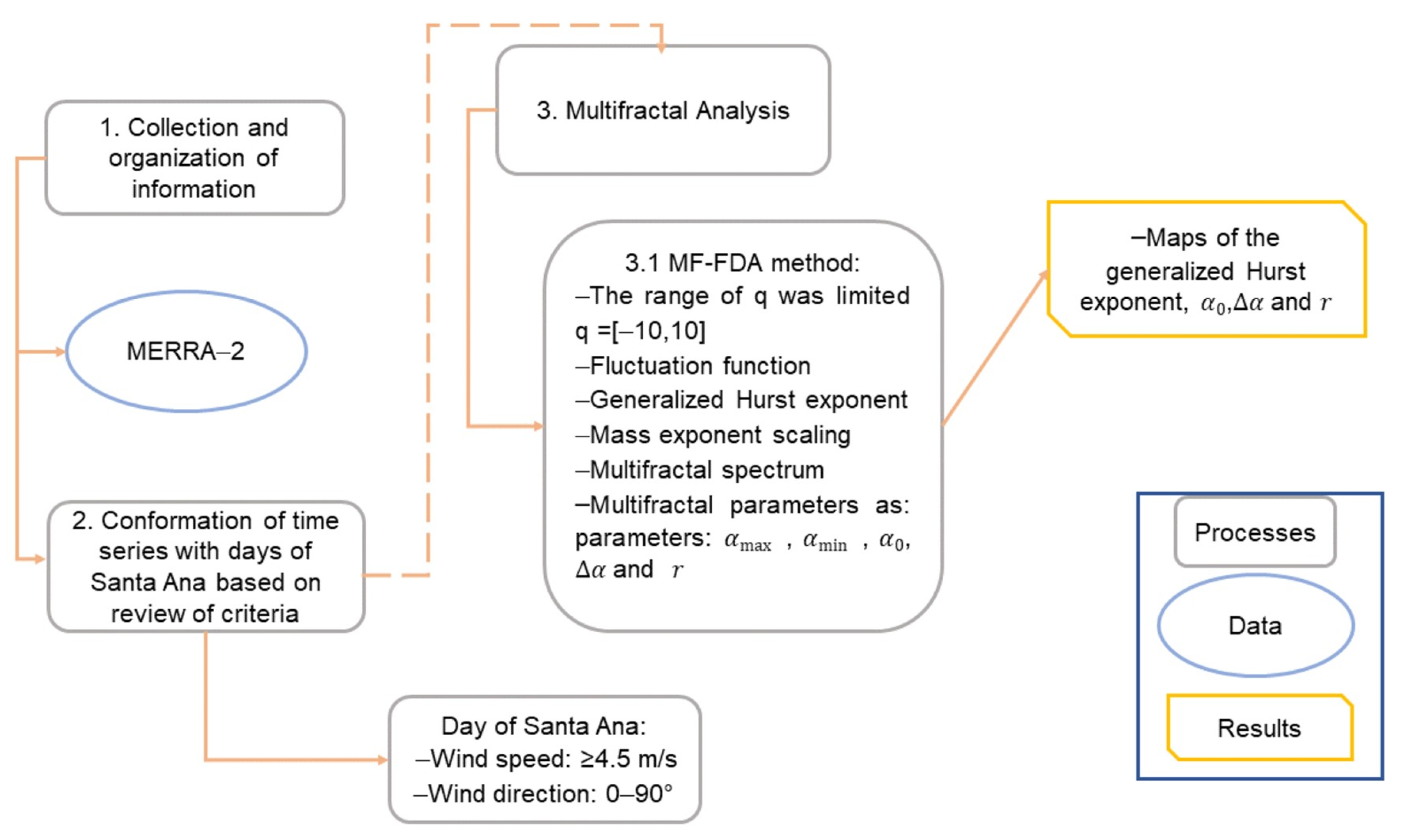
3. Materials and Methods
3.1. Santa Ana Time Series
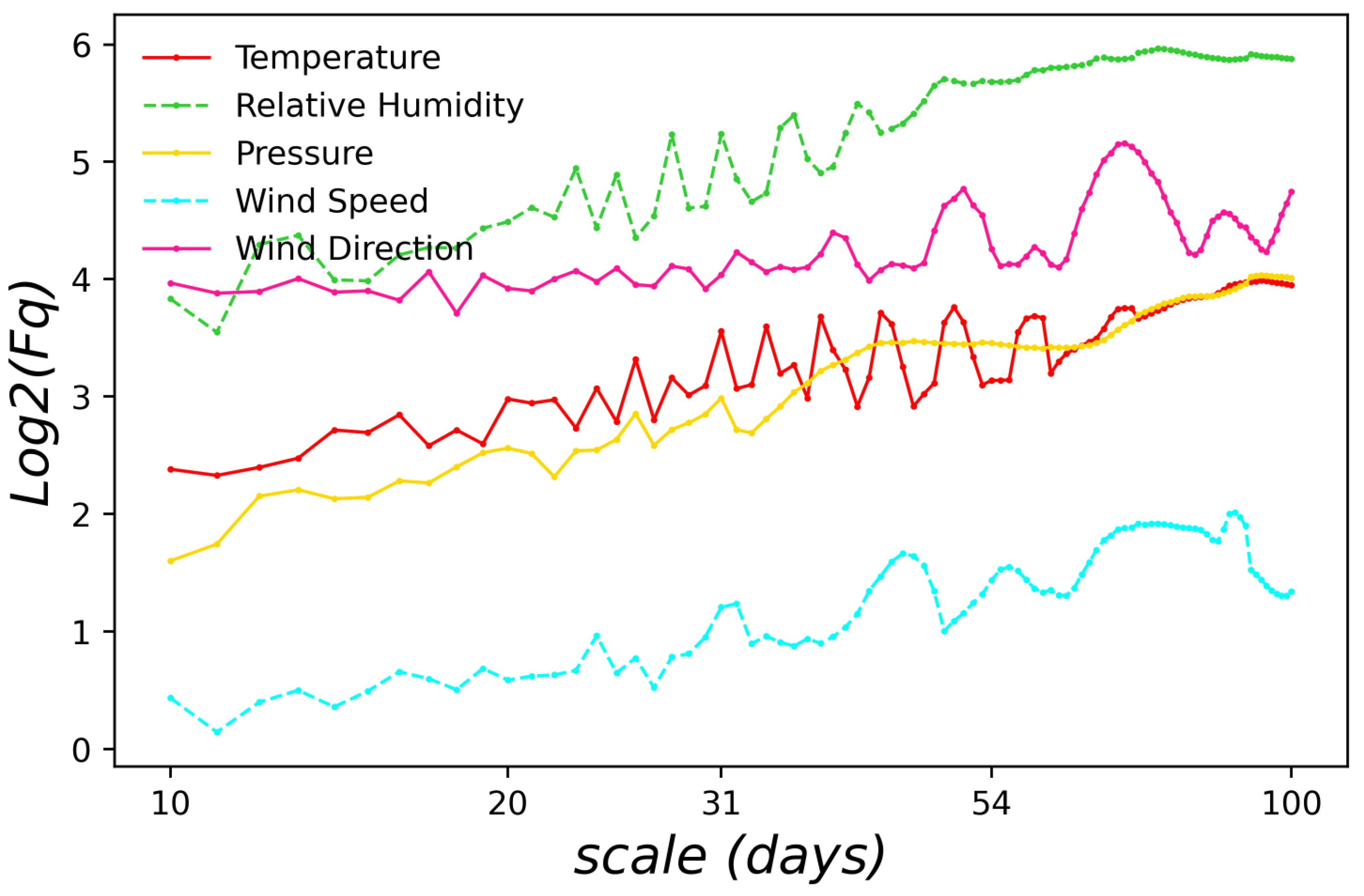
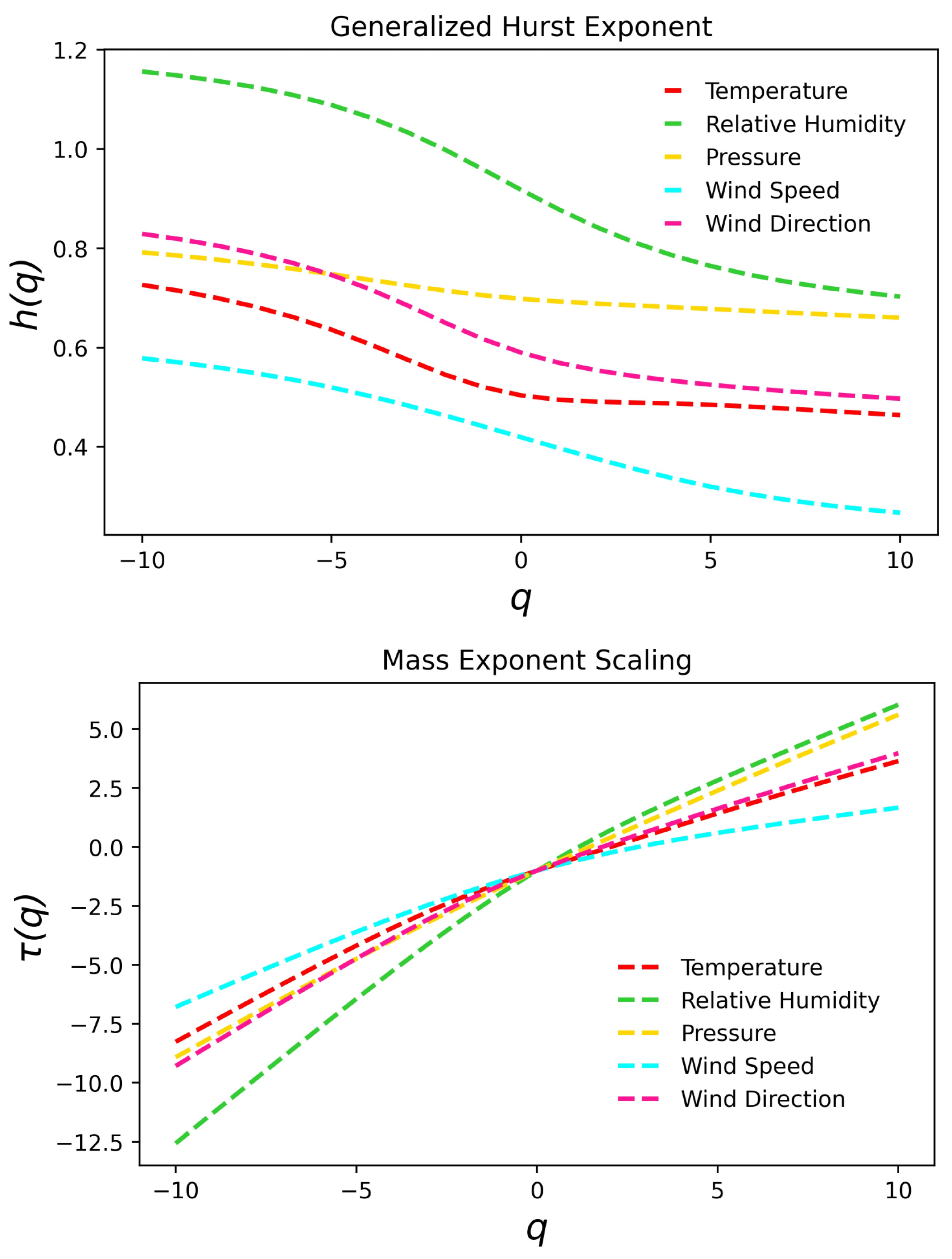
3.2. Multifractal Analysis
3.3. Spatialization
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Santa Ana Time Series: Wind Direction, Wind Speed and Temperature
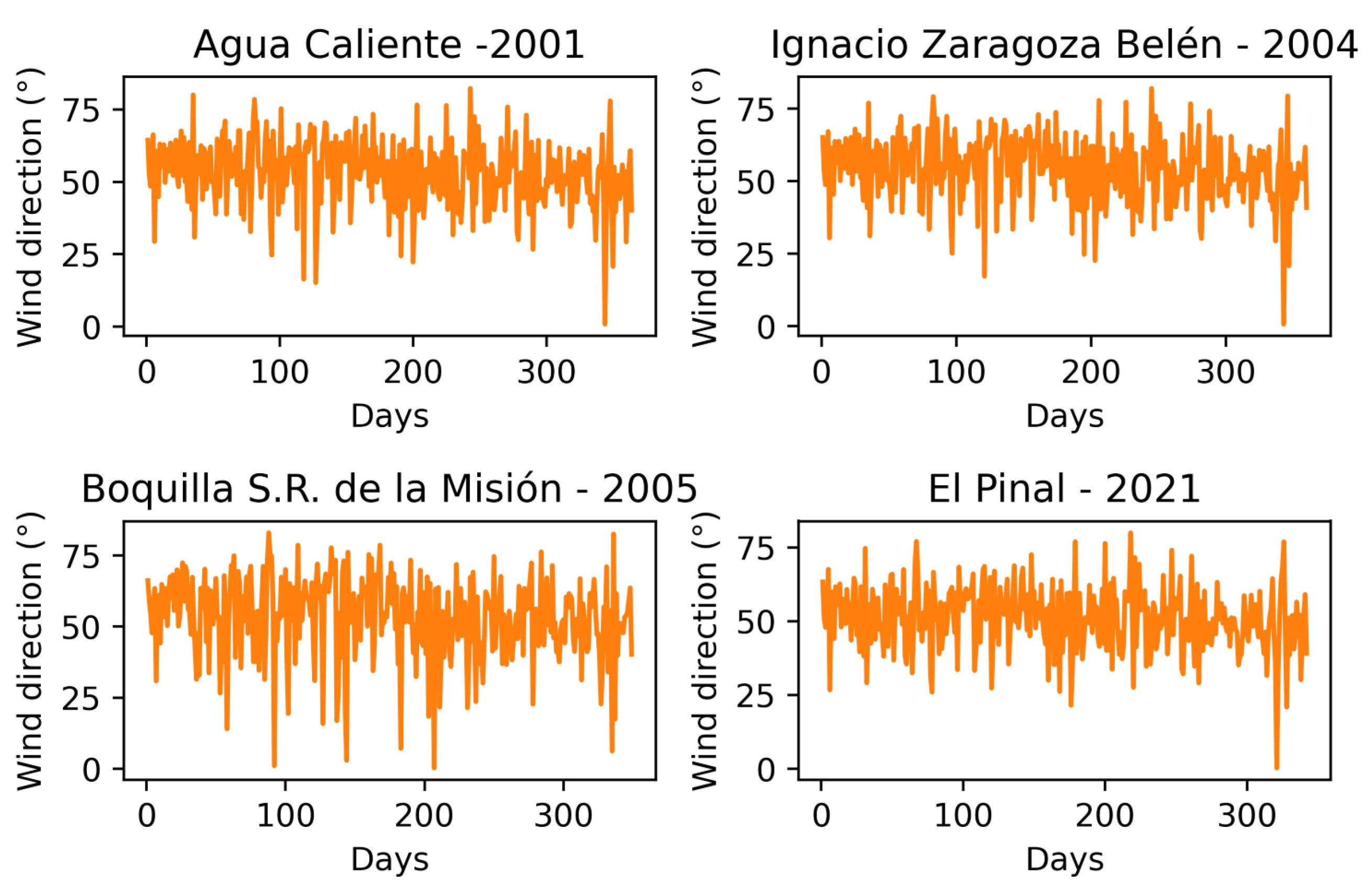
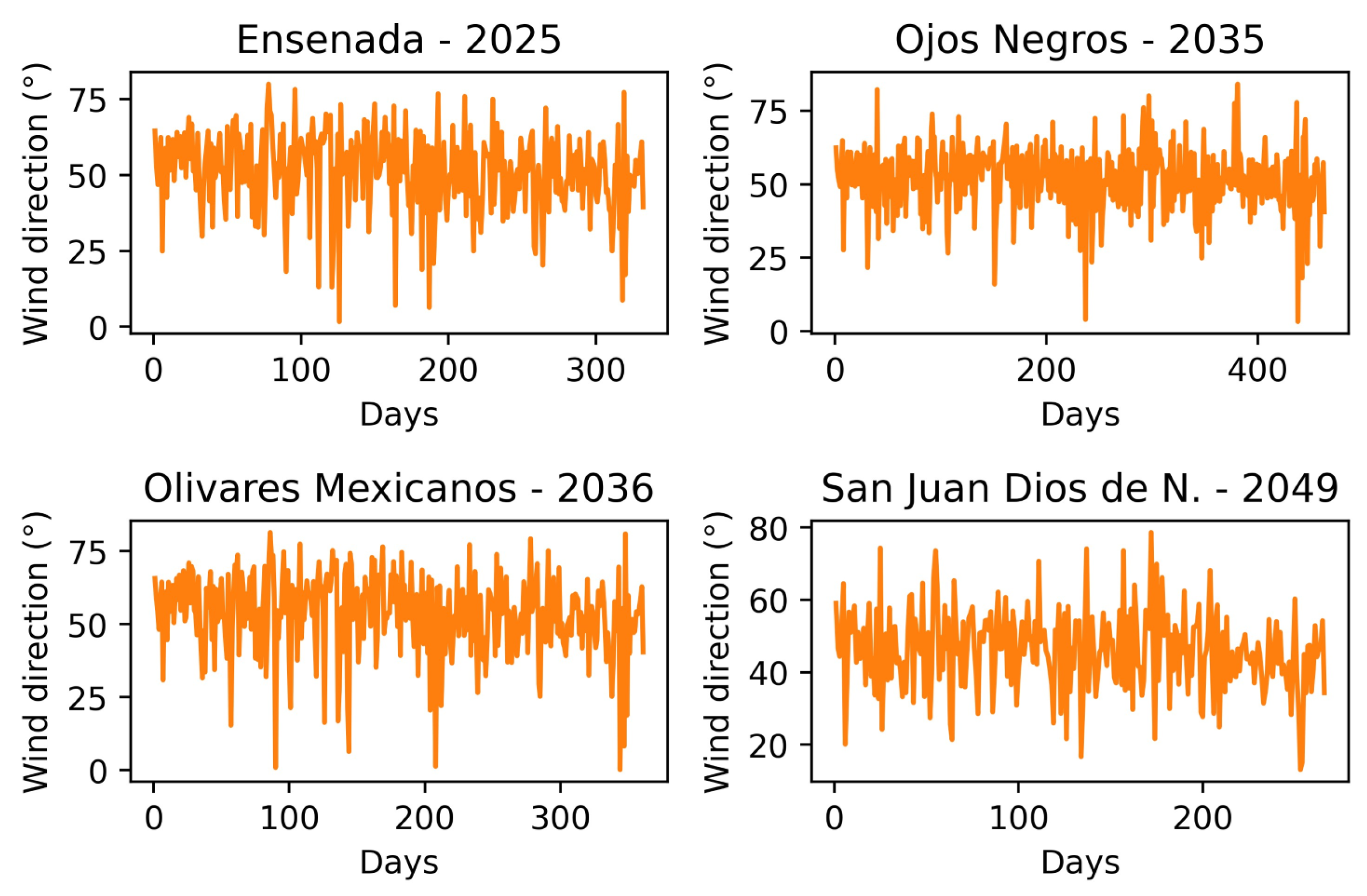
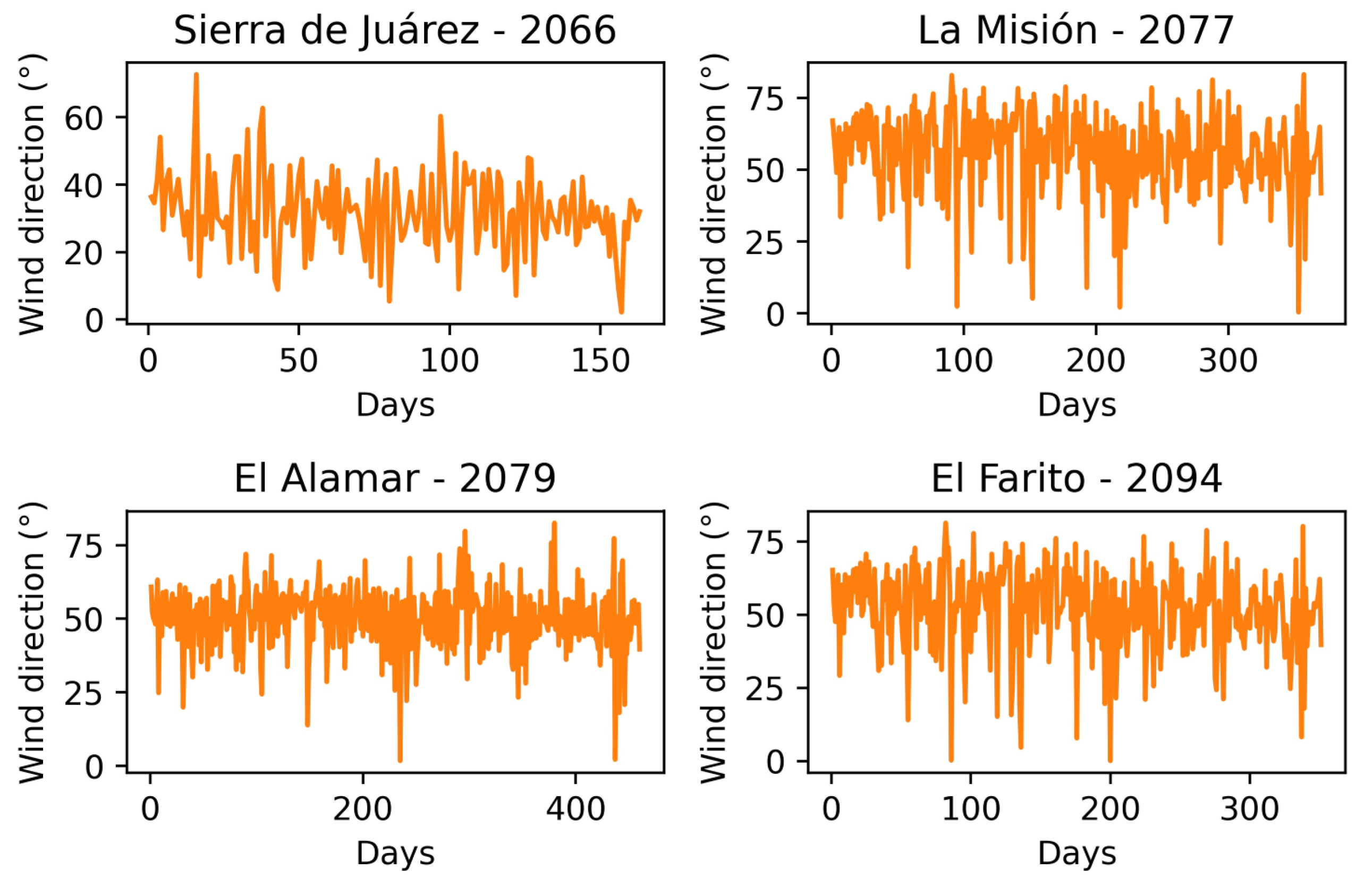
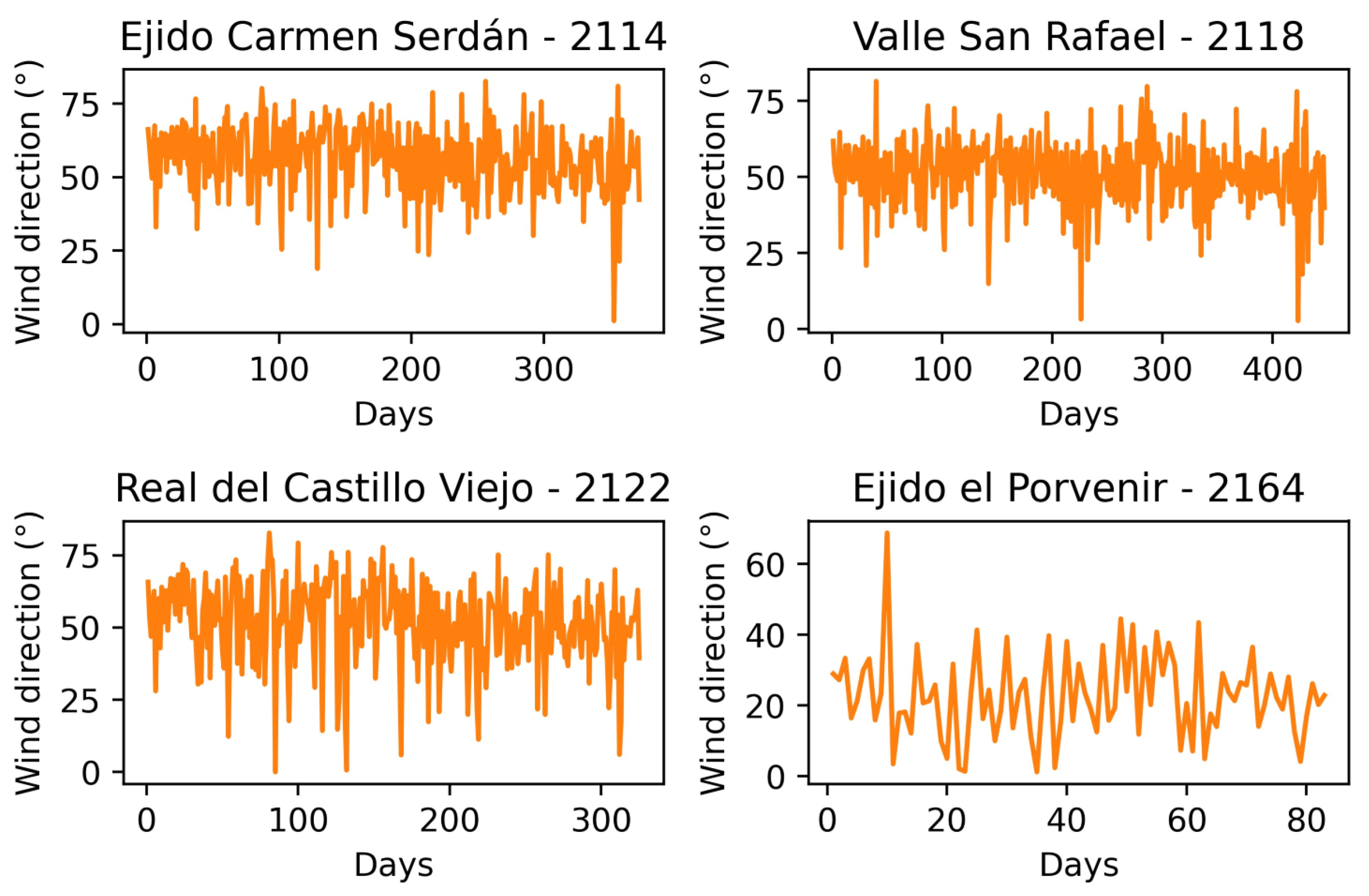


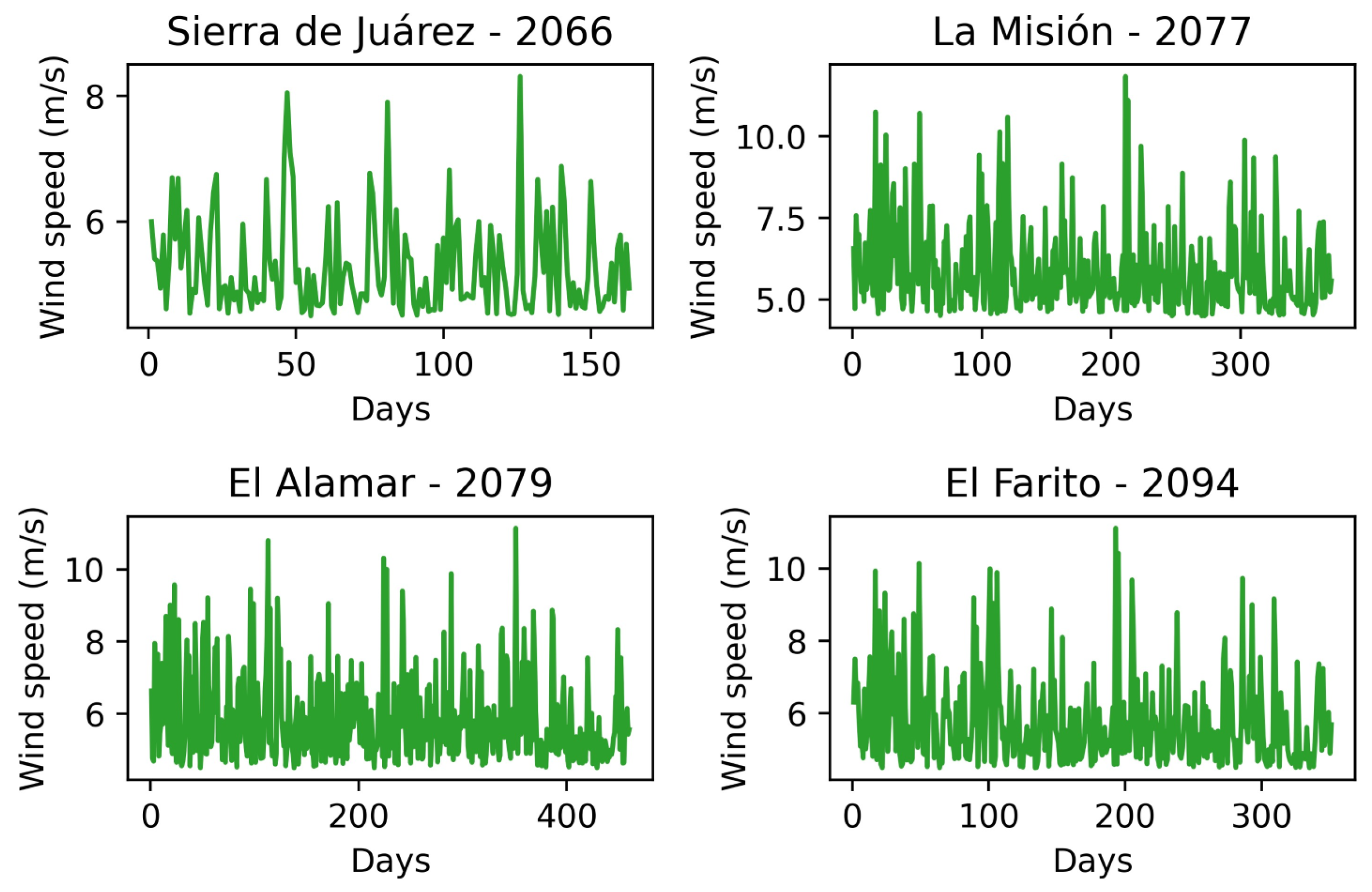
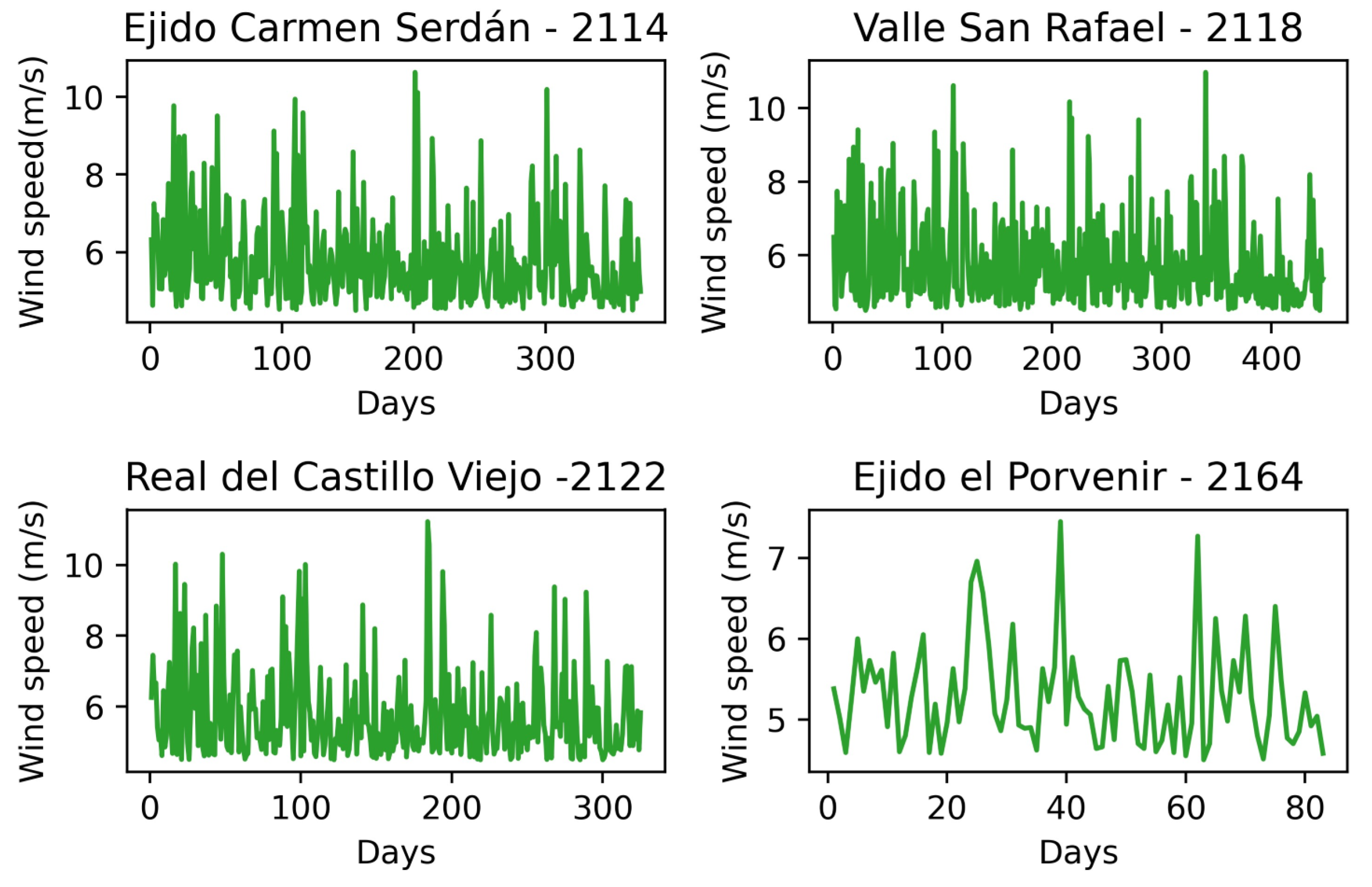

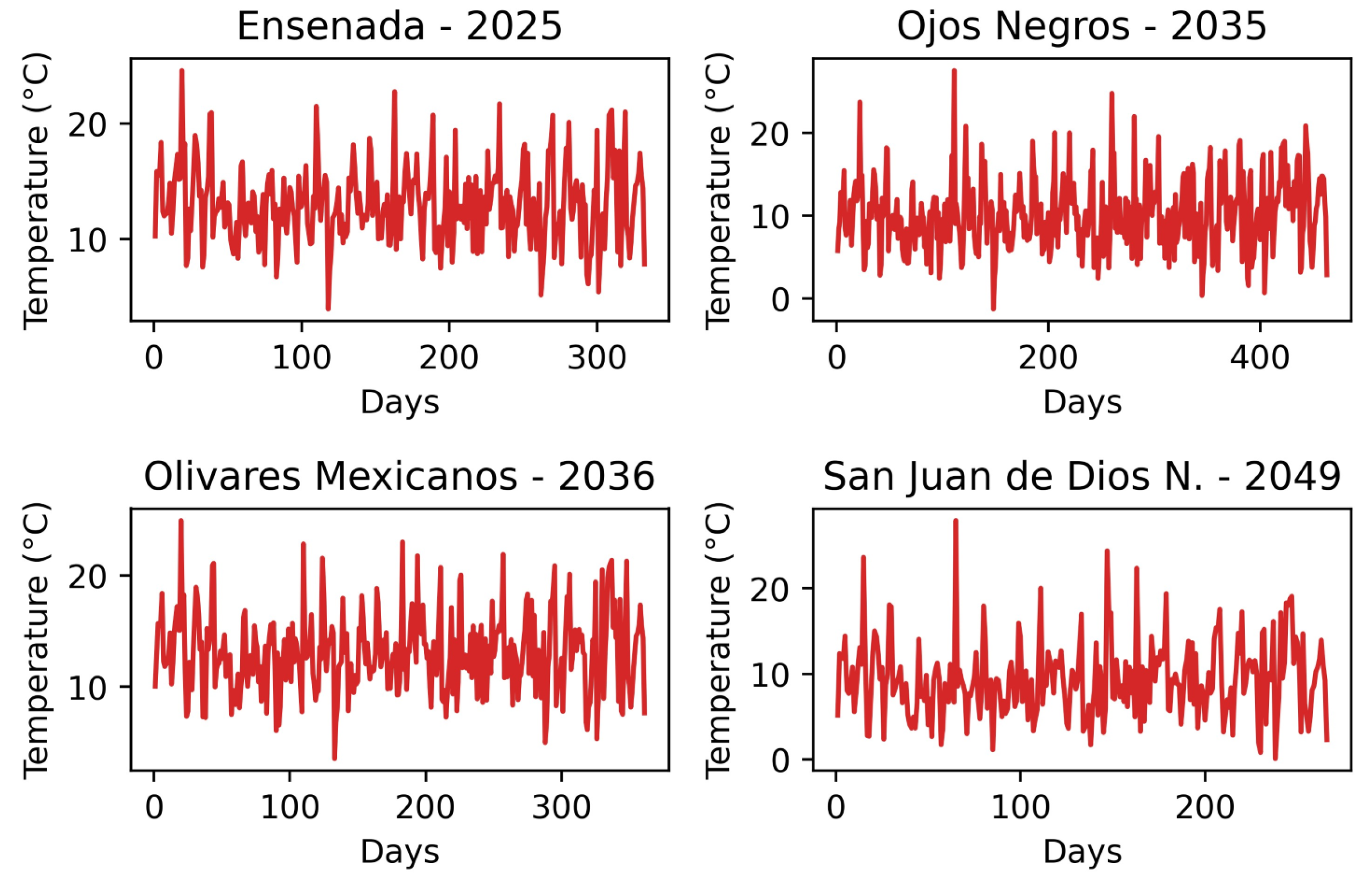

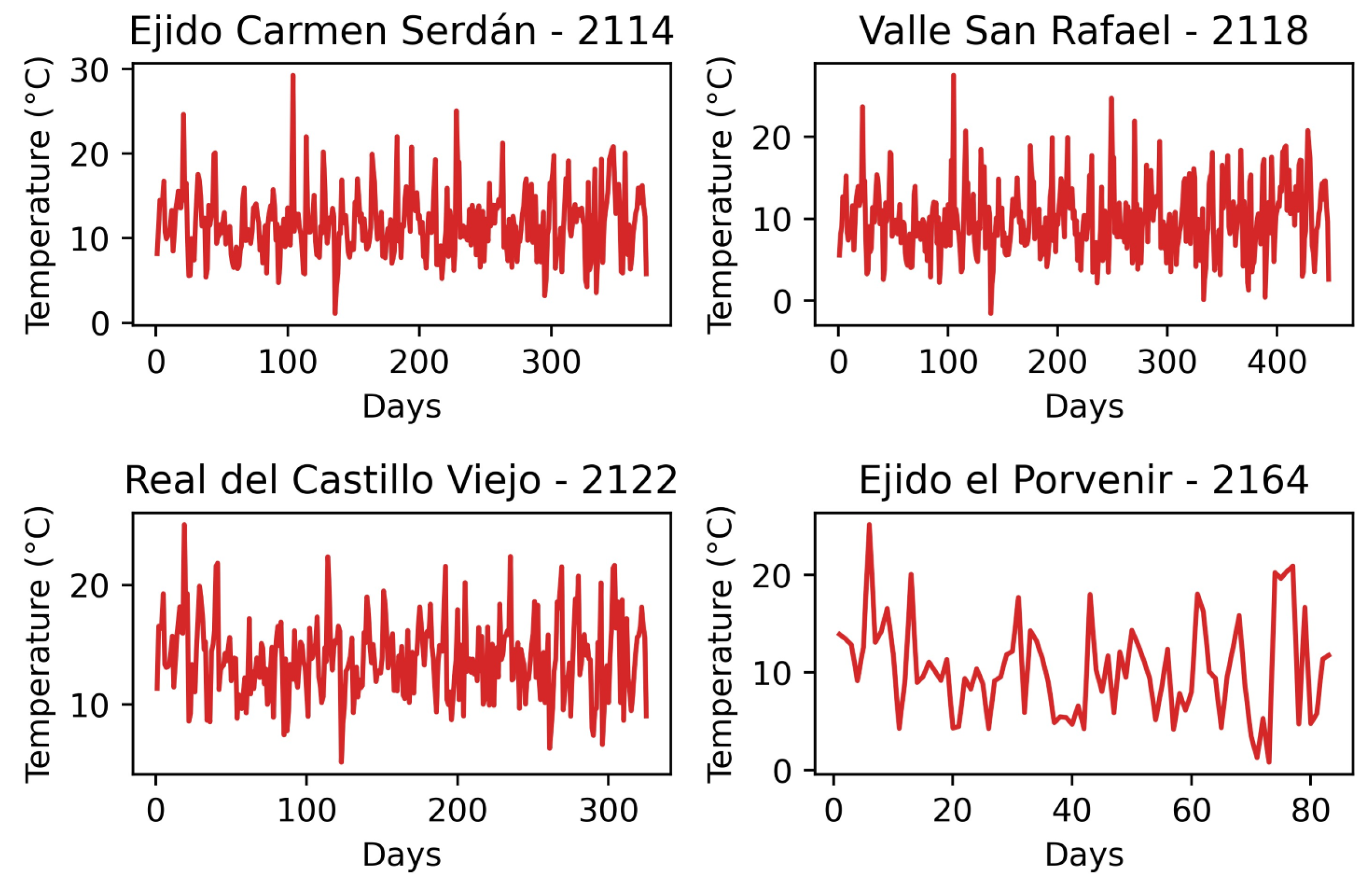
References
- Álvarez, C.A.; Carbajal, N. Regions of Influence and Environmental Effects of Santa Ana Wind Event. Air Qual. Atmos. Health 2019, 12, 1019–1034. [Google Scholar] [CrossRef]
- Glickman, T.S. Glossary of Meteorology, 2nd ed.; American Meteorogical Society: Boston, MA, USA, 2021. [Google Scholar]
- Serpa-Usta, Y.; López-Lambraño, A.A.; Flores, D.-L.; Gámez-Balmaceda, E.; Martínez-Acosta, L.; Medrano-Barboza, J.P.; López, J.F.R.; López-Ramos, A.; López-Lambraño, M. Santa Ana Winds: Fractal-Based Analysis in a Semi-Arid Zone of Northern Mexico. Atmosphere 2021, 13, 48. [Google Scholar] [CrossRef]
- Baranowski, P.; Gos, M.; Krzyszczak, J.; Siwek, K.; Kieliszek, A.; Tkaczyk, P. Multifractality of Meteorological Time Series for Poland on the Base of MERRA-2 Data. Chaos Solitons Fractals 2019, 127, 318–333. [Google Scholar] [CrossRef]
- De Lima, M.I.P. Multifractals and the Temporal Structure of Rainfall; Wageningen Agricultural University: Wageningen, The Netherlands, 1998. [Google Scholar]
- Zeleke, T.B.; Si, B.C. Scaling Properties of Topographic Indices and Crop Yield: Multifractal and Joint Multifractal Approaches. Agron. J. 2004, 96, 1082–1090. [Google Scholar] [CrossRef]
- López Lambraño, A. Análisis Multifractal y Modelación de La Precipitación. Ph.D. Thesis, Universidad Autónoma de Querétaro, Santiago de Querétaro, Mexico, 2012. [Google Scholar]
- Xiong, G.; Yu, W.; Zhang, S. Singularity Power Spectrum Distribution. Phys. A Stat. Mech. Its Appl. 2015, 431, 63–73. [Google Scholar] [CrossRef]
- Grassberger, P. On the Hausdorff Dimension of Fractal Attractors. J. Stat. Phys. 1981, 26, 173–179. [Google Scholar] [CrossRef]
- Gómez-Gómez, J.; Ariza-Villaverde, A.B.; Gutiérrez De Ravé, E.; Jiménez-Hornero, F.J. Relationships between Reference Evapotranspiration and Meteorological Variables in the Middle Zone of the Guadalquivir River Valley Explained by Multifractal Detrended Cross-Correlation Analysis. Fractal Fract. 2023, 7, 54. [Google Scholar] [CrossRef]
- Gómez-Gómez, J.; Carmona-Cabezas, R.; Sánchez-López, E.; Gutiérrez De Ravé, E.; Jiménez-Hornero, F.J. Multifractal Fluctuations of the Precipitation in Spain (1960–2019). Chaos Solitons Fractals 2022, 157, 111909. [Google Scholar] [CrossRef]
- Sankaran, A.; Plocoste, T.; Nourani, V.; Vahab, S.; Salim, A. Assessment of Multifractal Fingerprints of Reference Evapotranspiration Based on Multivariate Empirical Mode Decomposition. Atmosphere 2023, 14, 1219. [Google Scholar] [CrossRef]
- Devi, R.R.; Chattopadhyay, S. A Modified Multifractal Detrended Fluctuation Analysis to Study the Precipitation across Northeast India. Dyn. Atmos. Ocean. 2023, 104, 101402. [Google Scholar] [CrossRef]
- Balkissoon, S.; Fox, N.; Lupo, A. Fractal Characteristics of Tall Tower Wind Speeds in Missouri. Renew. Energy 2020, 154, 1346–1356. [Google Scholar] [CrossRef]
- Philippopoulos, K.; Kalamaras, N.; Tzanis, C.G.; Deligiorgi, D.; Koutsogiannis, I. Multifractal Detrended Fluctuation Analysis of Temperature Reanalysis Data over Greece. Atmosphere 2019, 10, 336. [Google Scholar] [CrossRef]
- Laib, M.; Golay, J.; Telesca, L.; Kanevski, M. Multifractal Analysis of the Time Series of Daily Means of Wind Speed in Complex Regions. Chaos Solitons Fractals 2018, 109, 118–127. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, J.; Liu, X.; Li, F. Multifractal Scaling Comparison of the Air Temperature and the Surface Temperature over China. Phys. A Stat. Mech. Its Appl. 2016, 462, 783–792. [Google Scholar] [CrossRef]
- Akinsusi, J.; Ogunjo, S.; Fuwape, I. Nonlinear Dynamics and Multifractal Analysis of Minimum–Maximum Temperature and Solar Radiation over Lagos State, Nigeria. Acta Geophys. 2022, 70, 2171–2178. [Google Scholar] [CrossRef]
- de Lima, M.I.P.; Grasman, J. Multifractal Analysis of 15-Min and Daily Rainfall from a Semi-Arid Region in Portugal. J. Hydrol. 1999, 220, 1–11. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y. Multifractality of Canadian Precipitation and Streamflow. Int. J. Climatol. 2017, 37, 1221–1236. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, J.; Chen, Z.; Nie, Q.; Wei, C. Multifractal and Long Memory of Humidity Process in the Tarim River Basin. Stoch. Environ. Res. Risk Assess. 2014, 28, 1383–1400. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Estévez, J.; Jiménez-Hornero, F.J.; Ayuso-Muñoz, J.L. Multifractal Analysis of Validated Wind Speed Time Series. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 013133. [Google Scholar] [CrossRef]
- dos Santos, F.S.; do Nascimento, K.K.F.; Jale, J.d.S.; Stosic, T.; Marinho, M.H.N.; Ferreira, T.A.E. Mixture Distribution and Multifractal Analysis Applied to Wind Speed in the Brazilian Northeast Region. Chaos Solitons Fractals 2021, 144, 110651. [Google Scholar] [CrossRef]
- Zeng, Z.; Yang, H.; Zhao, R.; Meng, J. Nonlinear Characteristics of Observed Solar Radiation Data. Sol. Energy 2013, 87, 204–218. [Google Scholar] [CrossRef]
- Varotsos, C.; Kirk-Davidoff, D. Long-Memory Processes in Ozone and Temperature Variations at the Region 60° S−60° N. Atmos. Chem. Phys. 2006, 6, 4093. [Google Scholar] [CrossRef]
- Stosic, T.; Stosic, B.; Tošić, M.; Lazić, I.; Djurdjević, V.; Tošić, I. Climate Change Effects through MFDFA Study of Temperature in Serbia. Atmosphere 2023, 14, 1532. [Google Scholar] [CrossRef]
- Adarsh, S.; Nourani, V.; Archana, D.S.; Dharan, D.S. Multifractal Description of Daily Rainfall Fields over India. J. Hydrol. 2020, 586, 124913. [Google Scholar] [CrossRef]
- Yuval; Broday, D.M. Studying the Time Scale Dependence of Environmental Variables Predictability Using Fractal Analysis. Environ. Sci. Technol. 2010, 44, 4629–4634. [Google Scholar] [CrossRef] [PubMed]
- Sadegh Movahed, M.; Jafari, G.R.; Ghasemi, F.; Rahvar, S.; Reza Rahimi Tabar, M. Multifractal Detrended Fluctuation Analysis of Sunspot Time Series. J. Stat. Mech. Theory Exp. 2006, 2006, P02003. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- López, A.; Fuentes, C.; López Ramos, A.; Mata, J.; López, M. Spatial and Temporal Hurst Exponent Variability of Rainfall Series Based on the Climatological Distribution in a Semiarid Region in Mexico. Atmosfera 2018, 31, 199–219. [Google Scholar] [CrossRef]
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Kazandjiev, V.; Georgieva, V.; Sławiński, C.; Siwek, K.; Kozyra, J.; Nieróbca, A. Multifractal Characterization and Comparison of Meteorological Time Series from Two Climatic Zones. Theor. Appl. Clim. 2019, 137, 1811–1824. [Google Scholar] [CrossRef]
- Kalamaras, N.; Philippopoulos, K.; Deligiorgi, D.; Tzanis, C.G.; Karvounis, G. Multifractal Scaling Properties of Daily Air Temperature Time Series. Chaos Solitons Fractals 2017, 98, 38–43. [Google Scholar] [CrossRef]
- Dos Santos, F.S.; Do Nascimento, K.K.F.; Jale, J.S.; Xavier Júnior, S.F.A.; Ferreira, T.A.E. Multifractal Analysis of Solar Radiation in the Northeastern Region of Brazil. Fractals 2023, 31, 2350026. [Google Scholar] [CrossRef]
- da Silva, H.S.; Silva, J.R.S.; Stosic, T. Multifractal Analysis of Air Temperature in Brazil. Phys. A Stat. Mech. Its Appl. 2020, 549, 124333. [Google Scholar] [CrossRef]
- Aguilar-Molina, A.M.; Angulo-Brown, F.; Muñoz-Diosdado, A. Multifractal Spectrum Curvature of RR Tachograms of Healthy People and Patients with Congestive Heart Failure, a New Tool to Assess Health Conditions. Entropy 2019, 21, 581. [Google Scholar] [CrossRef] [PubMed]
- Munoz-Diosdado, A.; Del Rio-Correa, J.L. Further Study of the Asymmetry for Multifractal Spectra of Heartbeat Time Series. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; IEEE: New York, NY, USA, 2006; pp. 1450–1453. [Google Scholar] [CrossRef]
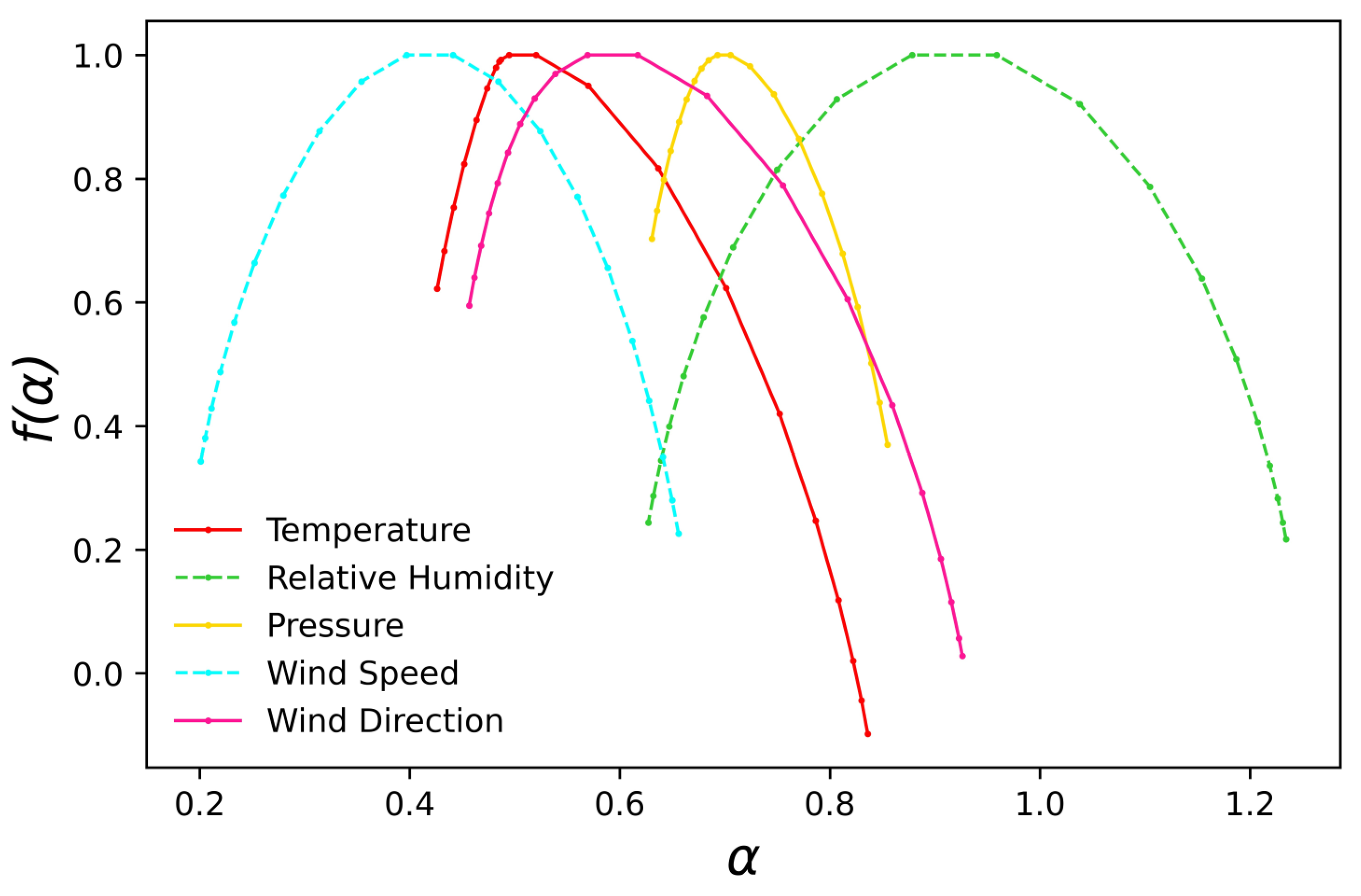
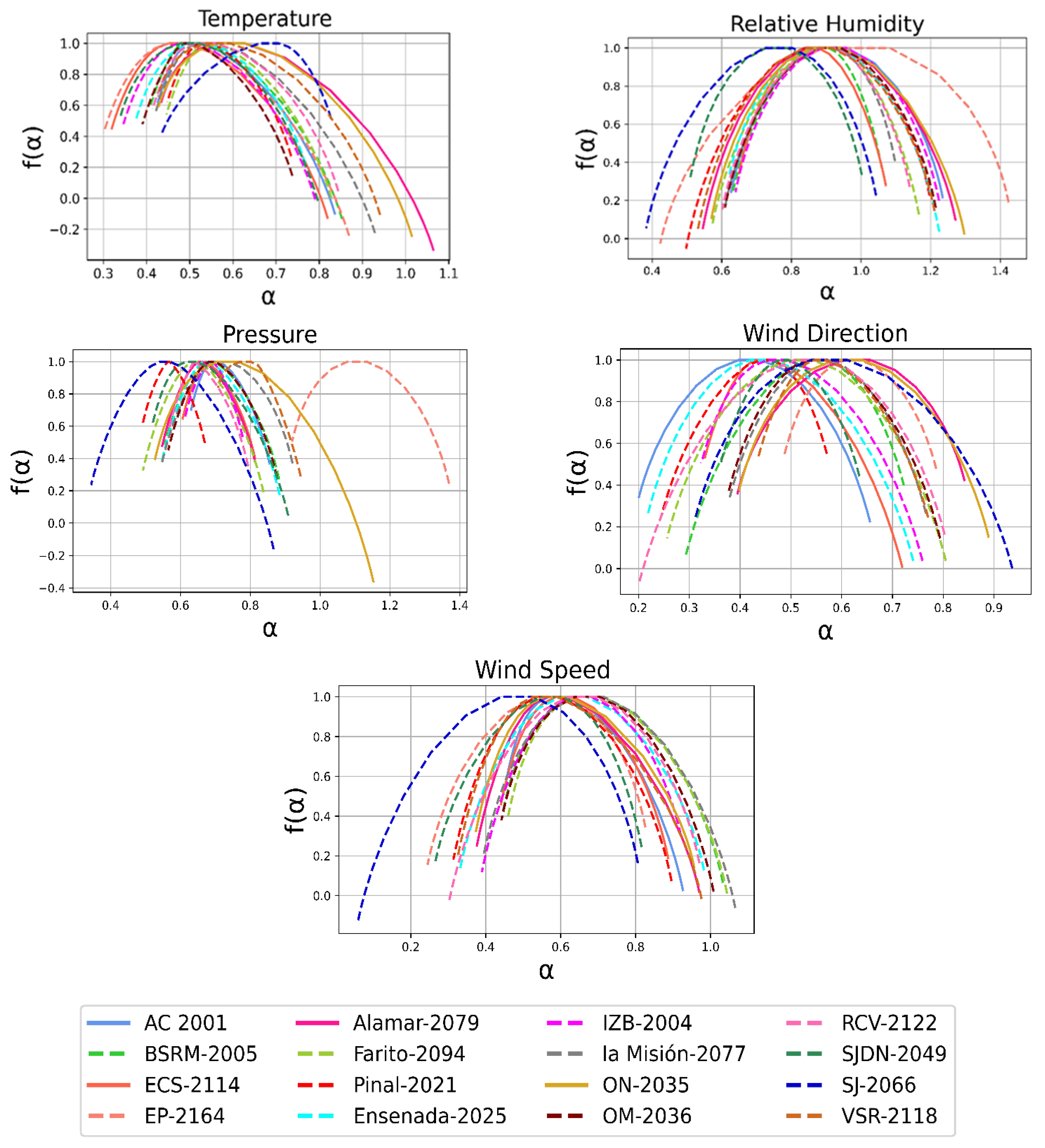
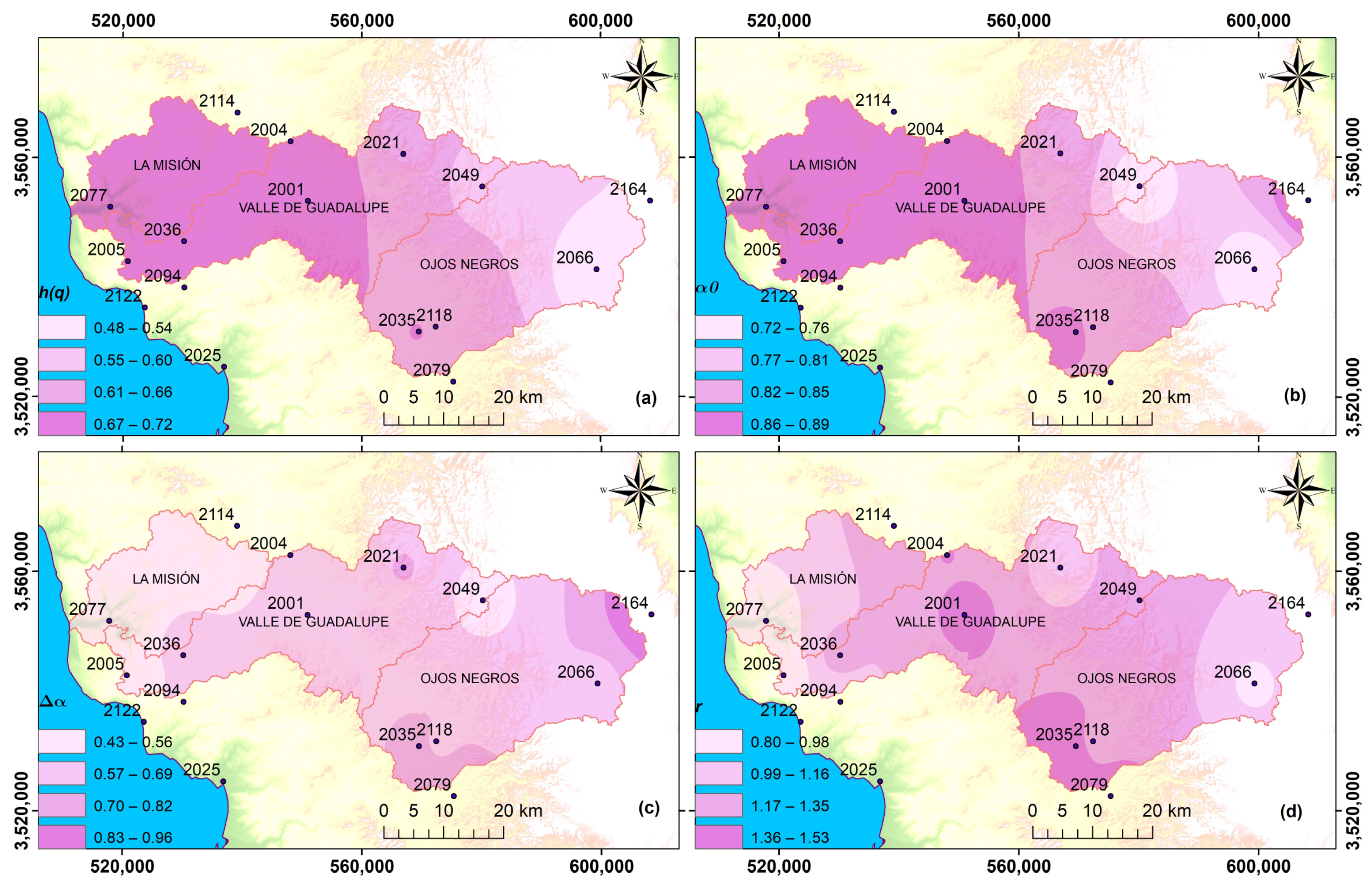
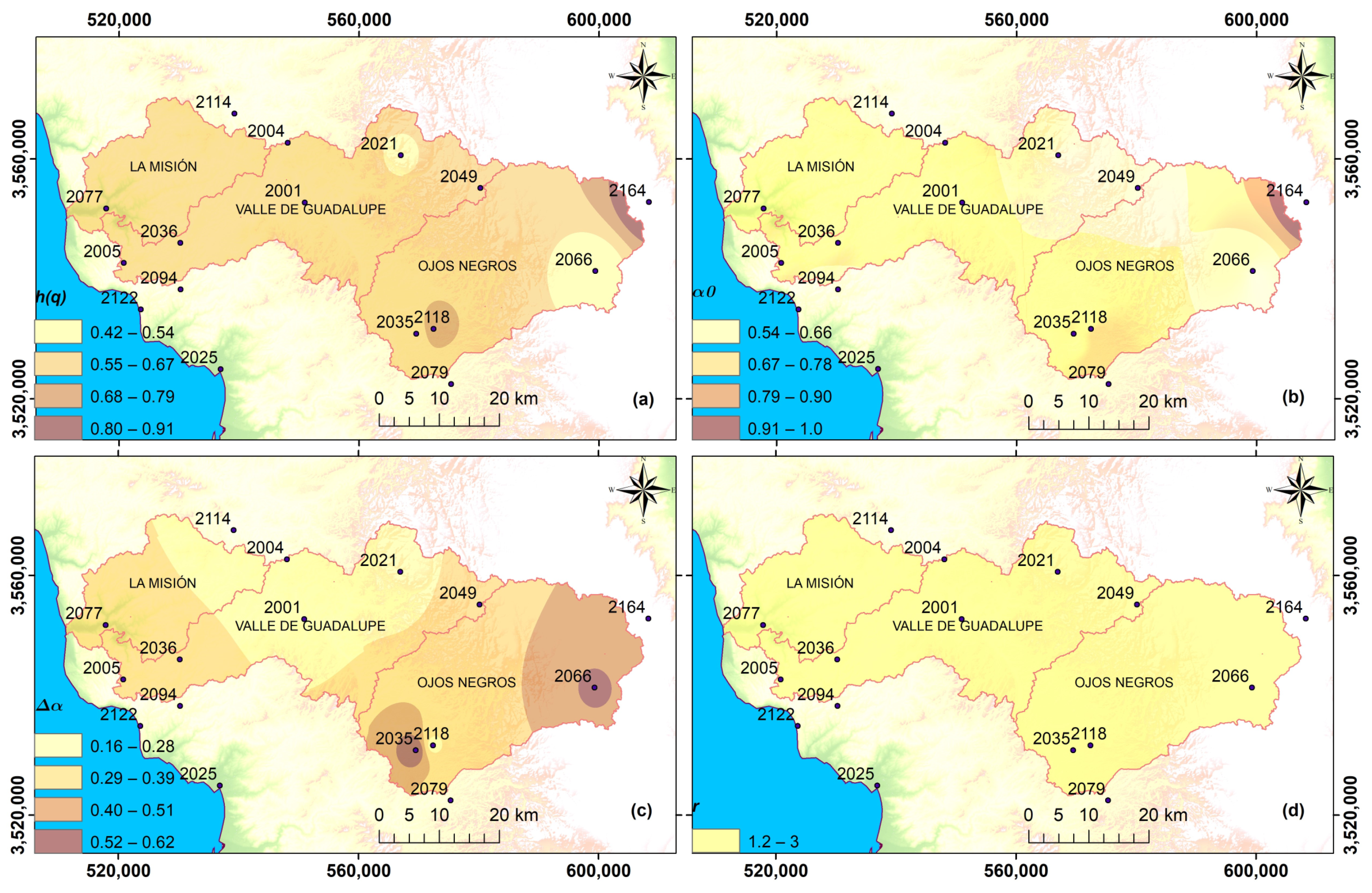
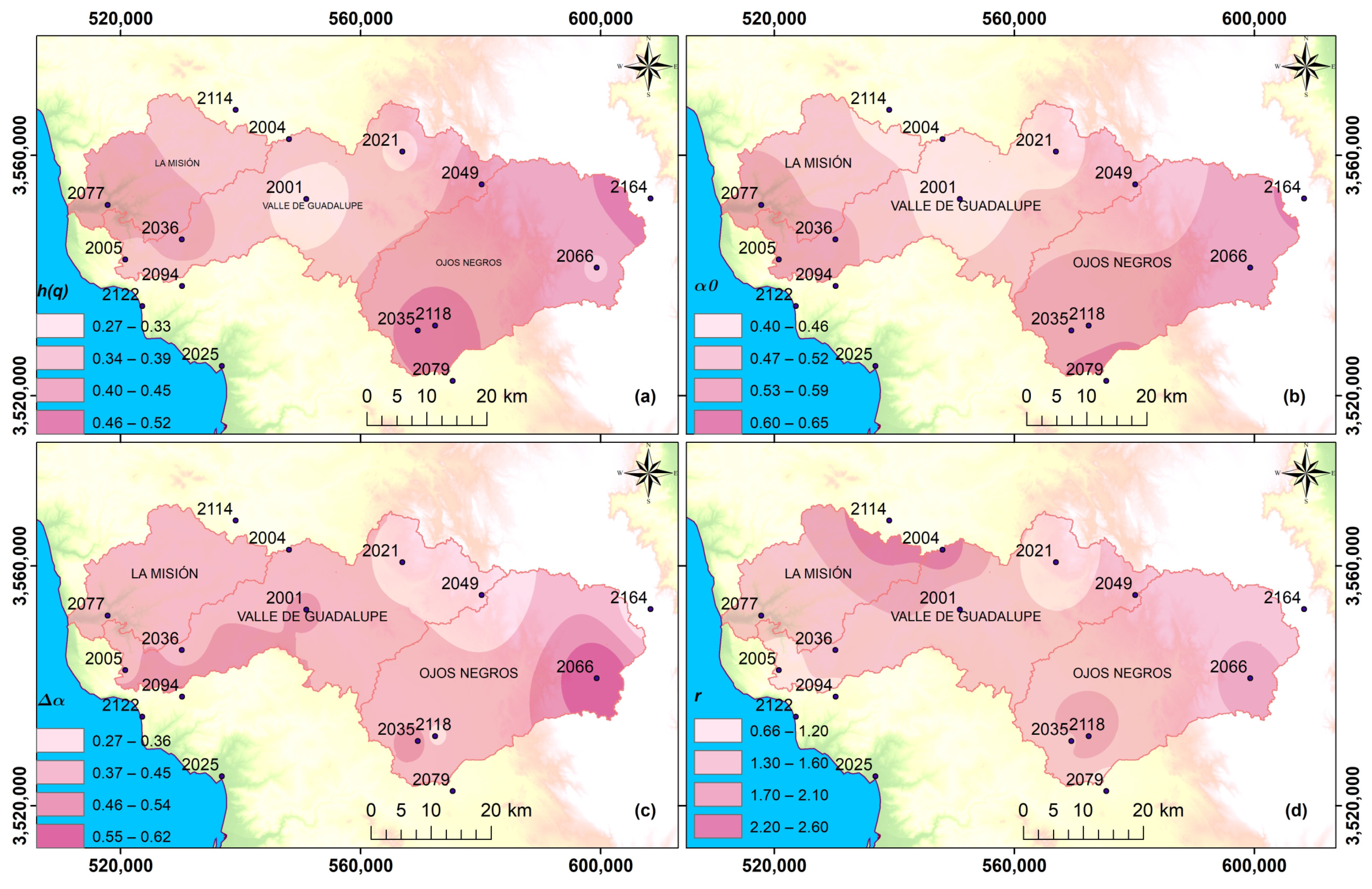
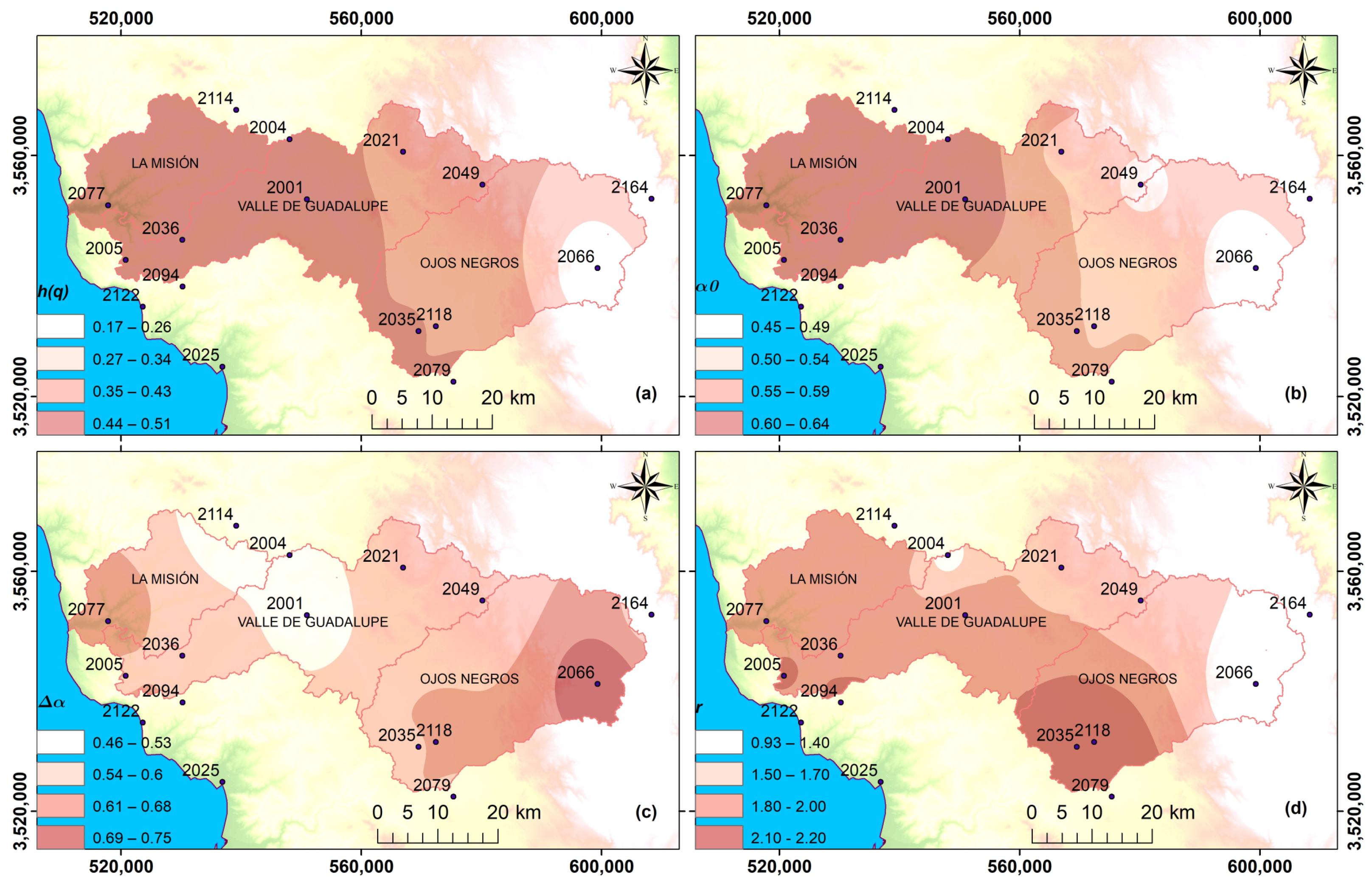
| Code | Name | Latitude | Longitude | Altitude |
|---|---|---|---|---|
| 2035 | Ojos Negros | 31.910 | −116.270 | 680 |
| 2066 | Sierra de Juárez | 32.000 | −115.950 | 1580 |
| 2079 | El Alamar | 31.840 | −116.200 | 710 |
| 2118 | Valle San Rafael | 31.920 | −116.230 | 721 |
| 2164 | Ejido El Porvenir | 32.110 | −115.850 | 330 |
| 2001 | Agua Caliente | 32.110 | −116.450 | 400 |
| 2004 | Ignacio Zaragoza Belén | 32.200 | −116.490 | 540 |
| 2005 | Boquilla Santa Rosa de la Misión | 32.020 | −116.780 | 250 |
| 2021 | El Pinal | 32.180 | −116.290 | 1320 |
| 2025 | Ensenada (Obs) | 31.860 | −116.610 | 21 |
| 2036 | Olivares Mexicanos | 32.050 | −116.680 | 340 |
| 2049 | San Juan de Dios Norte | 32.130 | −116.170 | 1280 |
| 2094 | El Farito | 31.980 | −116.670 | 250 |
| 2122 | Real del Castillo Viejo | 31.950 | −116.750 | 610 |
| 2077 | La Misión | 32.100 | −116.810 | 20 |
| 2114 | Ejido Carmen Serdán | 32.240 | −116.580 | 560 |
| Code Station | 2118 | 2035 | 2066 | 2079 | 2164 | 2001 | 2004 | 2005 | 2021 | 2025 | 2036 | 2049 | 2094 | 2122 | 2077 | 2114 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Temperature | m for q− | 0.86 | 0.92 | 0.79 | 0.96 | 0.74 | 0.70 | 0.69 | 0.74 | 0.68 | 0.70 | 0.67 | 0.71 | 0.75 | 0.77 | 0.83 | 0.73 |
| m for q+ | 0.45 | 0.46 | 0.47 | 0.46 | 0.35 | 0.48 | 0.40 | 0.45 | 0.48 | 0.50 | 0.44 | 0.38 | 0.49 | 0.45 | 0.46 | 0.37 | |
| hq(q = 10) | 0.46 | 0.47 | 0.49 | 0.47 | 0.36 | 0.46 | 0.40 | 0.45 | 0.49 | 0.42 | 0.44 | 0.39 | 0.49 | 0.46 | 0.47 | 0.37 | |
| Df | 1.54 | 1.53 | 1.51 | 1.53 | 1.64 | 1.54 | 1.60 | 1.55 | 1.51 | 1.58 | 1.56 | 1.61 | 1.51 | 1.54 | 1.53 | 1.63 | |
| 0.94 | 1.01 | 0.83 | 1.06 | 0.87 | 0.84 | 0.79 | 0.85 | 0.74 | 0.77 | 0.74 | 0.80 | 0.83 | 0.84 | 0.93 | 0.82 | ||
| 0.43 | 0.43 | 0.43 | 0.43 | 0.30 | 0.43 | 0.35 | 0.41 | 0.45 | 0.38 | 0.39 | 0.34 | 0.45 | 0.41 | 0.42 | 0.32 | ||
| 0.52 | 0.59 | 0.39 | 0.63 | 0.57 | 0.41 | 0.44 | 0.44 | 0.29 | 0.39 | 0.35 | 0.46 | 0.38 | 0.43 | 0.51 | 0.50 | ||
| Relative humidity | m for q− | 1.15 | 1.23 | 0.98 | 1.21 | 1.37 | 1.18 | 1.16 | 1.01 | 1.14 | 1.15 | 1.15 | 0.95 | 1.10 | 1.08 | 1.05 | 1.01 |
| m for q+ | 0.60 | 0.64 | 0.45 | 0.62 | 0.49 | 0.68 | 0.70 | 0.69 | 0.58 | 0.67 | 0.67 | 0.56 | 0.64 | 0.67 | 0.67 | 0.70 | |
| hq(q = 10) | 0.63 | 0.66 | 0.48 | 0.64 | 0.53 | 0.70 | 0.72 | 0.71 | 0.60 | 0.69 | 0.69 | 0.58 | 0.67 | 0.69 | 0.69 | 0.72 | |
| Df | 1.37 | 1.34 | 1.52 | 1.36 | 1.47 | 1.30 | 1.28 | 1.29 | 1.40 | 1.31 | 1.31 | 1.42 | 1.33 | 1.31 | 1.31 | 1.28 | |
| 1.21 | 1.30 | 1.04 | 1.27 | 1.42 | 1.23 | 1.22 | 1.06 | 1.20 | 1.22 | 1.21 | 1.00 | 1.17 | 1.14 | 1.10 | 1.07 | ||
| 0.53 | 0.57 | 0.38 | 0.55 | 0.42 | 0.63 | 0.64 | 0.63 | 0.50 | 0.62 | 0.61 | 0.51 | 0.57 | 0.60 | 0.61 | 0.65 | ||
| 0.68 | 0.73 | 0.66 | 0.73 | 1.00 | 0.61 | 0.58 | 0.43 | 0.70 | 0.60 | 0.61 | 0.49 | 0.59 | 0.54 | 0.49 | 0.42 | ||
| Pressure | m for q− | 0.88 | 1.04 | 0.77 | 0.76 | 1.31 | 0.80 | 0.74 | 0.82 | 0.63 | 0.82 | 0.82 | 0.83 | 0.77 | 0.80 | 0.87 | 0.76 |
| m for q+ | 0.72 | 0.57 | 0.41 | 0.59 | 0.96 | 0.66 | 0.64 | 0.60 | 0.53 | 0.60 | 0.61 | 0.55 | 0.55 | 0.54 | 0.60 | 0.64 | |
| hq(q = 10) | 0.72 | 0.59 | 0.42 | 0.60 | 0.97 | 0.66 | 0.65 | 0.61 | 0.53 | 0.61 | 0.62 | 0.56 | 0.56 | 0.55 | 0.61 | 0.64 | |
| Df | 1.28 | 1.41 | 1.58 | 1.40 | 1.03 | 1.34 | 1.35 | 1.39 | 1.47 | 1.39 | 1.38 | 1.44 | 1.44 | 1.45 | 1.39 | 1.36 | |
| 0.94 | 1.15 | 0.87 | 0.81 | 1.37 | 0.85 | 0.78 | 0.88 | 0.67 | 0.88 | 0.88 | 0.91 | 0.84 | 0.79 | 0.92 | 0.81 | ||
| 0.71 | 0.53 | 0.34 | 0.55 | 0.92 | 0.63 | 0.61 | 0.56 | 0.49 | 0.55 | 0.57 | 0.52 | 0.49 | 0.57 | 0.55 | 0.61 | ||
| 0.24 | 0.63 | 0.52 | 0.27 | 0.45 | 0.22 | 0.16 | 0.33 | 0.18 | 0.34 | 0.31 | 0.39 | 0.35 | 0.23 | 0.37 | 0.21 | ||
| Wind speed | m for q− | 0.91 | 0.90 | 0.74 | 0.90 | 0.78 | 0.85 | 0.87 | 0.96 | 0.83 | 0.92 | 0.93 | 0.76 | 0.97 | 0.91 | 0.99 | 0.82 |
| m for q+ | 0.39 | 0.43 | 0.14 | 0.44 | 0.31 | 0.49 | 0.46 | 0.49 | 0.38 | 0.40 | 0.49 | 0.33 | 0.51 | 0.38 | 0.04 | 0.48 | |
| hq(q = 10) | 0.41 | 0.44 | 0.17 | 0.45 | 0.33 | 0.50 | 0.48 | 0.50 | 0.40 | 0.42 | 0.50 | 0.35 | 0.52 | 0.41 | 0.47 | 0.49 | |
| Df | 1.59 | 1.56 | 1.83 | 1.55 | 1.67 | 1.50 | 1.52 | 1.50 | 1.60 | 1.58 | 1.50 | 1.65 | 1.48 | 1.59 | 1.53 | 1.51 | |
| 0.98 | 0.96 | 0.81 | 0.97 | 0.83 | 0.93 | 0.92 | 1.03 | 0.90 | 0.98 | 1.01 | 0.82 | 1.04 | 0.97 | 1.07 | 0.89 | ||
| 0.33 | 0.37 | 0.06 | 0.38 | 0.24 | 0.46 | 0.39 | 0.45 | 0.31 | 0.33 | 0.44 | 0.26 | 0.46 | 0.30 | 0.39 | 0.44 | ||
| 0.65 | 0.58 | 0.75 | 0.59 | 0.58 | 0.47 | 0.53 | 0.59 | 0.58 | 0.65 | 0.57 | 0.55 | 0.59 | 0.67 | 0.67 | 0.45 | ||
| Wind direction | m for q− | 0.71 | 0.82 | 0.86 | 0.80 | 0.75 | 0.59 | 0.68 | 0.67 | 0.53 | 0.66 | 0.72 | 0.59 | 0.73 | 0.74 | 0.71 | 0.64 |
| m for q+ | 0.48 | 0.45 | 0.37 | 0.44 | 0.52 | 0.25 | 0.36 | 0.37 | 0.31 | 0.28 | 0.43 | 0.40 | 0.32 | 0.29 | 0.43 | 0.37 | |
| hq(q = 10) | 0.48 | 0.46 | 0.39 | 0.46 | 0.53 | 0.27 | 0.37 | 0.39 | 0.32 | 0.29 | 0.44 | 0.41 | 0.34 | 0.31 | 0.45 | 0.38 | |
| Df | 1.52 | 1.54 | 1.61 | 1.54 | 1.47 | 1.73 | 1.63 | 1.61 | 1.68 | 1.71 | 1.56 | 1.59 | 1.66 | 1.69 | 1.55 | 1.62 | |
| 0.77 | 0.89 | 0.94 | 0.84 | 0.79 | 0.66 | 0.76 | 0.72 | 0.57 | 0.74 | 0.79 | 0.64 | 0.81 | 0.80 | 0.77 | 0.72 | ||
| 0.43 | 0.40 | 0.31 | 0.40 | 0.49 | 0.20 | 0.32 | 0.29 | 0.24 | 0.22 | 0.38 | 0.36 | 0.26 | 0.20 | 0.38 | 0.33 | ||
| 0.34 | 0.49 | 0.63 | 0.45 | 0.30 | 0.45 | 0.44 | 0.43 | 0.33 | 0.52 | 0.42 | 0.27 | 0.55 | 0.60 | 0.39 | 0.39 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serpa-Usta, Y.; López-Lambraño, A.A.; Fuentes, C.; Flores, D.-L.; González-Durán, M.; López-Ramos, A. Santa Ana Winds: Multifractal Measures and Singularity Spectrum. Atmosphere 2023, 14, 1751. https://doi.org/10.3390/atmos14121751
Serpa-Usta Y, López-Lambraño AA, Fuentes C, Flores D-L, González-Durán M, López-Ramos A. Santa Ana Winds: Multifractal Measures and Singularity Spectrum. Atmosphere. 2023; 14(12):1751. https://doi.org/10.3390/atmos14121751
Chicago/Turabian StyleSerpa-Usta, Yeraldin, Alvaro Alberto López-Lambraño, Carlos Fuentes, Dora-Luz Flores, Mario González-Durán, and Alvaro López-Ramos. 2023. "Santa Ana Winds: Multifractal Measures and Singularity Spectrum" Atmosphere 14, no. 12: 1751. https://doi.org/10.3390/atmos14121751
APA StyleSerpa-Usta, Y., López-Lambraño, A. A., Fuentes, C., Flores, D.-L., González-Durán, M., & López-Ramos, A. (2023). Santa Ana Winds: Multifractal Measures and Singularity Spectrum. Atmosphere, 14(12), 1751. https://doi.org/10.3390/atmos14121751








