Prediction of PM2.5 Concentration Using Spatiotemporal Data with Machine Learning Models
Abstract
:1. Introduction
2. Data and Model Implementation
2.1. Data Description
2.2. Development of Predictive Models
2.2.1. Random Forest Model
- (1)
- Create the original dataset D;
- (2)
- A subset is randomly selected from the dataset as the training dataset, where Dj is the training dataset of the jth iteration and j is the iteration number of the classifier (j = 1, 2 …, J). Each decision tree is constructed using a random subspace partition strategy, from which the optimal features are selected to split. After repeated training, Q decision trees are obtained and a random forest is formed.
- (3)
- The prediction result is the average value of each decision tree.
2.2.2. Ridge Regression Model
2.2.3. Support Vector Machine Model
2.2.4. Extremely Randomized Trees Model
2.3. Evaluation Metrics
3. Results
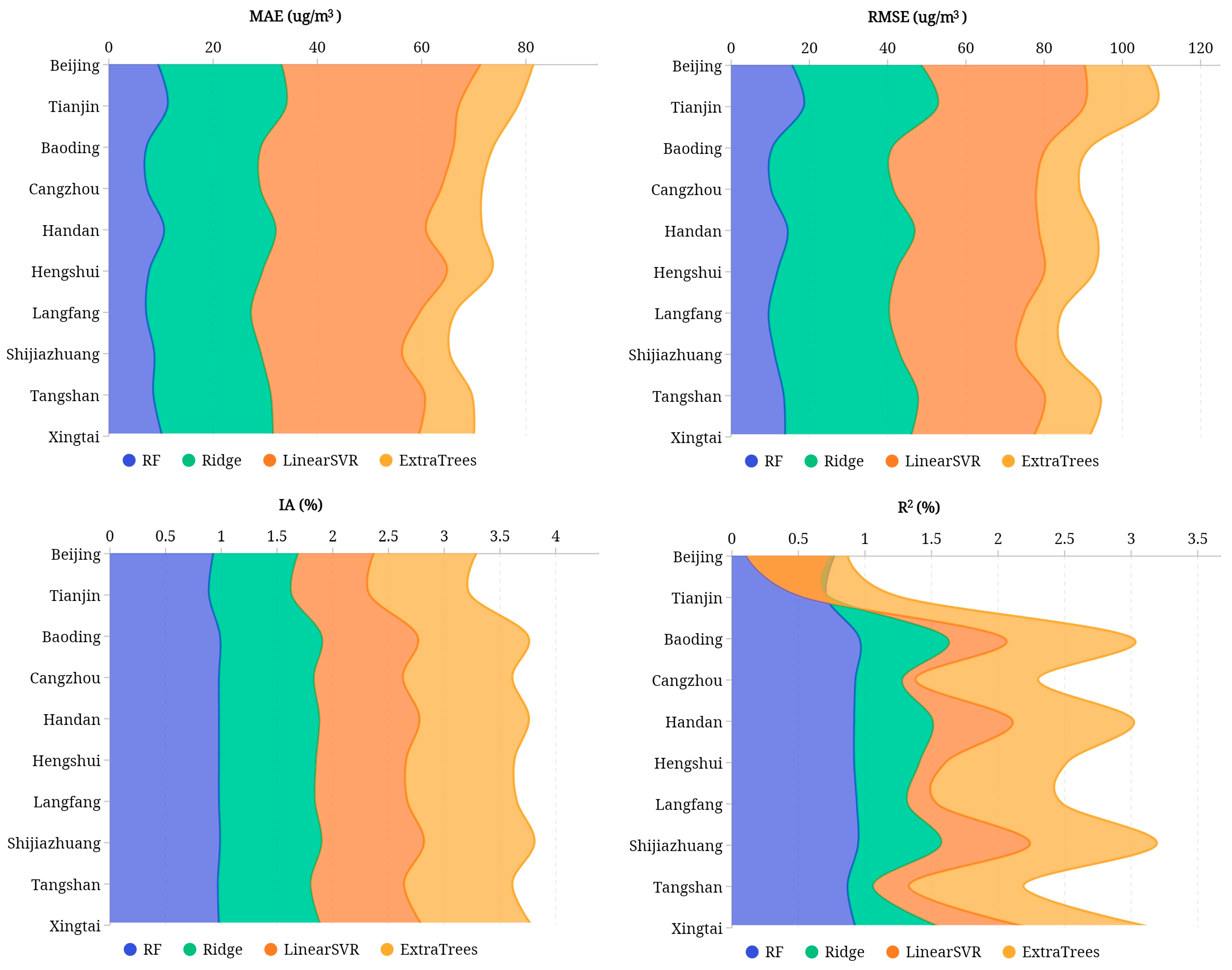
3.1. Prediction Comparison Based on City Level
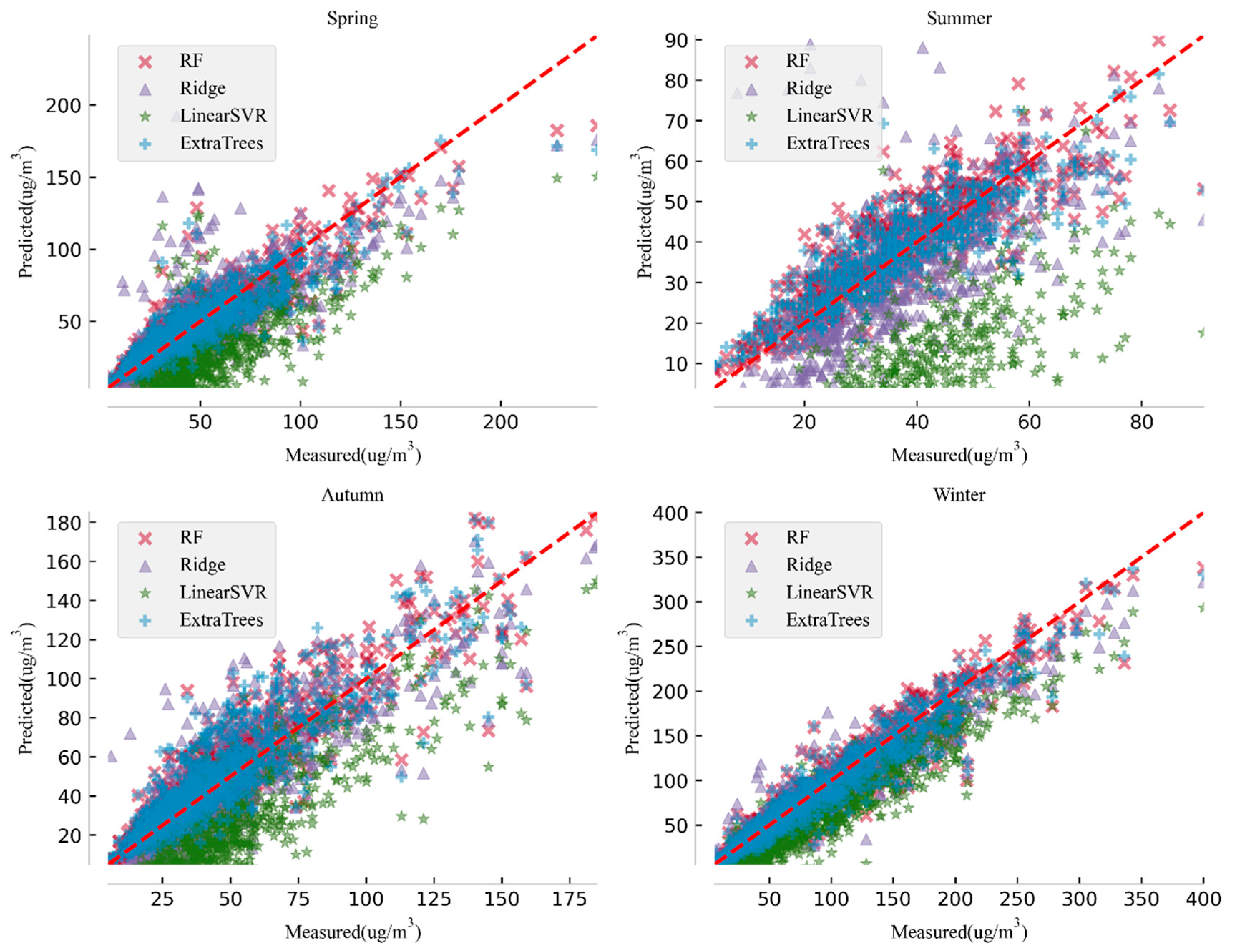
3.2. Prediction Comparison Based on Seasons
3.3. Overall Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lewis, S.L.; Maslin, M.A. Defining the anthropocene. Nature 2015, 519, 171–180. [Google Scholar] [CrossRef]
- Steffen, W.; Grinevald, J.; Crutzen, P.; McNeill, J. The Anthropocene: Conceptual and historical perspectives. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 842–867. [Google Scholar] [CrossRef]
- Lelieveld, J. Clean air in the Anthropocene. Faraday Discuss. 2017, 200, 693–703. [Google Scholar] [CrossRef]
- Xing, Y.; Xu, Y.; Shi, M.; Lian, Y. The impact of PM2.5 on the human respiratory system. J. Thorac. Dis. 2016, 8, E69. [Google Scholar]
- Apte, J.S.; Brauer, M.; Cohen, A.J.; Ezzati, M.; Pope, C.A., III. Ambient PM2.5 reduces global and regional life expectancy. Environ. Sci. Technol. Lett. 2018, 5, 546–551. [Google Scholar] [CrossRef]
- Al-Hemoud, A.; Gasana, J.; Al-Dabbous, A.; Alajeel, A.; Al-Shatti, A.; Behbehani, W.; Malak, M. Exposure levels of air pollution (PM2.5) and associated health risk in Kuwait. Environ. Res. 2019, 179, 108730. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Gao, D.; Liao, F.; Zhou, F.; Wang, X. The health effects of ambient PM2.5 and potential mechanisms. Ecotoxicol. Environ. Saf. 2016, 128, 67–74. [Google Scholar] [CrossRef] [PubMed]
- McDuffie, E.E.; Martin, R.V.; Spadaro, J.V.; Burnett, R.; Smith, S.J.; O’Rourke, P.; Hammer, M.S.; van Donkelaar, A.; Bindle, L.; Shah, V. Source sector and fuel contributions to ambient PM2.5 and attributable mortality across multiple spatial scales. Nat. Commun. 2021, 12, 3594. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Hu, J.; Xue, T.; Xu, H.; Wang, M. High-resolution spatiotemporal modeling for ambient PM2.5 exposure assessment in China from 2013 to 2019. Environ. Sci. Technol. 2021, 55, 2152–2162. [Google Scholar] [CrossRef]
- Chakrabarty, R.K.; Beeler, P.; Liu, P.; Goswami, S.; Harvey, R.D.; Pervez, S.; van Donkelaar, A.; Martin, R.V. Ambient PM2.5 exposure and rapid spread of COVID-19 in the United States. Sci. Total Environ. 2021, 760, 143391. [Google Scholar] [CrossRef]
- Cao, J.; Chow, J.C.; Lee, F.S.; Watson, J.G. Evolution of PM2.5 measurements and standards in the US and future perspectives for China. Aerosol Air Qual. Res. 2013, 13, 1197–1211. [Google Scholar] [CrossRef]
- Chow, J.; Watson, J.; Cao, J. Highlights from Leapfrogging Opportunities for Air Quality Improvement. EM 2010, 16, 38–43. [Google Scholar]
- Shin, S.E.; Jung, C.H.; Kim, Y. Analysis of the measurement difference for the PM10 concentrations between Beta-ray absorption and gravimetric methods at Gosan. Aerosol Air Qual. Res. 2011, 11, 846–853. [Google Scholar] [CrossRef]
- Takahashi, K.; Minoura, H.; Sakamoto, K. Examination of discrepancies between beta-attenuation and gravimetric methods for the monitoring of particulate matter. Atmos. Environ. 2008, 42, 5232–5240. [Google Scholar] [CrossRef]
- Tasić, V.; Jovašević-Stojanović, M.; Vardoulakis, S.; Milošević, N.; Kovačević, R.; Petrović, J. Comparative assessment of a real-time particle monitor against the reference gravimetric method for PM10 and PM2.5 in indoor air. Atmos. Environ. 2012, 54, 358–364. [Google Scholar] [CrossRef]
- Karagulian, F.; Belis, C.A.; Dora, C.F.C.; Prüss-Ustün, A.M.; Bonjour, S.; Adair-Rohani, H.; Amann, M. Contributions to cities’ ambient particulate matter (PM): A systematic review of local source contributions at global level. Atmos. Environ. 2015, 120, 475–483. [Google Scholar] [CrossRef]
- Singh, N.; Murari, V.; Kumar, M.; Barman, S.C.; Banerjee, T. Fine particulates over South Asia: Review and meta-analysis of PM2.5 source apportionment through receptor model. Environ. Pollut. 2017, 223, 121–136. [Google Scholar] [CrossRef]
- Saraga, D.E.; Tolis, E.I.; Maggos, T.; Vasilakos, C.; Bartzis, J.G. PM2.5 source apportionment for the port city of Thessaloniki, Greece. Sci. Total Environ. 2019, 650, 2337–2354. [Google Scholar] [CrossRef]
- Zheng, M.; Salmon, L.G.; Schauer, J.J.; Zeng, L.; Kiang, C.S.; Zhang, Y.; Cass, G.R. Seasonal trends in PM2.5 source contributions in Beijing, China. Atmos. Environ. 2005, 39, 3967–3976. [Google Scholar] [CrossRef]
- Zhang, X.; Ji, G.; Peng, X.; Kong, L.; Zhao, X.; Ying, R.; Yin, W.; Xu, T.; Cheng, J.; Wang, L. Characteristics of the chemical composition and source apportionment of PM2.5 for a one-year period in Wuhan, China. J. Atmos. Chem. 2022, 79, 101–115. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, J.; Wang, S.; He, K.; Zheng, M. Review of receptor-based source apportionment research of fine particulate matter and its challenges in China. Sci. Total Environ. 2017, 586, 917–929. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, C.; Xue, C.; Mu, Y.; Liu, J.; Zhang, Y.; Tian, D.; Ye, C.; Zhang, H.; Guan, J. The contribution of residential coal combustion to atmospheric PM2.5 in northern China during winter. Atmos. Chem. Phys. 2017, 17, 11503–11520. [Google Scholar] [CrossRef]
- Askariyeh, M.H.; Khreis, H.; Vallamsundar, S. Chapter 5—Air pollution monitoring and modeling. In Traffic-Related Air Pollution; Khreis, H., Nieuwenhuijsen, M., Zietsman, J., Ramani, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 111–135. [Google Scholar]
- Hu, J.; Ostro, B.; Zhang, H.; Ying, Q.; Kleeman, M.J. Using chemical transport model predictions to improve exposure assessment of PM2.5 constituents. Environ. Sci. Technol. Lett. 2019, 6, 456–461. [Google Scholar]
- Polat, E.; Gunay, S. The comparison of partial least squares regression, principal component regression and ridge regression with multiple linear regression for predicting pm10 concentration level based on meteorological parameters. J. Data Sci. 2015, 13, 663–692. [Google Scholar] [CrossRef]
- Singh, K.P.; Gupta, S.; Kumar, A.; Shukla, S.P. Linear and nonlinear modeling approaches for urban air quality prediction. Sci. Total Environ. 2012, 426, 244–255. [Google Scholar] [CrossRef] [PubMed]
- Sampson, P.D.; Richards, M.; Szpiro, A.A.; Bergen, S.; Sheppard, L.; Larson, T.V.; Kaufman, J.D. A regionalized national universal kriging model using Partial Least Squares regression for estimating annual PM2.5 concentrations in epidemiology. Atmos. Environ. 2013, 75, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Faganeli Pucer, J.; Pirš, G.; Štrumbelj, E. A Bayesian approach to forecasting daily air-pollutant levels. Knowl. Inf. Syst. 2018, 57, 635–654. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, H.; Mao, G.; Yang, P. A Bayesian hierarchical model for urban air quality prediction under uncertainty. Atmos. Environ. 2008, 42, 8464–8469. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, H.; Palazoglu, A.; Singh, A.; Zhang, W.; Liu, S. Prediction of 24-h-average PM2.5 concentrations using a hidden Markov model with different emission distributions in Northern California. Sci. Total Environ. 2013, 443, 93–103. [Google Scholar] [CrossRef]
- Ni, X.Y.; Huang, H.; Du, W. Relevance analysis and short-term prediction of PM2.5 concentrations in Beijing based on multi-source data. Atmos. Environ. 2017, 150, 146–161. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, Z.; Meng, X.; Cheng, S.; Sun, W. Research on prediction method of api based on the enhanced moving average method. In Proceedings of the 2012 International Conference on Systems and Informatics (ICSAI2012), Yantai, China, 19–20 May 2012. [Google Scholar]
- Kumar, U.; Jain, V.K. ARIMA forecasting of ambient air pollutants (O3, NO, NO2 and CO). Stoch. Environ. Res. Risk Assess. 2010, 24, 751–760. [Google Scholar] [CrossRef]
- Abhilash, M.; Thakur, A.; Gupta, D.; Sreevidya, B. Time series analysis of air pollution in Bengaluru using ARIMA model. In Ambient Communications and Computer Systems; Springer: Berlin/Heidelberg, Germany, 2018; pp. 413–426. [Google Scholar]
- Bhatti, U.A.; Yan, Y.; Zhou, M.; Ali, S.; Hussain, A.; Qingsong, H.; Yu, Z.; Yuan, L. Time series analysis and forecasting of air pollution particulate matter (PM2.5): An SARIMA and factor analysis approach. IEEE Access 2021, 9, 41019–41031. [Google Scholar] [CrossRef]
- Niu, M.; Wang, Y.; Sun, S.; Li, Y. A novel hybrid decomposition-and-ensemble model based on CEEMD and GWO for short-term PM2.5 concentration forecasting. Atmos. Environ. 2016, 134, 168–180. [Google Scholar] [CrossRef]
- Liao, K.; Huang, X.; Dang, H.; Ren, Y.; Zuo, S.; Duan, C. Statistical approaches for forecasting primary air pollutants: A review. Atmosphere 2021, 12, 686. [Google Scholar] [CrossRef]
- Masood, A.; Ahmad, K. A model for particulate matter (PM2.5) prediction for Delhi based on machine learning approaches. Procedia Comput. Sci. 2020, 167, 2101–2110. [Google Scholar] [CrossRef]
- Ordieres, J.B.; Vergara, E.P.; Capuz, R.S.; Salazar, R.E. Neural network prediction model for fine particulate matter (PM2.5) on the US–Mexico border in El Paso (Texas) and Ciudad Juárez (Chihuahua). Environ. Model. Softw. 2005, 20, 547–559. [Google Scholar] [CrossRef]
- Khan, N.U.; Shah, M.A.; Maple, C.; Ahmed, E.; Asghar, N. Traffic flow prediction: An intelligent scheme for forecasting traffic flow using air pollution data in smart cities with bagging ensemble. Sustainability 2022, 14, 4164. [Google Scholar] [CrossRef]
- Liu, H.; Jin, K.; Duan, Z. Air PM2.5 concentration multi-step forecasting using a new hybrid modeling method: Comparing cases for four cities in China. Atmos. Pollut. Res. 2019, 10, 1588–1600. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, H.; Qin, Z.; Zhang, G. A novel hybrid-Garch model based on ARIMA and SVM for PM2.5 concentrations forecasting. Atmos. Pollut. Res. 2017, 8, 850–860. [Google Scholar] [CrossRef]
- Yu, B.; Huang, C.; Liu, Z.; Wang, H.; Wang, L. A chaotic analysis on air pollution index change over past 10 years in Lanzhou, northwest China. Stoch. Environ. Res. Risk Assess. 2011, 25, 643–653. [Google Scholar] [CrossRef]
- Kumar, U.; Prakash, A.; Jain, V. Characterization of chaos in air pollutants: A Volterra–Wiener–Korenberg series and numerical titration approach. Atmos. Environ. 2008, 42, 1537–1551. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, F. How industrial transfer processes impact on haze pollution in China: An analysis from the perspective of spatial effects. Int. J. Environ. Res. Public. Health 2019, 16, 423. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Wang, S.; Zhang, W.; Wang, H.; Wang, H.; Wang, S.; Li, H. Characteristics and influencing factors of urban air quality in Beijing-Tianjin-Hebei and its surrounding areas (‘2 + 26’ cities). Res. Environ. Sci. 2021, 34, 172–184. [Google Scholar]
- Han, J.; Chen, W.-Q.; Zhang, L.; Liu, G. Uncovering the Spatiotemporal Dynamics of Urban Infrastructure Development: A High Spatial Resolution Material Stock and Flow Analysis. Environ. Sci. Technol. 2018, 52, 12122–12132. [Google Scholar] [CrossRef] [PubMed]
- Dong, L.; Wang, Y.; Scipioni, A.; Park, H.-S.; Ren, J. Recent progress on innovative urban infrastructures system towards sustainable resource management. Resour. Conserv. Recycl. 2018, 128, 355–359. [Google Scholar] [CrossRef]
- Zhang, G.; Ge, R.; Lin, T.; Ye, H.; Li, X.; Huang, N. Spatial apportionment of urban greenhouse gas emission inventory and its implications for urban planning: A case study of Xiamen, China. Ecol. Indic. 2018, 85, 644–656. [Google Scholar] [CrossRef]



| Selected Features | ||||||
|---|---|---|---|---|---|---|
| PM10 | SO2 | NO2 | CO | O3 | Lowest temperature | Highest temperature |
| Wind speed | Year | Month | Season | PM2.5_L1 | PM2.5_L2 | PM2.5_L3 |
| PM2.5_L4 | PM2.5_L5 | AQI_L5 | AQI ranking_L5 | PM10_L5 | SO2_L5 | NO2_L5 |
| CO_L5 | O3_L5 | Lowest temperature _L5 | Highest temperature _L5 | Wind speed _L5 | Year_L5 | Month_L5 |
| Season_L5 | ||||||
| Unit | Mean | Variance | Minimum | 25% Quantile | Median | 75% Quantile | Maximum | |
|---|---|---|---|---|---|---|---|---|
| AQI | ____ | 116.41 | 5156.15 | 16 | 69 | 96 | 138 | 500 |
| PM2.5 | μg/m3 | 78.66 | 4374.42 | 0 | 36 | 59 | 98 | 796 |
| PM10 | μg/m3 | 134.76 | 8786.33 | 0 | 72 | 110 | 168 | 937 |
| SO2 | μg/m3 | 32.60 | 1220.53 | 0 | 11 | 21 | 40 | 437 |
| NO2 | μg/m3 | 48.32 | 559.85 | 0 | 31 | 44 | 61 | 235 |
| CO | μg/m3 | 1.40 | 1.11 | 0 | 0.75 | 1.09 | 1.7 | 18.92 |
| O3 | μg/m3 | 57.98 | 1491.04 | 0 | 26 | 51 | 83 | 234 |
| Lowest temperature | °C | 8.72 | 117.92 | −20 | −2 | 9 | 19 | 29 |
| Highest temperature | °C | 19.05 | 123.20 | −12 | 9 | 20 | 29 | 40 |
| Wind speed | Force (Beaufort scale) | 2.41 | 1.00 | 0 | 2 | 3 | 3 | 8 |
| City | RF | Ridge | LinearSVR | ExtraTrees | |
|---|---|---|---|---|---|
| Beijing | MAE | 9.47 | 23.64 | 38.26 | 10.08 |
| RMSE | 15.56 | 32.98 | 41.85 | 16.09 | |
| IA | 0.93 | 0.76 | 0.68 | 0.92 | |
| R2 | 0.77 | −0.02 | −0.64 | 0.76 | |
| Tianjin | MAE | 11.33 | 22.72 | 33.13 | 11.30 |
| RMSE | 18.64 | 34.17 | 37.50 | 18.23 | |
| IA | 0.89 | 0.74 | 0.70 | 0.90 | |
| R2 | 0.71 | 0.02 | −0.19 | 0.72 | |
| Baoding | MAE | 7.26 | 21.92 | 36.98 | 7.59 |
| RMSE | 10.57 | 30.57 | 39.48 | 11.07 | |
| IA | 0.99 | 0.91 | 0.86 | 0.99 | |
| R2 | 0.96 | 0.66 | 0.43 | 0.96 | |
| Cangzhou | MAE | 7.36 | 21.69 | 34.73 | 7.81 |
| RMSE | 10.21 | 31.22 | 36.60 | 10.99 | |
| IA | 0.98 | 0.85 | 0.80 | 0.98 | |
| R2 | 0.93 | 0.35 | 0.10 | 0.92 | |
| Handan | MAE | 10.65 | 21.40 | 28.79 | 10.79 |
| RMSE | 14.51 | 32.44 | 31.75 | 14.72 | |
| IA | 0.98 | 0.90 | 0.90 | 0.98 | |
| R2 | 0.92 | 0.59 | 0.60 | 0.91 | |
| Hengshui | MAE | 7.80 | 21.72 | 35.40 | 8.58 |
| RMSE | 11.87 | 30.33 | 37.96 | 12.66 | |
| IA | 0.98 | 0.87 | 0.81 | 0.97 | |
| R2 | 0.92 | 0.49 | 0.20 | 0.91 | |
| Langfang | MAE | 7.17 | 20.10 | 32.44 | 6.77 |
| RMSE | 9.62 | 30.79 | 34.52 | 9.46 | |
| IA | 0.98 | 0.86 | 0.83 | 0.98 | |
| R2 | 0.94 | 0.38 | 0.22 | 0.94 | |
| Shijiazhuang | MAE | 8.77 | 20.40 | 27.09 | 9.12 |
| RMSE | 11.15 | 31.99 | 29.97 | 11.70 | |
| IA | 0.99 | 0.91 | 0.92 | 0.99 | |
| R2 | 0.95 | 0.62 | 0.67 | 0.95 | |
| Tangshan | MAE | 8.57 | 22.50 | 29.54 | 9.01 |
| RMSE | 13.49 | 34.28 | 32.46 | 14.10 | |
| IA | 0.97 | 0.83 | 0.84 | 0.97 | |
| R2 | 0.87 | 0.19 | 0.27 | 0.86 | |
| Xingtai | MAE | 10.26 | 21.23 | 27.94 | 10.58 |
| RMSE | 13.85 | 32.08 | 31.42 | 14.16 | |
| IA | 0.98 | 0.91 | 0.91 | 0.98 | |
| R2 | 0.93 | 0.64 | 0.66 | 0.93 | |
| City | RF | Ridge | LinearSVR | ExtraTrees | ||||
|---|---|---|---|---|---|---|---|---|
| 90% | 75% | 90% | 75% | 90% | 75% | 90% | 75% | |
| Beijing | −20–32 | −14–9 | −29–159 | −26–60 | −55–61 | −52–−20 | −21–36 | −17–7 |
| Tianjin | −22–44 | −17–10 | −25–173 | −18–65 | −54–70 | −45–−13 | −23–44 | −16–9 |
| Baoding | −13–40 | −10–9 | −25–145 | −20–58 | −52–47 | −48–−21 | −13–33 | −11–10 |
| Cangzhou | −14–39 | −10–11 | −21–176 | −18–63 | −48–78 | −45–−19 | −15–41 | −11–10 |
| Handan | −7–47 | −5–21 | −18–107 | −16–67 | −46–42 | −41–−8 | −11–52 | −7–20 |
| Hengshui | −16–34 | −12–9 | −24–91 | −20–60 | −52–12 | −48–−19 | −19–32 | −13–8 |
| Langfang | −7–34 | −6–14 | −19–166 | −16–65 | −46–63 | −43–−17 | −9–38 | −6–11 |
| Shijiazhuang | −9–39 | −6–16 | −16–105 | −14–69 | −44–47 | −39–−9 | −10–35 | −6–16 |
| Tangshang | −7–88 | −5–17 | −20–187 | −17–65 | −45–87 | −43–−11 | −8–93 | −4–17 |
| Xingtai | −14–60 | −9–16 | −19–110 | −15–65 | −45–47 | −41–−9 | −16–56 | −11–15 |
| RF | Ridge | LinearSVR | ExtraTrees | ||
|---|---|---|---|---|---|
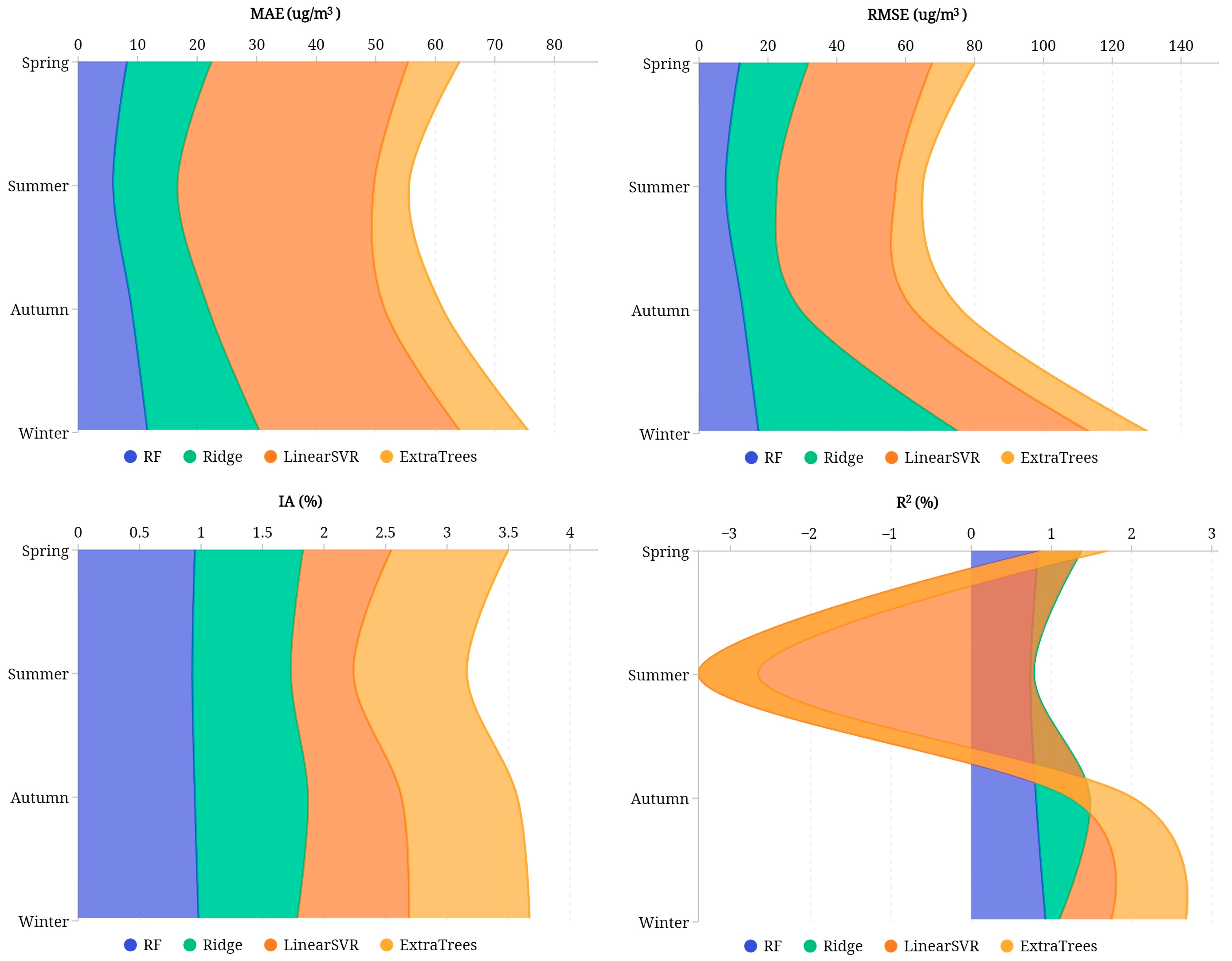
| Spring | MAE | 8.26 | 14.21 | 33.02 | 8.61 |
| RMSE | 11.87 | 19.94 | 35.98 | 12.31 | |
| IA | 0.95 | 0.88 | 0.72 | 0.95 | |
| R2 | 0.84 | 0.54 | −0.49 | 0.82 | |
| Summer | MAE | 5.91 | 10.77 | 33.04 | 5.84 |
| RMSE | 7.75 | 14.89 | 34.55 | 7.78 | |
| IA | 0.93 | 0.80 | 0.51 | 0.92 | |
| R2 | 0.74 | 0.04 | −4.18 | 0.74 | |
| Autumn | MAE | 9.02 | 12.86 | 29.58 | 9.73 |
| RMSE | 12.71 | 16.72 | 32.78 | 13.84 | |
| IA | 0.95 | 0.92 | 0.76 | 0.94 | |
| R2 | 0.81 | 0.67 | −0.25 | 0.78 | |
| Winter | MAE | 11.68 | 18.89 | 33.74 | 11.50 |
| RMSE | 17.35 | 58.81 | 38.01 | 16.94 | |
| IA | 0.98 | 0.80 | 0.91 | 0.98 | |
| R2 | 0.93 | 0.16 | 0.65 | 0.93 | |
| Model | Occupied Memory Size (KB) | Model Construction Time (S) |
|---|---|---|
| RF | 136,192 | 63.96 |
| Ridge | 3.79 | 2.27 |
| Linear SVR | 3.81 | 8.07 |
| Extra Trees | 227,328 | 28.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Chen, T.; Ge, R.; Xv, F.; Cui, C.; Li, J. Prediction of PM2.5 Concentration Using Spatiotemporal Data with Machine Learning Models. Atmosphere 2023, 14, 1517. https://doi.org/10.3390/atmos14101517
Ma X, Chen T, Ge R, Xv F, Cui C, Li J. Prediction of PM2.5 Concentration Using Spatiotemporal Data with Machine Learning Models. Atmosphere. 2023; 14(10):1517. https://doi.org/10.3390/atmos14101517
Chicago/Turabian StyleMa, Xin, Tengfei Chen, Rubing Ge, Fan Xv, Caocao Cui, and Junpeng Li. 2023. "Prediction of PM2.5 Concentration Using Spatiotemporal Data with Machine Learning Models" Atmosphere 14, no. 10: 1517. https://doi.org/10.3390/atmos14101517
APA StyleMa, X., Chen, T., Ge, R., Xv, F., Cui, C., & Li, J. (2023). Prediction of PM2.5 Concentration Using Spatiotemporal Data with Machine Learning Models. Atmosphere, 14(10), 1517. https://doi.org/10.3390/atmos14101517







