Abstract
Previous studies have successfully assessed the extent to which a kinetic model accurately represents a specific reaction mechanism by comparing the kinetic parameters derived from the kinetic model to those obtained using isoconversional methods. However, this approach remains underdeveloped for the important steam gasification reaction of char. This study addresses this issue by conducting a series of steam-assisted char gasification tests, using thermogravimetric analysis at five different heating rates. The results indicate that the carbon conversion ratio of the char gasification reaction increases with the increasing heating rate. The activation energies of the reaction process are determined with different carbon conversion ratios using three isoconversional methods, including the Flynn–Wall–Ozawa, Kissinger–Akahira–Sunose, and Starink methods. The gasification mechanism is also analyzed using model-fitting methods with a wide variety of carbon conversion models, and the accuracies of the models are evaluated, firstly, by comparing the obtained goodness of fit values of the models with the experimental results, and, secondly, by comparing the obtained activation energies with those derived using the isoconversional methods. The goodness of fit results and the results of the comparisons between the activation energies obtained using the various models with the isoconversional values demonstrate that the three-dimensional Avrami–Erofeev model best represents the steam gasification char reaction, where the difference between the two activation energy values is only 0.70 KJ.mol−1. The reliability of the proposed approach for evaluating the applicability of a given kinetic model to the steam gasification reaction of char is tested by comparing the results obtained for char samples derived from three different bituminous coal sources.
1. Introduction
Coal gasification is a well-developed means of converting coal into a clean energy source for heating and electricity generation purposes and for the production of chemical feedstocks. Typically, coal gasification is a two-step process, involving reactions that are categorized into pyrolysis, gasification, and gas-phase reaction mechanisms. The first stage, the pyrolysis process, generates vaporous components by heating the coal at a relatively low temperature (450–600 °C) in the absence of air. The separation of these vaporous components leaves behind a residue of charcoal, which is converted, in a second stage, the char gasification process, into carbon monoxide (CO) through reactions with oxygen-bearing compounds at a relatively high temperature (700–1200 °C). Clearly, char gasification represents the rate-limiting step of the coal gasification process, and numerous methods have been developed for analyzing the reaction kinetics of char gasification [1,2,3] in an effort to enhance the gasification rate at lower temperatures, which is crucial for supporting efficient coal gasification applications. These analytical methods can be divided into two categories, including model-fitting methods and model-free, or isoconversional, methods. [4,5,6].
The model-fitting method has been frequently used because it facilitates the direct analysis of reaction kinetics [7,8]. Complex models can be developed with a large number of kinetic parameters that lead to data with an improved fit with the experimental results, where the goodness of fit is generally assessed based on calculations of the coefficient of determination (R2). However, while these models may fit better with the experimental data, the kinetic parameters obtained through fitting can be inconsistent, and thereby lead to incorrect assessments of the reaction mechanism. Hence, an indication of good model fitting, such as high R2 values, alone is no longer considered as a valid basis for choosing the best reaction kinetics model [9].
The above-discussed shortcomings of model-fitting methods have led to the increased use of model-free methods, which require no assumptions regarding the char gasification reaction process when determining the kinetic parameters. However, this absence of model assumptions renders these methods incapable of facilitating a detailed analysis of the reaction mechanisms. As such, only the kinetic parameter values themselves are of substantial benefit.
The respective shortcomings of model-fitting and model-free methods have led researchers to develop new criteria for determining whether a given kinetic model adequately represents a specific reaction mechanism by comparing the kinetic parameters derived using a kinetic model with those obtained using model-free approaches [10,11]. For example, Czerski et al. [12] compared the kinetic parameters calculated using two first-order models and a combination of the model-free isoconversional method and model-dependent Coats–Redfern method in order to investigate the impact of direct and indirect char gasification processes conducted in CO2 atmospheres on the activation energy of the reactions. Khaled O. Sebakhy et al. [13] studied the transformation of cubic molybdenum carbide into hexagonal β-Mo2C through an Avrami–Erofeev kinetic model. Other studies have also focused on the kinetic parameters of char gasification reactions in CO2 atmospheres [14,15]. However, research focusing on the evaluation of the kinetic parameters of the steam gasification of char is lacking.
In the present study, we addressed the above-mentioned issue by conducting a series of steam gasification tests for three types of bituminous chars using thermogravimetry analysis (TGA) and derivative thermogravimetry (DTG). The activation energy (Ea) of the steam gasification reaction of char was evaluated based on the experimental results, using three isoconversional methods, including the Flynn–Wall–Ozawa (FWO), Kissinger–Akahira-Sunose (KAS), and Starink methods, and it was also evaluated independently using a wide variety of kinetic models. The goodness of fit of these kinetic models (i.e., R2 values) was applied as the first criterion for selecting the candidate models best representing the steam gasification reaction process. Then, the difference between the Ea values obtained using the model-free and those obtained using the model-fitting methods was examined as the second criterion for selecting the best possible kinetic model for this reaction process. The reliability of the proposed approach for the evaluation of the applicability of a given kinetic model to the steam gasification reaction of char was tested by comparing the results obtained for char samples derived from three different bituminous coal sources.
2. Experiments and Theory
2.1. Coal Samples and Char Preparation
Coal samples were collected from the Ningdong (NX), Shaanxi (SX), and Xinjiang (XJ) coalfields in western China, which can be seen in Figure S1. The main reasons for choosing these three places were their abundant coal reserves, distinctive characteristics, and energy bases. The nature of the coal differed. The XRD and SEM-EDS of the NX, SX, and XJ coal can be seen in Figures S2 and S3. The CuFe2O4 oxygen carriers were characterized using a Japanese MiniFlex 600 X-ray diffraction (XRD) instrument with a tube current and voltage of 15 mA and 40 kV, respectively. The morphology of the sample was established using a JEOL JSM-7900F scanning electron microscopy (SEM) instrument (JEOL Ltd., Tokyo, Japan). The inorganic constituents mass fraction in coal was analyzed by an X diffraction fluorescence (XRF), as shown in Table S1. The heavy metal content of the initial coal samples was determined using ICP methods, which can be seen Table S2. Measurements were conducted using an Agilent 7000 ICP-OES instrument. The sample preparation process can be seen in the Supplementary Information, Section S3. According to the solid waste identification standard GB 34330-2017 and the hazardous waste identification standard for immersion toxicity, standard GB 5085.3-2007, the samples were judged to be non-hazardous substances before and after coal gasification.
The char was prepared from coal placed in a packed column in an inert atmosphere with a continuous nitrogen flow. It was heated at a rate of 10 K·min−1 up to 850 °C, which was maintained for 60 min so as to achieve full devolatilization. The generated chars had a mean particle size of 75–150 µm. The detailed proximate and ultimate analyses of the coal samples and their major ash constituents are listed in Table 1.

Table 1.
Proximate and ultimate analyses of the coal samples.
2.2. Steam Gasification
The steam gasification of the char samples was conducted in atmospheric pressure using a thermogravimetric analyzer (NETZSCH STA 449F3, Eltmann, Germany). During gasification, 10 mg of a given char sample was placed in an alumina (Al2O3) crucible with a 12 mm internal diameter and heated from 373 K to 1173 K at five different rates of 4, 8, 12, 16, and 20 K·min−1, while gaseous H2O with a partial pressure of 50% and the remaining partial pressure adjusted by argon (Ar) was introduced at a flow rate of 200 mL/min. The weight loss of the sample was not maintained for 30 min so as to ensure complete gasification. To avoid inter-particle diffusion and intra-pore diffusion, we used a sample particle size of 100 μm [16,17].
2.3. Kinetics Analysis
2.3.1. Activation Energy Calculation
The degree of conversion (X) obtained at any point in time t during the char gasification reaction process:
where w0 is the initial char sample weight (i.e., 10 mg), wt is the char sample weight at time t (mg), and w∞ is the final char sample weight (mg). This variable, along with Ea, the heating rate β (K·min−1), the gas constant R = 8.314462 J⋅K−1⋅mol−1, and temperature T, represent the core variables employed when using the FWO, KAS, and Starink methods, each of which produces a straight line with a slope of Ea. These straight lines were plotted and fitted based on the appropriate pairs of data points obtained for 5 values of X in the range of 0.1–0.9 at each of the five heating rates.
The FWO method establishes the following relationship:
where A is the rate constant of the reaction (min−1) and G(X) is an integral function, which is defined in the following subsection. Here, the associated fitting is conducted based on the lnβ and 1000/T data point pairs. The KAS method establishes the following relationship:
Here, the associated fitting is conducted based on the ln(β/T2) and 1000/T data point pairs. The Starink method establishes the following relationship:
Here, the associated fitting is conducted based on the ln(β/T1.92) and 1000/T data point pairs.
2.3.2. Kinetic Model Analysis Methodology
According to Equations (2)–(4), the value of Ea, as the slope of the plotted lines, is unaffected by any of the terms in the given intercepts of the relationships. As such, Ea is independent of the reaction mechanism, while all the terms reflecting the reaction mechanism itself are contained within the intercepts. The kinetic model, reflecting the reaction mechanism, was determined using the methodology established by the ICTAC Kinetics Committee [18], and this method was employed to calculate G(X) [19]:
This represents a model-fitting approach for determining Ea based on the slope of a linear plot of ln[G(X)] versus 1000/T, obtained using a series of common candidate G(X) functions, including the power law (Xα), first-order Mampel (−ln(1 − X)), Avrami–Erofeev ([−ln(1 − X)]α), contracting sphere (1 − (1 − X)α), one-dimensional (1D) diffusion (X2), two-dimensional (2D) diffusion ((1 − X)ln(1 − X) + X), and three-dimensional (3D) diffusion 1 − (1 − X)1/3 or 1 − 2/3X − (1 − X)3/2) functions, where various exponent values of α are employed, such as 1/4, 1/3, 1/2, and 3/2. The R2 values obtained from the fitting results with the various candidate functions G(X) can then be employed in order to determine the best-fitting model for describing the reaction process. If several linear relations between ln[G(X)] and 1000/T were obtained, the model with the smallest difference between the Ea values obtained from the specific kinetic model and the model-free isoconversional methods was chosen as the best-fitting model.
2.3.3. Pre-Exponential Factor Calculation
The pre-exponential factor A was determined using the intercept of Equation (5) for the best-fitting kinetic model, obtained according to the methodology discussed in the preceding subsection [20].
3. Results and Discussion
3.1. Effect of the Heating Rate on the Char Conversion
The TGA and DTG results obtained for the char sample derived from the NX coal source during steam gasification at different values of β are presented in Figure 1, and the characteristic parameters of the gasification processes, including the temperature, corresponding to the weight loss peak (Tmax), the ultimate weight loss during char gasification (Mr), and the maximum rate of the weight loss (Rmax), are listed in Table 2. The results demonstrate that the heating rate had obvious positive effects on the rate of the carbon conversion. Here, the value of Tmax increased from 850 °C to 908 °C as β increased from 4 to 20 K·min−1. We also noted that the value of Rmax correspondingly increased from 3.48 to 15.69 wt%·min−1. However, the value of Mr increased only slightly with increasing β. These findings reveal that increasing heating rates led to increasingly rapid reaction processes with short reaction times, but it did not alter the reaction mechanism itself. Specifically, the values of the weight loss of the char in the steam atmosphere were relatively similar at different heating rates, while the value of X increased with increasing β. Therefore, increased values of Rmax were attained by increasing β. Nevertheless, the transfer of thermal energy from the external environment to the particle interiors is impeded at high heating rates, which is expected to result in a large temperature gradient within the particles. Consequently, this leads to thermal hysteresis patterns, and the value of Tmax tends to shift toward higher temperatures at higher heating rates.
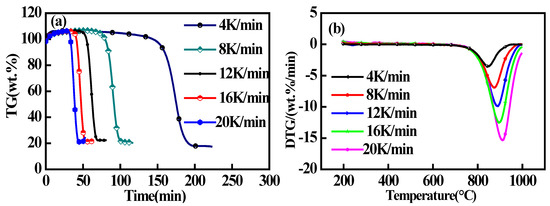
Figure 1.
Thermal analyses of the gasification of the char sample derived from the NX coal source at different heating rates: (a) TGA; (b) DTG.

Table 2.
Characteristic parameters of the steam gasification of char derived from Figure 1 at different heating rates β. The parameters include the temperature, corresponding to the weight loss peak (Tmax), the ultimate weight loss during char gasification (Mr), and the maximum rate of weight loss (Rmax).
3.2. Activation Energy Values Obtained Using Isoconversional Methods
The plots and fitted lines obtained from the TGA data in Figure 1, which are based on the three isoconversional methods at the carbon conversion ratios X in the range of 0.1–0.9, are presented in Figure 2. In addition, the Ea values and corresponding values of R2 obtained from the fitting results are listed in Table 3 for each value of X. We note that the values of R2 obtained using all three methods were generally greater than 0.9. In addition, the values of Ea nearly always increased monotonically with increasing X. From the initially low values of Ea at X = 0.1, the values of Ea increased more slowly from 135.28 to 176.19 KJ.mol−1 (FWO), 114.74 to 152.13 KJ.mol−1 (KAS), and 115.39 to 152.87 KJ.mol−1 (Starink) with increasing X in the range of 0.2–0.9.The relatively low values of Ea obtained at X = 0.1 may be attributable to changes in the surfaces of the char particles in this early stage of gasification, affecting various factors such as the gas adsorption behavior of the active components, mineral catalysis [21,22], and pore structure [23]. In addition, we note from the average values of Ea (Eave) derived from the FWO, KAS, and Starink methods for 0.2 ≤ X ≤ 0.8 that the value of Eave obtained using the FWO method is somewhat greater than those obtained using the KAS and Starink methods, while the values of Eave obtained using the KAS and Starink methods are in good agreement and differ by less than 0.1%, indicating that these Eave values have a high degree of confidence. Therefore, we employed the Eave value obtained using the Starink method (EStarink) as the standard value for the comparison with the Eave values obtained using the kinetic models.
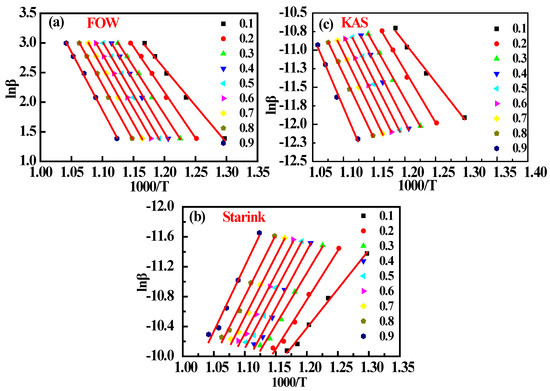
Figure 2.
Plots of the isoconversional methods for the carbon conversion ratios X in the range of 0.1–0.9: (a) FWO method (Equation (2)); (b) KAS method (Equation (3)); (c) Starink method (Equation (4)).

Table 3.
Activation energies Ea (KJ.mol−1) of the steam gasification reaction of the char obtained at different values of X using the FWO, KAS, and Starink methods. The average value of Ea (Eave) obtained for 0.2 ≤ X ≤ 0.8 is also presented.
3.3. Analysis of Kinetic Models
The values of R2 obtained by fitting the results to ln[G(X)] with respect to 1000/T in Equation (5) for 0.2 < X ≤ 0.8 at various heating rates and integral functions G(X) are listed in Table 4. The results indicate that all the models considered provided gradually decreasing values of R2 with increasing β. In addition, aside from the 3D diffusion models, which provided the poorest agreement with Equation (5) due to the small R2 values of less than 0.90, the power law, contacting sphere, and contacting cylinder models also yielded smaller values of R2 at each heating rate considered compared to all models involving G(X) = [−ln(1 − X)]α for the α values of 1/4, 1/3, 1/2, and 1. Considering these factors, the first-order Mampel model, also denoted as the 1D Avrami–Erofeev model (α = 1), and the 2D (α = 1/2), 3D (α = 1/3), and 4D (α = 1/4) Avrami–Erofeev models exhibited the best linear correlation between ln[G(X)] and 1000/T, indicating that these models may potentially represent accurate depictions of the steam gasification reaction of char.

Table 4.
Linear coefficient of determination R2 values obtained with respect to ln[G(X)] and 1000/T using Equation (5) for 0.2 < X ≤ 0.8 at various heating rates β (K·min−1) and integral functions G(X).
The plots and fitted lines obtained from the TGA data in Figure 1 at the carbon conversion ratios X in the range of 0.2–0.8 are presented in Figure 3 for the 1D, 2D, 3D, and 4D Avrami–Erofeev models. In addition, the Ea values obtained from the fitting results corresponding to each heating rate and the Eave values for each model are listed in Table 5, and the table also includes EStarink and the differences between EStarink and the Eave values obtained using the kinetic models. The results in Table 5 indicate that the 3D Avrami–Erofeev model provides the best agreement with EStarink. Hence, the 3D Avrami–Erofeev model was selected as the best kinetic model for describing the steam gasification of char in the subsequent investigation.
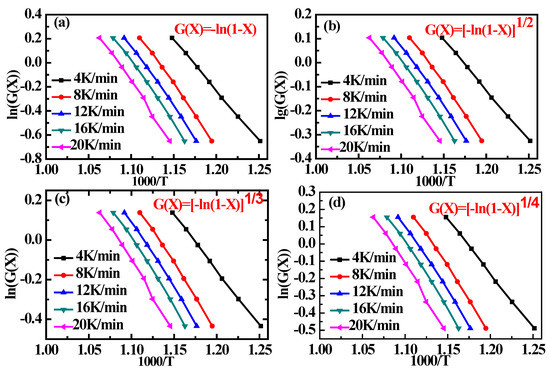
Figure 3.
Plots of Equation (5) with G(X) given by the different kinetic models in the form [−ln(1 − X)]α for X values in the range of 0.2–0.8: (a) 1D Avrami–Erofeev model (α = 1); (b) 2D Avrami–Erofeev model (α = 1/2); (c) 3D Avrami–Erofeev model (α = 1/3); (d) 4D Avrami–Erofeev model (α = 1/4).

Table 5.
Activation energies Ea and average Ea values Eave of the steam gasification reaction of char obtained using the various Avrami–Erofeev models at different heating rates β (K·min−1). The Eave value obtained using the Starink method is also given as EStarink.
The value of the pre-exponential factor A was determined for the fitted line in Figure 3c, as obtained under each heating rate, based on the discussion presented in Section 2.3.3. The results indicate that the value of A increased with increasing β, which further demonstrates that the kinetic parameters correlated with the heating rates. This issue is discussed further in the following subsection.
3.4. Application and Analysis
The Ea values obtained by the FWO, KAS, and Starink methods from the TGA results of the char samples derived from the NX, XJ, and NM coal sources (i.e., NX char, XJ char, and NM char) are presented in Figure 4 as a function of X. As observed previously, the Ea values increased with increasing X for all the char samples. The fact that the energetic feasibility of the steam gasification reaction decreased (i.e., Ea increases) with increasing X can be explained by the decreasing availability of active components as the degree of the carbon conversion increased. In addition, the minerals in the char act as a barrier for the diffusion of gaseous components, and the ash layer becomes thicker with increasing X, leading to enhanced gas diffusion resistance and increasing Ea values.
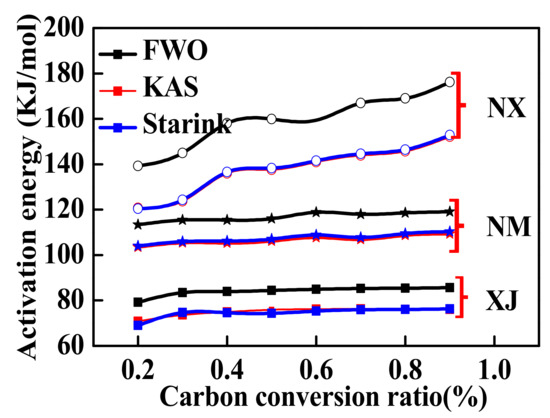
Figure 4.
Activation energy Ea values obtained using the FWO, KAS, and Starink methods as a function of X from the TGA results of the char samples derived from the NX, XJ, and NM coal sources (i.e., NX char, XJ char, and NM char).
Once again, we note that the Ea values obtained using the FWO method are somewhat greater than those obtained using the KAS and Starink methods, and that the KAS and Starink methods yield very similar values of Ea, which range from approximately 115–153 KJ.mol−1 for the NX char, 70–78 KJ.mol−1 for the XJ char, and 103–110 KJ.mol−1 for the NM char. Accordingly, the values of Ea obtained for these coal chars decreases in the order of NX char > NM char > XJ char.
The ranges of Ea obtained using the KAS and Starink methods can be compared with the values reported for steam gasification char reactions in the literature, such as Ea = 255 KJ.mol−1 for chars derived from low-rank Samhwa coal [24], 105.48–169.10 KJ.mol−1 for chars derived from Shenmu Chinese bituminous coal [25], and 282 KJ.mol−1 for chars derived from Australian bituminous coal [26,27]. We note that the resulting Ea values obtained here are not in good agreement with these previously reported findings. This can be attributed to variations in the experimental char gasification conditions, which can be affected by many factors, such as the parent coal properties [28], charring conditions [24], and mineral catalytic effects [22].
The values of the pre-exponential factors A were determined for the NX, NM, and XJ chars based on the discussion presented in Section 2.3.3, and the results are presented in Figure 5. Interestingly, the values of A obtained for these coal chars decrease in the same order, i.e., NX char > NM char > XJ char, as that obtained for Ea above. As discussed above, in regard to the NX char sample, the results indicate that the value of A increased with increasing β for all the char samples. This phenomenon is consistent with the results of previous findings and is probably due to the high heating rates applied during the char gasification reactions [29,30,31,32]. However, this effect can be limited by the heat and mass transfer. Limitations in the heat transfer can delay the sample heating process, and, thus, the internal temperature of the char particles is always less than the ambient temperature. However, the obtained data were quite similar across gradually increases in the temperature. These results essentially demonstrate that the effects of the heat and mass transfer on the reaction are less significant than those on the TGA.
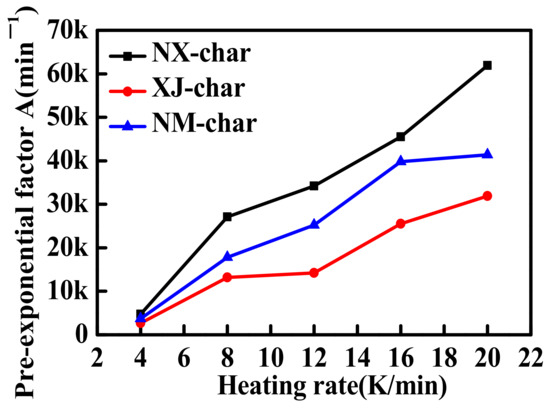
Figure 5.
Pre-exponential factors A obtained for the chars derived from the NX, XJ, and NM coal sources as a function of the heating rate.
4. Conclusions
This study addressed the lack of development of the methods for assessing the fitness of kinetic models in representing the important steam gasification reaction of char based on comparisons with kinetic parameters obtained using isoconversional methods. To this end, we conducted a series of steam-assisted char gasification tests using TGA and DTG at five different heating rates. We determined the values of Ea based on the FWO, KAS, and Starink isoconversional methods with different values of X for the NX char sample. Then, we evaluated the degree of fit of a wide variety of kinetic models with the experimental results and compared the average values of Ea obtained using these models with the optimal value obtained using the isoconversional methods. Finally, the reliability of the proposed approach for evaluating the applicability of a given kinetic model to the steam gasification reaction of char was tested by comparing the results obtained for char samples derived from three different bituminous coal sources. The results yielded the following conclusions:
- The weight loss of the char samples in the steam atmosphere was relatively similar at different heating rates, while the value of X increased with the increasing heating rate.
- The FWO method provided somewhat greater values of Ea than the KAS and Starink methods, while the latter two methods provided consistent Ea values for all the values of X. The average value of Ea obtained by the Starink method (EStarink) was deemed optimal.
- The 3D Avrami–Erofeev model provided the best fit with the data, while the 3D Avrami–Erofeev model yielded a value of Eave closest to EStarink. The two values differed by only 0.70 KJ.mol−1.
- The values of Ea obtained from the fitted 3D Avrami–Erofeev model for chars derived from the three coal sources decreased in the order of NX char (115–153 KJ.mol−1) > NM char (103–110 KJ.mol−1) > XJ char (70–78 KJ.mol−1). The pre-exponential factor A followed an order of decreasing values consistent with that obtained for Ea.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos13091480/s1, Table S1. Inorganic constituents mass fraction in coal; Table S2. the heavy metal content of initial coal samples;Figure S1. Coal samples were collected from the Ningdong (NX), Shenxi (SX), and Xinjiang (XJ) coalfields in western China; Figure S2. XRD of the Ningdong (NX), Shenxi (SX), and Xinjiang (XJ) coal.; Figure S3. SEM-EDS of the Ningdong (NX), Shenxi (SX), and Xinjiang (XJ) coal.
Author Contributions
M.A. designed and carried out the quality control, and wrote the manuscript, Q.G. helped with the analyses. Methodology and validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported financially by the Fundamental Research Funds for the Central Universities (Grant No. 2021QN1044), the Natural Science Foundation Project of Ningxia (Grant No. 2022AC03764), State Key Laboratory of High-efficiency Utilization of Coal and Green Chemical Engineering (Grant No.2021-K06). The key R&D projects of Ningxia (Talent special) (Grant No.2021BEB04083).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
The authors are appreciative for the reviewers’ helpful comments and suggestions, which have helped to improve the presentation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brown, M.E.; Maciejewski, M.; Vyazovkin, S.; Nomen, R.; Sempere, J.; Burnham, A.; Opfermann, J.; Strey, R.; Anderson, H.L.; Kemmler, A. Computational aspects of kinetic analysis.: Part A: The ICTAC kinetics project-data, methods and results. Thermochim. Acta 2000, 355, 125–143. [Google Scholar] [CrossRef]
- Kök, M.V. Recent developments in the application of thermal analysis techniques in fossil fuels. J. Therm. Anal. Calorim. 2008, 91, 763–773. [Google Scholar] [CrossRef]
- Vyazovkin, S. Computational aspects of kinetic analysis.: Part C. The ICTAC Kinetics Project—The light at the end of the tunnel. Thermochim. Acta 2000, 355, 155–163. [Google Scholar] [CrossRef]
- Wang, F.; Zeng, X.; Wang, Y.; Su, H.; Yu, J.; Xu, G. Non-isothermal coal char gasification with CO2 in a micro fluidized bed reaction analyzer and a thermogravimetric analyzer. Fuel 2016, 164, 403–409. [Google Scholar] [CrossRef]
- Ashraf, A.; Sattar, H.; Munir, S. A comparative applicability study of model-fitting and model-free kinetic analysis approaches to non-isothermal pyrolysis of coal and agricultural residues. Fuel 2019, 240, 326–333. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, P.; Bie, K.; Xu, T.; Ahsan, M. Non-isothermal kinetics of coal char oxyfuel combustion by isothermal model-fitting method. Energy Rep. 2022, 8, 2062–2071. [Google Scholar] [CrossRef]
- Yang, S.; Ding, J.; Zhang, X.; Ye, S.; Guo, Z.; Chen, W. Fusion method of model-free and model-fitting for complex reactions in accelerating rate calorimetry. Thermochim. Acta 2022, 712, 179212. [Google Scholar] [CrossRef]
- Mahmood, H.; Shakeel, A.; Abdullah, A.; Khan, M.; Moniruzzaman, M. A Comparative Study on Suitability of Model-Free and Model-Fitting Kinetic Methods to Non-Isothermal Degradation of Lignocellulosic Materials. Polymers 2021, 13, 2504. [Google Scholar] [CrossRef]
- Gomez, A.; Mahinpey, N. A new method to calculate kinetic parameters independent of the kinetic model: Insights on CO2 and steam gasification. Chem. Eng. Res. Des. 2015, 95, 346–357. [Google Scholar] [CrossRef]
- Mahinpey, N.; Gomez, A. Review of gasification fundamentals and new findings: Reactors, feedstock, and kinetic studies. Chem. Eng. Sci. 2016, 148, 14–31. [Google Scholar] [CrossRef]
- Jain, A.A.; Mehra, A.; Ranade, V.V. Processing of TGA data: Analysis of isoconversional and model fitting methods. Fuel 2016, 165, 490–498. [Google Scholar] [CrossRef]
- Czerski, G.; Zubek, K.; Grzywacz, P.; Porada, S. Effect of Char Preparation Conditions on Gasification in a Carbon Dioxide Atmosphere. Energy Fuels 2016, 31, 815–823. [Google Scholar] [CrossRef]
- Sebakhy, K.O.; Vitale, G.; Hassan, A.; Pereira-Almao, P. New Insights into the Kinetics of Structural Transformation and Hydrogenation Activity of Nano-crystalline Molybdenum Carbide. Catal. Lett. 2018, 148, 904–923. [Google Scholar] [CrossRef]
- Byambajav, E.; Hachiyama, Y.; Kudo, S.; Norinaga, K.; Hayashi, J. Kinetics and Mechanism of CO2 Gasification of Chars from 11 Mongolian Lignites. Energy Fuels 2015, 30, 1636–1646. [Google Scholar] [CrossRef]
- Korotkikh, A.G.; Slyusarskiy, K.V. Kinetic study of coals gasification into carbon dioxide atmosphere. MATEC Web Conf. 2015, 23, 1020. [Google Scholar] [CrossRef]
- Gomez, A.; Mahinpey, N. Kinetic study of coal steam and CO2 gasification: A new method to reduce interparticle diffusion. Fuel 2015, 148, 160–167. [Google Scholar] [CrossRef]
- Gomez, A.; Silbermann, R.; Mahinpey, N. A comprehensive experimental procedure for CO2 coal gasification: Is there really a maximum reaction rate? Appl. Energy 2014, 124, 73–81. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, M.; Wang, Y.; Bai, Y.; Li, F. Identification for the behavior of maximum reaction rate during the initial stage of coal char gasification. J. Therm. Anal. Calorim. 2017, 128, 1183–1194. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Doyle, C.D. Estimating isothermal life from thermogravimetric data. J. Appl. Polym. Sci. 1962, 6, 639–642. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, H.; Kaneko, M.; Kato, S.; Kojima, T. High-Temperature Gasification Reactivity with Steam of Coal Chars Derived under Various Pyrolysis Conditions in a Fluidized Bed. Energy Fuels 2010, 24, 68–75. [Google Scholar] [CrossRef]
- Zhang, Y.; Hara, S.; Kajitani, S.; Ashizawa, M. Modeling of catalytic gasification kinetics of coal char and carbon. Fuel 2010, 89, 152–157. [Google Scholar] [CrossRef]
- Wang, Y.L.; Zhu, S.H.; Gao, M.Q.; Yang, Z.R.; Yan, L.J.; Bai, Y.H.; Li, F. A study of char gasification in H2O and CO2 mixtures: Role of inherent minerals in the coal. Fuel Process. Technol. 2015, 141, 9–15. [Google Scholar] [CrossRef]
- Dai, P.; Dennis, J.S.; Scott, S.A. Using an experimentally-determined model of the evolution of pore structure for the gasification of chars by CO2. Fuel 2016, 171, 29–43. [Google Scholar] [CrossRef][Green Version]
- Jayaraman, K.; Gokalp, I.; Bonifaci, E.; Merlo, N. Kinetics of steam and CO2 gasification of high ash coal–char produced under various heating rates. Fuel 2015, 154, 370–379. [Google Scholar] [CrossRef]
- Fan, D.; Zhu, Z.; Na, Y.; Lu, Q. Thermogravimetric analysis of gasification reactivity of coal chars with steam and CO2 at moderate temperatures. J. Therm. Anal. Calorim. 2013, 113, 599–607. [Google Scholar] [CrossRef]
- Everson, R.C.; Okolo, G.N.; Neomagus, H.W.J.P.; Dos Santos, J. X-ray diffraction parameters and reaction rate modeling for gasification and combustion of chars derived from inertinite-rich coals. Fuel 2013, 109, 148–156. [Google Scholar] [CrossRef]
- Everson, R.C.; Neomagus, H.W.J.P.; Kaitano, R.; Falcon, R.; du Cann, V.M. Properties of high ash coal-char particles derived from inertinite-rich coal: II. Gasification kinetics with carbon dioxide. Fuel 2008, 87, 3403–3408. [Google Scholar] [CrossRef]
- Fermoso, J.; Gil, M.V.; Garciía, S.; Pevida, C.; Pis, J.J.; Rubiera, F. Kinetic Parameters and Reactivity for the Steam Gasification of Coal Chars Obtained under Different Pyrolysis Temperatures and Pressures. Energy Fuels 2011, 25, 3574–3580. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Q.; Zou, Z.; Tan, G. Arrhenius parameters determination in non-isothermal conditions for the uncatalyzed gasification of carbon by carbon dioxide. Thermochim. Acta 2011, 512, 1–4. [Google Scholar] [CrossRef]
- Ding, H.; Jiang, Y.; Chen, Y.F.; Li, W.H. Experimental study on gasification kinetics of Lu’an coal char with steam by non-isothermal thermogravimetry. J. China Coal Soc. 2010, 35, 666–669. [Google Scholar]
- Edreis, E.M.A.; Luo, G.; Yao, H. Investigations of the structure and thermal kinetic analysis of sugarcane bagasse char during non-isothermal CO2 gasification. J. Anal. Appl. Pyrol. 2014, 107, 107–115. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).