Two Decades of Satellite Observations of Carbon Monoxide Confirm the Increase in Northern Hemispheric Wildfires
Abstract
:1. Introduction
2. Materials and Methods
2.1. AIRS Data and Validation
2.2. Validation Results
2.3. Mass-Balance Box Model
- Satellite-measured CO volume mixing ratio (VMR) profiles were supplied for 24 standard air layers from the surface to pressure 1.0 hPa with different pressure thicknesses Δp(i) in hPa, where i was from 1 to 24. VMR weighted by Δp(i) averages were calculated for the sake of comparability with the validation network TCCON. The conversion of Xco (ppb) into TC (molec cm−2) was performed as follows: TC = Xco · 2.12 · 1013 · Σ(Δp(i)).
- A standard HNH seasonal cycle was calculated for the period between January 2004 and December 2007. After subtracting the overall Xco mean for 4 years of data, the obtained seasonal cycle (Table A2) was employed for deseasonalizing the measured Xco.
- The data were also required to be detrended. The February-March points were chosen as the cold season with negligible biomass burning. The fifth-order polynomial for these points with the subtracted overall mean was obtained and assumed as the trend for the entire data set (Table A3)
- The HNH box-averaged CO TC was subtracted by the trend and the seasonal cycle to represent the TC perturbed by fires. Then it was multiplied by the area of the HNH to obtain the monthly fire-induced total mass anomaly M’HNH in Tg.
- The anomaly was divided by 0.73 to correct for reduced sensitivity of measured CO (see Validation section above).
- Loss terms in Equations (2) and (3) were calculated.
- The wildfire emission P’ was calculated as a sum of the monthly changes in M’HNH and two loss terms, transport into the LNH, Ltrans, and loss of CO due to a reaction with hydroxyl (OH), Lchem; quotation marks indicate deviations from the 2004–2007 background (Equation (1)).
2.4. Global Fire Emission Data
3. Results
3.1. Xco Measured by AIRS
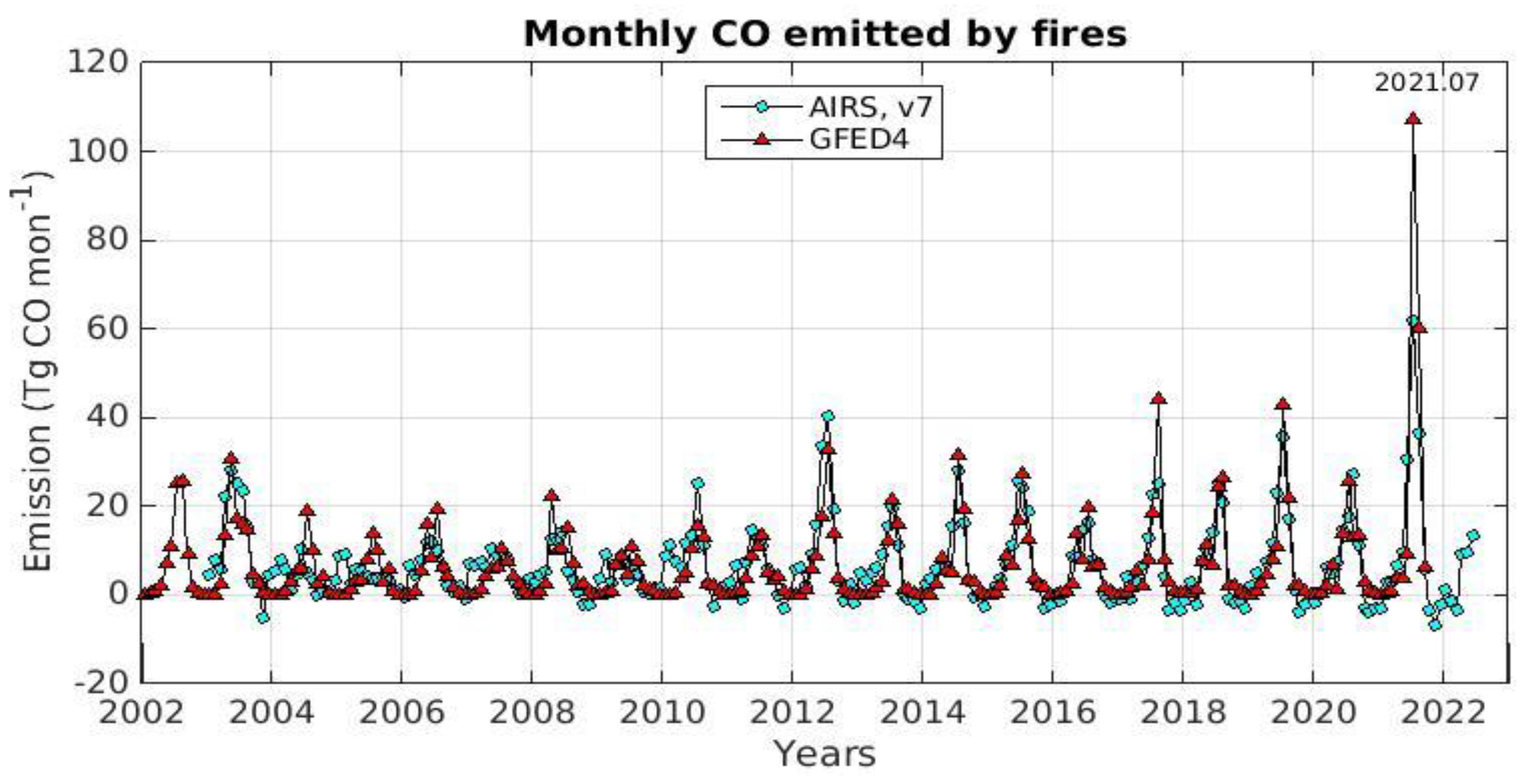
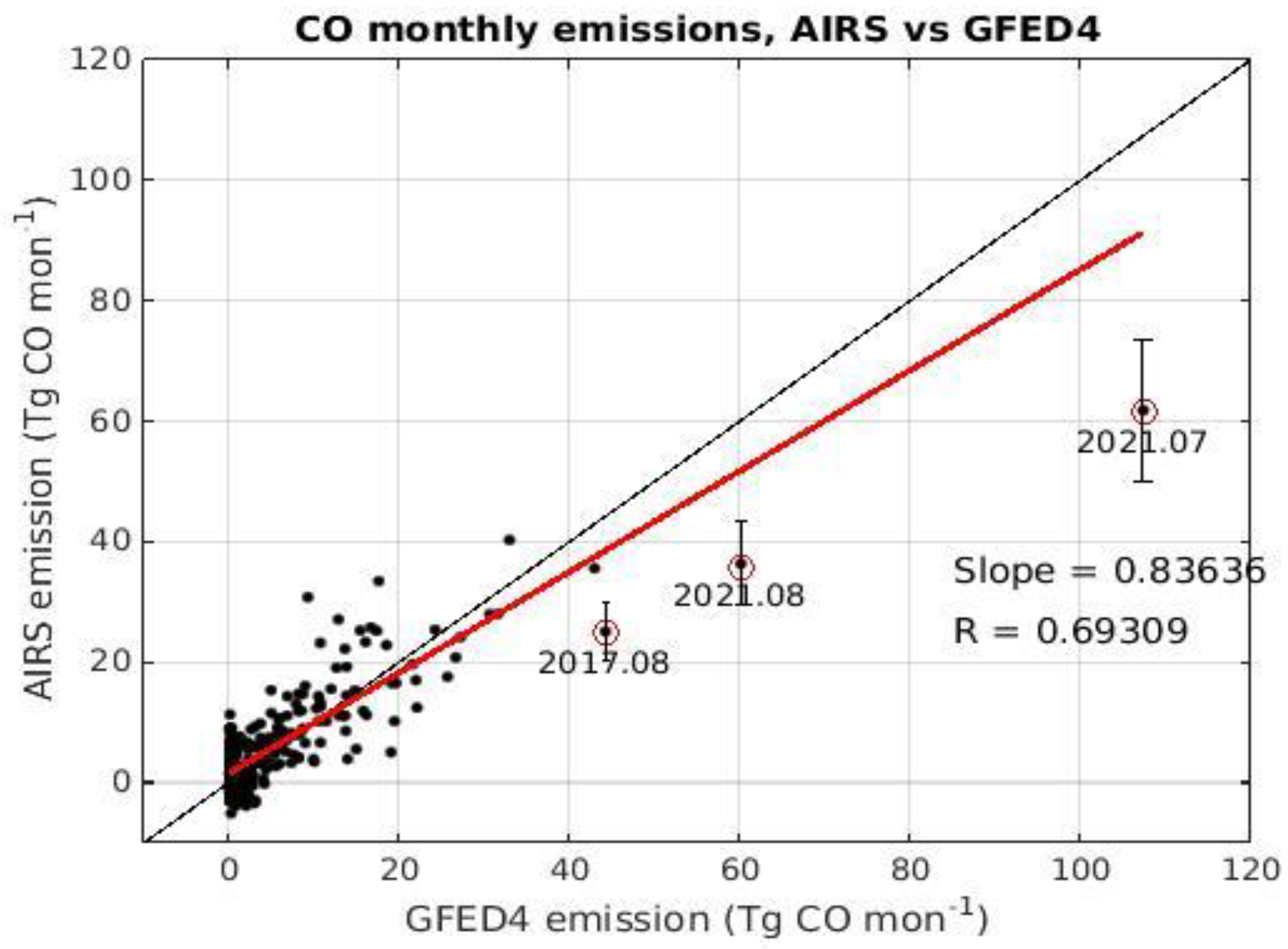
3.2. Fire Emissions
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Month | τtrans (Months) | τchem (Months) |
|---|---|---|
| 1 | 1.7 | 23.8 |
| 2 | 2.1 | 14.0 |
| 3 | 3.5 | 6.5 |
| 4 | 3.4 | 3.4 |
| 5 | 2.1 | 2.1 |
| 6 | 1.5 | 1.4 |
| 7 | 1.5 | 1.4 |
| 8 | 1.6 | 1.8 |
| 9 | 2.4 | 3.5 |
| 10 | 2.6 | 7.3 |
| 11 | 2.8 | 15.8 |
| 12 | 1.5 | 27.2 |
| Month | Seasonal Cycle, ppb |
|---|---|
| 1 | 8.0 |
| 2 | 13.5 |
| 3 | 17.5 |
| 4 | 17.7 |
| 5 | 7.1 |
| 6 | −6.8 |
| 7 | −12.6 |
| 8 | −13.3 |
| 9 | −14.0 |
| 10 | −11.9 |
| 11 | −6.1 |
| 12 | 0.9 |
| Month/Year | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 10.4 | 10 | 9.1 | 7.7 | 6.2 | 4.7 | 3.3 | 2.1 | 1 | 0.1 |
| 2 | 10.4 | 10 | 9 | 7.6 | 6.1 | 4.6 | 3.2 | 2 | 0.9 | 0 |
| 3 | 10.4 | 9.9 | 8.9 | 7.5 | 5.9 | 4.4 | 3.1 | 1.9 | 0.8 | −0.1 |
| 4 | 10.4 | 9.9 | 8.8 | 7.3 | 5.8 | 4.3 | 3 | 1.8 | 0.8 | −0.1 |
| 5 | 10.3 | 9.8 | 8.6 | 7.2 | 5.7 | 4.2 | 2.9 | 1.7 | 0.7 | −0.2 |
| 6 | 10.3 | 9.7 | 8.5 | 7.1 | 5.6 | 4.1 | 2.8 | 1.6 | 0.6 | −0.3 |
| 7 | 10.3 | 9.6 | 8.4 | 7 | 5.4 | 4 | 2.7 | 1.5 | 0.5 | −0.3 |
| 8 | 10.2 | 9.5 | 8.3 | 6.8 | 5.3 | 3.9 | 2.6 | 1.4 | 0.5 | −0.4 |
| 9 | 10.2 | 9.4 | 8.2 | 6.7 | 5.2 | 3.8 | 2.5 | 1.4 | 0.4 | −0.5 |
| 10 | 10.2 | 9.3 | 8.1 | 6.6 | 5.1 | 3.6 | 2.4 | 1.3 | 0.3 | −0.5 |
| 11 | 10.1 | 9.2 | 7.9 | 6.4 | 4.9 | 3.5 | 2.3 | 1.2 | 0.2 | −0.6 |
| 12 | 10.1 | 9.2 | 7.8 | 6.3 | 4.8 | 3.4 | 2.2 | 1.1 | 0.2 | −0.7 |
| Month/Year | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | |
| 1 | -0.8 | −1.6 | −2.4 | −3.3 | −4.2 | −5.3 | −6.4 | −7.5 | −8.3 | |
| 2 | −0.8 | −1.6 | −2.4 | −3.3 | −4.3 | −5.4 | −6.5 | −7.6 | −8.4 | |
| 3 | −0.9 | −1.7 | −2.5 | −3.4 | −4.4 | −5.5 | −6.6 | −7.6 | −8.4 | |
| 4 | −1 | −1.8 | −2.6 | −3.5 | −4.5 | −5.6 | −6.7 | −7.7 | −8.5 | |
| 5 | −1 | −1.8 | −2.7 | −3.6 | −4.6 | −5.7 | −6.8 | −7.8 | −8.5 | |
| 6 | −1.1 | −1.9 | −2.7 | −3.7 | −4.7 | −5.8 | −6.9 | −7.8 | −8.5 | |
| 7 | −1.2 | −2 | −2.8 | −3.7 | −4.8 | −5.9 | −6.9 | −7.9 | −8.6 | |
| 8 | −1.2 | −2 | −2.9 | −3.8 | −4.9 | −5.9 | −7 | −8 | −8.6 | |
| 9 | −1.3 | −2.1 | −3 | −3.9 | −4.9 | −6 | −7.1 | −8 | −8.6 | |
| 10 | −1.4 | −2.2 | −3 | −4 | −5 | −6.1 | −7.2 | −8.1 | −8.7 | |
| 11 | −1.4 | −2.2 | −3.1 | −4.1 | −5.1 | −6.2 | −7.3 | −8.2 | −8.7 | |
| 12 | −1.5 | −2.3 | −3.2 | −4.2 | −5.2 | −6.3 | −7.4 | −8.3 | −8.7 |
References
- Kasischke, E.; Stocks, B. Fire, Climate Change, and Carbon Cycling in the Boreal Forest; Springer: New York, NY, USA, 2000; 461p. [Google Scholar]
- Seiler, W.; Crutzen, P.J. Estimates of gross and net fluxes of carbon between the biosphere and the atmosphere from biomass burning. Clim. Change 1980, 2, 207–247. [Google Scholar] [CrossRef]
- Van der Werf, G.R.; Randerson, J.T.; Giglio, L.; van Leeuwen, T.T.; Chen, Y.; Rogers, B.M.; Mu, M.; van Marle, M.J.E.; Morton, D.C.; Collatz, J.; et al. Global fire emissions estimates during 1997–2016. Earth Syst. Sci. Data 2017, 9, 697–720. [Google Scholar] [CrossRef]
- Giglio, L.; Csiszar, I.; Justice, C.O. Global distribution and seasonality of active fires as observed with the Terra and Aqua Moderate Resolution Imaging Spectroradiometer (MODIS) sensors. J. Geophys. Res. Biogeosci. 2006, 111, G02016. [Google Scholar] [CrossRef]
- Dekker, I.N.; Houweling, S.; Aben, I.; Röckmann, T.; Krol, M.; Martínez-Alonso, S.; Deeter, M.N.; Worden, H.M. Quantification of CO emissions from the city of Madrid using MOPITT satellite retrievals and WRF simulations. Atmos. Chem. Phys. 2017, 17, 14675–14694. [Google Scholar] [CrossRef]
- Bela, M.M.; Kille, N.; McKeen, S.A.; Romero-Alvarez, J.; Ahmadov, R.; James, E.; Pereira, G.; Schmidt, C.; Pierce, R.B.; O’Neill, S.M.; et al. Quantifying carbon monoxide emissions on the scale of large wildfires. Geophys. Res. Lett. 2021, 49, e2021GL095831. [Google Scholar] [CrossRef]
- Deeter, M.; Francis, G.; Gille, J.; Mao, D.; Martínez-Alonso, S.; Worden, H.; McKain, K. The MOPITT Version 9 CO product: Sampling enhancements and validation. Atmosph. Meas. Tech. 2022, 15, 2325–2344. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.P.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the Aqua mission: Design, science objectives, data products and processing systems. IEEE Trans. Geosci. Rem. Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Yurganov, L.N.; Duchatelet, P.; Dzhola, A.V.; Edwards, D.P.; Hase, F.; Kramer, I.; Mahieu, E.; Mellqvist, J.; Notholt, J.; Novelli, P.C.; et al. Increased Northern Hemispheric carbon monoxide burden in the troposphere in 2002 and 2003 detected from the ground and from space. Atmos. Chem. Phys. 2005, 5, 563–573. [Google Scholar] [CrossRef]
- Yurganov, L.N.; Blumenstock, T.; Grechko, E.I.; Hase, F.; Hyer, E.J.; Kasischke, E.S.; Koike, M.; Kondo, Y.; Kramer, I.; Le-ung, F.-Y.; et al. A quantitative assessment of the 1998 carbon monoxide emission anomaly in the northern Hemisphere based on total column and surface concentration measurements. J. Geophys. Res. 2004, 109, D15305. [Google Scholar] [CrossRef]
- Zheng, B.; Chevallier, F.; Yin, Y.; Ciais, P.; Fortems-Cheiney, A.; Deeter, M.N.; Parker, R.J.; Wang, Y.; Worden, H.M.; Zhao, Y. Global atmospheric carbon monoxide budget 2000-2017 inferred from multi-species atmospheric inversions. Earth Syst. Sci. Data 2019, 11, 1411–1436. [Google Scholar] [CrossRef] [Green Version]
- Zheng, B.; Ciais, P.; Chevallier, А.; Chuvieco, E.; Chen, Y.; Yang, H. Increasing forest fire emissions despite the decline in global burned area. Sci. Adv. 2021, 7, eabh2646. [Google Scholar] [CrossRef] [PubMed]
- Tian, B.; Manning, R.J.; Thrastarson, H.; Fetzer, E.; Monarrez, R. AIRS Version 7 Level 3 Product User Guide. 2020. Available online: https://docserver.gesdisc.eosdis.nasa.gov/public/project/AIRS/V7_L3_User_Guide.pdf (accessed on 18 August 2022).
- Wunch, D.; Toon, G.C.; Blavier, J.-F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The Total Carbon Column Observing Network. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2087–2112. [Google Scholar] [CrossRef] [PubMed]
- Rakitin, V.S.; Elansky, N.F.; Skorokhod, A.I.; Dzhola, A.V.; Rakitina, A.V.; Shilkin, A.V.; Kirillova, N.S.; Kazakov, A.V. Long-Term Tendencies of Carbon Monoxide in the Atmosphere of the Moscow Megapolis. Izv. Atmos. Ocean Phys. 2021, 57, 116–125. [Google Scholar] [CrossRef]
- Holloway, T.; Levy, H., II; Kasibhatla, P. Global distribution of carbon monoxide. J. Geophys. Res. 2000, 105, 12123–12147. [Google Scholar] [CrossRef]
- Spivakovsky, C.M.; Logan, J.A.; Montzka, S.A.; Balkanski, Y.J.; Foreman-Fowler, M.; Jones, D.B.A.; Horowitz, L.W.; Fusco, A.C.; Brenninkmeijer, C.A.M.; Prather, M.J.; et al. Three-dimensional climatological distribution of tropospheric OH: Update and evaluation. J. Geophys. Res. 2000, 105, 8931–8980. [Google Scholar] [CrossRef]
- DeMore, W.B.; Sander, S.P.; Golden, D.M.; Hampson, R.F.; Kurylo, M.J.; Howard, C.J.; Ravishankara, A.R.; Kolb, C.E.; Molina, M.J. Chemical kinetics and photochemical data for use in stratospheric modeling. JPL Publ. 1997, 3, 94–97. [Google Scholar]
- Dianov-Klokov, V.I.; Yurganov, L.N. A spectroscopic study of the global space-time distribution of atmospheric CO. Tellus 1981, 33, 262–273. [Google Scholar] [CrossRef]
- Chatterjee, S.; Hadi, A.S. Influential observations, high leverage points, and outliers in linear regression. Stat. Sci. 1986, 1, 379–416. [Google Scholar]




| Site | Latitude; Longitude | Slope | Interception | R |
|---|---|---|---|---|
| E. Trout Lake, Canada | 54.35; −104.99 | 0.82 | 5.43 | 0.71 |
| Karlsruhe, Germany | 49.1; 8.438 | 0.74 | 9.23 | 0.76 |
| Lamont, OK, USA | 36.604; −97.486 | 0.58 | 23.25 | 0.52 |
| Ny-Alesund, Svalbard | 78.9; 11.9 | 0.90 | 13.01 | 0.81 |
| Park Falls, PA, USA | 45.945; −90.273 | 0.71 | 14.41 | 0.63 |
| Rikubetsu, Japan | 43.4567; 143.7661 | 0.61 | 26.37 | 0.61 |
| Sodankyla, Finland | 67.3668; 26.631 | 0.79 | 9.67 | 0.86 |
| Tsukuba, Japan | 36.0513; 140.1215 | 0.51 | 35.38 | 0.53 |
| Zvenigorod, Russia | 55.6957; 36.4454 | 0.89 | −2.64 | 0.24 |
| Year | AIRS (This Paper) | GFED4c (This Paper) | FTIR [9] | MOPITT [9] |
|---|---|---|---|---|
| 1998 | - | 114 | 151.4 | |
| 1999 | - | 48 | 32.3 | |
| 2000 | - | 50 | −1.8 | 1.8 |
| 2001 | - | 43 | 5.1 | −0.9 |
| 2002 | - | 83 | 120.6 | 118 |
| 2003 | 125 | 103 | - | - |
| 2004 | 49 | 51 | - | - |
| 2005 | 53 | 50 | - | - |
| 2006 | 63 | 63 | - | - |
| 2007 | 75 | 44 | - | - |
| 2008 | 57 | 74 | - | - |
| 2009 | 51 | 43 | - | - |
| 2010 | 99 | 53 | - | - |
| 2011 | 62 | 51 | - | - |
| 2012 | 135 | 85 | - | - |
| 2013 | 70 | 58 | - | - |
| 2014 | 87 | 79 | - | - |
| 2015 | 93 | 82 | - | - |
| 2016 | 61 | 61 | - | - |
| 2017 | 69 | 93 | - | - |
| 2018 | 71 | 84 | - | - |
| 2019 | 101 | 97 | - | - |
| 2020 | 78 | 80 | - | - |
| 2021 | 142 | 192 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yurganov, L.; Rakitin, V. Two Decades of Satellite Observations of Carbon Monoxide Confirm the Increase in Northern Hemispheric Wildfires. Atmosphere 2022, 13, 1479. https://doi.org/10.3390/atmos13091479
Yurganov L, Rakitin V. Two Decades of Satellite Observations of Carbon Monoxide Confirm the Increase in Northern Hemispheric Wildfires. Atmosphere. 2022; 13(9):1479. https://doi.org/10.3390/atmos13091479
Chicago/Turabian StyleYurganov, Leonid, and Vadim Rakitin. 2022. "Two Decades of Satellite Observations of Carbon Monoxide Confirm the Increase in Northern Hemispheric Wildfires" Atmosphere 13, no. 9: 1479. https://doi.org/10.3390/atmos13091479
APA StyleYurganov, L., & Rakitin, V. (2022). Two Decades of Satellite Observations of Carbon Monoxide Confirm the Increase in Northern Hemispheric Wildfires. Atmosphere, 13(9), 1479. https://doi.org/10.3390/atmos13091479





