Study of the Mesosphere and Lower Thermosphere by the Method of Creating Artificial Periodic Irregularities of the Ionospheric Plasma
Abstract
1. Introduction
- Electron density profiles in the E region, including the interlayer E–F valley;
- The vertical plasma velocity;
- The neutral component velocity in the mesosphere and lower thermosphere (60–130 km);
- Turbulent velocity and turbo pause level;
- Temperature and density of the neutral atmosphere at the E region heights (90–120 km);
- Molecular masses and densities of prevailing metal ions in the sporadic-E layer;
- Relative concentration of negative ions of oxygen, concentration of atomic oxygen, and raised molecular oxygen 1Δg in the D region;
- Electron and ion temperatures in the F region.
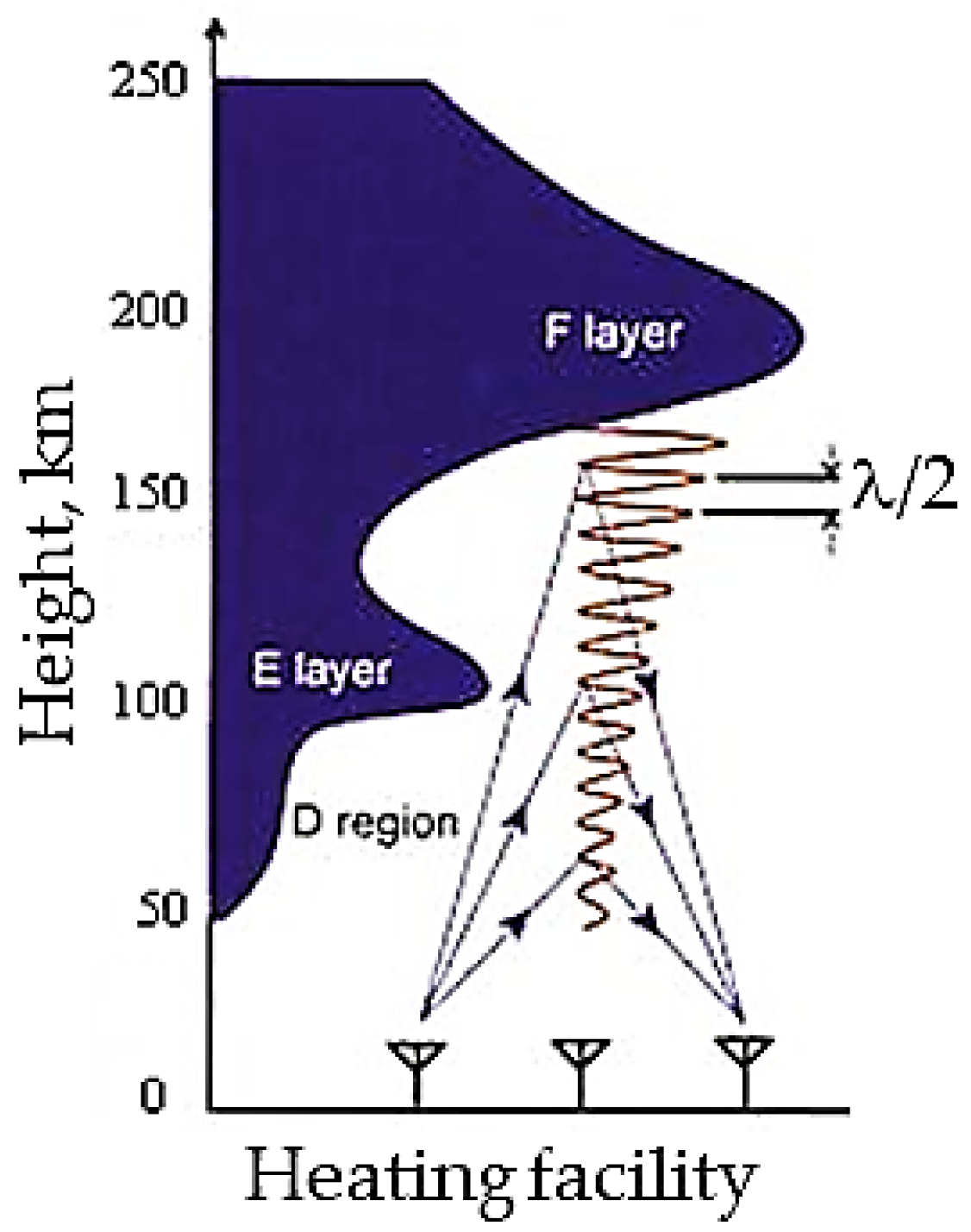
2. API Technique and Experiment Description
2.1. Equipment and Methodic of the Experiment
2.2. The Method for Determining the Ionized and Neutral Components
3. API Technique and the Ionized Component Parameters
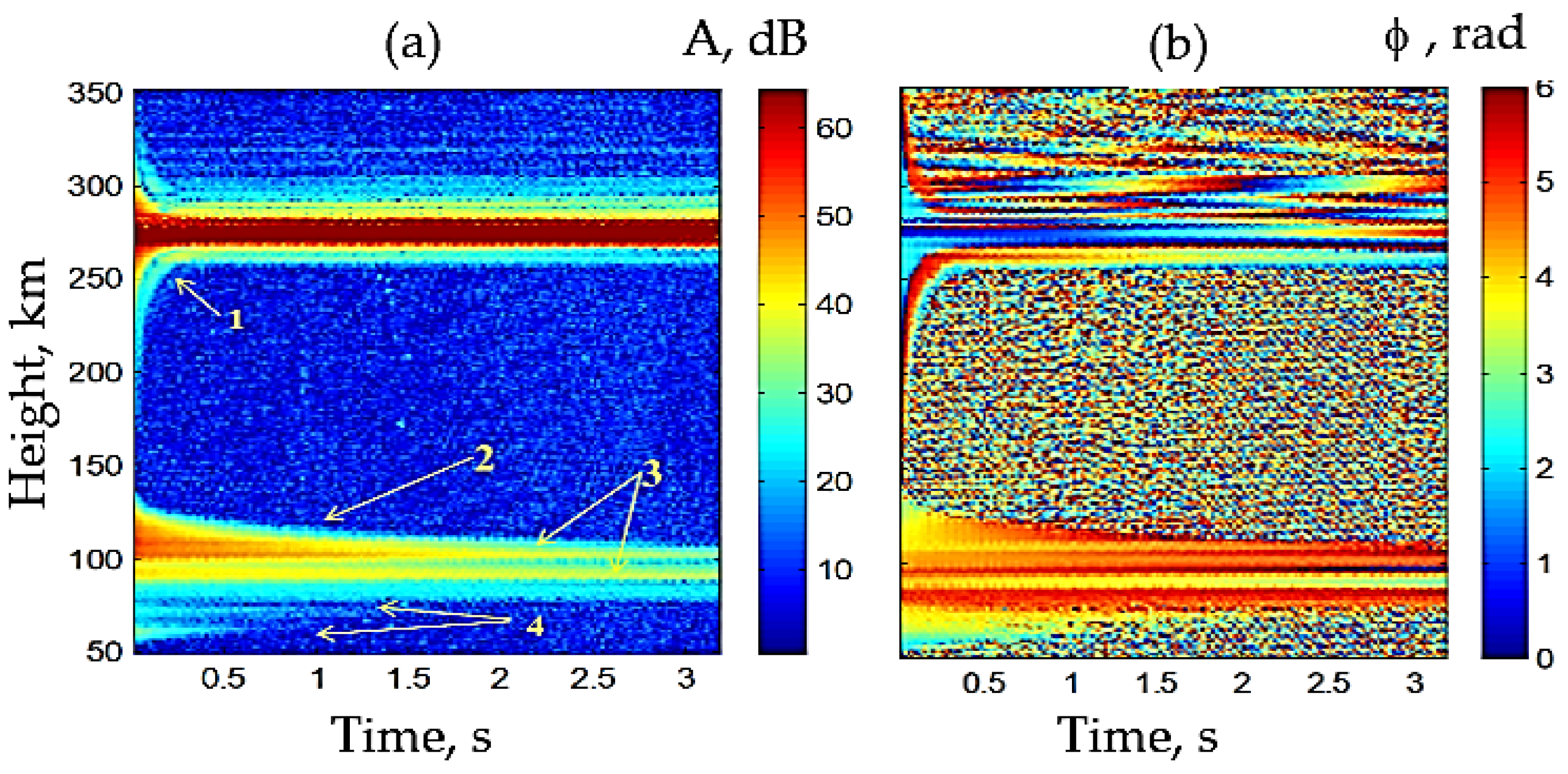
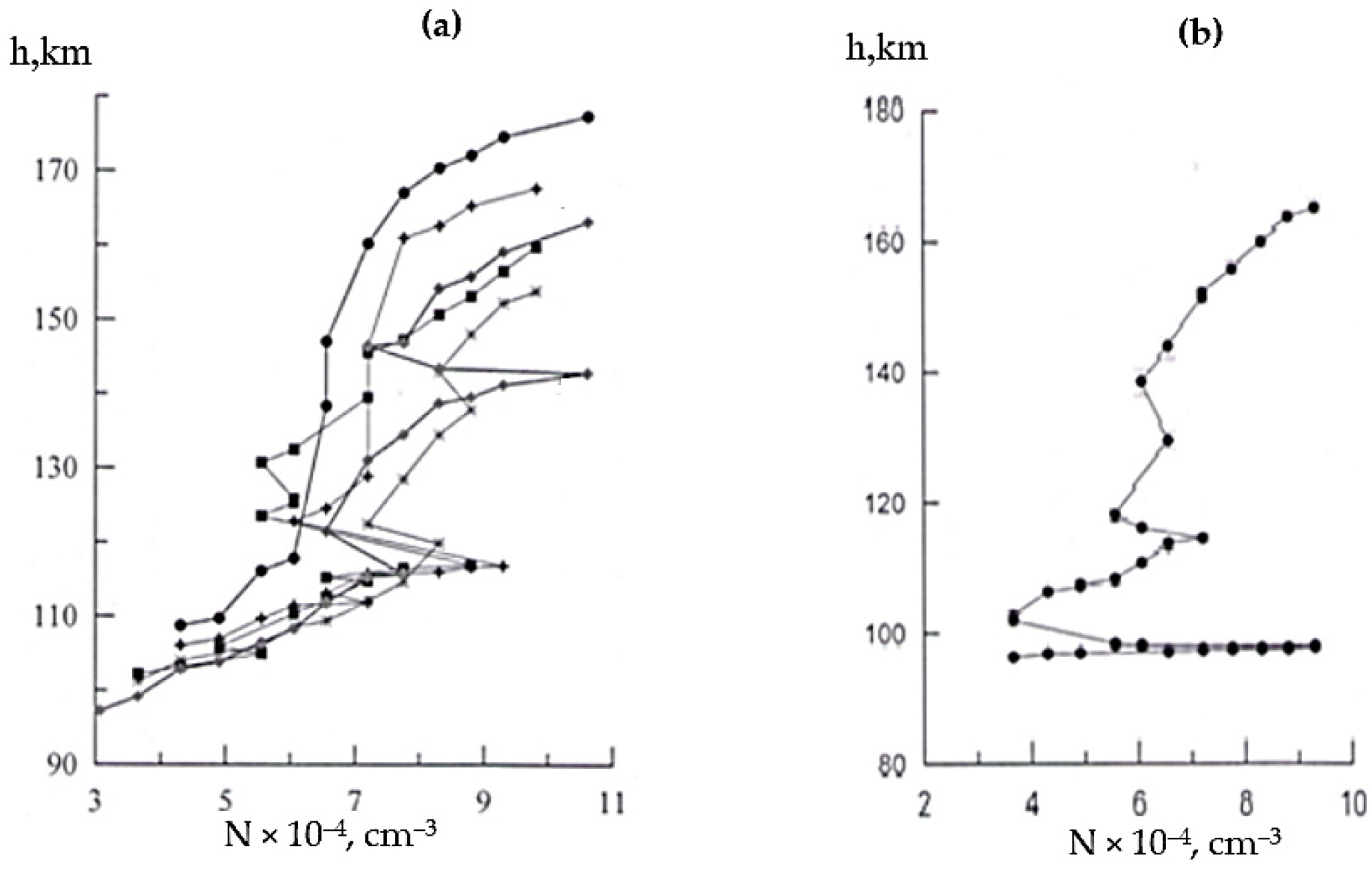
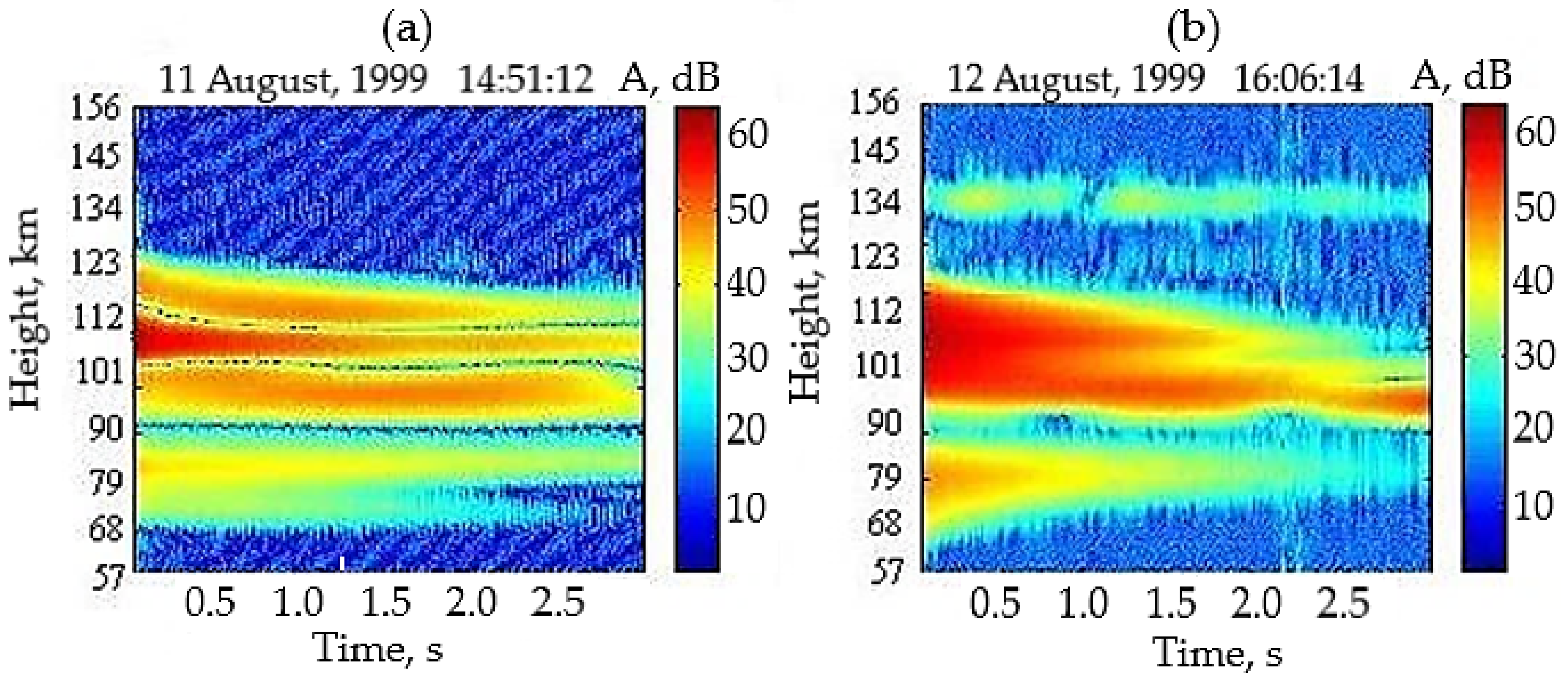
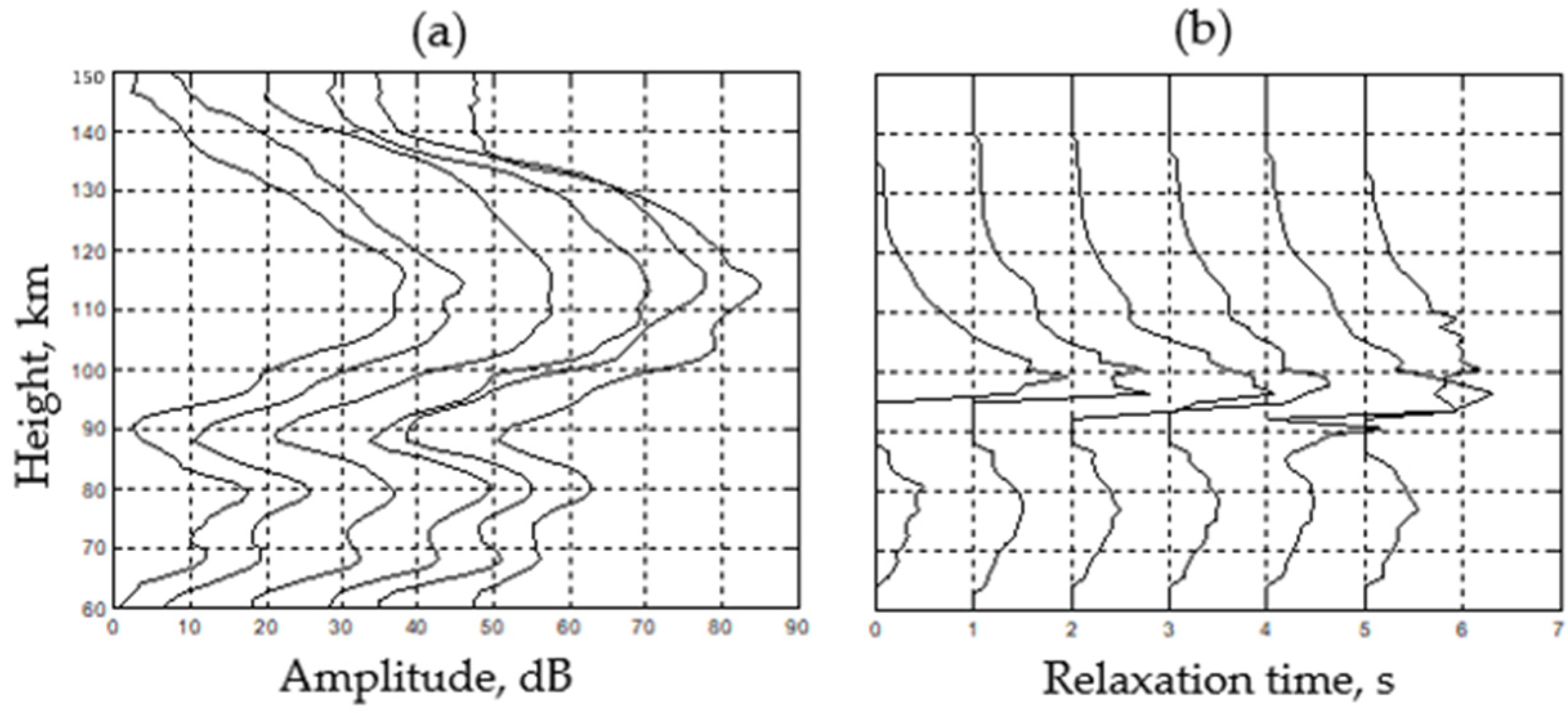
3.1. N(h)-Profile
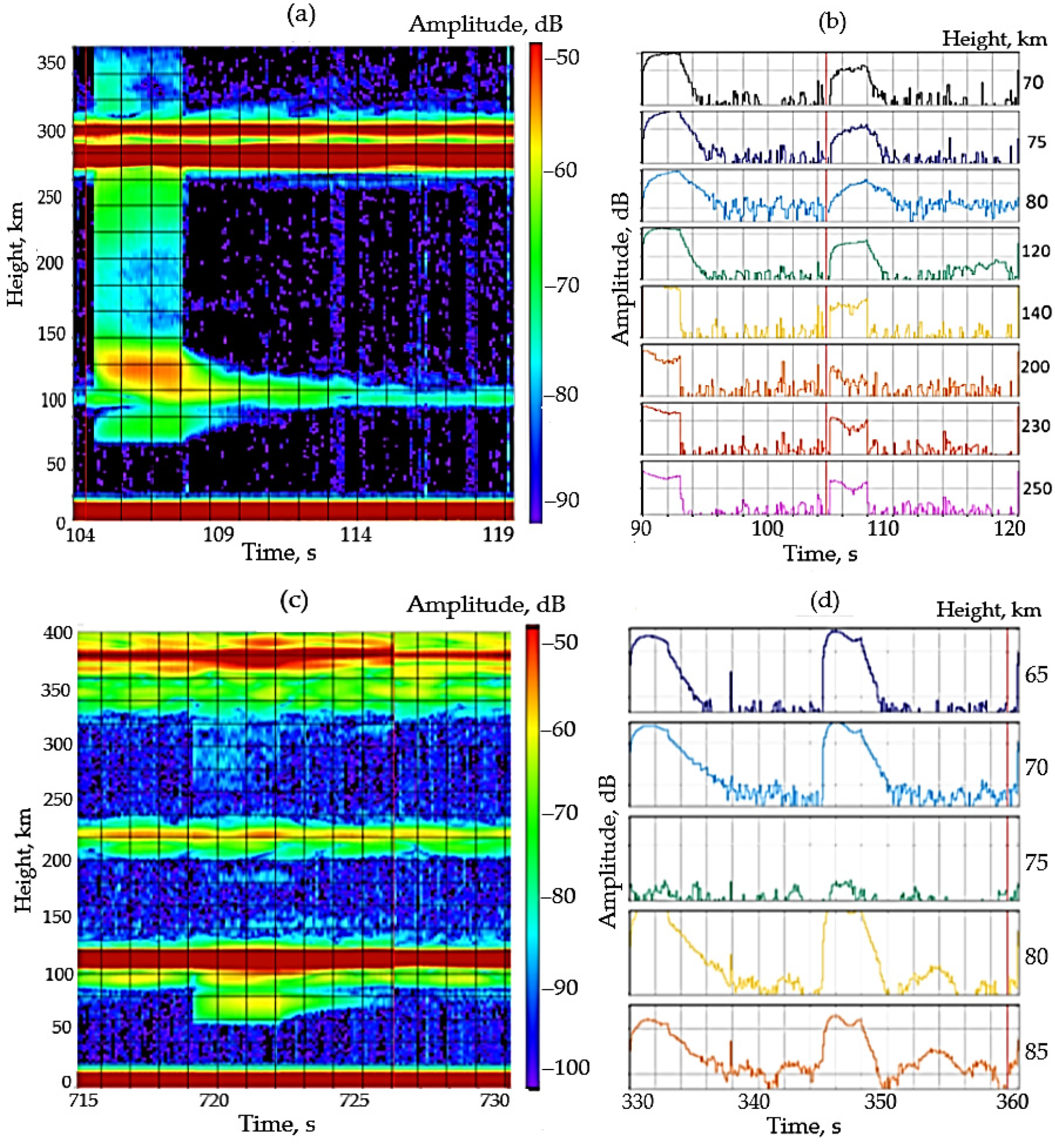
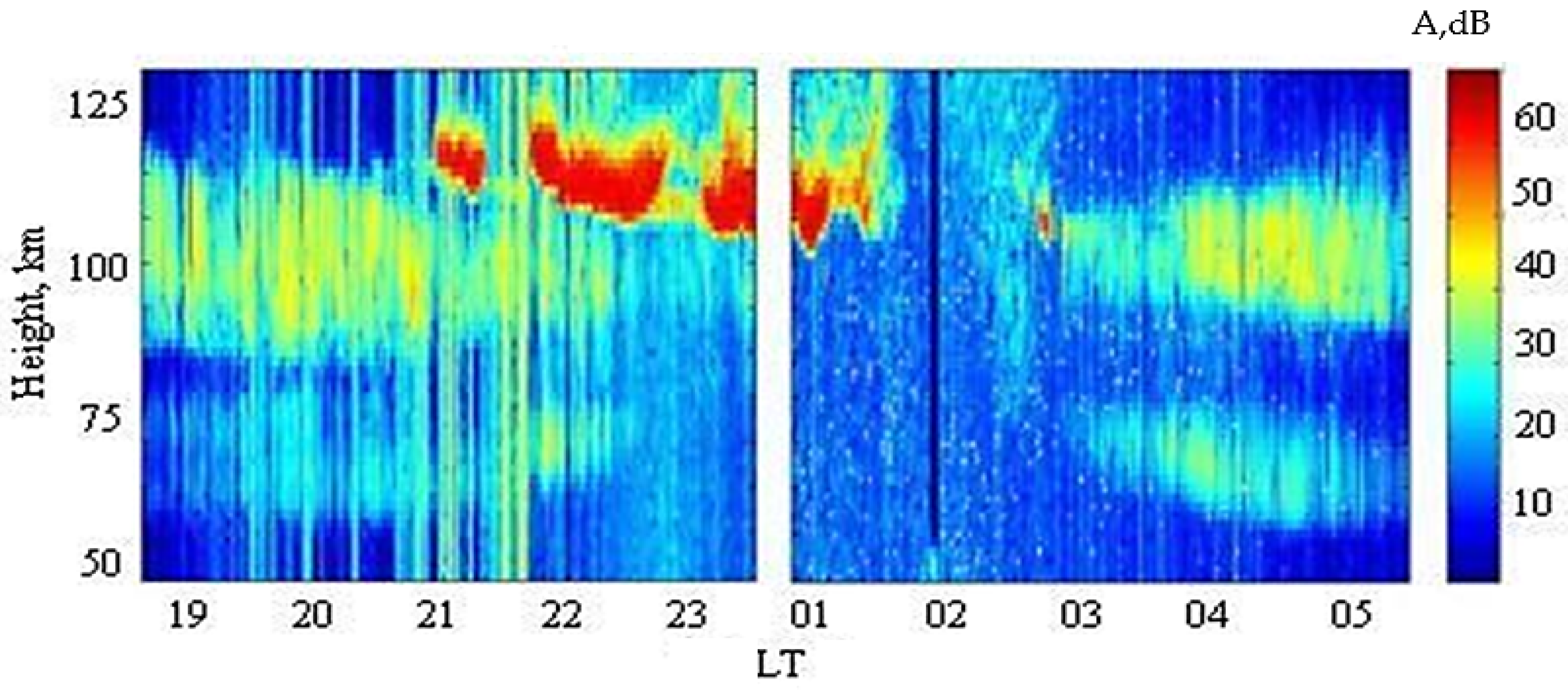
3.2. APIs and Sporadic E Layers
3.3. Ionization in the D Region
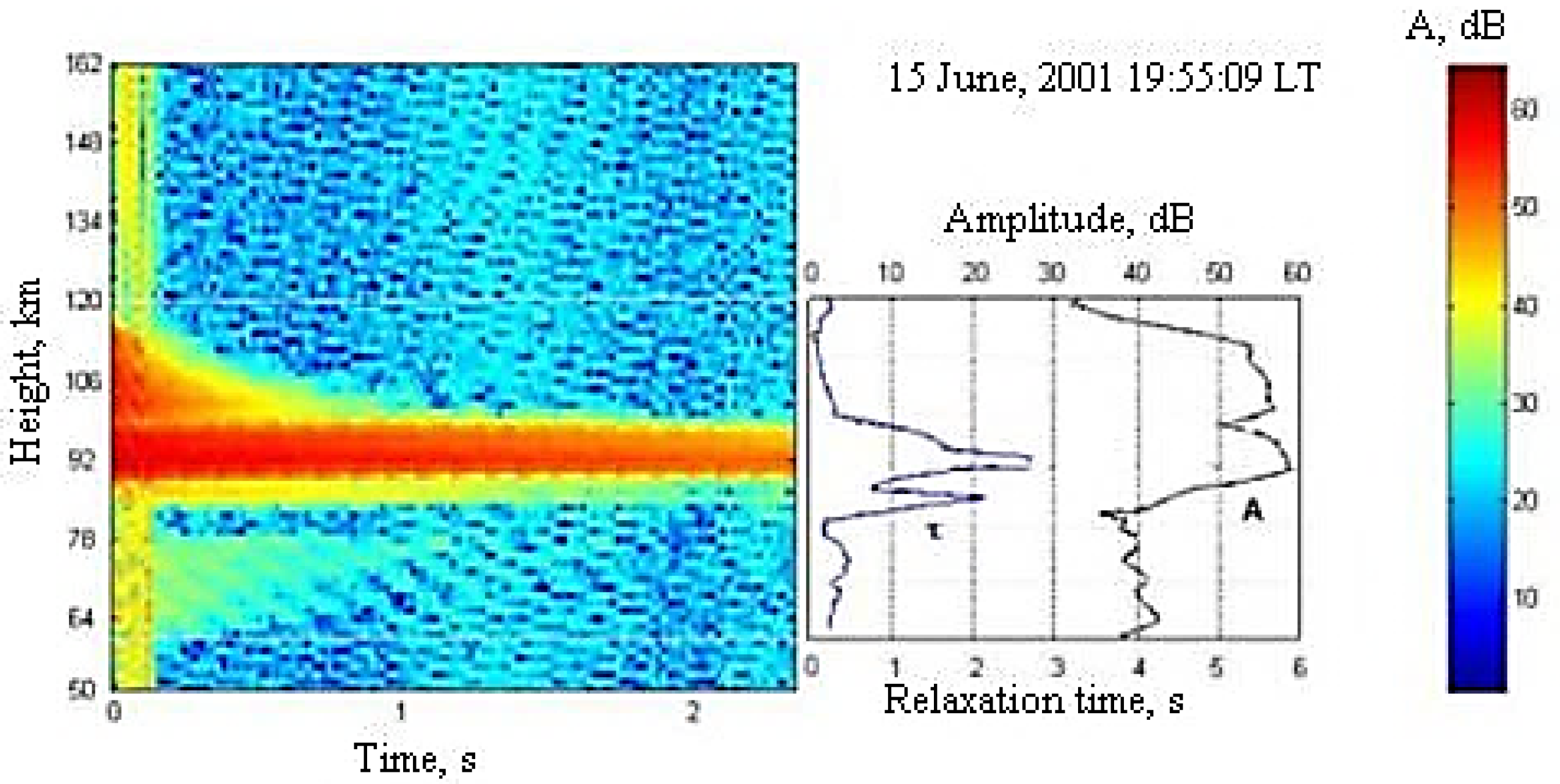
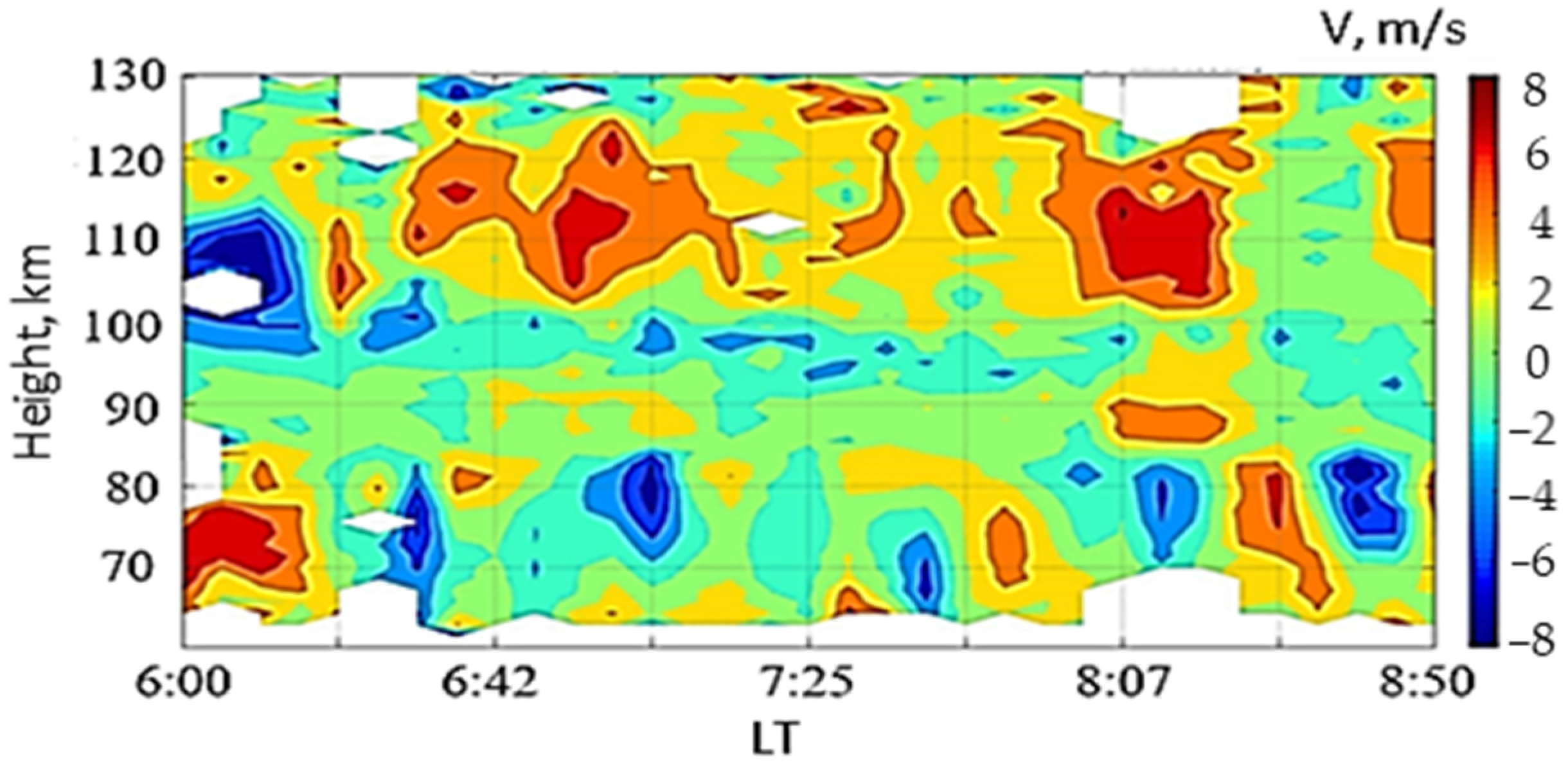
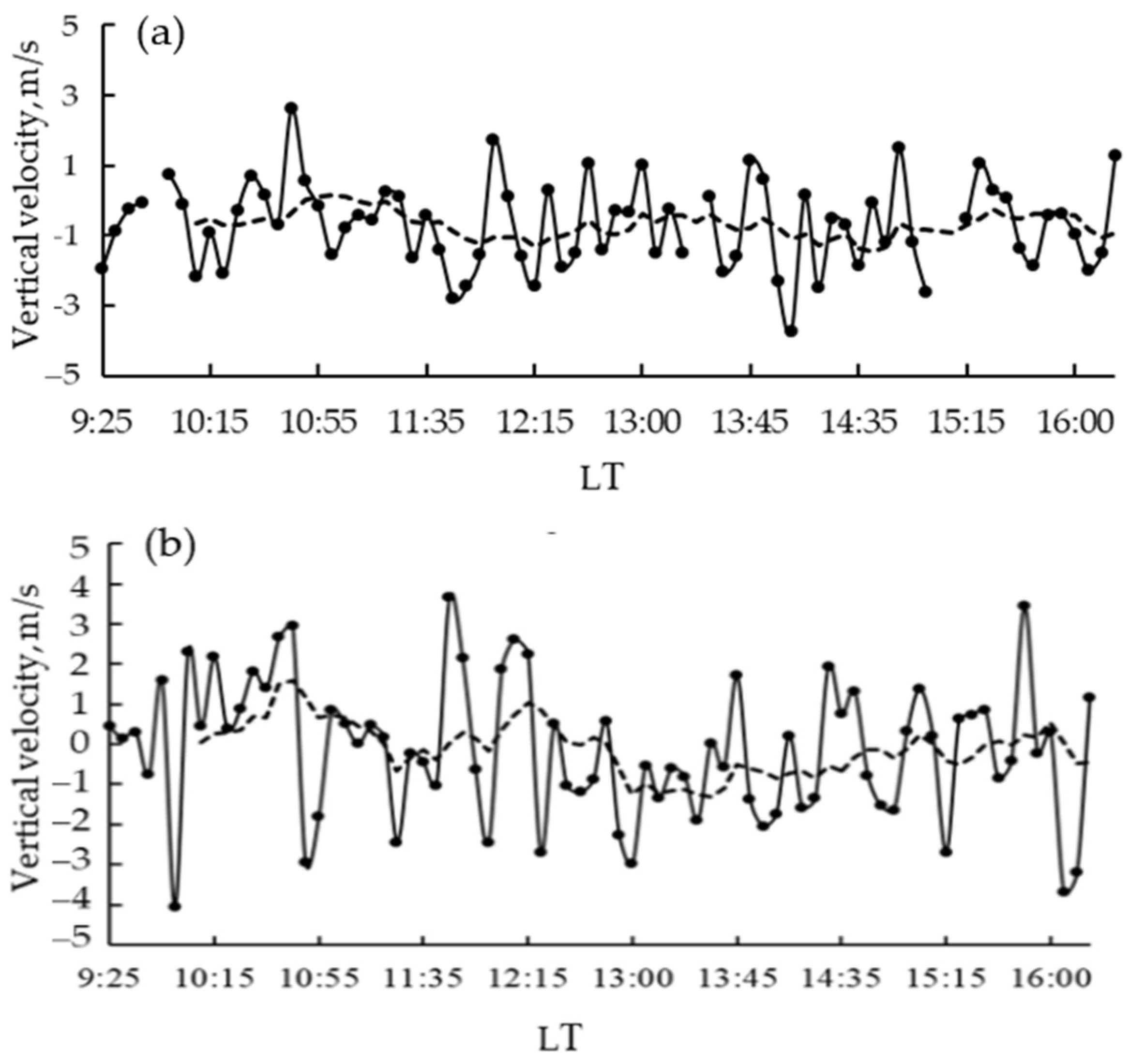
3.4. Plasma Vertical Velocity
4. API Technique and the Neutral Atmosphere
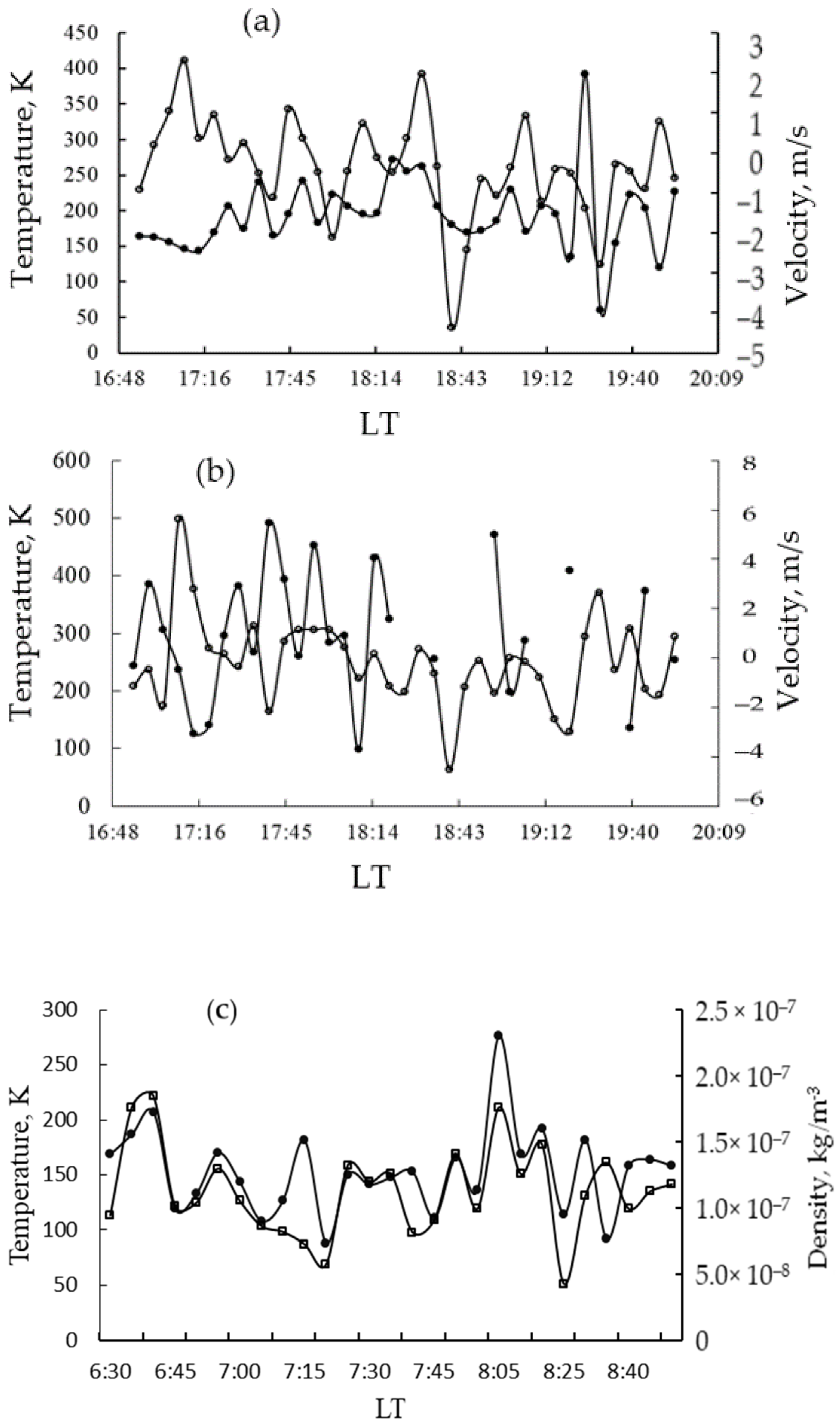
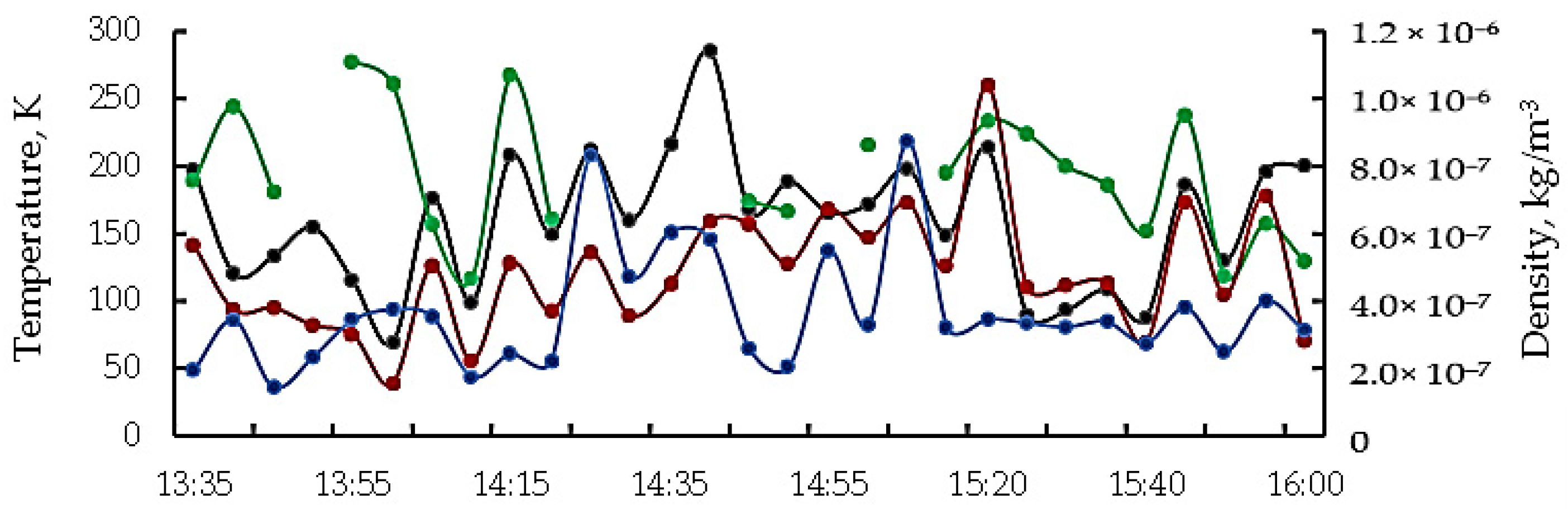
4.1. Temperature and Density in the E Region
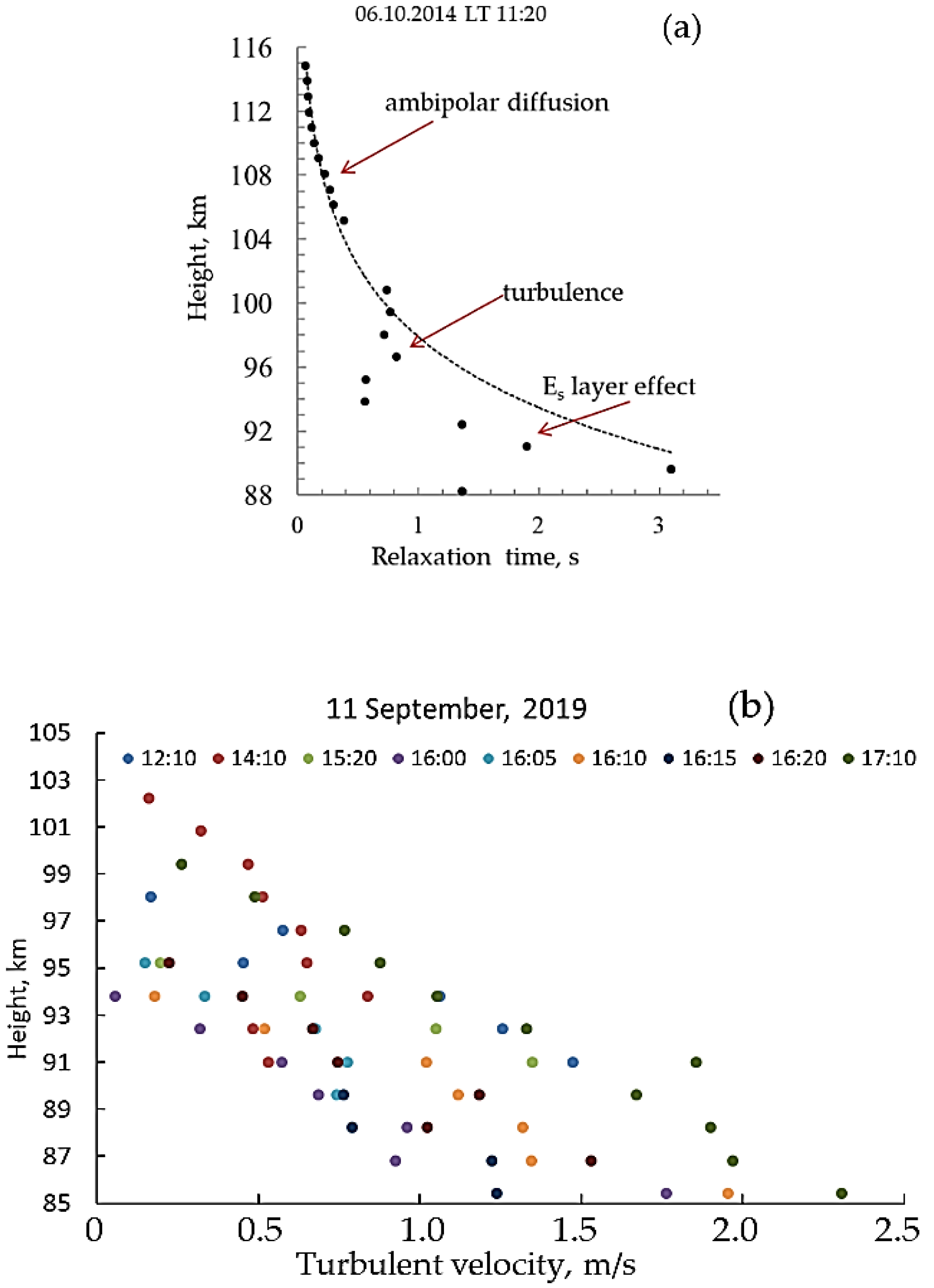
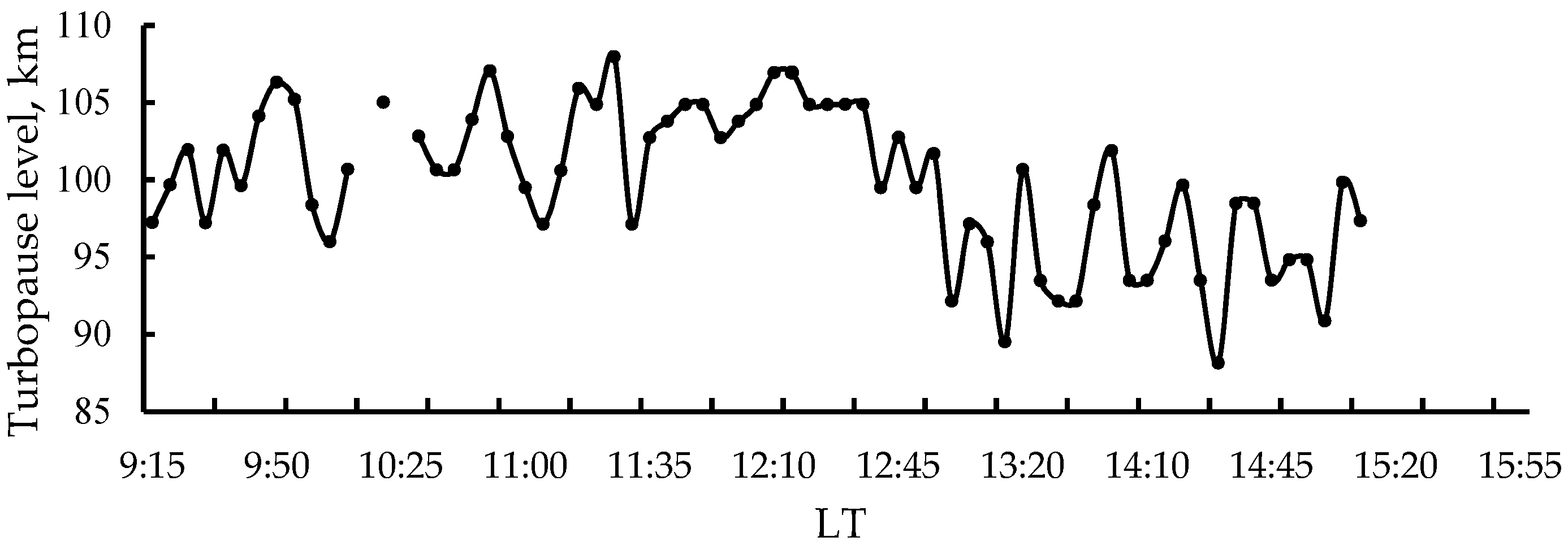
4.2. Turbulent Velocity and Turbopause Level
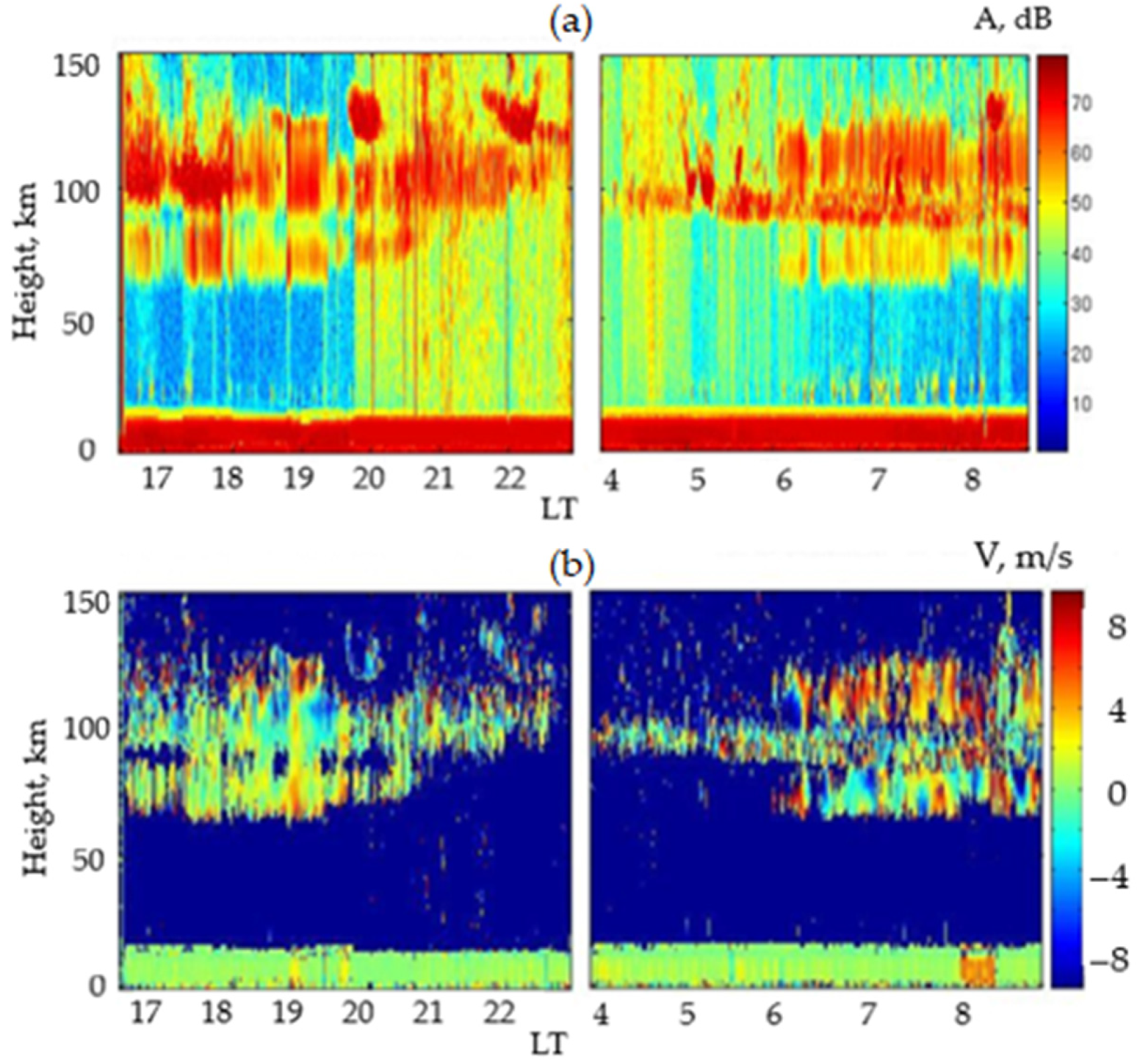
5. Study of Natural Phenomena Using the API Technique
5.1. Sunset–Sunrise Phenomena
5.2. Solar Eclipse
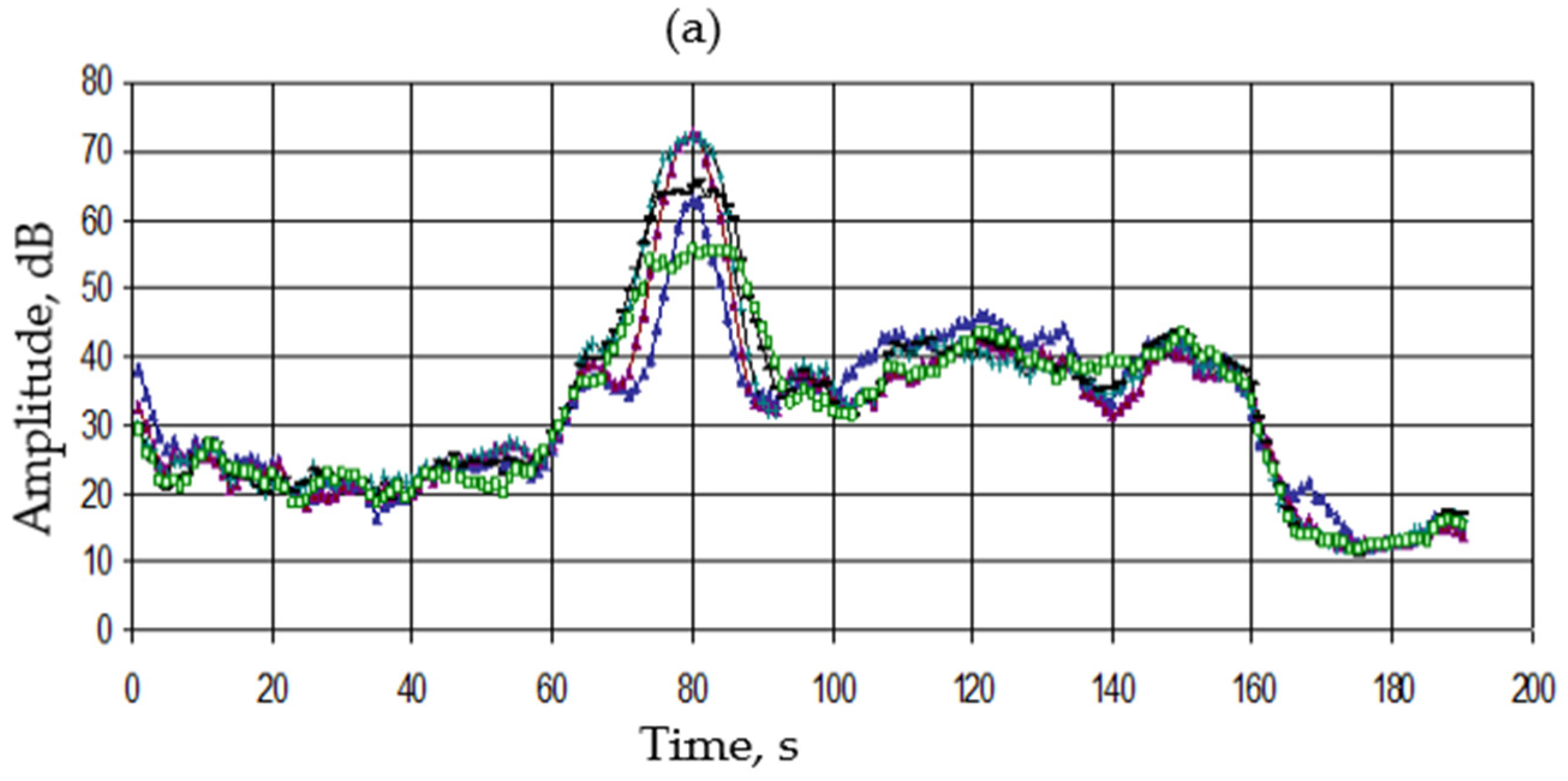
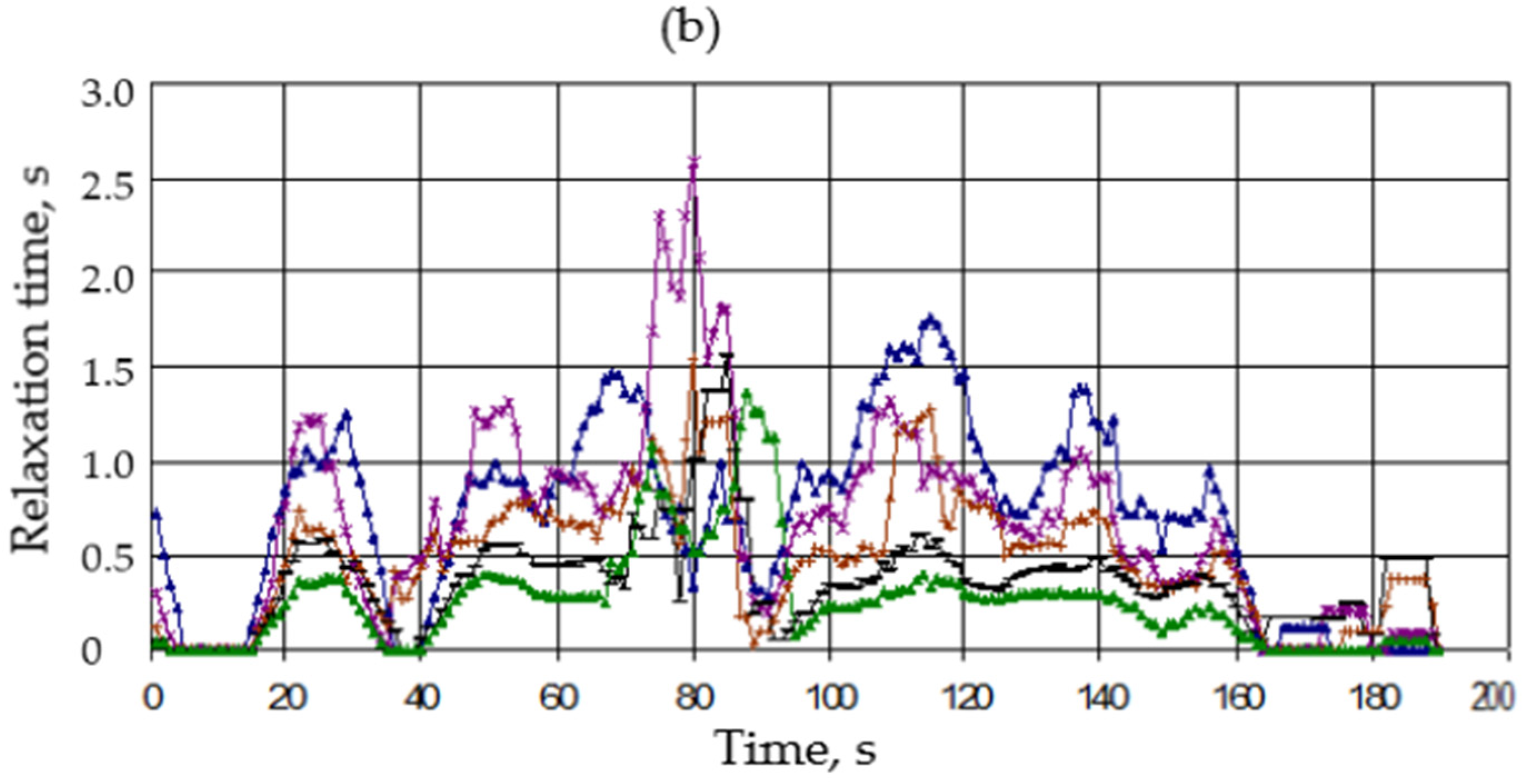
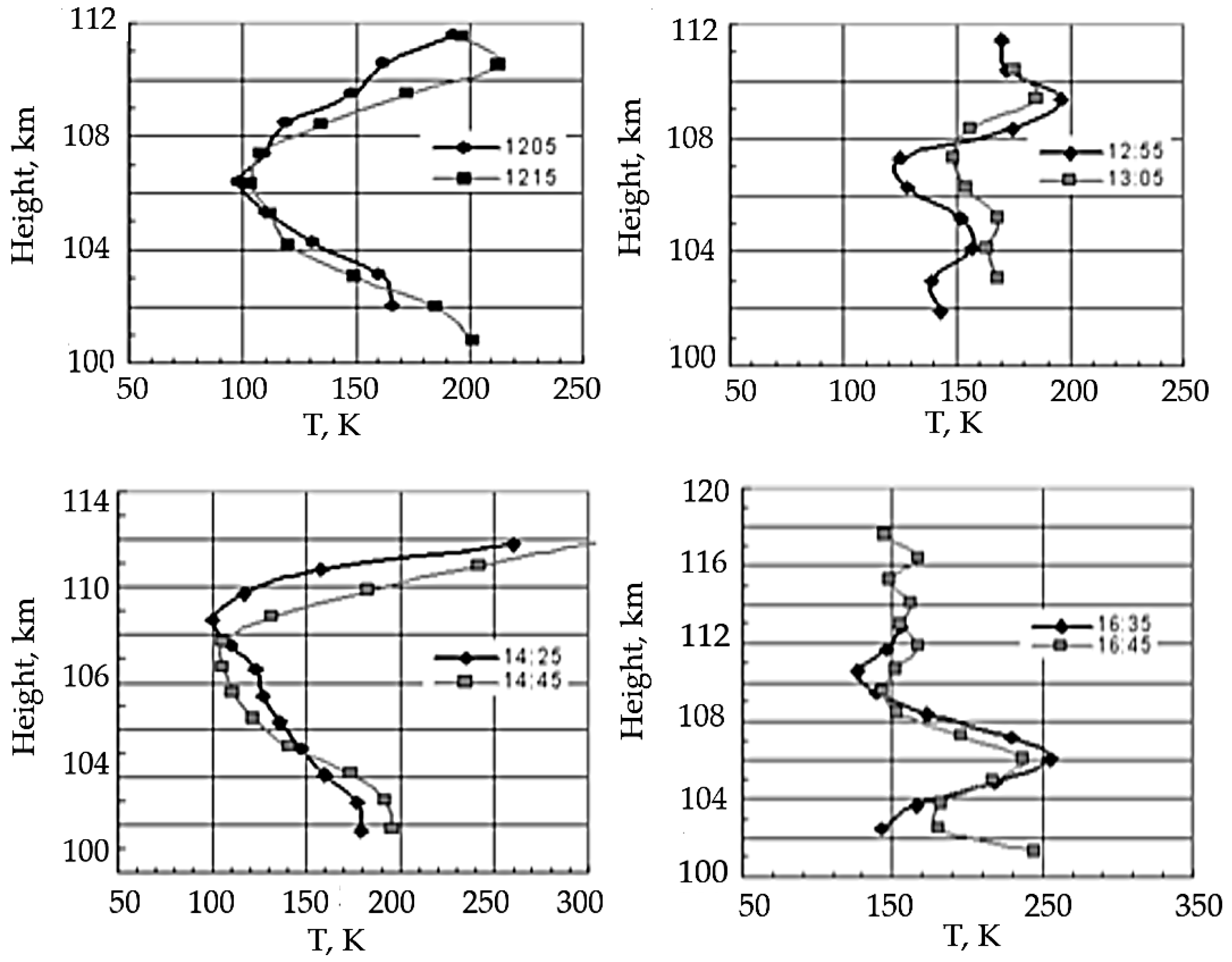
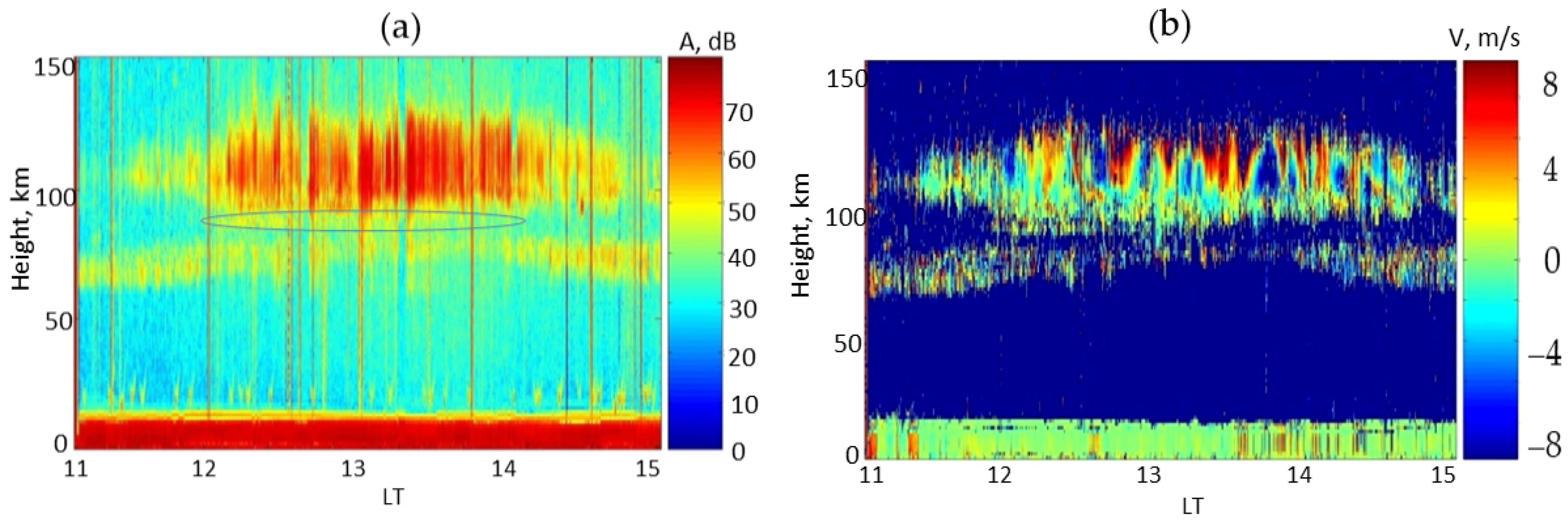
5.3. Atmospheric Waves
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vilenskii, I.M.; Izraileva, N.I.; Kapel’zon, A.A.; Plotkin, V.V.; Freiman, M.E. Artificial Quasi-Periodic Irregularities in the Lower Ionosphere; Nauka: Novosibirsk, Russia, 1987; p. 188. (In Russian) [Google Scholar]
- Belikovich, V.V.; Benediktov, E.A.; Getmantsev, G.G.; Ignat’ev, Y.A.; Komrakov, G.P. Scattering of radio waves from the artificially perturbed F region of the ionosphere (Engl. Translation). JETP Lett. 1975, 22, 243–244. [Google Scholar]
- Fejer, I.A.; Djuth, F.T.; Gonzales, C.A. Bragg backscatter from plasma inhomogeneities due to a powerful ionospherically reflected radio waves. J. Geophys. Res. 1984, 89, 9145–9147. [Google Scholar] [CrossRef]
- Djuth, F.T.; Groves, K.M.; Elder, J.H.; Shinn, E.R.; Quinn, J.M.; Villasenor, J.; Wong, A.Y. Measurements of artificial periodic inhomogeneities at HIPAS observatory. J. Geophys. Res. 1997, 102, 24023–24035. [Google Scholar] [CrossRef]
- Rietveld, M.T.; Goncharov, N.P. Artificial periodic irregularities from the Tromso heating facility. Adv. Space Res. 1998, 21, 693–696. [Google Scholar] [CrossRef]
- Rietveld, M.T.; Turunen, E.; Matveinen, H.; Goncharov, N.P.; Pollari, P. Artificial periodic irregularities in the auroral ionosphere. Ann. Geophys. 1996, 14, 1437–1453. [Google Scholar] [CrossRef]
- Vierinen, J.; Kero, A.; Rietveld, M.T. High latitude artificial periodic irregularity observations with the upgraded EISCAT heating facility. J. Atmos. Sol. Terr. Phys. 2013, 105–106, 253–261. [Google Scholar] [CrossRef]
- Hyssel, D.L.; McCarrick, M.J.; Fallen, C.T.; Vierinen, J. First artificial periodic inhomogeneity experiments at HAARP. GRL. 2015, 42, 1033–1297. [Google Scholar] [CrossRef]
- Grach, S.M.; Sergeev, E.N.; Bakhmetieva, N.V.; Milikh, G.; Shindin, A.V. Preliminary results of the artificial periodic irregularities excited by the HAARP HF heater. In Proceedings of the 14th Ionospheric Effects Symposium (IES2015), Alexandria, VA, USA, 12–14 May 2015; Available online: http://ies2015.bc.edu/wp-content/uploads/2015/05/051-Grach-Paper.pdf (accessed on 15 July 2022).
- Bakhmetieva, N.V.; Grach, S.M.; Sergeev, E.N.; Shindin, A.V.; Milikh, G.M.; Siefring, C.L.; Bernhardt, P.A.; McCarrick, M. Artificial periodic irregularities in the high-latitude ionosphere excited by the HAARP facility. Radio Sci. 2016, 51, 999–1009. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Benediktov, E.A.; Tolmacheva, A.V.; Bakhmet’eva, N.V. Ionospheric Research by Means of Artificial Periodic Irregularities; Copernicus GmbH: Katlenburg-Lindau, Germany, 2002; p. 160. [Google Scholar]
- Belikovich, V.V.; Benediktov, E.A. Investigation of the lower D-region of the ionosphere using artificial periodic irregularities. Radiofizika 1986, 29, 1283–1296. (In Russian) [Google Scholar]
- Belikovich, V.V.; Benediktov, E.A.; Terina, G.I. Diagnostics of the lower ionosphere by the method of resonance scattering of radio waves. J. Atmos. Terr. Phys. 1986, 48, 1247–1253. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Benediktov, E.A.; Vyakhirev, V.D.; Goncharov, N.P.; Tolmacheva, A.V.; Korotina, G.S. Studies of the ionosphere and neutral atmosphere using artificial periodic inhomogeneities in the ionospheric plasma. Radio Sci. 1998, 33, 583–594. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Bakhmet’eva, N.V.; Vyakhirev, V.D.; Bubukina, V.N.; Kalinina, E.E. Altitude–time variations in electron number density in the ionospheric E layer. Radiophys. Quantum Electron. 2011, 54, 365–375. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Benediktov, E.A.; Bubukina, V.N.; Ignat’ev, Y.A. Investigation of wave motions in the lower ionosphere by the method of resonance scattering of radio waves from artificial periodic inhomogeneities. Radiophys. Quantum Electron. 1997, 40, 196–205. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Bakhmeteva, N.V.; Kalinina, E.E.; Tolmacheva, A.V. A New method for determination of the electron number density in the e region of the ionosphere from relaxation times of artificial periodic inhomogeneities. Radiophys. Quantum Electron. 2006, 49, 669–674. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Benediktov, E.A.; Goncharov, N.P.; Tolmacheva, A.V. Diagnostics of the ionosphere and neutral atmosphere at e-region heights using artificial periodic inhomogeneities. J. Atmos. Sol.-Terr. Phys. 1997, 59, 2447–2460. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Kagan, L.M.; Ponyatov, A.A. Sunset–sunrise characteristics of sporadic layers of ionization in the lower ionosphere observed by the method of resonance scattering of radio waves from artificial periodic inhomogeneities of the ionospheric plasma. Radiophys. Quantum Electron. 2005, 48, 14–28. [Google Scholar] [CrossRef][Green Version]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Benediktov, E.A.; Tolmacheva, A.V. Studies of the irregular structure of the ionosphere using scattering of radio waves on artificial periodic inhomogeneities. Radiophys. Quantum Electron. 2001, 44, 924–934. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Benediktov, E.A.; Trunov, D.V. Height profiles of the amplitude and relaxation time of artificial periodic irregularities in the D-region. Geomagn. Aeron. 2000, 40, 733–738. [Google Scholar]
- Benediktov, E.A.; Belikovich, V.V.; Tolmacheva, A.K. Some results of measurement of atmospheric temperature and density using artificial periodic inhomogeneities of the ionospheric plasma. Radiophys. Quantum Electron. 1998, 41, 229–235. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Belikovich, V.V. Measurements of the temperature and density of the upper atmosphere using artificial periodic irregularities during the summer seasons of 1999–2002. Int. J. Geomagn. Aeron. 2004, 5, GI1008. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Benediktov, E.A.; Bubukina, V.N.; Vyakhirev, V.D. Artificial periodic inhomogeneities and a model for the lower part of the D region. Radiophys. Quantum Electron. 1999, 42, 431–437. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Ponyatov, A.A.; Tolmacheva, A.V.; Kagan, L.M.; Kelley, M.C.; Nicolls, M.J. New results of studying the lower ionosphere by the method of resonance scattering of radio waves from artificial periodic inhomogeneities. Radiophys. Quantum Electron. 2005, 48, 673–685. [Google Scholar] [CrossRef]
- Tolmacheva, A.V. Results of the ion–neutral collision frequency measurements in the lower thermosphere by the method of resonance scattering of the radio waves by artificial periodic irregularities. Radiophys. Quantum Electron. 2015, 58, 245–251. [Google Scholar] [CrossRef]
- Frolov, V.L.; Bakhmet’eva, N.V.; Belikovich, V.V.; Vertogradov, G.G.; Vertogradov, V.G.; Komrakov, G.P.; Kotik, D.S.; Mityakov, N.A.; Polyakov, S.V.; Rapoport, V.O.; et al. Modification of the Earth’s ionosphere by high power high frequency radio waves. Phys.-Uspekhi 2007, 50, 315–324. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Bakhmet’eva, N.V.; Bubukina, V.N.; Vyakhirev, V.D.; Kalinina, E.E.; Komrakov, G.P.; Tolmacheva, A.V. Results of determining the electron number density in the ionospheric E region from relaxation times of artificial periodic irregularities of different scales. Radiophys. Quantum Electron. 2008, 51, 431–437. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigor’ev, G.I.; Tolmacheva, A.V.; Kalinina, E.E. Atmospheric turbulence and internal gravity waves examined by the method of artificial periodic irregularities. Russ. J. Phys. Chem. B 2018, 12, 510–521. [Google Scholar]
- Yusupov, K.M.; Bakhmetieva, N.V. Sporadic E layer with a structure of double cusp in the vertical sounding ionogram. Atmosphere 2021, 12, 1093. [Google Scholar] [CrossRef]
- Wilkinson, P.J.; Szuszczewicz, E.P.; Roble, R.G. Measurements and modeling of intermediate, descending, and sporadic layers in the lower ionosphere: Results and implications for global-scale ionospheric-thermospheric studies. Geophys. Res. Lett. 1992, 19, 95–98. [Google Scholar] [CrossRef]
- Haldoupis, C.; Meek, C.; Christakis, N.; Pancheva, D.; Bourdillon, A. Ionogram height–time–intensity observations of descending sporadic E layers at mid-latitude. J. Atmos. Sol.-Terr. Phys. 2006, 68, 539–557. [Google Scholar] [CrossRef]
- Mathews, J.D.; Bekeny, F.S. Upper atmospheric tides and the vertical motion of ionospheric sporadic layers at Arecibo. J. Geophys. Res. 1979, 84, 2743–2750. [Google Scholar] [CrossRef]
- Shalimov, S.; Kozlovsky, A. High-latitude E and F region coupling signature: A case study results from rapid-run ionosonde. J. Geophys. Res. Space Phys. 2015, 120, 3033–3041. [Google Scholar] [CrossRef]
- Yusupov, K.M.; Mathews, J.D.; Maruyama, T.; Akchurin, A.D.; Tolstikov, M.V.; Sherstyukov, O.N.; Filippova, E.A.; Safiullin, A.S. Amplitude variations of the reflected signal during vertical sounding of the ionosphere at middle latitudes. Sol.-Terr. Phys. 2020, 6, 72–80. [Google Scholar]
- Bakhmetieva, N.V.; Belikovich, V.V. Results of studying the sporadic E layer by the method of resonant scattering of radio waves by artificial periodic inhomogeneities of the ionospheric plasma. Radiophys. Quantum Electron. 2008, 51, 862–873. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Belikovich, V.V.; Grigor’ev, G.I.; Tolmacheva, A.V. Effect of acoustic gravity waves on variations in the lower-ionosphere parameters as observed using artificial periodic inhomogeneities. Radiophys. Quantum Electron. 2002, 45, 211–219. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Ignat’ev, Y.A.; Ponyatov, A.A. Vertical motions in the lower ionosphere and a sporadic E layer. Radiophys. Quantum Electron. 1999, 42, 22–30. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Egerev, M.N.; Tolmacheva, A.V. Artificial periodic irregularities, wave phenomena in the lower ionosphere and the sporadic E-layer. Radiophys. Quantum Electron. 2010, 53, 77–90. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Bakhmetieva, N.V.; Grigoriev, G.I.; Kalinina, E.E. The main results of the long-term measurements of the neutral atmosphere parameters by the artificial periodic irregularities techniques. Adv. Space Res. 2015, 56, 1185–1193. [Google Scholar] [CrossRef]
- Bakhmet’eva, N.V.; Belikovich, V.V.; Benediktov, E.A.; Bubukina, V.N.; Goncharov, N.P.; Ignat’ev, Y.A. Investigation of acoustic gravity waves in the upper atmosphere by the artificial periodic inhomogeneities method at Nizhny Novgorod. Radiophys. Quantum Electron. 1996, 39, 224–228. [Google Scholar] [CrossRef]
- Huuskonen, A.; Nygren, T.; Jalonen, L.L.; Bjorn, N.; Hansen, T.L.; Brekke, A. Ion composition in sporadic E layers measured by the EISCAT UHF radar. J. Geophys. Res. 1988, 93, 14603. [Google Scholar] [CrossRef]
- Kopp, E. On the abundance of metal ions in the lower ionosphere. J. Geophys. Res. Space Phys. 1997, 102, 9967–9974. [Google Scholar] [CrossRef]
- Belikovich, V.V.; Benediktov, E.A. Study of the twilight D-region of the Ionosphere using artificial periodic inhomogeneities. Radiophys. Quantum Electron. 2002, 45, 458–464. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Kulikov, Y.Y.; Zhemyakov, I.N. Mesosphere Ozone and the lower Ionosphere under plasma disturbance by powerful high-frequency radio emission. Atmosphere 2020, 11, 1154. [Google Scholar] [CrossRef]
- Gershman, B.N. Dynamics of the Ionospheric Plasma; Nauka: Moscow, Russia, 1974; p. 256. (In Russian) [Google Scholar]
- Benediktov, E.A.; Belikovich, V.V.; Bakhmet’eva, N.V.; Tolmacheva, A.V. Artificial periodic inhomogeneities of the ionosperic plasma as a promising line in the ionospheric research. Radiophys. Quantum Electron. 2002, 45, 343–357. [Google Scholar] [CrossRef]
- Benediktov, E.A.; Belikovich, V.V.; Bakhmet’eva, N.V.; Tolmacheva, A.V. Seasonal and daily variations of the velocity of vertical motions at altitudes of the mesosphere and lower thermosphere near Nizhny Novgorod. Geomag. Aeron. 1997, 37, 88. [Google Scholar]
- Tolmacheva, A.V.; Grigoriev, G.I.; Bakhmetieva, N.V. The variations of the atmospherical parameters on measurements using the artificial periodic irregularities of plasma. Russ. J. Phys. Chem. B 2013, 7, 663–669. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigoriev, G.I.; Tolmacheva, A.V.; Zhemyakov, I.N. Investigations of Atmospheric Waves in the Earth Lower Ionosphere by Means of the Method of the Creation of the Artificial Periodic Irregularities of the Ionospheric Plasma. Atmosphere 2019, 10, 450. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Vyakhirev, V.D.; Grigoriev, G.I.; Egerev, M.N.; Kalinina, E.E.; Tolmacheva, A.V.; Zhemyakov, I.N.; Vinogradov, G.R.; Yusupov, K.M. Dynamics of the mesosphere and lower thermosphere based on results of observations on the SURA facility. Geomag. Aeron. 2020, 60, 96–111. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigor’ev, G.I.; Tolmacheva, A.V. Artificial periodic irregularities, hydrodynamic instabilities, and dynamic processes in the mesosphere-lower thermosphere. Radiophys. Quantum Electron. 2011, 53, 623–637. [Google Scholar]
- Bakhmetieva, N.V.; Zhemyakov, I.N. Vertical plasma motions in the dynamics of the mesosphere and lower thermosphere of the Earth. Russ. J. Phys. Chem. B 2022, 16. in press. [Google Scholar]
- Bakhmetieva, N.V.; Grigoriev, G.I.; Vinogradov, G.R.; Zhemyakov, I.N.; Kalinina, E.E.; Pershin, A.V. Parameters of Atmospheric Turbulence and the Dynamics of the Lower Ionosphere in Studies at the SURA Facility. Geomag. Aeron. 2021, 61, 871–887. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Bakhmetieva, N.V.; Grigoriev, G.I.; Egerev, M.N. Turbopause range measured by the method of the artificial periodic irregularities. Adv. Space Res. 2019, 64, 1968–1974. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Vyakhirev, V.D.; Kalinina, E.E.; Komrakov, G.P. Earth’s lower ionosphere during partial solar eclipses according to observations near Nizhny Novgorod. Geomagn. Aeron. 2017, 57, 58–71. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Bubukina, V.N.; Vyakhirev, V.D.; Kalinina, E.E.; Komrakov, G.P. Response of the lower ionosphere to the partial solar eclipses of 1 August 2008 and 20 March 2015 based on observations of radio-wave scattering by the ionospheric plasma irregularities. Radiophys. Quantum Electron. 2017, 59, 782–793. [Google Scholar] [CrossRef]
- Gossard, E.E.; Hooke, W.H. Waves in the Atmosphere; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 1975; p. 456. [Google Scholar]
- Grigoriev, G.I. Acoustic-gravity waves in the earth’s atmosphere (Review). Radiophys. Quanum Electron. 1999, 42, 1–21. [Google Scholar] [CrossRef]
- Offermann, D.; Jarisch, M.; Oberheide, J.; Gusev, O.; Wohltmann, I.; Russel, J.M., III; Mlynczak, M.G. Global wave activity from upper stratosphere to lower thermosphere: A new turbopause concept. J. Atmos. Sol. Terr. Phys. 2006, 68, 1709–1729. [Google Scholar] [CrossRef]
- Tsuda, T.; Kato, S.; Yokol, T.; Inoue, T.; Yamamoto, M.; VanZand, T.E.; Fukao, S.; Sato, T. Gravity waves in the mesosphere observed with the middle and upper atmosphere radar. Radio Sci. 1990, 26, 1005–1018. [Google Scholar] [CrossRef]
- Hines, C.O. Internal atmospheric gravity waves at atmospheric heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Grigor’ev, G.I.; Bakhmetieva, N.V.; Tolmacheva, A.V.; Kalinina, E.E. Relaxation time of artificial periodic irregularities of the ionospheric plasma and diffusion in the inhomogeneous atmosphere. Radiophys. Quantum Electron. 2013, 56, 187–196. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigor’ev, G.I.; Tolmacheva, A.V.; Kalinina, E.E.; Egerev, M.N. Internal gravity waves in the lower thermosphere with linear temperature profile: Theory and experiment. Radiophys. Quantum Electron. 2017, 60, 103–112. [Google Scholar] [CrossRef]
- Bakhmetieva, N.V.; Grigoriev, G.I.; Kalinina, E.E. Acoustic gravity waves with a heterogeneous temperature profile of the neutral component in the earth’s atmosphere. Russ. J. Phys. Chem. B 2022, 16, 499–507. [Google Scholar] [CrossRef]
- Tolmacheva, A.V.; Grigoriev, G.I. Polytropic Processes in the Lower Thermosphere. Russ. J. Phys. Chem. B 2021, 15, 582–589. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhmetieva, N.V.; Grigoriev, G.I. Study of the Mesosphere and Lower Thermosphere by the Method of Creating Artificial Periodic Irregularities of the Ionospheric Plasma. Atmosphere 2022, 13, 1346. https://doi.org/10.3390/atmos13091346
Bakhmetieva NV, Grigoriev GI. Study of the Mesosphere and Lower Thermosphere by the Method of Creating Artificial Periodic Irregularities of the Ionospheric Plasma. Atmosphere. 2022; 13(9):1346. https://doi.org/10.3390/atmos13091346
Chicago/Turabian StyleBakhmetieva, Nataliya V., and Gennadiy I. Grigoriev. 2022. "Study of the Mesosphere and Lower Thermosphere by the Method of Creating Artificial Periodic Irregularities of the Ionospheric Plasma" Atmosphere 13, no. 9: 1346. https://doi.org/10.3390/atmos13091346
APA StyleBakhmetieva, N. V., & Grigoriev, G. I. (2022). Study of the Mesosphere and Lower Thermosphere by the Method of Creating Artificial Periodic Irregularities of the Ionospheric Plasma. Atmosphere, 13(9), 1346. https://doi.org/10.3390/atmos13091346






