Diurnal and Seasonal Variation of High-Frequency Gravity Waves at Mohe and Wuhan
Abstract
1. Introduction
2. Datasets and Methods
2.1. Datasets
2.2. Method
3. Results and Analysis
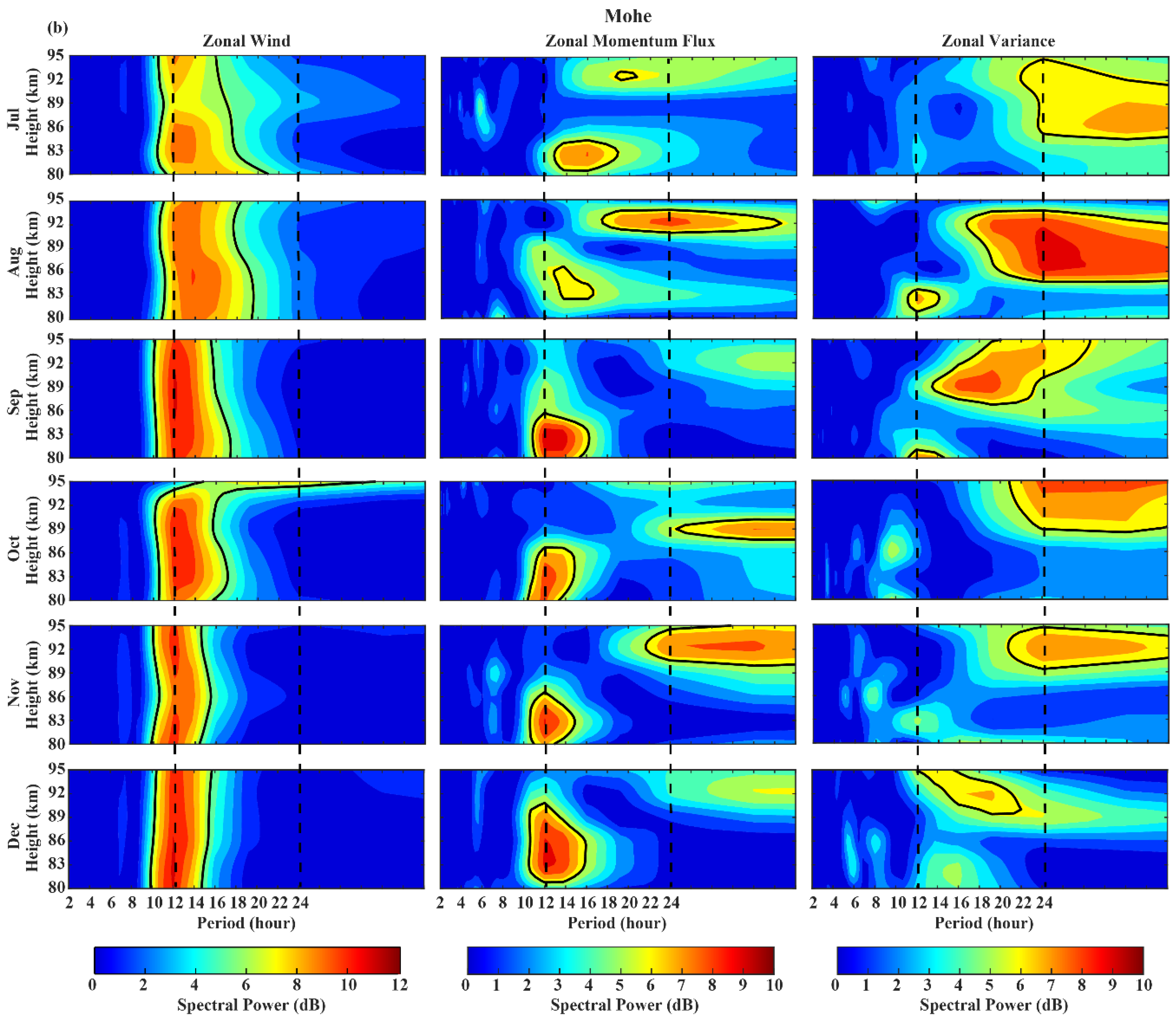
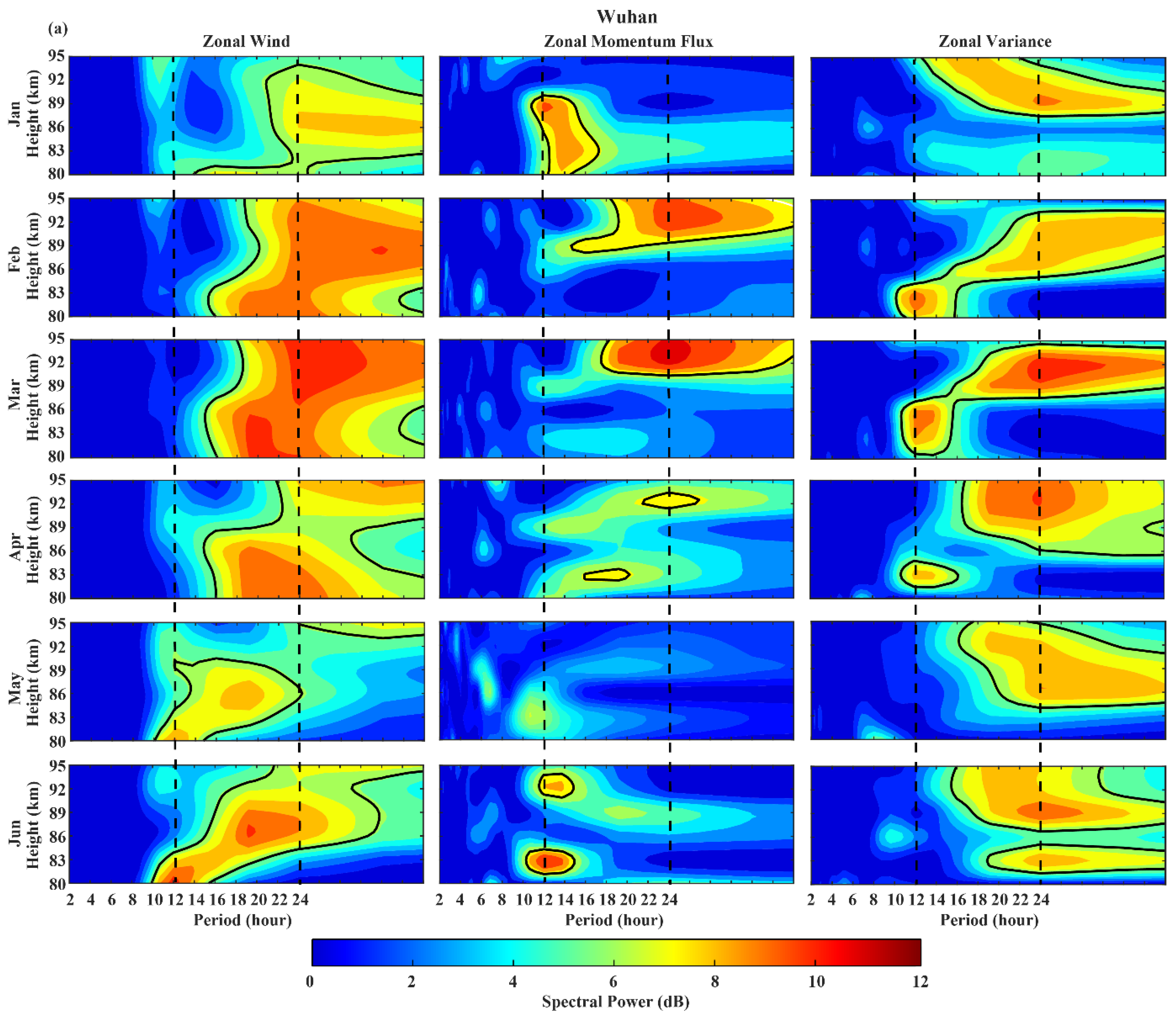
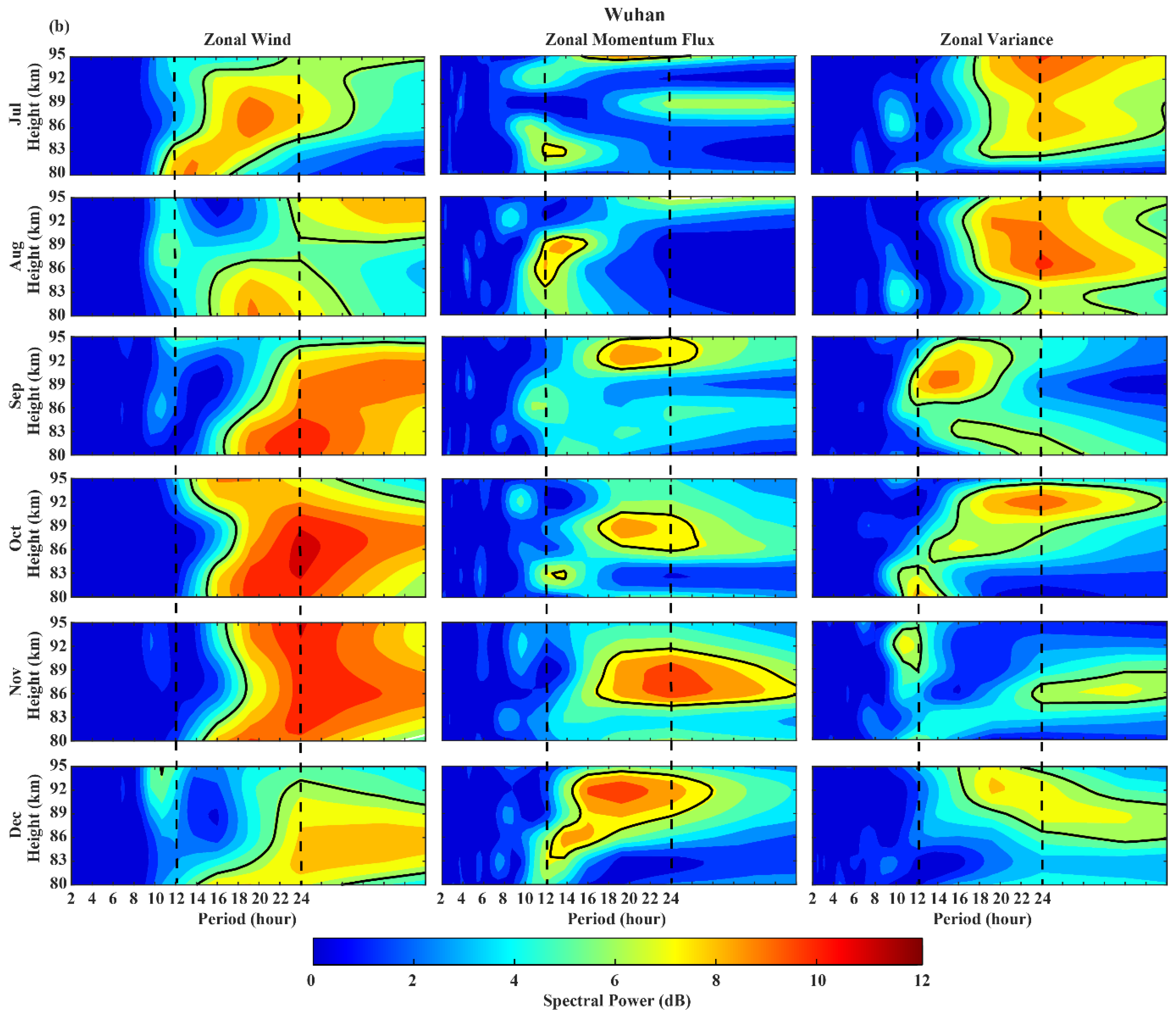
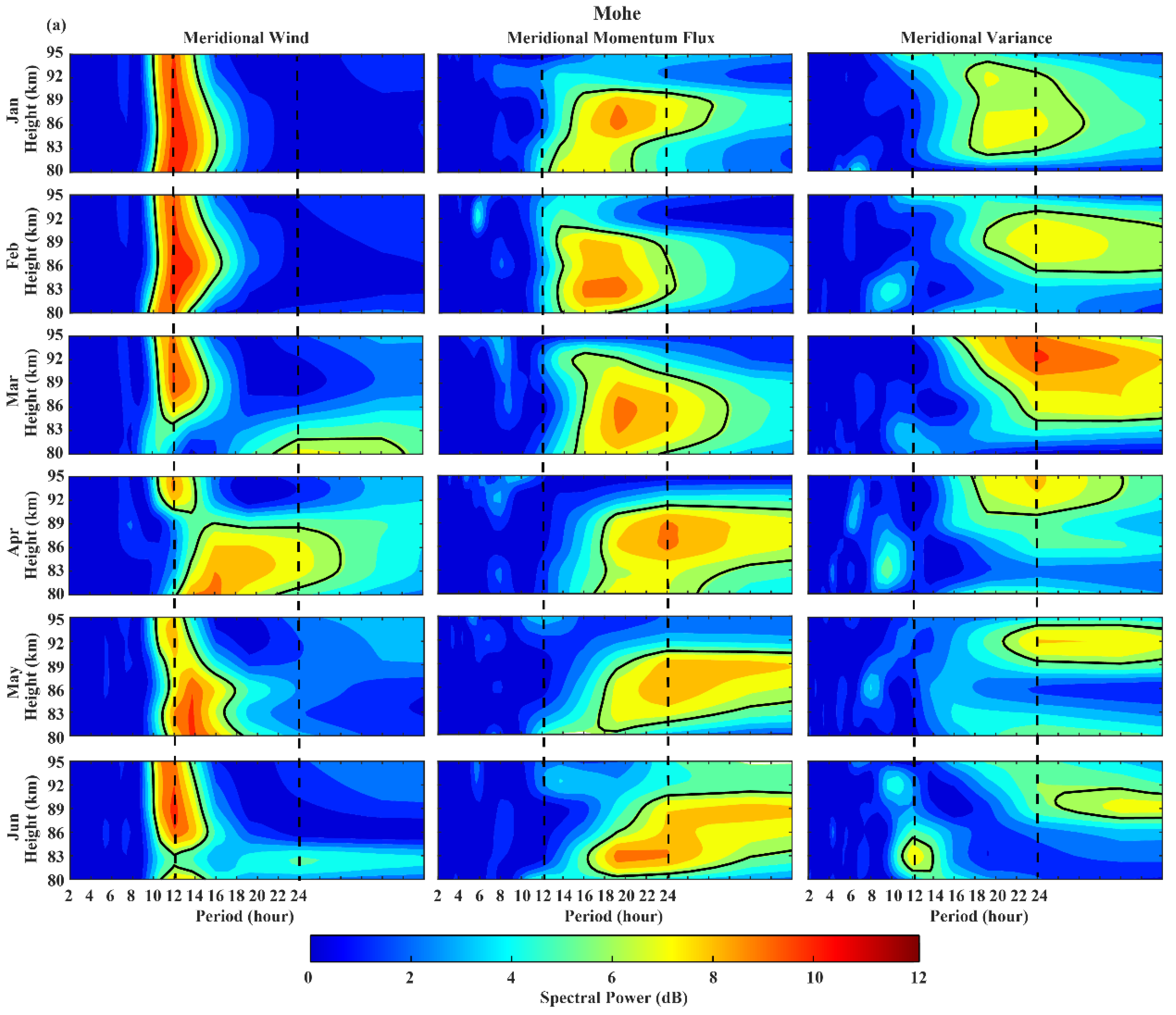
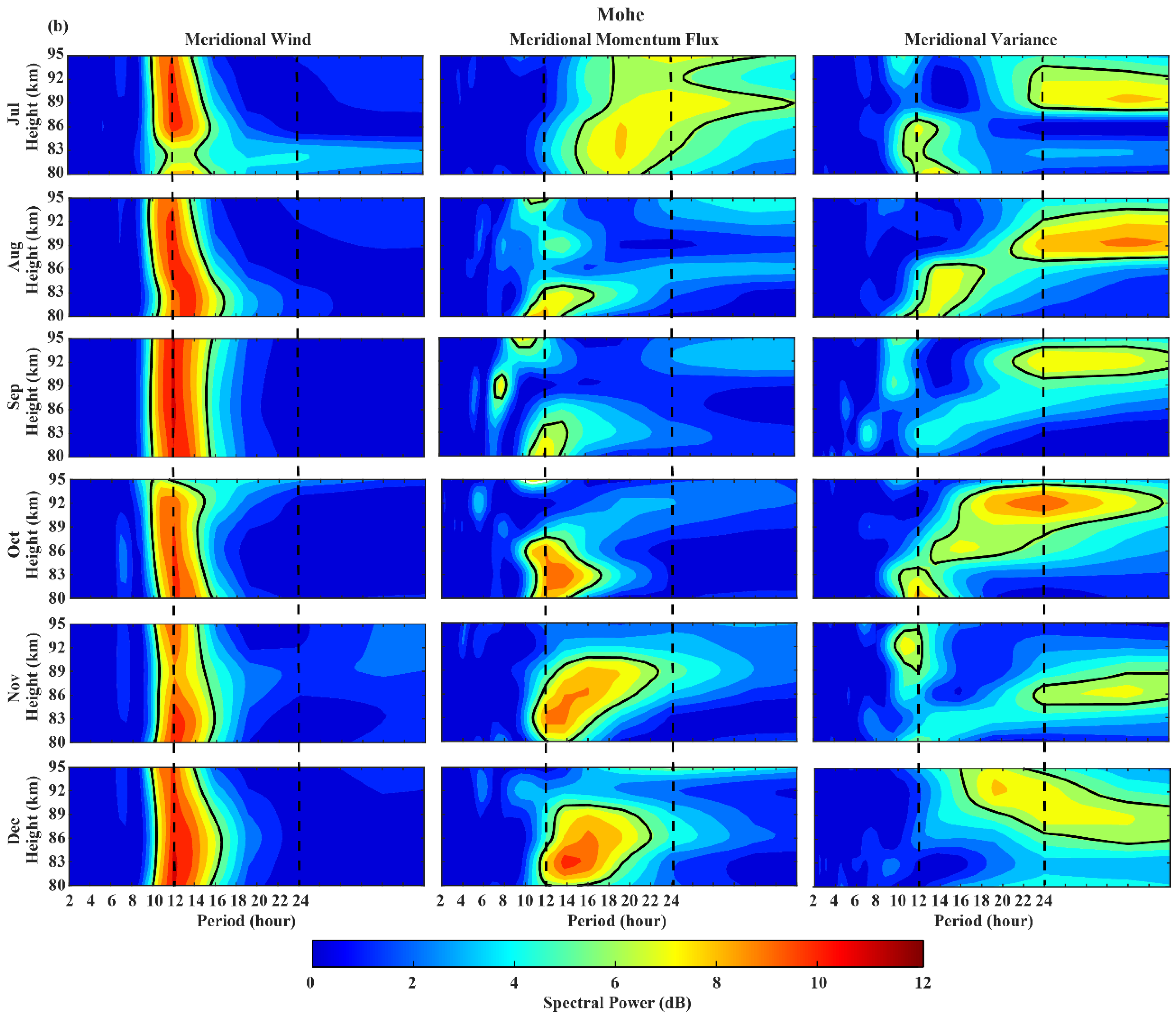
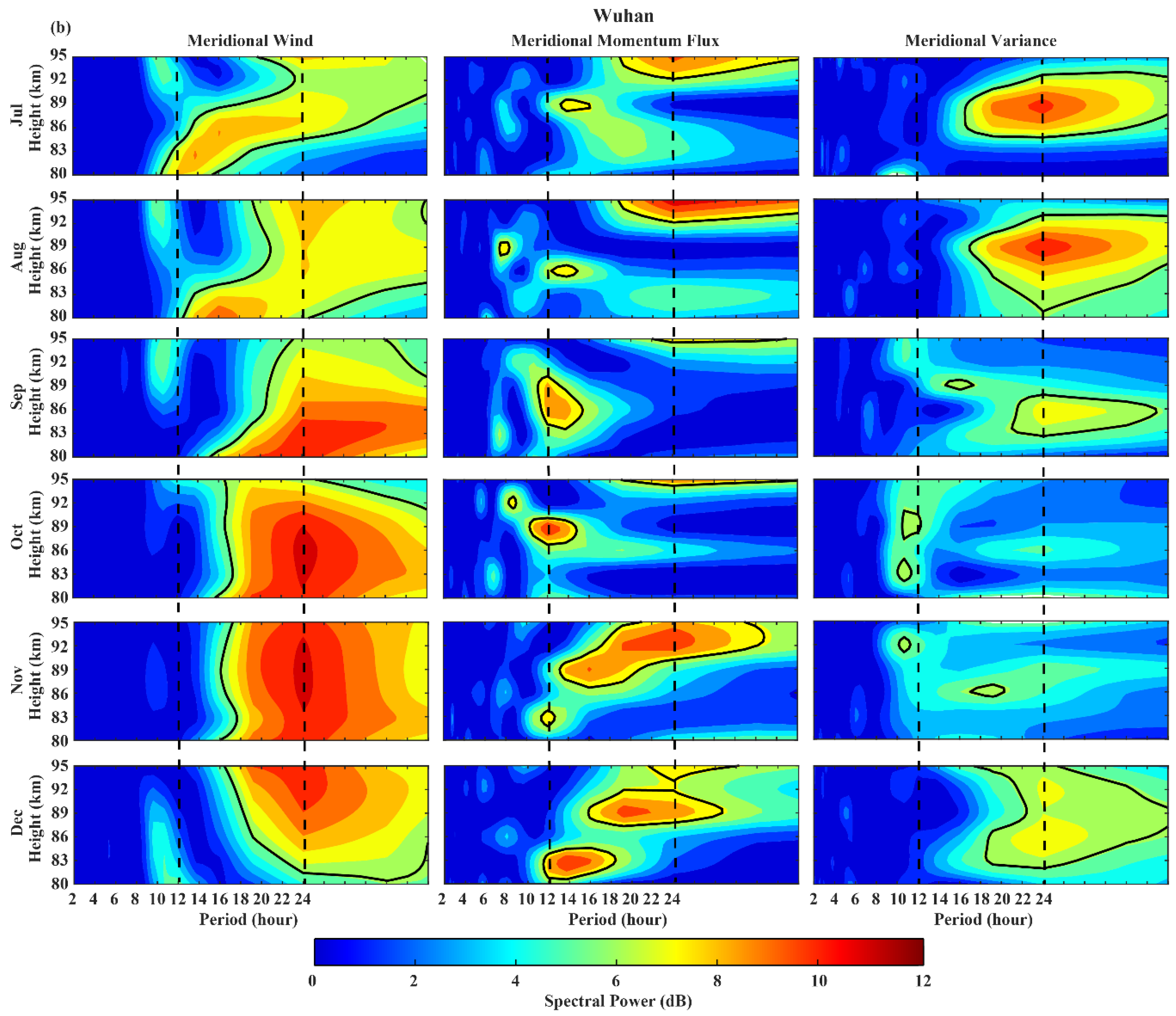
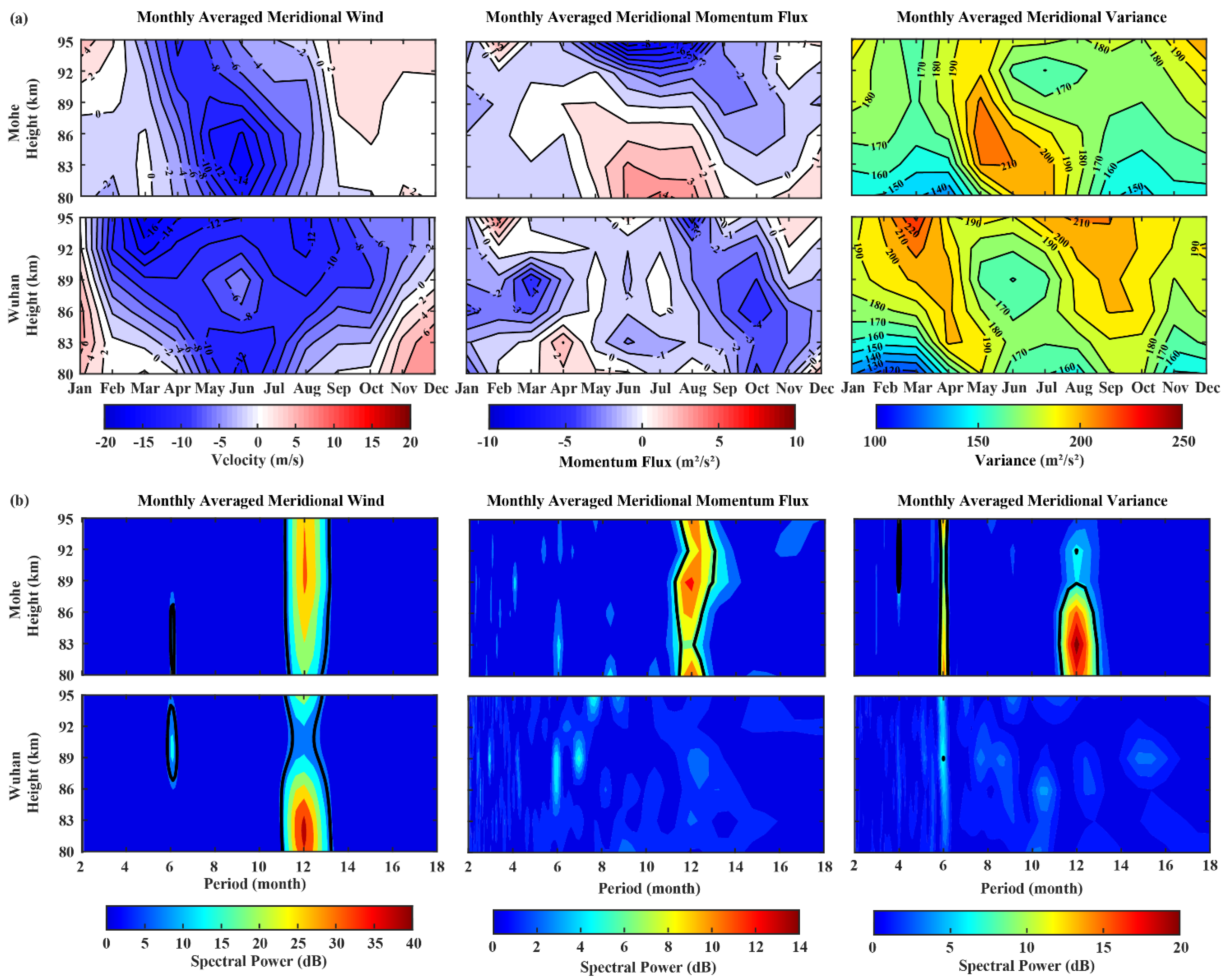
3.1. Diurnal Variation
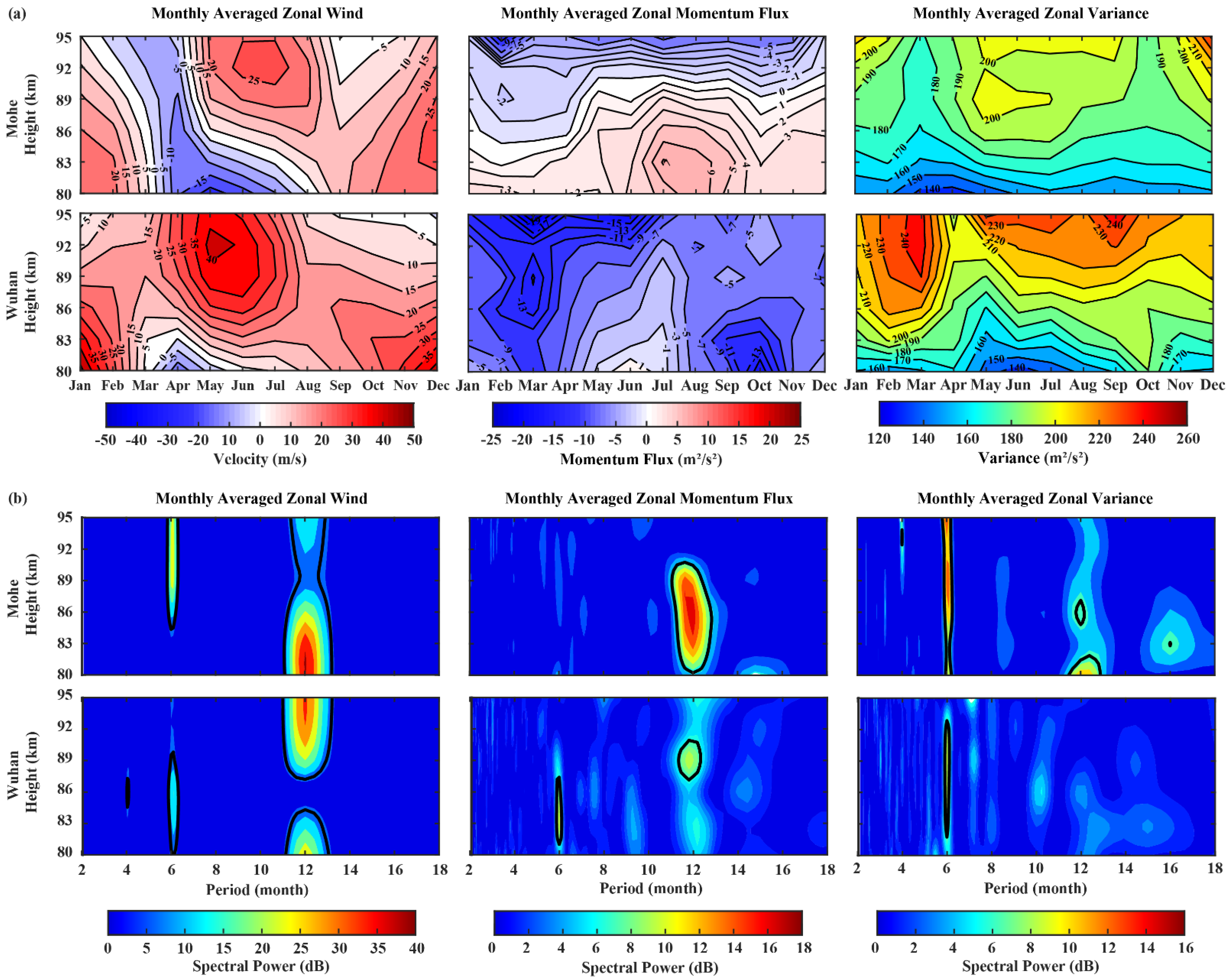
3.2. Seasonal Variation
4. Discussion
5. Summary
- The meridional momentum flux of GWs presents an anti-correlated pattern to the meridional wind pattern at Mohe, which is due to the wind filtering of GWs, while the meridional momentum flux is almost southward at Wuhan without the correlation with the background meridional wind.
- The 24 h variation of the high-frequency GWs activity is observed more frequently at both stations.
- The high-frequency GWs activity at Mohe shows obvious annual and semiannual oscillations, while that at Wuhan only presents a weak semiannual oscillation. In addition, a quasi-4-month oscillation is observed at Mohe.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Placke, M. Gravity Waves and Momentum Fluxes in the Mesosphere and Lower Thermosphere Region. Master’s Thesis, University of Rostock, Rostock, Germany, 2014. [Google Scholar]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Lindzen, R.S. Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. Ocean. 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Holton, J.R. The Role of Gravity Wave Induced Drag and Diffusion in the Momentum Budget of the Mesosphere. J. Atmos. Sci. 1982, 39, 791–799. [Google Scholar] [CrossRef]
- Andrioli, V.F.; Batista, P.P.; Clemesha, B.R.; Schuch, N.J.; Buriti, R.A. Multi-year observations of gravity wave momentum fluxes at low and middle latitudes inferred by all-sky meteor radar. Ann. Geophys. 2015, 33, 1183–1193. [Google Scholar] [CrossRef]
- Ern, M.; Preusse, P.; Gille, J.C.; Hepplewhite, C.L.; Mlynczak, M.G.; Russell, J.M.; Riese, M. Implications for atmospheric dynamics derived from global observations of gravity wave momentum flux in stratosphere and mesosphere. J. Geophys. Res. Atmos. 2011, 116, D19107. [Google Scholar] [CrossRef]
- Hoffmann, P.; Jacobi, C.; Borries, C. Possible planetary wave coupling between the stratosphere and ionosphere by gravity wave modulation. J. Atmos. Sol. Terr. Phy. 2012, 75, 71–80. [Google Scholar] [CrossRef]
- Holton, J.R.; Alexander, M.J. The role of waves in the transport circulation of the middle atmosphere. In Atmospheric Science across the Stratopause, 1st ed.; Siskind, D.E., Eckermann, S.D., Summers, M.E., Eds.; American Geophysical Union: Washington, DC, USA, 2000; Volume 123, pp. 21–35. [Google Scholar]
- Manson, A.H.; Meek, C.E.; Luo, Y.; Hocking, W.K.; MacDougall, J.; Riggin, D.; Fritts, D.C.; Vincent, R.A. Modulation of gravity waves by planetary waves (2 and 16 d): Observations with the North American-Pacific MLT-MFR radar network. J. Atmos. Sol. Terr. Phys. 2003, 65, 85–104. [Google Scholar] [CrossRef]
- Jacobi, C.; Gavrilov, M.N.; Kürschner, D.; Fröhlich, K. Gravity wave climatology and trends in the mesosphere/lower thermosphere region deduced from low-frequency drift measurements 1984–2003 (52.1° N, 13.2° E). J. Atmos. Sol. Terr. Phys. 2006, 68, 1913–1923. [Google Scholar] [CrossRef]
- Matsumoto, N.; Shinbori, A.; Riggin, D.M.; Tsuda, T. Measurement of momentum flux using two meteor radars in Indonesia. Ann. Geophys. 2016, 34, 369–377. [Google Scholar] [CrossRef]
- Placke, M.; Stober, G.; Jacobi, C. Gravity wave momentum fluxes in the MLT—Part I: Seasonal variation at Collm (51.3° N, 13.0° E). J. Atmos. Sol. Terr. Phy. 2011, 73, 904–910. [Google Scholar] [CrossRef]
- Liu, A.Z.; Lu, X.; Franke, S.J. Diurnal variation of gravity wave momentum flux and its forcing on the diurnal tide. J. Geophys. Res. Atmos. 2013, 118, 1668–1678. [Google Scholar] [CrossRef]
- Manson, A.H.; Meek, C.E.; Hall, G.E. Correlations of gravity waves and tides in the mesosphere over Saskatoon. J. Atmos. Sol. Terr. Phy. 1998, 60, 1089–1107. [Google Scholar] [CrossRef]
- Beldon, C.L.; Mitchell, N.J. Gravity waves in the mesopause region observed by meteor radar, 2: Climatologies of gravity waves in the Antarctic and Arctic. J. Atmos. Sol. Terr. Phy. 2009, 71, 875–884. [Google Scholar] [CrossRef]
- Jia, M.; Xue, X.; Gu, S.Y.; Chen, T.D.; Ning, B.Q.; Wu, J.F.; Zeng, X.Y.; Dou, X.K. Multiyear Observations of Gravity Wave Momentum Fluxes in the Midlatitude Mesosphere and Lower Thermosphere Region by Meteor Radar. J. Geophys. Res. Space Phys. 2018, 123, 5684–5703. [Google Scholar] [CrossRef]
- Andrioli, V.F.; Fritts, D.C.; Batista, P.P.; Clemesha, B.R.; Janches, D. Diurnal variation in gravity wave activity at low and middle latitudes. Ann. Geophys. 2013, 31, 2123–2135. [Google Scholar] [CrossRef]
- Rauthe, M.; Gerding, M.; Lubken, F.J. Seasonal changes in gravity wave activity measured by lidars at mid-latitudes. Atmos. Chem. Phys. Discuss. 2008, 8, 13741–13773. [Google Scholar] [CrossRef]
- Rapp, M.; Strelnikov, B.; Müllemann, A.; Lübken, F.J.; Fritts, D.C. Turbulence measurements and implications for gravity wave dissipation during the MaCWAVE/MIDAS rocket program. Geophys. Res. Lett. 2004, 31, L24S07. [Google Scholar] [CrossRef]
- Krebsbach, M.; Preusse, P. Spectral analysis of gravity wave activity in SABER temperature data. Geophys. Res. Lett. 2007, 34, L03814. [Google Scholar] [CrossRef]
- Hocking, W.K.; Fuller, B.; Vandepeer, B. Real-time determination of meteor-related parameters utilizing modern digital technology. J. Atmos. Sol. Terr. Phy. 2001, 63, 155–169. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Reid, I.M.; Cervera, M.A. Buckland Park all-sky interferometric meteor radar. Radio. Sci. 2004, 39, RS5009. [Google Scholar] [CrossRef]
- Reid, J.D.; Choi, C.H.; Oldroyd, N.O. Calcium oxalate crystals in the thyroid: Their identification, prevalence, origin, and possible significance. Am. J. Clin. Pathol. 1987, 87, 443–454. [Google Scholar] [CrossRef]
- Hocking, W.K. A new approach to momentum flux determinations using SKiYMET meteor radars. Ann. Geophys. 2005, 23, 2433–2439. [Google Scholar] [CrossRef]
- Vincent, R.A.; Kovalam, S.; Reid, I.M.; Younger, J.P. Gravity wave flux retrievals using meteor radars. Geophys. Res. Lett. 2010, 37, L14802. [Google Scholar] [CrossRef]
- de Wit, R.J.; Hibbins, R.E.; Espy, P.J.; Orsolini, Y.J.; Limpasuvan, V.; Kinnison, D.E. Observations of gravity wave forcing of the mesopause region during the January 2013 major Sudden Stratospheric Warming. Geophys. Res. Lett. 2014, 41, 4745–4752. [Google Scholar] [CrossRef]
- Spargo, A.J.; Reid, I.M.; Mackinnon, A.D. Multistatic meteor radar observations of gravity-wave–tidal interaction over southern Australia. Atmos. Meas. Tech. 2019, 12, 4791–4812. [Google Scholar] [CrossRef]
- Beldon, C.L.; Mitchell, N.J. Gravity wave–tidal interactions in the mesosphere and lower thermosphere over Rothera, Antarctica (68° S, 68° W). J. Geophys. Res. Atmos. 2010, 115, D18101. [Google Scholar] [CrossRef]
- Espy, P.J. Tidal modulation of the gravity-wave momentum flux in the Antarctic mesosphere. Geophys. Res. Lett. 2004, 31, L11111. [Google Scholar] [CrossRef]
- Hall, C.M.; Nozawa, S.; Manson, A.H.; Meek, C.E. Tidal signatures in mesospheric turbulence. Ann. Geophys. 2006, 24, 453–465. [Google Scholar] [CrossRef][Green Version]
- Charles, K.; Jones, G. Mesospheric mean winds and tides observed by the imaging Doppler interferometer (IDI) at Halley, Antarctica. J. Atmos. Sol. Terr. Phys. 1999, 61, 351–362. [Google Scholar] [CrossRef]
- Fritts, D.C.; Vincent, R.A. Mesospheric momentum flux studies at Adelaide, Australia: Observations and a gravity wave-tidal interaction model. J. Atmos. Sci. 1987, 44, 605–619. [Google Scholar] [CrossRef]
- Thayaparan, T.; Hocking, W.K.; MacDougall, J. Observational evidence of tidal/gravity wave interactions using the UWO 2MHz radar. Geophys. Res. Lett. 1995, 22, 373–376. [Google Scholar] [CrossRef]
- Nakamura, T.; Fritts, D.C.; Isler, J.R.; Tsuda, T.; Vincent, R.A.; Reid, I.M. Short-period fluctuations of the diurnal tide observed with low-latitude MF and meteor radars during CADRE: Evidence for gravity wave/tidal interactions. J. Geophys. Res. 1997, 102, 26225–26238. [Google Scholar] [CrossRef]
- Walterscheid, R.L. Inertio-gravity wave induced accelerations of mean flow having an imposed periodic component: Implications for tidal observations in the meteor region. J. Geophys. Res. 1981, 86, 9698–9706. [Google Scholar] [CrossRef]
- Isler, J.R.; Fritts, D.C. Gravity wave variability and interaction with lower-frequency motions in the mesosphere and lower thermosphere over Hawaii. J. Atmos. Sci. 1996, 53, 37–48. [Google Scholar] [CrossRef]
- Placke, M.; Hoffmann, P.; Latteck, R.; Rapp, M. Gravity wave momentum fluxes from MF and meteor radar measurements in the polar MLT region. J. Geophys. Res. Space 2015, 120, 736–750. [Google Scholar] [CrossRef]
- de Wit, R.; Hibbins, R.; Espy, P.J. The seasonal cycle of gravity wave momentum flux and forcing in the high latitude northern hemisphere mesopause region. J. Atmos. Sol. Terr. Phys. 2015, 127, 21–29. [Google Scholar] [CrossRef]
- Lilly, D.K. Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 1983, 40, 749–761. [Google Scholar] [CrossRef]
- Satomura, T.; Sato, K. Secondary generation of gravity waves associated with the breaking of mountain waves. J. Atmos. Sci. 1999, 56, 3847–3858. [Google Scholar] [CrossRef]
- Smith, R.B.; Woods, B.K.; Jensen, J.; Cooper, W.A.; Doyle, J.D.; Jiang, Q.; Grubisic, V. Mountain waves entering the stratosphere. J. Atmos. Sci. 2008, 65, 2543–2562. [Google Scholar] [CrossRef]
- Wit, R.D.; Janches, D.; Fritts, D.C.; Stockwell, R.G.; Coy, L. Unexpected climatological behavior of MLT gravity wave momentum flux in the lee of the Southern Andes hot spot. Geophys. Res. Lett. 2017, 44, 1182–1191. [Google Scholar] [CrossRef]
- Zhao, R.; Dou, X.; Xue, X.; Sun, D.; Han, Y.; Chen, C.; Zheng, J.; Li, Z.; Zhou, A.; Han, Y.; et al. Stratosphere and lower mesosphere wind observation and gravity wave activities of the wind field in China using a mobile Rayleigh Doppler lidar. J. Geophys. Res. Space 2017, 122, 8847–8857. [Google Scholar] [CrossRef]
- Gavrilov, N.M.; Fukao, S.; Nakamura, T.; Jacobi, C.; Kürschner, D.; Manson, A.H.; Meek, C.E. Comparative study of interannual changes of the mean winds and gravity wave activity in the middle atmosphere over Japan, Central Europe and Canada. J. Atmos. Sol. Terr. Phy. 2002, 64, 1003–1010. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Tang, Q.; Chen, Z.; Liu, Y.; Zhou, C. Diurnal and Seasonal Variation of High-Frequency Gravity Waves at Mohe and Wuhan. Atmosphere 2022, 13, 1069. https://doi.org/10.3390/atmos13071069
Wu Y, Tang Q, Chen Z, Liu Y, Zhou C. Diurnal and Seasonal Variation of High-Frequency Gravity Waves at Mohe and Wuhan. Atmosphere. 2022; 13(7):1069. https://doi.org/10.3390/atmos13071069
Chicago/Turabian StyleWu, Yiyun, Qiong Tang, Zhou Chen, Yi Liu, and Chen Zhou. 2022. "Diurnal and Seasonal Variation of High-Frequency Gravity Waves at Mohe and Wuhan" Atmosphere 13, no. 7: 1069. https://doi.org/10.3390/atmos13071069
APA StyleWu, Y., Tang, Q., Chen, Z., Liu, Y., & Zhou, C. (2022). Diurnal and Seasonal Variation of High-Frequency Gravity Waves at Mohe and Wuhan. Atmosphere, 13(7), 1069. https://doi.org/10.3390/atmos13071069








