Investigation of a Gaussian Plume in the Vicinity of an Urban Cyclotron Using Helium as a Tracer Gas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Campaigns and the Site
- Bituminous, up to 100 m heading north and north west, and up to 50 m heading north east;
- Vegetation up to 100 m heading south and south west and up to 50 m heading east. A 15–20 m hedge comprising deciduous trees contains the cyclotron area in the area ranging from north east to south west, at a distance not exceeding 50 m towards the east.
2.2. Weather Conditions
2.3. Tracing Experiments
2.3.1. Discharging the Passive Tracer, Helium
2.3.2. Air Sampling
2.3.3. Helium Concentrations
2.4. Gaussian Plume Models
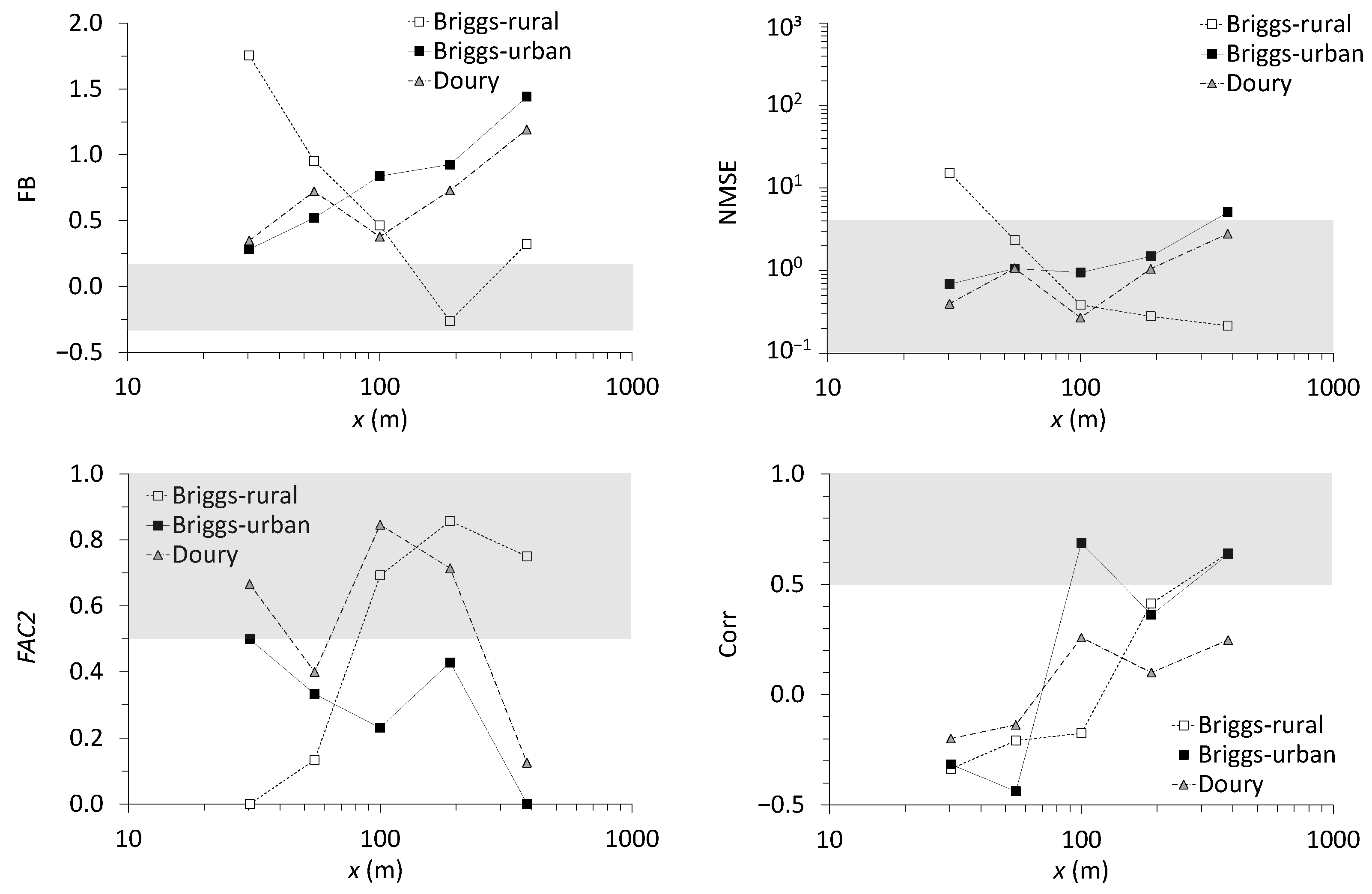
2.5. Evaluation Criteria for Gaussian Models
3. Results
3.1. Weather Conditions
3.2. Significant Helium Concentrations
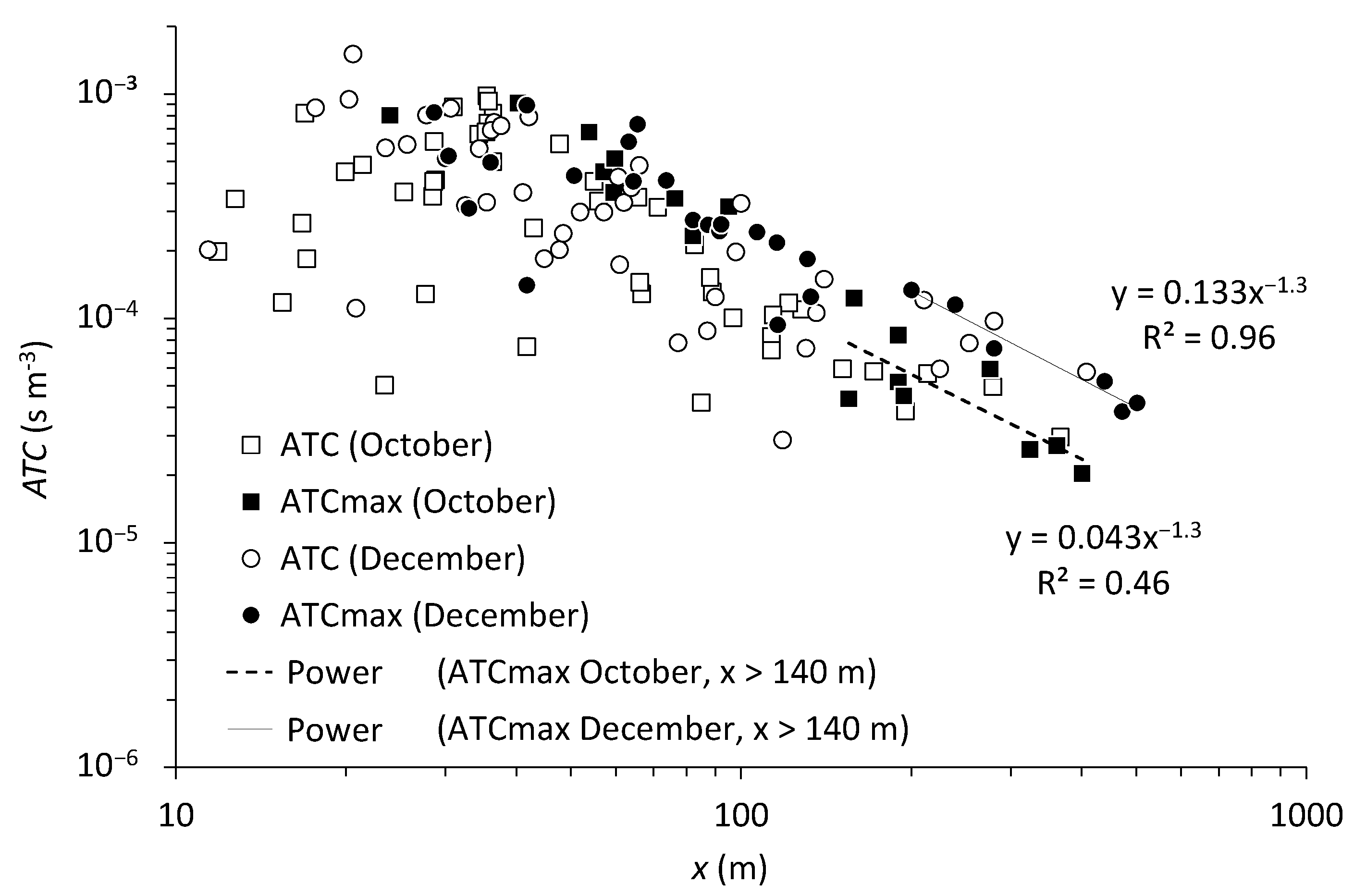
3.3. Atmospheric Transfer Coefficients
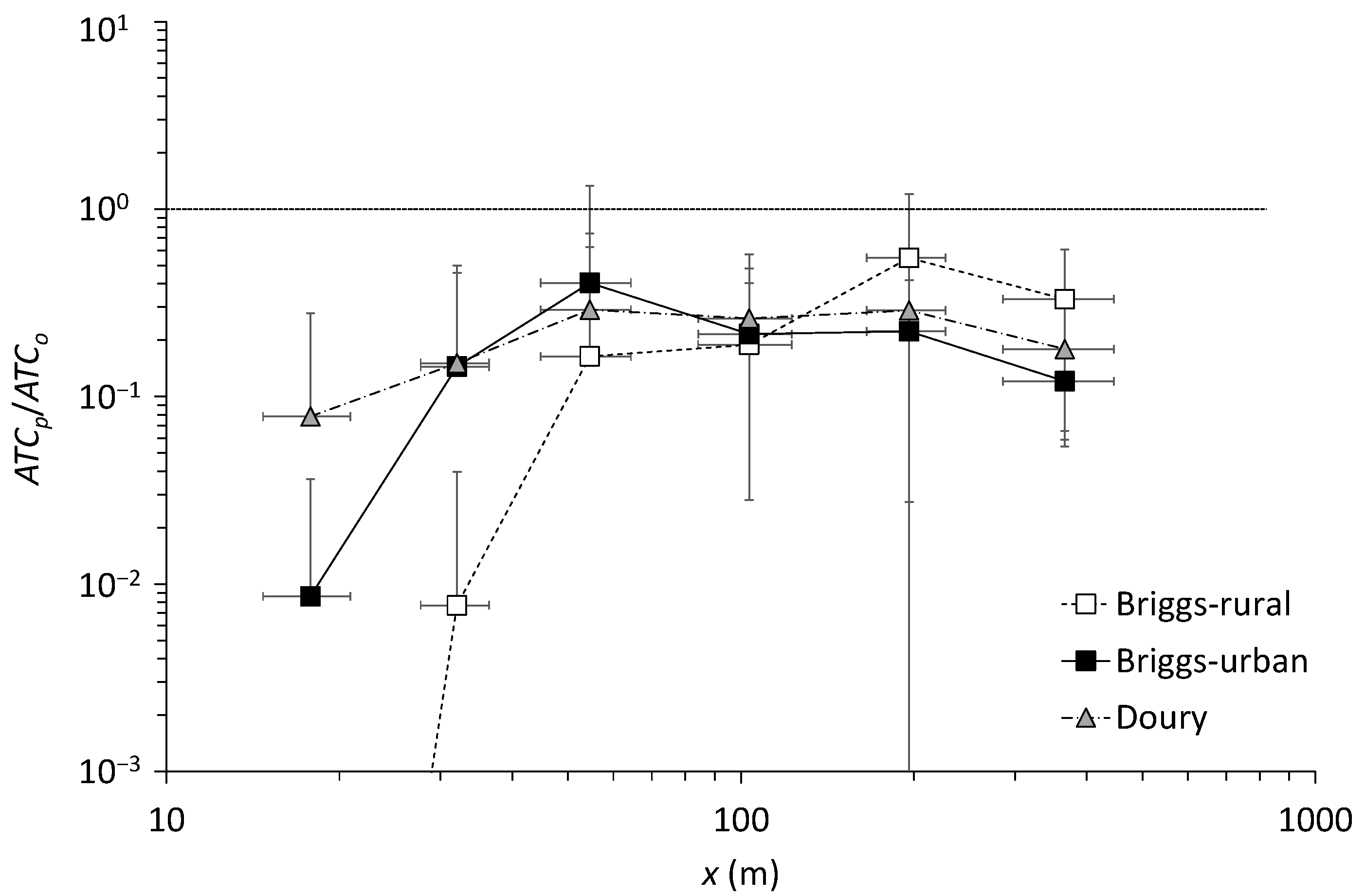
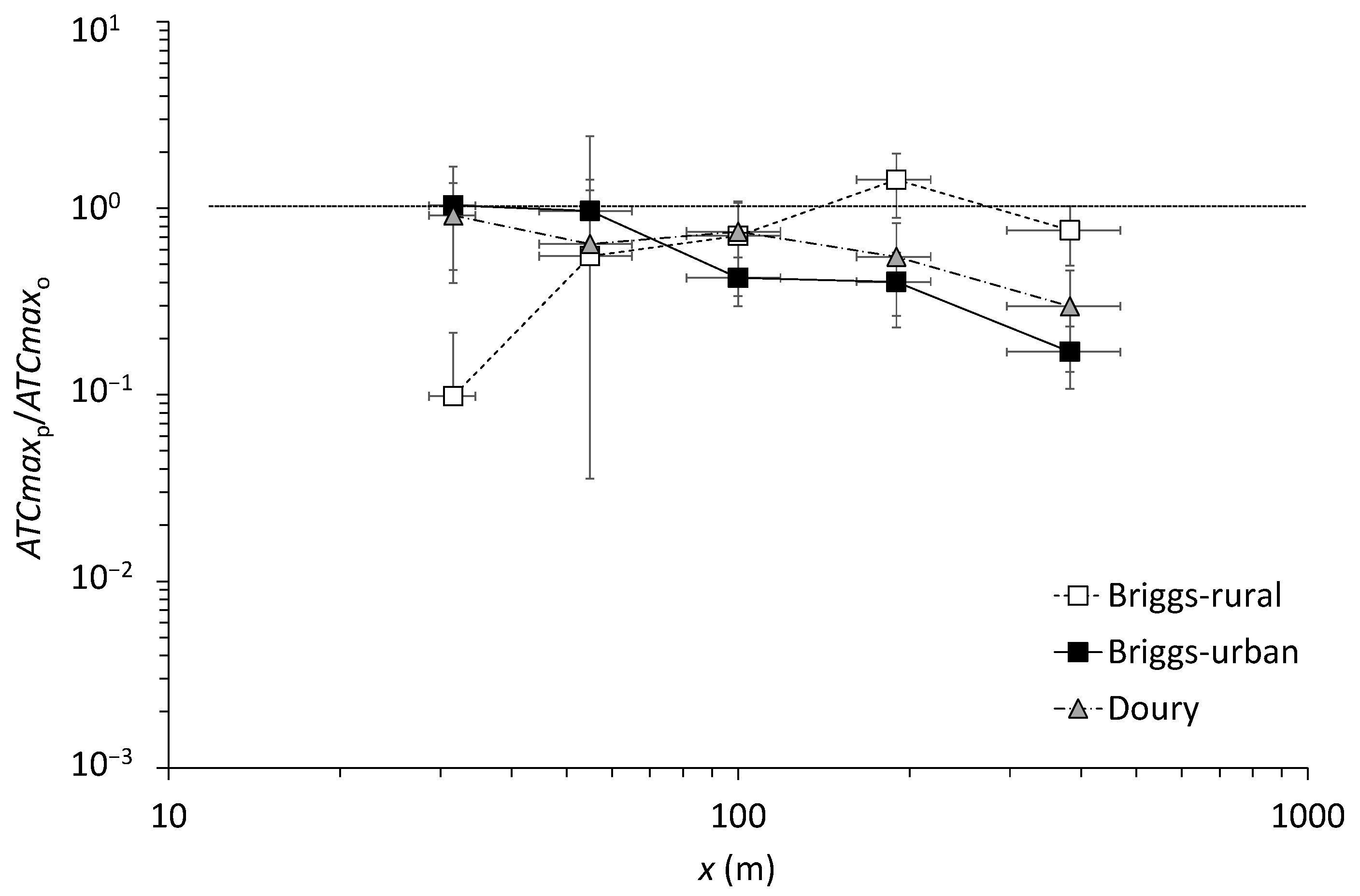
3.4. Evaluation of Gaussian Models
4. Discussion
4.1. Atmospheric Transfer Coefficients Measured
4.2. Atmospheric Transfer Coefficients Modeled
- The 10–50 m interval characterized by turbulent airflow in the wake of buildings and probably recirculating zones due to the fact that the cyclotron is near to a row of 15–20 m high trees;
- The 50–150 m interval with porous (two rows of trees) and non-porous (piles of materials) vertical obstacles;
- The 150–500 m interval with a housing estate of uniform roughness located at the bottom of the pile of material.
4.3. Parametrization of as a Function of the Distance x from the Discharge Point
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martin, D.; Petersson, K.F.; Shallcross, D.E. The Use of Cyclic Perfluoroalkanes and SF6 in Atmospheric Dispersion Experiments. Q. J. R. Meteorol. Soc. 2011, 137, 2047–2063. [Google Scholar] [CrossRef]
- Lac, C.; Bonnardot, F.; Connan, O.; Camail, C.; Maro, D.; Hebert, D.; Rozet, M.; Pergaud, J. Evaluation of a Mesoscale Dispersion Modelling Tool during the CAPITOUL Experiment. Meteorol. Atmos. Phys. 2008, 102, 263. [Google Scholar] [CrossRef]
- Connan, O.; Laguionie, P.; Maro, D.; Hébert, D.; Mestayer, P.G.; Rodriguez, F.; Rodrigues, V.; Rosant, J.M. Vertical and Horizontal Concentration Profiles from a Tracer Experiment in a Heterogeneous Urban Area. Atmos. Res. 2015, 154, 126–137. [Google Scholar] [CrossRef]
- Trini Castelli, S.; Armand, P.; Tinarelli, G.; Duchenne, C.; Nibart, M. Validation of a Lagrangian Particle Dispersion Model with Wind Tunnel and Field Experiments in Urban Environment. Atmos. Environ. 2018, 193, 273–289. [Google Scholar] [CrossRef]
- Briggs, G.A. Diffusion Estimation for Small Emissions. Preliminary Report; Technical Report TID-28289; National Oceanic and Atmospheric Administration, Atmospheric Turbulence and Diffusion Lab.: Oak Ridge, TN, USA, 1973; 62p.
- Doury, A. Une Méthode de Calcul Pratique et Générale Pour la Prévision Numérique des Pollutions Véhiculées Par l’Atmosphère [A Practical and General Method of Calculating for Numerical Forecasting of Pollution Transported in the Atmosphere]; Technical Report; CEA: Paris, France, 1976. [Google Scholar]
- Vanderborght, B.; Kretzschmar, J. A Literature Survey on Tracer Experiments for Atmospheric Dispersion Modelling Studies. Atmos. Environ. 1984, 18, 2395–2403. [Google Scholar] [CrossRef]
- Lines, I.G.; Deaves, D.M.; Atkins, W.S. Practical Modelling of Gas Dispersion in Low Wind Speed Conditions, for Application in Risk Assessment. J. Hazard. Mater. 1997, 54, 201–226. [Google Scholar] [CrossRef]
- De Melo Lisboa, H.; Guillot, J.-M.; Fanlo, J.-L.; Le Cloirec, P. Dispersion of Odorous Gases in the Atmosphere—Part I: Modeling Approaches to the Phenomenon. Sci. Total Environ. 2006, 361, 220–228. [Google Scholar] [CrossRef] [PubMed]
- Korsakissok, I.; Mallet, V. Comparative Study of Gaussian Dispersion Formulas within the Polyphemus Platform: Evaluation with Prairie Grass and Kincaid Experiments. J. Appl. Meteorol. Climatol. 2009, 48, 2459–2473. [Google Scholar] [CrossRef] [Green Version]
- Leroy, C.; Maro, D.; Hébert, D.; Solier, L.; Rozet, M.; Le Cavelier, S.; Connan, O. A Study of the Atmospheric Dispersion of a High Release of Krypton-85 above a Complex Coastal Terrain, Comparison with the Predictions of Gaussian Models (Briggs, Doury, ADMS4). J. Environ. Radioact. 2010, 101, 937–944. [Google Scholar] [CrossRef] [PubMed]
- Connan, O.; Solier, L.; Hébert, D.; Maro, D.; Lamotte, M.; Voiseux, C.; Laguionie, P.; Cazimajou, O.; Le Cavelier, S.; Godinot, C.; et al. Near-Field Krypton-85 Measurements in Stable Meteorological Conditions around the AREVA NC La Hague Reprocessing Plant: Estimation of Atmospheric Transfer Coefficients. J. Environ. Radioact. 2014, 137, 142–149. [Google Scholar] [CrossRef] [PubMed]
- Mao, S.; Lang, J.; Chen, T.; Cheng, S.; Wang, C.; Zhang, J.; Hu, F. Impacts of Typical Atmospheric Dispersion Schemes on Source Inversion. Atmos. Environ. 2020, 232, 117572. [Google Scholar] [CrossRef]
- Turner, D.B. Workbook of Atmospheric Dispersion Estimates; Public Health Service Publication No. 999-AP-26; National Center for Air Pollution Control: Cincinnati, OH, USA, 1969. [Google Scholar]
- IAEA Atmospheric Dispersion Models for Application in Relation to Radionuclide Releases; Technical Document IAEA-TECDOC-379; International Atomic Energy Agency: Vienna, Austria, 1986; p. 138.
- Glueckauf, E. A Micro-Analysis of the Helium and Neon Contents of Air. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1946, 185, 98–119. [Google Scholar] [CrossRef]
- Sano, Y.; Marty, B.; Burnard, P. Noble Gases in the Atmosphere. In The Noble Gases as Geochemical Tracers; Advances in Isotope, Geochemistry; Burnard, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 17–31. [Google Scholar]
- Brun, J.; Hugon, J.; Le Quinio, R. Influence de La Durée d’exposition Sur l’évaluation Des Coefficients de Diffusion Atmosphérique. In Physical Behaviour of Radioactive Contaminants in the Atmosphere, Proceedings of the a Symposium, Vienna, Austria, 12–16 November 1973; IAEA-SM-181/11; IAEA: Vienna, Austria, 1973. [Google Scholar]
- Griffiths, R.F. Errors in the use of the Briggs parameterization for atmospheric dispersion coefficients. Atmos. Environ. 1994, 28, 2861–2865. [Google Scholar] [CrossRef]
- Pasquill, F.; Smith, F.B. Experimental studies of the basic features of atmospheric diffusion. In Atmospheric Diffusion, 3rd ed.; Scorer, R.S., Ed.; Ellis Horwood Limited: Chichester, UK, 1983; pp. 179–232. [Google Scholar]
- Chang, J.; Hanna, S. Air Quality Model Performance Evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Hanna, S. Applications in Air Pollution Modelling. In Atmospheric Turbulence and Air Pollution Modeling; Niewstadt, F., van Dop, H., Eds.; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1984; pp. 275–309. [Google Scholar]
- Roupsard, P.; Amielh, M.; Maro, D.; Coppalle, A.; Branger, H.; Connan, O.; Laguionie, P.; Hébert, D.; Talbaut, M. Measurement in a Wind Tunnel of Dry Deposition Velocities of Submicron Aerosol with Associated Turbulence onto Rough and Smooth Urban Surfaces. J. Aerosol Sci. 2013, 55, 12–24. [Google Scholar] [CrossRef] [Green Version]
- Pellerin, G.; Maro, D.; Damay, P.; Gehin, E.; Connan, O.; Laguionie, P.; Hébert, D.; Solier, L.; Boulaud, D.; Lamaud, E.; et al. Aerosol Particle Dry Deposition Velocity above Natural Surfaces: Quantification According to the Particles Diameter. J. Aerosol Sci. 2017, 114, 107–117. [Google Scholar] [CrossRef]






| Experiment | Date * and Time | Helium Discharge | Significant Sampling | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Duration | Flowrate | Duration | Number | ||||||
| (and %) | median | min | max | median | |||||
| (Reference) | (UTC) | (min) | (g s−1) | (min) | (m) | (m) | (m) | ||
| 1-1 | 15 October 2019 13:45 | 10.0 | 2.68 | 15 | 11 (79%) | 54 | 17 | 190 | 0.25 |
| 1-2 | 16 October 2019 07:10 | 10.0 | 2.38 | 15 | 11 (79%) | 29 | 12 | 67 | 1.07 |
| 1-3 | 16 October 2019 09:30 | 10.0 | 2.38 | 15 | 13 (93%) | 60 | 13 | 113 | 0.38 |
| 1-4 | 16 October 2019 12:00 | 10.0 | 5.29 | 20 | 8 (57%) | 84 | 17 | 401 | 0.22 |
| 1-5 | 17 October 2019 07:05 | 10.0 | 5.49 | 20 | 8 (57%) | 83 | 21 | 367 | 0.28 |
| 1-6 | 17 October 2019 09:30 | 10.0 | 5.36 | 15 | 13 (93%) | 151 | 35 | 279 | 0.35 |
| 1-7 | 17 October 2019 12:45 | 10.0 | 2.53 | 15 | 4 (29%) | 32 | 20 | 56 | 0.61 |
| 2-1 | 10 December 2019 09:30 | 10.0 | 2.38 | 15 | 8 (67%) | 51 | 21 | 100 | 0.49 |
| 2-2 | 10 December 2019 12:40 | 10.0 | 2.38 | 15 | 12 (100%) | 90 | 34 | 136 | 0.25 |
| 2-3 | 10 December 2019 14:20 | 10.0 | 2.38 | 15 | 10 (91%) | 86 | 34 | 133 | 0.21 |
| 2-4 | 11 December 2019 08:45 | 10.0 | 2.38 | 15 | 6 (46%) | 33 | 20 | 42 | 0.13 |
| 2-5 | 11 December 2019 10:15 | 10.0 | 2.38 | 15 | 10 (83%) | 36 | 26 | 66 | 0.17 |
| 2-6 | 11 December 2019 13:00 | 8.3 | 5.06 | 15 | 12 (92%) | 69 | 18 | 280 | 0.19 |
| 2-7 | 11 December 2019 15:00 | 9.0 | 5.06 | 15 | 10 (91%) | 267 | 38 | 502 | 0.20 |
| 2-8 | 12 December 2019 08:15 | 10.0 | 2.38 | 15 | 12 (100%) | 46 | 11 | 64 | 0.66 |
| Experiment | Weather Conditions | |||||
|---|---|---|---|---|---|---|
| Wind Speed | Wind Direction | Solar Radiation | Stability Class | |||
| (Reference) | (m s−1) | (m s−1) | (°) | (°) | (W m−2) | (Pasquill-Turner) |
| 1-1 | 2.5 | 1.0 | 222 | 27 | 195 | C |
| 1-2 | 2.1 | 1.1 | 166 | 36 | 14 | C |
| 1-3 | 3.3 | 1.4 | 205 | 33 | 114 | C |
| 1-4 | 3.1 | 1.4 | 210 | 35 | 78 | C |
| 1-5 | 2.0 | 0.9 | 196 | 32 | 53 | C |
| 1-6 | 2.9 | 1.1 | 186 | 38 | 201 | C |
| 1-7 | 2.1 | 1.1 | 192 | 32 | 438 | C |
| 2-1 | 3.3 | 1.3 | 183 | 24 | 118 | C |
| 2-2 | 4.3 | 1.5 | 187 | 20 | 79 | C |
| 2-3 | 4.2 | 1.9 | 184 | 24 | 22 | C |
| 2-4 | 0.9 | 0.4 | 233 | 27 | 36 | B |
| 2-5 | 1.7 | 0.7 | 197 | 19 | 110 | B |
| 2-6 | 2.0 | 0.7 | 213 | 21 | 67 | C |
| 2-7 | 2.4 | 0.9 | 195 | 19 | 4 | C |
| 2-8 | 1.7 | 0.7 | 183 | 28 | 90 | B |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laguionie, P.; Connan, O.; Tien, T.L.; Vecchiola, S.; Chardeur, J.; Cazimajou, O.; Solier, L.; Charvolin-Volta, P.; Chen, L.; Korsakissok, I.; et al. Investigation of a Gaussian Plume in the Vicinity of an Urban Cyclotron Using Helium as a Tracer Gas. Atmosphere 2022, 13, 1223. https://doi.org/10.3390/atmos13081223
Laguionie P, Connan O, Tien TL, Vecchiola S, Chardeur J, Cazimajou O, Solier L, Charvolin-Volta P, Chen L, Korsakissok I, et al. Investigation of a Gaussian Plume in the Vicinity of an Urban Cyclotron Using Helium as a Tracer Gas. Atmosphere. 2022; 13(8):1223. https://doi.org/10.3390/atmos13081223
Chicago/Turabian StyleLaguionie, Philippe, Olivier Connan, Thinh Lai Tien, Sophie Vecchiola, Johann Chardeur, Olivier Cazimajou, Luc Solier, Perrine Charvolin-Volta, Liying Chen, Irène Korsakissok, and et al. 2022. "Investigation of a Gaussian Plume in the Vicinity of an Urban Cyclotron Using Helium as a Tracer Gas" Atmosphere 13, no. 8: 1223. https://doi.org/10.3390/atmos13081223
APA StyleLaguionie, P., Connan, O., Tien, T. L., Vecchiola, S., Chardeur, J., Cazimajou, O., Solier, L., Charvolin-Volta, P., Chen, L., Korsakissok, I., Guellec, M. L., Soulhac, L., Tripathi, A., & Maro, D. (2022). Investigation of a Gaussian Plume in the Vicinity of an Urban Cyclotron Using Helium as a Tracer Gas. Atmosphere, 13(8), 1223. https://doi.org/10.3390/atmos13081223








