Variability of Precipitation Recycling and Moisture Sources over the Colombian Pacific Region: A Precipitationshed Approach
Abstract
:1. Introduction
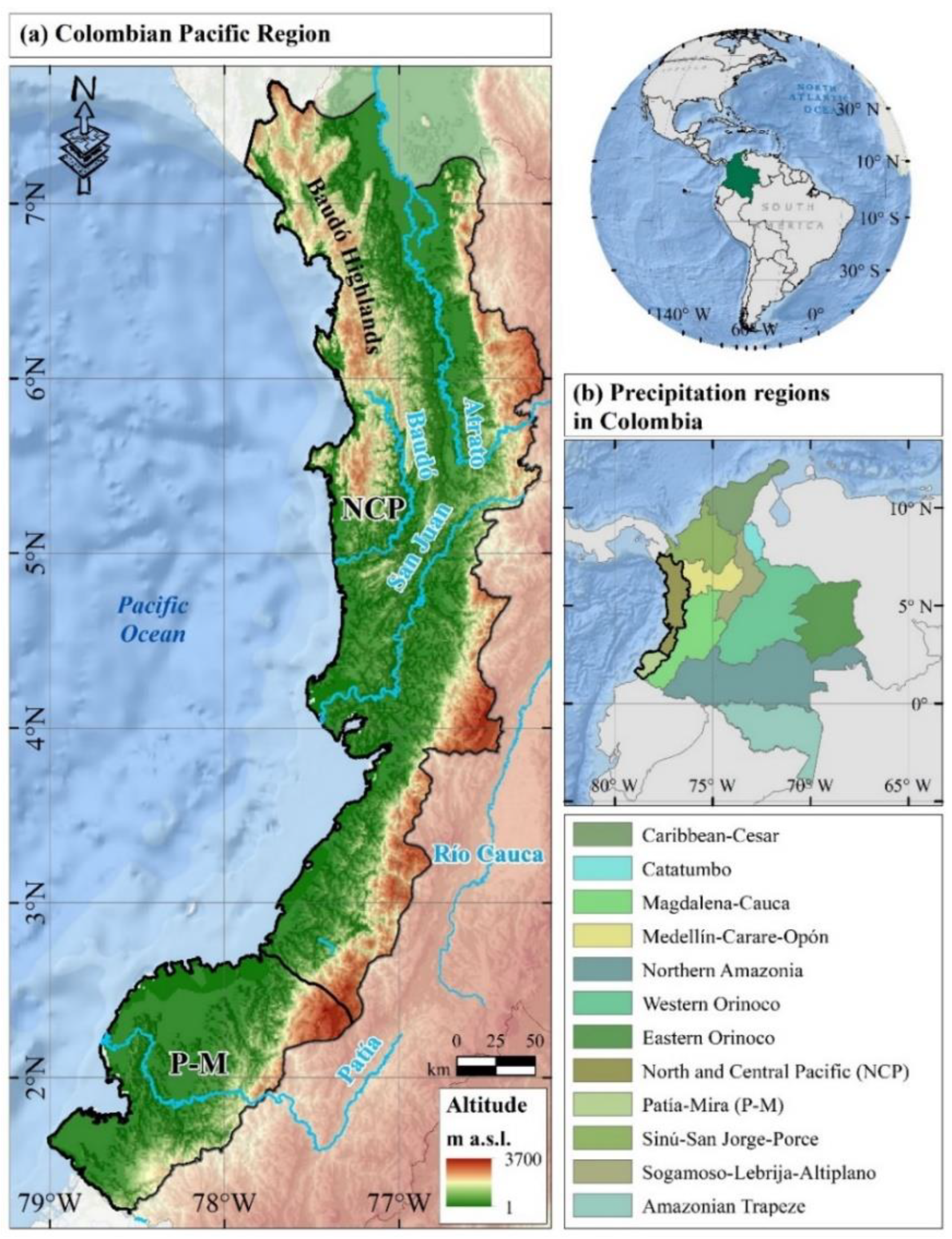
2. Materials and Methods
3. Results and Discussion
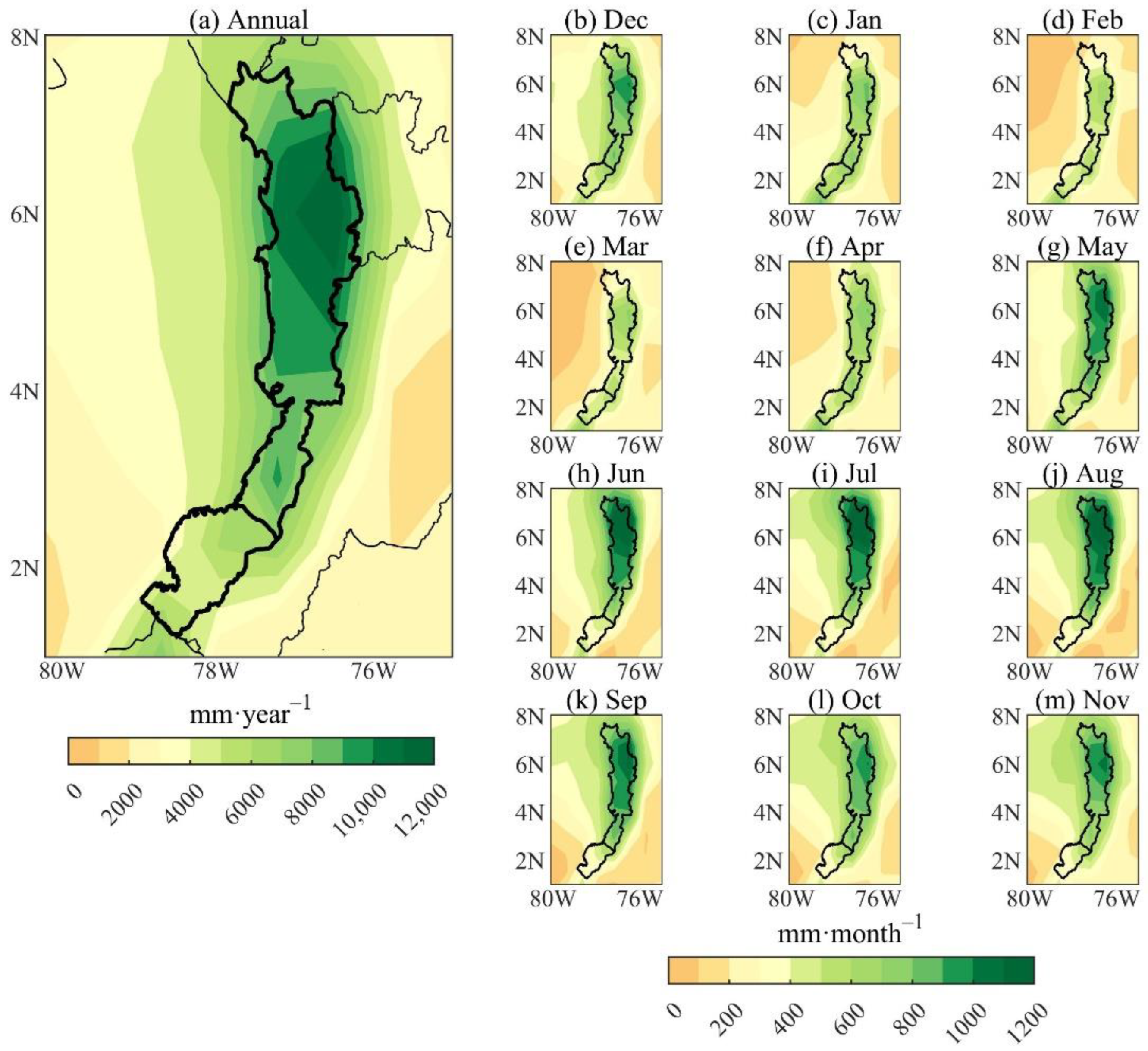
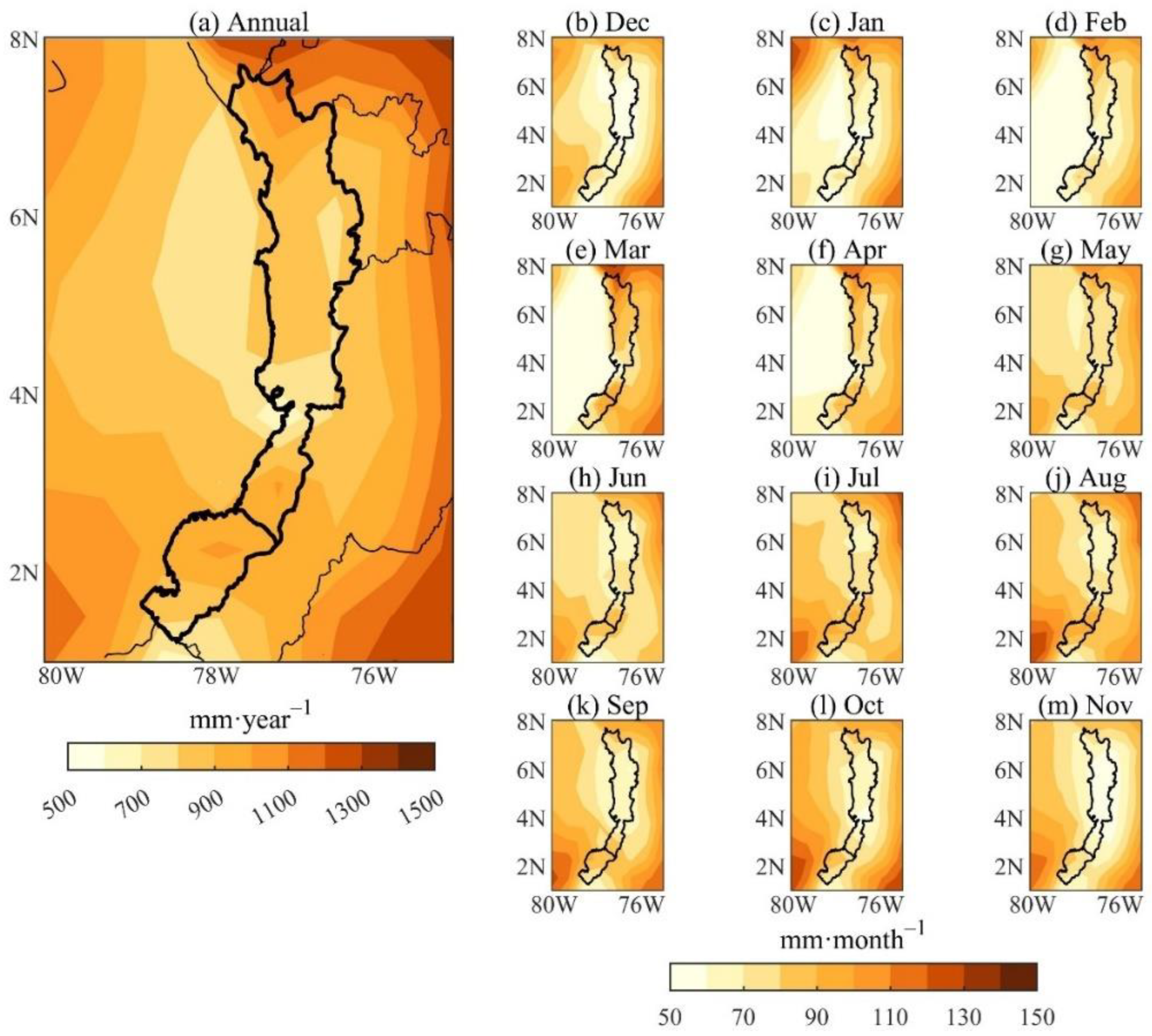
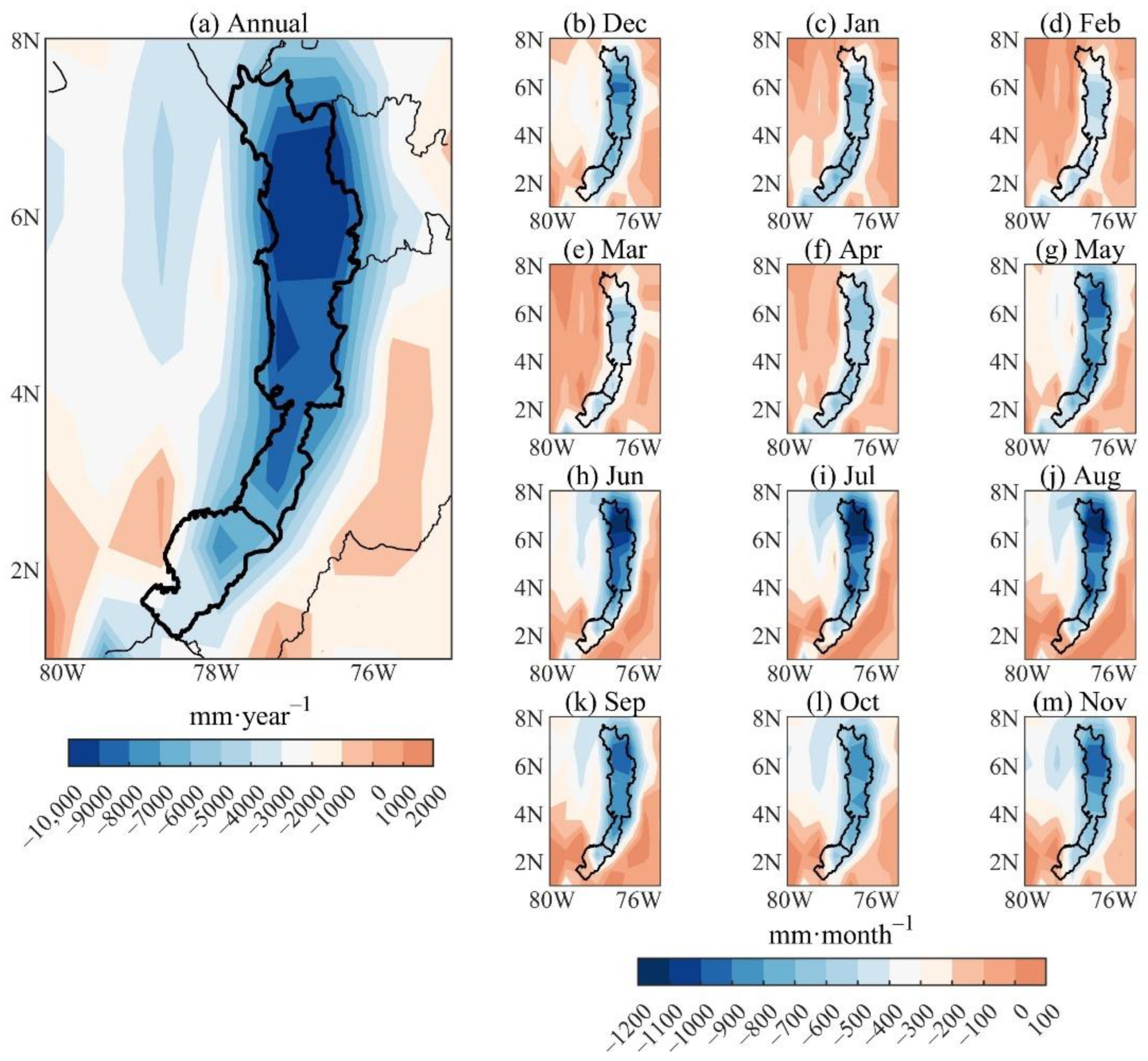
3.1. Water Balance
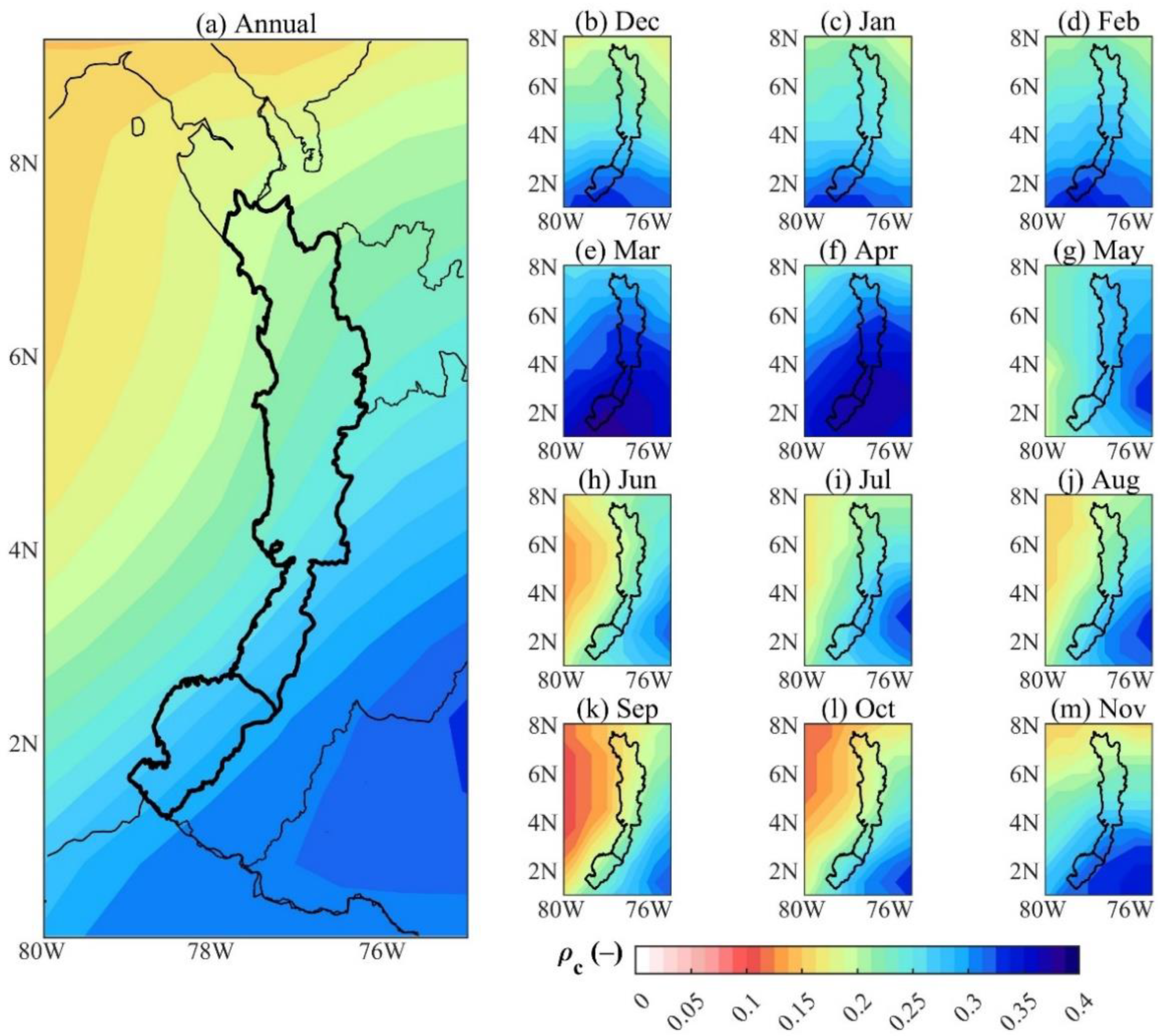
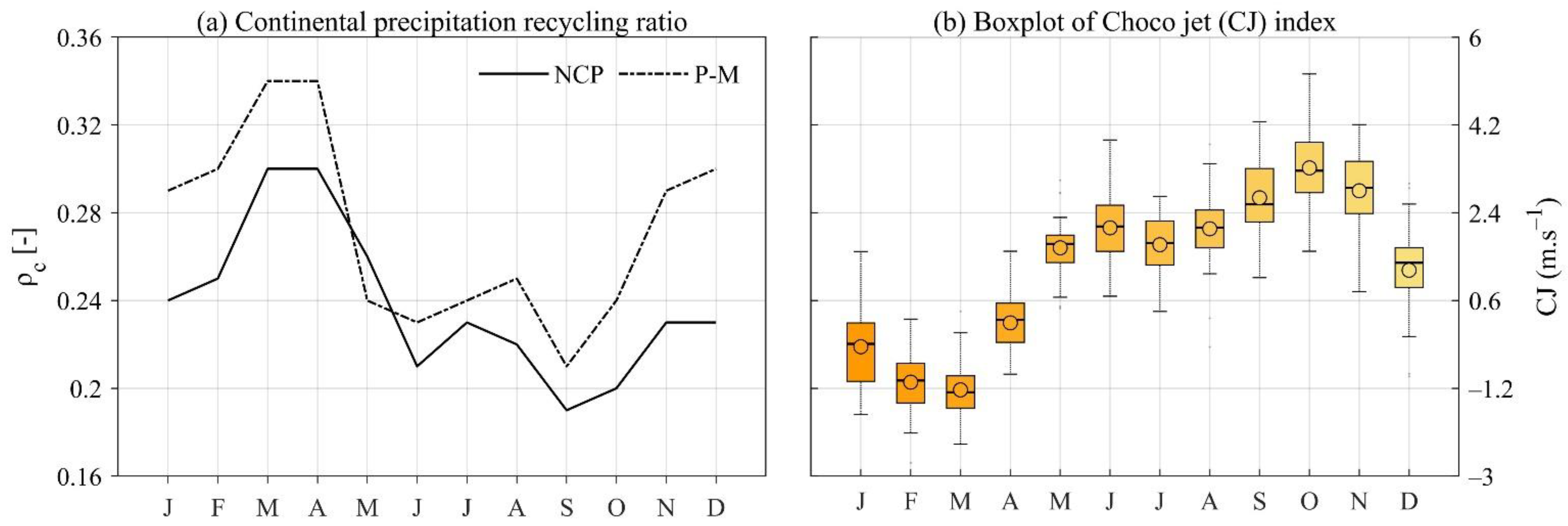
3.2. Continental Precipitation Recycling Ratio
3.3. Precipitationshed
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brubaker, K.L.; Entekhabi, D.; Eagleson, P.S. Estimation of continental precipitation recycling. J. Clim. 1993, 6, 1077–1089. [Google Scholar] [CrossRef] [Green Version]
- Cuartas, A.; Poveda, G. Balance atmosférico de humedad y estimación de la precipitación reciclada en colombia según el reanális ncep/ncar. Meteorol. Colomb. 2002, 5, 57–65. [Google Scholar]
- Sánchez, C. Estimation of the Precipitation Recycling Ratio; Delft University of Technology—National University of Singapore: Delft, The Netherlands, 2016. [Google Scholar]
- Eltahir, E.; Bras, R. Precipitation Recycling. Rev. Geophys. 1996, 34, 367–378. [Google Scholar] [CrossRef]
- Van Der Ent, R. A New View on the Hydrological Cycle over Continents. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2014. [Google Scholar]
- Van Der Ent, R.J.; Savenije, H.H.G.; Schaefli, B.; Steele-Dunne, S.C. Origin and fate of atmospheric moisture over continents. Water Resour. Res. 2010, 46, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Van Der Ent, R.J.; Wang-Erlandsson, L.; Keys, P.W.; Savenije, H.H.G. Contrasting roles of interception and transpiration in the hydrological cycle—Part 2: Moisture recycling. Earth Syst. Dyn. 2014, 5, 471–489. [Google Scholar] [CrossRef] [Green Version]
- Keys, P.W. The Precipitationshed: Concepts, Methods, and Applications; Stockholm University, Faculty of Science, Stockholm Resilience Centre: Stockholm, Sweden, 2016; ISBN 9789176494646. [Google Scholar]
- Hoyos, I. Transporte de Humedad Atmosférica en Colombia: Origen, Variabilidad y Acople con Fenómenos Climáticos Globales; Universidad de Antioquia: Medellín, Colombia, 2017. [Google Scholar]
- Hoyos, I.; Dominguez, F.; Cañón-Barriga, J.; Martínez, J.A.; Nieto, R.; Gimeno, L.; Dirmeyer, P.A. Moisture origin and transport processes in Colombia, northern South America. Clim. Dyn. 2018, 50, 971–990. [Google Scholar] [CrossRef]
- Vallejo, L. Dinámica Espacio-Temporal de Los Ríos Aéreos en el Norte de sur América y Posibles Efectos del Cambio Climático; Universidad Nacional de Colombia: Medellín, Colombia, 2014. [Google Scholar]
- Satyamurty, P.; da Costa, C.P.W.; Manzi, A.O. Moisture source for the Amazon Basin: A study of contrasting years. Theor. Appl. Climatol. 2013, 111, 195–209. [Google Scholar] [CrossRef]
- Eltahir, E.A.B.; Bras, R.L. Precipitation recycling in the Amazon basin. Q. J. R. Meteorol. Soc. 1994, 120, 861–880. [Google Scholar] [CrossRef]
- Van Der Ent, R.J.; Savenije, H.H.G. Oceanic sources of continental precipitation and the correlation with sea surface temperature. Water Resour. Res. 2013, 49, 3993–4004. [Google Scholar] [CrossRef]
- Poveda, G.; Jaramillo, L.; Vallejo, L.F. Seasonal precipitation patterns along pathways of South American low-level jets and aerial rivers. Water Resour. Res. 2014, 50, 98–118. [Google Scholar] [CrossRef]
- Arias, P.A.; Martínez, J.A.; Vieira, S.C. Moisture sources to the 2010–2012 anomalous wet season in northern South America. Clim. Dyn. 2015, 45, 2861–2884. [Google Scholar] [CrossRef]
- Morales, J.; Arias, P.; Martínez, J. Role of Caribbean low-level jet and Choco jet in the transport of moisture patterns towards Central America. Conf. Proc. Pap. 2017, 1, 4861. [Google Scholar]
- Gallego, D.; García-Herrera, R.; Gómez-Delgado, F.D.P.; Ordoñez-Perez, P.; Ribera, P. Tracking the moisture transport from the Pacific towards Central and northern South America since the late 19th century. Earth Syst. Dyn. 2019, 10, 319–331. [Google Scholar] [CrossRef] [Green Version]
- Drumond, A.; Nieto, R.; Gimeno, L.; Ambrizzi, T. A Lagrangian identification of major sources of moisture over Central Brazil and la Plata Basin. J. Geophys. Res. Atmos. 2008, 113, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Martinez, A.J.; Dominguez, F. Sources of atmospheric moisture for the La Plata River Basin. J. Clim. 2014, 27, 6737–6753. [Google Scholar] [CrossRef]
- Gimeno, L.; Stohl, A.; Trigo, R.M.; Dominguez, F.; Yoshimura, K.; Yu, L.; Drumond, A.; Durán-quesada, A.M.; Nieto, R. Oceanic and terrestrial sources of continental precipitation. Rev. Geophys. 2012, 50, 1–41. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O. La corriente de chorro superficial del oeste (“del Chocó”) y otras dos corrientes del chorro en Colombia: Climatología y variabilidad durante las fases ENSO. Rev. Académica Colomb. Ciencias Tierra 1999, 23, 517–528. [Google Scholar]
- Yepes, J.; Poveda, G.; Mejía, J.F.; Moreno, L.; Rueda, C. Choco-jex: A research experiment focused on the Chocó low-level jet over the far eastern Pacific and western Colombia. Bull. Am. Meteorol. Soc. 2019, 100, 779–796. [Google Scholar] [CrossRef]
- Cerón, W.L.; Kayano, M.T.; Andreoli, R.V.; Avila-Diaz, A.; de Souza, I.P.; Souza, R.A.F. Pacific and atlantic multidecadal variability relations with the choco and caribbean low-level jets during the 1900–2015 period. Atmosphere 2021, 12, 1120. [Google Scholar] [CrossRef]
- Jaramillo, L.; Poveda, G.; Mejía, J.F. Mesoscale convective systems and other precipitation features over the tropical Americas and surrounding seas as seen by TRMM. Int. J. Climatol. 2017, 37, 380–397. [Google Scholar] [CrossRef]
- Velásquez-Restrepo, M.; Poveda, G. Estimación del balance hídrico de la región Pacífica. Dyna 2019, 86, 297–306. [Google Scholar] [CrossRef]
- Cuartas, L. Balance Atmosférico de Humedad Para Colombia (Tesis de Maestría); Universidad Nacional de Colombia: Medellín, Columbia, 2001. [Google Scholar]
- Savenije, H.H.G. New definitions for moisture recycling and the relationship with land-use changes in the Sahel. J. Hydrol. 1995, 167, 57–78. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and life; Budyko, M.I., Miller, D.H., Eds.; Academic Press: London, UK; New York, NY, USA, 1974; ISBN 978-0-12-139450-9. Available online: https://www.sciencedirect.com/bookseries/international-geophysics/vol/18/suppl/C (accessed on 22 July 2022).
- Dominguez, F.; Liang, X.; Ting, M. Impact of Atmospheric Moisture Storage on Precipitation Recycling. J. Clim. 2006, 19, 1513–1530. [Google Scholar] [CrossRef]
- Dirmeyer, P.; Brubaker, K. Characterization of the Global Hydrologic Cycle from a Back-Trajectory Analysis of Atmospheric Water Vapor. J. Hydrometeorol. 2007, 8, 20–37. [Google Scholar] [CrossRef]
- Burde, G.; Zangvil, A. The estimation of regional precipitation recycling. Part I: Review of recycling models. J. Clim. 2001, 14, 2509–2527. [Google Scholar] [CrossRef]
- Knoche, H.R.; Kunstmann, H. Tracking atmospheric water pathways by direct evaporation tagging: A case study for West Africa. J. Geophys. Res. Atmos. 2013, 118, 12345–12358. [Google Scholar] [CrossRef]
- Van Der Ent, R.J.; Tuinenburg, O.A.; Knoche, H.R.; Kunstmann, H.; Savenije, H.H.G. Should we use a simple or complex model for moisture recycling and atmospheric moisture tracking? Hydrol. Earth Syst. Sci. 2013, 17, 4869–4884. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts Interim Reanalysis (ECMWF/ERA-I) Atmospheric Data. Available online: http://apps.ecmwf.int/datasets/data/interim-full-moda/levtype=pl/ (accessed on 6 June 2019).
- Hoyos, I.; Baquero-Bernal, A.; Jacob, D.; Rodríguez, B. Variability of extreme events in the Colombian Pacific and Caribbean catchment basins. Clim. Dyn. 2013, 40, 1985–2003. [Google Scholar] [CrossRef]
- Cerón, W.L.; Andreoli, R.V.; Kayano, M.T.; Souza, R.A.F.; Jones, C.; Carvalho, L.M.V. The Influence of the Atlantic Multidecadal Oscillation on the Choco Low-Level Jet and Precipitation in Colombia. Atmosphere 2020, 11, 174. [Google Scholar] [CrossRef] [Green Version]
- Cerón, W.L.; Kayano, M.T.; Andreoli, R.V.; Avila, A.; Canchala, T.; Francés, F.; Ayes Rivera, I.; Alfonso-Morales, W.; Ferreira de Souza, R.A.; Carvajal-Escobar, Y. Streamflow Intensification Driven by the Atlantic Multidecadal Oscillation (AMO) in the Atrato River Basin, Northwestern Colombia. Water 2020, 12, 216. [Google Scholar] [CrossRef] [Green Version]
- Institute of Hydrology, Meteorology and Environmental Studies (IDEAM). Atlas climatológico de Colombia; IDEAM: Bogotá, Colombia, 2017.
- Keys, P.; Van Der Ent, R.; Gordon, L.; Hoff, H.; Nikoli, R.; Savenije, H. Analyzing precipitationsheds to understand the vulnerability of rainfall dependent regions. Biogeosciences 2012, 9, 733–746. [Google Scholar] [CrossRef] [Green Version]
- Cerón, W.L.; Andreoli, R.V.; Kayano, M.T.; Avila-Diaz, A. Role of the eastern Pacific-Caribbean Sea SST gradient in the Choco low-level jet variations from 1900–2015. Clim. Res. 2021, 83, 61–74. [Google Scholar] [CrossRef]
- Cerón, W.L.; Andreoli, R.V.; Kayano, M.T.; Ferreria, D.S.R.; Canchala, N.T.; Carvajal-Escobar, Y. Comparison of spatial interpolation methods for annual and seasonal rainfall in two hotspots of biodiversity in South America. An. Acad. Bras. Ciencias 2021, 93, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Guzmán, D.; Ruíz, J.F.; Cadena, M. Regionalización de Colombia Según la Estacionalidad de la Precipitación Media Mensual; A Través Análisis de Componentes Principales (ACP): Bogotá, Colombia, 2014. [Google Scholar]
- Estupiñan, A.R.C. Estudio de la Variabilidad Espacio Temporal de la Precipitación en Colombia. Ph.D. Thesis, Universidad Nacional de Colombia, Medellín, Colombia, 2016. Available online: http://bdigital.unal.edu.co/54014/1/1110490004.2016.pdf (accessed on 5 October 2019).
- Cerón, W.L.; Andreoli, R.V.; Kayano, M.T.; Canchala, T.; Ocampo-marulanda, C.; Avila-diaz, A.; Antunes, J. Trend Pattern of Heavy and Intense Rainfall Events in Colombia from 1981–2018: A Trend-EOF Approach. Atmosphere 2022, 13, 156. [Google Scholar] [CrossRef]
- Canchala, T.; Cerón, W.L.; Francés, F.; Carvajal-Escobar, Y.; Andreoli, R.V.; Kayano, M.T.; Alfonso-Morales, W.; Caicedo-Bravo, E.; de Souza, R.A.F. Streamflow variability in colombian pacific basins and their teleconnections with climate indices. Water 2020, 12, 526. [Google Scholar] [CrossRef] [Green Version]
- Canchala, T.; Alfonso-Morales, W.; Cerón, W.L.; Carvajal-Escobar, Y.; Caicedo-Bravo, E. Teleconnections between monthly rainfall variability and large-scale climate indices in Southwestern Colombia. Water 2020, 12, 1863. [Google Scholar] [CrossRef]
- Poveda, G. La hidroclimatología de Colombia: Una síntesis desde la escala inter-decadal hasta la escala diurna. Rev. Acad. Colomb. Cienc. 2004, 28, 201–222. [Google Scholar]
- Velasco, I.; Fritsch, J.M. Mesoscale convective complexes in the Americas. J. Geophys. Res. Atmos. 1987, 92, 9591–9613. [Google Scholar] [CrossRef]
- Zipser, E.J.; Cecil, D.J.; Liu, C.; Nesbitt, S.W.; Yorty, D.P. Where are the most: Intense thunderstorms on Earth? Bull. Am. Meteorol. Soc. 2006, 87, 1057–1071. [Google Scholar] [CrossRef] [Green Version]
- Zuluaga, M.D.; Houze, R.A. Extreme convection of the near-equatorial Americas, Africa, and adjoining oceans as seen by TRMM. Mon. Weather Rev. 2015, 143, 298–316. [Google Scholar] [CrossRef] [Green Version]
- Marengo, J.A. Characteristics and spatio-temporal variability of the Amazon river basin water budget. Clim. Dyn. 2005, 24, 11–22. [Google Scholar] [CrossRef]
- Do Nascimento, M.G.; Herdies, D.L.; De Souza, D.O. The south American water balance: The influence of low-level jets. J. Clim. 2016, 29, 1429–1449. [Google Scholar] [CrossRef]
- Poveda, G.; Álvarez, D.M.; Rueda, Ó.A. Hydro-climatic variability over the Andes of Colombia associated with ENSO: A review of climatic processes and their impact on one of the Earth’s most important biodiversity hotspots. Clim. Dyn. 2011, 36, 2233–2249. [Google Scholar] [CrossRef]
- Sakamoto, M.S.; Ambrizzi, T.; Poveda, G. Moisture Sources and Life Cycle of Convective Systems over Western Colombia. Adv. Meteorol. 2011, 2011, 1–11. [Google Scholar] [CrossRef]
- Durán-Quesada, A.M.; Gimeno, L.; Amador, J. Role of moisture transport for Central American precipitation. Earth Syst. Dyn. 2017, 8, 147–161. [Google Scholar] [CrossRef] [Green Version]
- Bosilovich, M.G. On the vertical distribution of local and remote sources of water for precipitation. Meteorol. Atmos. Phys. 2002, 80, 31–41. [Google Scholar] [CrossRef] [Green Version]
- Builes-Jaramillo, A.; Yepes, J.; Salas, H.D. The Orinoco Low-Level Jet and Its Association with the Hydroclimatology of Northern South America. J. Hydrometeorol. 2022, 23, 209–223. [Google Scholar] [CrossRef]

| Surface Variables | ||
|---|---|---|
| Symbol | Variable | Unit |
| Precipitation | m·day–1 | |
| Evaporation | m·day–1 | |
| Total column water | kg·m–2 | |
| Total column of water vapor | kg·m–2 | |
| Vertical integral of eastward water vapor flux | kg·m−1·s−1 | |
| Vertical integral of northward water vapor flux | kg·m−1·s−1 | |
| Vertical integral of eastward cloud liquid water flux | kg·m−1·s−1 | |
| Vertical integral of northward cloud liquid water flux | kg·m−1·s−1 | |
| Vertical integral of eastward cloud solid water flux | kg·m−1·s−1 | |
| Vertical integral of northward cloud solid water flux | kg·m−1·s−1 | |
| Surface pressure | Pa | |
| Pressure levels variables | ||
| Specific humidity | kg·kg–1 | |
| Zonal component of wind | m·s–1 | |
| Meridional component of wind | m·s–1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Enciso, A.M.; Baquero, O.L.; Escobar-Carbonari, D.; Tapasco, J.; Cerón, W.L. Variability of Precipitation Recycling and Moisture Sources over the Colombian Pacific Region: A Precipitationshed Approach. Atmosphere 2022, 13, 1202. https://doi.org/10.3390/atmos13081202
Enciso AM, Baquero OL, Escobar-Carbonari D, Tapasco J, Cerón WL. Variability of Precipitation Recycling and Moisture Sources over the Colombian Pacific Region: A Precipitationshed Approach. Atmosphere. 2022; 13(8):1202. https://doi.org/10.3390/atmos13081202
Chicago/Turabian StyleEnciso, Angelica M., Olga Lucia Baquero, Daniel Escobar-Carbonari, Jeimar Tapasco, and Wilmar L. Cerón. 2022. "Variability of Precipitation Recycling and Moisture Sources over the Colombian Pacific Region: A Precipitationshed Approach" Atmosphere 13, no. 8: 1202. https://doi.org/10.3390/atmos13081202
APA StyleEnciso, A. M., Baquero, O. L., Escobar-Carbonari, D., Tapasco, J., & Cerón, W. L. (2022). Variability of Precipitation Recycling and Moisture Sources over the Colombian Pacific Region: A Precipitationshed Approach. Atmosphere, 13(8), 1202. https://doi.org/10.3390/atmos13081202






