Optimizing Analog Ensembles for Sub-Daily Precipitation Forecasts
Abstract
1. Introduction
2. Materials and Methods
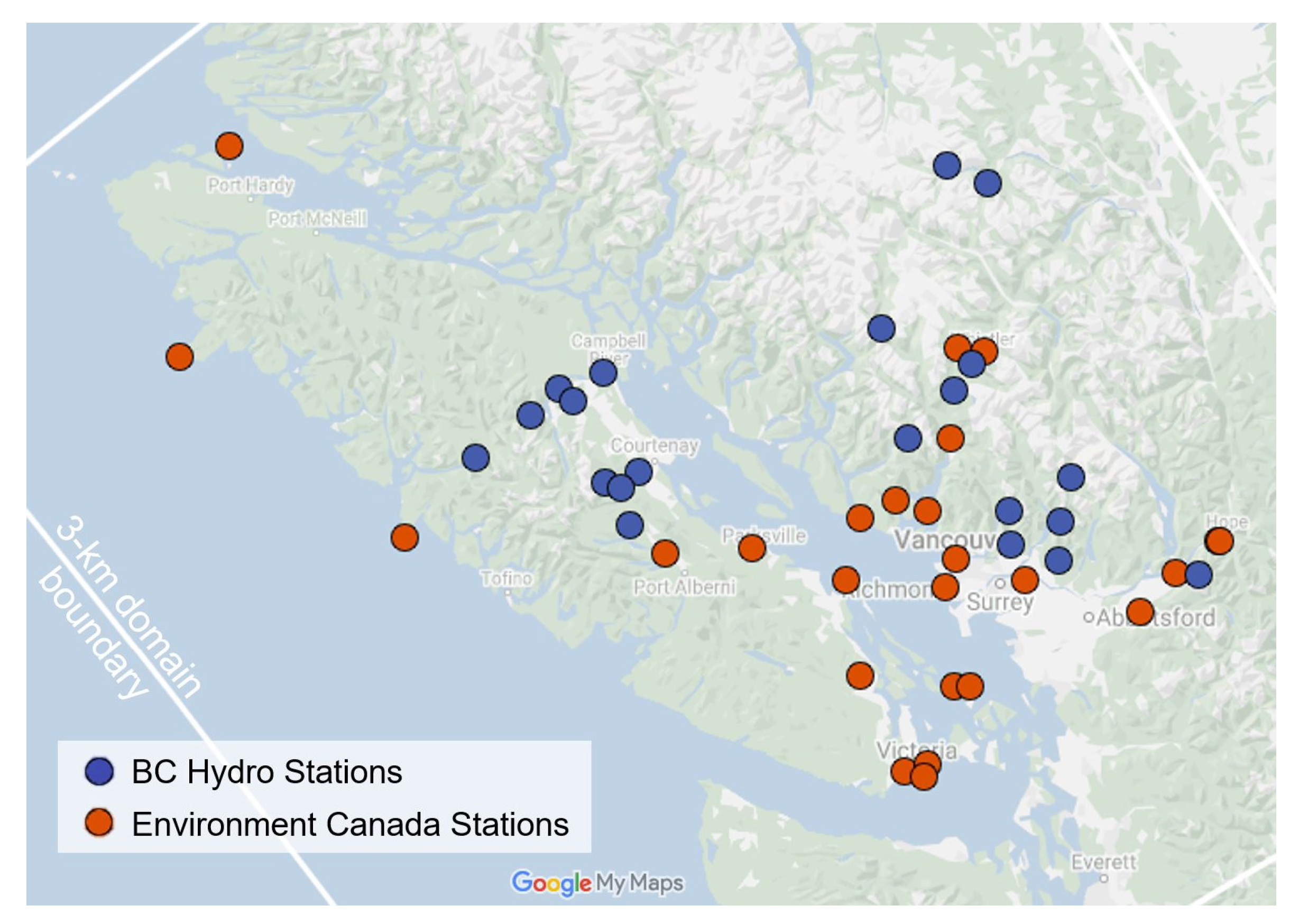
2.1. Data
- each station has at least 90% of data available, and missing data is not systematically distributed (e.g., in the same season, at the same time of day, or over a large consecutive period); and
- outliers are reasonable considering the synoptic situation (e.g., convection), nearby stations, and the available station climatology.
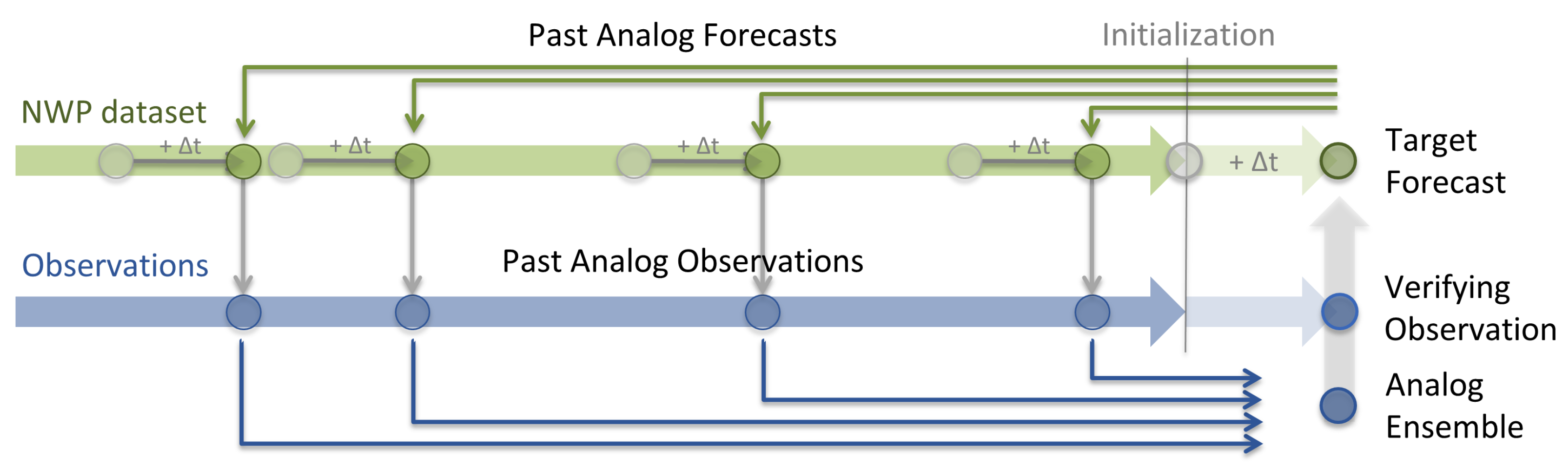
2.2. Analog Ensemble Methodology
2.2.1. Predictor Selection Procedures
- All-EFS: Using the EFS to test all 40 variables in addition to PCP as predictors.
- DC-EFS: Using the EFS to test the same subset of 10 predictor candidates as in DC-FS.
- DCV-EFS: Using the EFS to test a subset of 10 variables as predictors, except here, the predictor candidates are based on the best DCorr, as well as the variance inflation factor (VIF, a measure of multicollinearity among variables). Specifically, we grow a set of 10 predictor candidates by sequentially adding one variable at a time, starting from the best ranking DCorr, provided the VIF among the growing set of predictor candidates stays below a threshold value of 10. If this threshold is exceeded it means that the variable exhibits strong correlation with other variables that were already selected and we assume that this variable contributes no additional value as a predictor for the AnEn. Since some of our 41 variables are related (e.g., the same variables at different vertical levels), the VIF check limits the use of correlated and presumably redundant variables in the FS.
2.2.2. The Supplemental-Lead-Time (SLT) Approach
3. Results and Discussion
3.1. Predictor Selection Optimization
3.2. Temporal Trend Similarity
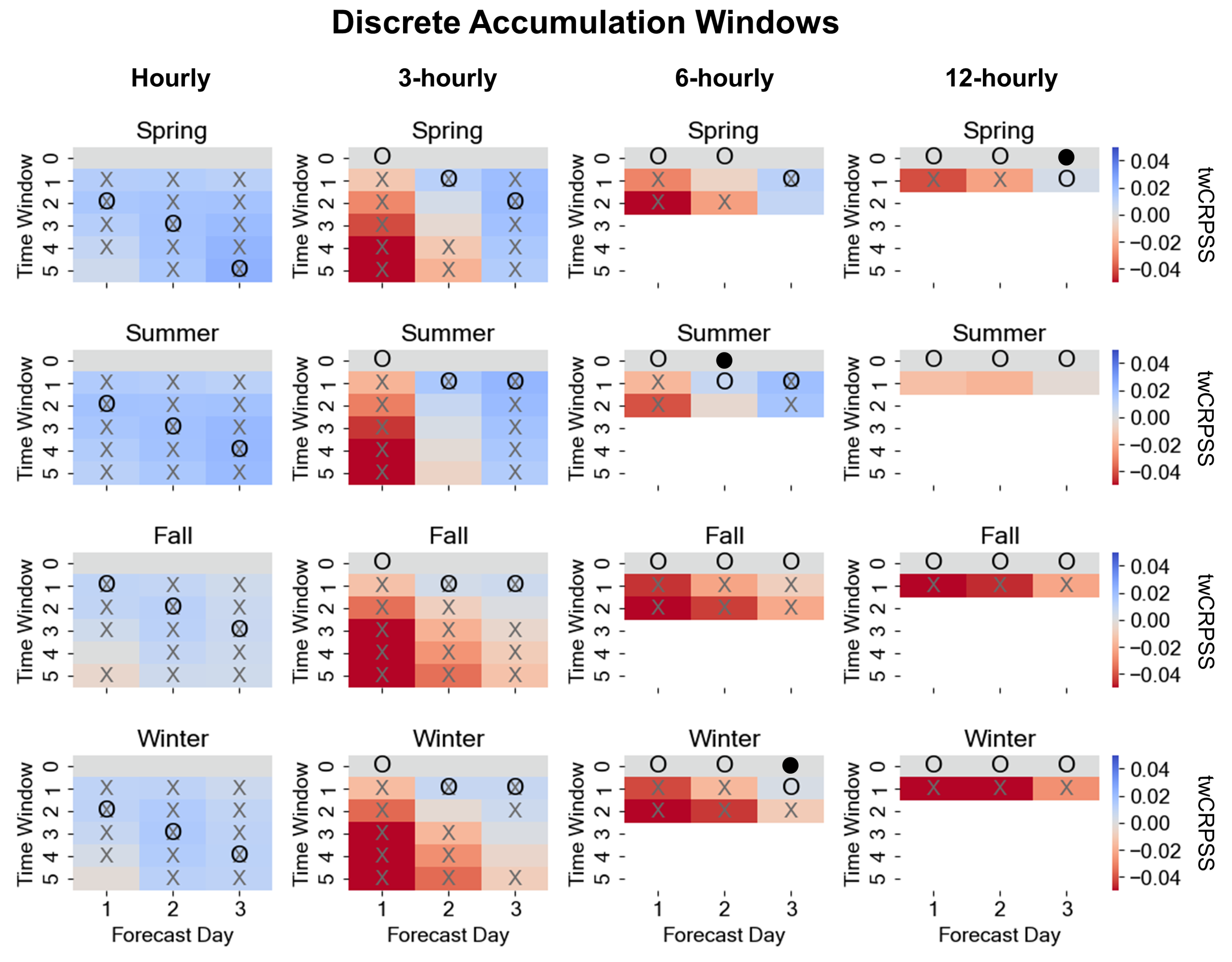
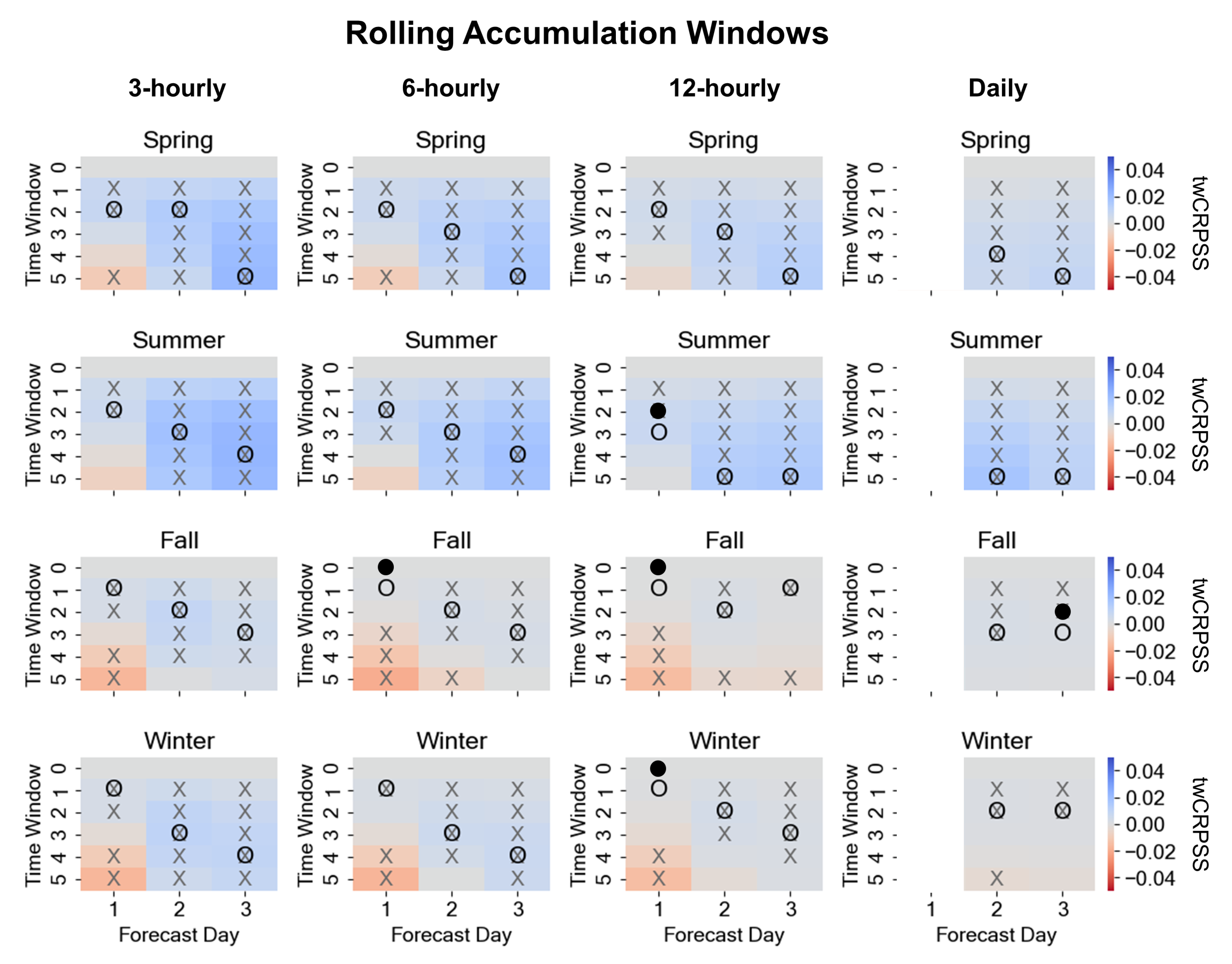
3.3. Supplemental Lead Times (SLTs)
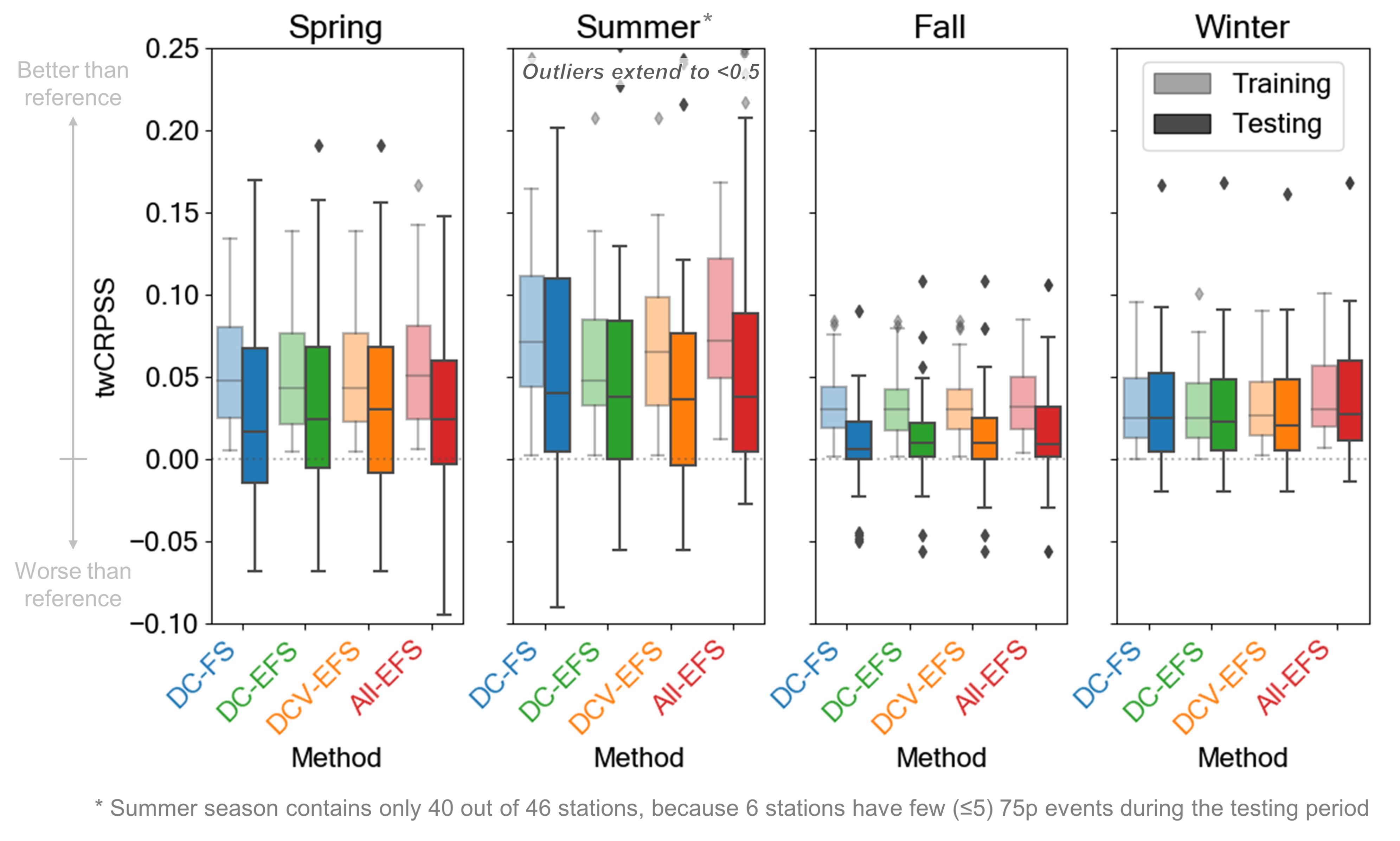
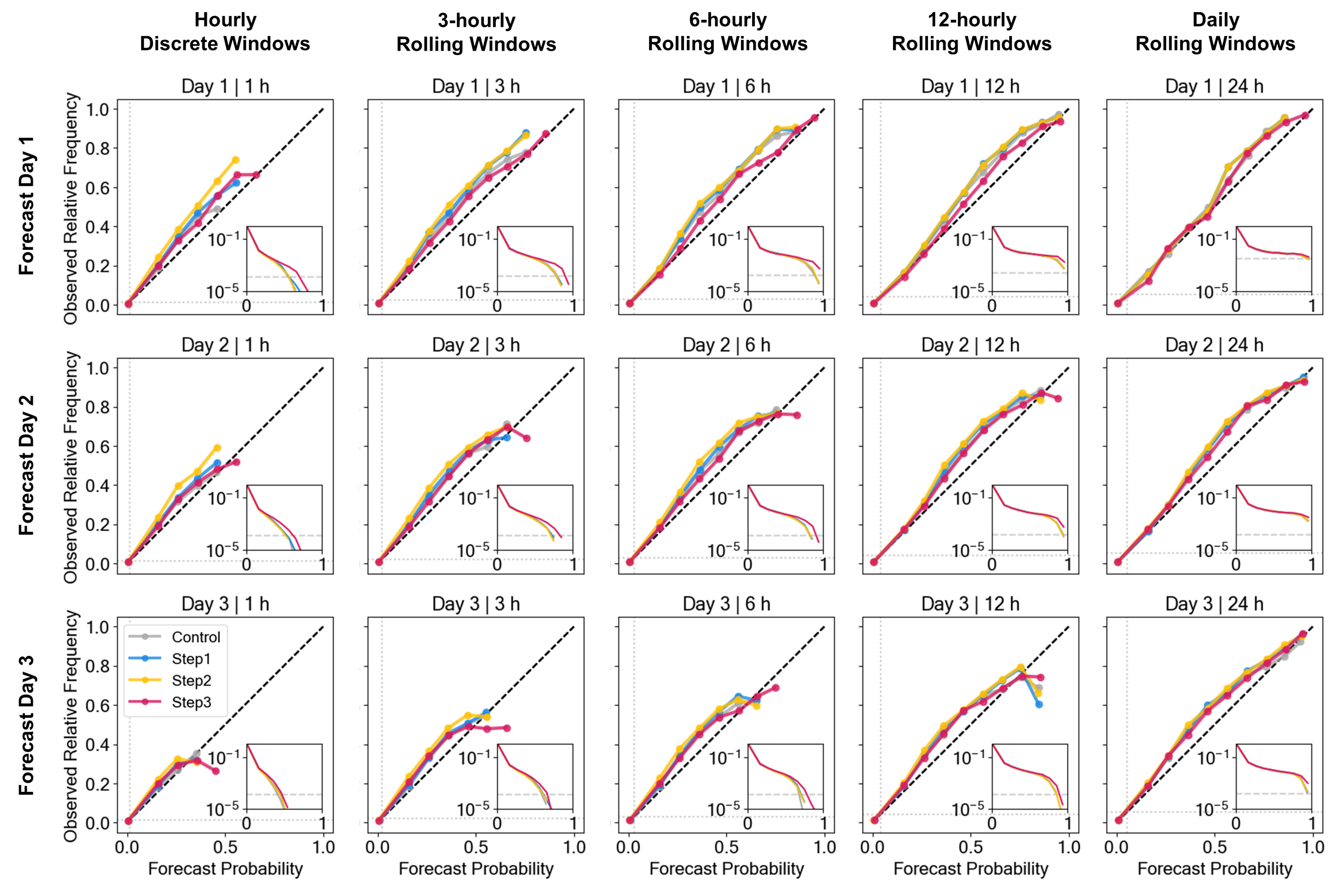
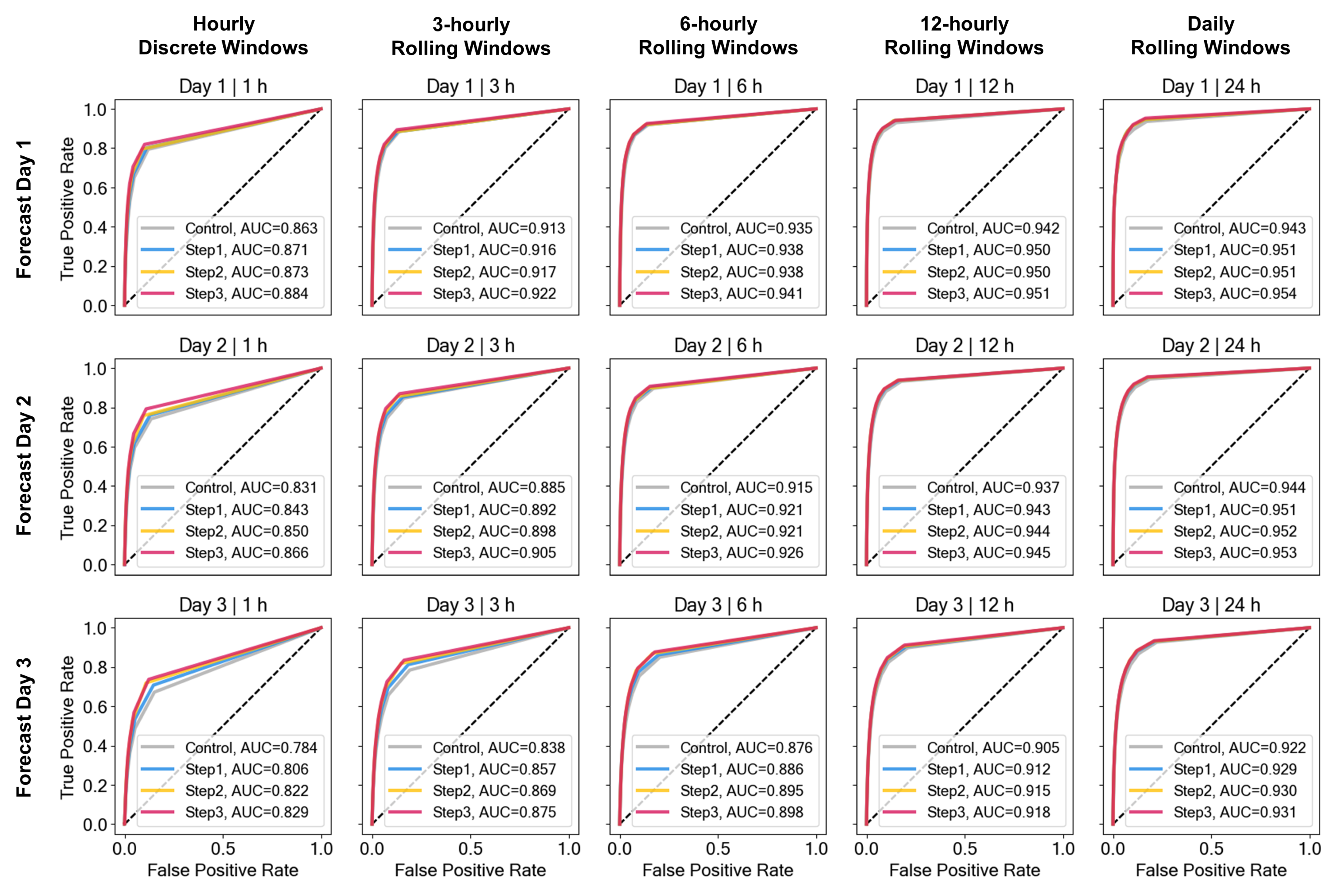
3.4. Verification
- the control AnEn using reference predictors, no TTS, and no SLTs (Control),
- the AnEn with optimized predictors, but no TTS, and no SLTs (Step 1),
- the AnEn with optimized predictors and optimized TTS consideration, but no SLT (Step 2), and
- the AnEn with optimized predictors and optimized TTS consideration, and using SLTs in a window of (Step 3).
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AnEn(s) | Analog Ensemble(s) |
| AnFcst(s) | Analog Forecast(s) |
| AnObs | Analog Observation(s) |
| TaFcst(s) | Target Forecast(s) |
| VerifObs | Verifying Observation(s) |
| TTS | Temporal Trend Similarity |
| SLT(s) | Supplemental Lead Time(s) |
| FS | Forward Selection |
| EFS | Efficient Forward Selection |
Appendix A. Percentiles
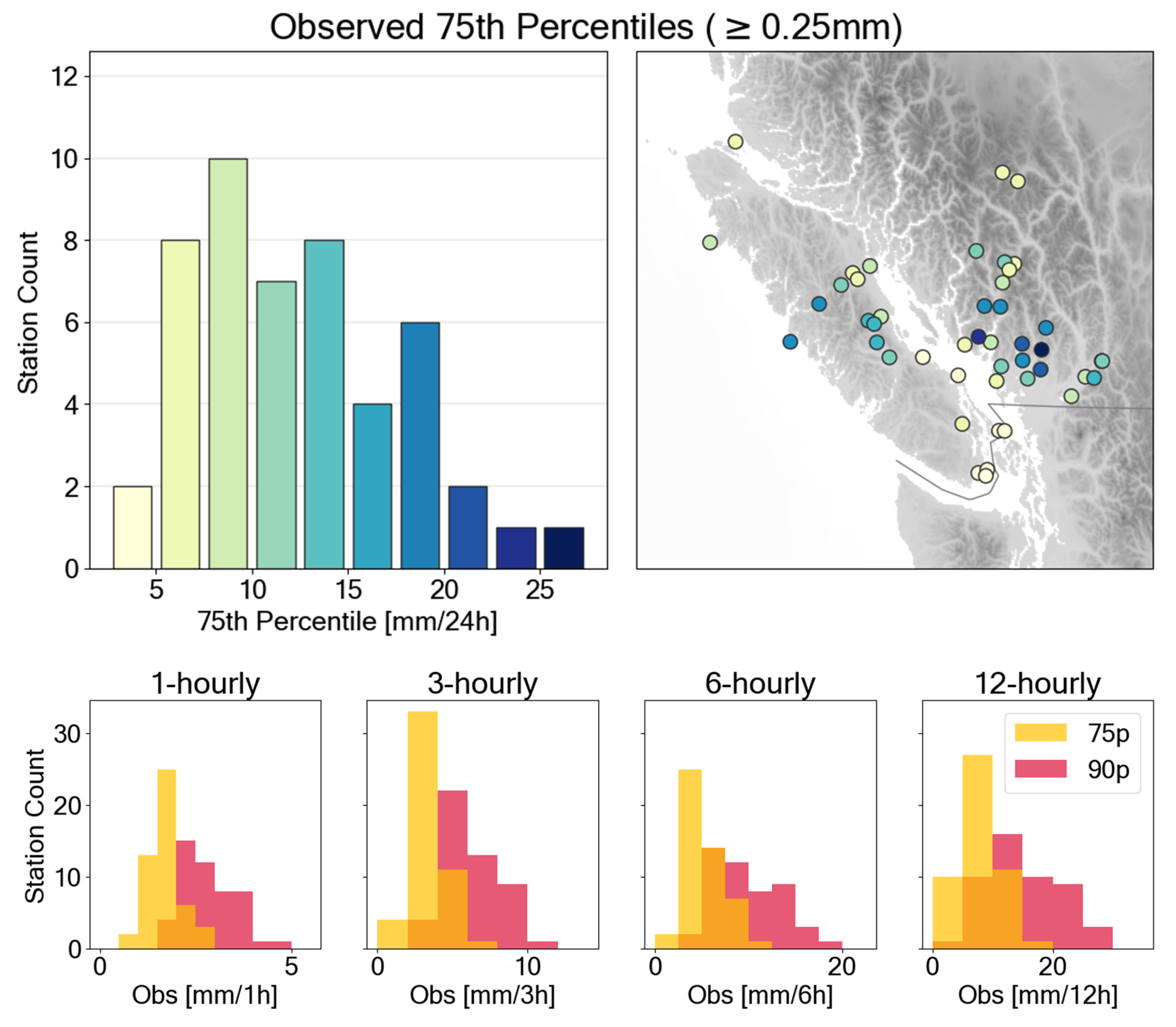
Appendix B. Evaluation
Appendix B.1. Threshold-Weighted Continuous Ranked Probability Score
Appendix B.2. Statistical Tests
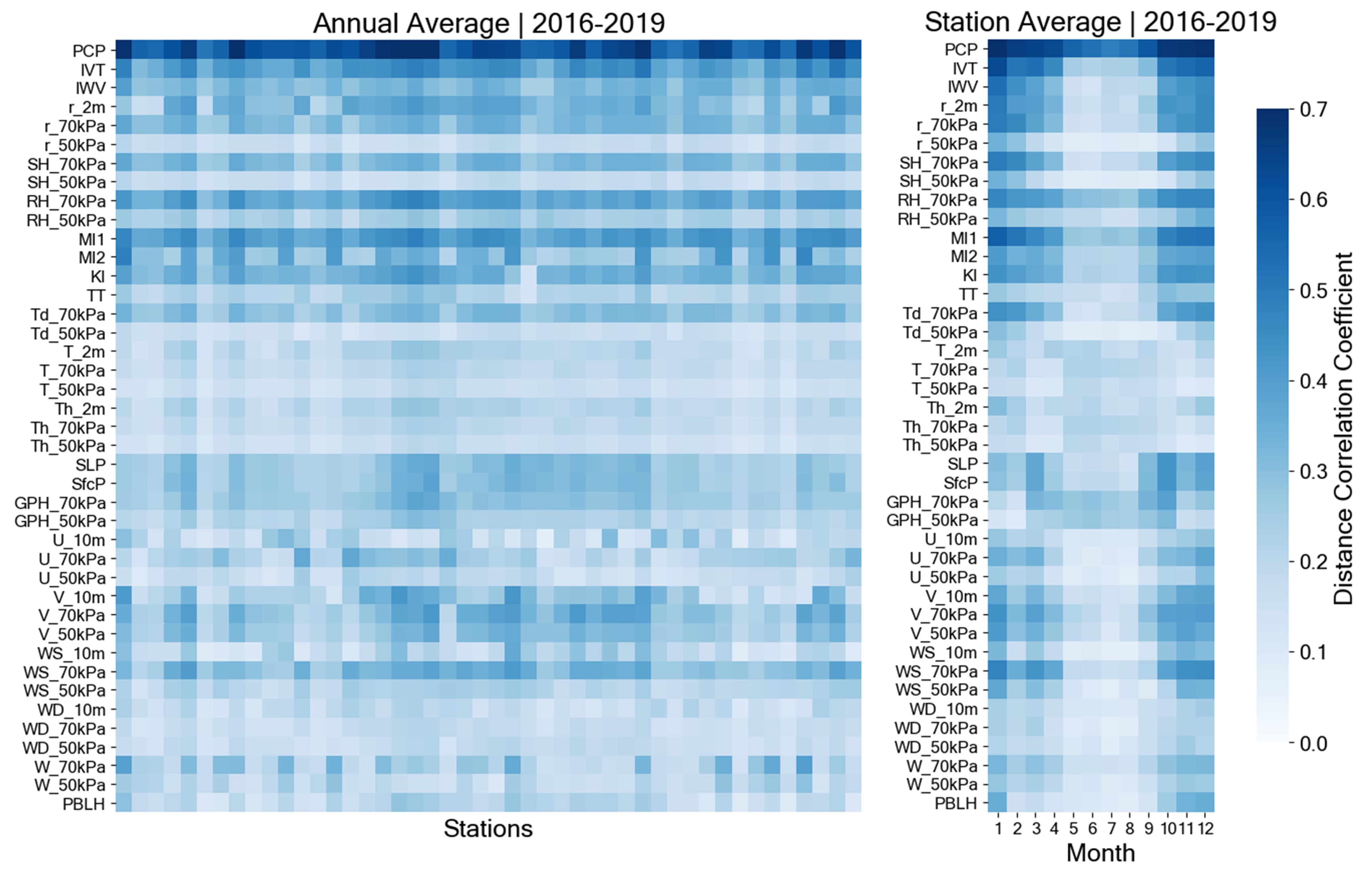
Appendix C. Correlation Analysis
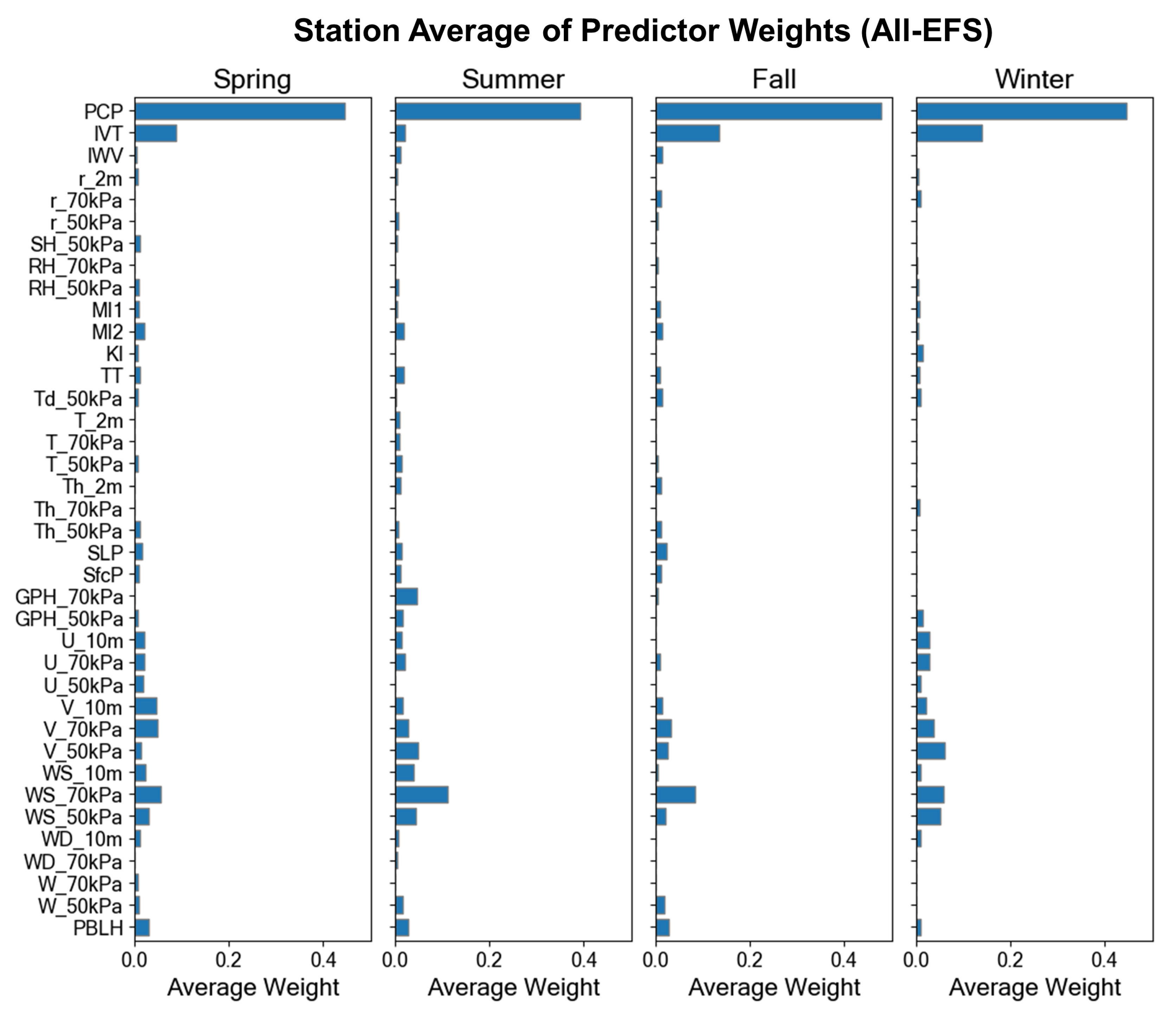
Appendix D. Predictor Weights
References
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Elsevier/Academic Press: Cambridge, MA, USA, 2011; p. 676. [Google Scholar]
- Wilks, D.S. Extending logistic regression to provide full-probability-distribution MOS forecasts. Meteorol. Appl. 2009, 16, 361–368. [Google Scholar] [CrossRef]
- Roulin, E.; Vannitsem, S. Postprocessing of Ensemble Precipitation Predictions with Extended Logistic Regression Based on Hindcasts. Mon. Weather Rev. 2012, 140, 874–888. [Google Scholar] [CrossRef]
- Bakker, K.; Whan, K.; Knap, W.; Schmeits, M. Comparison of statistical post-processing methods for probabilistic NWP forecasts of solar radiation. Sol. Energy 2019, 191, 138–150. [Google Scholar] [CrossRef]
- Carter, G.M.; Dallavalle, J.P.; Glahn, H.R. Statistical Forecasts Based on the National Meteorological Center’s Numerical Weather Prediction System. Weather Forecast. 1989, 4, 401–412. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Yussouf, N. Short-range ensemble predictions of 2-m temperature and dewpoint temperature over New England. Mon. Weather Rev. 2003, 131, 2510–2524. [Google Scholar] [CrossRef]
- Gneiting, T.; Ranjan, R. Comparing density forecasts using threshold and quantile-weighted scoring rules. J. Bus. Econ. Stat. 2011, 29, 411–422. [Google Scholar] [CrossRef]
- Scheuerer, M. Probabilistic quantitative precipitation forecasting using Ensemble Model Output Statistics. Q. J. R. Meteorol. Soc. 2014, 140, 1086–1096. [Google Scholar] [CrossRef]
- Delle Monache, L.; Nipen, T.; Liu, Y.; Roux, G.; Stull, R. Kalman Filter and Analog Schemes to Postprocess Numerical Weather Predictions. Mon. Weather Rev. 2011, 139, 3554–3570. [Google Scholar] [CrossRef]
- McCollor, D.; Stull, R. Hydrometeorological accuracy enhancement via postprocessing of numerical weather forecasts in complex terrain. Weather Forecast. 2008, 23, 131–144. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Faidah, D.Y.; Kuswanto, H.; Suhartono. The comparison of Bayesian model averaging with gaussian and gamma components for probabilistic precipitation forecasting. AIP Conf. Proc. 2019, 2192, 090003. [Google Scholar] [CrossRef]
- Yuan, H.; Gao, X.; Mullen, S.L.; Sorooshian, S.; Du, J.; Juang, H.M.H. Calibration of Probabilistic Quantitative Precipitation Forecasts with an Artificial Neural Network. Weather Forecast. 2007, 22, 1287–1303. [Google Scholar] [CrossRef]
- Sha, Y.; Gagne, D.J., II; West, G.; Stull, R. A hybrid analog-ensemble, convolutional-neural-network method for post-processing precipitation forecasts. Mon. Weather. Rev. 2022, 150, 1495–1515. [Google Scholar] [CrossRef]
- Cho, D.; Yoo, C.; Son, B.; Im, J.; Yoon, D.; Cha, D.H. A novel ensemble learning for post-processing of NWP Model’s next-day maximum air temperature forecast in summer using deep learning and statistical approaches. Weather Clim. Extrem. 2022, 35, 100410. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S. Probabilistic Quantitative Precipitation Forecasts Based on Reforecast Analogs: Theory and Application. Mon. Weather Rev. 2006, 134, 3209–3229. [Google Scholar] [CrossRef]
- Delle Monache, L.; Eckel, F.A.; Rife, D.L.; Nagarajan, B.; Searight, K. Probabilistic Weather Prediction with an Analog Ensemble. Mon. Weather Rev. 2013, 141, 3498–3516. [Google Scholar] [CrossRef]
- Eckel, F.A.; Delle Monache, L. A Hybrid NWP–Analog Ensemble. Mon. Weather Rev. 2016, 144, 897–911. [Google Scholar] [CrossRef]
- Junk, C.; Monache, L.D.; Alessandrini, S. Analog-Based Ensemble Model Output Statistics. Mon. Weather Rev. 2015, 143, 2909–2917. [Google Scholar] [CrossRef]
- Frediani, M.E.B.; Hopson, T.M.; Hacker, J.P.; Anagnostou, E.N.; Delle Monache, L.; Vandenberghe, F. Object-Based Analog Forecasts for Surface Wind Speed. Mon. Weather Rev. 2017, 145, 5083–5102. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; Delle Monache, L. Gridded probabilistic weather forecasts with an analog ensemble. Q. J. R. Meteorol. Soc. 2017, 143, 2874–2885. [Google Scholar] [CrossRef]
- Odak Plenković, I.; Delle Monache, L.; Horvath, K.; Hrastinski, M. Deterministic Wind Speed Predictions with Analog-Based Methods over Complex Topography. J. Appl. Meteorol. Climatol. 2018, 57, 2047–2070. [Google Scholar] [CrossRef]
- Yang, J.; Astitha, M.; Monache, L.D.; Alessandrini, S. An Analog Technique to Improve Storm Wind Speed Prediction Using a Dual NWP Model Approach. Mon. Weather Rev. 2018, 146, 4057–4077. [Google Scholar] [CrossRef]
- Davò, F.; Alessandrini, S.; Sperati, S.; Delle Monache, L.; Airoldi, D.; Vespucci, M.T. Post-processing techniques and principal component analysis for regional wind power and solar irradiance forecasting. Sol. Energy 2016, 134, 327–338. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Nissen, J. A novel application of an analog ensemble for short-term wind power forecasting. Renew. Energy 2015, 76, 768–781. [Google Scholar] [CrossRef]
- Martín, M.; Valero, F.; Pascual, A.; Sanz, J.; Frias, L. Analysis of wind power productions by means of an analog model. Atmos. Res. 2014, 143, 238–249. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Cervone, G. An analog ensemble for short-term probabilistic solar power forecast. Appl. Energy 2015, 157, 95–110. [Google Scholar] [CrossRef]
- Djalalova, I.; Delle Monache, L.; Wilczak, J. PM2.5 analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model. Atmos. Environ. 2015, 108, 76–87. [Google Scholar] [CrossRef]
- Delle Monache, L.; Alessandrini, S.; Djalalova, I.; Wilczak, J.; Knievel, J.C.; Kumar, R. Improving Air Quality Predictions over the United States with an Analog Ensemble. Weather Forecast. 2020, 35, 2145–2162. [Google Scholar] [CrossRef]
- Raman, A.; Arellano, A.F.; Delle Monache, L.; Alessandrini, S.; Kumar, R. Exploring analog-based schemes for aerosol optical depth forecasting with WRF-Chem. Atmos. Environ. 2021, 246, 118134. [Google Scholar] [CrossRef]
- Horton, P.; Jaboyedoff, M.; Metzger, R.; Obled, C.; Marty, R. Spatial relationship between the atmospheric circulation and the precipitation measured in the western Swiss Alps by means of the analogue method. Nat. Hazards Earth Syst. Sci. 2012, 12, 777–784. [Google Scholar] [CrossRef][Green Version]
- Ben Daoud, A.; Sauquet, E.; Bontron, G.; Obled, C.; Lang, M. Daily quantitative precipitation forecasts based on the analogue method: Improvements and application to a French large river basin. Atmos. Res. 2016, 169, 147–159. [Google Scholar] [CrossRef]
- Keller, J.D.; Monache, L.D.; Alessandrini, S. Statistical Downscaling of a High-Resolution Precipitation Reanalysis Using the Analog Ensemble Method. J. Appl. Meteorol. Climatol. 2017, 56, 2081–2095. [Google Scholar] [CrossRef]
- Yang, C.; Yuan, H.; Su, X. Bias correction of ensemble precipitation forecasts in the improvement of summer streamflow prediction skill. J. Hydrol. 2020, 588, 124955. [Google Scholar] [CrossRef]
- Junk, C.; Delle Monache, L.; Alessandrini, S.; Cervone, G.; von Bremen, L. Predictor-weighting strategies for probabilistic wind power forecasting with an analog ensemble. Meteorol. Z. 2015, 24, 361–379. [Google Scholar] [CrossRef]
- Li, N.; Ran, L.; Jiao, B. An analogy-based method for strong convection forecasts in China using GFS forecast data. Atmos. Ocean. Sci. Lett. 2020, 13, 97–106. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Li, L.; Liu, Y.S.; Chan, P.W.; Zhang, W.H.; Zhang, L. Estimation of precipitation induced by tropical cyclones based on machine-learning-enhanced analogue identification of numerical prediction. Meteorol. Appl. 2021, 28, e1978. [Google Scholar] [CrossRef]
- Hamill, T.M.; Scheuerer, M.; Bates, G.T. Analog Probabilistic Precipitation Forecasts Using GEFS Reforecasts and Climatology-Calibrated Precipitation Analyses. Mon. Weather Rev. 2015, 143, 3300–3309. [Google Scholar] [CrossRef]
- Obled, C.; Bontron, G.; Garçon, R. Quantitative precipitation forecasts: A statistical adaptation of model outputs through an analogues sorting approach. Atmos. Res. 2002, 63, 303–324. [Google Scholar] [CrossRef]
- Marty, R.; Zin, I.; Obled, C.; Bontron, G.; Djerboua, A. Toward Real-Time Daily PQPF by an Analog Sorting Approach: Application to Flash-Flood Catchments. J. Appl. Meteorol. Climatol. 2012, 51, 505–520. [Google Scholar] [CrossRef]
- Bellier, J.; Zin, I.; Siblot, S.; Bontron, G. Probabilistic flood forecasting on the Rhone River: Evaluation with ensemble and analogue-based precipitation forecasts. E3S Web Conf. 2016, 7, 18011. [Google Scholar] [CrossRef]
- Horton, P.; Jaboyedoff, M.; Obled, C. Global Optimization of an Analog Method by Means of Genetic Algorithms. Mon. Weather Rev. 2017, 145, 1275–1294. [Google Scholar] [CrossRef][Green Version]
- Horton, P.; Brönnimann, S. Impact of global atmospheric reanalyses on statistical precipitation downscaling. Clim. Dyn. 2019, 52, 5189–5211. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Rozoff, C.M.; Lewis, W.E. Probabilistic Prediction of Tropical Cyclone Intensity with an Analog Ensemble. Mon. Weather Rev. 2018, 146, 1723–1744. [Google Scholar] [CrossRef]
- Fernández, J.; Sáenz, J. Improved field reconstruction with the analog method: Searching the CCA space. Clim. Res. 2003, 24, 199–213. [Google Scholar] [CrossRef]
- Cannon, A.J. Nonlinear analog predictor analysis: A coupled neural network/analog model for climate downscaling. Neural Netw. 2007, 20, 444–453. [Google Scholar] [CrossRef] [PubMed]
- Horton, P.; Jaboyedoff, M.; Obled, C. Using genetic algorithms to optimize the analogue method for precipitation prediction in the Swiss Alps. J. Hydrol. 2018, 556, 1220–1231. [Google Scholar] [CrossRef]
- Alessandrini, S.; Sperati, S.; Delle Monache, L. Improving the Analog Ensemble Wind Speed Forecasts for Rare Events. Mon. Weather Rev. 2019, 147, 2677–2692. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Rozoff, C.; Lewis, W. Probabilistic Prediction of Hurricane Intensity with an Analog Ensemble. In Proceedings of the 96th American Meteorological Society Annual Meeting, New Orleans, LA, USA, 10–14 January 2016. [Google Scholar]
- Odak Plenković, I.; Schicker, I.; Dabernig, M.; Horvath, K.; Keresturi, E. Analog-based post-processing of the ALADIN-LAEF ensemble predictions in complex terrain. Q. J. R. Meteorol. Soc. 2020, 146, 1842–1860. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S.; Mullen, S.L. Reforecasts: An Important Dataset for Improving Weather Predictions. Bull. Am. Meteorol. Soc. 2006, 87, 33–46. [Google Scholar] [CrossRef]
- Meech, S.; Alessandrini, S.; Chapman, W.; Delle Monache, L. Post-processing rainfall in a high-resolution simulation of the 1994 Piedmont flood. Bull. Atmos. Sci. Technol. 2020, 1, 373–385. [Google Scholar] [CrossRef]
- Dayon, G.; Boé, J.; Martin, E. Transferability in the future climate of a statistical downscaling method for precipitation in France. J. Geophys. Res. Atmos. 2015, 120, 1023–1043. [Google Scholar] [CrossRef]
- Horton, P.; Obled, C.; Jaboyedoff, M. The analogue method for precipitation prediction: Finding better analogue situations at a sub-daily time step. Hydrol. Earth Syst. Sci. 2017, 21, 3307–3323. [Google Scholar] [CrossRef]
- Gibergans-Báguena, J.; Llasat, M. Improvement of the analog forecasting method by using local thermodynamic data. Application to autumn precipitation in Catalonia. Atmos. Res. 2007, 86, 173–193. [Google Scholar] [CrossRef]
- Ren, F.; Ding, C.; Zhang, D.L.; Chen, D.; li Ren, H.; Qiu, W. A Dynamical-Statistical-Analog Ensemble Forecast Model: Theory and an Application to Heavy Rainfall Forecasts of Landfalling Tropical Cyclones. Mon. Weather Rev. 2020, 148, 1503–1517. [Google Scholar] [CrossRef]
- Saminathan, S.; Medina, H.; Mitra, S.; Tian, D. Improving short to medium range GEFS precipitation forecast in India. J. Hydrol. 2021, 598, 126431. [Google Scholar] [CrossRef]
- Jeworrek, J.; West, G.; Stull, R. WRF Precipitation Performance and Predictability for Systematically Varied Parameterizations over Complex Terrain. Weather Forecast. 2021, 36, 893–913. [Google Scholar] [CrossRef]
- Marty, R.; Zin, I.; Obled, C. Sensitivity of hydrological ensemble forecasts to different sources and temporal resolutions of probabilistic quantitative precipitation forecasts: Flash flood case studies in the Cévennes-Vivarais region (Southern France). Hydrol. Process. 2013, 27, 33–44. [Google Scholar] [CrossRef]
- Hamill, T.M.; Hagedorn, R.; Whitaker, J.S. Probabilistic forecast calibration using ECMWF and GFS ensemble reforecasts. Part II: Precipitation. Mon. Weather Rev. 2008, 136, 2620–2632. [Google Scholar] [CrossRef]
- Fernández-Ferrero, A.; Sáenz, J.; Ibarra-Berastegi, G. Comparison of the performance of different analog-based bayesian probabilistic precipitation forecasts over Bilbao, Spain. Mon. Weather Rev. 2010, 138, 3107–3119. [Google Scholar] [CrossRef]
- Chapman, W.E.; Delle Monache, L.; Alessandrini, S.; Subramanian, A.C.; Ralph, F.M.; Xie, S.P.; Lerch, S.; Hayatbini, N. Probabilistic Predictions from Deterministic Atmospheric River Forecasts with Deep Learning. Mon. Weather Rev. 2021, 150, 215–234. [Google Scholar] [CrossRef]
- PCIC. Atmospheric Rivers State of Knowledge Report; Technical Report; Pacific Climate Impacts Consortium: Victoria, BC, Canada, 2013; Available online: https://www.pacificclimate.org/sites/default/files/publications/Atmospheric%20Report%20Final%20Revised.pdf (accessed on 2 November 2021).
- Gillett, N.P.; Cannon, A.J.; Malinina, E.; Schnorbus, M.; Anslow, F.; Sun, Q.; Kirchmeier-Young, M.; Zwiers, F.; Seiler, C.; Zhang, X.; et al. Human influence on the 2021 British Columbia floods. Weather Clim. Extrem. 2022, 36, 100441. [Google Scholar] [CrossRef]
- Vasquez, T. How an Atmopsheric River Flooded British Columbia. Weatherwise 2022, 75, 19–23. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhi, J.; Gill, D.; Barker, D.; Duda, M.; Huang, X.Y.; Wang, W.; Powers, J. A Description of the Advanced Research WRF Version 3; Technical Report; University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Côté, J.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The Operational CMC–MRB Global Environmental Multiscale (GEM) Model. Part I: Design Considerations and Formulation. Mon. Weather Rev. 1998, 126, 1373–1395. [Google Scholar] [CrossRef]
- Girard, C.; Plante, A.; Desgagné, M.; McTaggart-Cowan, R.; Côté, J.; Charron, M.; Gravel, S.; Lee, V.; Patoine, A.; Qaddouri, A.; et al. Staggered Vertical Discretization of the Canadian Environmental Multiscale (GEM) Model Using a Coordinate of the Log-Hydrostatic-Pressure Type. Mon. Weather Rev. 2014, 142, 1183–1196. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A Revised Approach to Ice Microphysical Processes for the Bulk Parameterization of Clouds and Precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch Convective Parameterization: An Update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. Atmos. 2011, 116, 1–19. [Google Scholar] [CrossRef]
- Yang, Z.L.; Niu, G.Y.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Longuevergne, L.; Manning, K.; Niyogi, D.; Tewari, M.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 2. Evaluation over global river basins. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Sha, Y.; Gagne, D.J., II; West, G.; Stull, R. Deep-Learning-Based Precipitation Observation Quality Control. J. Atmos. Ocean. Technol. 2021, 38, 1075–1091. [Google Scholar] [CrossRef]
- Székely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- Smith, L.A.; Suckling, E.B.; Thompson, E.L.; Maynard, T.; Du, H. Towards improving the framework for probabilistic forecast evaluation. Clim. Chang. 2015, 132, 31–45. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]



| Variable | Abbreviation | Levels |
|---|---|---|
| Total Precipitation | PCP | Surface |
| Integrated Water Vapor * | IWV | Column |
| Integrated Vapor Transport * | IVT | Column |
| Water Vapor Mixing Ratio | r | 2 m, 70 kPa, 50 kPa |
| Specific Humidity * | SH | 70 kPa, 50 kPa |
| Relative Humidity * | RH | 70 kPa, 50 kPa |
| Moisture Index 1 * () | MI1 | |
| Moisture Index 2 * () | MI2 | |
| Temperature | T | 2 m, 70 kPa, 50 kPa |
| Potential Temperature | Th | 2 m, 70 kPa, 50 kPa |
| Dewpoint Temperature | Td | 70 kPa, 50 kPa |
| Total Totals Index * | TT | |
| K-Index * | KI | |
| U-component Wind | U | 10 m, 70 kPa, 50 kPa |
| V-component Wind | V | 10 m, 70 kPa, 50 kPa |
| W-component Wind | W | 70 kPa, 50 kPa |
| Wind Direction * | WD | 10 m, 70 kPa, 50 kPa |
| Wind Speed * | WS | 10 m, 70 kPa, 50 kPa |
| Sea Level Pressure | SLP | Sea Level |
| Surface Pressure | SfcP | Surface |
| Geopotential Height | GPH | 70 kPa, 50 kPa |
| Boundary Layer Height | PBLH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeworrek, J.; West, G.; Stull, R. Optimizing Analog Ensembles for Sub-Daily Precipitation Forecasts. Atmosphere 2022, 13, 1662. https://doi.org/10.3390/atmos13101662
Jeworrek J, West G, Stull R. Optimizing Analog Ensembles for Sub-Daily Precipitation Forecasts. Atmosphere. 2022; 13(10):1662. https://doi.org/10.3390/atmos13101662
Chicago/Turabian StyleJeworrek, Julia, Gregory West, and Roland Stull. 2022. "Optimizing Analog Ensembles for Sub-Daily Precipitation Forecasts" Atmosphere 13, no. 10: 1662. https://doi.org/10.3390/atmos13101662
APA StyleJeworrek, J., West, G., & Stull, R. (2022). Optimizing Analog Ensembles for Sub-Daily Precipitation Forecasts. Atmosphere, 13(10), 1662. https://doi.org/10.3390/atmos13101662








