A Simple Parameterization to Enhance the Computational Time in the Three Layer Dry Deposition Model for Smooth Surfaces
Abstract
:1. Introduction
2. Materials and Methods
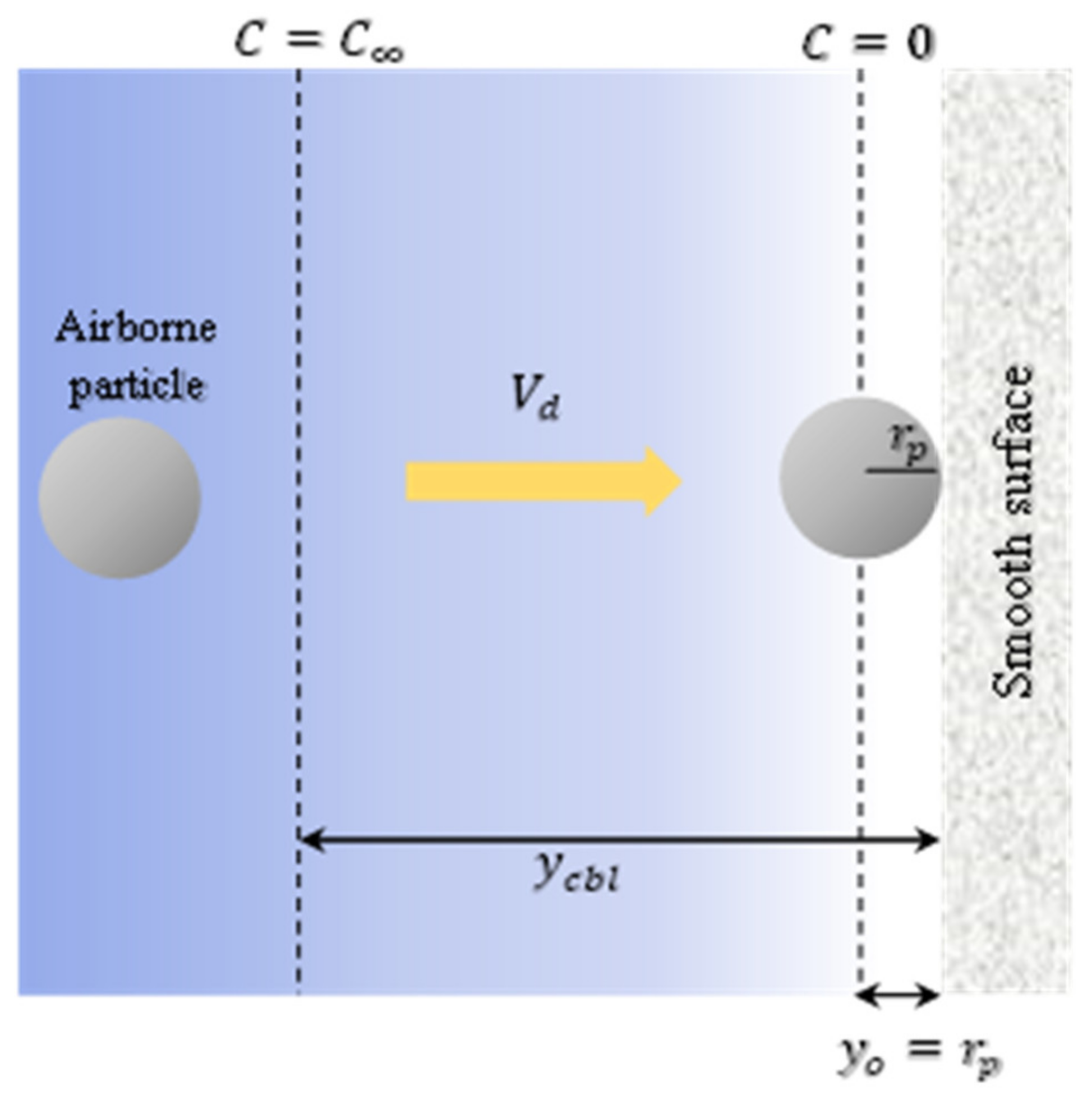
2.1. Three-Layer Dry Deposition Model
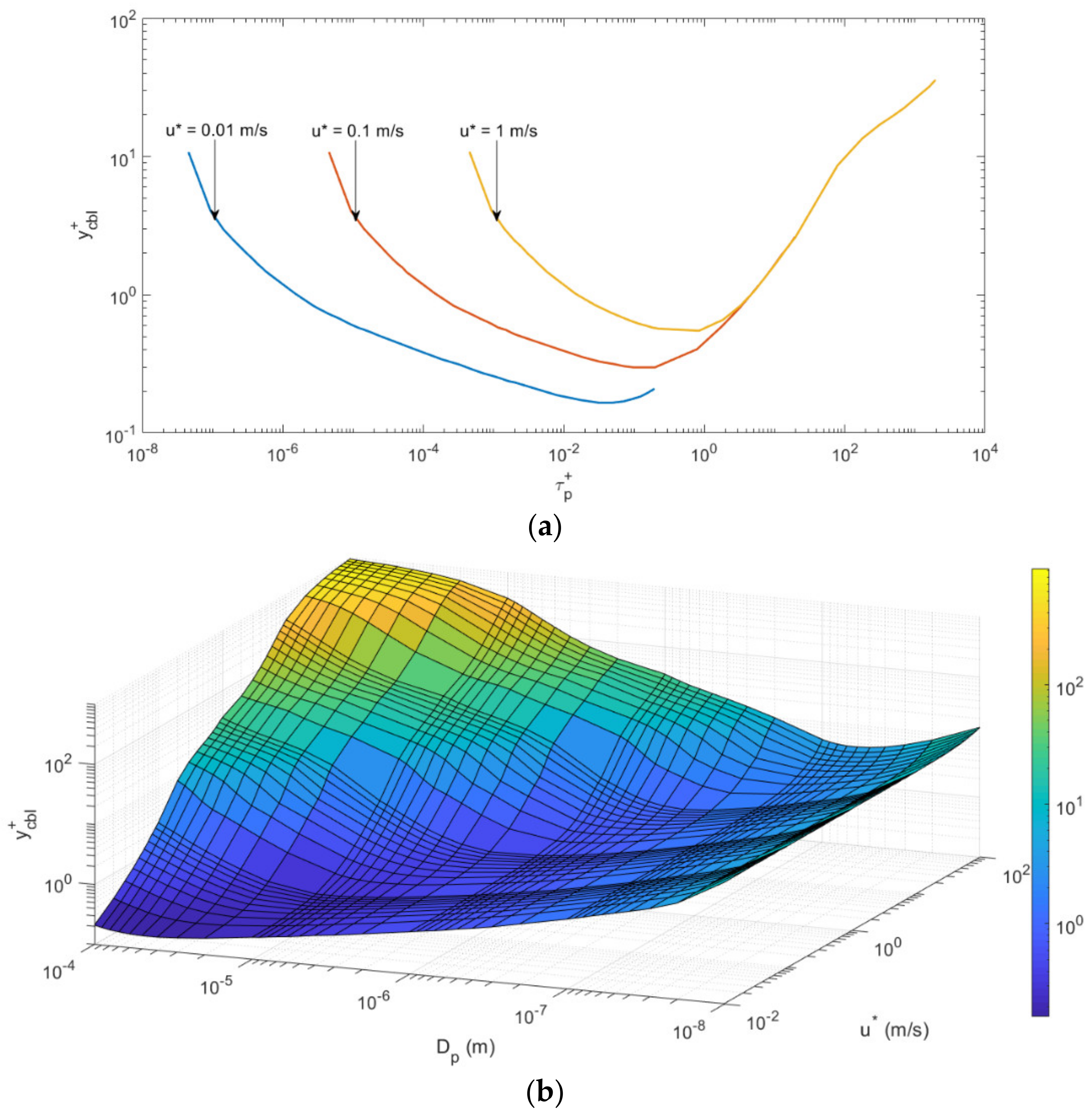
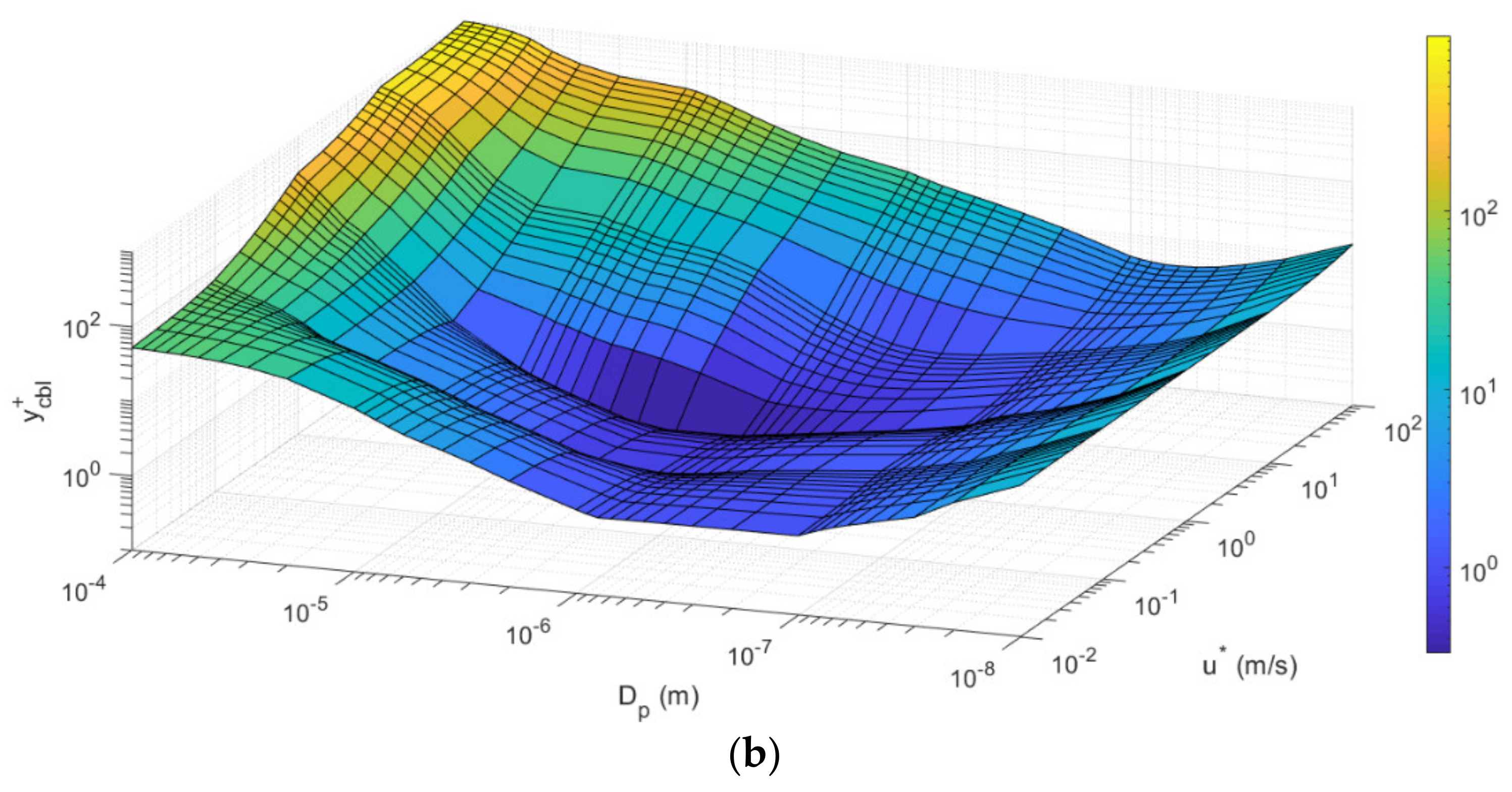
2.2. Parametrization for y+cbl
3. Results and Discussion
3.1. A Parameterization for Fickian Diffusion
3.2. The Inclusion of Gravitational Settling
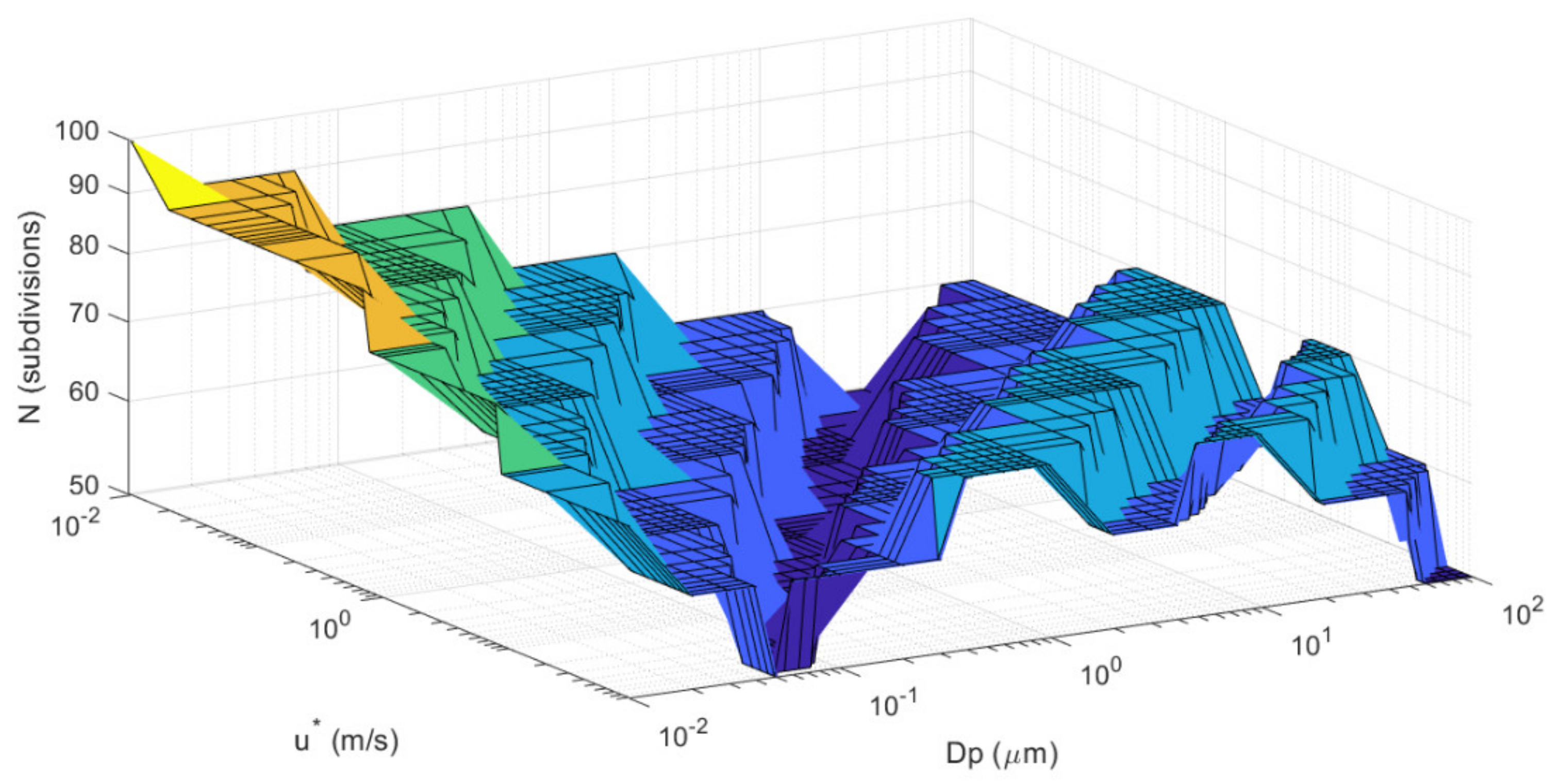
3.3. Computation Advantage by the Parameterization
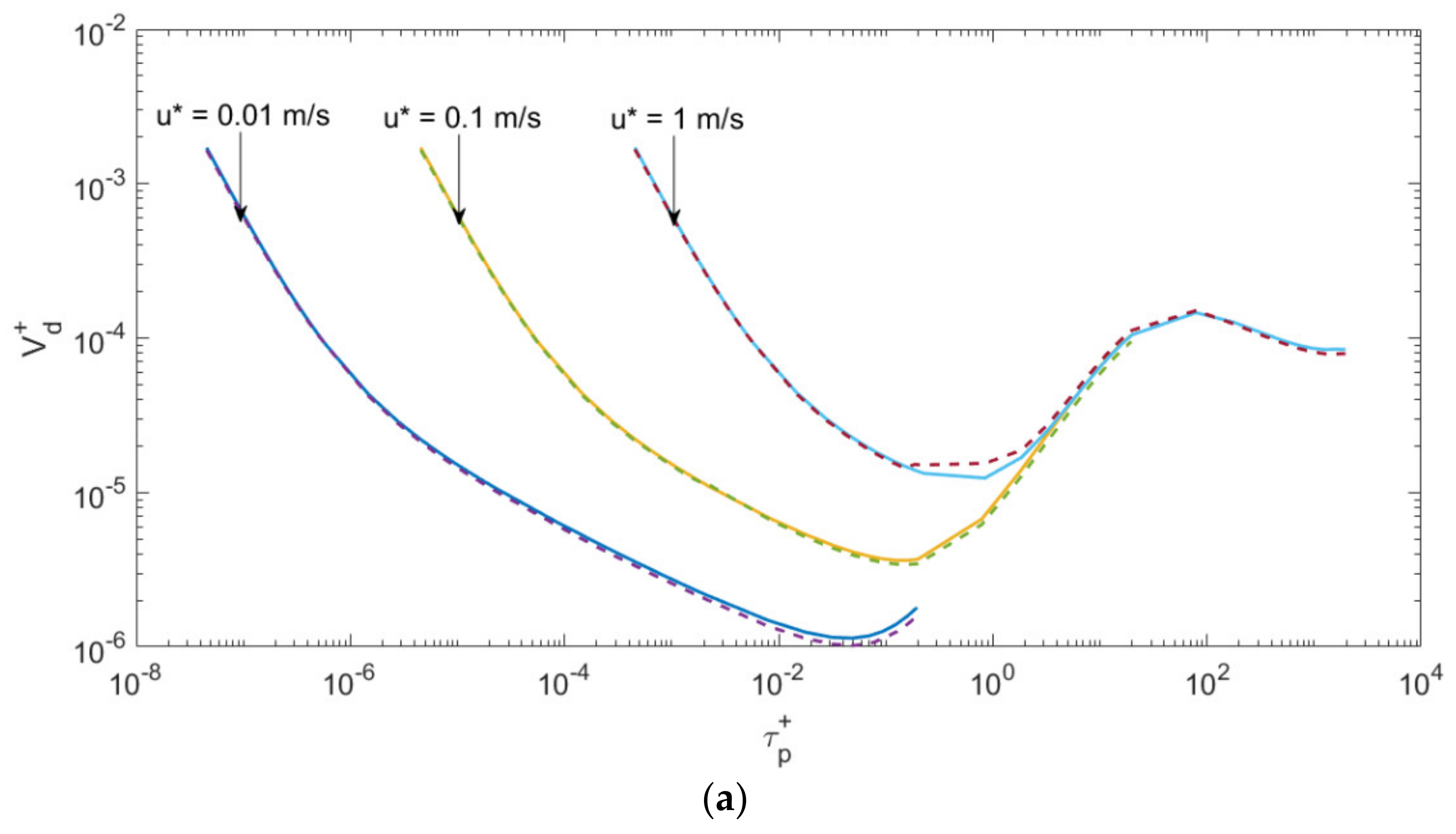
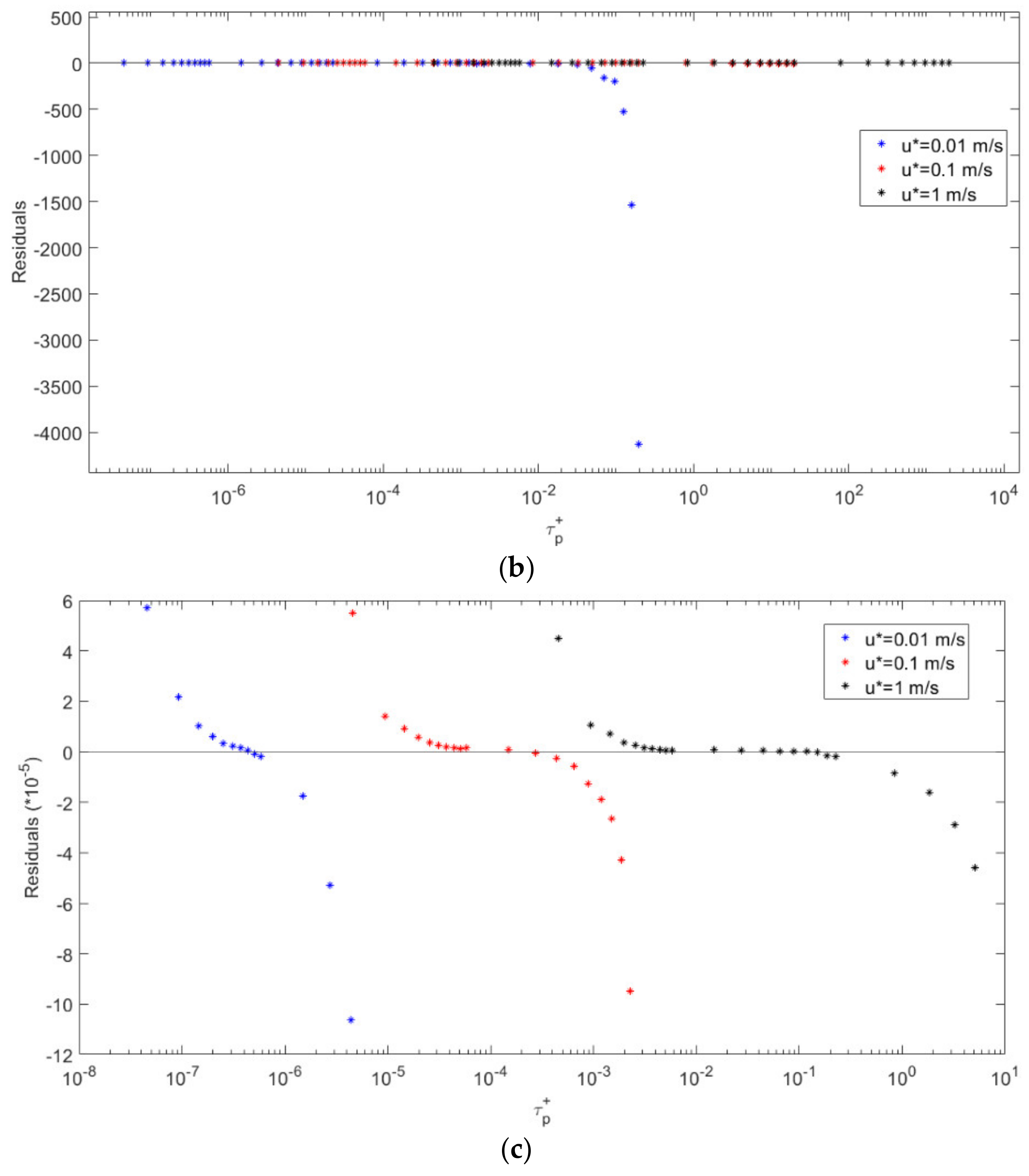
3.4. The Effect of Parameterization on V+d Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Unit | Description |
| C | m−3 | Particle concentration within the boundary layer. In dimensionless form C+ = C/C∞ C∞ is the particle concentration above the boundary layer or far away from the surface |
| Cc | -- | Cunningham slip correction coefficient |
| D | m2 s−1 | Brownian diffusivity of the particle, D = kB T Cc/3πμ Dp in dimensionless form D+ = (εp + D)/ν |
| Dp | m | Particle diameter, in dimensionless form D+p = Dp u*/ν |
| J | m−2 s−1 | Total particle flux across the concentration boundary layer towards the surface. is particle flux due to Brownian and Eddy diffusions. is the particle flux across the concentration boundary layer due to other mechanisms to be included in the model in the future |
| kB | Joule/K | Boltzmann constant |
| mp | kg | Particle mass |
| rp | m | Particle radius, in dimensionless form r+p = rp u*/ν |
| T | K | Absolute temperature |
| u* | m s−1 | Friction velocity |
| Vd | m s−1 | Deposition velocity onto a surface, in dimensionless form V+d = Vd/u* |
| m2 s−2 | Air wall normal fluctuating velocity intensity, in dimensionless [16,22]: | |
| m2 s−2 | Particle wall normal fluctuating velocity intensity [31]: | |
| y | m | Vertical distance from the surface, in dimensionless form y+ = y u*/ν |
| y0 | m | Distance from the surface at which the particle with a radius rp is deposited, in dimensionless form y+o = y0 u*/ν |
| ycbl | m | Depth of the concentration boundary layer above which dC/dy = 0 in dimensionless form y+cbl = ycbl u*/ν |
| μ | kg m−1 s−1 | Dynamic viscosity of the fluid |
| ρ | kg m−3 | Fluid density |
| τL | s | Lagrangian time-scale of the fluid [31]: |
| τp | s | Particle relaxation time |
| εp | m2 s−1 | Eddy diffusivity of the particle. For relatively small particles and homogeneous isotropic turbulence [18] For any particle size [21,29] |
| ν | m2 s−1 | Kinematic viscosity of the fluid, ν = μ/ρ |
| ντ | m2 s−1 | Air turbulent viscosity. For smooth surfaces it is [17] and for rough surfaces it is [16] |
References
- Bozlaker, A.; Muezzinoglu, A.; Odabasi, M. Atmospheric concentrations, dry deposition and air-soil exchange of polycyclic aromatic hydrocarbons (PAHs) in an industrial region in Turkey. J. Hazard Mater. 2008, 153, 1093–1102. [Google Scholar] [CrossRef] [PubMed]
- El-Batsh, H. Modelling Particle Deposition on Compressor and Turbine Blades. Ph.D. Thesis, Vienna University of Technology, Vienna, Austria, 2001. [Google Scholar]
- Liu, B.Y.H.; Ahn, K.H. Particle Deposition on Semiconductor Wafers. Aerosol Sci. Technol. 1987, 6, 215–224. [Google Scholar] [CrossRef]
- Lobo, P.; Durdina, L.; Brem, B.T.; Crayford, A.P.; Johnson, M.P.; Smallwood, G.J.; Siegerist, F.; Williams, P.I.; Black, E.A.; Llamedo, A.; et al. Comparison of Standardized Sampling and Measurement Reference Systems for Aircraft Engine Non-Volatile Particulate Matter Emissions. J. Aerosol Sci. 2020, 145, 105557. [Google Scholar] [CrossRef]
- Pui, D.Y.H.; Ye, Y.; Liu, B.Y.H. Experimental Study of Particle Deposition on Semiconductor Wafers. Aerosol Sci. Technol. 1990, 12, 795–804. [Google Scholar] [CrossRef]
- Song, L.; Elimelech, M. Particle Deposition onto a Permeable Surface in Laminar Flow. J. Colloid Interface Sci. 1995, 173, 165–180. [Google Scholar] [CrossRef]
- Tong, X.; Dong, J.; Shang, Y.; Inthavong, K.; Tu, J. Effects of Nasal Drug Delivery Device and Its Orientation on Sprayed Particle Deposition in a Realistic Human Nasal Cavity. Comput. Biol. Med. 2016, 77, 40–48. [Google Scholar] [CrossRef] [PubMed]
- Tong, Z.X.; Li, M.J.; He, Y.L.; Tan, H.Z. Simulation of Real Time Particle Deposition and Removal Processes on Tubes by Coupled Numerical Method. Appl. Energy 2017, 185, 2181–2193. [Google Scholar] [CrossRef]
- Andersson, K.G.; Roed, J.; Byrne, M.A.; Hession, H. Deposition of contaminant aerosol on human skin. J. Environ. Radioact. 2006, 85, 182–195. [Google Scholar] [CrossRef]
- Casal, J.; Planas-Cuchi, E.; Moreso, J.M.; Casal, J. Forecasting virus atmospherical dispersion. Studies with foot-and-mouth disease. J. Hazard. Mater. 1995, 43, 229–244. [Google Scholar] [CrossRef]
- Karlsson, E.; Huber, U. Influence of desorption on the indoor concentration of toxic gases. J. Hazard. Mater. 1996, 49, 15–27. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Zhang, Z.; Li, Z. Modeling airflow and particle transport/deposition in pulmonary airways. Respir. Physiol. Neurobiol. 2008, 163, 128–138. [Google Scholar] [CrossRef] [PubMed]
- Londah, J.; Pagels, J.; Swietlicki, E.; Zhou, J.; Ketzel, M.; Massling, A.; Bohgard, M. A set-up for field studies of respiratory tract deposition of fine and ultrafine particles in humans. J. Aerosol Sci. 2006, 37, 1152–1163. [Google Scholar] [CrossRef]
- Goosse, H.; Barriat, P.Y.; Lefebvre, W.; Loutre, M.F.; Zunz, V. Introduction to Climate Dynamics and Climate Modeling. Online Textbook. Available online: http://www.climate.be/textbook (accessed on 17 July 2022).
- Hussein, T.; Smolik, J.; Kerminen, V.M.; Kulmala, M. Modeling Dry Deposition of Aerosol Particles onto Rough Surfaces. Aerosol Sci. Technol. 2012, 46, 44–59. [Google Scholar] [CrossRef] [Green Version]
- Guha, A. A Unified Eulerian Theory of Turbulent Deposition to Smooth and Rough Surfaces. J. Aerosol Sci. 1997, 28, 1517–1537. [Google Scholar] [CrossRef]
- Corner, J.; Pendlebury, E.D. The Coagulation and Deposition of a Stirred Aerosol. Proc. Phys. Soc. Sect. B 1951, 64, 645–654. [Google Scholar] [CrossRef]
- Lai, A.C.K.; Nazaroff, W.W. Modeling Indoor Particle Deposition from Turbulent Flow onto Smooth Surfaces. J. Aerosol Sci. 2000, 31, 463–476. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, J. Modeling Particle Deposition from Fully Developed Turbulent Flow in Ventilation Duct. Atmos. Environ. 2006, 40, 457–466. [Google Scholar] [CrossRef]
- Hussein, T.; Ibrahim, S.; Malek, S. Basic Concepts and Development of Dry Deposition Modelling. Jordan J. Phys. 2019, 12, 113–132. [Google Scholar]
- Zhao, B.; Wu, J. Modeling Particle Deposition onto Rough Walls in Ventilation Duct. Atmos. Environ. 2006, 40, 6918–6927. [Google Scholar] [CrossRef]
- Kallio, G.A.; Reeks, M.W. A Numerical Simulation of Particle Deposition in Turbulent Boundary Layers. Int. J. Multiph. Flow 1989, 15, 433–446. [Google Scholar] [CrossRef]
- Kim, J.; Moin, P.; Moser, R. Turbulence Statistics in Fully Developed Channel Flow at Low Reynolds Number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef] [Green Version]
- Crump, J.G.; Flagan, R.C.; Seinfeld, J.H. Particle Wall Loss Rates in Vessels. Aerosol Sci. Technol. 1982, 2, 303–309. [Google Scholar] [CrossRef]
- McMurry, P.H.; Rader, D.J. Aerosol Wall Losses in Electrically Charged Chambers. Aerosol Sci. Technol. 1985, 4, 249–268. [Google Scholar] [CrossRef] [Green Version]
- Nazaroff, W.W.; Cass, G.R. Mathematical Modeling of Indoor Aerosol Dynamics. Environ. Sci. Technol. 1984, 23, 157–166. [Google Scholar] [CrossRef]
- Bejan, A. Convection Heat Transfer, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Hinze, J.O. Turbulence, 2nd ed.; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Hinds, W.C. Aerosol Technology, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Johansen, S.T. The Deposition of Particles on Vertical Walls. Int. J. Multiph. Flow 1991, 17, 355–376. [Google Scholar] [CrossRef]
- Boyce, W.E.; DiPrima, R.C. Elementary Differential Equations and Boundary Value Problems, 10th ed.; John Wiley & Sons: New York, NY, USA, 2012. [Google Scholar]
- Piskunov, V.N. Parameterization of Aerosol Dry Deposition Velocities onto Smooth and Rough Surfaces. J. Aerosol Sci. 2009, 40, 664–679. [Google Scholar] [CrossRef]
- Pidwirny, M. Surface Area of Our Planet Covered by Oceans and Continents; University of British Columbia: Kelowna, BC, Canada, 2006. [Google Scholar]




| Computer | Processor (CPU) | Memory (RAM) | Storage |
|---|---|---|---|
| PC-1 | Core i7 10th, generation | 8 GB | 256 SSD |
| PC-2 | Core i5 2nd, generation | 4 GB | 256 SSD |
| PC-3 | AMD RYZON 3, 3rd generation | 4 GB | 256 SSD |
| PC-4 | Core i7 3rd, generation | 8 GB | 250 SSD |
| PC | Dp (µm) | Calculation Time (s) | % Time | Time Difference (s) | |
|---|---|---|---|---|---|
| Without Parameterization | With Parameterization | ||||
| PC-1 | 0.01 | 0.60 | 0.15 | 75% | 0.45 |
| 0.1 | 0.67 | 0.17 | 75% | 0.50 | |
| 1 | 0.63 | 0.15 | 76% | 0.48 | |
| 10 | 0.61 | 0.13 | 78% | 0.48 | |
| 100 | 0.56 | 0.14 | 74% | 0.42 | |
| PC-2 | 0.01 | 1.6 | 0.38 | 76% | 1.2 |
| 0.1 | 1.5 | 0.40 | 73% | 1.1 | |
| 1 | 1.5 | 0.38 | 74% | 1.1 | |
| 10 | 1.4 | 0.37 | 74% | 1.0 | |
| 100 | 1.3 | 0.36 | 72% | 0.94 | |
| PC-3 | 0.01 | 2.5 | 0.52 | 79% | 2.0 |
| 0.1 | 2.8 | 0.52 | 81% | 2.3 | |
| 1 | 2.3 | 0.51 | 78% | 1.8 | |
| 10 | 2.4 | 0.48 | 80% | 1.9 | |
| 100 | 2.7 | 0.46 | 83% | 2.2 | |
| PC-4 | 0.01 | 1.4 | 0.31 | 78% | 1.1 |
| 0.1 | 1.4 | 0.28 | 80% | 1.1 | |
| 1 | 1.3 | 0.30 | 77% | 1.0 | |
| 10 | 1.3 | 0.26 | 80% | 1.0 | |
| 100 | 1.3 | 0.25 | 80% | 1.0 | |
| PC | Dp (µm) | Calculation Time (s) | % Time | Time Difference (s) | |
|---|---|---|---|---|---|
| Without Parameterization | With Parameterization | ||||
| PC-1 | 0.01 | 0.70 | 0.10 | 86% | 0.60 |
| 0.1 | 0.66 | 0.15 | 77% | 0.51 | |
| 1 | 0.63 | 0.13 | 79% | 0.50 | |
| 10 | 0.60 | 0.13 | 78% | 0.47 | |
| 100 | 0.58 | 0.13 | 77% | 0.45 | |
| PC-2 | 0.01 | 1.6 | 0.40 | 76% | 1.2 |
| 0.1 | 1.5 | 0.37 | 75% | 1.1 | |
| 1 | 1.4 | 0.36 | 75% | 1.0 | |
| 10 | 1.4 | 0.40 | 70% | 1.0 | |
| 100 | 1.2 | 0.37 | 68% | 0.8 | |
| PC-3 | 0.01 | 2.7 | 0.49 | 82% | 2.2 |
| 0.1 | 2.2 | 0.48 | 78% | 1.7 | |
| 1 | 2.4 | 0.46 | 81% | 1.9 | |
| 10 | 2.2 | 0.50 | 78% | 1.7 | |
| 100 | 2.7 | 0.55 | 79% | 2.2 | |
| PC-4 | 0.01 | 1.5 | 0.27 | 81% | 1.2 |
| 0.1 | 1.3 | 0.25 | 81% | 1.0 | |
| 1 | 1.8 | 0.24 | 87% | 1.6 | |
| 10 | 1.2 | 0.30 | 74% | 0.9 | |
| 100 | 1.4 | 0.26 | 82% | 1.1 | |
| PC | Dp (µm) | Calculation Time (s) | % Time | Time Difference (s) | |
|---|---|---|---|---|---|
| Without Parameterization | With Parameterization | ||||
| PC-1 | 0.01 | 0.68 | 0.13 | 81% | 0.55 |
| 0.1 | 0.65 | 0.13 | 80% | 0.52 | |
| 1 | 0.75 | 0.13 | 83% | 0.62 | |
| 10 | 0.62 | 0.13 | 79% | 0.49 | |
| 100 | 0.59 | 0.13 | 78% | 0.46 | |
| PC-2 | 0.01 | 1.6 | 0.41 | 74% | 1.2 |
| 0.1 | 1.6 | 0.38 | 76% | 1.2 | |
| 1 | 1.5 | 0.39 | 74% | 1.1 | |
| 10 | 1.2 | 0.38 | 69% | 0.82 | |
| 100 | 1.1 | 0.26 | 77% | 0.84 | |
| PC-3 | 0.01 | 2.7 | 0.46 | 83% | 2.2 |
| 0.1 | 2.4 | 0.50 | 79% | 1.9 | |
| 1 | 2.6 | 0.53 | 80% | 2.1 | |
| 10 | 2.4 | 0.45 | 81% | 2.0 | |
| 100 | 2.3 | 0.44 | 81% | 1.9 | |
| PC-4 | 0.01 | 1.2 | 0.26 | 78% | 0.94 |
| 0.1 | 1.2 | 0.24 | 80% | 1.0 | |
| 1 | 1.5 | 0.26 | 83% | 1.2 | |
| 10 | 1.3 | 0.30 | 77% | 1.0 | |
| 100 | 1.7 | 0.26 | 85% | 1.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nofal, O.M.M.; Al-Jaghbeer, O.; Bakri, Z.; Hussein, T. A Simple Parameterization to Enhance the Computational Time in the Three Layer Dry Deposition Model for Smooth Surfaces. Atmosphere 2022, 13, 1190. https://doi.org/10.3390/atmos13081190
Nofal OMM, Al-Jaghbeer O, Bakri Z, Hussein T. A Simple Parameterization to Enhance the Computational Time in the Three Layer Dry Deposition Model for Smooth Surfaces. Atmosphere. 2022; 13(8):1190. https://doi.org/10.3390/atmos13081190
Chicago/Turabian StyleNofal, Omar M. M., Omar Al-Jaghbeer, Zaid Bakri, and Tareq Hussein. 2022. "A Simple Parameterization to Enhance the Computational Time in the Three Layer Dry Deposition Model for Smooth Surfaces" Atmosphere 13, no. 8: 1190. https://doi.org/10.3390/atmos13081190
APA StyleNofal, O. M. M., Al-Jaghbeer, O., Bakri, Z., & Hussein, T. (2022). A Simple Parameterization to Enhance the Computational Time in the Three Layer Dry Deposition Model for Smooth Surfaces. Atmosphere, 13(8), 1190. https://doi.org/10.3390/atmos13081190






