Performance Evaluation of the RANS Models in Predicting the Pollutant Concentration Field within a Compact Urban Setting: Effects of the Source Location and Turbulent Schmidt Number
Abstract
1. Introduction
2. Fundamentals and Governing Equations
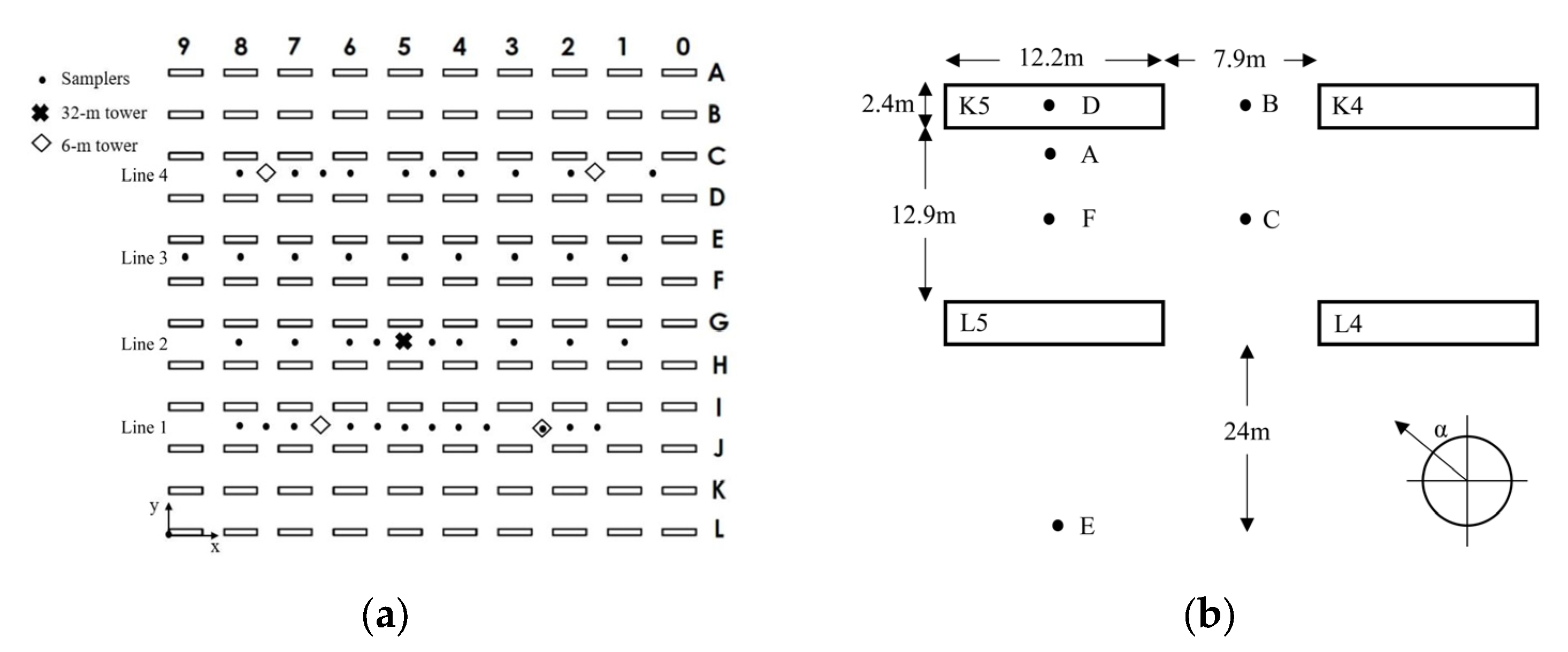
3. Description of Case Studies
- Source type A: located 1 m upstream of container J3 within the array ().
- Source type D: located on the rooftop of container J9 within the array ().
- Source type E: located 24 m upstream of container L1 outside the array ().
- Source type F: located on the road, centered between containers K8 and L8 long sides ().
4. CFD Model Description
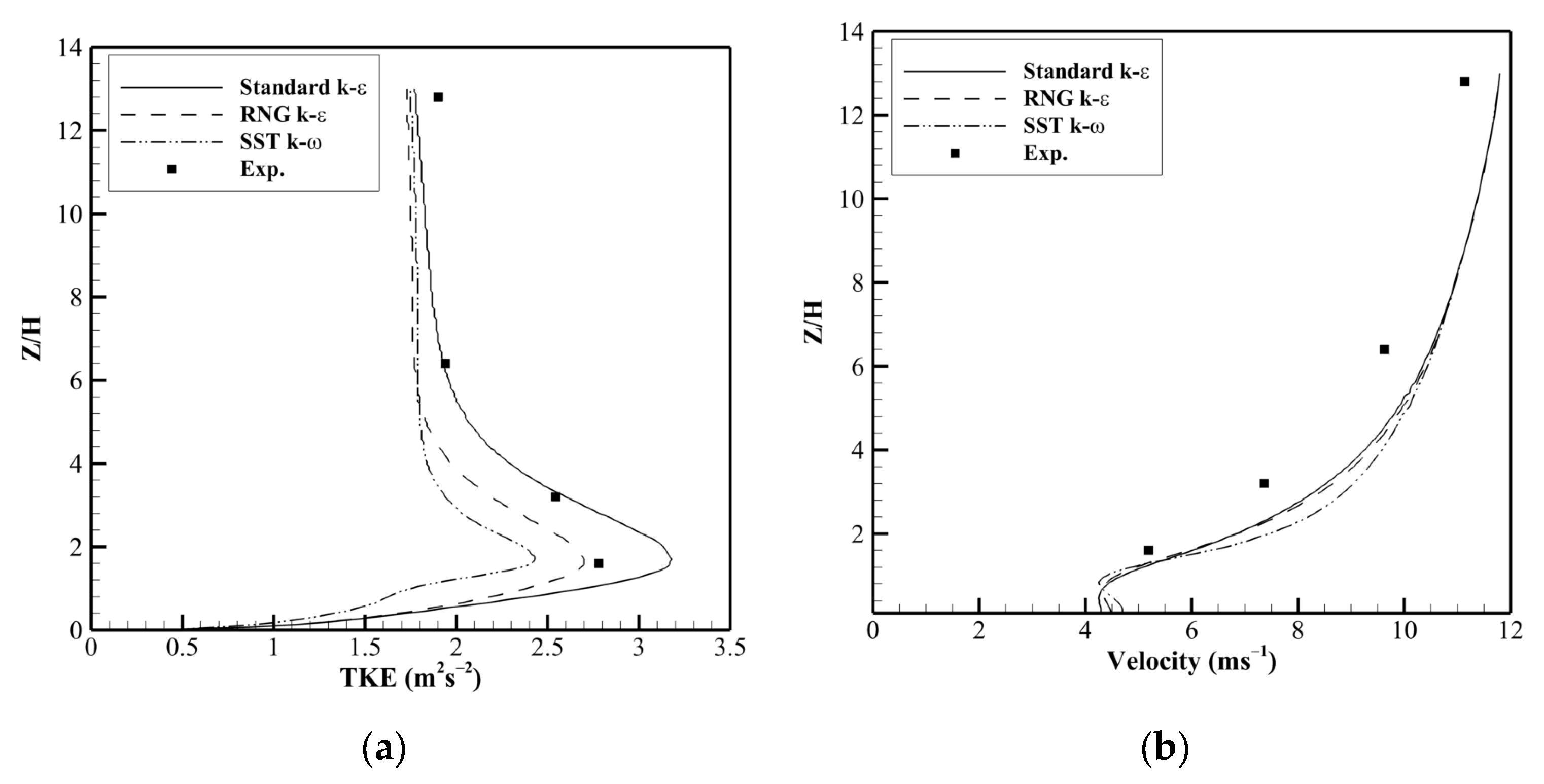
4.1. General Settings
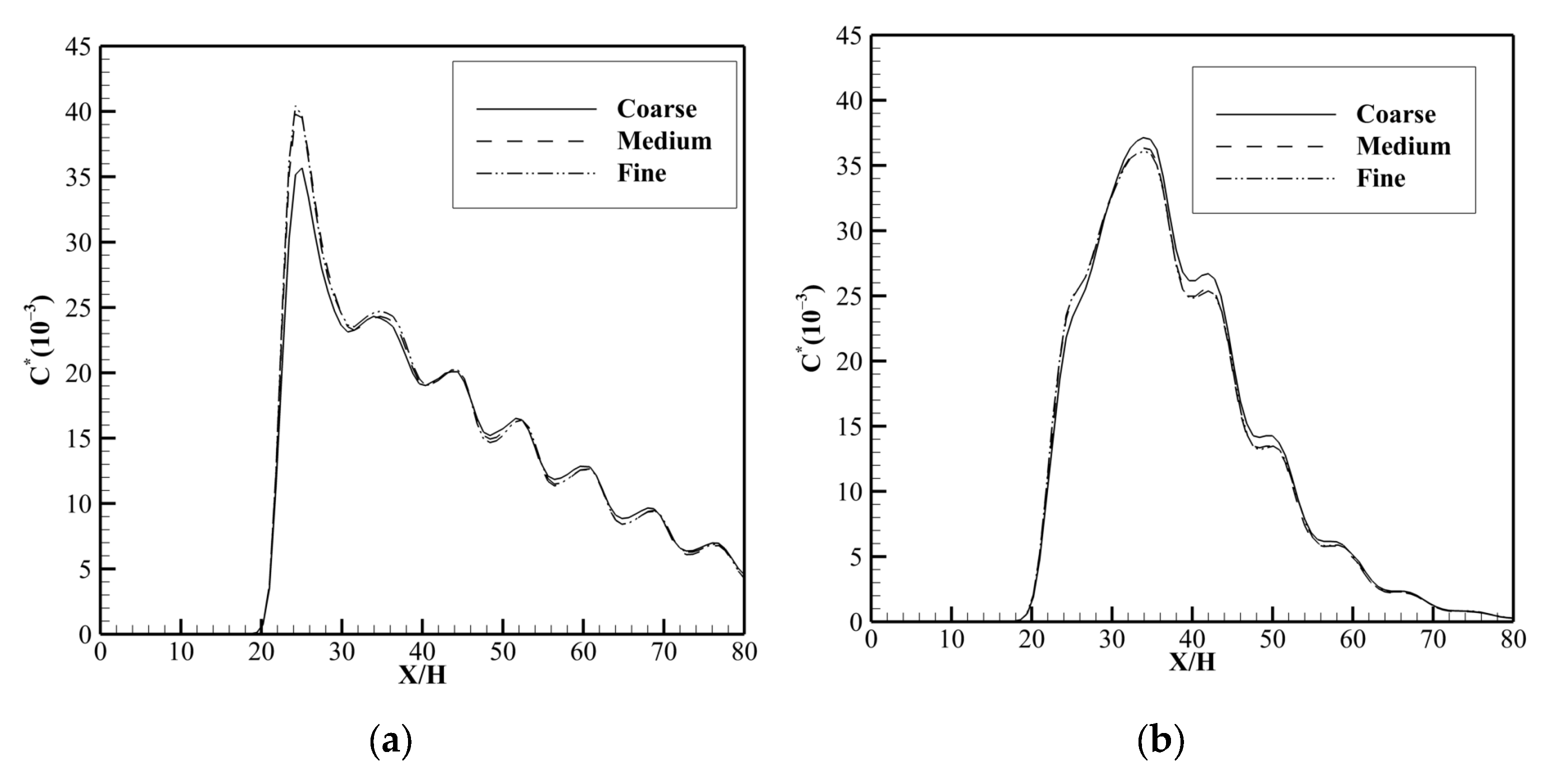
4.2. Grid Sensitivity Study
5. Statistical Analysis Method
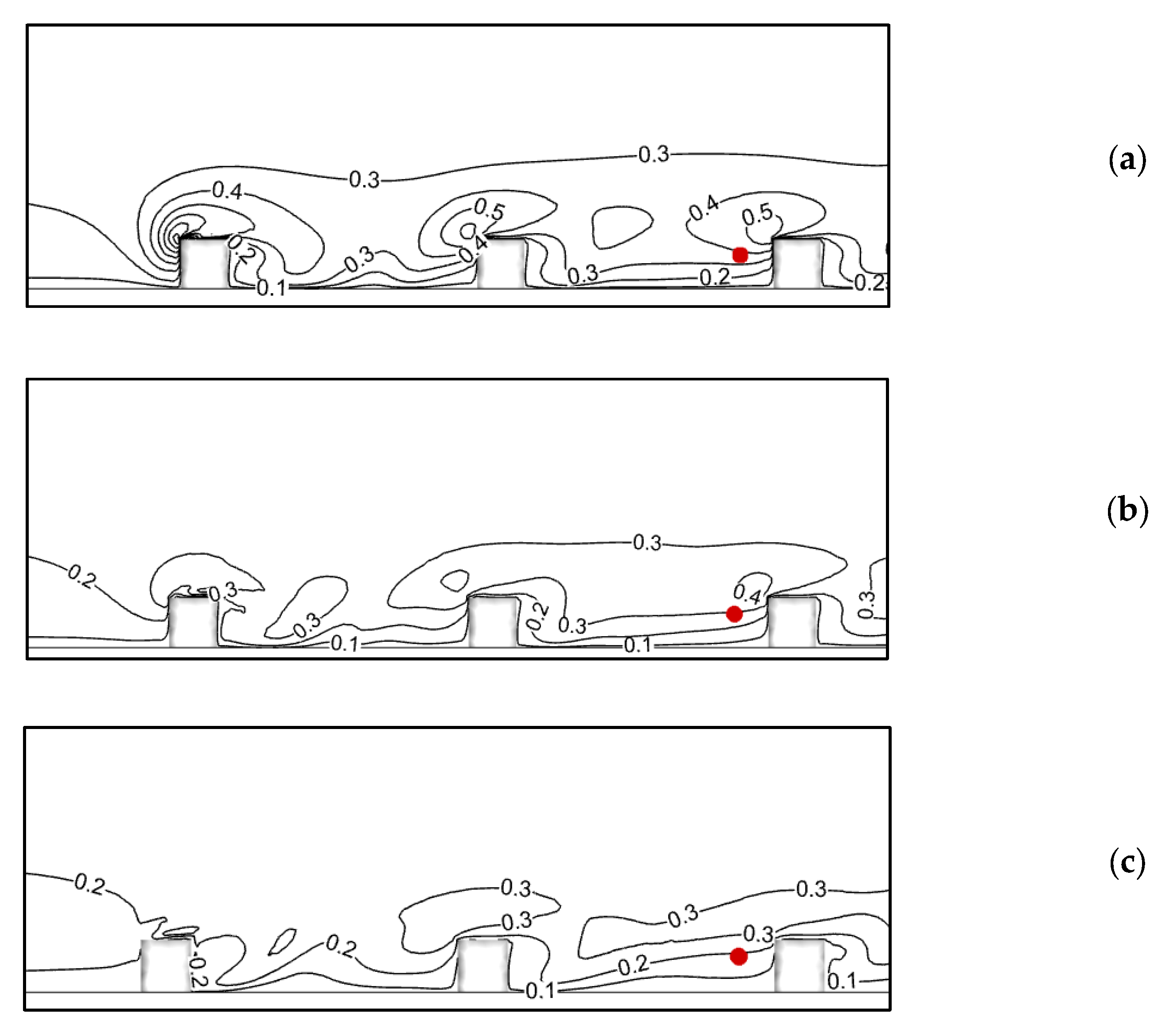
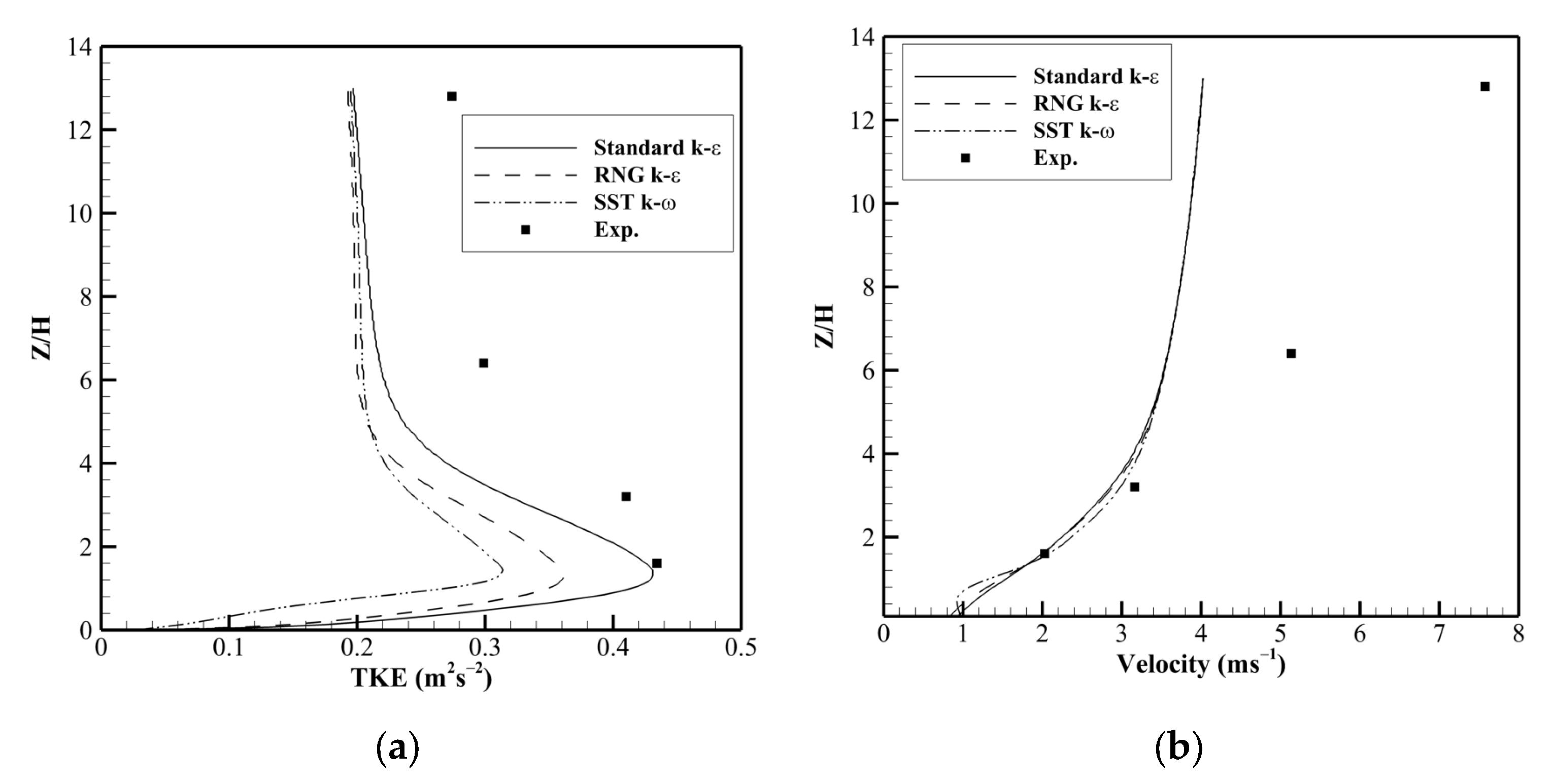
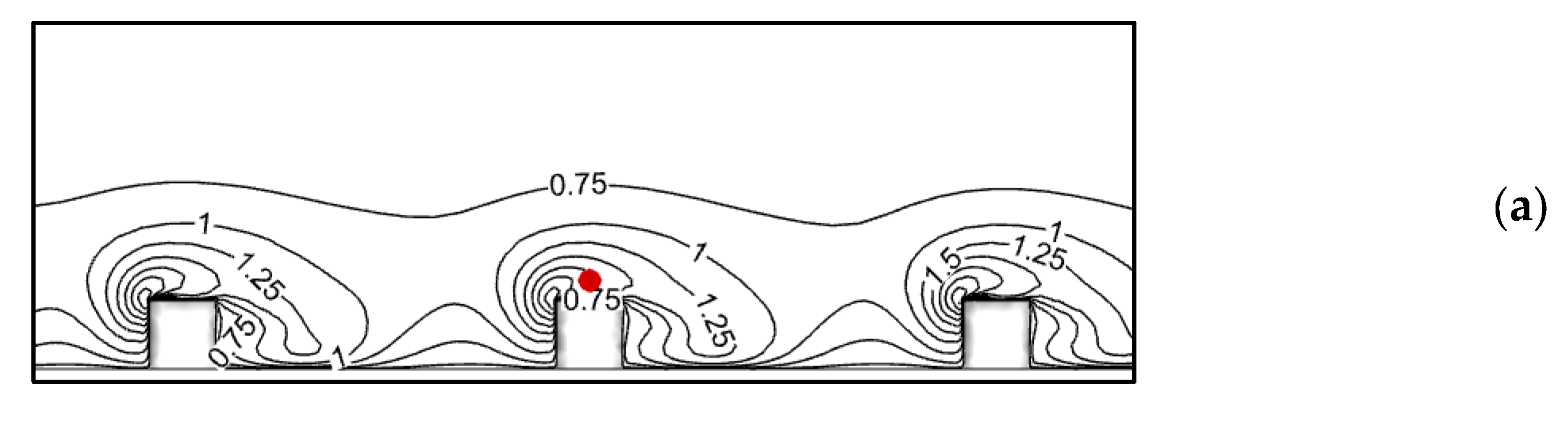
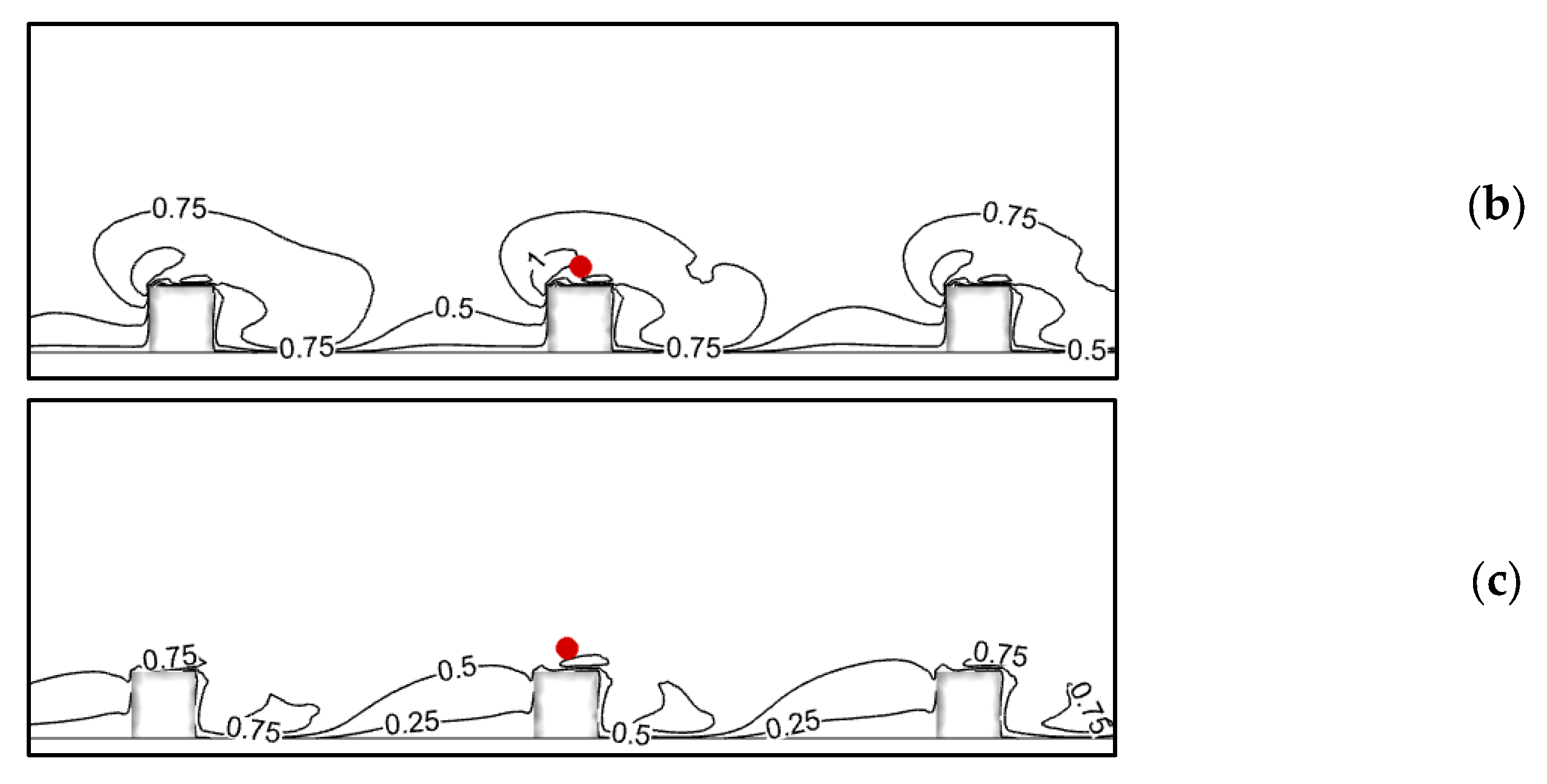
6. Results and Discussion
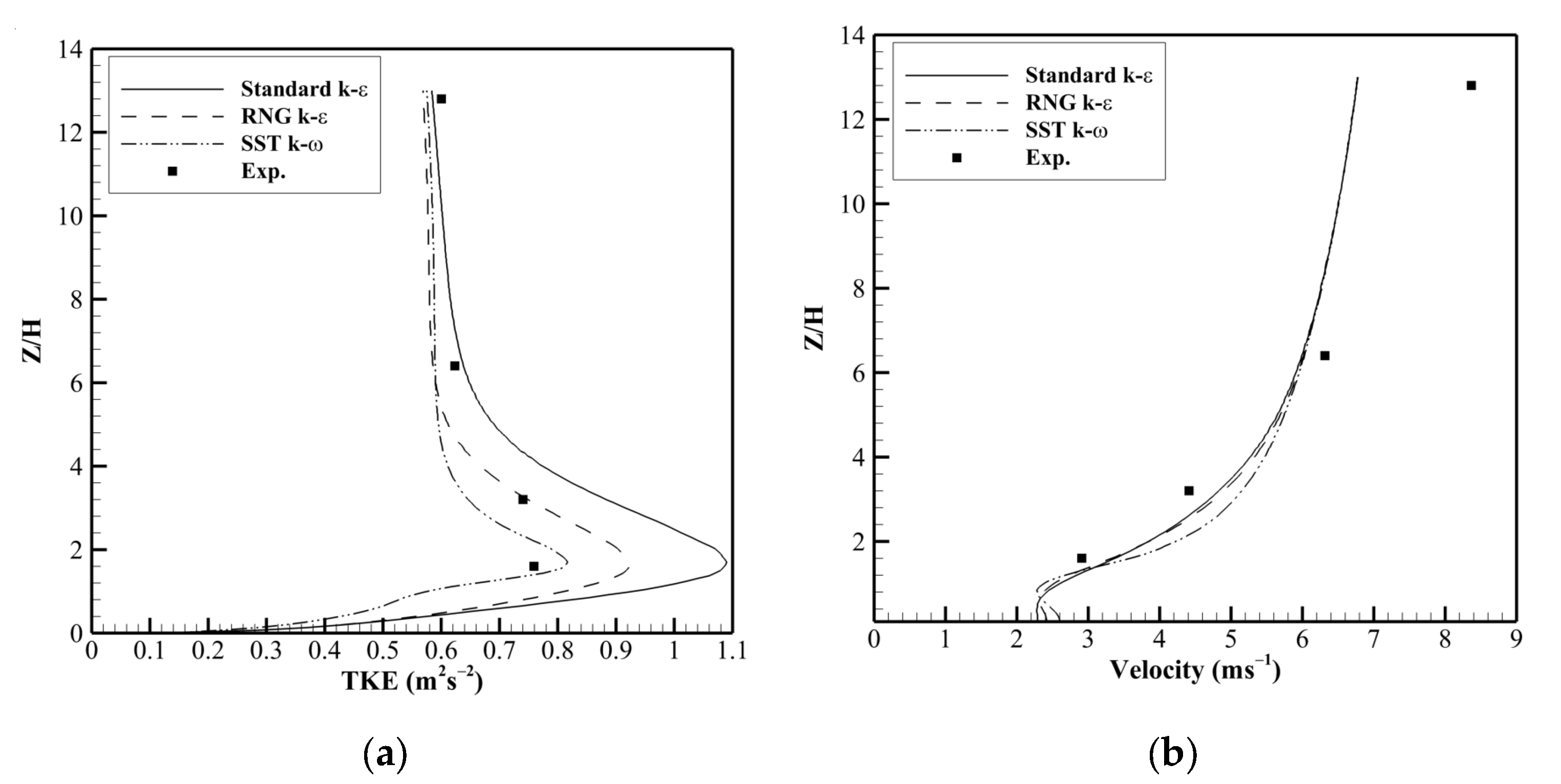
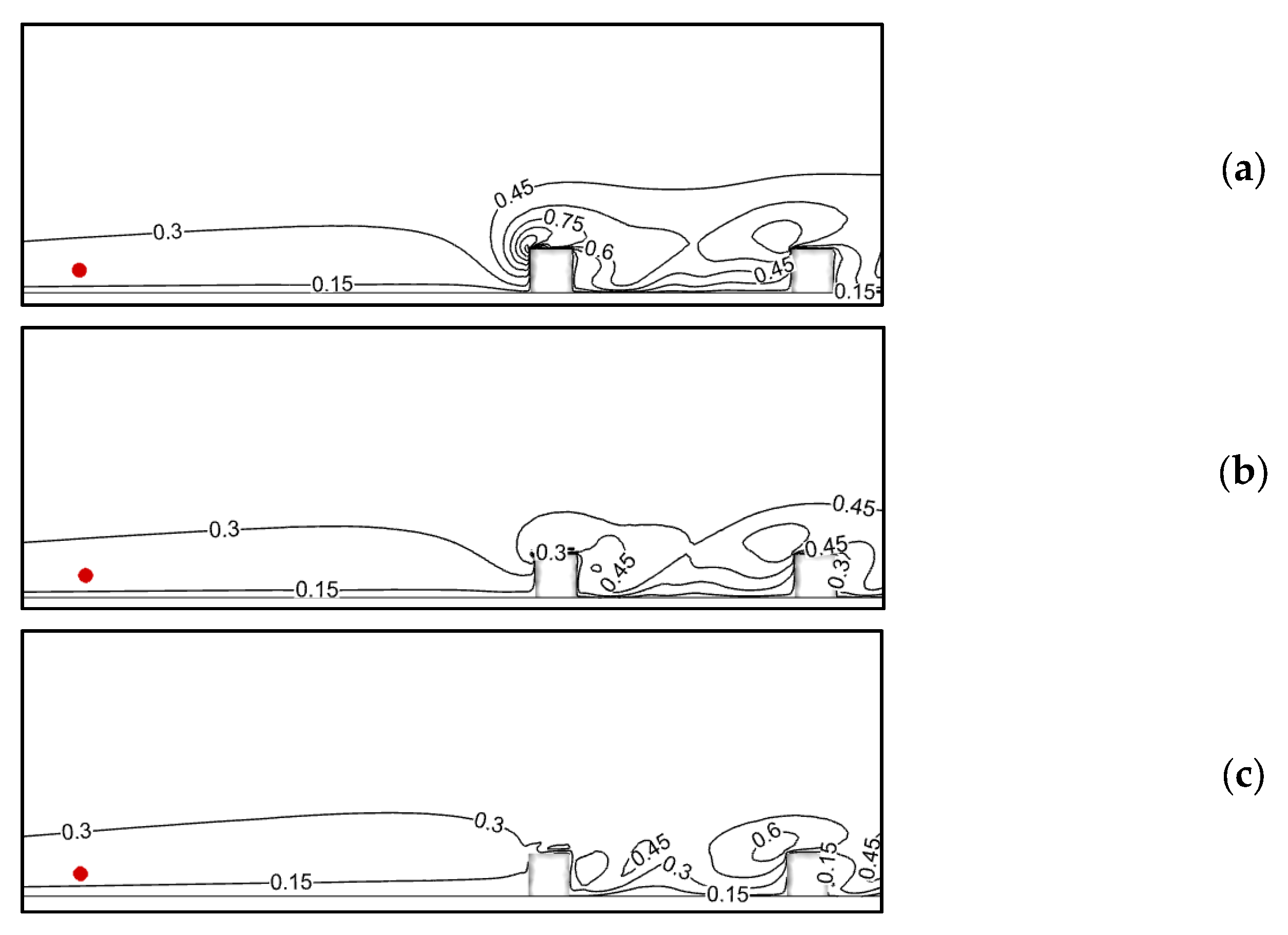
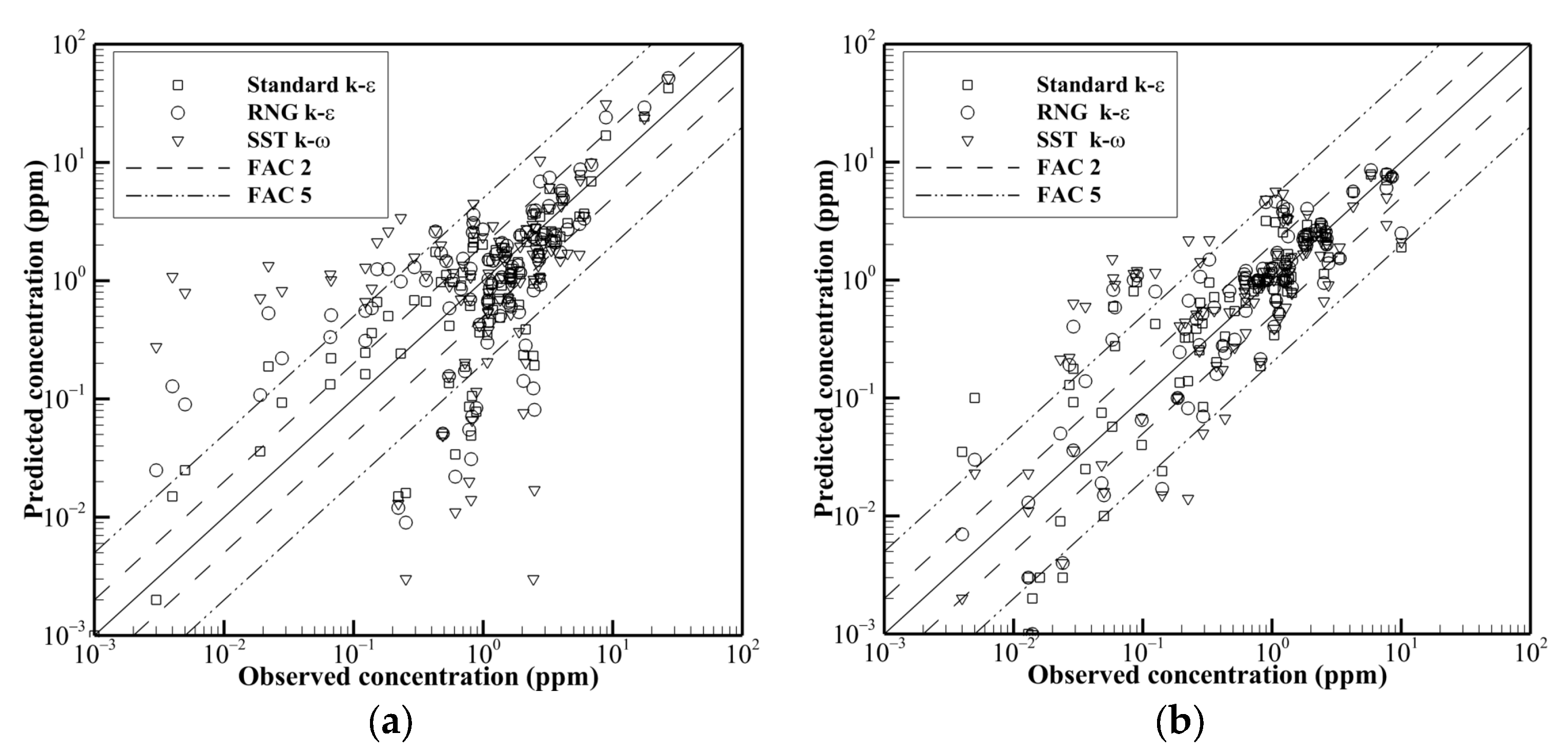
6.1. Performance Evaluation of Closure Models: Source Location Effects
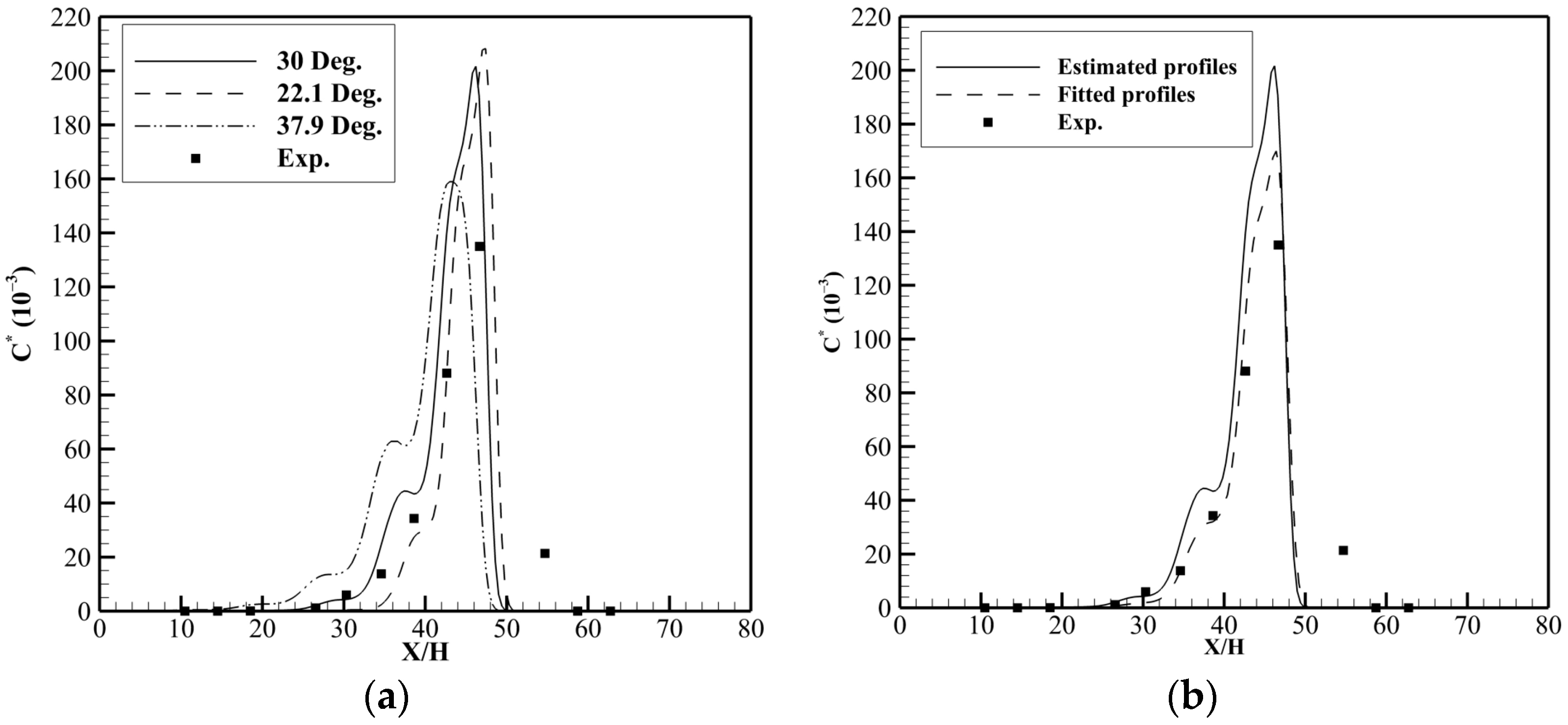
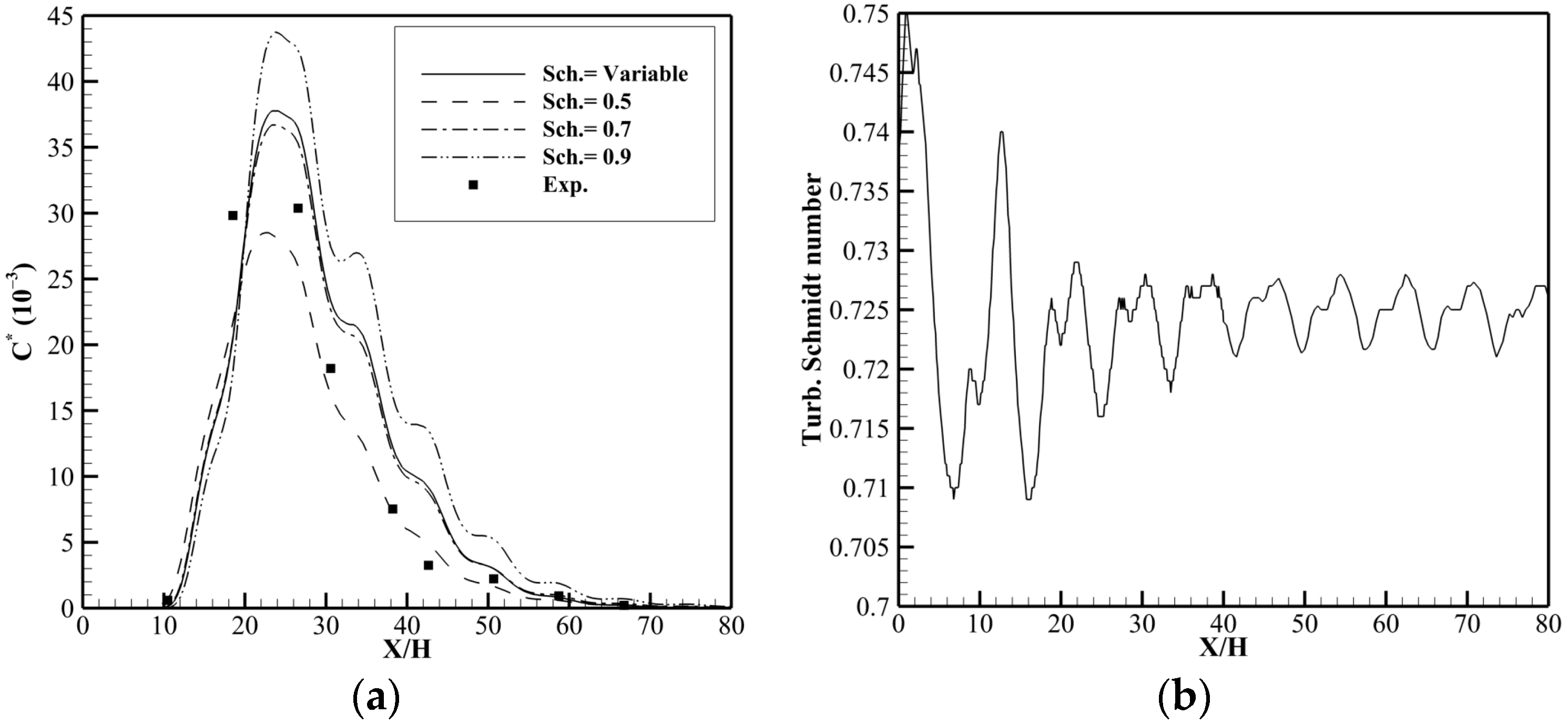
6.2. Turbulent Schmidt Number
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- 2018 Revision of World Urbanization Prospects, Technical Report; United Nations Department of Economics and Social Affairs (UNDESA): New York, NY, USA, 2018.
- Wilson, D.J.; Britter, R.E. Estimates of building surface concentrations from nearby point sources. Atmos. Environ. 1982, 16, 2631–2646. [Google Scholar] [CrossRef]
- ASHRAE. Airflow around the buildings. In ASHRAE Fundamental Handbook; American Society of Heating, Refrigerating and Air-conditioning Engineers: Atlanta, GA, USA, 2009. [Google Scholar]
- Hajra, B.; Stathopoulos, T.; Bahloul, A. Assessment of pollutant dispersion from rooftop stacks: ASHRAE, ADMS and wind tunnel simulation. Build. Environ. 2010, 45, 2768–2777. [Google Scholar] [CrossRef]
- Holmes, N.S.; Morawska, L. A review of dispersion modeling and its application to the dispersion of particles: An overview of different dispersion models available. Atmos. Environ. 2006, 40, 5902–5928. [Google Scholar] [CrossRef]
- Riddle, A.; Carruthers, D.; Sharpe, A.; McHugh, C.; Stocker, J. Comparisons between FLUENT and ADMS for atmospheric dispersion modeling. Atmos. Environ. 2004, 38, 1029–1038. [Google Scholar] [CrossRef]
- Lateb, M.; Masson, C.; Stathopoulos, T.; Bedard, C. Effect of stack height and exhaust velocity on pollutant dispersion in the wake of a building. Atmos. Environ. 2011, 45, 5150–5163. [Google Scholar] [CrossRef]
- Li, Z.; Ming, T.; Liu, S.; Peng, C.; Richter, R.; Li, W.; Zhang, H.; Wen, C.Y. Review on pollutant dispersion in urban areas-part A: Effects of mechanical factors and urban morphology. Build. Environ. 2021, 190, 107534. [Google Scholar] [CrossRef]
- Du, Y.; Blocken, B.; Abbasi, S.; Pirker, S. Efficient and high-resolution simulation of pollutant dispersion in complex urban environments by island-based recurrence CFD. Environ. Model. Softw. 2021, 145, 105172. [Google Scholar] [CrossRef]
- Ricci, A.; Kalkman, I.; Blocken, B.; Burlando, M.; Freda, A.; Repetto, M. Local-scale forcing effects on wind flows in an urban environment: Impact of geometrical simplifications. J. Wind. Eng. Ind. Aerodyn. 2017, 170, 238–255. [Google Scholar] [CrossRef]
- Lee, D.S.H.; Mauree, D. RANS based CFD simulations for urban wind prediction–field verification against MoTUS. Wind. Struct. 2021, 33, 29–40. [Google Scholar]
- Silva, F.T.; Reis, N.C.; Santos, J.M.; Goulart, E.V.; Alvarez, C.E. The impact of urban block typology on pollutant dispersion. J. Wind. Eng. Ind. Aerodyn. 2021, 210, 104524. [Google Scholar] [CrossRef]
- Mattar, S.J.; Kavian Nezhad, M.R.; Versteege, M.; Lange, C.F.; Fleck, B.A. Validation Process for Rooftop Wind Regime CFD Model in Complex Urban Environment Using an Experimental Measurement Campaign. Energies 2021, 14, 2497. [Google Scholar] [CrossRef]
- Wilson, D.J.; Lamb, B.K. Dispersion of exhaust gases from roof-level stacks and vents on a laboratory building. Atmos. Environ. 1994, 28, 3099–3111. [Google Scholar] [CrossRef]
- Yang, C.; Hong, Z.; Chen, j.; Xu, L.; Zhuang, M.; Huang, Z. Characteristics of secondary organic aerosols tracers in PM2.5 in three central cities of the Yangtze river delta, China. Chemosphere 2022, 293, 133637. [Google Scholar] [CrossRef]
- Dai, Y.; Mak, C.M.; Hang, J.; Zhang, F.; Ling, H. Scaled outdoor experimental analysis of ventilation and interunit dispersion with wind and buoyancy effects in street canyons. Energy Build. 2022, 255, 111688. [Google Scholar] [CrossRef]
- Lateb, M.; Meroney, R.N.; Yataghene, M.; Fellouah, H.; Saleh, F.; Boufadel, B.C. On the use of numerical modeling for near-field pollutant dispersion in urban environment. Environ. Pollut. 2016, 208, 271–283. [Google Scholar] [CrossRef]
- Hajra, B.; Stathopoulos, T.; Bahloul, A. A wind tunnel study of the effects of adjacent buildings on near-field pollutant dispersion from rooftop emissions in an urban environment. J. Wind. Eng. Ind. Aerodyn. 2013, 119, 133–145. [Google Scholar] [CrossRef]
- Zou, J.; Yu, Y.; Liu, J.; Niu, J.; Chauhan, K.; Lei, C. Field measurement of the urban pedestrian level wind turbulence. Build. Environ. 2021, 194, 107713. [Google Scholar] [CrossRef]
- Lateb, M.; Masson, C.; Stathopoulos, T.; Bedard, C. Numerical simulation of pollutant dispersion around a building complex. Build. Environ. 2010, 45, 1788–1798. [Google Scholar] [CrossRef]
- Mirzaei, P.A. CFD modeling of micro and urban climates: Problems to be solved in the new decade. Sustain. Cities Soc. 2021, 69, 102839. [Google Scholar] [CrossRef]
- Du, Y.; Blocken, B.; Pirkar, S. A novel approach to simulate pollutant dispersion in the built environment: Transport-based recurrence CFD. Build. Environ. 2020, 170, 106604. [Google Scholar] [CrossRef]
- Jiang, G.; Yoshie, R. Side ratio effects on flow and pollutant dispersion around an isolated high-rise building in a turbulent boundary layer. Build. Environ. 2020, 180, 107078. [Google Scholar] [CrossRef]
- Huang, X.; Gao, L.; Guo, D.; Yao, R. Impacts of high-rise building on urban airflows and pollutant dispersion under different temperature stratifications: Numerical investigations. Atmos. Pollut. Res. 2021, 12, 100–112. [Google Scholar] [CrossRef]
- Chavez, M.; Hajra, B.; Stathopoulos, T.; Bahloul, A. Assessment of near-field pollutant dispersion: Effect of upstream buildings. J. Wind. Eng. Ind. Aerodyn. 2012, 104, 509–515. [Google Scholar] [CrossRef]
- Lauriks, T.; Longo, R.; Baetens, D.; Derudi, M.; Parente, A.; Bellemans, A.; Van Beeck, J.; Denys, S. Application of improved CFD modeling for prediction and mitigation of traffic related air pollution hotspots in a realistic urban street. Atmos. Environ. 2021, 246, 118127. [Google Scholar] [CrossRef]
- Salim, S.M.; Buccolieri, R.; Chan, A.; Sabatino, S.D. Numerical simulation of atmospheric pollutant dispersion in an urban street canyon: Comparison between RANS and LES. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 103–113. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, J. CFD simulation of wind flow and pollutant dispersion in a street canyon with traffic flow: Comparison between RANS and LES. Sustain. Cities Soc. 2021, 75, 103307. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. Introduction to Computational Fluid Dynamics, 2nd ed.; Pearson Education Limited: Harlow, UK, 2007. [Google Scholar]
- Narjisse, A.; Abdellatif, K. Assessment of RANS turbulence closure models for predicting airflow in neutral ABL over hilly terrain. Int. Rev. Apllied Sci. Eng. 2021, 12, 238–256. [Google Scholar] [CrossRef]
- Tominaga, Y. Flow around a high-rise building using steady and unsteady RANS CFD; Effect of large-scale fluctuations on the velocity statics. J. Wind. Eng. Ind. Aerodyn. 2015, 142, 93–103. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.; Keshmiri, A. Computational simulation of wind microclimate in complex urban models and mitigation using tress. Buildings 2021, 11, 112. [Google Scholar] [CrossRef]
- Lateb, M.; Masson, C.; Stathopoulos, T.; Bedard, C. Comparison of various types of k–e models for pollutant emissions around a two-building configuration. J. Wind. Eng. Ind. Aerodyn. 2013, 115, 9–21. [Google Scholar] [CrossRef]
- An, K.; Fung, J.C.H. An improved SST k-w model for pollutant dispersion simulations within an isothermal boundary layer. J. Wind. Eng. Ind. Aerodyn. 2018, 179, 369–384. [Google Scholar] [CrossRef]
- Keshavarzian, E.; Jin, R.; Dong, K.; Kwok, K.C.S.; Zhang, Y.; Zhao, M. Effect of pollutant source location on air pollutant dispersion around a high-rise building. Appl. Math. Modeling 2020, 81, 582–602. [Google Scholar] [CrossRef] [PubMed]
- Hassan, A.M.; ELMokadem, A.A.; Megahed, N.A.; Abo Eleinen, O.M. Urban morphology as a passive strategy in promoting outdoor air quality. J. Build. Eng. 2020, 29, 101204. [Google Scholar] [CrossRef]
- Ming, T.; Shi, T.; Han, H.; Liu, S.; Wu, Y.; Li, W. Assessment of pollutant dispersion in urban street canyons based on field synergy theory. Atmos. Pollut. Res. 2021, 12, 341–356. [Google Scholar] [CrossRef]
- Pirhalla, M.; Heist, D.; Perry, S.; Tang, W.; Brouwer, L. Simulations of dispersion through an irregular urban building array Michael. Atmos. Environ. 2021, 258, 118500. [Google Scholar] [CrossRef]
- Elfverson, D.; Lejon, C. Use and scalability of OpenFOAM for wind fields and pollution dispersion with building- and ground-resolving topography. Atmosphere 2021, 12, 1124. [Google Scholar] [CrossRef]
- Blocken, B. LES over RANS in building simulation for outdoor and indoor applications: A foregone conclusion? Build. Simul. 2018, 11, 821–870. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD simulation of the atmospheric boundary layer: Wall function problems. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Turbulent Schmidt numbers for CFD analysis with various types of flowfield. Atmos. Environ. 2007, 41, 8091–8099. [Google Scholar] [CrossRef]
- Di Sabatino, S.; Buccolieri, R.; Pulvirenti, B.; Britter, R. Simulations of pollutant dispersion within idealised urban-type geometries with cfd and integral models. Atmos. Environ. 2007, 41, 8316–8329. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Saathoff, P.; Wang, X. Numerical evaluation of pollutant dispersion in the built environment: Comparisons between models and experiments. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1817–1831. [Google Scholar] [CrossRef]
- Emeis, S. Wind Energy Meteorology Atmospheric Physics for Wind Power Generation, 2nd ed.; Springer International Publishing AG: Zug, Switzerland, 2018; pp. 31–56. [Google Scholar]
- Speranza, A.; Lucarini, V. Environmental science, physical principles and applications. Encycl. Condens. Matter Phys. 2005, 146–156. [Google Scholar]
- Mohamed, M.A.; Wood, D.H. Computational modeling of wind flow over the University of Calgary campus. Wind. Eng. 2016, 40, 228–249. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence modes for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS CFX-Solver Theory Guide Release 2020-R1; ANSYS, Inc.: Canonsburg, PA, USA, 2020; pp. 79–90. [Google Scholar]
- Milliez, M.; Carissimo, B. Numerical simulations of pollutant dispersion in an idealized urban area, for different meteorological conditions. Bound. Layer Meteorol. 2007, 122, 321–342. [Google Scholar] [CrossRef]
- Donnelly, R.P.; Lyons, T.J.; Flassak, T. Evaluation of results of a numerical simulation of dispersion in an idealised urban area for emergency response modelling. Atmos. Environ. 2009, 43, 4416–4423. [Google Scholar] [CrossRef][Green Version]
- Kumar, P.; Feiz, A.; Singh, S.K.; Ngae, P. An urban scale inverse modelling for retrieving unknown elevated emissions with building-resolving simulations. Atmos. Environ. 2016, 140, 135–146. [Google Scholar] [CrossRef]
- Bahlali, M.L.; Dupont, E.; Carissimo, B. Atmospheric dispersion using a Lagrangian stochastic approach: Application to an idealized urban area under neutral and stable meteorological conditions. J. Wind. Eng. Ind. Aerodyn. 2019, 193, 103976. [Google Scholar] [CrossRef]
- Tee, C.; Ng, E.Y.K.; Xu, G. Analysis of transport methodologies for pollutant dispersion modelling in urban environments. J. Environ. Chem. Eng. 2020, 8, 103937. [Google Scholar] [CrossRef]
- Biltoft, C.A. Customer Report for Mock Urban Setting Test; Technical Report, DPG Document No. WDTC-FR-01–121; US Army Dugway Proving Ground: Dugway, UT, USA, 2001. [Google Scholar]
- Yee, E.; Biltoft, C. Concentration fluctuation measurements in a plume dispersing through a regular array of obstacles. Bound. Layer Meteorol. 2004, 111, 363–415. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, K. Quantifying and adjusting the impact of urbanization on the observed surface wind speed over China from 1985 to 2017. Fundam. Res. 2021, 1, 785–791. [Google Scholar] [CrossRef]
- Franke, J.; Hellsten, A.; Schlünzen, H.; Carissimo, B. Best Practice Guideline for the CFD Simulation of Flows in the Urban Environment: COST Action 732 Quality Assurance and Improvement of Microscale Meteorological Models; Meteorological Inst.: Hamburg, Germany, 2007. [Google Scholar]
- Tian, L.; Zhao, N.; Wang, T.; Zhu, W.; Shen, W. Assessment of inflow boundary conditions for RANS simulations of neutral ABL and wind turbine wake flow. J. Wind. Eng. Ind. Aerodyn. 2018, 179, 215–228. [Google Scholar] [CrossRef]
- Richards, P.J.; Hoxey, R.P. Appropriate boundary conditions for computational wind engineering models using the k-ε turbulence model. J. Wind. Eng. Ind. Aerodyn. 1993, 46, 145–153. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Chang, J.C.; Hanna, S.R. Air quality model performance evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical simulation of dispersion around an isolated cubic building: Comparison of various types of k-e models. Atmos. Environ. 2009, 20, 3200–3210. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. CFD simulation of near-field pollutant dispersion in the urban environment: A review of current modeling techniques. Atmos. Environ. 2013, 79, 716–730. [Google Scholar] [CrossRef]
- Murakami, S. Comparison of various turbulence models applied to a bluff body. J. Wind. Eng. Ind. Aerodyn. 1993, 46, 21–36. [Google Scholar] [CrossRef]
- Tominaga, Y.; Stathopoulos, T. Numerical simulation of dispersion around an isolated cubic building: Model evaluation of RANS and LES. Build. Environ. 2010, 45, 2231–2239. [Google Scholar] [CrossRef]
- Hanna, S.R.; Hansen, O.R.; Dharmavaram, S. FLACS CFD air quality model performance evaluation with Kit Fox, MUST, Prairie Grass, and EMU observations. Atmos. Environ. 2004, 38, 4675–4687. [Google Scholar] [CrossRef]
- Koeltzsch, K. The height dependence of the turbulent Schmidt number within the boundary layer. Atmos. Environ. 2000, 34, 1147–1151. [Google Scholar] [CrossRef]
- Longo, R.; Fürsta, M.; Bellemansa, A.; Ferrarottia, M.; Derudib, M.; Parentea, A. CFD dispersion study based on a variable Schmidt formulation for flows around different configurations of ground-mounted buildings. Build. Environ. 2019, 154, 336–347. [Google Scholar] [CrossRef]
- Longo, R.; Bellemansa, A.; Derudib, M.; Parentea, A. A multi-fidelity framework for the estimation of the turbulent Schmidt number in the simulation of atmospheric dispersion. Build. Environ. 2020, 185, 107066. [Google Scholar] [CrossRef]

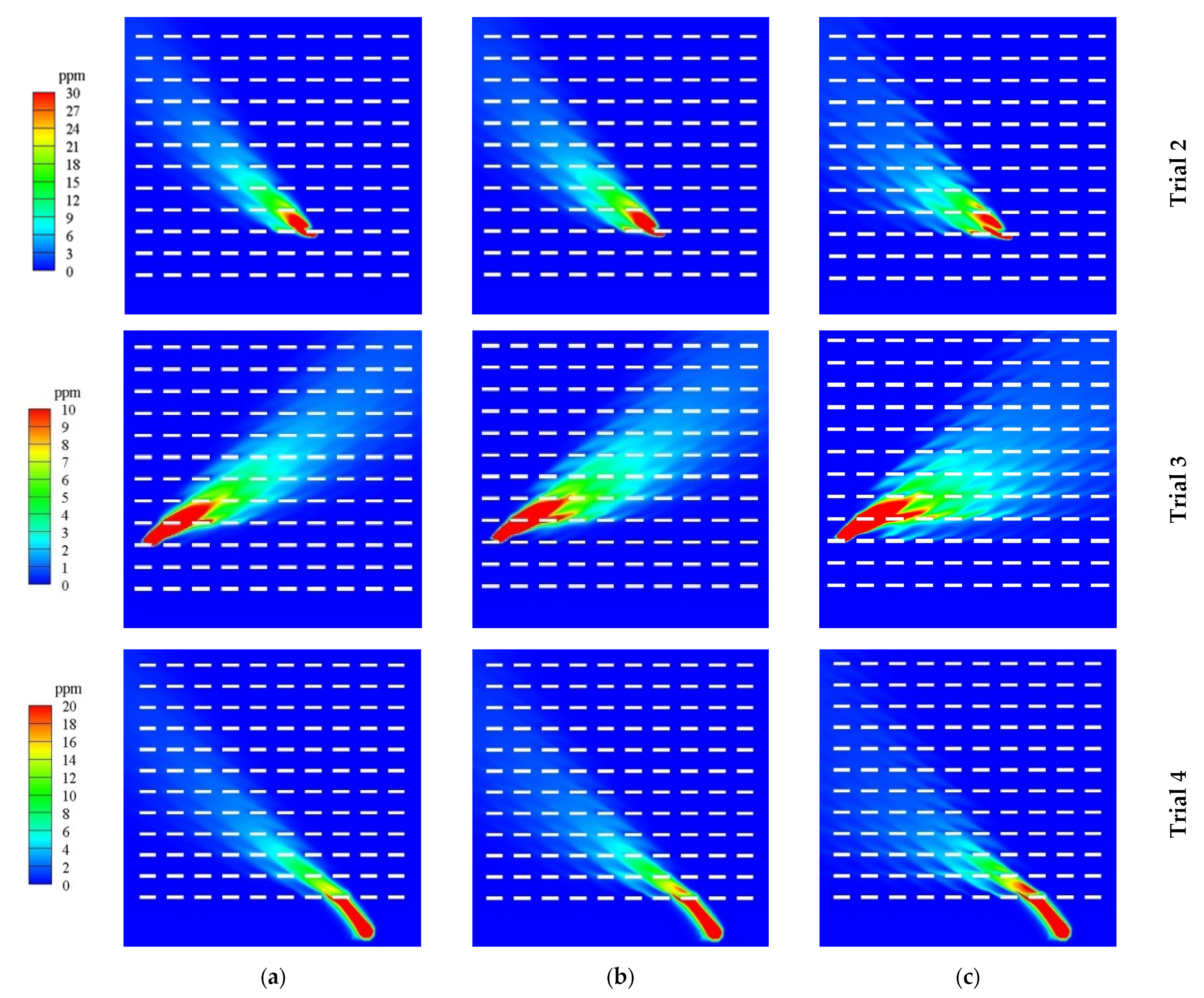


| Trial No. | Trial I.D. | Source Type | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2681829 | 225 | F | 1.8 | 7.93 | −41 | 1.10 | 28,000 | 1.46 |
| 2 | 2672213 | 200 | A | 1.8 | 2.68 | 30 | 0.35 | 150 | 0.428 |
| 3 | 2682320 | 225 | D | 2.6 | 4.55 | −39 | 0.50 | 170 | 0.718 |
| 4 | 2692250 | 225 | E | 1.3 | 3.38 | 36 | 0.37 | 130 | 0.537 |
| Turbulence Closure Model | Coarse-Medium | Medium-Fine | |||||
|---|---|---|---|---|---|---|---|
| Coarse | Medium | Fine | |||||
| SST | 7.65 | 11.59 | 17.50 | 14.00 | 39.77 | 1.97 | 5.60 |
| based models | 6.39 | 9.68 | 14.62 | 5.61 | 15.94 | 2.33 | 6.62 |
| Case | Model | FB | NMSE | VG | MG | FAC2 |
|---|---|---|---|---|---|---|
| Trial 1 | Standard | −0.01 | 0.79 | 2.65 | 0.98 | 0.62 |
| RNG | −0.17 | 1.45 | 3.11 | 0.84 | 0.59 | |
| SST | −0.23 | 2.06 | 3.81 | 0.80 | 0.59 | |
| Trial 2 | Standard | −0.11 | 1.04 | 2.35 | 1.24 | 0.70 |
| RNG | −0.25 | 2.21 | 3.76 | 1.13 | 0.65 | |
| SST | −0.20 | 2.23 | 5.65 | 1.06 | 0.64 | |
| Trial 3 | Standard | −0.02 | 0.59 | 3.13 | 0.85 | 0.68 |
| RNG | −0.22 | 0.76 | 3.25 | 0.94 | 0.58 | |
| SST | −0.29 | 0.66 | 5.36 | 0.97 | 0.53 | |
| Trial 4 | Standard | 0.07 | 0.46 | 1.98 | 1.01 | 0.65 |
| RNG | 0.00 | 0.62 | 2.54 | 0.86 | 0.65 | |
| SST | 0.01 | 1.01 | 3.51 | 0.78 | 0.61 |
| Sampling line | Model | FB | NMSE | VG | MG | FAC2 |
|---|---|---|---|---|---|---|
| Line 1 | Standard | −0.18 | 1.36 | 1.86 | 0.91 | 0.67 |
| RNG | −0.39 | 2.92 | 2.42 | 0.79 | 0.50 | |
| SST | −0.48 | 3.21 | 5.67 | 0.84 | 0.38 | |
| Line 2 | Standard | −0.04 | 0.56 | 2.88 | 0.83 | 0.58 |
| RNG | −0.18 | 0.95 | 5.69 | 0.71 | 0.50 | |
| SST | −0.11 | 0.90 | 5.85 | 0.53 | 0.53 | |
| Line 3 | Standard | 0.25 | 0.88 | 3.86 | 0.86 | 0.64 |
| RNG | 0.17 | 1.15 | 4.12 | 0.93 | 0.58 | |
| SST | 0.38 | 1.66 | 6.81 | 1.16 | 0.53 | |
| Line 4 | Standard | 0.59 | 1.56 | 4.55 | 1.39 | 0.56 |
| RNG | 0.67 | 1.99 | 4.64 | 1.56 | 0.56 | |
| SST | 0.81 | 2.56 | 6.66 | 1.81 | 0.53 | |
| Vertical | Standard | −0.08 | 1.49 | 1.74 | 0.99 | 0.68 |
| RNG | −0.18 | 1.16 | 2.37 | 0.84 | 0.61 | |
| SST | −0.12 | 1.66 | 3.22 | 0.85 | 0.61 |
| Turb. Schmidt Number | FB | NMSE | VG | MG | FAC2 |
|---|---|---|---|---|---|
| 0.3 | 0.86 | 1.48 | 4.57 | 2.40 | 0.50 |
| 0.5 | 0.42 | 0.44 | 1.97 | 1.22 | 0.76 |
| 0.7 | 0.16 | 0.40 | 1.74 | 0.97 | 0.71 |
| 0.9 | −0.02 | 0.59 | 3.13 | 0.85 | 0.68 |
| 1.1 | −0.15 | 0.85 | 7.79 | 0.79 | 0.62 |
| 1.3 | −0.23 | 1.12 | 22.27 | 0.78 | 0.55 |
| Variable | 0.13 | 0.41 | 1.82 | 0.98 | 0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kavian Nezhad, M.R.; Lange, C.F.; Fleck, B.A. Performance Evaluation of the RANS Models in Predicting the Pollutant Concentration Field within a Compact Urban Setting: Effects of the Source Location and Turbulent Schmidt Number. Atmosphere 2022, 13, 1013. https://doi.org/10.3390/atmos13071013
Kavian Nezhad MR, Lange CF, Fleck BA. Performance Evaluation of the RANS Models in Predicting the Pollutant Concentration Field within a Compact Urban Setting: Effects of the Source Location and Turbulent Schmidt Number. Atmosphere. 2022; 13(7):1013. https://doi.org/10.3390/atmos13071013
Chicago/Turabian StyleKavian Nezhad, Mohammad Reza, Carlos F. Lange, and Brian A. Fleck. 2022. "Performance Evaluation of the RANS Models in Predicting the Pollutant Concentration Field within a Compact Urban Setting: Effects of the Source Location and Turbulent Schmidt Number" Atmosphere 13, no. 7: 1013. https://doi.org/10.3390/atmos13071013
APA StyleKavian Nezhad, M. R., Lange, C. F., & Fleck, B. A. (2022). Performance Evaluation of the RANS Models in Predicting the Pollutant Concentration Field within a Compact Urban Setting: Effects of the Source Location and Turbulent Schmidt Number. Atmosphere, 13(7), 1013. https://doi.org/10.3390/atmos13071013








