Effect of Multiple GNSS Integration on the Number and Spatiotemporal Coverage of Radio Occultation Events
Abstract
1. Introduction
2. GNSS RO Event Simulation and Assessment Approaches
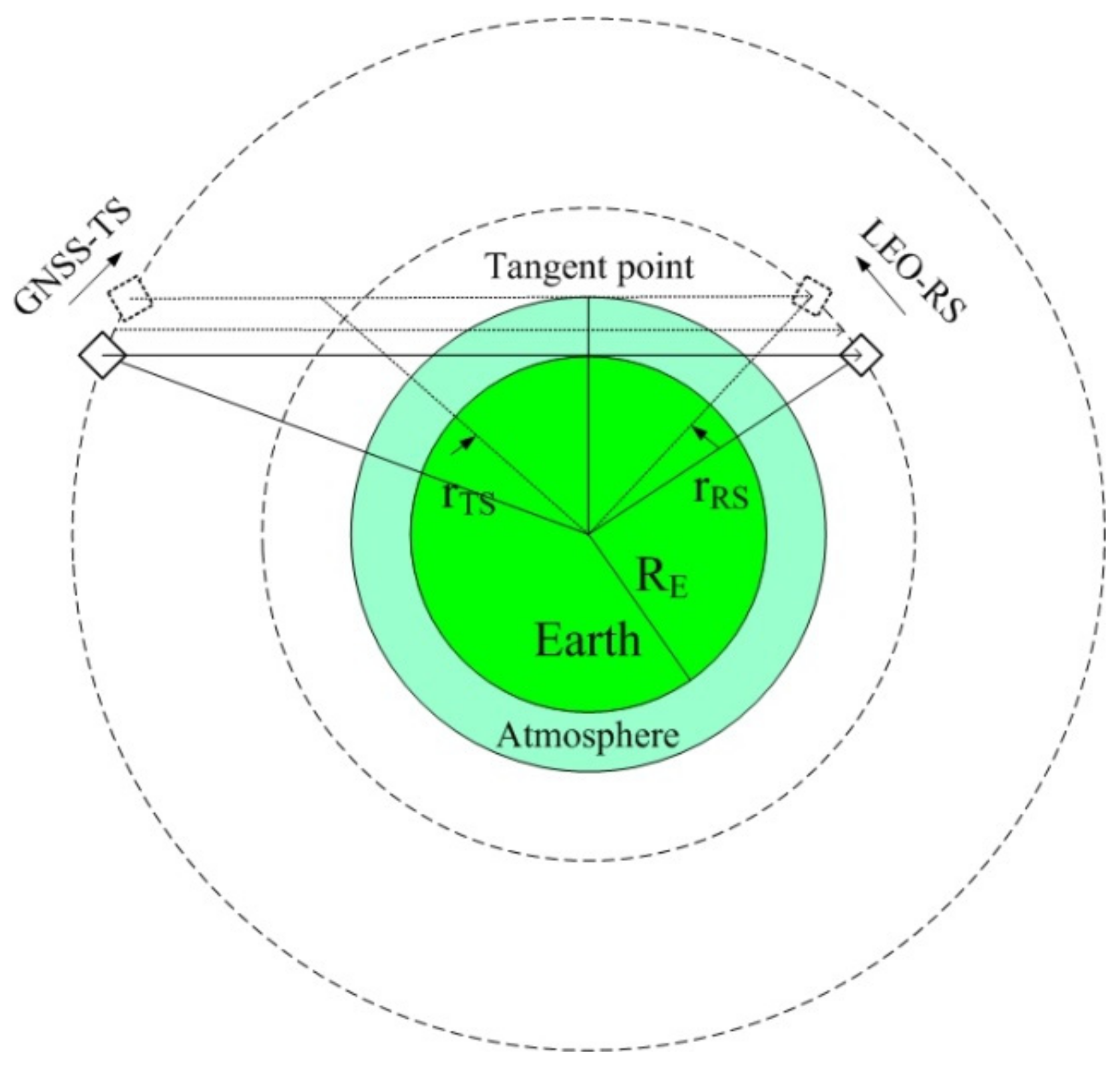
2.1. GNSS RO Event Simulation
2.2. Global Coverage Fraction and Uniformity of GNSS RO Events
2.3. GNSS and LEO Satellite Orbital Data
2.4. Experimental Programs
3. Results
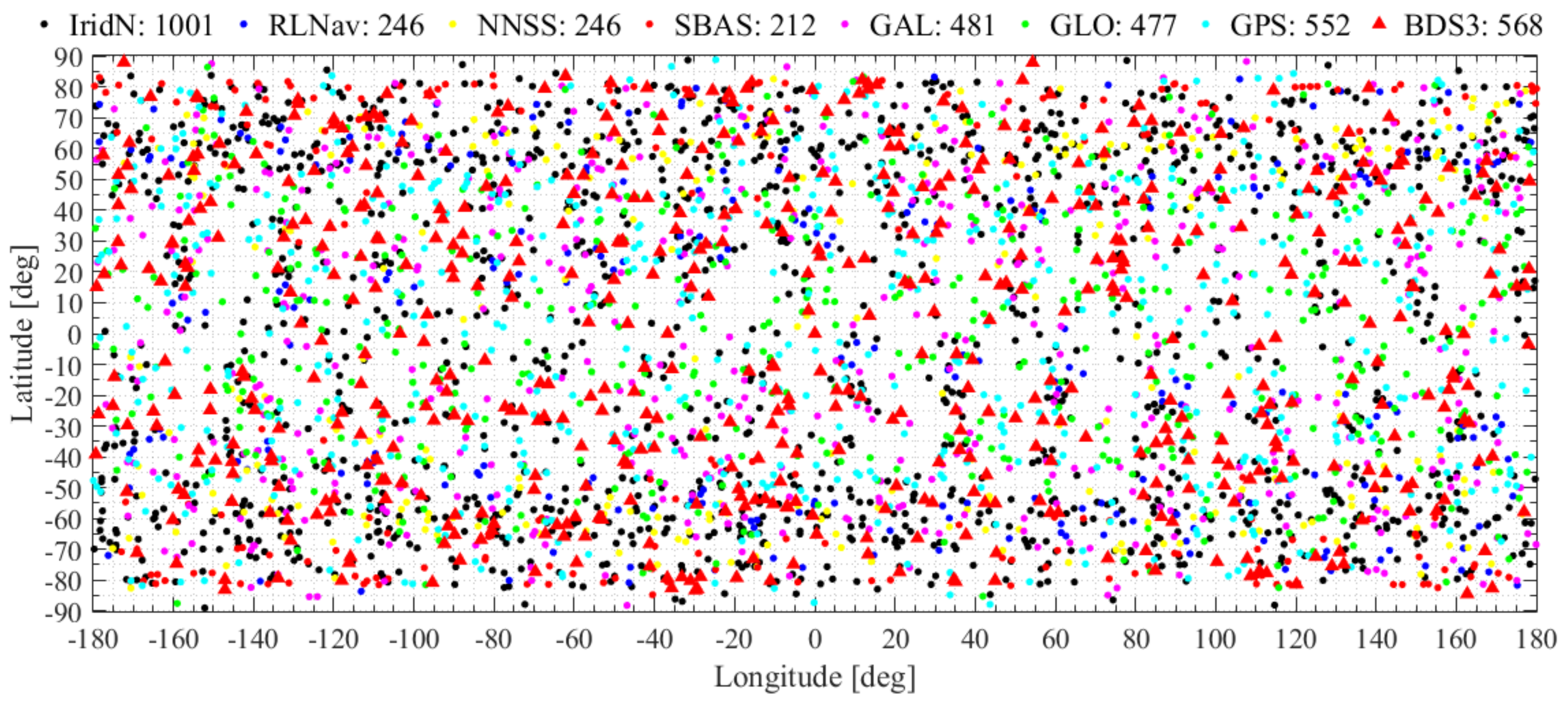
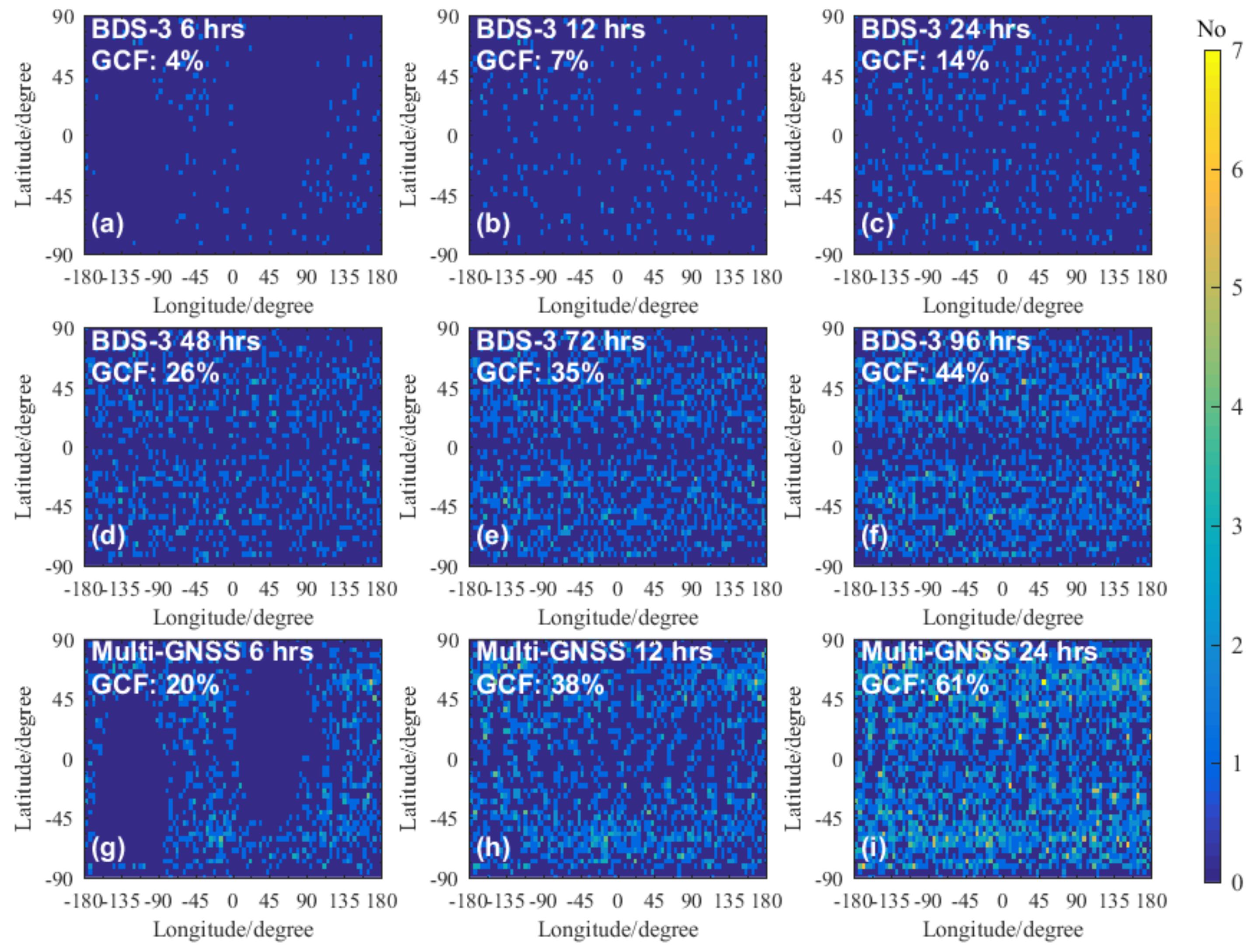
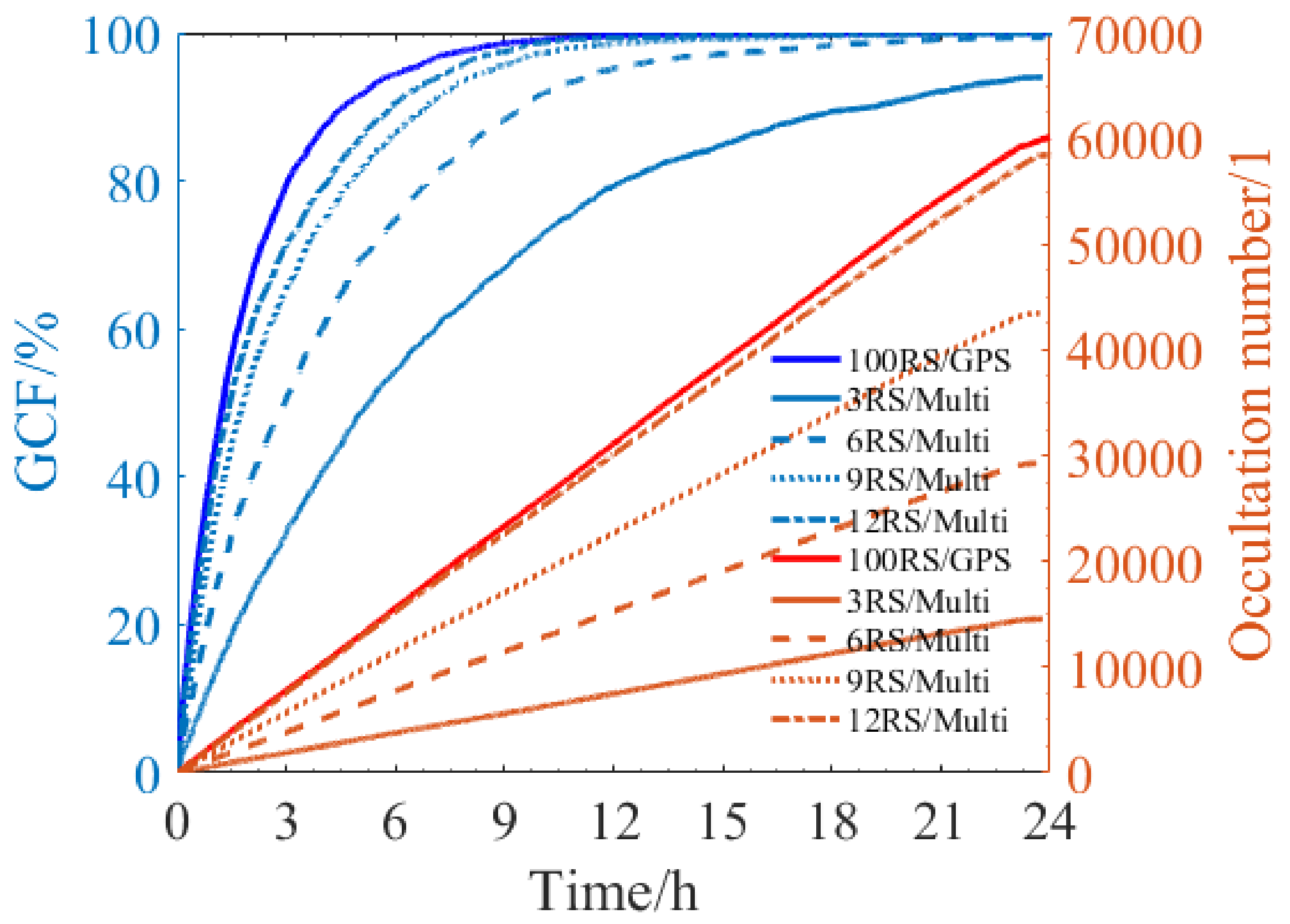
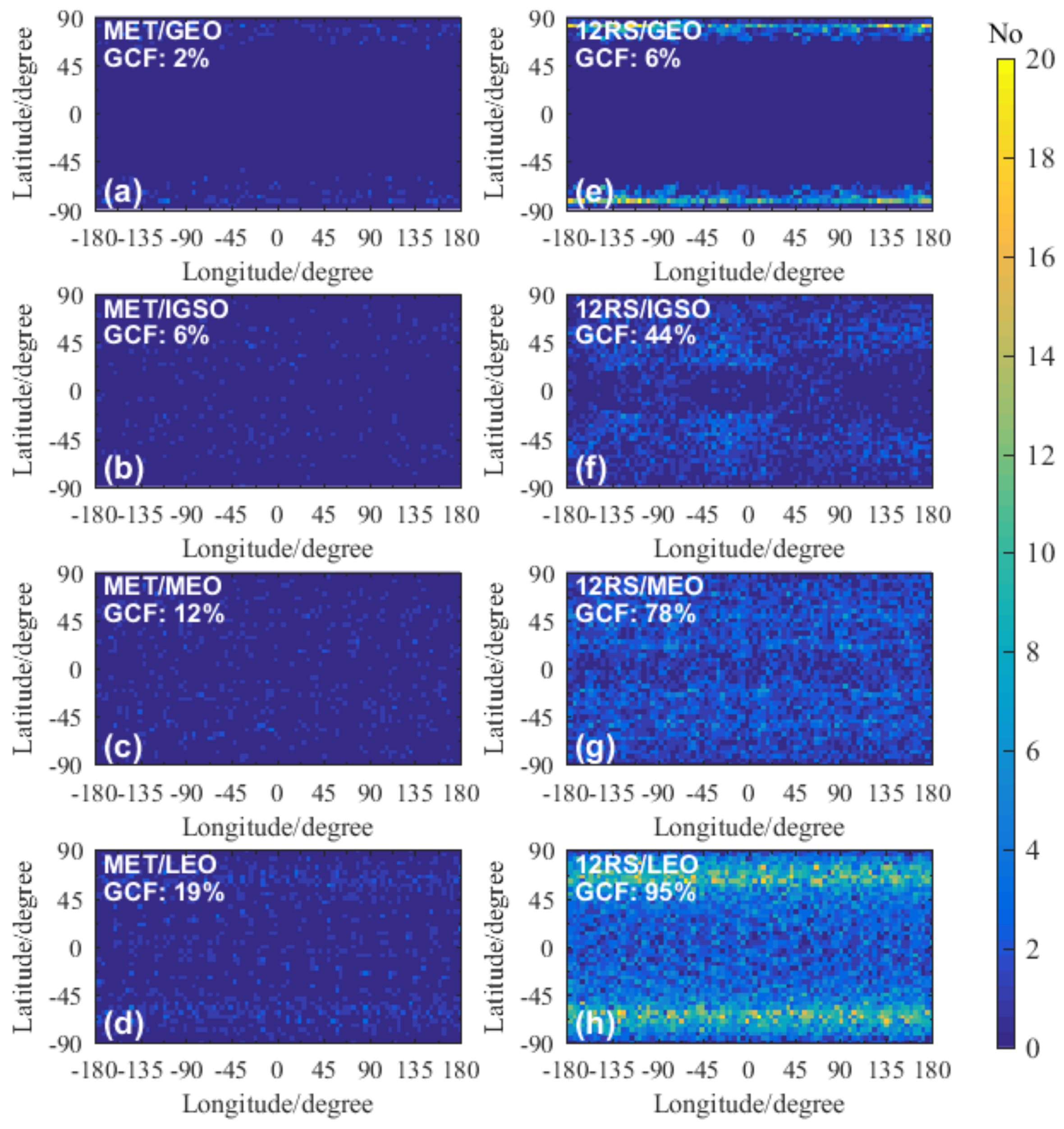
3.1. Detection Capability Improvement of Multi-GNSS for a Single Polar-Orbit Satellite
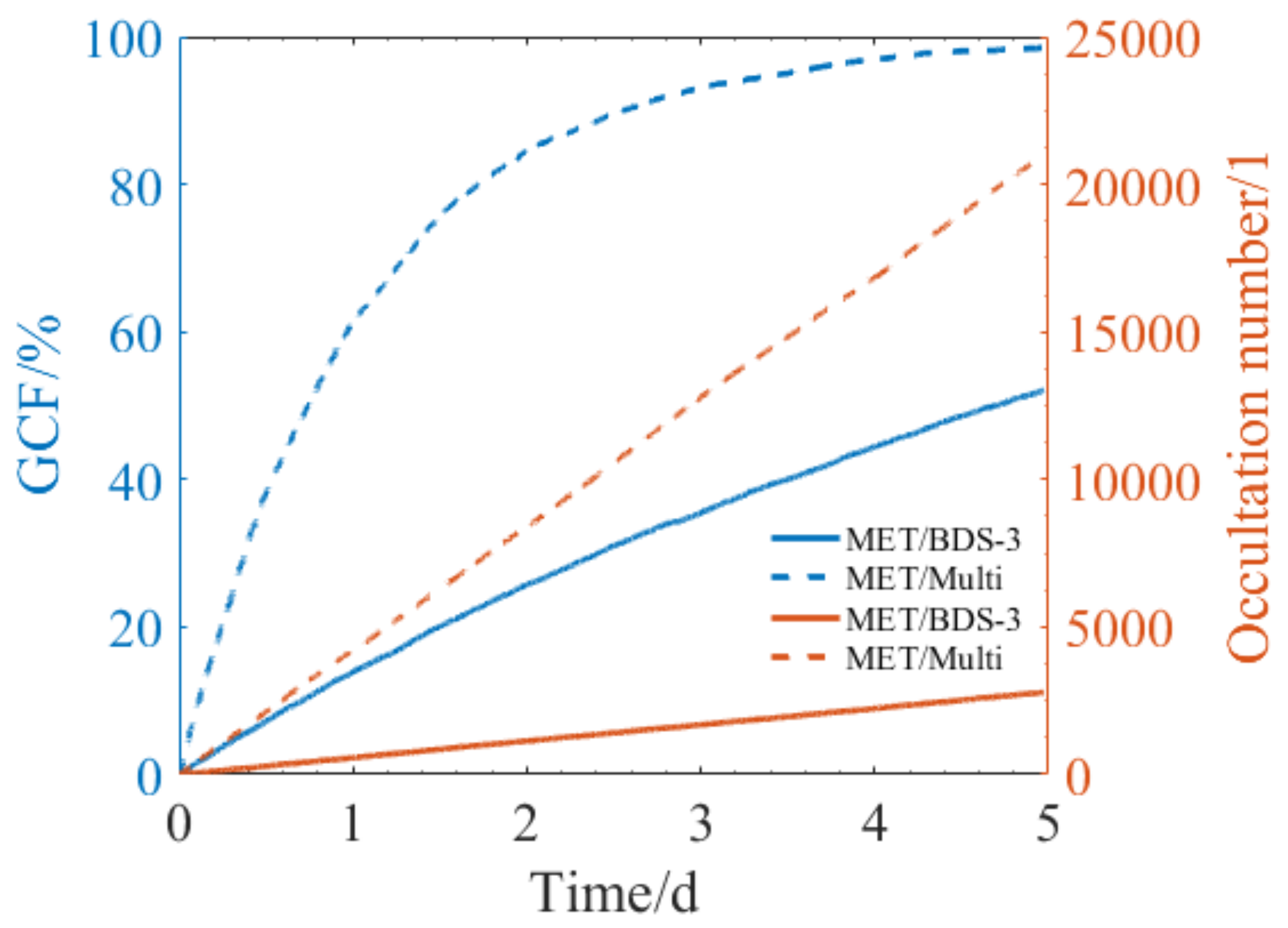
3.2. Comparing Polar-Orbit Constellation Detection Capability with the Spire Constellation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melbourne, W.G.; Davis, E.S.; Duncan, C.B.; Hajj, G.A.; Hardy, K.R.; Kursinski, E.R.; Meehan, T.K.; Yong, L.E.; Yunck, T.P. The Application of Spaceborne GPS to Atmospheric Limb Sounding and Global Change Monitoring; Jet Propulsion Laboratory: Pasadena, CA, USA, 1994. [Google Scholar]
- Kursinski, E.R.; Hajj, G.A.; Bertiger, W.I.; Leroy, S.S.; Meehan, T.K.; Romans, L.J.; Schofield, J.T.; McCleese, D.J.; Melbourne, W.G.; Thornton, C.L.; et al. Initial results of radio occultation observations of Earth’s atmosphere using the global positioning system. Science 1996, 271, 1107–1110. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Steiner, A.K.; Kirchengast, G.; Foelsche, U.; Kornblueh, L.; Manzini, E.; Bengtsson, L. GNSS occultation sounding for climate monitoring. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 113–124. [Google Scholar] [CrossRef]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertiger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultation. J. Atmos. Sol. -Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- Liu, C.; Kirchengast, G.; Syndergaard, S.; Schwaerz, M.; Danzer, J.; Sun, Y. New Higher-Order Correction of GNSS RO Bending Angles Accounting for Ionospheric Asymmetry: Evaluation of Performance and Added Value. Remote Sens. 2020, 12, 3637. [Google Scholar] [CrossRef]
- Gleisner, H.; Lauritsen, K.B.; Nielsen, J.K.; Syndergaard, S. Evaluation of the 15-year ROM SAF monthly mean GPS radio occultation climate data record. Atmos. Meas. Tech. 2020, 13, 3081–3098. [Google Scholar] [CrossRef]
- Stocker, M.; Ladstadter, F.; Wilhelmsen, H.; Steiner, A.K. Quantifying Stratospheric Temperature Signals and Climate Imprints From Post-2000 Volcanic Eruptions. Geophys Res Lett 2019, 46, 12486–12494. [Google Scholar] [CrossRef]
- Ladstädter, F.; Steiner, A.K.; Schwärz, M.; Kirchengast, G. Climate intercomparison of GPS radio occultation, RS90/92 radiosondes and GRUAN from 2002 to 2013. Atmos. Meas. Tech. 2015, 8, 1819–1834. [Google Scholar] [CrossRef]
- Steiner, A.K.; Hunt, D.; Ho, S.P.; Kirchengast, G.; Mannucci, A.J.; Scherllin-Pirscher, B.; Gleisner, H.; von Engeln, A.; Schmidt, T.; Ao, C.; et al. Quantification of structural uncertainty in climate data records from GPS radio occultation. Atmos. Chem. Phys. 2013, 13, 1469–1484. [Google Scholar] [CrossRef]
- Ho, S.-p.; Hunt, D.; Steiner, A.K.; Mannucci, A.J.; Kirchengast, G.; Gleisner, H.; Heise, S.; von Engeln, A.; Marquardt, C.; Sokolovskiy, S.; et al. Reproducibility of GPS radio occultation data for climate monitoring: Profile-to-profile inter-comparison of CHAMP climate records 2002 to 2008 from six data centers. J. Geophys. Res. Atmos. 2012, 117, D18111. [Google Scholar] [CrossRef]
- Ao, C.O.; Mannucci, A.J.; Kursinski, E.R. Improving GPS Radio occultation stratospheric refractivity retrievals for climate benchmarking. Geophys. Res. Lett. 2012, 39, 229–240. [Google Scholar] [CrossRef]
- Lackner, B.C.; Steiner, A.K.; Hegerl, G.C.; Kirchengast, G. Atmospheric climate change detection by radio occultation data using a fingerprinting method. J. Clim. 2011, 24, 5275–5291. [Google Scholar] [CrossRef]
- Kirchengast, G.; Schweitzer, S. Climate benchmark profiling of greenhouse gases and thermodynamic structure and wind from space. Geophys. Res. Lett. 2011, 38, 142–154. [Google Scholar] [CrossRef]
- Foelsche, U.; Scherllin-Pirscher, B.; Ladstädter, F.; Steiner, A.K.; Kirchengast, G. Refractivity and temperature climate records from multiple radio occultation satellites consistent within 0.05%. Atmos. Meas. Tech. 2011, 4, 2007–2018. [Google Scholar] [CrossRef]
- Anthes, R.A. Exploring Earth’s atmosphere with radio occultation: Contributions to weather, climate and space weather. Atmos. Meas. Tech. 2011, 4, 1077–1103. [Google Scholar] [CrossRef]
- Ho, S.-p.; Kirchengast, G.; Leroy, S.; Wickert, J.; Mannucci, A.J.; Steiner, A.; Hunt, D.; Schreiner, W.; Sokolovskiy, S.; Ao, C.; et al. Estimating the uncertainty of using GPS radio occultation data for climate monitoring: Intercomparison of CHAMP refractivity climate records from 2002 to 2006 from different data centers. J. Geophys. Res. 2009, 114, 1470–1478. [Google Scholar] [CrossRef]
- Foelsche, U.; Pirscher, B.; Borsche, M.; Kirchengast, G.; Wickert, J. Assessing the climate monitoring utility of radio occultation data: From CHAMP to FORMOSAT-3/COSMIC. Terr. Atmos. Ocean. Sci. 2009, 20, 155–170. [Google Scholar] [CrossRef][Green Version]
- Gobiet, A.; Kirchengast, G.; Manney, G.L.; Borsche, M.; Retscher, C.; Stiller, G. Retrieval of temperature profiles from CHAMP for climate monitoring: Intercomparison with Envisat MIPAS and GOMOS and different atmospheric analyses. Atmos. Chem. Phys. 2007, 7, 3519–3536. [Google Scholar] [CrossRef]
- Gobiet, A.; Kirchengast, G. Advancements of Global Navigation Satellite System radio occultation retrieval in the upper stratosphere for optimal climate monitoring utility. J. Geophys. Res. 2004, 109, 1. [Google Scholar] [CrossRef]
- Foelsche, U.; Kirchengast, G.; Steiner, A.K. Global Climate Monitoring based on CHAMP/GPS Radio Occultation Data. In First CHAMP Mission Results for Gravity, Magnetic and Atmospheric Studies; Springer: Berlin/Heidelberg, Germany, 2003; pp. 397–407. [Google Scholar]
- Kursinski, E.R.; Ward, D.; Otarola, A.C.; McGhee, J.; Stovern, M.; Sammler, K.; Reed, H.; Erickson, D.; McCormick, C.; Griggs, E. Atmospheric profiling via satellite to satellite occultations near water and ozone absorption lines for weather and climate. In Earth Observing Missions and Sensors: Development, Implementation, and Characterization IV; SPIE: Bellingham, WA, USA, 2016; Volume 9881, pp. 140–159. [Google Scholar]
- Cook, K.; Chen-Joe, F.; Wenkel, M.J.; Wilczynski, P.; Yen, N.; Chang, G.S. COSMIC-2/FORMOSAT-7: The future of global weather monitoring and prediction. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Aparicio, J.M.; Laroche, S. Estimation of the Added Value of the Absolute Calibration of GPS Radio Occultation Data for Numerical Weather Prediction. Mon. Weather Rev. 2015, 143, 1259–1274. [Google Scholar] [CrossRef]
- Cucurull, L.; Anthes, R.A.; Tsao, L.L. Radio Occultation Observations as Anchor Observations in Numerical Weather Prediction Models and Associated Reduction of Bias Corrections in Microwave and Infrared Satellite Observations. J. Atmos. Ocean. Technol. 2014, 31, 20–32. [Google Scholar] [CrossRef]
- Cucurull, L.; Anthes, R.A. Impact of Infrared, Microwave, and Radio Occultation Satellite Observations on Operational Numerical Weather Prediction. Mon. Weather Rev. 2014, 142, 4164–4186. [Google Scholar] [CrossRef]
- Cucurull, L.; Kuo, Y.H.; Barker, D.; Rizvi, S.R.H. Assessing the Impact of Simulated COSMIC GPS Radio Occultation Data on Weather Analysis over the Antarctic: A Case Study. Mon. Weather Rev. 2006, 134, 3283–3296. [Google Scholar] [CrossRef]
- Steiner, A.K.; Kirchengast, G.; Ladreiter, H.-P. Inversion, error analysis, and validation of GPS/MET occultaiton data. In Annales Geophysicae; Springer: Berlin/Heidelberg, Germany, 1999; pp. 122–138. [Google Scholar]
- Wickert, J.; Schmidt, T.; Michalak, G.; Heise, S.; Arras, C.; Beyerle, G.; Falck, C.; König, R.; Pingel, D.; Rothacher, M. GPS Radio Occultation with CHAMP, GRACE-A, SAC-C, TerraSAR-X, and FORMOSAT-3/COSMIC: Brief Review of Results from GFZ. In New Horizons in Occultation Research; Springer: Berlin/Heidelberg, Germany, 2009; pp. 3–15. [Google Scholar]
- Gobiet, A.; Foelsche, U.; Steiner, A.K.; Borsche, M.; Kirchengast, G.; Wickert, J. Climatological validation of stratospheric temperatures in ECMWF operational analyses with CHAMP radio occultation data. Geophys. Res. Lett. 2005, 32, 161–179. [Google Scholar] [CrossRef]
- Wickert, J.; Reigber, C.; Beyerle, G.; Konig, R.; Marquardt, C.; Schmidt, T.; Grunwaldt, L.; Galas, R.; Meehan, T.K.; Melbourne, W.G.; et al. Atmosphere sounding by GPS radio occultation: First results from CHAMP. Geophys. Res. Lett. 2001, 28, 3263–3266. [Google Scholar] [CrossRef]
- Beyerle, G. GPS radio occultation with GRACE: Atmospheric profiling utilizing the zero difference technique. Geophys. Res. Lett. 2005, 32, L13806. [Google Scholar] [CrossRef]
- Luntama, J.P.; Kirchengast, G.; Borsche, M.; Foelsche, U.; Steiner, A.; Healy, S.; von Engeln, A.; O’Clerigh, E.; Marquardt, C. Prospects of the Eps Gras Mission for Operational Atmospheric Applications. Bull. Am. Meteorol. Soc. 2008, 89, 1863. [Google Scholar] [CrossRef]
- Anthes, R.A.; Ector, D.; Hunt, D.C.; Kuo, Y.H.; Rocken, C.; Schreiner, W.S.; Sokolovskiy, S.V.; Syndergaard, S.; Wee, T.K.; Zeng, Z.; et al. The COSMIC/FORMOSAT-3 Mission: Early Results. Bull. Am. Meteorol. Soc. 2008, 89, 313–333. [Google Scholar] [CrossRef]
- Schreiner, W.; Rocken, C.; Sokolovskiy, S.; Syndergaard, S.; Hunt, D. Estimates of the precision of GPS radio occultations from the COSMIC/FORMOSAT-3 mission. Geophys. Res. Lett. 2007, 34, 545–559. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Bai, W.H.; Liu, C.L.; Liu, Y.; Du, Q.F.; Wang, X.Y.; Yang, G.L.; Liao, M.; Yang, Z.D.; Zhang, X.X.; et al. The FengYun-3C radio occultation sounder GNOS: A review of the mission and its early results and science applications. Atmos. Meas. Tech. 2018, 11, 5797–5811. [Google Scholar] [CrossRef]
- Bai, W.H.; Liu, C.L.; Meng, X.G.; Sun, Y.Q.; Kirchengast, G.; Du, Q.F.; Wang, X.Y.; Yang, G.L.; Liao, M.; Yang, Z.D.; et al. Evaluation of atmospheric profiles derived from single- and zero-difference excess phase processing of BeiDou radio occultation data from the FY-3C GNOS mission. Atmos. Meas. Tech. 2018, 11, 819–833. [Google Scholar] [CrossRef]
- Liao, M.; Zhang, P.; Yang, G.-L.; Bi, Y.-M.; Liu, Y.; Bai, W.-H.; Meng, X.-G.; Du, Q.-F.; Sun, Y.-Q. Preliminary validation of the refractivity from the new radio occultation sounder GNOS/FY-3C. Atmos. Meas. Tech. 2016, 9, 781–792. [Google Scholar] [CrossRef]
- Adhikari, L.; Ho, S.-P.; Zhou, X. Inverting COSMIC-2 Phase Data to Bending Angle and Refractivity Profiles Using the Full Spectrum Inversion Method. Remote Sens. 2021, 13, 1793. [Google Scholar] [CrossRef]
- Wang, L.; Li, D.R.; Chen, R.Z.; Fu, W.J.; Shen, X.; Jiang, H. Low Earth Orbiter (LEO) Navigation Augmentation: Opportunities and Challenges. Eng. Sci. 2020, 22, 144–152. [Google Scholar]
- Wang, S.Z.; Liu, C.L.; Zhu, G.W.; Bai, W.H.; Du, Q.F.; Sun, Y.Q.; Xia, J.M.; Meng, X.G.; Wang, X.Y.; Zhao, D.Y.; et al. Simulation Study on GRO and LRO Events. Chin. J. Space Sci. 2017, 37, 207–213. [Google Scholar]
- Wang, S.Z.; Zhu, G.W.; Bai, W.H.; Liu, C.L.; Sun, Y.Q.; Du, Q.F.; Wang, X.Y.; Meng, X.G.; Yang, G.L.; Yang, Z.D.; et al. For the first time fengyun3 C satellite-global navigation satellite system occultation sounder achieved spaceborne Bei Dou system radio occultation. Acta Phys. Sin. 2015, 64, 408–415. [Google Scholar]
- Wang, X.Y.; Sun, Y.Q.; Bai, W.H.; Du, Q.F.; Wang, D.W.; Wu, D.; Yu, Q.L.; Han, Y. Simulation of Numver and Distribution of Compass Occultation Events. Chin. J. Geophys. 2013, 56, 2522–2530. [Google Scholar]
- Zhang, X.H.; Ma, F.J. Review of the Development of LEO Navigation Augmented GNSS. Acta Geod. Cartogr. Sin. 2019, 48, 1073–1087. [Google Scholar]
- Harnisch, F.; Healy, S.B.; Bauer, P.; English, S.J. Scaling of GNSS Radio Occultation Impact with Observation Number Using an Ensemble of Data Assimilations. Mon. Weather Rev. 2013, 141, 4395–4413. [Google Scholar] [CrossRef]
- Steiner, A.K.; Ladstädter, F.; Ao, C.O.; Gleisner, H.; Ho, S.-P.; Hunt, D.; Schmidt, T.; Foelsche, U.; Kirchengast, G.; Kuo, Y.-H.; et al. Consistency and structural uncertainty of multi-mission GPS radio occultation records. Atmos. Meas. Tech. 2020, 13, 2547–2575. [Google Scholar] [CrossRef]
- Wang, J.Y.; Fu, Y.; Bai, W.H.; Wei, S.L.; Guo, B.B.; Yan, F.; Xie, C.Q. Design of GNSS Remotesening Satellite Constellation. Chin. J. Space Sci. 2021, 41, 475–482. [Google Scholar] [CrossRef]
- Liang, B.; Wang, J.Y.; Li, C.; Wei, S.L. Design of Multi-GNSS Occultation Sounding Satellite Constellation. J. Astronaut. 2016, 37, 334–340. [Google Scholar]
- Liang, B.; Wang, J.Y. Research on the Multi-Constellation Design for GNSS RO Atmosphere Sounding. Navig. Position. Timing 2016, 3, 58–64. [Google Scholar]
- Xu, X.H.; Li, Z.H.; Luo, J. Simulation Research on the Impact of LEO Constellation’s Parameters on the Number and Space-time Distribution of GPS Occultation Events. Acta Geod. Cartogr. Sin. 2015, 4, 27–33. [Google Scholar]
- Xu, X.H.; Li, Z.H.; Luo, J. Simulation of the Impacts of Single LEO Satellite Orbit Parameters on the Distribution and Number of Occultation Events. Geomat. Inf. Sci. Wuhan Univ. 2015, 7, 609–612. [Google Scholar]
- Mousa, A.; Aoyama, Y.; Tsuda, T. A simulation analysis to optimize orbits for a tropical GPS radio occultation mission. Earth Planets Space 2006, 58, 919–925. [Google Scholar] [CrossRef]
- Zhao, S.J.; Sun, X.J.; Zhu, Y.C.; Liao, F.Y. Effect of LEO Satellite’s Orbit Parameter on GPS Occultation Event’s Number and Distribution. J. PLA Univ. Sci. Technol. (Nat. Sci. Ed.) 2002, 2, 85–89. [Google Scholar]
- Asgarimehr, M.; Hossainali, M.M. GPS radio occultation constellation design with the optimal performance in Asia Pacific region. J. Geod. 2015, 89, 519–536. [Google Scholar] [CrossRef]
- Ghoniem, I.F.; Mousa, A.E.-K.; El-Fiky, G. GNSS-RO LEO satellite orbit optimization for Egypt and the Middle East region. Alex. Eng. J. 2020, 59, 389–397. [Google Scholar] [CrossRef]
- Ghoniem, I.; Mousa, A.E.-K.; El-Fiky, G. Distribution of the GNSS-LEO occultation events over Egypt. NRIAG J. Astron. Geophys. 2019, 6, 97–103. [Google Scholar] [CrossRef]
- Juang, J.-C.; Tsai, Y.-F.; Chu, C.-H. On constellation design of multi-GNSS radio occultation mission. Acta Astronaut. 2013, 82, 88–94. [Google Scholar] [CrossRef]
- Xu, X.; Han, Y.; Luo, J.; Wickert, J.; Asgarimehr, M. Seeking Optimal GNSS Radio Occultation Constellations Using Evolutionary Algorithms. Remote Sens. 2019, 11, 571. [Google Scholar] [CrossRef]
- Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. J. Geo-Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef]
- Liu, C.; Kirchengast, G.; Sun, Y.; Proschek, V.; Wang, X.; Tian, L.; Du, Q.; Bai, W.; Wu, C.; Hu, P.; et al. Impacts of Orbital and Constellation Parameters on the Number and Spatiotemporal Coverage of LEO-LEO Occultation Events. Remote Sens. 2021, 13, 4849. [Google Scholar] [CrossRef]
- Vallado, D.; Crawford, P.; Hujsak, R.; Kelso, T. Revisiting Spacetrack Report #3. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006; Volume 6753, pp. 1–88. [Google Scholar]
- Du, X.-Y.; Fu, Y.; Xue, Z.-G.; Guo, Y.-N.; Mao, J.-T. Simulation of the Impacts of Satellite Orbit Parameters on the Number and Distribution of LEO-LEO Occultation Events. Chin. J. Geophys. 2007, 50, 1107–1116. [Google Scholar] [CrossRef]

| Satellite ID | Inclination/(°) | RAAN/(°) | Eccentricity | Argument of Perigee/(°) | Mean Anomaly/(°) | Height/(km) |
|---|---|---|---|---|---|---|
| BDS-3 (C59) | 1 | 226.6 | 0.0003 | 356.3 | 149.4 | 35,787 |
| BDS-3 (C38) | 56 | 56.9 | 0.0019 | 191.9 | 341.8 | 35,787 |
| BDS-3 (C19) | 55.4 | 123.8 | 0.0012 | 293.4 | 66.5 | 21,528 |
| GPS (13) | 55.5 | 169.8 | 0.0048 | 53.4 | 307.1 | 20,182 |
| COSMOS (2425) | 64.8 | 255.3 | 0.0024 | 342.9 | 16.3 | 19,129 |
| GSAT (E11) | 56.8 | 31.2 | 0.0004 | 31.7 | 328.3 | 23,222 |
| IRIDIUM (109) | 86.4 | 129.2 | 0 | 92.1 | 268.1 | 778 |
| COSMOS (2361) | 82.9 | 112.9 | 0.0032 | 129.8 | 43.7 | 989 |
| NNSS (19) | 89.9 | 242.6 | 0.0171 | 349.6 | 10.2 | 1069 |
| QZSS (184) | 42.4 | 269.3 | 0.0758 | 269.1 | 89.6 | 35,787 |
| QZSS (189) | 0.02 | 188.6 | 0.0002 | 271.7 | 154.3 | 35,787 |
| Satellite ID | Inclination/(°) | RAAN/(°) | Eccentricity | Argument of Perigee/(°) | Mean Anomaly/(°) | Height/(km) |
|---|---|---|---|---|---|---|
| RS01 | 93.6 | 151 | 0.0001 | 90 | 30 | 600 |
| RS02 | 93.9 | 215 | 0.0001 | 90 | 150 | 600 |
| RS03 | 94.6 | 330 | 0.0001 | 90 | 270 | 600 |
| RS04 | 95.5 | 183 | 0.0001 | 90 | 90 | 600 |
| RS05 | 96.6 | 245 | 0.0001 | 90 | 210 | 600 |
| RS06 | 96.9 | 280 | 0.0001 | 90 | 330 | 600 |
| RS07 | 96.5 | 330 | 0.0001 | 90 | 90 | 600 |
| RS08 | 95.9 | 215 | 0.0001 | 90 | 330 | 600 |
| RS09 | 95.3 | 151 | 0.0001 | 90 | 210 | 600 |
| RS10 | 53 | 15 | 0.0001 | 90 | 330 | 600 |
| RS11 | 53 | 60 | 0.0001 | 90 | 150 | 600 |
| RS12 | 53 | 105 | 0.0001 | 90 | 30 | 600 |
| MET | 98.8 | 348.5 | 0.00004 | 185.7 | 174.4 | 827 |
| Spire01 | 6 | 198.4 | 0.00134 | 155.9 | 204.1 | 635 |
| Spire02 | 51.6 | 11.3 | 0.00001 | 327.4 | 32.7 | 388 |
| Spire03 | 97.6 | 136.6 | 0.00224 | 296.5 | 63.4 | 524 |
| MET/BDS-3/(%) | MET/Multi/(%) | 3RS/Multi/(%) | 6RS/Multi/(%) | 9RS/Multi/(%) | 12RS/Multi/(%) | 100RS/GPS/(%) | |
|---|---|---|---|---|---|---|---|
| 4 | 20 | 54 | 75 | 87 | 90 | 94 | |
| 4 | 20 | 54 | 51 | 47 | 45 | 54 | |
| 7 | 38 | 79 | 95 | 99 | 99 | 100 | |
| 7 | 38 | 50 | 48 | 45 | 43 | 55 | |
| 14 | 61 | 94 | 99 | 100 | 100 | 100 | |
| 14 | 28 | 44 | 40 | 46 | 44 | 57 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Sun, Y.; Bai, W.; Du, Q.; Li, W.; Wang, X.; Li, P. Effect of Multiple GNSS Integration on the Number and Spatiotemporal Coverage of Radio Occultation Events. Atmosphere 2022, 13, 654. https://doi.org/10.3390/atmos13050654
Liu C, Sun Y, Bai W, Du Q, Li W, Wang X, Li P. Effect of Multiple GNSS Integration on the Number and Spatiotemporal Coverage of Radio Occultation Events. Atmosphere. 2022; 13(5):654. https://doi.org/10.3390/atmos13050654
Chicago/Turabian StyleLiu, Congliang, Yueqiang Sun, Weihua Bai, Qifei Du, Wei Li, Xi Wang, and Peixian Li. 2022. "Effect of Multiple GNSS Integration on the Number and Spatiotemporal Coverage of Radio Occultation Events" Atmosphere 13, no. 5: 654. https://doi.org/10.3390/atmos13050654
APA StyleLiu, C., Sun, Y., Bai, W., Du, Q., Li, W., Wang, X., & Li, P. (2022). Effect of Multiple GNSS Integration on the Number and Spatiotemporal Coverage of Radio Occultation Events. Atmosphere, 13(5), 654. https://doi.org/10.3390/atmos13050654






