Signal Simulation of Dual-Polarization Weather Radar and Its Application in Range Ambiguity Mitigation
Abstract
:1. Introduction
2. Methods
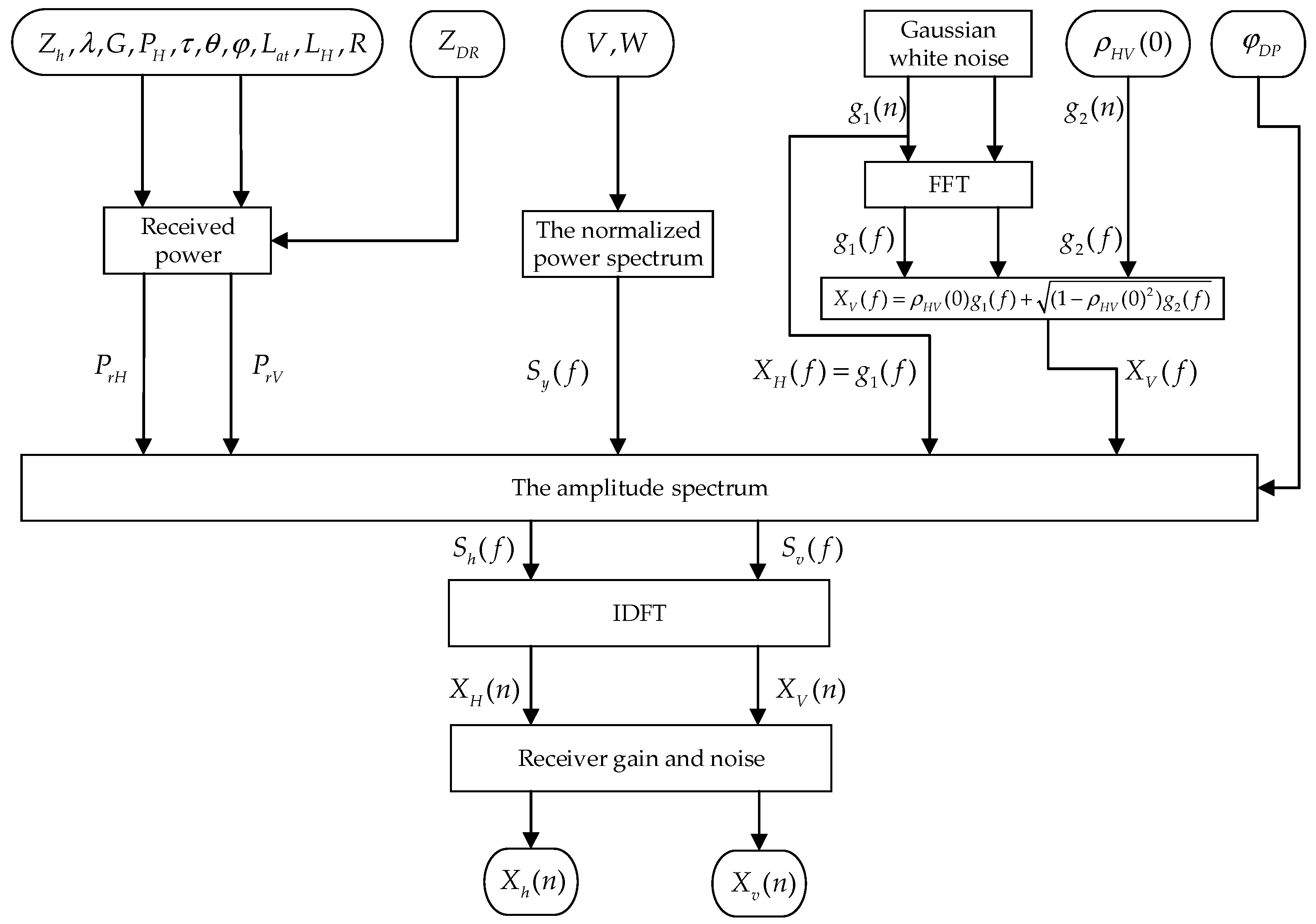
2.1. Simulation Algorithm of Dual-Polarization Weather Radar Echo Signal
- (1)
- Modeling of radar signal power
- (2)
- Power spectrum modeling of H−channel and V−channel echo signal
- (3)
- Time-domain generation of echo signal for H−channel and V−channel
- (4)
- Modeling of the effect of radar receiver noise and gain into radar signal
2.2. Batch Work Mode and Phase-Encoded Work Mode Echo Signal Simulation
2.2.1. Batch Working Mode Echo Simulation Modeling
2.2.2. Phase-Coded Mode Echo Simulation Modeling
- (a)
- First, the echo signal sequences and of the H−channel and V−channel of a single range gate are generated according to the echo signal simulation algorithm in Section 2.1.
- (b)
- Second, the phase modulation of and is formulated as follows:where m and M are phase encoding parameters. Weather radar often uses SZ(8/64) coding for modulation output, namely m = 8, M = 64. The phases in Equations (20) and (21) change repeatedly with a period of 8, and the 8 duplicate phases are −0, −π/8, −4π/8, −9π/8, 0, −9π/8, −4π/8, −πh/8.
- (c)
- Third, the range folding judgment and folding position calculation are used for each range gate, which is consistent with the PRT2 working in the batch working mode. Thus, the additional echo signal of the position R1 and R2 is calculated as follows:
- (d)
- Finally, other range gates’ echo signals are generated according to the above (a)–(b) process until the entire scan is simulated.
3. Results
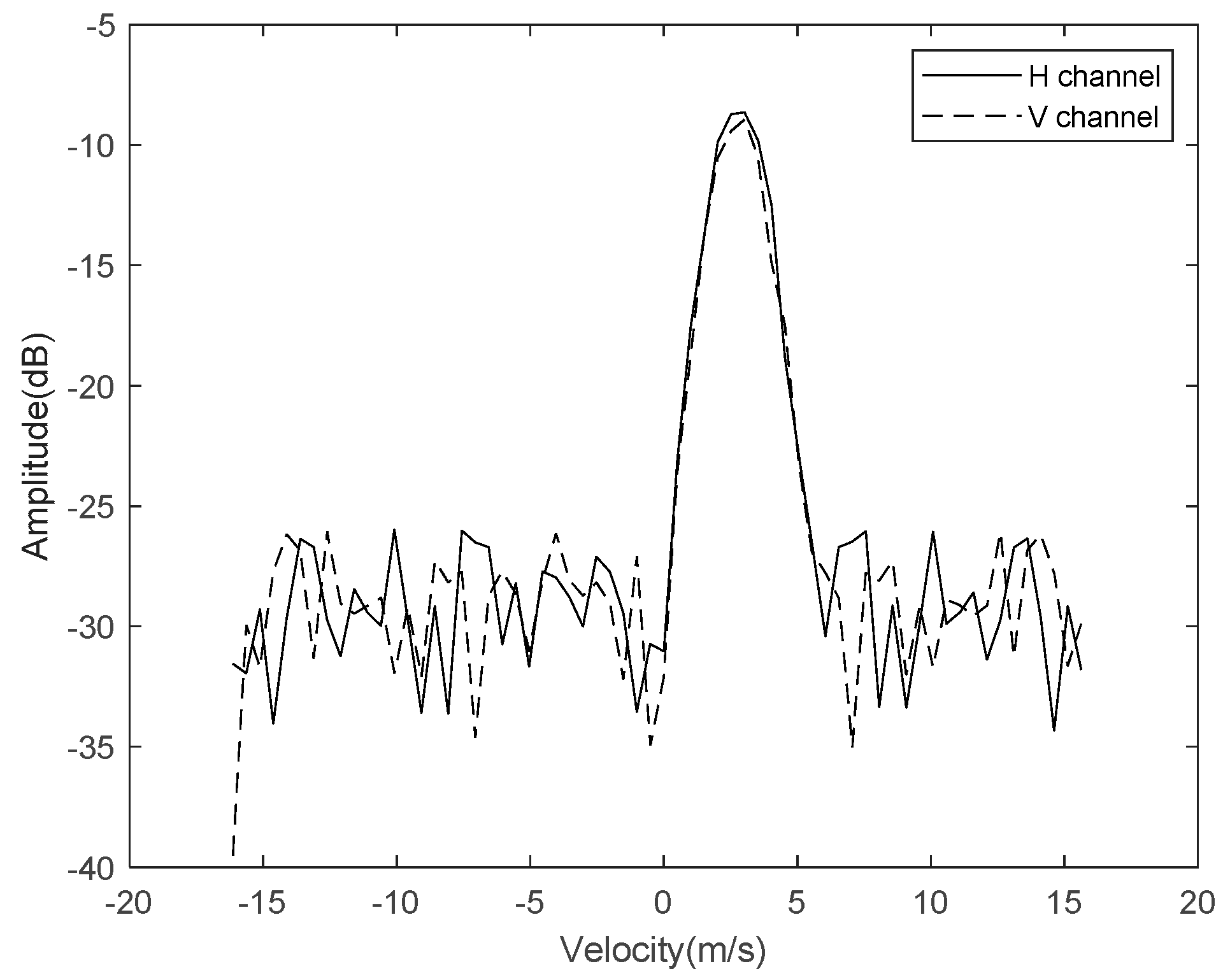
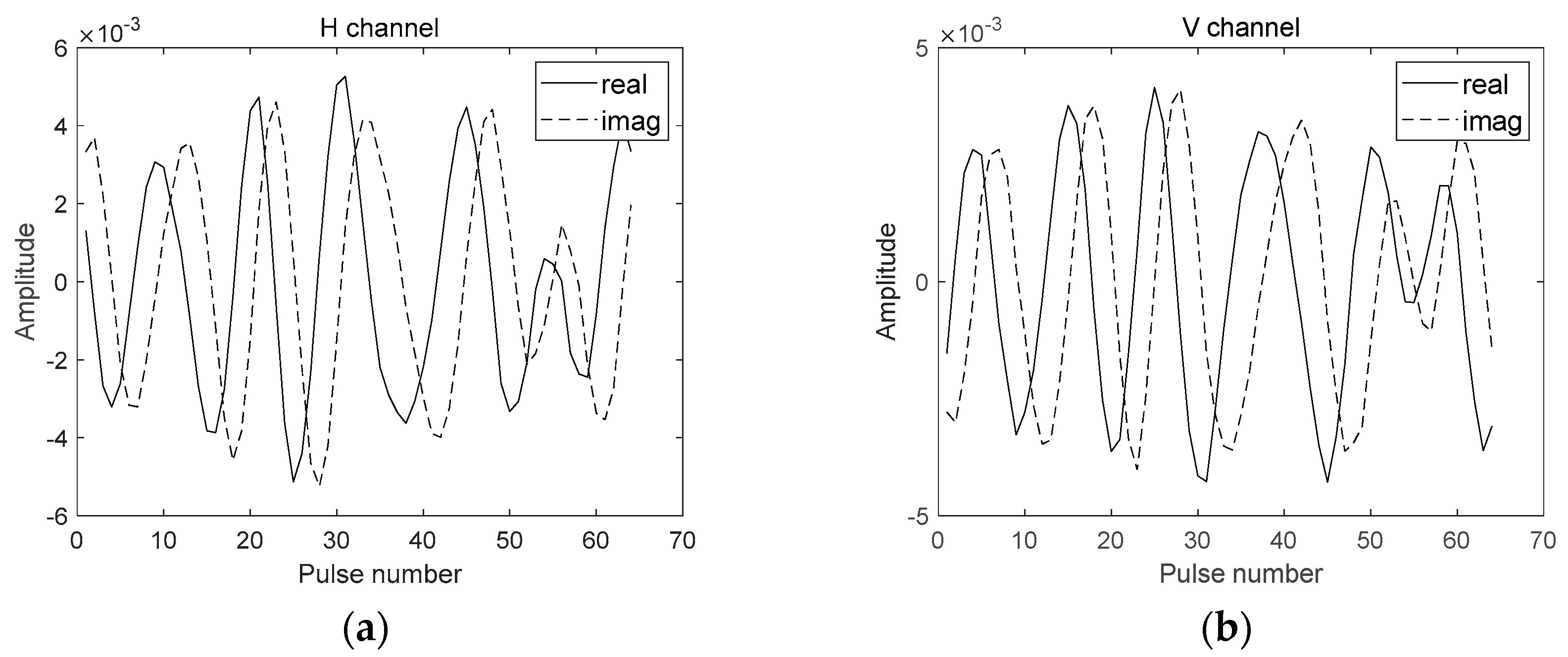
3.1. Verification of Simulation Results of Dual-Polarization Weather Radar Echo Signals
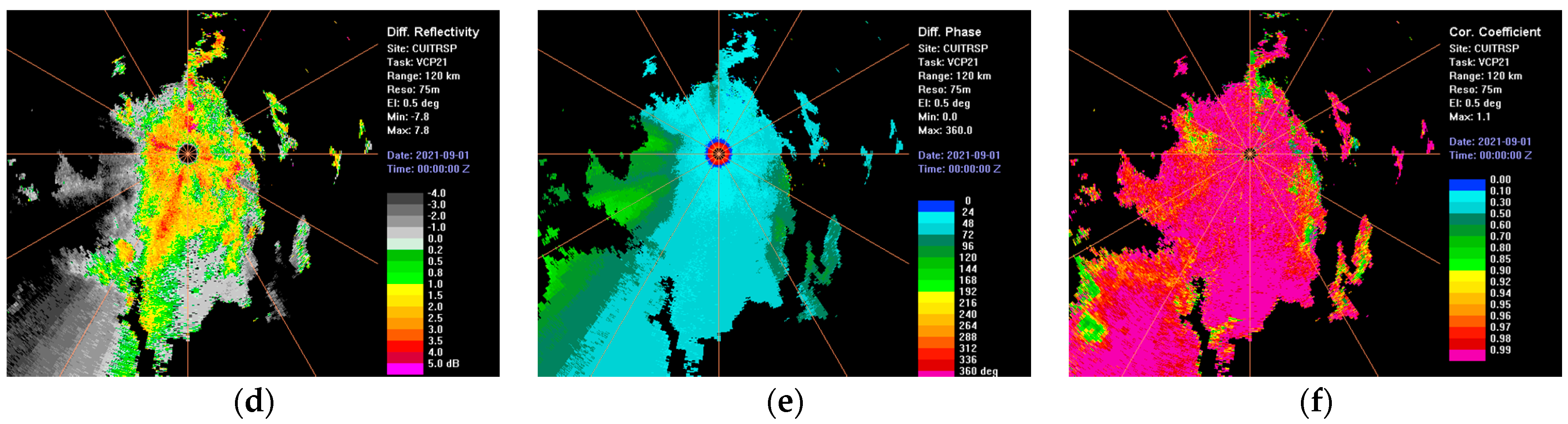
3.2. Verification of Batch Work Mode and Phase-Encoded Work Mode Echo Signal Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumjian, M. Principles and applications of dual-polarization weather radar. Part I: Description of the polarimetric radar variables. J. Oper. Meteorol. 2013, 1, 226–242. [Google Scholar] [CrossRef]
- Lim, S.; Cifelli, R.; Chandrasekar, V.; Matrosov, S.Y. Precipitation Classification and Quantification Using X-Band Dual-Polarization Weather Radar: Application in the Hydrometeorology Testbed. J. Atmos. Ocean. Technol. 2013, 30, 2108–2120. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Krajewski, W.F. Simulation of radar reflectivity fields: Algorithm formulation and evaluation. Water Resour. Res. 1997, 33, 1419–1428. [Google Scholar] [CrossRef]
- Capsoni, C.; D’Amico, M.; Nebuloni, R. A Multiparameter Polarimetric Radar Simulator. J. Atmos. Ocean. Technol. 2001, 18, 1799–1809. [Google Scholar] [CrossRef]
- Lupidi, A.; Moscardini, C.; Garzelli, A.; Berizzi, F.; Cuccoli, F.; Bernabò, M. Polarimetry applied to avionic weather radar: Improvement on meteorological phenomena detection and classification. In Proceedings of the 2011 Tyrrhenian International Workshop on Digital Communications—Enhanced Surveillance of Aircraft and Vehicles, Capri, Italy, 12–14 September 2011; pp. 73–77. [Google Scholar]
- Augros, C.; Caumont, O.; Ducrocq, V.; Tabary, P. Development and validation of a full polarimetric radar simulator. In Proceedings of the 36th Conference on Radar Meteorology, Breckenridge, CO, USA, 16–20 September 2013; American Meteorological Society: Boston, MA, USA, 2013; Volume 387. [Google Scholar]
- Ivic, I.R.; Doviak, R.J. Evaluation of Phase Coding to Mitigate Differential Reflectivity Bias in Polarimetric PAR. IEEE Trans. Geosci. Remote Sens. 2015, 54, 431–451. [Google Scholar] [CrossRef]
- Zrnić, D.S.; Doviak, R.J.; Melnikov, V.M.; Ivić, I.R. Signal Design to Suppress Coupling in the Polarimetric Phased Array Radar. J. Atmos. Ocean. Technol. 2014, 31, 1063–1077. [Google Scholar] [CrossRef]
- Nai, F.; Boettcher, J.; Curtis, C.; Schvartzman, D.; Torres, S. The Impact of Elevation Sidelobe Contamination on Radar Data Quality for Operational Interpretation. J. Appl. Meteorol. Clim. 2020, 59, 707–724. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Wang, C.; Qin, Z.; He, J.; Liu, F.; Sun, Q. A Velocity Dealiasing Algorithm on Frequency Diversity Pulse-Pair for Future Geostationary Spaceborne Doppler Weather Radar. Atmosphere 2018, 9, 234. [Google Scholar] [CrossRef] [Green Version]
- Schvartzman, D.; Curtis, C.D. Signal Processing and Radar Characteristics (SPARC) Simulator: A Flexible Dual-Polarization Weather-Radar Signal Simulation Framework Based on Preexisting Radar-Variable Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 12, 135–150. [Google Scholar] [CrossRef]
- Doviak, R.; Zrnic, S. Doppler Radar and Weather Observations; Courier Corporation: Chelmsford, MA, USA, 2006. [Google Scholar]
- Zrnic, D.S.; Mahapatra, P. Two Methods of Ambiguity Resolution in Pulse Doppler Weather Radars. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 470–483. [Google Scholar]
- Sachidananda, M.; Zrnic, D.S. Systematic Phase Codes for Resolving Range Overlaid Signals in a Doppler Weather Radar. J. Atmos. Ocean. Technol. 1999, 16, 1351–1363. [Google Scholar] [CrossRef]
- Zhang, S.; Min, J.; Zhang, C.; Huang, X.; Liu, J.; Wei, K. Hybrid Method to Identify Second-trip Echoes Using Phase Modulation and Polarimetric Technology. Adv. Atmos. Sci. 2021, 38, 480–492. [Google Scholar] [CrossRef]
- Zrnić, D.S. Simulation of Weatherlike Doppler Spectra and Signals. J. Appl. Meteorol. 1975, 14, 619–620. [Google Scholar] [CrossRef]
- Galati, G.; Pavan, G. Computer simulation of weather radar signals. Simul. Pract. Theory 1995, 3, 17–44. [Google Scholar] [CrossRef]
- Melnikov, V.M.; Zrnić, D.S. On the Alternate Transmission Mode for Polarimetric Phased Array Weather Radar. J. Atmos. Ocean. Technol. 2015, 32, 220–233. [Google Scholar] [CrossRef]
- Doviak, R.J.; Zrnic, D.S. Doppler Radar & Weather Observations; Published Online. 2014. Available online: https://www.numilog.com/355287/Doppler-Radar--Weather-Observations.ebook (accessed on 20 February 2022).
- Torres, S.M.; Zrnic, D.S. Range and velocity ambiguity mitigation techniques for the WSR-88D weather radar. In Proceedings of the IGARSS 2004: 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1727–1729. [Google Scholar]
- Meymaris, G.; Hubbert, J.; Ellis, S. Quanitative Analysis of the SZ(8/64) Phase Code for the Mitigation of Range and Velocity Ambiquities in the WSR-88D. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.604.2132&rep=rep1&type=pdf (accessed on 20 February 2022).
- Zrnic, D. Spectrum Width Estimtes for Weather Echoes. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 613–619. [Google Scholar] [CrossRef]
- Sachidananda, M.; Zrnic, D.S. ZDR measurement considerations for a fast scan capability radar. Radio Sci. 1985, 20, 907–922. [Google Scholar] [CrossRef]
- Li, X.; He, J.; Wang, C.; Tang, S.; Hou, X. Evaluation of Surface Clutter for Future Geostationary Spaceborne Weather Radar. Atmosphere 2017, 8, 14. [Google Scholar] [CrossRef] [Green Version]


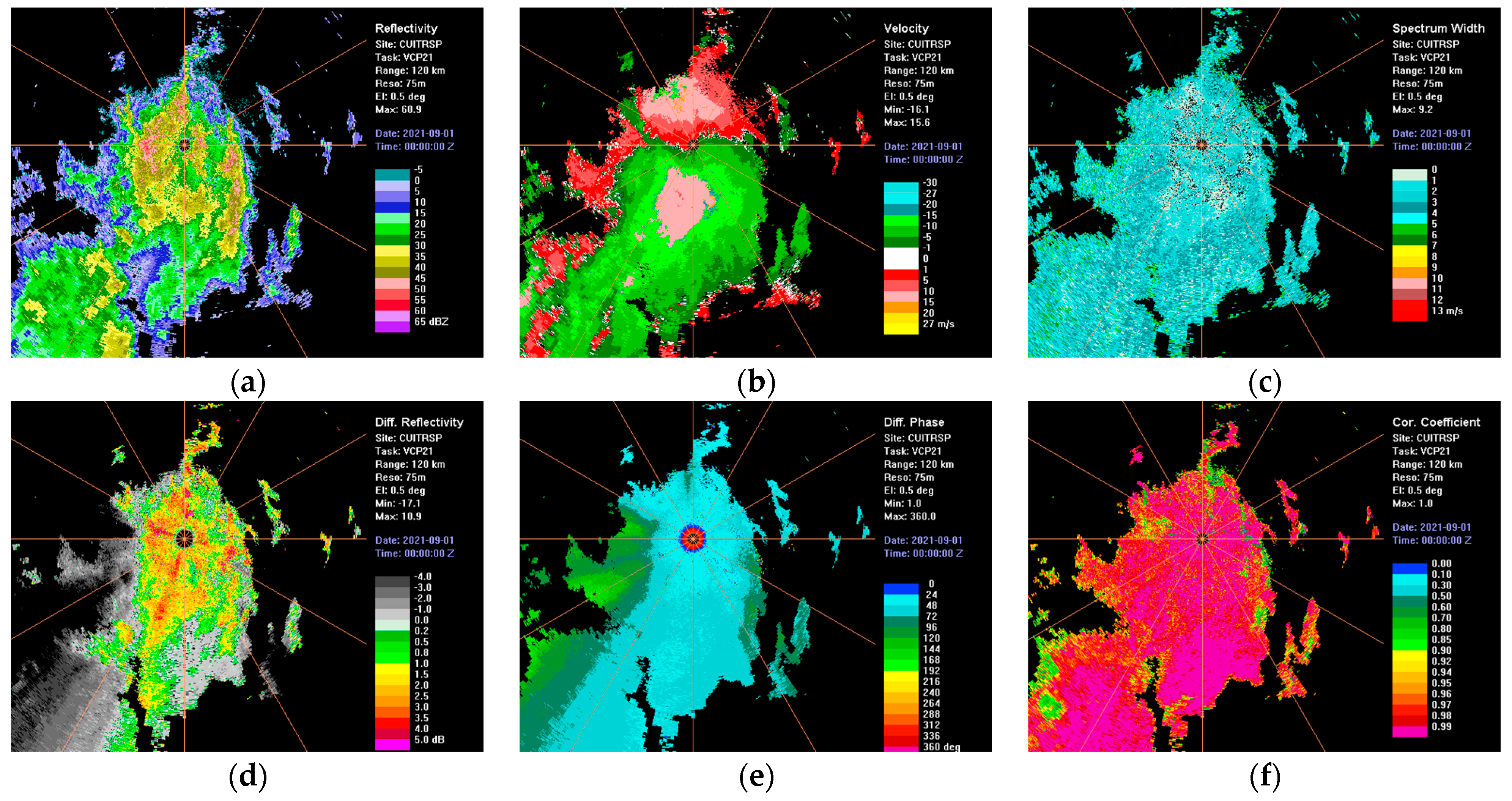
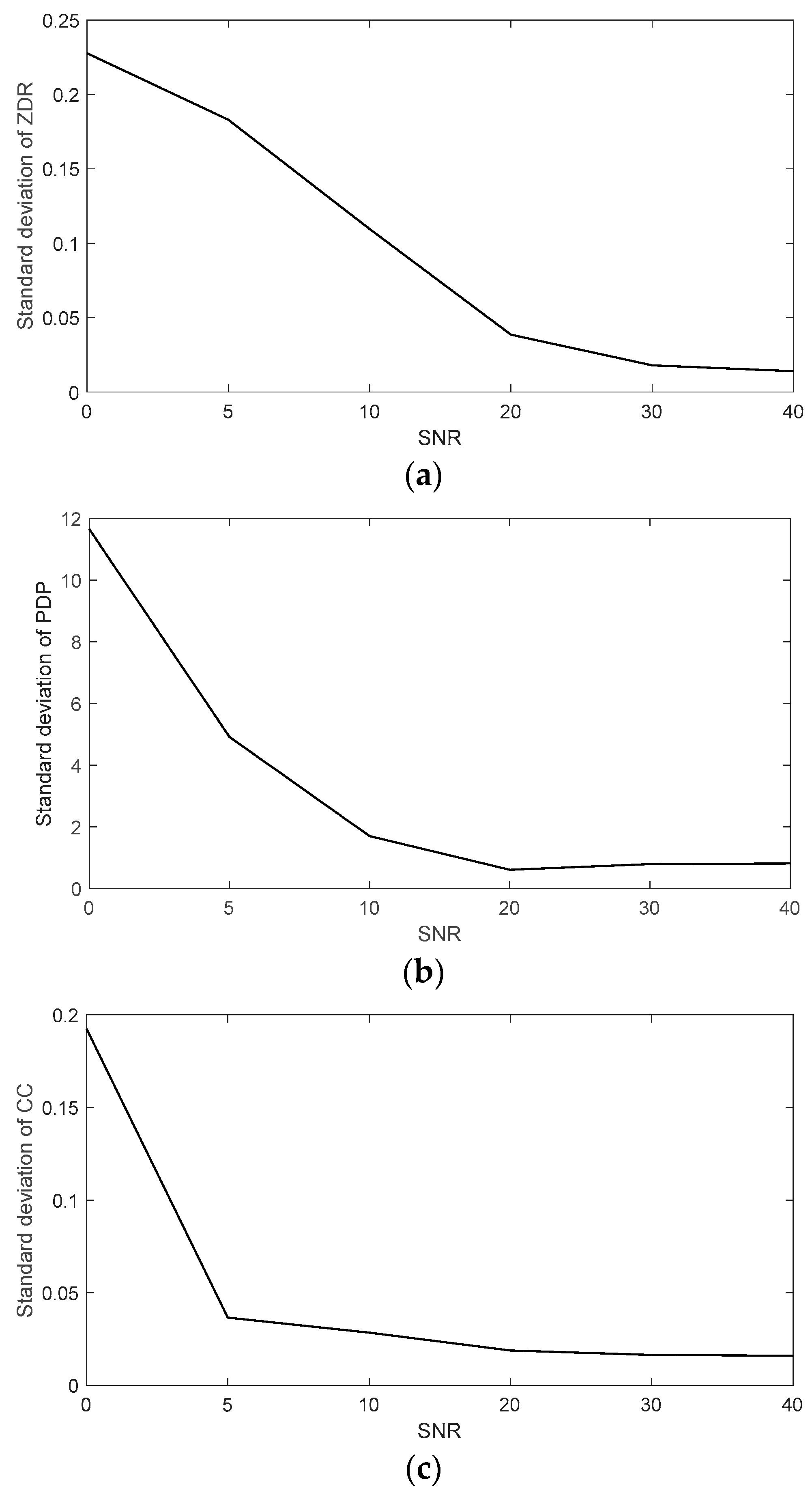
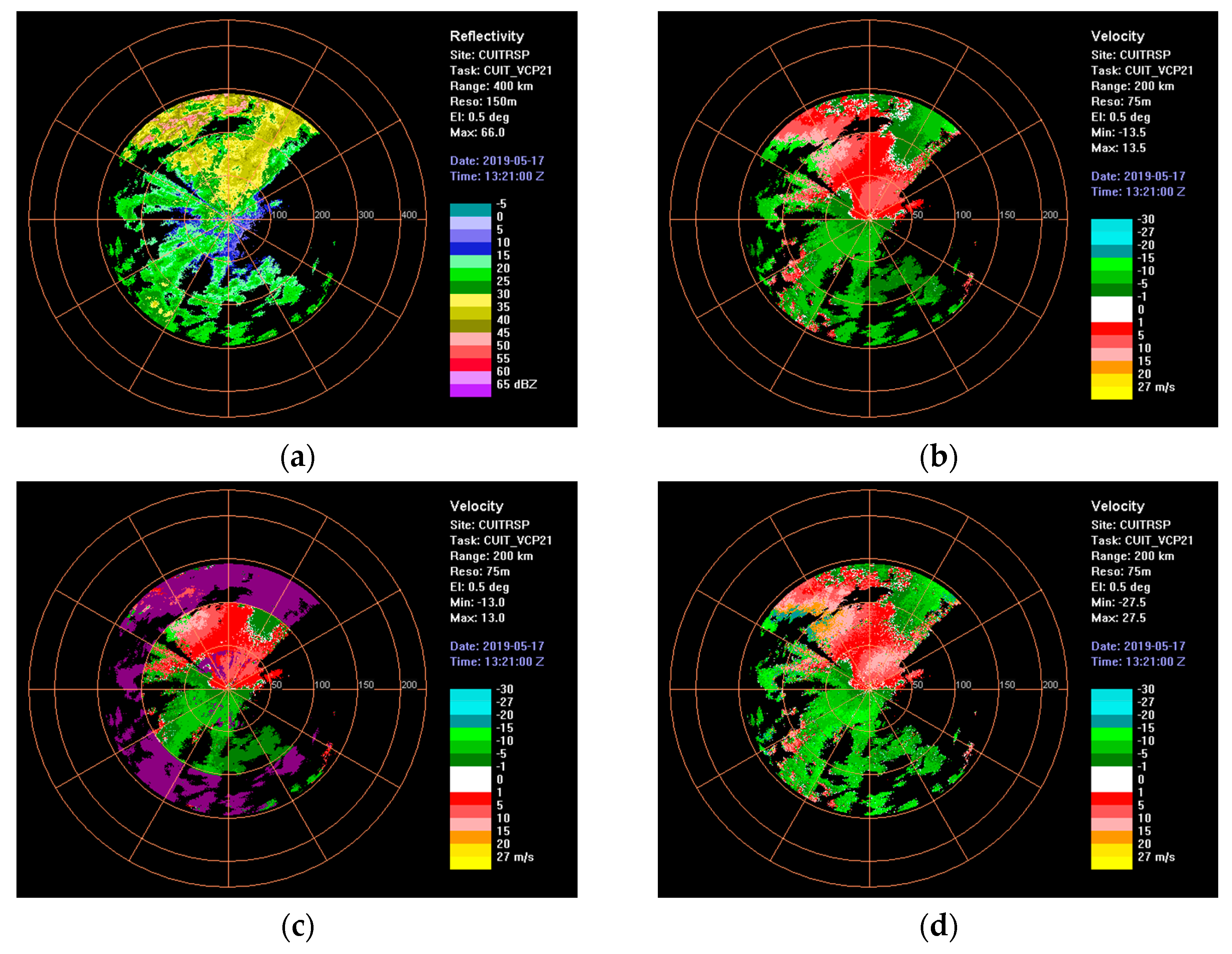
| Parameter | Parameter Value |
|---|---|
| Emissive power | 250 kw |
| Pulse width | |
| Horizontal beam width | |
| Vertical beam width | |
| Pulse repetition frequency | 2000 hz |
| Wave length | 5.3571 cm |
| Receiver gain | 35 dB |
| Antenna gain | 45 dB |
| Atmospheric loss | 0.016 dB |
| Noise power | −112 dB |
| Range Gate Number | Simulation Time (s) |
|---|---|
| 1 | 0.125 |
| 431,430 | 70.348 |
| Working Modes | |||
|---|---|---|---|
| Batch | 1000 | 150 | 13.3929 |
| 1500 | 100 | 20.0893 | |
| SZ(8/64) | 1000 (no phase code) | 150 | 13.3929 |
| 1500 (phase code) | 100 | 20.0893 |
| Working Modes | PO |
|---|---|
| Batch | 59.75% |
| SZ(8/64) | 0 |
| Working Modes | Standard Deviation |
|---|---|
| Batch | 1.2312 |
| SZ(8/64) | 1.1915 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, S.; Li, X.; Bu, Z.; Chen, Y.; He, J.; Li, M.; Xiong, M. Signal Simulation of Dual-Polarization Weather Radar and Its Application in Range Ambiguity Mitigation. Atmosphere 2022, 13, 432. https://doi.org/10.3390/atmos13030432
Dai S, Li X, Bu Z, Chen Y, He J, Li M, Xiong M. Signal Simulation of Dual-Polarization Weather Radar and Its Application in Range Ambiguity Mitigation. Atmosphere. 2022; 13(3):432. https://doi.org/10.3390/atmos13030432
Chicago/Turabian StyleDai, Shaojun, Xuehua Li, Zhichao Bu, Yajun Chen, Jianxin He, Minghua Li, and Maojie Xiong. 2022. "Signal Simulation of Dual-Polarization Weather Radar and Its Application in Range Ambiguity Mitigation" Atmosphere 13, no. 3: 432. https://doi.org/10.3390/atmos13030432
APA StyleDai, S., Li, X., Bu, Z., Chen, Y., He, J., Li, M., & Xiong, M. (2022). Signal Simulation of Dual-Polarization Weather Radar and Its Application in Range Ambiguity Mitigation. Atmosphere, 13(3), 432. https://doi.org/10.3390/atmos13030432






