Impact of Meteorological Uncertainties in the Methane Retrieval Ground Segment of the MERLIN Lidar Mission
Abstract
:1. Introduction
2. Materials and Methods
2.1. Meteorological Data in IPDA Lidar Methane Retrieval
2.2. Meteorological Data Availability
2.3. Time and Horizontal Interpolations
2.4. Vertical Interpolation and Extrapolation under the Model Topography
2.4.1. Different Methods
2.4.2. Comparison of the Different Methods on Two Examples
2.5. Intrinsic Uncertainties in Weather Forecasts
3. Results
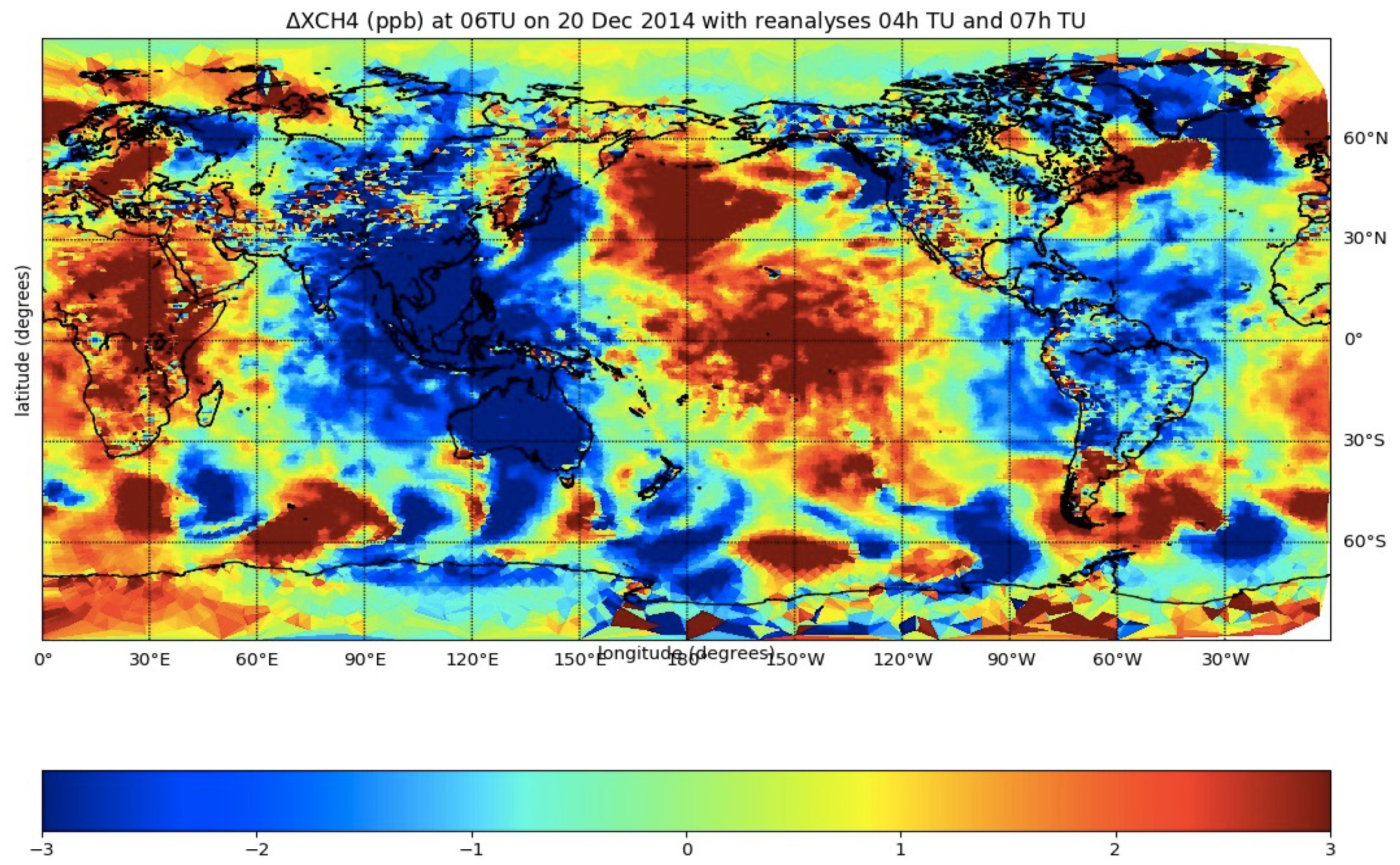
3.1. Time Interpolation and Tide Waves
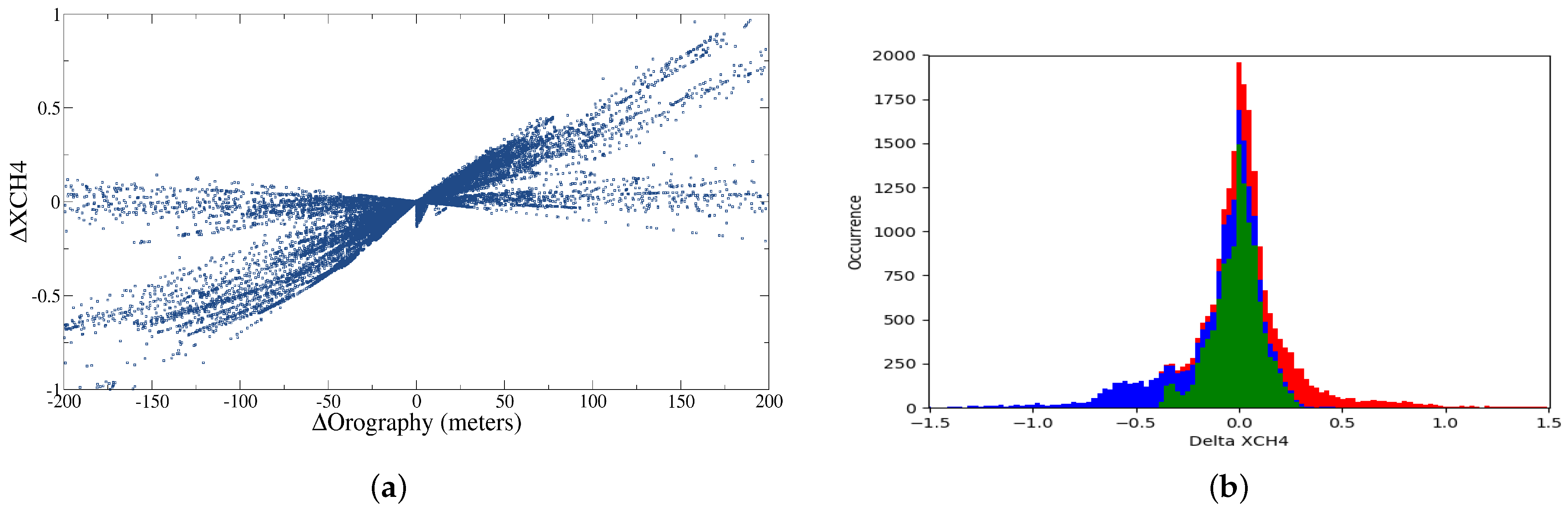
3.2. Impact on the Methane Retrieval of Vertical Interpolation Methods
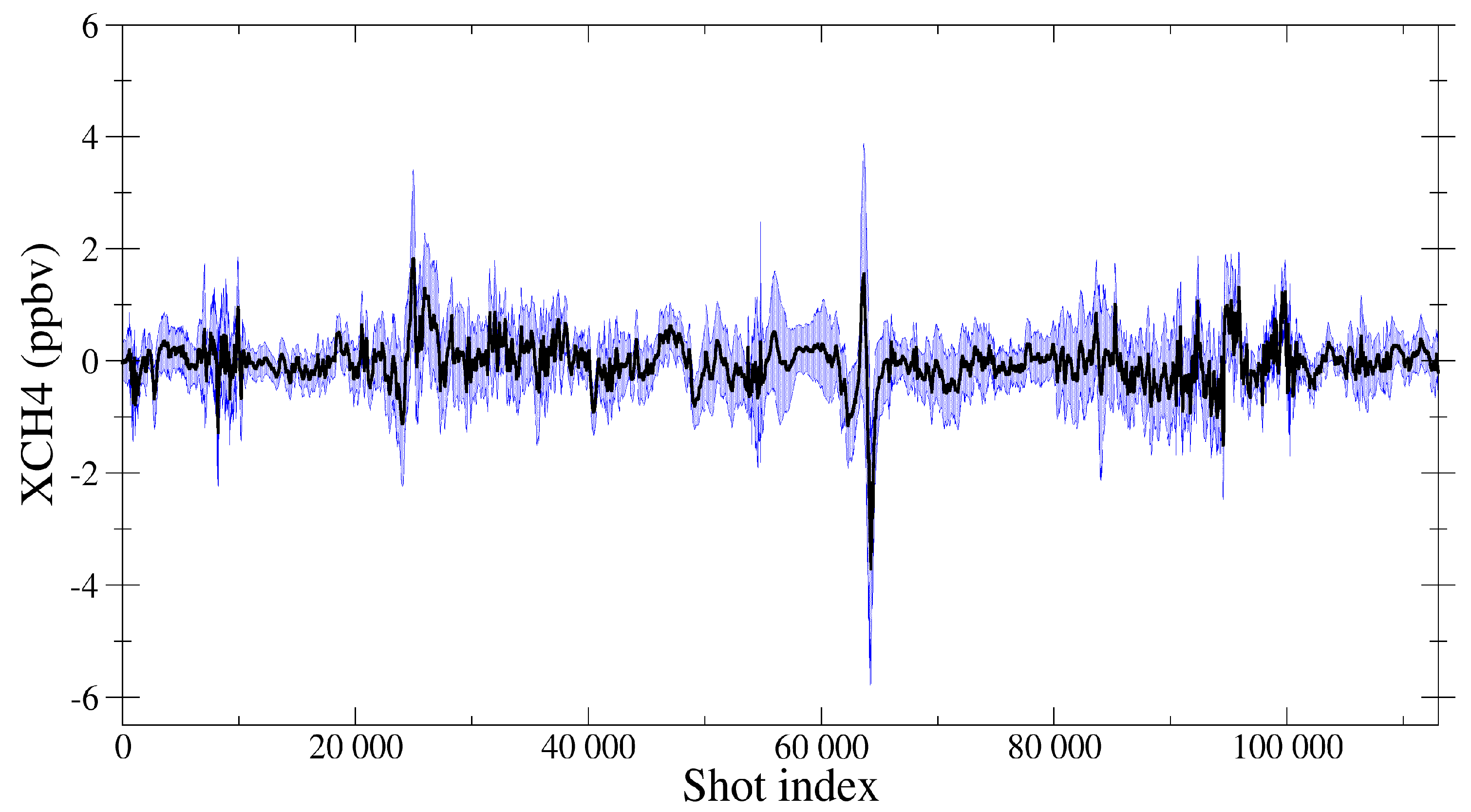
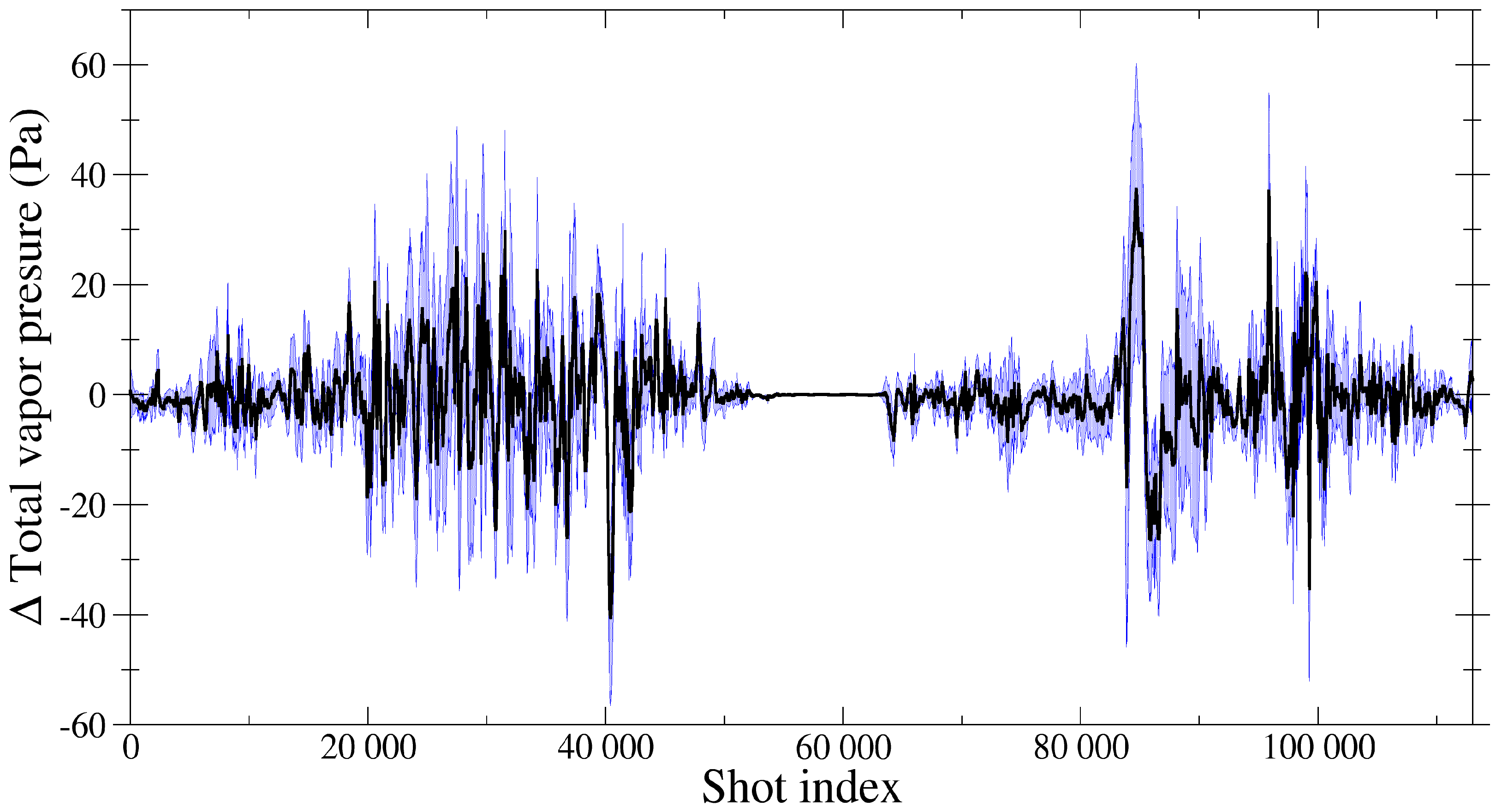
3.3. Sensitivity to the Analysis Errors
4. Discussion
4.1. Forecasting Errors
4.2. Horizontal Interpolations
4.3. Vertical Extrapolations
4.4. Time Interpolations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Standard Atmosphere
| Layer Number | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Layer limits in kmgp | 0–11 | 11–20 | 20–32 | 32–47 | 47–51 | 51–71 | 71–86 |
| Lapse rate in K/kmgp | −6.5 | 0 | +1.0 | +2.8 | 0 | −2.8 | −2.0 |
Appendix B. Standard Extrapolation
Appendix C. APACHE a Method for Maintaining the Boundary Layer
References
- Bousquet, P.; Pierangelo, C.; Bacour, C.; Marshall, J.; Peylin, P.; Ayar, P.V.; Ehret, G.; Bréon, F.M.; Chevallier, F.; Crevoisier, C.; et al. Error Budget of the MEthane Remote LIdar missioN and Its Impact on the Uncertainties of the Global Methane Budget. JGR Atmos. 2018, 123, 766–785. [Google Scholar] [CrossRef]
- Myhre, G.; Shindell, D.; Bréon, F.-M.; Collins, W.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.-F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/WG1AR5_Chapter08_FINAL.pdf (accessed on 18 February 2022).
- Ehret, G.; Bousquet, P.; Pierangelo, C.; Alpers, M.; Millet, B.; Abshire, J.B.; Bovensmann, H.; Burrows, J.P.; Chevallier, F.; Ciais, P.; et al. MERLIN: A French-German Space Lidar Mission Dedicated to Atmospheric Methane. Remote Sens. 2017, 9, 1052. [Google Scholar] [CrossRef] [Green Version]
- Nikolov, S.; Wührer, C.; Kühl, C.; Bode, M.; Hupfer, W.; Lucarelli, S. MERLIN: Design of an IPDA LIDAR instrument. CEAS Space J. 2019, 11, 437–457. [Google Scholar] [CrossRef]
- Wirth, M. (DLR, Oberpfaffenhofen, Germany). MERLIN ATBD: Algorithm Theoretical Basis Document Part 1/Top Level Algorithms for Primary L1/2 Products. MLN-PLDP-ATBD-90001-PI Version 1 Rev 2, published by CNES and DLR, Toulouse. 2018; unpublished internal document. [Google Scholar]
- Cassé, V.; Armante, R.; Bousquet, P.; Chomette, O.; Crevoisier, C.; Delahaye, T.; Edouart, D.; Gibert, F.; Millet, B.; Nahan, F.; et al. Development and Validation of an End-to-End Simulator and Gas Concentration Retrieval Processor Applied to the MERLIN Lidar Mission. Remote Sens. 2021, 13, 2679. [Google Scholar] [CrossRef]
- Han, G.; Gong, W.; Lin, H.; Ma, X.; Xiang, Z. Study on Influences of Atmospheric Factors on Vertical CO2 Profile Retrieving from Ground-Based DIAL at 1.6 μm. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3221–3234. [Google Scholar] [CrossRef]
- Buchwitz, M.; Reuter, M.; Bovensmann, H.; Pillai, D.; Heymann, J.; Schneising, O.; Rozanov, V.; Krings, T.; Burrows, J.P.; Boesch, H.; et al. Carbon Monitoring Satellite (CarbonSat): Assessment of atmospheric CO2 and CH4 retrieval errors by error parameterization. Atmos. Meas. Tech. 2013, 6, 3477–3500. [Google Scholar] [CrossRef] [Green Version]
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, CH4, and N2O by integrated path differential absorption Lidar: A sensitivity analysis. Appl. Phys. B Lasers Opt. 2008, 90, 593–608. [Google Scholar] [CrossRef] [Green Version]
- Jacquinet-Husson, N.; Armante, R.; Scott, N.A.; Chedin, A.; Crépeau, L.; Boutammine, C.; Bouhdaoui, A.; Crevoisier, C.; Capelle, V.; Boonne, C.; et al. The 2015 edition of the GEISA spectroscopic database. J. Mol. Spectrosc. 2016, 327, 31–72. [Google Scholar] [CrossRef] [Green Version]
- Delahaye, T.; Maxwell, S.E.; Reed, Z.D.; Lin, H.; Hodges, J.T.; Sung, K.; Devi, V.; Warneke, T.; Tran, H. Precise methane absorption measurements in the 1.64 μm spectral region for the MERLIN mission. JGR Atmos. 2016, 121, 7360–7370. [Google Scholar] [CrossRef] [PubMed]
- Delahaye, T.; Ghysels, M.; Hodges, J.T.; Sung, K.; Armante, R.; Tran, H. Measurement and modeling of air-broadened methane absorption in the MERLIN spectral region at low temperatures. JGR Atmos. 2019, 124, 3556–3564. [Google Scholar] [CrossRef]
- ECMWF, MARS—The ECMWF Meteorological Archive. Available online: https://www.ecmwf.int/node/18124 (accessed on 18 February 2022).
- ECMWF. IFS Documentation Cy47r1, Part II: Data Assimilation; ECMWF: Reading, UK, 2020. [Google Scholar] [CrossRef]
- Robinson, N.; Regetz, J.; Guralnick, R.P. EarthEnv-DEM90: A nearly-global, void-free, multi-scale smoothed, 90 m digital elevation model from fused ASTER and SRTM data. ISPRS J. Photogramm. Remote Sens. 2014, 87, 57–67. [Google Scholar] [CrossRef]
- ECMWF. IFS Documentation Cy47r1, Part III: Dynamics and Numerical Procedures; ECMWF: Reading, UK, 2020. [Google Scholar] [CrossRef]
- Simmons, A.J.; Chen, J. The calculation of geopotential and the pressure gradient in the ECMWF atmospheric model: Influence on the simulation of the polar atmosphere and on temperature analyses. Q. J. R. Meteorol. Soc. 1991, 117, 29–58. [Google Scholar] [CrossRef]
- ECMWF. IFS Documentation Cy47r1, Part I: Observations; ECMWF: Reading, UK, 2020. [Google Scholar] [CrossRef]
- Bubnová, R. Pouziti Souradnice “Hydrostaticky Tlak” pro Integraci Elastického Modelu Dynamiky Atmosféry v Numerickém Predpovednim Systému ARPEGE/ALADIN. Ph.D. Thesis, Paul Sabatier University, Toulouse, France, Charles University, Prague, Czech Republic, 25 April 1995. [Google Scholar]
- Chinaud, J.; Pierangelo, C.; Tyrou, V.; Millet, B. (CNES, Toulouse, France). MERLIN Level 2 error budget. MLN-SYS-TN-0399-CNS, Issue 5. 2021; unpublished internal document. [Google Scholar]
- ECMWF. IFS Documentation Cy47r1, Part V: Ensemble Prediction System; ECMWF: Reading, UK, 2020. [Google Scholar] [CrossRef]
- Isaksen, L.; Bonavita, M.; Buizza, R.; Fisher, M.; Haseler, J.; Leutbecher, M.; Raynaud, L. Ensemble of Data Assimilations at ECMWF; Technical Report 636; ECMWF: Reading, UK, 2010. [Google Scholar] [CrossRef]
- Martins, E.; Chinaud, J. Impact of the interpolation of the meteorological profiles on XCH4 retrievals. «Groupe Mission MERLIN» Meeting, LMD Palaiseau (France). 2020; unpublished internal document. [Google Scholar]
- Li, Z.; Chen, W.; Jiang, W.; Deng, L.; Yang, R. The Magnitude of Diurnal/Semidiurnal Atmospheric Tides (S1/S2) and Their Impacts on the Continuous GPS Coordinate Time Series. Remote Sens. 2018, 10, 1125. [Google Scholar] [CrossRef] [Green Version]
- Chevallier, F.; Chédin, A.; Chéruy, F.; Morcrette, J.-J. TIGR-like atmospheric-profile databases for accurate radiative-flux computation. Q. J. R. Meteorol. Soc. 2000, 126, 777–785. [Google Scholar] [CrossRef]
- Kiemle, C.; Quatrevalet, M.; Ehret, G.; Amediek, A.; Fix, A.; Wirth, M. Sensitivity studies for a space-based methane lidar mission. Atmos. Meas. Tech. 2011, 4, 2195–2211. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Ray, R.D.; Ponte, R.M. Barometric tides from ECMWF operational analyses. Ann. Geophys. 2003, 21, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Amediek, A.; Ehret, G.; Fix, A.; Wirth, M.; Budenbender, C.; Quatrevalet, M.; Kiemle, C.; Gerbig, C. CHARM-F a new airborne integrated-path differential-absorption lidar for carbon dioxide and methane observations: Measurement performance and quantification of strong point source emissions. Appl. Opt. 2017, 56, 5182–5197. [Google Scholar] [CrossRef] [PubMed]
- Crevoisier, C.; Bes, C.; Joly, L.; Té, Y.; Ramonet, M.; Herbin, H.; Catoire, V.; Fix, A.; Cézard, N.; Bourdon, A.; et al. Overview of the MAGIC Initiative for GHG and Future Plans. In Proceedings of the International Workshop on Greenhouse Gas Measurements from Space, IWGGMS-17, Online Conference, 15 June 2021; Available online: https://cce-datasharing.gsfc.nasa.gov/files/conference_presentations/Talk_Crevoisier_148_25.pdf (accessed on 18 February 2022).
- COESA (Committee on Extension to the Standard Atmosphere). U.S. Standard Atmosphere, 1976; U.S. Government Printing Office: Washington, DC, USA, 1976. Available online: https://www.ngdc.noaa.gov/stp/space-weather/online-publications/miscellaneous/us-standard-atmosphere-1976/us-standard-atmosphere_st76-1562_noaa.pdf (accessed on 18 February 2022).
- Simmons, A.J.; Burridge, D.M. An energy and angular momentum conserving vertical finite difference scheme and hybrid vertical coordinates. Mon. Weather Rev. 1981, 109, 758–766. [Google Scholar] [CrossRef] [Green Version]
- ECMWF. IFS Documentation Cy47r1, Part IV: Physical Processes; ECMWF: Reading, UK, 2020. [Google Scholar] [CrossRef]
- Buck, A.L. New Equations for Computing Vapor Pressure and Enhancement Factor. J. Appl. Meteorol. Climatol. 1981, 20, 1527–1532. [Google Scholar] [CrossRef] [Green Version]


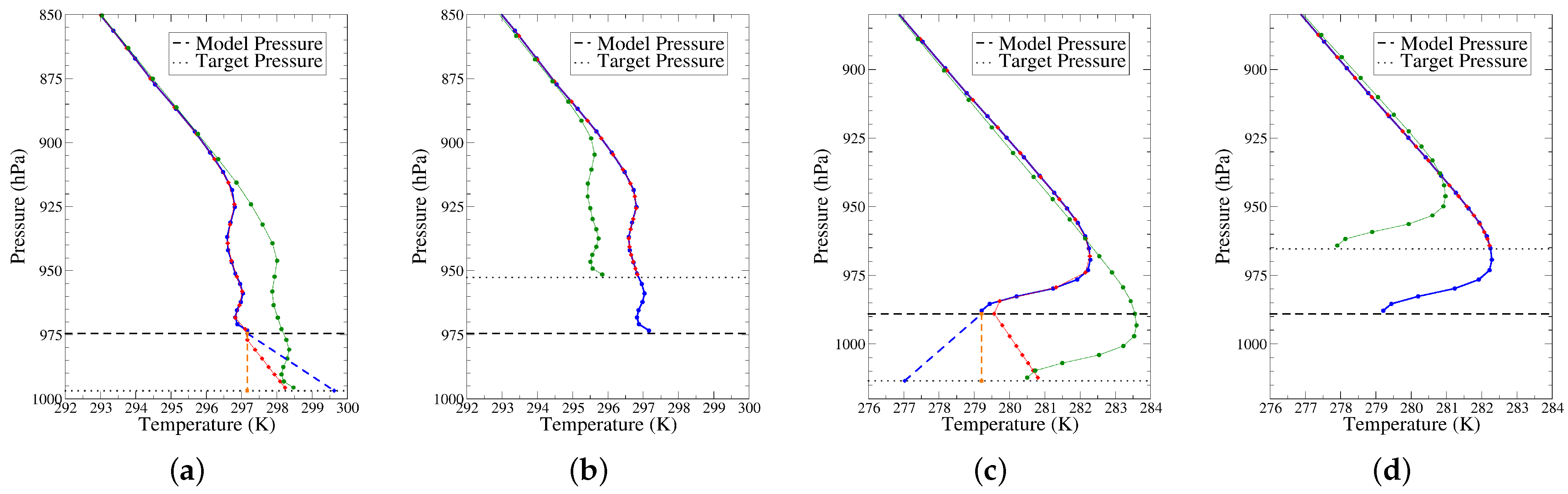
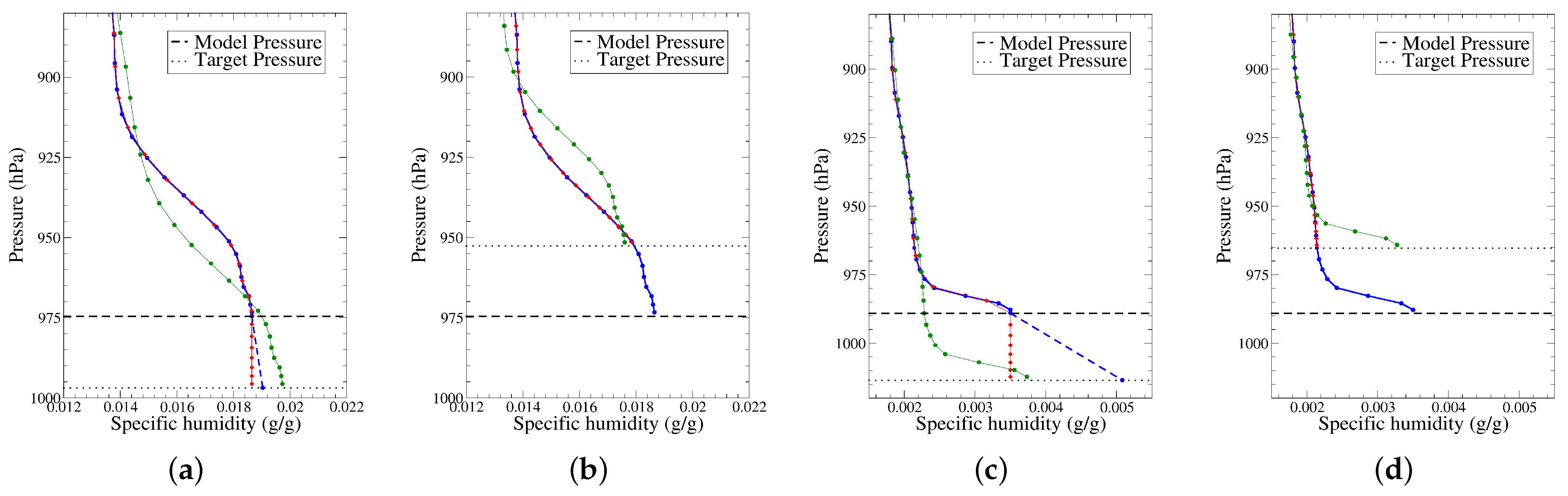
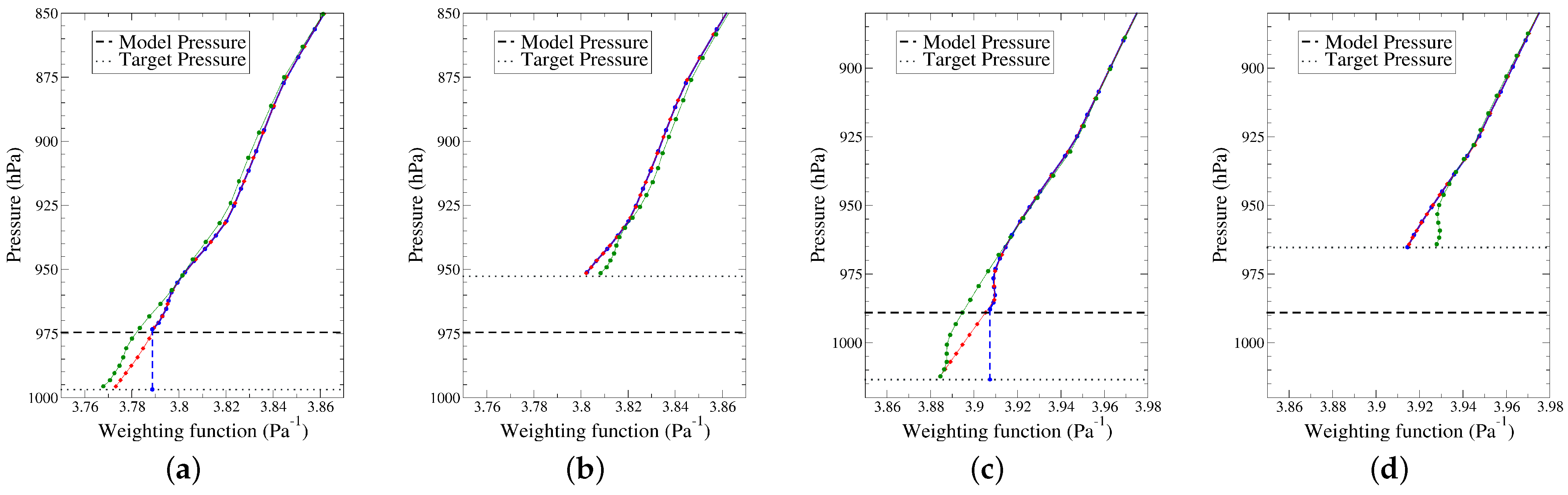

| Method | Zero Gradient | Last Gradient | Standard Gradient | APACHE |
|---|---|---|---|---|
| Extrapolation with | zero gradient | gradient determined from the latest levels of the weather model | standard gradient | |
| Conservative properties | potential temperature gradient and relative humidity | |||
| Resampling | no | no | yes | yes |
| Extrapolation in LIDSIM with | ||||
|---|---|---|---|---|
| Extrapolation in PROLID with | Zero Gradient | Last Gradient | Standard Gradient | APACHE |
| zero gradient | 0.239/11.3 | 0.091/5.93 | 0.112/2.90 | |
| last gradient | ||||
| standard gradient | 0.266/13.1 | 0.063/0.30 | 0.114/2.85 | |
| APACHE | 0.268/12.3 | 0.100/3.17 | 0.066/0.34 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cassé, V.; Chomette, O.; Crevoisier, C.; Gibert, F.; Brožková, R.; El Khatib, R.; Nahan, F. Impact of Meteorological Uncertainties in the Methane Retrieval Ground Segment of the MERLIN Lidar Mission. Atmosphere 2022, 13, 431. https://doi.org/10.3390/atmos13030431
Cassé V, Chomette O, Crevoisier C, Gibert F, Brožková R, El Khatib R, Nahan F. Impact of Meteorological Uncertainties in the Methane Retrieval Ground Segment of the MERLIN Lidar Mission. Atmosphere. 2022; 13(3):431. https://doi.org/10.3390/atmos13030431
Chicago/Turabian StyleCassé, Vincent, Olivier Chomette, Cyril Crevoisier, Fabien Gibert, Radmila Brožková, Ryad El Khatib, and Frédéric Nahan. 2022. "Impact of Meteorological Uncertainties in the Methane Retrieval Ground Segment of the MERLIN Lidar Mission" Atmosphere 13, no. 3: 431. https://doi.org/10.3390/atmos13030431
APA StyleCassé, V., Chomette, O., Crevoisier, C., Gibert, F., Brožková, R., El Khatib, R., & Nahan, F. (2022). Impact of Meteorological Uncertainties in the Methane Retrieval Ground Segment of the MERLIN Lidar Mission. Atmosphere, 13(3), 431. https://doi.org/10.3390/atmos13030431






