Mid-Latitude Detection of High Schmidt-Number Turbulent Echoes, and Comparison to PMSE and Geomagnetic Variations

Abstract

Unexpected observations of strong radiowave scatter at a ~85–90 km altitude with very high frequency radars were explained in the early 1990s, when it was demonstrated that these were due to special turbulent and small-scale scatterers with high Schmidt number. Studies of these phenomena have primarily been concentrated in polar regions, and the events seem most prominent in regions of very cold air (below 140 K). Such radar echoes are referred to as polar mesosphere summer echoes (PMSE), and are rare at lower latitudes. In this paper we report observations of similar scatterers at sites below 50° latitude. The nature of these scatterers is discussed and results are compared to observations at the polar site of Eureka, Canada. Mid-latitude observations at frequencies of 48.92 and 45.47 MHz were made, respectively, at Abitibi Canyon (49.9° N latitude) and Markstay (46.5° N latitude) in Ontario, Canada. In particular, we look at the relationship of these scatterers to geophysical parameters, especially the A_p index. Our results suggest that mesospheric air with temperatures less than 140 K now exists below 50° latitude. This may be an indication of an equator-ward creep of global mesospheric cooling (which is associated with the well-known tropospheric global warming), but the scatterers at lower latitudes also demonstrate correlation with the A_p index. On the other hand, the polar scatterers at Eureka demonstrated no correlation of any significance with A_p. The importance of these results in regard to the global distribution of mesospheric temperatures is discussed, and comparisons to other measurements are made.

1. Introduction

Radiowave scatter from the mesosphere and lower thermosphere at frequencies of 2 to 100 MHz has been discussed for many years. Medium frequency (MF: 0.3–3 MHz) and high frequency (HF: 3–30 MHz) radars have been used since the 1960s to determine winds and study turbulence at 60 to 95 km altitude (e.g., [1,2,3], and references therein). A review is presented by [4]. In the 1970s, reports were published of observations at higher frequencies of the order of 50 MHz, which demonstrated detectable scatterers in the troposphere, stratosphere, and mesosphere [5]. The discovery of these scatterers led to the development of so-called wind profiler radars, which were used for studies of winds and turbulence in the troposphere, lower stratosphere, and mesosphere. This became a large field of endeavour, and the reasons for the existence of the scatterers became fairly well understood. However, predictions of scatter from heights above 80 km suggested that due to properties of atmospheric turbulence, no scatter should be expected at ~50 MHz frequencies above typically 80–85 km. However, on occasions such scatterers were observed, (e.g., [6,7], among others), although scatter from these upper levels was often confined to summer.

It was not until the early 1990s that the unusual nature of scatterers from these upper levels was fully appreciated. Ref. [8] was the first to recognise the unique nature of these scattering layers, and established that these echoes could not be explained by traditional theories of turbulence: subsequent reviews can be found in Refs. [9,10], among others.

Detailed investigations demonstrated that the scatterers could be explained by anomalously large Schmidt numbers S_c, where S_c defines the rates of diffusion of neutral turbulence relative to ion diffusion. It was proposed that diffusion of charged particles was adversely affected by the existence of large clusters of charged ions, each of which had a surrounding cloud of electrons (“dressed aerosols”). This suppresses the rates of diffusion of electrons and hence allows the so-called inertial range of turbulence to extend to smaller scales.

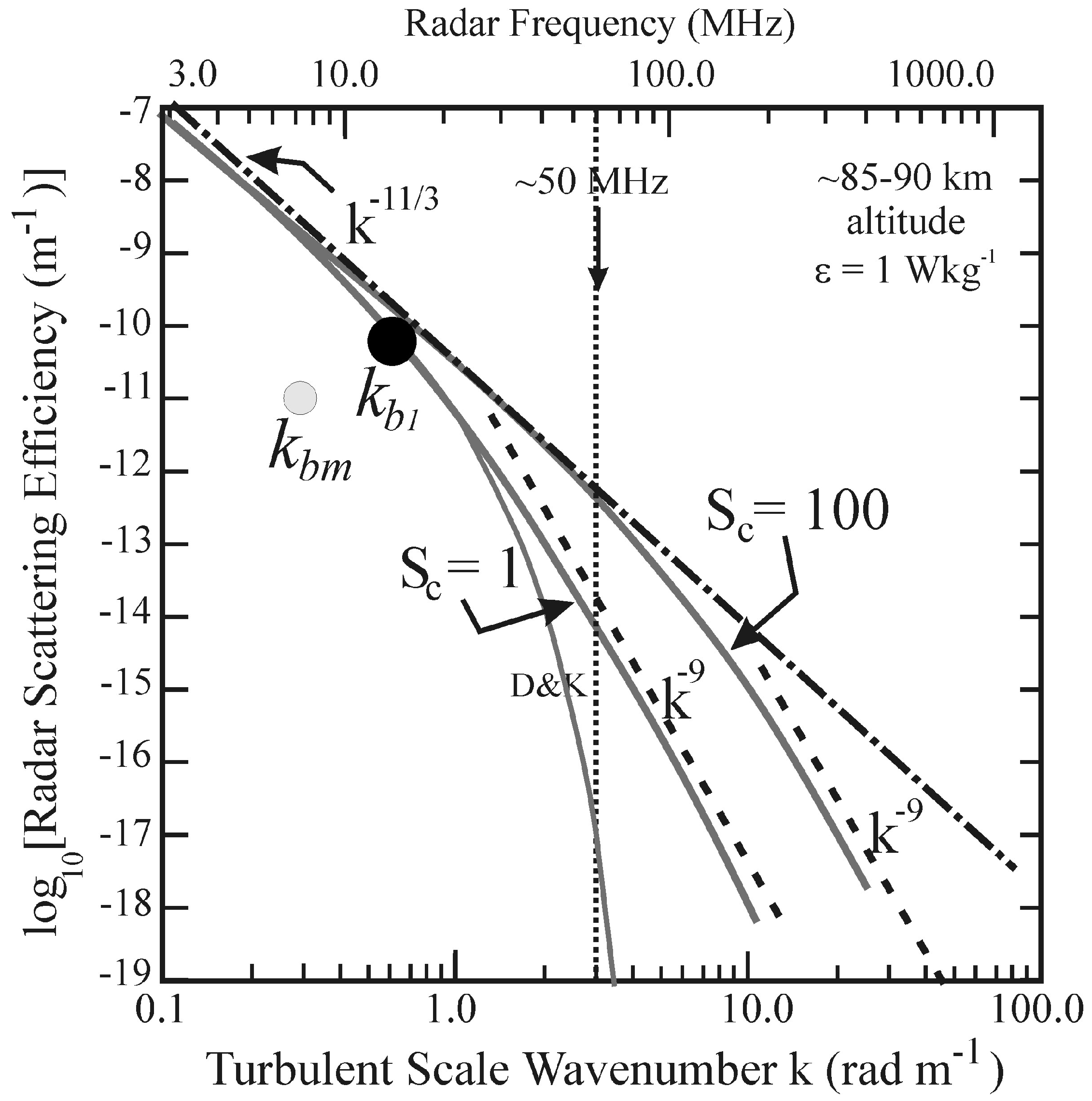
Figure 1 (which is a significant expansion of Figure 8 from Ref. [8]) shows the impact of the large Schmidt number. The spectral density of a nominally isotropic turbulent patch is shown as a function of the wavenumber along any direction in a 3-D spectral decomposition. Radar backscattered power is proportional to this quantity, but needs to be multiplied by k⁴. (To understand the need for this, see Equation (3.196) in Ref. [11], where a “k” term is observed to appear in the Poynting vector, and this carries through from Equation (3.197) to Equation (3.233) and (3.238)). As we are only interested in relative impact, the k⁴ term is not included for now. The lower abscissa can be interpreted in two ways. First, it can be considered as k = 2π/λ_t, where λ_t is the “wavelength” of the turbulent Fourier component (“scale”) of interest. Because radar scattering is a resonant Bragg scattering process, the radar wavelength that will scatter most dominantly from the scale λ_t will have a wavelength of λ = 2λ_t, so secondly, k can also be considered as 4π/λ. The scale across the top refers only to the radar, and gives the frequency of the radar required to produce a wavelength λ (=4π/k), so f = c/λ = ck/(4π).

The spectral density varies proportionally to k^−11/3 in the inertial range of turbulence. As the wavenumber increases, the spectrum enters the so-called “viscous range”, at which point Ref. [12] predicted that the slope would become closer to k⁻⁹. This occurs close to the “inner scale”, drawn as the wavenumber approximately at the point labelled k_b1. The behaviour for “normal” atmospheric turbulence is shown by the curve labelled as S_c = 1.

The point k_b1 can be determined from the inner scale of turbulence, which is determined from the structure function; here, the inner scale is denoted as ℓ₀. The value of ℓ₀ is given by ℓ₀ ≈ 7(ν³/ε)^0.25 (e.g., [11], Equation (10.1)), where ν is the kinematic molecular diffusion coefficient and ε is the turbulent kinetic energy dissipation rate. Taking ε = 1 W kg⁻¹ (as specified in the figure), and using ν as approximately 2 m² s⁻¹ (see Figure 11.33 in Ref. [11] for ~80–85 km altitude), gives ℓ₀ ≈ 12 m. Because the structure functions and spectra are both power laws (the Fourier transform of a power law is another power law), this expression can be converted to k_b1 via k_b1 = 2π/ℓ₀, so k_b1 ≈ 0.5, as plotted in Figure 1. Additional evidence that k_b1 can indeed be written as ≈2π/ℓ₀ can be observed in Ref. [13], Figure 3, where the intercepts of a change in power law in both the structure function and in the spectrum are related by k_b1 = 2π/ℓ₀ (after adjusting for the fact that the spectra are plotted there as inverse wavelengths).

A choice of ε = 1 W kg⁻¹, as used by Ref. [8], is somewhat on the high side, and represents the most extreme turbulence observed in the mesosphere. More typically, ε is in the range 0.01 to 0.1 W kg⁻¹ (see Figure 11.28 in Ref. [11], and Ref. [14]), so for ε = 0.05, the point k_b1 shifts to k_bm in the figure, and the whole curve “S_c = 1” shifts along with it. It will be noticed that this value of k_bm is also consistent with Ref. [3] and also with Figure 11.25 from Ref. [11], which show ℓ₀ to be between 20 and 40 m. Notice also that in the process of moving to k_bm, the “radar scattering efficiency” is also diminished. For our purposes here, Figure 1 stands as a representation of high values of turbulence strengths, but still serves as at least a guide for our discussions in regard to weaker turbulence.

Returning to the implications of Figure 1 for radar scatter, we first note that a rapid drop-off in scattering cross-section at larger scales (>k_b1) is apparent. More sophisticated modelling (e.g., [15]) demonstrate that the drop-off may be even more rapid (as indicated by the thin line labelled “D&K”). The decrease of scatter in the viscous region relative to the inertial-range prediction at a radar frequency of ~50 MHz is at least a factor of 100, and ~10⁵ if the “D&K” curve is used. This effect ensures that 50 MHz radio wave scatter from 85–90 km altitude should not be detectable if the scatterers are due to “classical” turbulence.

As seen from the curve labelled S_c = 100, the existence of a large Schmidt number allows the inertial range to extend to larger wavenumbers (smaller scales), which means that the scatter at ~50 MHz is now potentially detectable (remembering that the spectral densities need to be rescaled by k⁴, as discussed earlier).

The primary factor that leads to large Schmidt numbers at these heights is related to very cold temperatures. These cold temperatures permit ice crystals to form, which then become the nuclei for the “dressed aerosols”. Temperatures as low as 140 K and less are necessary for this model to work, and measurements demonstrated that indeed such low temperatures did exist in the polar mesosphere at 80 to 90 km altitude. In fact, Ref. [16] demonstrated that over 80% of PMSE existed in atmospheric regions where the temperatures were less than 140 K. This has also been discussed by Ref. [10]. Of course in order for such crystals to be formed, there is also a need for water vapour, and the absence or existence of water vapour has also been discussed by various authors (e.g., [17], and references therein). The potential importance of methane for formation of noctilucent clouds (and by likely extension, the formation of PMSE) has also been discussed by Ref. [18].

The SOUSY radar in Germany (52 N) did see echoes at 52° N, which could (retrospectively) be interpreted as PMSE-like phenomena (see Ref. [6], for example), and more recently, PMSE-like echoes have been reported using a 53.5 MHz radar near Kühlungsborn, Germany at latitude 54° N [19]. Mid-latitude signals measured with a HF SuperDARN radar at 43.5° N have also been reported by Ref. [20], and while interesting, this comes as no surprise.

In order to understand this last sentence, it is necessary to emphasise an important point. While echoes at 80–90 km have indeed been reported using a SuperDARN radar working at 9 and 11 MHz [20], this does not necessarily indicate a cold mesopause. As can be observed from Figure 1, scatter at frequencies of 10 MHz and less is fully expected even without dressed aerosols. Observations at frequencies above ~20 MHz must be made before the need for dressed aerosols arises (even for ε as low at 0.05 Wkg⁻¹), so the SuperDARN echoes reported in Ref. [20] do not tell us much about temperatures. Of course the temperatures could have been cold, but these HF observations do not tell us anything about it. The observation of true VHF echoes with the radar at Wakkanai, reported in Ref. [20] (and also reported in earlier papers referenced within Ref. [20]), are more significant, as they suggest true PMSE-type echoes at 45.4° N, though the echoes were only observed on one or two occasions. The SuperDARN echoes may be called mesospheric summer echoes, but they do not possess the special properties discussed in regard to Figure 1, and could equally occur at any time of year. For this reason, no further references to MF and HF observations of “mid-latitude summer echoes” will be made in this paper. Correlations between HF and VHF observations have been performed, with mixed results, but these comparisons need to be made recognizing our forgoing comments. These studies are not the focus of our work.

Returning to our general discussion, it is also important to note that scatter does not only have to be due to turbulence, and other small-scale events, such as viscosity waves and similar small-scale wavelike events, could explain the observed radar signatures, e.g., [21,22]. Nevertheless, regardless of whether the scatterers are due to turbulence or waves, the importance of low temperatures, water vapour and high Schmidt numbers remains necessary for these entities to produce radar scatter at ~40–50 MHz.

This altitude region is already expected to be cold relative to the lower altitudes because it is a region from which infrared radiation is emitted to space, (complementing the greenhouse warming that occurs in the troposphere) but temperatures as low as 140 K cannot be explained solely by such thermal radiation. The existence of even further cooling, leading to extremely cold temperatures at 80 to 90 km altitude in the summer, was originally explained by Ref. [23], who demonstrated the impact of gravity waves on inducing upper level (~80–90 km altitude) meridional flow out of the summer polar regions and into the winter polar regions. This results in rising air and subsequent adiabatic cooling at the summer poles, leading to these extreme temperature minima (e.g., see Ref. [11], Figure 11.19, for a suitable illustration and discussion).

Hence, the combination of these physical processes leads to the altitude-region at ~85 km to 90 km in the summer being the coldest place on Earth, with temperature so low that some super-conducting materials could operate there. The radar signals produced by the scatterers discussed above are referred to as “Polar Mesosphere Summer Echoes”, or PMSE. They have been a focus of much study, and are often coincident with noctilucent clouds (NLC) (e.g., [24]), which also require cold temperatures and ice particles.

As a brief summary, the following sequence gives a guide to PMSE formation. Ice particles form in the upper atmosphere, and we focus on the 85–90 km altitude region, where temperatures are coldest due to the effects of radiative cooling to space plus adiabatic cooling of the rising air. As the ice crystals grow, they become as large as 20 nm in diameter. As a consequence, they fall in altitude, but usually stay within the 80–90 km range. They are then subject to plasma immersion, in which the ice particles are ionised [10]. This process leads to the formation of charged aerosols surrounded by clusters of electrons, producing “dressed aerosols”, which have very slow diffusion rates. As it is the electrons that principally produce radio-wave scatter, the scatterers which produce the radar scatter are dominated in their motions by these dressed aerosols, leading to extension of the turbulence spectrum, as discussed in regard to Figure 1 (also see Ref. [25]). It has also been demonstrated that around 50% of the free electrons need to be bound to the charged aerosols for this process to take place [26]. The electron density of the atmosphere also plays a large role in PMSE formation. It has been observed that PMSE’s will form during the day if the density rises to above 500 electrons/cm³ [19].

By far the majority of studies of these phenomena have taken place in polar regions (e.g., [27,28,29,30,31], among others), but with hindsight, it appears that they may also have been detected earlier at lower latitudes, and recent studies (discussed above) have confirmed “dressed aerosol”-type scatterers at 45−55° latitude [19,20]. It is worth remembering that some of these are quite powerful radars. For example, as discussed, Ref. [6] used a peak power of 600 kW (e.g., [32]).

This paper will focus on these mid-latitude mesospheric summer echoes, which we will refer to as MMSE. Section 2 presents details about our radars and sites, and compares them to similar instruments elsewhere. Section 3 presents the main observations of mesospheric summer echoes that are pertinent to this paper. Section 4 compares our results to other potentially relevant parameters, including geomagnetic ones, and Section 5 discusses current and potential reasons for the effects observed.

2. Materials and Methods

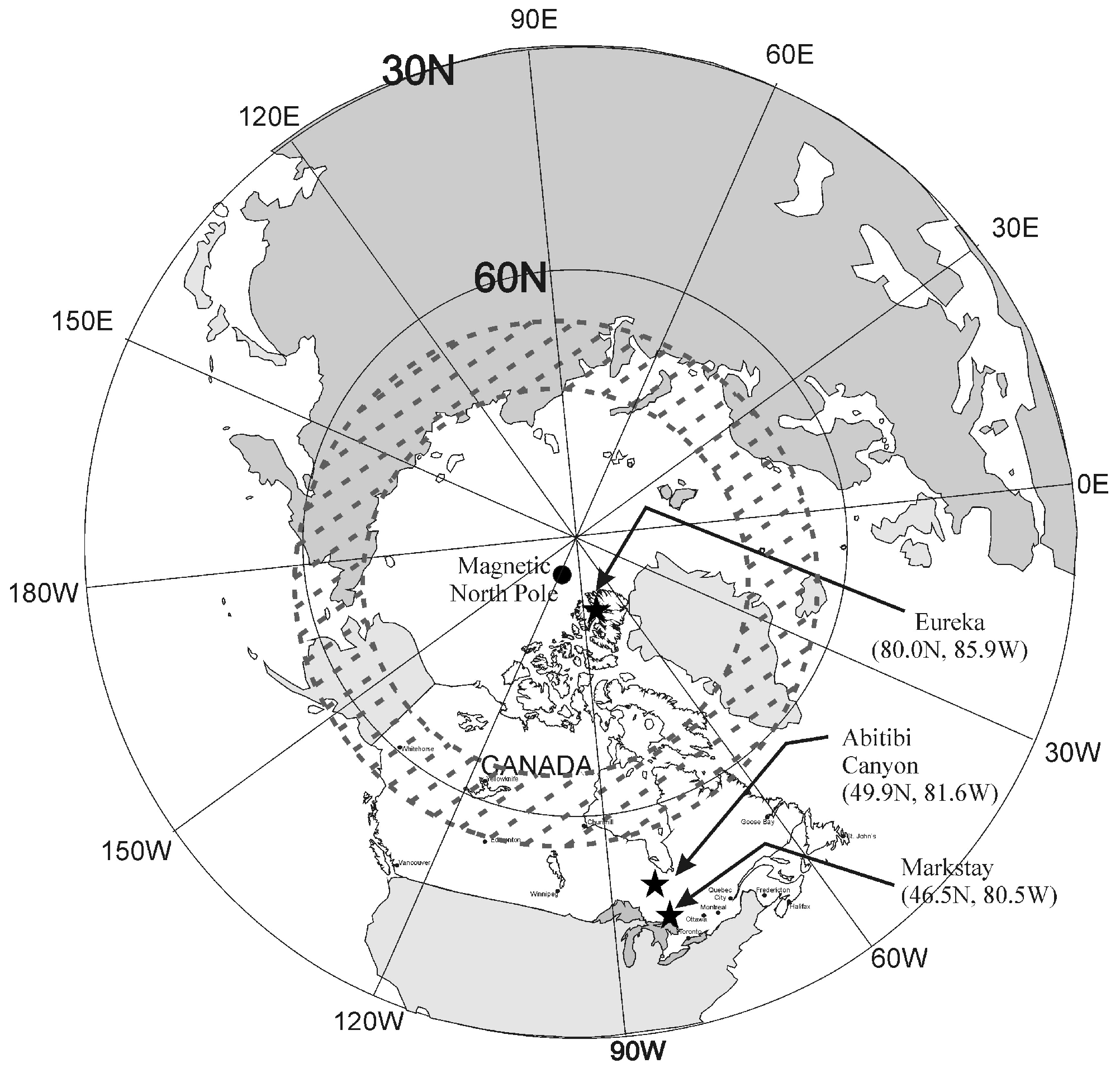
Figure 2 shows the locations of the three radars used in this study. All have a longitude between 80° W and 86° W, and the latitudes vary from 46.5° north to 80° N. It is noteworthy that the auroral oval reaches its lowest geographic latitude just north-west of Abitibi Canyon. The relevance of the auroral oval will be reported later in the paper; we will remind the reader, however, that the auroral oval is not generally a circle, but often stretches further into the night side than it does into the solar side, and expands and contracts in size depending on solar geomagnetic activity. The geomagnetic latitude of Abitibi Canyon is approximately 58° N, with a magnetic field inclination of 74° (year of 2018). The magnetic north pole is also currently drifting at a speed of ~40–50 km per annum, and 10–20 years ago was located south of Eureka. At that time, the auroral oval would have approached even closer to Abitibi Canyon. Our data were recorded in 2018–2019.

All three radars are VHF, ST-type radars with moderate power. This means they are really only designed to achieve backscatter from the lower stratosphere and troposphere. The peak power in each case is typically 32 kW and all have similar antenna designs. The antenna arrays each consist of 128 Yagi antennas, and each covers an area of typically 3500 m². The radars at Eureka and Markstay have standard recording procedures and use various types of pulse coding, including complementary codes and Barker codes. The system at Abitibi Canyon used the deconvolution procedure introduced by Ref. [33].

System parameters for the radars are given in

Table 1. (a) Parameters of the Abitibi radar. This table is also representative of Markstay and Eureka, although site-to-site variations do exist. Part (b) shows variations for the Markstay and Eureka radars.

(a)
Parameter		Value
Location		Abitibi Canyon, near Fraserdale Ont. (49.88 N, 81.57 W)
Operating frequency		48.92 MHz
One way half-power half-beam-width		2.75 degrees
Total area of antenna field		3500 m2 (Partially filled)
Typical mean power		1600 W
Peak power output		32 kW
Beam gain		25 dB
Wind measurement mode		Doppler
Pulse length		100, 250, 500, 1000 m (tunable)
Peak power aperture product		1.1 × 108 Wm2
Duty cycle		5–10%
Pulse compression mode		Real-time pulse deconvolution [33]
Height resolution		0.25–1.0 km
Number of beams		5 (Vertical + 10.9° off-vertical at 90° azimuthal steps)
Alignment of nominal north beam		12° clockwise from true geographic North
Suppression of ground-level gain		120 dB (2-way)
(b)
Site	Parameter	Value
Eureka	Location	Eureka Weather Station 79.98° N, 85.93° W
	Alignment of nominal north beam	30° anti-clockwise from true geographic North
	Operating frequency	51.00 MHz
	Pulse compression modes	Complementary, Barker codes, 1–8 bits
Markstay	Location	Markstay, Ont., Canada (46.54° N, 80.53° W)
	Alignment of nominal north beam	26° clockwise from true geographic North
	Operating frequency	45.47 MHz
	Pulse compression modes	Complementary, Barker codes, 1–8 bits

. The frequencies used at the radars are 45.47 MHz for Markstay, 48.92 for Abitibi, and 51.0 MHz at Eureka. (Antenna layouts and photographs of typical radars can be found in Refs. [34,35], and Supplementary Section 1 of Ref. [36], among others.) We will not delve further into the radar properties, as these can be found in such earlier references.

Note that the peak power of each of these three radars is ~20 times less than the power of that of the SOUSY radar in the 1970s. Our radars have peak power aperture products (PPAP’s) of about 1.1 × 10⁸ W m² and would normally be considered quite modest instruments, whereas the PPAP for SOUSY was 2.5 × 10⁹ W m² [6,32], or 23 times that of our radars. For comparison, we will also present the PPAP’s of two other radars at similar mid-latitudes and frequencies that we have discussed earlier. These are the OSWIN radar in Kühlungsborn, Germany (latitude = 54.1 N, frequency = 53.5 MHz) [19], and the Wakkanai VHF radar in Japan (latitude = 45.4 N, frequency = 46.5 MHz) [20]. These had PPAP’s of 6.8 × 10⁷ Wm² and 2.0 × 10⁸ W m², respectively. These are similar to our own radars. The OSWIN and Wakkanai radars used either long monopulses or 4 and 8-bit complementary codes; the Markstay radar used 4-bit complementary codes, while the Abitibi radar used a 2 km-long pulse with a swept frequency embedded inside it, and deconvolved the pulse down to 500 m resolution in real time [33]. As we shall see, all three of our radars observed significant quantities of summer mesospheric echoes, with our 2 mid-latitude radars detecting the echoes with similar signal-to-noise ratios as OSWIN and the Wakkanai radar.

The latitude at Abitibi Canyon is just below 50° north, and the site at Markstay in Ontario is at 46.5° latitude. The system at Eureka in northern Canada is at 80° N and has summer echoes, which are recognised as “traditional” PMSE. The observation of mesospheric summer echoes at Abitibi Canyon and Markstay represents some of the lowest latitudes at which such echoes have been observed up to this time, with only the Wakkanai detections having a comparably low latitude. The low peak power used at these radars makes the observation of these echoes surprising, and hence very important.

3. Observations

Figure 3 shows typical results for the Eureka radar. Such results for Eureka have been presented in various papers, e.g., [27,28,29,30,37].

The results presented for Eureka will be used as a “standard” against which the observations at lower altitudes will be compared. In general, a range-resolution of typically 500 m to 750 m was used, and data are averaged in 750 m bins. All radars used 5 beams—one vertical beam and 4 off vertical. The off-vertical beams were pointed at 10.9° off vertical, with directions at 90° steps azimuthally. The azimuthal directions of the tilted beams are summarised in Table 1.

In Figure 3, and in subsequent figures, we generally do not present all beams, in order to save space. Power units used in Figure 3 are arbitrary, but are the same for all beams. Generally the vertical beam and 1 or 2 off-vertical beams are presented, as confirmation that the scattering layer is spread over an area of several tens of km², and is not some artefact, such as a long-lived meteor trail. Careful examination of Figure 3 (and later ones) demonstrate that the range to the scattering layer as observed on the off-vertical beam is generally ~1.5 km larger than that on the vertical beam, as would be expected for an approximately horizontal scattering layer.

One point of considerable note is that in all cases shown in Figure 3 for Eureka, the signals seem most dominant in the hours between 12:00 GMT and 02:00 GMT, and are quite weak or non-existent between 04:00 and 12:00. The reasons for this will be discussed shortly.

In Figure 4, radar echoes recorded at Abitibi Canyon are presented. Again, a range-resolution of generally 500 m to 750 m was used, and data are presented at 750 m steps. In this case the signal-to-noise ratio is presented, where the “noise level” is taken as the mean noise across the full temporal width of the graph. The noise is calculated using averages of data at heights and times where no significant power increase is evident. The mean noise level was generally about 1 dB less on the vertical beam than the off-vertical beams, and was in the main dominated by galactic skynoise. In regard to scattering layers, it is clear that layers are evident on all beams shown, and such layers were evident on most days throughout the summer. As in the case of Figure 3, a 1.5 km offset in range is apparent on the off-vertical beams, confirming that these were extended layers with horizontal extents in excess of 30 km.

Figure 5 shows mesospheric echoes recorded with the Markstay radar on 28 July 2021. In this case the layers are shorter-lived than the ones at Eureka and Abitibi, being about 45–60 min in duration. Data on all beams are shown, in order to confirm that this truly was a mesospheric layer and not an artefact. Our MMSE research program at Markstay, encouraged by results from Abitibi Canyon, was only begun in mid July, 2021, so it was only possible to catch the end of the MMSE season. A more complete summer of observation is planned for 2022. Nevertheless, echoes, such as the ones shown in Figure 5, were detected on at least 5 occasions between mid-July and the end of August.

4. Results

4.1. Correlations with Geophysical Parameters

In order to develop further insight regarding the nature of these scattering entities, comparisons with other parameters were investigated. Concentration will be on Eureka and Abitibi Canyon: there is too little data available from Markstay for any useful correlative studies.

4.2. Eureka Temperatures

As a first step in examining the characteristics of these PMSE and MMSE, we have looked at the temperature dependence for the Eureka system. This has been possible because a meteor radar was established close to the profiler radar, and this can be used for temperature measurements [38,39]. In this case, data for an entire month were collocated according to universal time, but without recognition of the day of the month. This produced a composite characteristic temperature time-series of a “typical” day for that month. This was done both for both July and August. In one case (July), the mean temperature profile based on the simplest method [38] was used, which gives in essence average temperatures in the region 85–95 km altitude, while for August the method of Ref. [39] was used, which produced temperature profiles more specific to 88 km altitude. These temperatures have been verified extensively, most recently in the comparisons of Ref. 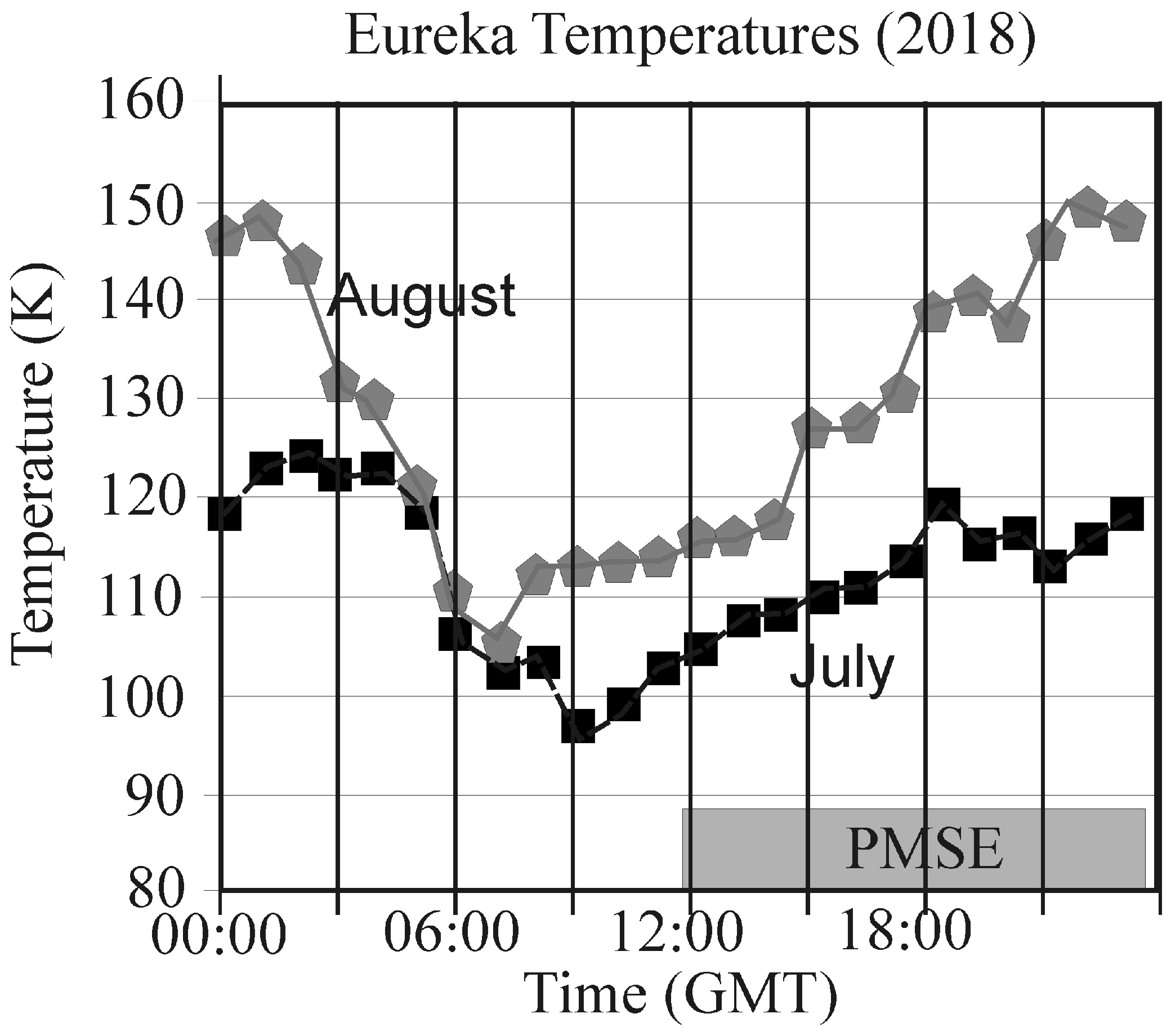[40]. In both cases, a clear diurnal oscillation is apparent, with the minimum between 06:00 and 09:00 GMT. At this time, temperatures reach lowest values between 95 and 110 K. These temperatures have an accuracy of typically +/−5 K, e.g., [40]; both sets of data show similar trends, and the low values around 06:00 to 09:00 GMT are robust.

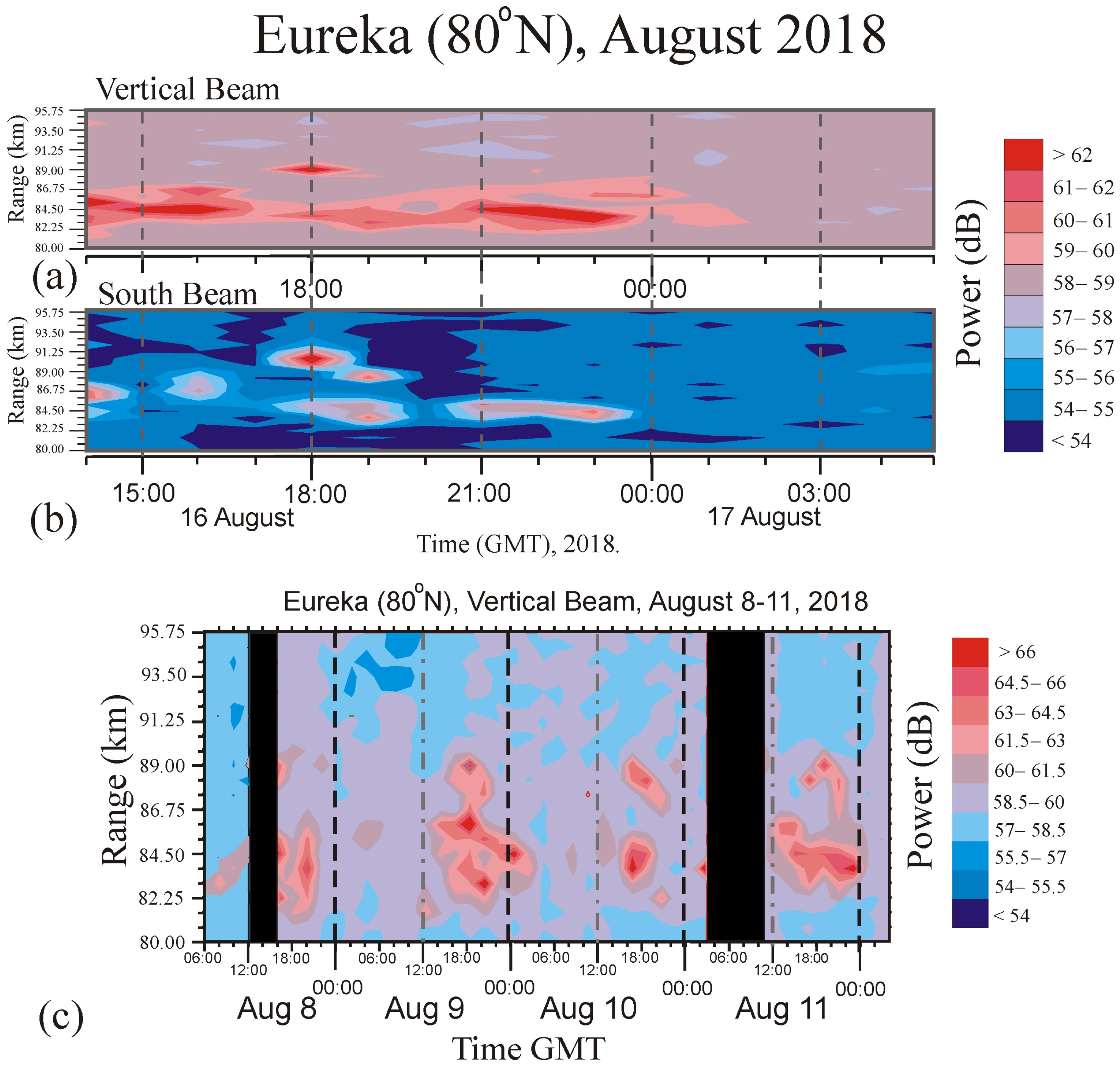
As is observed in Figure 6, temperatures are well below 140 K. The time of PMSE occurrence was generally repeatable from day to day (e.g., see Figure 3c), and is shaded in the figure. Such low temperatures are consistent with the observations of Ref. [16], who noted that over 80% of PMSE echoes occur at temperatures below 140 K.

An interesting point is that the PMSE only develop a couple of hours after the lowest temperatures are reached, and persist until the temperatures reach ~140 K, then disappear. They then do not generally reappear till the next day. This lag in the onset of PMSE of a few hours relative to the time of the lowest temperatures indicates that the PMSE take some time to develop and then take further time to disappear, indicating a form of hysteresis.

An alternative approach would have been to apply the tidal theory of Ref. [41], which is a little more sophisticated in determining a “composite-day” graph of temperature tides, but for our purposes, Figure 6 is sufficient and demonstrates that the expected temperature expectations are satisfied. It also gives some new insights into the sequence of development of the PMSE.

At Abitibi Canyon, there was no similar instrumentation for measuring upper-level temperatures; as a result, this type of analysis was not possible with the Abitibi data.

4.3. Geomagnetic Correlations

Our next sequence of analysis was to examine correlations with the geomagnetic indices. This is particularly pertinent to Abitibi Canyon, as it is close to the auroral oval. We will therefore consider the case at Abitibi Canyon first.

We have chosen the parameter of analysis to be the percentage of time per day for which the MMSE above Abitibi can be observed above the noise. This is suitable, as the site is remote and has little radio interference; therefore, the noise level is defined by cosmic noise and the receivers. There are no major astronomical sources that pass through the beams, and thus the noise is quite stable in time. As the signal rarely rises above 15 dB over the noise, the system only catches the strongest echoes; thus, this is a suitable measure of “activity”. A somewhat similar parameter was used by Ref. [19]. The percentage of time that these MMSE are observed per day will be compared with measurements of the geomagnetic index A_p, the latter being a well-established daily linear average of geomagnetic activity. Values of A_p were found on the worldwide web at https://www.spaceweatherlive.com/en/archive.html (accessed on 15 December 2021). Our largest values reached ~20—very strong magnetic sub-storms can have A_p values as high as 40 and more [42]. However, our data were recorded during a time of decreasing solar activity, approaching solar minimum. Larger values occurred in 1998–2003 and 2012–2016, during solar maxima.

Because of the relatively low latitudes of our non-polar sites, we do not expect the mesopause temperatures to persist at values below 140 K during the entire summer. Temperatures in early June can be warmer than this, and in August they return above 140 K for the latter part of the month. Analysis is therefore concentrated on the months of July in 2018 and June–July in 2019, when good MMSE were evident. In 2018, MMSE did not show until later in June; thus, these cases are excluded, as they may be limited by temperature effects and possibly a lack of water vapour. However, in 2019, MMSE appeared quite early in June, so June 2019 has been included in the analyses.

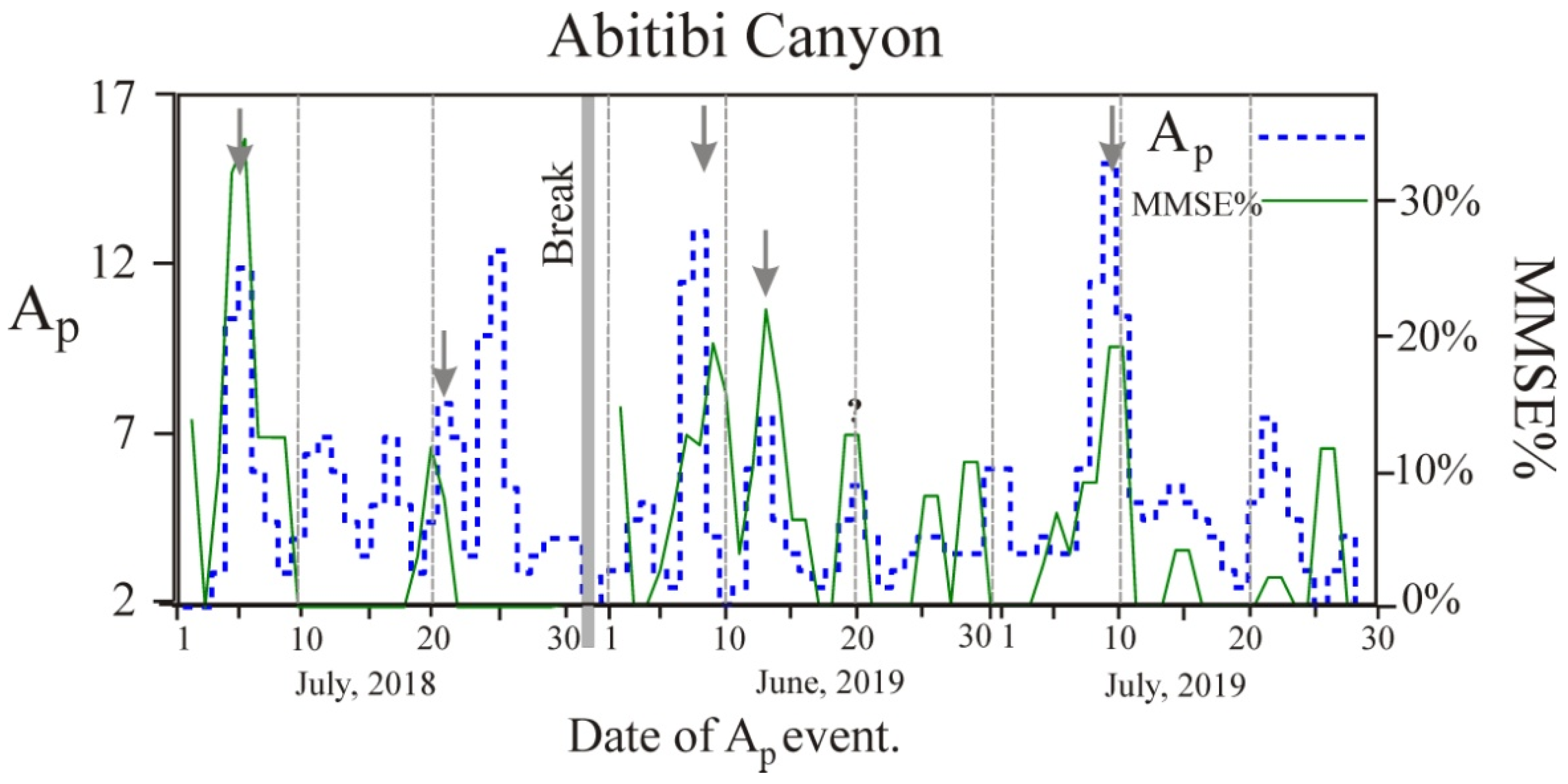
Raw data plots of the daily A_p and the percentage occurrence of MMSE are shown in Supplementary Section S1 for completeness, but have not been presented within the paper, as better ways will be used to display our conclusions.

Lags between A_p and MMSE occurrence varying from 0 to ~20 h were found by Ref. [43], and evidence of potentially relevant lags of 3 and even 4 days were found in Refs. [44,45,46]. In the following paragraphs, searches for similar lags will be undertaken.

As a first step, conditions indicating some significant geomagnetic activity were isolated for further study. Concentrating on values of A_p in excess of 8 (which, for want of a better wording, we will define as “significant events” for now), six events were found that deserved further investigation. Initial inspection of these events demonstrated that there were delays, with the percentage of MMSE lagging the peaks in A_p, but the lag varied between 2 and 4 days. As will be discussed in the next section, several other papers have recognised a possible link between MMSE occurrence at mid-latitudes and relativistic electron precipitation, and the electron precipitation can lag the A_p index by periods of a few hours to 3 or more days. For example, Figure 6 in Ref. [45] shows a broad region of good correlation between A_p and the so-called “geosynchronous relativistic electron enhancement” (GREE), with correlations maximizing with lags between 1 and 4 days.

Because of the possibility that the lag between A_p and MMSE% can vary from event to event, a two-point running mean was applied to both time series, and these averaged datasets were usefully employed at times. The use of a two-point running mean allowed coverage of 2, 3, and 4-day lags in a single data set, as both 2 and 4-day lags show up to some degree in a 3-day lagged comparison when such averaging is applied.

As a “first-look”, Figure 7 shows these 2-day running averages for both datasets. The averaged MMSE percentages have been moved in time by 3 days, as visual inspection demonstrated that that this produced the best visual agreement between datasets. Confirmation of this by statistical processes will be given shortly. Cases in which the MMSE% lag A_p by ~3 days show up at the vertical arrows. Five events can be observed where the coincidence of the two datasets is clear. For the case of 21 July 2018 (second vertical downward arrow in the sequence), the MMSE% appears to lead the A_p peak, but this really means it was a 2-day lag rather than a 3-day lag.

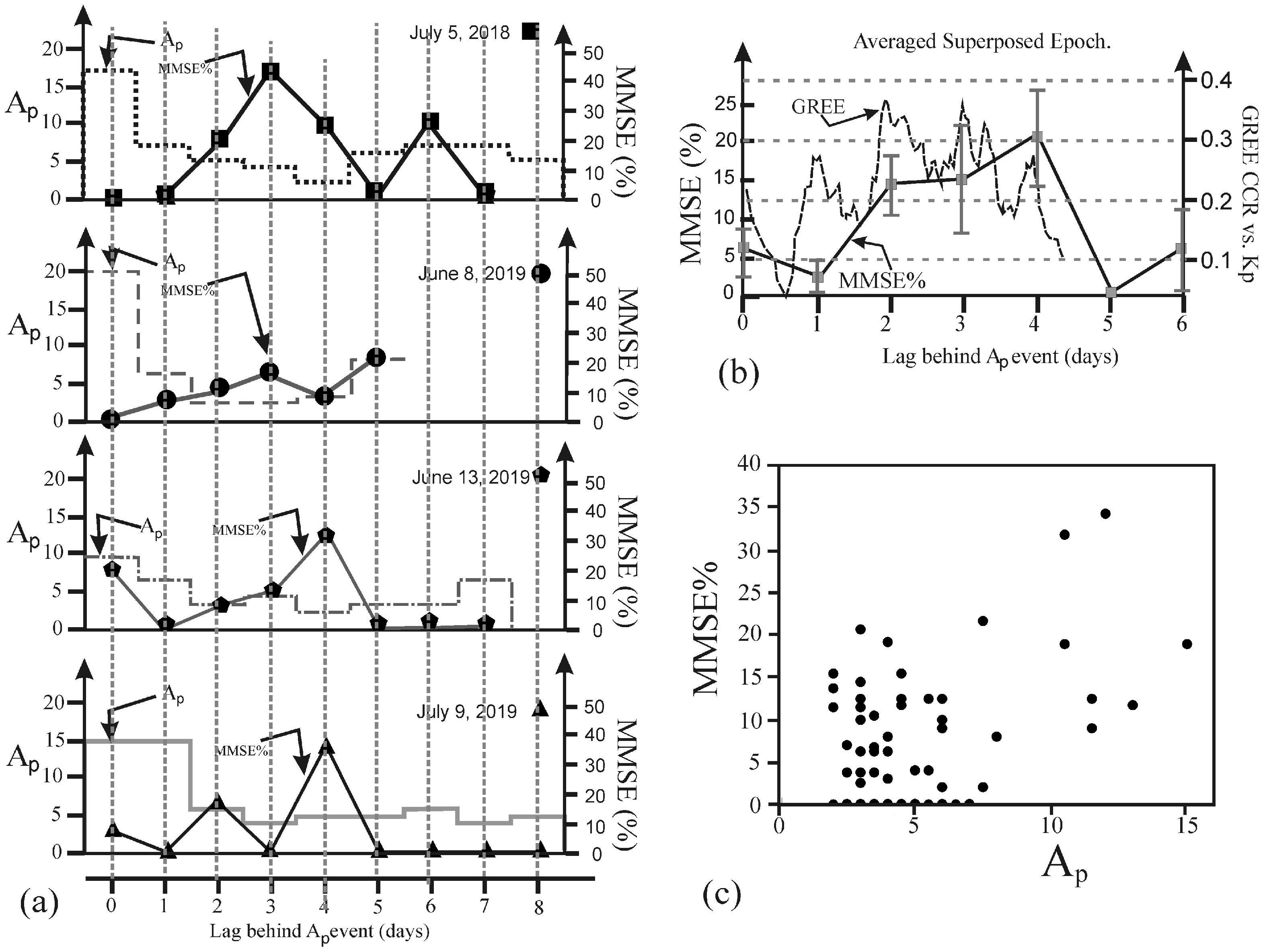
In order to investigate these lagged events more thoroughly, the original dataset (with no two-point running mean applied) was then re-examined using a “superposed Epoch” analysis. For each case of a significant A_p, the date of the event was set to zero, and then the time series of both A_p and MMSE% for the next 8 days were plotted. The result was the graphs shown in Figure 8a. Seven events were found with A_p in excess of 8, although two were on successive days (9 and 10 July 2019, as observed in Figure 7, last downward vertical arrow). These are therefore considered as a single extended event; thus, it is considered that we have six distinct events in all.

It is noticeable in Figure 8a that in general on the day of the large value of A_p, and the day following, MMSE% tends to be very small, and the greatest activity in MMSE activity seems to be most common three and four days later. For example, the event on 5 July 2018 had an A_p of 17, and the percentage of MMSE reached 44% three days after the significant A_p event. On 9 July 2019 an A_p of 15 occurred, and the percentage of MMSE reached a maximum of 38% 2–4 days afterwards. A significant value of A_p also occurred on 21 July 2018 (A_p = 10) and had a delay of only two days until the percentage of MMSE peaked. This point has not been included in Figure 8b, in order to save space, but it can clearly seen in Figure 7, and indeed has been discussed briefly already. It should be noted that the events on 8 June and 13 June 2019 were very close in time; thus, the delayed MMSE event from June 8 almost overlapped the new A_p event on 13 June—this explains why the lagged plot for 8 June 2019 terminates early.

Finally, an event on 24 July 2019 had an A_p of 17, but there were no MMSE after that time for the next 7 days; it is possible that as this occurred in late July in 2018, the temperatures in the region had risen above 140 K, or the water-vapour content could have been low, either of which would have precluded creation of MMSE.

Figure 8b shows the cumulative average of all superposed epoch plots, in which the MMSE% values for common lags have been averaged. Error bars refer to standard errors.

Two points deserve special recognition in Figure 8b. The first point to discuss is the one at zero lag, which has a value of 7.5%. This is almost entirely due to the value of MMSE% on 13 June 2019. It is the only individual zero-lag event in which MMSE% exceeded 10%, and in 4 out of the 6 events, the MMSE% was zero at zero-lag. The cause of this particular MMSE event on June 13 is therefore unclear. It could have been a lagged response to the larger value of A_p = 20 on 8 June, or it could have been a near-instantaneous response to the magnetic event on 13 June (or it could have been unrelated to either). In some senses it might have been justifiable to exclude it for reasons of uncertainty, but that could subjectively bias the statistics, so we retain it. Nevertheless, it should be born in mind that its origins are not clear. The second point to be discussed is the value at a lag of 4. This has a contribution from the dual-day A_p-event of 9–10 July 2019 (bottom graph of Figure 8a), and the peak at lag 4 could equally be considered as a consequence of geomagnetic activity on 10 July. If this were true, then it would be a case of a 3-day lag. Hence the lag-3 percentage in Figure 8b would increase, and the lag-4 case would decrease. There is therefore the possibility that the lag-3 value could be the position of peak percentage.

The average location of all of these lags, determined as a “centre-of-mass”, was at a lag of 3.1. If some of the contribution to lag-4 really belongs to lag-3, then the “centre of mass” would be a little less than 3. In either case, this graph verifies the original proposal that a mean lag of 3 days, used in Figure 7, was reasonable.

Next we turn to cross-correlations of the A_p indices and the MMSE%. In view of the fact that the results discussed in regard to Figure 8 showed a range of lags from 2 to 4 days, these cross-correlations focused initially on using the two-point running means discussed in Figure 7.

Maximum correlation coefficient occurred for a delay of 3 days (consistent with our conclusions above), demonstrating a cross-correlation coefficient of 0.35 (45 independent points), in contrast to near-zero and even negative values at all other temporal lags. In regard to statistical confidence, this corresponds to a probability of less than 2.5% that random data could generate this correlation, or a statistical confidence in excess of 97.5% (p = 0.025). More detailed examination demonstrated that this higher correlation was due to a few dominant cases of high A_p, though the confidence level remains valid. As a check, a cross-correlation coefficient was also found for the case in which no running means were used, and in this case the correlation coefficient for a 3-day lag was 0.28, with 89 independent points. This corresponds to a confidence level in excess of 98% (p = 0.02).

A scatter plot of MMSE% vs. A_p for a three-point lag is shown in Figure 8c, in this case using the two-point running mean data. A similar plot for a three-point lag using the raw data (not shown) looked similar but had fewer point-pairs in the region A_p > 10.

The evidence of a transition region in the scatter-plot at around A_p = 8–10, with essentially uncorrelated data to the left, and correlated data to the right, supports our original decision to consider A_p = 8 as a “significant value”.

While numbers are small, we can say that there is some indication that geomagnetic disturbances with values of A_p of 9 and more lead to MMSE peak-percentage occurrences 3 ± 1 days later at Abitibi Canyon. This occurred on five occasions out of the six cases that had a value of A_p in excess of eight. In the sixth case, there was no accompanying MMSE at all, but it was late in the season. The correlation coefficient of ρ = 0.353 is statistically significant at the 97.5% confidence level. Some further statistics of value are (i) MMSE occurred on 24 days out of the 89 days studied (27%), and of these 24 days, 16 were found within 4 days after an occurrence of A_p > 8; (ii) values of MMSE% were zero on 5 of the 6 days with A_p > 8; (iii) on the day after a value of A_p > 8, no values of MMSE% greater than 8% ever occurred (and three out of five were zero).

Finally, similar studies carried out at Eureka demonstrated no situations where significantly nonzero correlations between MMSE% and A_p could be found, regardless of time delays. Possible reasons are discussed in the next section.

5. Discussion

The delays of ~3 days between A_p and MMSE% may seem long, but in fact are not unreasonable. One possible geomagnetic impact on MMSE% has been discussed in the context of relativistic electron precipitation [42,43]. The likely importance of electron precipitation has particularly been promoted by Ref. [42]. These electrons are produced in the inner magnetosphere, particular in association with strong charged-particle flow from the sun during solar sub-storms. The process involves acceleration of electrons to relativistic energies by internal processes at those heights, with subsequent magnetospheric diffusion to lower altitudes. There may be delays of up to 2–4 days before the high-speed electrons are generated and arrive at the mesopause—the delay being related to the timescales for the magnetospheric acceleration processes to create relativistic electrons, and the subsequent time for downward diffusion processes to take place. The delay is not fixed, being dependent on local environmental conditions; thus, some variability is to be expected.

In Figure 8b, a curve labelled “GREE” is presented. This was adapted from Figure 6 of Ref. [45], and shows the correlation between solar sub-storm activity (defined by K_p) and relativistic electrons detected by satellite. It therefore is a measure of the time for relativistic electrons to be accelerated, but does not include the time for them to reach the mesopause. It can be observed in Figure 8b that the time lags of GREE correlation coefficients and the MMSE% lags are broadly similar in coverage. The agreement is even better when it is recognised that the lag at 4 days in our data has a possible contribution from a 3-day lag in the data from 9–14 July 2019, where the geomagnetic sub-storm lasted for 2 days (July 9 and 10), as discussed following Figure 8. A similar lag of ~3 days is also presented by Ref. [44], who demonstrated that this 3-day delay is especially dominant during the descending phase of the solar cycle. Our results were recorded near the end of solar cycle 24, and match this timing well.

A mechanism for generation of these relativistic electrons was suggested by Ref. [44], in which it was proposed that coronal holes on the sun in the declining phase of the solar cycle are sources of high-speed solar wind streams, and that the high-speed solar wind could excite large amplitude Pc5 pulsations through the action of the Kelvin-Helmholtz instability along the magnetopause. More recent data from the Van Allen satellites (e.g., [47]) allow such theories to be refined or corrected, but regardless of the causes, the measurements by Ref. [44] remain valid.

It is also worth noting that Ref. [43] found significant delays in their studies of PMSE/MMSE relative to days of high values of A_p, though in those cases the delays were generally less than 24 h. Their results were recorded in 2007–2011, so from 2007 to 2009 were in the descending phase of the solar cycle 23, but from 2009 to 2011 were largely at solar minimum.

In contrast to Ref. [44], Ref. [43] argued that such delays were due to nitric oxide transport and mesospheric diffusion. Arguments therein regarding the delayed response were based on Figure 10 of Ref. [43], which used data from the ODIN satellite [48] to produce approximate maps of NO distributions as a function of geomagnetic latitude. They further employed Figure 11 of Ref. [43], which showed a scatter plot of PMSE strength as a function of NO density. The correlation was weak, but perhaps plausible for their latitudes, but the geomagnetic latitude of Abitibi Canyon is around 58° N, well offset from the peak NO densities in Figure 10 of Ref. [43], so less likely to be applicable here. Of course, particle precipitation can directly generate NO in the mesosphere and lower thermosphere; thus, the effects of particle precipitation and NO transport can be somewhat intertwined. It is also important to note that Abitibi Canyon is sub-auroral on the equator-ward side of the auroral oval, whereas the sites used by Ref. [43] were (i) auroral and (ii) sub-auroral on the polar side of the auroral oval. Further, some of their results were taken close to the solar minimum, whereas ours were recorded in the descending phase of the solar cycle.

A set of analyses similar to the ones presented in this paper was applied to data acquired at Kühlungsborn, Germany [42]. This site had a somewhat similar latitude to Abitibi Canyon, being at 54° N (about 4° north in geographic latitude relative to Abitibi); thus, it is of interest to compare the results obtained there to ours. That dataset was quite large, covering the summers of 1998 and 2000–2006. Superposed Epoch analyses were applied, just as we did. However, the conclusion was that in general strong radar echoes were observed on the days of maximum geomagnetic activity, and the maximum values were typically detected one day after the geomagnetic disturbance. Enhanced radar echoes were also observed on the following 2–3 days. Results can be observed in Figure 1 of Ref. [43], and it is clear that there is no really dominant peak. In fact, as stated by the authors, “the significance level of the difference between the MMSE maximum (day 1) and minimum values (days 5 and −1, respectively) is however smaller than 90%”. This is not a high level of significance.

These results differ somewhat from our results, in that they had significant MMSE activity on the day of large A_p (we had very little MMSE at those times), and the values of MMSE% do not really show any strong systematic trends as a function of lag number. The fact that they did see activity up to 4 days after the geomagnetic maximum is at least similar to our results.

It is of interest to investigate why these contrasts appear. The sites have somewhat similar latitudes, but beyond that, there are some noticeable differences. Firstly, the data were recorded at very different times—1998–2006 for Kühlungsborn, 2018–2019 for Abitibi. Secondly, the data were also recorded at very different phases of the solar cycle: the Kühlungsborn data were recorded at the peak of the relatively active solar-cycle 23, while the Abitibi data were recorded at the declining edge of solar cycle 24, and in fact the Abitibi records were made very close to the solar minimum. Thirdly, while the geographical latitudes are similar, the geomagnetic ones are not. The magnetic inclination angle at Abitibi Canyon in 2018 was 74.3° in 2018, whereas at Kühlungsborn it was 68.8° throughout the measurements made there. This means that Kühlungsborn was somewhat south of the edge of the auroral oval, while Abitibi Canyon is closer to the southern edge of the oval. Fourthly, sunspot numbers during the Kühlungsborn records were up to 200, while in the Abitibi case the numbers were as low as 10–20. Correspondingly, values of A_p during the Kühlungsborn acquisition could reach as high as 35–40 and more, whereas for our data, our largest values were around 20. In fact while values of 20 were considered as active in the context of our data, on a larger scale they are considered relatively modest. Fifthly, while the geographic latitudes are similar, the band between 45° N and 54° N is a region where the mesopause temperatures cross over from being above 140 K at lower latitudes to colder values at greater latitudes.

With all these factors combined, Abitibi Canyon and Kühlungsborn are in fact quite different. The fact that data for Kühlungsborn were recorded during high geomagnetic disturbances may be especially important. It is conceivable that large values of A_p of 30 and more could lead to direct and more rapid injection of relativistic electrons into the mesosphere, generating MMSE even on the day of the A_p maximum. Such processes may not be possible at values of A_p of 20 or less, so such rapid-injection processes may be relatively less common for the more moderate values of A_p. Both datasets demonstrate good activity on days 2–4, which is a consistent feature between the two sites. In addition, the Kühlungsborn site, being geographically further north and therefore colder, could generate MMSE more easily without any assistance from electron precipitation, thereby reducing the correlation with A_p events. The closer proximity of Abitibi to the auroral oval is also likely to play a role in the increased correlation between MMSE% and A_p at Abitibi. Furthermore, the lower magnetic activity at Abitibi in 2018 allowed for less occurrences of high A_p, which in turn allowed the full history of an “event” to play out without interruption by a new event. In a situation such as the solar maximum of cycle 23, a new event would commonly intercede into a previous event, masking the consequences of the prior event.

In this regard, then, it is our conclusion that the data from Kühlungsborn and Abitibi, far from being contradictory, are in fact complementary. They show up different aspects of a complicated situation. Combining data from vigorous periods with data from quiet periods reveals far more than could be obtained from either set of investigations alone.

In regard to the PMSE above the auroral latitudes, both we and Ref. [42] agree that there is generally poorer correlation with A_p. Possible reasons for this are discussed in Ref. [42]. We do not want to repeat those discussions, but we need to make one point in this regard. It is assumed in Ref. [42] that the backscattered power should naturally increase as a function of the electron density. However, this is not true. The backscattered power is proportional to the refractive index structure constant $C_n^2$ (See Ref. [3], Equations (29) and (33b)), where

$$C_n^2\propto {\epsilon }^{2/3}{M}_e^2{\omega }_B^2,$$

with ε being the turbulent energy dissipation rate. M_e is the electron density potential refractive index gradient, and ω_B is the Vaisla-Brunt frequency (see Ref. [3], Equation (38)). Here,

$$M_e=\frac{\partial n}{\partial N}[N\frac{{\omega }_B^2}{g}-\frac{dN}{dz}+\frac{N}{\rho }\frac{d\rho }{dz}],$$

as can be seen in Equation (7.71) of Ref. [11]. It is often the gradient in electron density (dN/dz) that plays the key role in determining the backscattered power, rather than N. It is quite possible for the gradient to remain constant, or even diminish, as the electron density (or in the case of PMSE, the density of cluster ions) increases. This does not seem to have been fully appreciated in these discussions.

At this point it is not our intention to try to discriminate further between these different mechanisms. Our primary purpose has been to demonstrate some new, and potentially important, relations between A_p and MMSE%, and to further demonstrate how the MMSE evolve after occurrence of a value of A_p of between ~8 and ~20.

6. Conclusions

Measurements of mid-latitude mesospheric summer echoes (MMSE) at VHF frequencies have been presented at latitudes below 50° N, some as low as 46.5° N. These observations support other similar observations in Japan at 45.4° N. It has been clarified that only VHF (and higher frequency) studies can highlight regions of sub-140K temperatures, ice-crystal growth, and high Schmidt numbers—observations of MF and HF echoes will occur even without ice crystals, and therefore do not tell us much about the temperature of the scattering region. These low latitude echoes are especially important, as they lie on the equator-ward side of the auroral oval, and seem to demonstrate different characteristics to echoes from within the auroral oval. A dataset covering two summer seasons at a sub-50° N latitude has been compared to the geophysical A_p parameter; such a comparison for a long dataset has never been previously undertaken at sub-50° N geographic latitudes. Results demonstrate a good correlation between modestly high A_p values and MMSE activity, with five out of six significant A_p events being followed typically 3 (+/−1) days later by relatively strong MMSE. The statistical confidence level for our cross-correlations across all our data at a 3-day lag exceeds 97.5%. The sixth event may have occurred during a warm phase of mesospheric temperatures. Such correlations are not observed at the near-polar site of Eureka, Canada, although mesospheric echoes there (PMSE) are much stronger than their MMSE counterparts.