Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Climatic Data
2.3. Standardized Precipitation Evapotranspiration Index (SPEI)
2.4. Standardized Precipitation Actual Evapotranspiration Index (SPAEI)
2.5. Probability Distribution Functions
- Pearson type III (PE3)
- Generalized extreme value (GEV) distribution
- Generalized logistic (Genlog) distribution
2.6. Distribution Fitting Using Shorter Time Series Data
2.7. Evaluating Distribution Functions and the SPEI Values
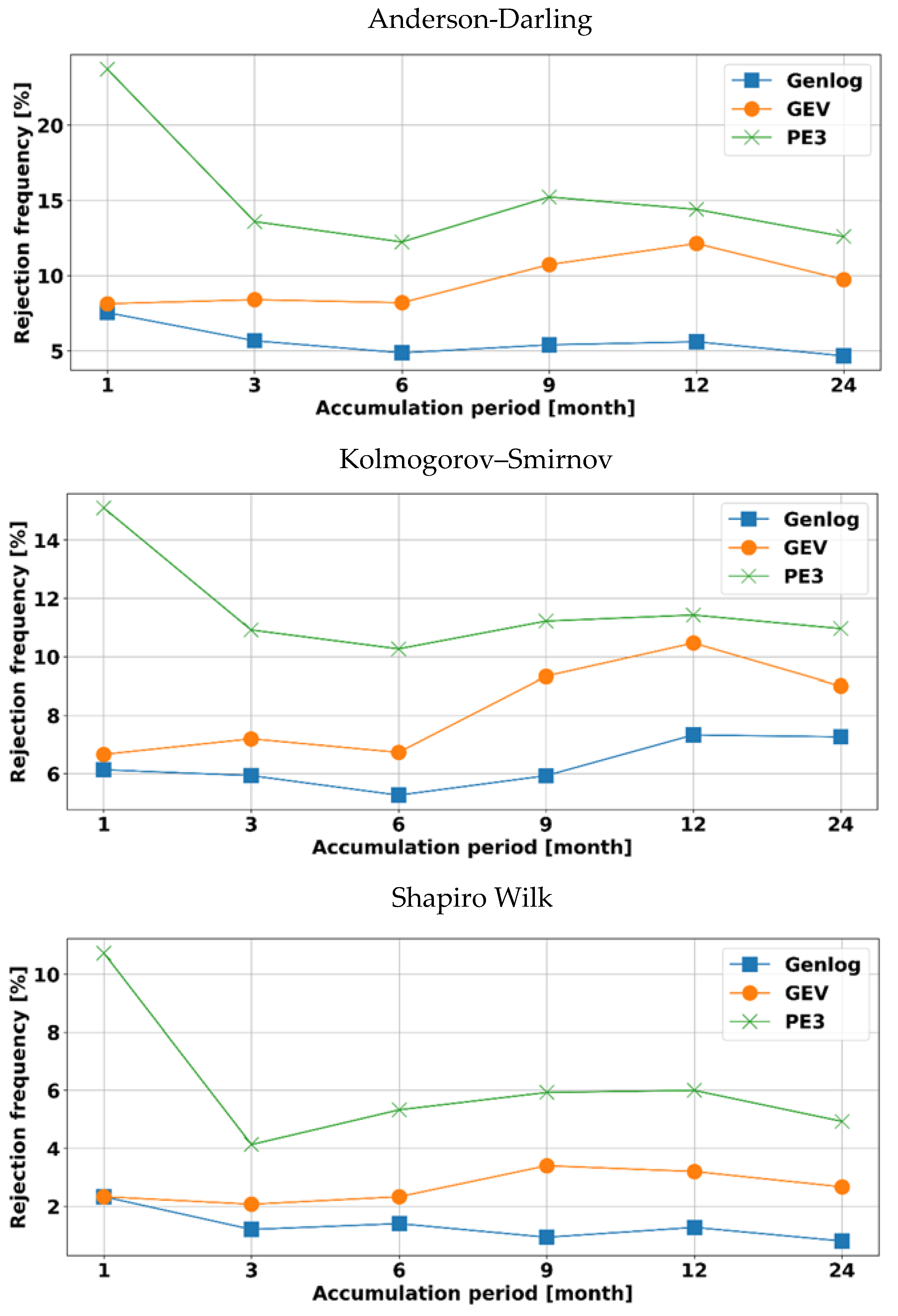
2.7.1. The Goodness-of-Fit Test (GOF)
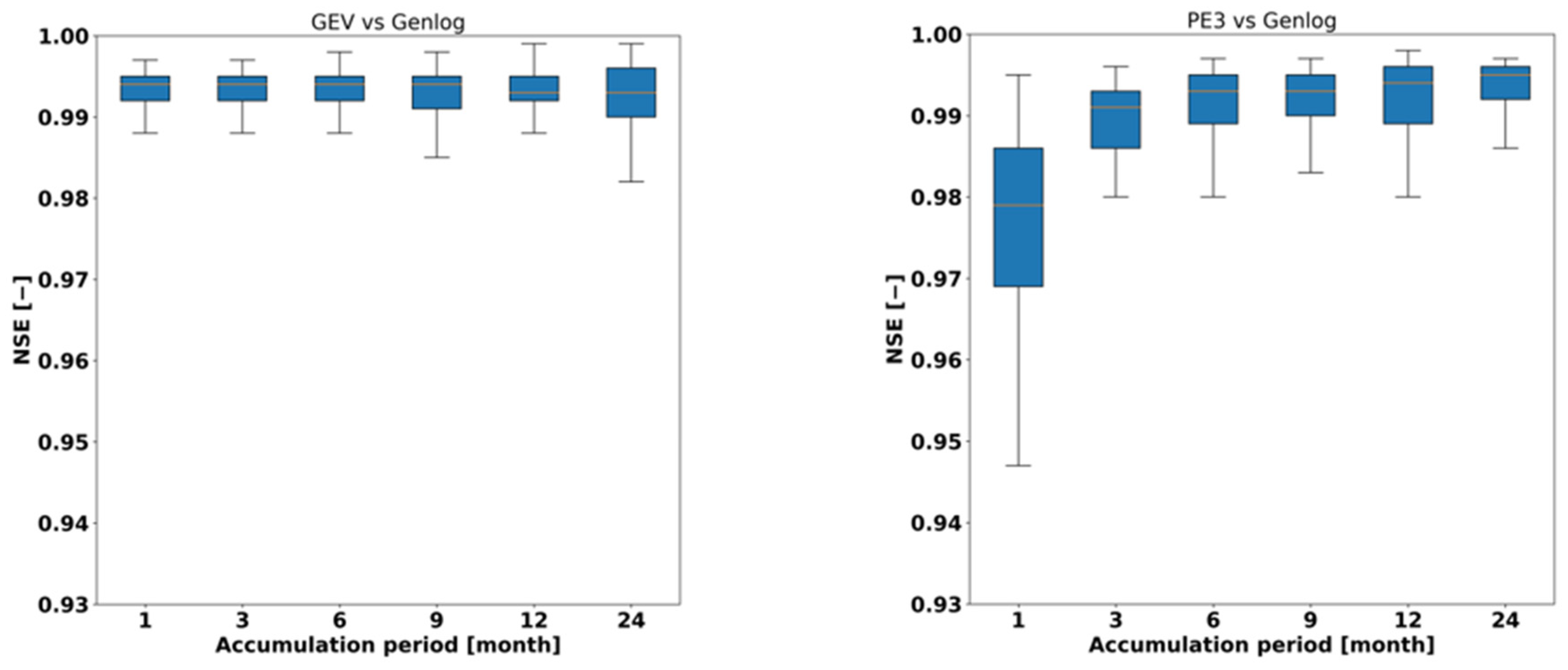
2.7.2. Nash–Sutcliffe Efficiency
3. Results and Discussion
3.1. Difficulty in Fitting Water Balance
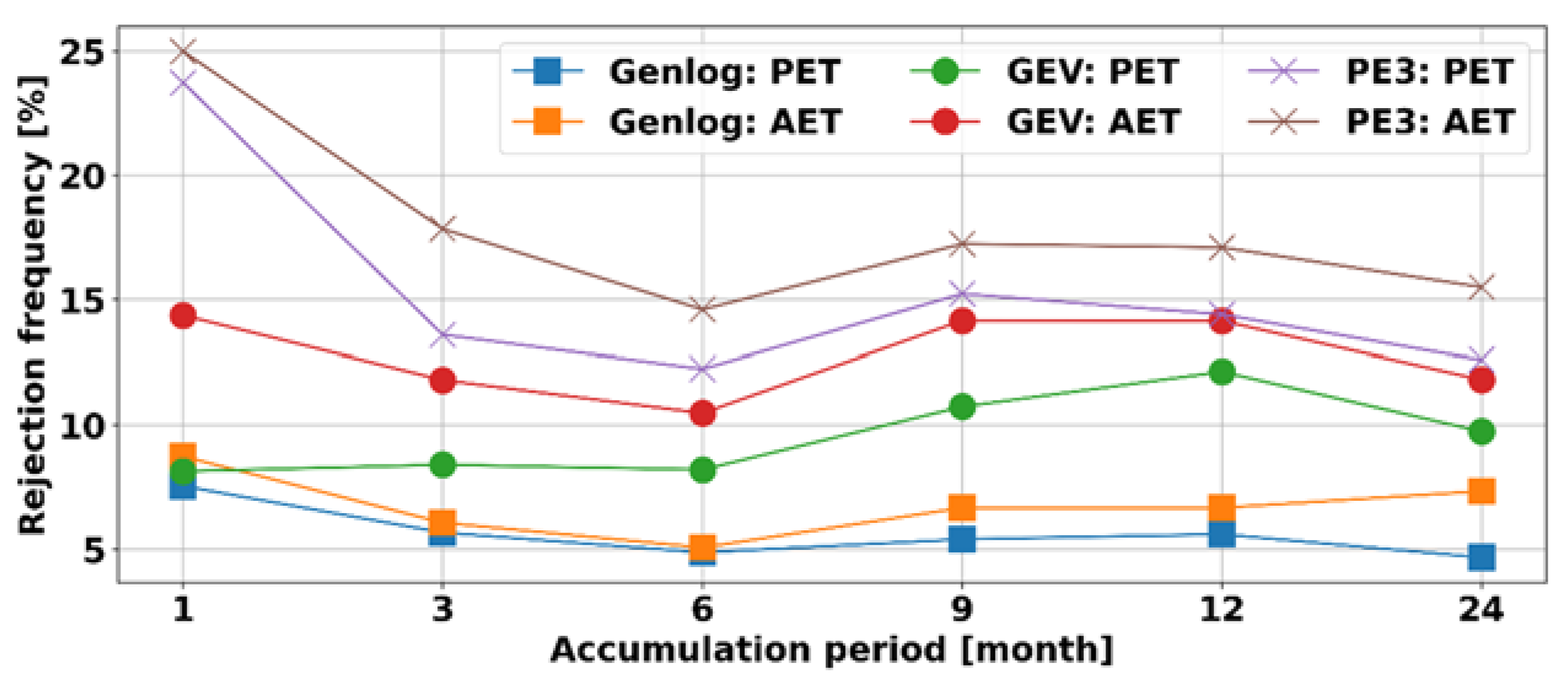
3.2. The Goodness-of-Fit Test
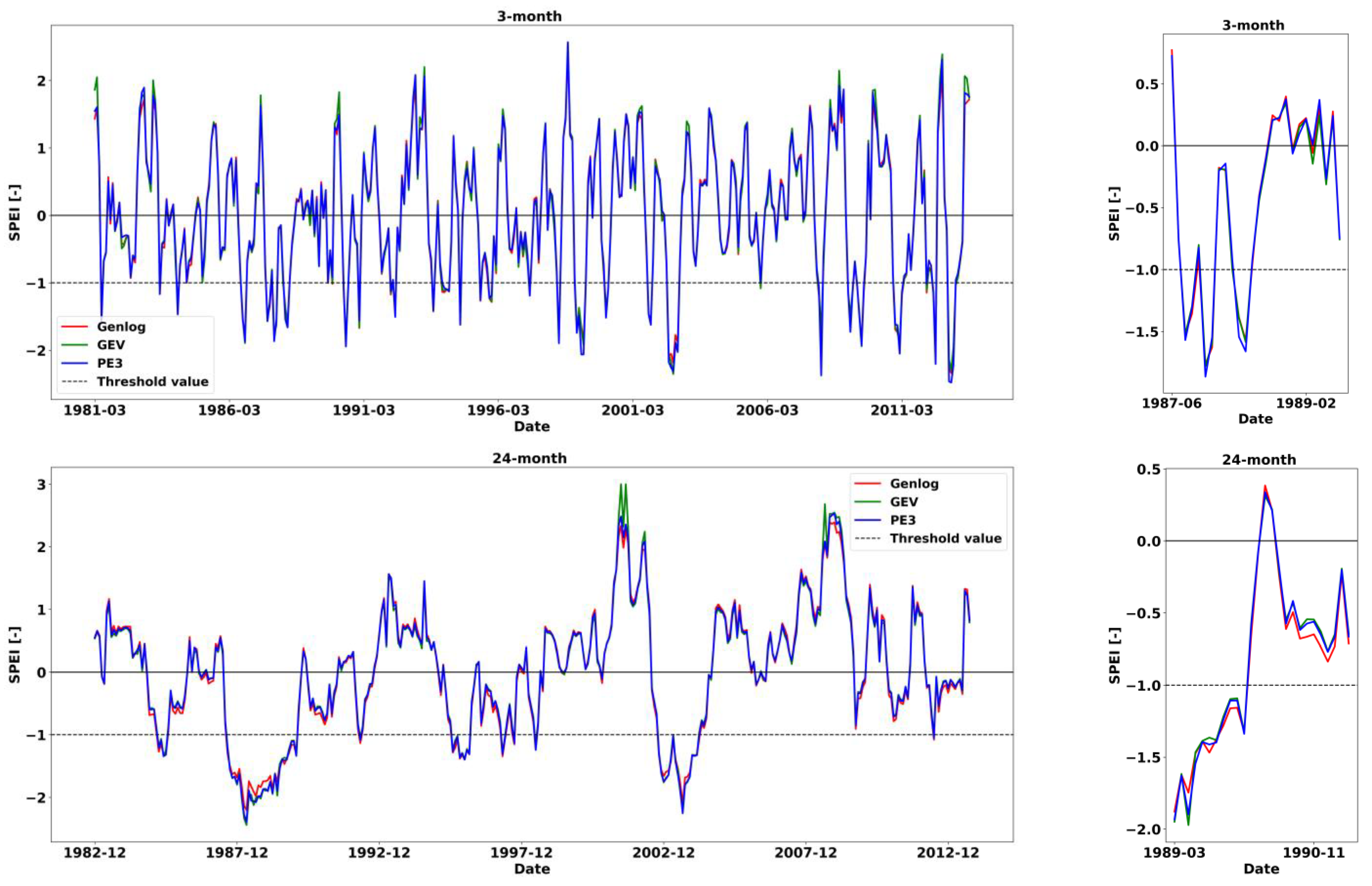
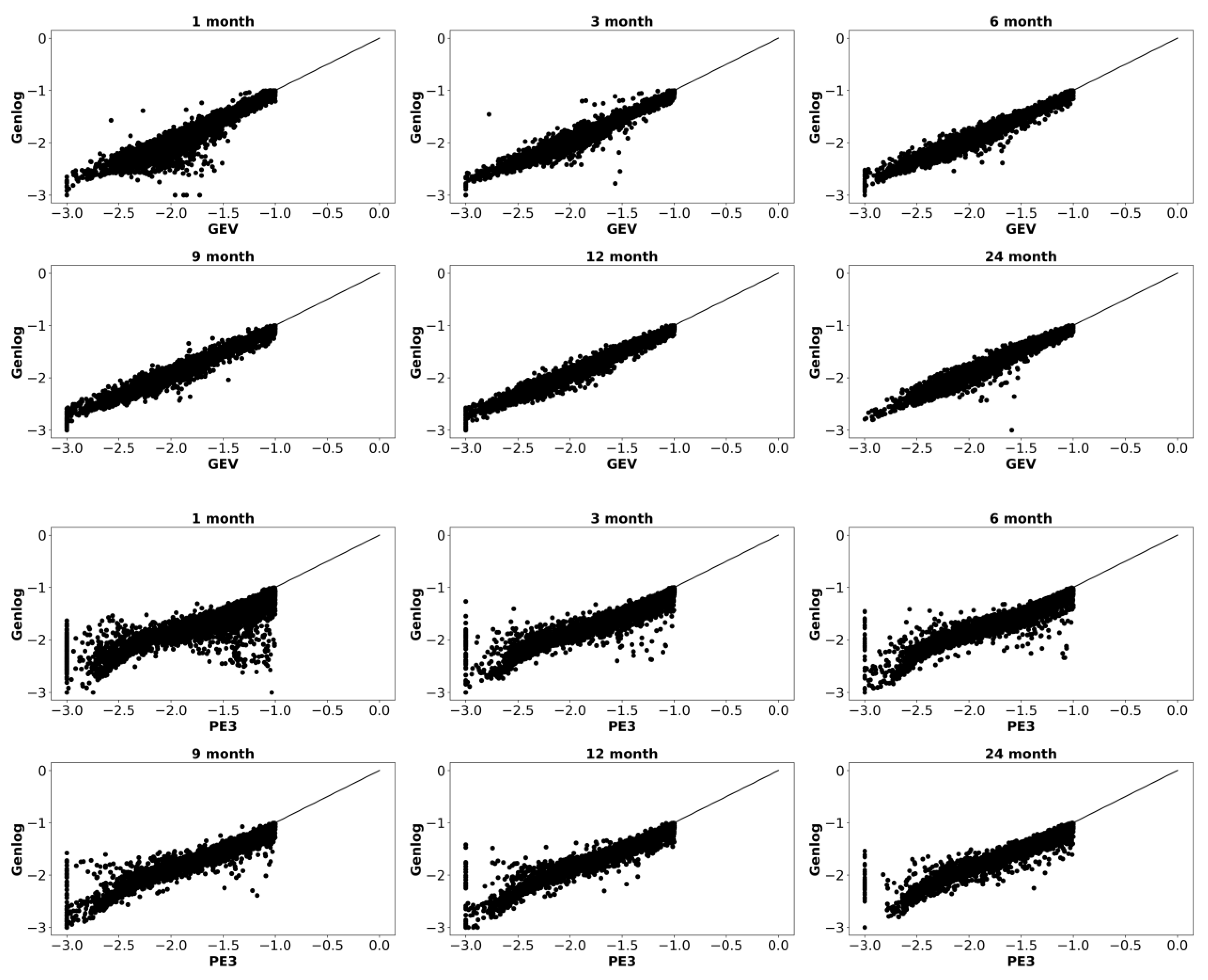
3.3. Comparison of SPEI Values Estimated from PE3, GEV, and Genlog
3.3.1. Visual Comparison of SPEI Values
3.3.2. Similarity Analysis Using NSE
3.3.3. Comparison Based on Drought Events
3.4. Standardized Precipitation Actual Evapotranspiration Index (SPAEI)
3.4.1. GOF Test
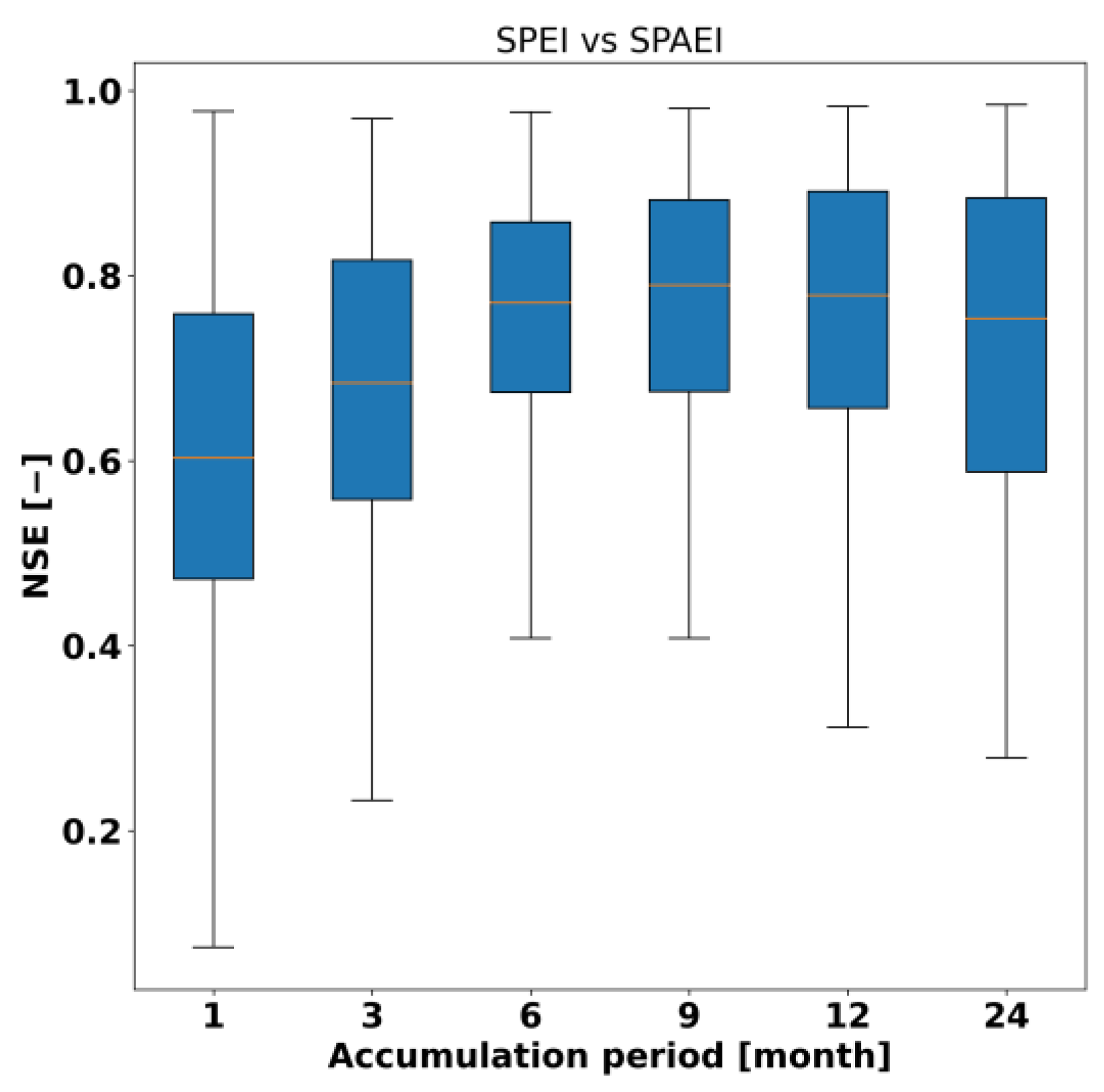
3.4.2. Comparison of the SPEI and SPAEI Values
3.5. Shorter Time Series Data Analysis
3.5.1. GOF Test
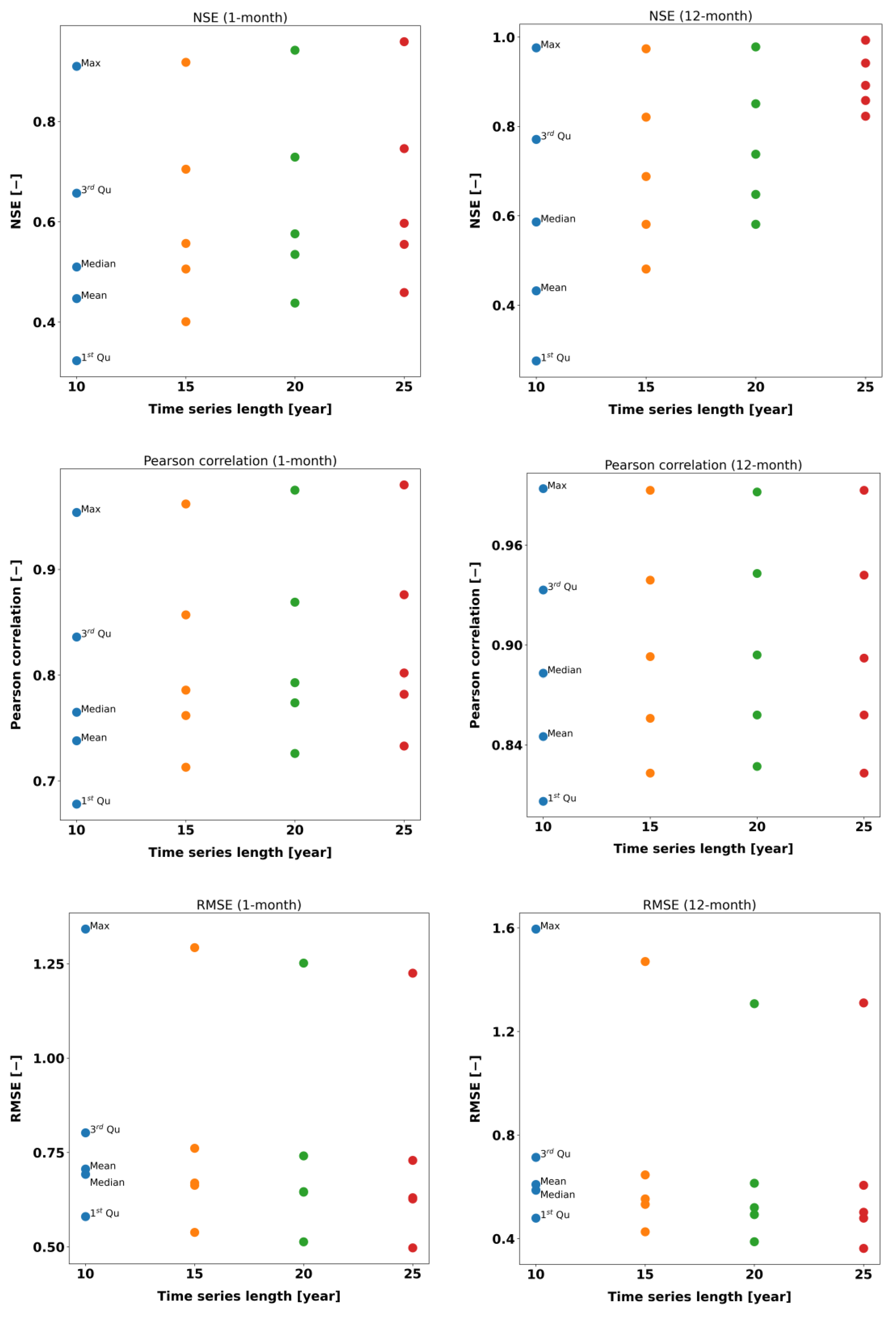
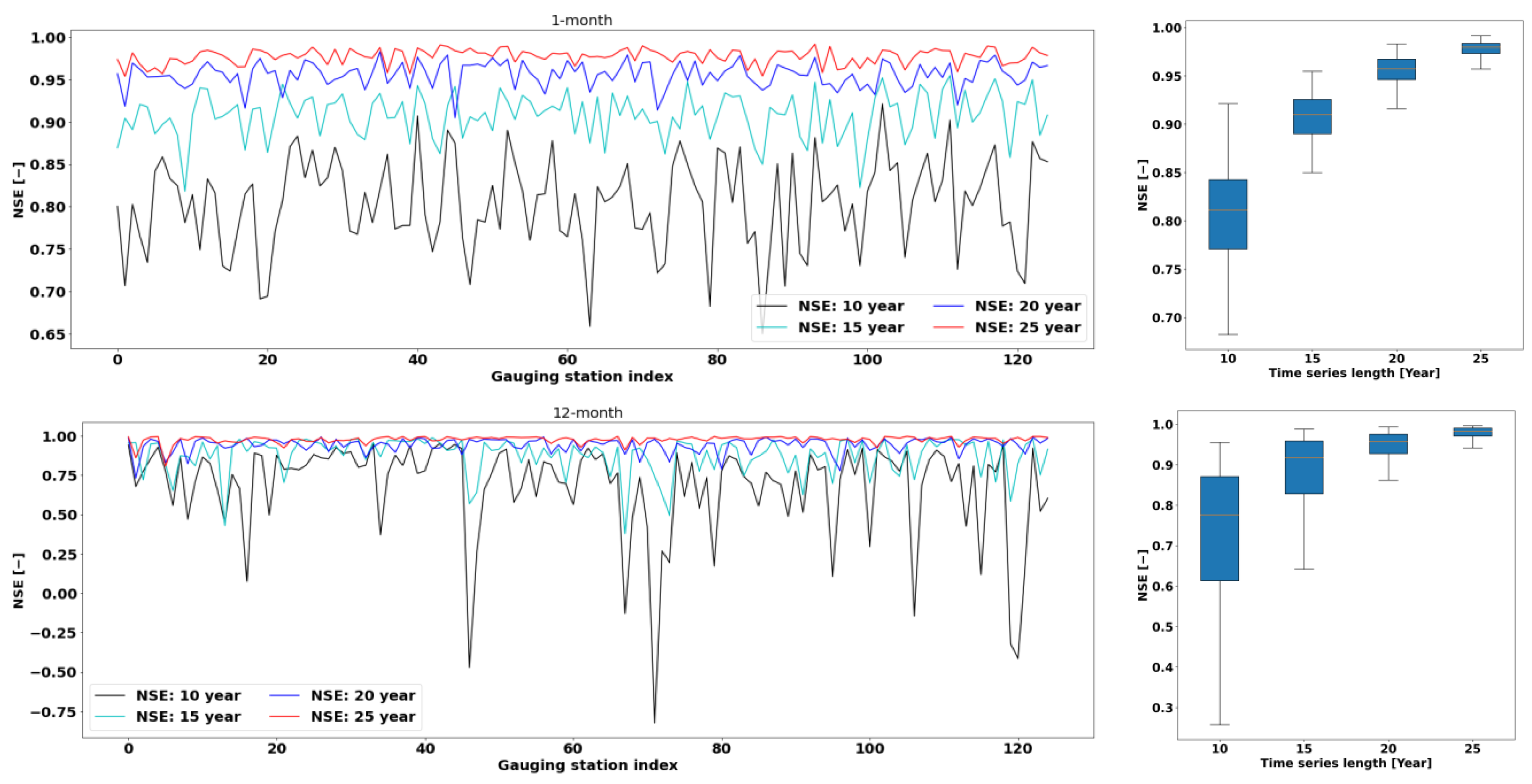
3.5.2. SPEI Value Comparison between Shorter Length and Benchmark Data
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bayissa, Y.; Maskey, S.; Tadesse, T.; Van Andel, S.J.; Moges, S.; Van Griensven, A.; Solomatine, D. Comparison of the performance of six drought indices in characterizing historical drought for the upper Blue Nile basin, Ethiopia. Geosciences 2018, 8, 81. [Google Scholar] [CrossRef] [Green Version]
- Wolde-Georgis, T. El Nino and drought early warning in Ethiopia. Internet J. Afr. Stud. 1997. Available online: https://ssrn.com/abstract=1589710 (accessed on 17 May 2021).
- Viste, E.; Korecha, D.; Sorteberg, A. Recent drought and precipitation tendencies in Ethiopia. Theor. Appl. Climatol. 2013, 112, 535–551. [Google Scholar] [CrossRef] [Green Version]
- Zeleke, T.T.; Giorgi, F.; Diro, G.T.; Zaitchik, B.F. Trend and periodicity of drought over Ethiopia. Int. J. Climatol. 2017, 37, 4733–4748. [Google Scholar] [CrossRef]
- Mera, G.A. Drought and its impacts in Ethiopia. Weather Clim. Extrem. 2018, 22, 24–35. [Google Scholar] [CrossRef]
- Liou, Y.-A.; Mulualem, G.M. Spatio–temporal assessment of drought in ethiopia and the impact of recent intense droughts. Remote Sens. 2019, 11, 1828. [Google Scholar] [CrossRef] [Green Version]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Van de Vyver, H.; Van den Bergh, J. The Gaussian copula model for the joint deficit index for droughts. J. Hydrol. 2018, 561, 987–999. [Google Scholar] [CrossRef]
- da Rocha Júnior, R.L.; dos Santos Silva, F.D.; Costa, R.L.; Gomes, H.B.; Pinto, D.D.C.; Herdies, D.L. Bivariate assessment of drought return periods and frequency in brazilian northeast using joint distribution by copula method. Geosciences 2020, 10, 135. [Google Scholar] [CrossRef] [Green Version]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Monish, N.T.; Rehana, S. Suitability of distributions for standard precipitation and evapotranspiration index over meteorologically homogeneous zones of India. J. Earth Syst. Sci. 2020, 129, 25. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Chen, Z.; Ren, Z. Assessment of candidate distributions for SPI/SPEI and sensitivity of drought to climatic variables in China. Int. J. Climatol. 2019, 39, 4392–4412. [Google Scholar] [CrossRef]
- García-Valdecasas Ojeda, M.; Yeste Donaire, P.; Góngora García, T.M.; Raquel Gámiz-Fortis, S.; Castro-Díez, Y.; Jesús Esteban-Parra, M. Evaluating the Feasibility of Using a Drought Index Based on the Actual Evapotranspiration. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 8–13 April 2018; p. 15169. [Google Scholar]
- Rehana, S.; Naidu, G.S. Development of hydro-meteorological drought index under climate change–Semi-arid river basin of Peninsular India. J. Hydrol. 2021, 594, 125973. [Google Scholar] [CrossRef]
- Zhang, G.; Gan, T.Y.; Su, X. Twenty-first century drought analysis across China under climate change. Clim. Dyn. 2021, 1–21. [Google Scholar] [CrossRef]
- Rehana, S.; Monish, N.T. Characterization of regional drought over water and energy limited zones of India using potential and actual evapotranspiration. Earth Space Sci. 2020, 7, e2020EA001264. [Google Scholar] [CrossRef]
- Faiz, M.A.; Liu, D.; Fu, Q.; Naz, F.; Hristova, N.; Li, T.; Niaz, M.A.; Khan, Y.N. Assessment of dryness conditions according to transitional ecosystem patterns in an extremely cold region of China. J. Clean. Prod. 2020, 255, 120348. [Google Scholar] [CrossRef]
- Bayissa, Y.A.; Moges, S.A.; Xuan, Y.; Van Andel, S.J.; Maskey, S.; Solomatine, D.P.; Griensven, A.V.; Tadesse, T. Spatio-temporal assessment of meteorological drought under the influence of varying record length: The case of Upper Blue Nile Basin, Ethiopia. Hydrol. Sci. J. 2015, 60, 1927–1942. [Google Scholar] [CrossRef]
- Lu, J.; Jia, L.; Menenti, M.; Yan, Y.; Zheng, C.; Zhou, J. Performance of the standardized precipitation index based on the TMPA and CMORPH precipitation products for drought monitoring in China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1387–1396. [Google Scholar] [CrossRef]
- Van den Hende, C.; Van Schaeybroeck, B.; Nyssen, J.; Van Vooren, S.; Van Ginderachter, M.; Termonia, P. Analysis of rain-shadows in the Ethiopian Mountains using climatological model data. Clim. Dyn. 2021, 56, 1663–1679. [Google Scholar] [CrossRef]
- Seleshi, Y.; Demarée, G. Identifying the major cause of the prevailing summer rainfall deficit over the North-Central Ethiopian highlands since the mid-60s. In Proceedings of the International Conference on Tropical Climatology, Meteorology and Hydrology in Memoriam Franz Bultot, Bruxelles, Belgium, 22–24 May 1996; Royal Meteorological Institute of Belgium (Brussels); Royal Academy of Overseas Sciences (Brussels): Brussels, Belgium, 1998. [Google Scholar]
- Seleshi, Y.; Demaree, G. The temporal distribution of Ethiopian meteorological droughts in the 20 century. In Proceedings of the Biological Indicators of Global Change, Brussels, Belgium, 7–9 May 1992. [Google Scholar]
- Seleshi, Y.; Camberlin, P. Recent changes in dry spell and extreme rainfall events in Ethiopia. Theor. Appl. Climatol. 2006, 83, 181–191. [Google Scholar] [CrossRef] [Green Version]
- Jury, M.R.; Funk, C. Climatic trends over Ethiopia: Regional signals and drivers. Int. J. Climatol. 2013, 33, 1924–1935. [Google Scholar] [CrossRef]
- Dosio, A.; Jones, R.G.; Jack, C.; Lennard, C.; Nikulin, G.; Hewitson, B. What can we know about future precipitation in Africa? Robustness, significance and added value of projections from a large ensemble of regional climate models. Clim. Dyn. 2019, 53, 5833–5858. [Google Scholar] [CrossRef] [Green Version]
- Keller, E.J. Drought, war, and the politics of famine in Ethiopia and Eritrea. J. Mod. Afr. Stud. 1992, 30, 609–624. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayissa, Y.; Tadesse, T.; Demisse, G.; Shiferaw, A. Evaluation of satellite-based rainfall estimates and application to monitor meteorological drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2017, 9, 669. [Google Scholar] [CrossRef] [Green Version]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Gleixner, S.; Demissie, T.; Diro, G.T. Did ERA5 improve temperature and precipitation reanalysis over East Africa? Atmosphere 2020, 11, 996. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar] [CrossRef] [Green Version]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Van der Schrier, G.; Jones, P.D.; Briffa, K.R. The sensitivity of the PDSI to the Thornthwaite and Penman-Monteith parameterizations for potential evapotranspiration. J. Geophys. Res. Atmos. 2011, 116, D03106. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Xu, C.Y.; Van Lanen, H.A. Standardized precipitation-evapotranspiration index (SPEI): Sensitivity to potential evapotranspiration model and parameters. In Proceedings of the Hydrology in a Changing World, Montpellier, France, 7–10 October 2014; Volume 363, pp. 367–373. [Google Scholar]
- Guttman, N.B. Accepting the standardized precipitation index: A calculation algorithm 1. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Stagge, J.H. SCI: Standardized Climate Indices such as SPI, SRI or SPEI, R Package Version 1.0.1. 2014. Available online: https://rdrr.io/cran/SCI/ (accessed on 17 May 2021).
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 8479–8519. [Google Scholar] [CrossRef] [Green Version]
- Martens, B.; Miralles, D.G.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.A.; Verhoest, N.E. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Dadson, S.; Hirpa, F.; Dyer, E.; Lees, T.; Miralles, D.G.; Vicente-Serrano, S.M.; Funk, C. A pan-African high-resolution drought index dataset. Earth Syst. Sci. Data 2020, 12, 753–769. [Google Scholar] [CrossRef] [Green Version]
- Singh, V.P. Pearson type III distribution. In Entropy-Based Parameter Estimation in Hydrology; Springer: Dordrecht, The Netherlands, 1998; pp. 231–251. [Google Scholar]
- Hosking, J.R. Algorithm as 215: Maximum-likelihood estimation of the parameters of the generalized extreme-value distribution. J. R. Stat. Soc. Ser. C Appl. Stat. 1985, 34, 301–310. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R.; Wood, E.F. Estimation of the generalized extreme-value distribution by the method of probability-weighted moments. Technometrics 1985, 27, 251–261. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized logistic distributions. J. Appl. Stat. Sci. 2010, 18, 51. [Google Scholar]
- Massey Jr, F.J. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Anderson, T.W.; Darling, D.A. A test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Chowdhury, J.U.; Stedinger, J.R.; Lu, L.-H. Goodness-of-fit tests for regional generalized extreme value flood distributions. Water Resour. Res. 1991, 27, 1765–1776. [Google Scholar] [CrossRef]
- Shin, H.; Jung, Y.; Jeong, C.; Heo, J.-H. Assessment of modified Anderson–Darling test statistics for the generalized extreme value and generalized logistic distributions. Stoch. Environ. Res. Risk Assess. 2012, 26, 105–114. [Google Scholar] [CrossRef]
- Song, S.; Singh, V.P. Meta-elliptical copulas for drought frequency analysis of periodic hydrologic data. Stoch. Environ. Res. Risk Assess. 2010, 24, 425–444. [Google Scholar] [CrossRef]
- Delignette-Muller, M.L.; Pouillot, R.; Denis, J.-B.; Dutang, C. Fitdistrplus: Help to Fit of a Parametric Distribution to Non-Censored or Censored Data, 2010; R Package Version 01-3. 2013. Available online: https://cran.r-project.org/web/packages/fitdistrplus/fitdistrplus.pdf (accessed on 17 May 2021).
- Asquith, W. Package ‘Lmomco.’ L-Moments, Trimmed L-Moments, L-Comoments, and Many. 2021. Available online: https://cran.r-project.org/web/packages/lmomco/lmomco.pdf (accessed on 17 May 2021).
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Xia, Y.; Ek, M.B.; Peters-Lidard, C.D.; Mocko, D.; Svoboda, M.; Sheffield, J.; Wood, E.F. Application of USDM statistics in NLDAS-2: Optimal blended NLDAS drought index over the continental United States. J. Geophys. Res. Atmos. 2014, 119, 2947–2965. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov test for normality with mean and variance unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Crutcher, H.L. A note on the possible misuse of the Kolmogorov-Smirnov test. J. Appl. Meteorol. 1975, 14, 1600–1603. [Google Scholar] [CrossRef] [Green Version]
- Steinskog, D.J.; Tjøstheim, D.B.; Kvamstø, N.G. A cautionary note on the use of the Kolmogorov–Smirnov test for normality. Mon. Weather Rev. 2007, 135, 1151–1157. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. Uncertainty analysis of Standardized Precipitation Index due to the effects of probability distributions and parameter errors. Front. Earth Sci. 2020, 8, 76. [Google Scholar] [CrossRef]
- Burke, E.J.; Brown, S.J. Evaluating uncertainties in the projection of future drought. J. Hydrometeorol. 2008, 9, 292–299. [Google Scholar] [CrossRef]
- Hoffmann, D.; Gallant, A.J.; Arblaster, J.M. Uncertainties in drought from index and data selection. J. Geophys. Res. Atmos. 2020, 125, e2019JD031946. [Google Scholar] [CrossRef]
- Xu, K.; Wu, C.; Zhang, C.; Hu, B.X. Uncertainty assessment of drought characteristics projections in humid subtropical basins in China based on multiple CMIP5 models and different index definitions. J. Hydrol. 2021, 600, 126502. [Google Scholar] [CrossRef]
- Homdee, T.; Pongput, K.; Kanae, S. A comparative performance analysis of three standardized climatic drought indices in the Chi River basin, Thailand. Agric. Nat. Resour. 2016, 50, 211–219. [Google Scholar] [CrossRef] [Green Version]
| Accumulation Period (Months) | ||||||
|---|---|---|---|---|---|---|
| Time Series Length | 1 | 3 | 6 | 9 | 12 | 24 |
| 10 | 4.04 | 4.79 | 5.74 | 7.27 | 8.13 | 12.83 |
| 15 | 3.67 | 2.48 | 2.09 | 2.17 | 2.16 | 3.00 |
| 20 | 5.87 | 4.03 | 4.05 | 3.78 | 4.31 | 3.61 |
| 25 | 7.13 | 5.19 | 4.57 | 4.43 | 5.38 | 5.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yimer, E.A.; Van Schaeybroeck, B.; Van de Vyver, H.; van Griensven, A. Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia. Atmosphere 2022, 13, 364. https://doi.org/10.3390/atmos13030364
Yimer EA, Van Schaeybroeck B, Van de Vyver H, van Griensven A. Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia. Atmosphere. 2022; 13(3):364. https://doi.org/10.3390/atmos13030364
Chicago/Turabian StyleYimer, Estifanos Addisu, Bert Van Schaeybroeck, Hans Van de Vyver, and Ann van Griensven. 2022. "Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia" Atmosphere 13, no. 3: 364. https://doi.org/10.3390/atmos13030364
APA StyleYimer, E. A., Van Schaeybroeck, B., Van de Vyver, H., & van Griensven, A. (2022). Evaluating Probability Distribution Functions for the Standardized Precipitation Evapotranspiration Index over Ethiopia. Atmosphere, 13(3), 364. https://doi.org/10.3390/atmos13030364







