Abstract
A method to estimate the sensible heat flux (H) for unstable atmospheric condition requiring measurements taken in half-hourly basis as input and involving the land surface temperature (LST), HLST, was tested over a tall and dense aspen stand. The method avoids the need to estimate the zero-plane displacement and the roughness length for momentum. The net radiation (Rn) and the latent heat flux (λE) dominated the surface energy balance (SEB). Therefore, λE was estimated applying the residual method using HLST as input, λER-LST. The sum of H and λE determined with the eddy covariance (EC) method led to a surface energy imbalance of 20% Rn. Thus, the reference taken for the comparisons were determined forcing the SEB using the EC Bowen ratio (BREB method). For clear sky days, HLST performed close to HBREB. Therefore, it showed potential in the framework of remote sensing because the input requirements are similar to current methods widely used. For cloudy days, HLST scattered HBREB and nearly matched the accumulated sensible hear flux. Regardless of the time basis and cloudiness, λER-LST was close to λEBREB. For all the data, both HLST and λER-LST were not biased and showed, respectively, a mean absolute relative error of 24.5% and 12.5% and an index of agreement of 68.5% and 80%.
1. Introduction
In non-dry climates, the evapotranspiration or latent heat flux (λE) is one of the dominant components of both the land-surface water and energy budgets. In dry and semi-arid climates λE is a critical component of living things. Therefore, among other issues, monitoring evapotranspiration rates is of interest to understand ecosystem sustainability/vulnerability regardless of the climate [1,2,3,4,5]. Different methodologies are available to determine λE and micrometeorological methods often involve the surface energy balance and similarity theory [6,7,8,9,10]. The latter methods require the identification of the dominant terms in the surface energy balance. On a half-hourly basis, for instance, the energy storage in tall and dense canopies is significant [11,12,13]. When the dominant surface fluxes can be determined using measurements taken at low frequency, the method becomes friendlier because the instrumentation involved is more robust and affordable and requires minor power supply. In addition, most similarity-based formulations allow involving remote sensing products. Hence, provided they are used on clear-sky days, they can be applied at non-local scales [14,15,16,17,18,19,20].
During the day, the sensible heat flux (H) on a half-hourly basis is a dominant term in the surface energy balance. Thus, the aim of this paper was to continue research on testing a recent method to estimate the H under unstable cases which involves measurements taken at low frequency including the land surface temperature (LST), HLST [21]. Currently, HLST has been tested over agricultural landscapes and mountain meadows, showing potential in the framework of remote sensing [22,23,24]. The good performance obtained in different scenarios aimed here to adapt HLST for a tall and dense canopy. Here, the scenario selected to test HLST was a Boreal Forest at a site which allowed estimation of the latent heat flux (LE) as a residual of the surface energy balance. In this study the data analysis was mainly based on the unstable condition and the criterion for the selection of unstable data was through the sign of sensible heat flux, because under stable condition the measured surface fluxes are expected to have major errors using the eddy covariance method [25,26]. Therefore, it was omitted with the aim of excluding errors in the estimated HSR. The testing included clear and cloudy days.
2. Materials
The campaign was carried out in a forest located in Prince Albert National Park (Saskatchewan, Canada; 53.629° N, 106.200° W, 600.63 m asl) in 1996. A brief description of the campaign accessed on (28 December 2021) (http:///boreas/TF/tf01tflx/comp/TF01_Tower_Flux.txt; Black, 2000) is the following. The forest consisted in an even-aged 70-year-old aspen stand with a mean height of 21.5 m. Hazelnut (2.0 m tall) dominated the understory. The forest had a minimum fetch of 3 km extending on a gentle rolling topography and the aspen canopy closure averaged 89% from June to August. For July and August, the mean leaf area index was 5.4 m2m−2 and 5.25 m2m−2, respectively [27] and the following measurements on a half-hourly basis were obtained from the dataset tf01_tower_flux.dat (freely downloadable). The soil heat flux was sampled at 3 cm below the ground at seven points. The mean soil temperature and the volumetric fraction of water were placed in a sublayer (3 cm thick) above the soil heat flux plates. The temperature and pressure of the air, the wind speed, the friction velocity and the sensible heat and latent heat fluxes (determined using the eddy covariance (EC) system) were measured at 39 m above the ground. The wind speed was measured at the canopy top and the downwelling and upwelling shortwave and longwave radiation were measured at 33 m above the ground.
3. Theory and Methods
3.1. Monin–Obukhov Similarity Theory (MOST)
The atmospheric surface layer is also known as the constant flux layer because fluxes are nearly constant with height, with variations of less than 10 % under steady-state and horizontal homogeneous conditions [28]. Monin and Obukhov (1954) introduced two scaling parameters, which are independent of height in the surface layer for the structure of turbulence [29]. The friction velocity expressed as Equation (1) is [30]:
where u′, v′ and w′ are the fluctuations from the mean three-dimensional windspeed of u, v and w respectively. The second scaling parameter, which is a function of momentum and sensible heat fluxes, is the Obukhov length, (Lo) expressed as Equation (2):
where ρ is the density of air, cp the specific heat capacity of air at constant pressure, Ta the absolute air temperature, k the von Karman constant and g the acceleration due to gravity. The negative sign is the sign of the sensible heat flux corresponding to the vertical air temperature difference between two heights. The Obukhov length can be interpreted as the height, above (do + z), for which free convection dominates [31,32]. Another, similar key scaling parameter which determines the structure of turbulence is the turbulent temperature scale (Ta) expressed as Equation (3) [30,31]:
On the other hand, turbulent characteristics depend upon a dimensionless stability parameter (ζ) expressed as Equation (4):
where z is the height above the surface and d is the zero-plane displacement height. The dimensionless stability parameter ζ is a theoretical indicator of the atmospheric stability.
3.2. Sensible Heat Flux
The summary of the method, fully described in Castellví and González-Dugo (2021) [24], to estimate the sensible heat flux (half-hourly basis) is as follows. It combines similarity and surface renewal formulation through Equations (5)–(7):
where
In Equation (5), z is the measurement height above the zero-plane displacement (d), thus z = Z − d where Z is measurement height above the ground, Φh is the stability correction function for heat transfer, λ and A, namely ramp period and amplitude, are two parameters that identify a coherent motion in the surface sublayer above the canopy top. By defining a macro parcel of air as a parcel of air which volume, per unit area, may cover all the sources of scalar at the surface, a coherent motion (regular eddy motion of macro parcels of air) is carried out by a coherent structure which is defined as an eddy capable to impose some organization in the turbulence in the surface layer. Thus, the ramp period accounts for the time that a macro parcel of air remained in contact with the surface and the ramp amplitude for the net temperature increase (for an unstable case) while it remained in contact with the surface [33,34,35].
Coherent structures near the canopy are mostly driven by shear rather than by buoyancy [36]. Thus, Chen et al. (1997b) proposed to relate the ramp frequency and u∗/z [34]. Approaching the shear at the canopy top by u∗/hc (hc is the canopy height), the semi-empirical Equation (6) was proven reliable for a variety of canopies. Assuming that the maximum temperature to be reached by the parcel of air is LST, Equation (7) proposes a linear relationship between quantities (LST–T) and A where T is the potential temperature of the air measured at a reference height above the canopy [21,22]. In Equation (7), b is a coefficient (hereafter referred to as offset) that corrects for the fact that (LST–T) may not necessarily follow the adiabatic lapse rate at neutral conditions (i.e., case where A = 0 K) and z0m is the roughness length for momentum. Because the factor [8k/π]1/2 approaches to one, combining Equations (5)–(7) the sensible heat flux can be estimated above the canopy as Equation (8):
3.3. Latent Heat Flux
The latent heat flux can be estimated as a residual of the surface energy balance (the residual method) as Equation (9):
where Rn is the net radiation, G is the soil heat flux and S is the energy storage (per unit time and surface) below the measurement height. The net radiation (Rn) was calculated using four radiative components. The soil heat flux (Wm−2) and the total storage in a column were estimated using Equations (10) and (11), respectively [37]:
where .
λER = Rn − G − S − H
S = 44.5∆ + 1.66
In Equation (10), overbar denotes spatial average, zs is the depth at which the soil heat flux plates were collocated and the second term in the right hand denotes heat storage in the soil above zs where Cs is the soil heat capacity (MJm−3K−1) and θw is the soil water content. In Equation (10), ΔT is the change of temperature of the air at the reference height on a half-hourly basis. Hereafter, λER determined using as input HLST and HEC is denoted as λER-LST and λER-EC, respectively.
3.4. Solving the Sensible and Latent Heat Fluxes
For tall canopies, the zero-plane displacement and the roughness length for momentum are related to each other and depend on the stability parameter [15,38,39]. It was accounted here and Appendix A describes an iterative procedure to simultaneously estimate d, z0m, u∗, HLST and λER-LST.
The land surface temperature was retrieved from the Stefan–Boltzman law and the effective emissivity of the surface (ε0) was estimated as [40]; ε0 = εv(1 − fs) + εsfs(1.74fs − 0.74) + 1.7372fs(1 − fs) where fs is the fraction cover and εv and εs are representative emissivities for the canopy and understories. During the experiment, the fraction cover remained fairly constant (fs = 0.89) and the emissivities for the aspen canopy and understories (hazelnut and soil) were set to 0.97 and 0.96, respectively [41]. Thus, ε0 was set to 0.97. The offset in Equation (7) was determined as in Castellví et al. (2016) [22]. Thus, the coefficient b at sunrise and sunset was determined setting A = 0 K, at noon the offset was set to zero and for the rest of the day it was calculated using a linear relationship from sunrise to noon and from noon to sunset.
3.5. The Reference, Datasets and Performance Evaluation
The sum of the EC sensible heat flux and latent heat flux was significantly smaller that the available net surface energy (shown in Section 4.1) which has implications on how HEC and λEEC should be interpreted. Kidstone et al. (2010) conducted experiments over two different land surfaces and implications for CO2 fluxes measurement using eddy covariance method. Results suggested that spatio-temporal distributions of total surface fluxes were in good agreement and difference between the relative magnitudes of the fluxes for several investigated energy balance closure classes was observed [42]. Noman et al. (2019) estimated surface fluxes including sensible and latent heat fluxes along variable fetch using flux variance technique, linear regression was performed between the sum of turbulent fluxes and the available energy fluxes and energy balance closure was well behaved with linear regression of R2 = 0.83 [43]. J. L. Chavez et al. (2009) evaluated the performance of eddy covariance over cotton with large weighing lysimeters; results suggested the estimated surface fluxes were underestimated with average error of about 30%. Energy balance closure was 73.2–78.0% for daytime fluxes [44]. R. Ding et al. (2019) conducted experiments in maize field of northwest China for evaluating performance of eddy covariance using lysimeters. Energy balance ratio was 0.84 for stable conditions, indicating that lack of energy balance closure occurred and estimated ET was adjusted by Bowen ratio forced closure method [45]. Noman et al. investigated performance of flux variance method at different heights and results suggested relatively better agreement between the energy balance closure with slope of regression 0.55 and RMSE of 33.95 Wm−2 [46]. X. Wang et al. (2010) performed experiments in maize fields for the estimation of energy fluxes and evapotranspiration in arid area with shallow groundwater. Estimated latent heat flux was adjusted using Bowen ratio with linear regression of R2 = 0.94 and slope of regression was 0.732 and 0.634 respectively for half-hourly data in 2017 and 2018. The water balance results showed average water table depth of 1.52 and 1.76 m for the growing season of 2017 and 2018 [47]. Here, the EC Bowen ratio (βEC) was used to refine the EC sensible heat and latent heat fluxes, Equation (12), which were taken as a reference [27]:
A dataset was formed excluding rainy events [25]. July only included cloudy days. August had 11 clear sky days and the rest were cloudy. Datasets were formed with samples having different friction velocity thresholds (up to 0.6 m/s).
The performance of the flux estimates, Fest, was analyzed determining the sum of the estimates over the sum of the reference (D), the mean absolute difference or error (MAE) and the index of agreement (IA) expressed as below [48]:
where F is the flux taken as reference, N is the total number of samples and overbar denotes average. The expression given in Equation (12) is valid when [48] and, here, the full expression to calculate IA was omitted because the datasets formed accomplished this constrain. The performance of HLST (determined as proposed in the Appendix A) was compared with the estimates obtained by assuming a fixed value for the zero-plane displacement (selected by rule of thumb in a range of 0.6–0.85 times the canopy height) and, in addition, by assuming that the offset may be neglected.
4. Results
4.1. Surface Energy Balance Using HEC and λEEC
Figure 1 shows the accumulated HEC, λEEC and (HEC + λEEC + G + S) standardized by the net radiation for different friction velocity thresholds. Regardless of the month, it is shown that the weight of the latent heat flux in the surface energy balance was much higher than of the sensible heat flux. The energy partitioning in Figure 1 showed the need to refine the EC fluxes. For all the data, about 20% of Rn was unexplained by (HEC + λEEC + G + S). The surface energy balance improved as the friction velocity threshold increased. A good closure (of about 10%) was obtained for a short dataset, for friction velocities higher than 0.5 m/s. Table 1 shows the coefficients D, MAE and IA for the sensible heat fluxes HEC and HLST and the latent heat fluxes determined using the EC method, λEEC, and the residual method, λER-EC and λER-LST. Regardless of the month, Table 1 shows that λER-EC was closer to λEBREB than λEEC. The reasons of the surface energy imbalance are unknown (i.e., yet an unresolved problem), however, (on the basis of forcing the closure using the Bowen ratio) Table 1 shows that the residual method was suitable to estimate the latent heat flux. This is of interest because estimation of the Bowen ratio in the present context appears difficult given that over very tall vegetation, measurements are expected in the roughness sublayer (i.e., a layer where gradients are weak).
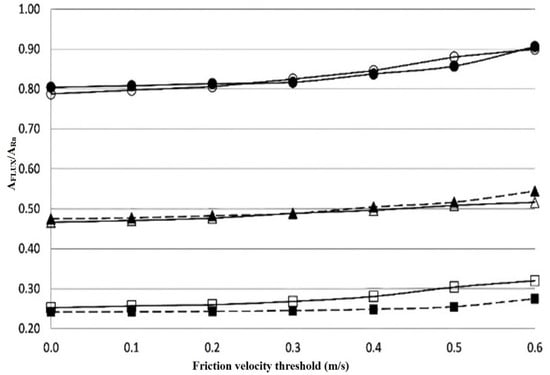
Figure 1.
Accumulated surface flux estimates, HEC (squares), λEEC (triangles) and (HEC + λEEC + G + S) (circles), standardized by the net radiation (AFlux/ARn) for different friction velocity thresholds in July (solid) and August (open).

Table 1.
EC and LST sensible heat and latent heat flux estimates.
4.2. Sensible Heat Flux
Figure 2 compares HEC and HLST against HBREB and Figure 3 shows the coefficients D, MAE and IA for HEC and HLST determined for different friction velocity thresholds and cloudiness. Regardless of the month, Figure 2 shows that HECt ended to underestimate HBREB while HLST scattered around HBREB. Therefore, the coefficients D in Figure 3 show that the accumulated HLST was consistently closer to the reference than using HEC. On a half-hourly basis, the MAE and IA obtained for clear sky days showed that HLST and HEC performed similarly. For cloudy days HEC was closer than HLST to HBREB, though the MAE coefficients differed about 10 Wm−2 (regardless of the month and friction velocity threshold). It is difficult to explain why the accumulated HLST was closer to HBREB than HEC. The lack of closure of the EC surface energy balance was, partly, attributed to lack of stationarity [49]. Though a steady flow on a half-hourly basis is also assumed in HLST, perhaps the use of measurements taken at low frequency as input tended to balance such source of error. On the other hand, the higher IA coefficients obtained using HEC than HLST can be attributed to the use of measurements taken at high frequency. That is, the EC method requires as input direct measurements of the turbulence and, therefore, it is expected to be highly correlated with the actual eddy flux.
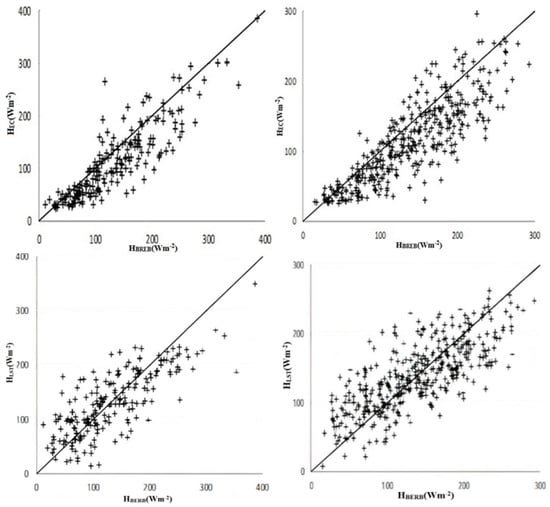
Figure 2.
Sensible heat flux determined using the EC method (upper panel) and the LST method (lower panel) against the BREB method in July (left panel) and August (right panel).
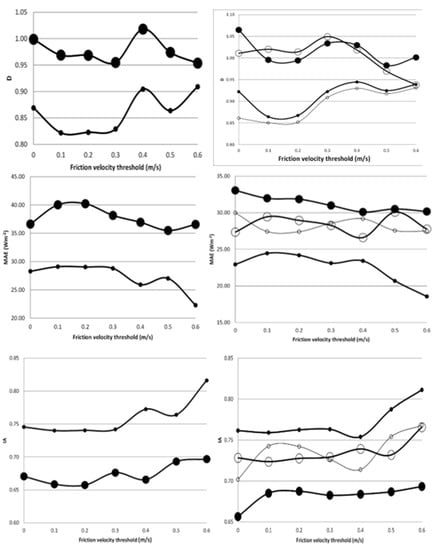
Figure 3.
Coefficients D (top), MAE (middle) and IA (bottom) for sensible heat flux estimates using the EC method (thin solid) and the LST method (thick solid) for different friction velocity thresholds in clear sky days (open circle) and cloudy days (solid circle) in July (left panel) and August (right panel).
4.3. Latent Heat Flux
Figure 4 shows the coefficients D and IA obtained for λER-EC and λER-LST for different friction velocity thresholds and cloudiness. Here, Figure 4 was included for completeness (i.e., the results shown can qualitatively be inferred from Figure 3), however, the MAE values were not shown (i.e., they are identical to the values shown in Figure 3). Regardless of the cloudiness and friction velocity threshold and for all the data (Table 1), it is shown that λER-LST nearly matched λEBREB. λER-EC tended to overestimate (7% and 9% in July and August, respectively) λEBREB and the worst performance was obtained using λEEC. For clear sky days, λER-EC and λER-LST performed close to λEBREB. For cloudy days, λER-EC was closer to λEBREB than λER-LST but in August (which includes cloudy and clear sky days), Figure 5, which compared λEEC, λER-EC and λER-LST against λEBREB, shows that λER-LST scattered the 1:1 line and λER-EC tended to overestimate.
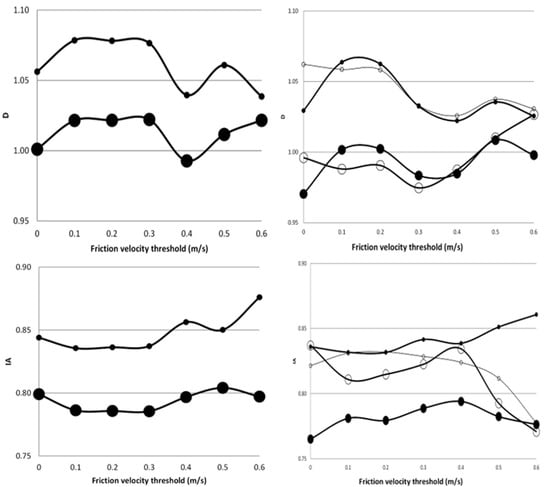
Figure 4.
Coefficients D (top) and IA (bottom) for latent heat flux estimates using the EC (thin solid) and the LST (thick solid) sensible heat flux as input for different friction velocity thresholds in clear sky days (open circle) and cloudy days (solid circle) in July (left panel) and August (right panel).
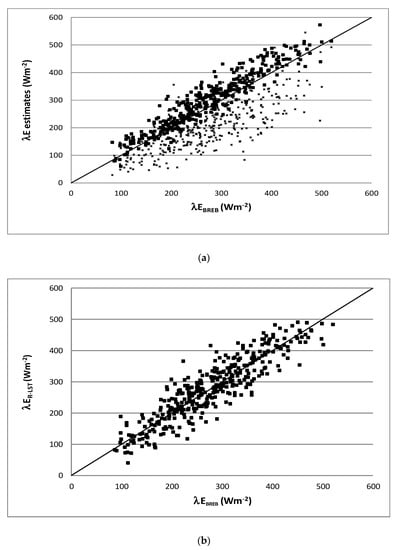
Figure 5.
Latent heat flux estimates against the BREB method in August. (a) λER-EC (square) and λEEC (cross) and (b) λER-LST.
The results of the linear regression analysis obtained for the samples collected during clear sky days (August) showed the λER-LST performed close to λEBREB, λER-LST = 0.98 λEBREB + 4 Wm−2, with a coefficient of determination (R2) of 0.89. The bias was negligible (1 Wm−2) and the mean absolute relative error was 9%. For cloudy days in July, it was found: λER-LST = 0.96 λEBREB + 13 Wm−2, R2 = 0.85; bias = 0 Wm−2, and the mean relative absolute error was 14% (Table 1). For cloudy days in August: λER-LST = 0.98 λEBREB + 3 Wm−2, R2 = 0.82, bias = 8 Wm−2 and the mean relative absolute error was 12%. Thus, −λER-LST performed excellently.
4.4. The Zero-Plane Displacement and the Offset
Table 2 shows the coefficients D, MAE and IA for HLST obtained for each month, setting a given value for the zero-plane displacement and setting the offset to zero. For completeness, the comparisons between λER-LST and λEBREB were also included.

Table 2.
LST sensible heat and latent heat flux estimates determined using different zero-plane displacements at neutral conditions and neglecting the offset.
4.4.1. Setting a Fixed Value for the Zero-Plane Displacement
The half-hourly difference, E, in closing Equation (A6) for a fixed dN/hc ratio, E = z0m − (2.05 dN/d − 1.05)z0mN), was averaged for samples collected in cloudy days, clear sky days and for all the data, hereafter referred to as Error. Figure 6 shows the Error obtained for dN/hc ratios in the range 0.6–0.85. The smallest Errors were obtained for dN values close to 0.75 hc . Comparing the results obtained in Table 1 for HEC with those obtained in Table 2, it is inferred that HLST would be neither close to HEC nor HBREB using approaches close to d = 0.65 hc , which are often taken as a rule of thumb [50,51]. Thus, the procedure to objectively select the zero-plane displacement for each sample is recommended.
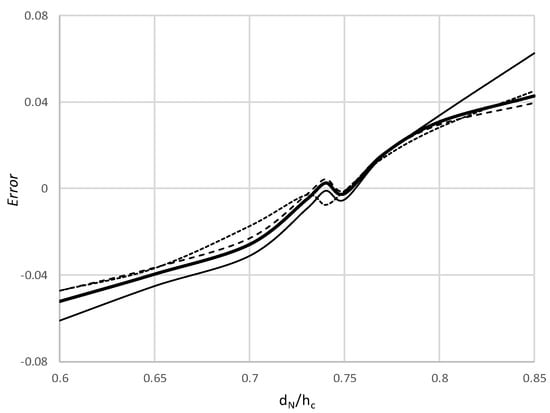
Figure 6.
Error (averaged (z0m/z0mN − 2.05 dN/d + 1.05)) for different ratios of the zero-plane displacement at neutral conditions over the canopy height in July (dotted), clear sky (thin solid) and cloudy (dashed) days in August and for all the data in August (thick solid).
4.4.2. The Offset
The accumulated frequency of the offset (Figure 7) shows that, in general, the offset ranged between −1 K and 1.25 K. The probability to observe an offset equal and smaller than 0 K in August doubled July because for clear sky days the offset ranged between 0.18 K and 0.15 K. Thus, in practice, for clear sky days the offset could be neglected. While Table 1 shows that the coefficient D was, in practice, one, Table 2 shows that when the offset was neglected HLST overestimated HBREB by 21% and 13% in July and August, respectively. The MAE and IA coefficients were worse, especially in July because August included clear sky days. Therefore, it is not recommended to neglect the offset for cloudy days.
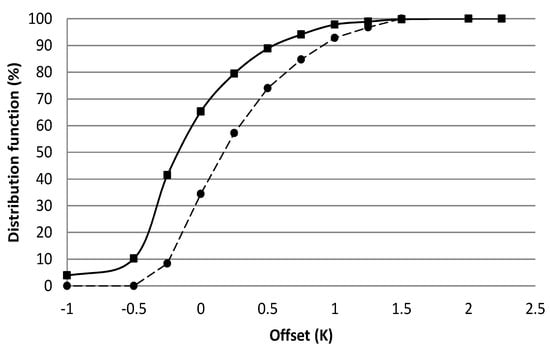
Figure 7.
Probability distribution function for the offset in July (circle) and August (square).
5. Concluding Remarks
A method based on similarity and surface renewal formulation to estimate the sensible heat flux for unstable cases was adapted to operate over tall canopies avoiding the need to estimate the zero-plane displacement and roughness length for momentum. The input requirements are the potential temperature of the air and wind speed at a reference height above the canopy, the land surface temperature, the canopy height, the leaf area index and the wind speed at the canopy top, though the latter is not required as input when the reference height is in the inertial sublayer. The method includes an offset to adjust the adiabatic temperature lapse rate which can be neglected for clear sky days. The latter implies that, except for bare soils (research is pending), the offset can be neglected regardless of the canopy type implying that (for clear sky days) the method shows potential of application in the framework of remote sensing over forests. Given that the net radiation and the latent heat flux dominated the surface energy balance, the latent heat flux was determined using the residual method and, regardless of the cloudiness, the role of the offset played a minor role. Thus, for cloudy days HLST scattered the reference and the accumulated HLST closely matched the reference. Further research is required to compare it with other models requiring the same or similar input. However, here it is concluded that the method proposed to estimate the sensible heat flux is an alternative to consider for modelling surface energy budgets in tall and dense canopies. In particular, it showed potential in remote sensing applications.
Author Contributions
Writing—original draft, Project administration, F.C.; Writing—review and editing, N.A.B.; Supervision, Y.H.; Data curation, K.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
This work was supported under project RTI2018-098693-B-C31 (Ministerio de Ciencia, Economia y Universidades of Spain). The data was freely downloadable at http://daac.ornl.gov/BOREAS/boreas.shtml (accessed on 28 December 2021). Key R&D Program of Jiangsu Province (BE2021340) and Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD-2018-87).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Solving the Sensible Heat and the Latent Heat Fluxes for Unstable Cases
The procedure combined flux-gradient and semi-empirical relationships to simultaneously solve the sensible heat flux (HLST, Equation (8)), the latent heat flux (λER-LST, where λis latent heat of vaporization and subscript R-LST denotes that the latent heat flux was determined as a residual of the surface energy balance using HLST as input, Equation (9)), the stability parameter, the friction velocity, the zero-plane displacement and the roughness length for momentum [15,39,40,52,53,54,55]. Because measurements over tall canopies are likely taken below the inertial sublayer, the procedure preserves the continuity of the mean profiles for the wind speed and the potential temperature of the air above the canopy (i.e., there is no need to know if the reference height is in the roughness or in the inertial sublayer).
In the following, the origin of the vertical axis is placed at the canopy top. Hence, the mean wind profile (u(z)) extrapolated within the canopy decays to zero, u(zc) = 0 at height (negative) zc = −dt + z0m where dt is dt = hc − d (hc is the canopy height and d is the zero-plane displacement) and z0mis the roughness length for momentum. By defining dt as the height that is enacting the total drag force on the canopy, it can be expressed as (A1) [39,52]:
where u∗ is the friction velocity, uh is the wind speed at the canopy top and Lc is a penetration depth into the canopy of a characteristic eddy size. It is estimated as Lc = 1/ (cda), where cd is the drag coefficient at leaf scale and a is the leaf area per unit volume. For unstable cases, it can be set to cd = 0.11 [56,57]. Denoting the stability function for the transfer of momentum in a generalized form as Φm, the local shear above the canopy is expressed as Equation (A2) [39,53]:
where k is the von-Kármán constant and ISL and RSL denote inertial and roughness (above the canopy) sublayers, respectively. The ISL is described by the Obukhov length (L), For unstable conditions, Φm(x) = (1 − 16x)−1/4 [58] the RLS is described by the Obukhov length and the shear length scale at the canopy top (Ls), [54] which can be expressed as Equation (A3):
In Equation (A2), φm(x) = 1 − c1mexp[−c2mx], where c1m and c2m are two coefficients:
and
Integrating Equation (A2) from the canopy top to up to a reference height, the friction velocity is expressed as Equation (A4):
where being (it only admits numerical solution) and the roughness length for momentum, z0m, is
.
Similar for the temperature profile, the generalized stability function for the transfer of heat, Φh, above the canopy is expressed as Equation (A5) [53,55]:
For unstable conditions, Φh(x) = (1 − 16x)−1/2 [58] and φh(x) = 1 − c1hexp[−c2hx] where the coefficients c1h and c2h are
and
being Pt the turbulent Prandtl number at the canopy top, .
Solving HLST and λER-LST. Provided that the zero-plane displacement at neutral conditions is known, Equations (A1)–(A5), HLST and λER-LST can be iterated until a criterion of convergence is achieved. Starting at neutral conditions, L = ∞ and dtN = hc − dN (subscript N denotes neutral case), β and Ls are determined which allows for the calculation of z0m, u∗, and a first proxy for HLST and λER-LST. The next iteration starts calculating a proxy for the Obukhov length. Thus, a new proxy is obtained for z0m, u∗, β, dt, Ls, HLST and λER-LST. The loop can be iterated until the difference in u∗between two consecutive iterations is smaller than a given threshold, here 0.01 m/s.
Selection of the zero-plane displacement at neutral conditions. For unstable cases, the zero-plane displacement and the roughness length for momentum decreases and increases, respectively, with respect to their value at neutral stratification as; z0m = z0mN [1 + 1.15 (−hc/L)1/3] and d = dN/[1 + 0.56 (−hc/L)1/3][39]. Combining the latter two relationships,
z0m − (2.05dN/d − 1.05); z0m N = 0
After solving HLST and λER-LST using a given dN value (selected as a rule of thumb), the values obtained in the iteration process for z0mN, d (i.e., once dt is solved) and z0m can be used to check the closure of Equation (A6). The best closure obtained for a given dN value within the range 0.6 hc ≤ dN ≤ 0.85 hc [15] can be used to objectively determine HLST and λER-LST.
References
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Wagener, T.; Sivapalan, M.; Troch, P.A.; McGlynn, B.L.; Harman, C.J.; Gupta, H.V.; Kumar, P.; Rao, P.S.C.; Basu, N.B.; Wilson, J.S. The future of hydrology: An evolving science for a changing world. Water Resour. Res. 2010, 46, W05301. [Google Scholar] [CrossRef]
- Chen, L.; Wang, L.; Ma, Y.; Liu, P. Overview of Ecohydrological Models and Systems at the Watershed Scale. IEEE Syst. J. 2015, 9, 1091–1099. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.F.; Barbosa, H.M.J.; Hirota, M.; Montade, V.; Sampaio, G.; Staal, A.; Wang-Erlandsson, L.; Rammig, A. Self-amplified Amazon forest loss due to vegetation-atmosphere feedbacks. Nat. Commun. 2017, 8, 14681. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere; (Environmental Fluid Mechanics); Springer: Dordrecht, The Nethelrands, 1982; 299p. [Google Scholar]
- Brotzge, J.A.; Crawford, K.C. Examination of the Surface Energy Budget: A Comparison of Eddy Correlation and Bowen Ratio Measurement Systems. J. Hydrometeorol. 2003, 4, 160–178. [Google Scholar] [CrossRef]
- Cuxart, J.; Boone, A.A. Evapotranspiration over Land from a Boundary-Layer Meteorology Perspective. Bound. Layer Meteorol. 2020, 177, 427–459. [Google Scholar] [CrossRef]
- Brunet, Y. Turbulent Flow in Plant Canopies: Historical Perspective and Overview. Bound. Layer Meteorol. 2020, 177, 315–364. [Google Scholar] [CrossRef]
- Hu, Y.; Buttar, N.A.; Tanny, J.; Snyder, R.L.; Savage, M.J.; Lakhiar, I.A. Surface Renewal Application for Estimating Evapotranspiration: A Review. Adv. Meteorol. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Meyers, T.P.; Hollinger, S.E. An assessment of storage terms in the surface energy balance of maize and soybean. Agric. For. Meteorol. 2004, 125, 105–115. [Google Scholar] [CrossRef]
- Castellví, F.; Medina, E.T.; Cavero, J. Surface eddy fluxes and friction velocity estimates taking measurements at the canopy top. Agric. Water Manag. 2020, 241, 106358. [Google Scholar] [CrossRef]
- Jackson, R.D. Evaluating Evapotranspiration at Local and Regional Scales. Proc. IEEE 1985, 73, 1086–1096. [Google Scholar] [CrossRef]
- Graefe, J. Roughness layer corrections with emphasis on SVAT model applications. Agric. For. Meteorol. 2004, 124, 237–251. [Google Scholar] [CrossRef]
- Allen, R.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Andreu, A.; Kustas, W.P.; Polo, M.J.; Carrara, A.; González-Dugo, M.P. Modeling surface energy fluxes over a dehesa (oak savanna) ecosystem using a thermal based two-source energy balance model (TSEB) I. Remote Sens. 2018, 10, 567. [Google Scholar] [CrossRef]
- Mohan, M.M.P.; Kanchirapuzha, R.; Varma, M.R.R. Review of approaches for the estimation of sensible heat flux in remote sensing-based evapotranspiration models. J. Appl. Remote Sens. 2020, 14, 041501. [Google Scholar] [CrossRef]
- Buttar, N.A.; Yongguang, H.; Shabbir, A.; Lakhiar, I.A.; Ullah, I.; Ali, A.; Aleem, M.; Yasin, M.A. Estimation of evapotranspiration using Bowen ratio method. IFAC Pap. 2018, 51, 807–810. [Google Scholar] [CrossRef]
- Wang, J.; Buttar, N.A.; Hu, Y.; Lakhiar, I.A.; Javed, Q.; Shabbir, A. Estimation of sensible and latent heat fluxes using surface renewal method: Case study of a tea plantation. Agronomy 2021, 11, 179. [Google Scholar] [CrossRef]
- Castellví, F.; Gavilán, P.; González-Dugo, M.P. Combining the bulk transfer formulation and surface renewal analysis for estimating the sensible heat flux without involving the parameter kB-1. Water Resour. Res. 2014, 50, 8179–8190. [Google Scholar] [CrossRef]
- Castellví, F.; Cammalleri, C.; Ciraolo, G.; Maltese, A.; Rossi, F. Daytime sensible heat flux estimation over heterogeneous surfaces usingmultitemporal land-surface temperature observations. Water Resour. Res. 2016, 52, 1–20. [Google Scholar] [CrossRef]
- Castellví, F.; Oliphant, A.J. Daytime sensible and latent heat flux estimates for a mountain meadow using in-situ slow-response measurements. Agric. For. Meteorol. 2017, 236, 135–144. [Google Scholar] [CrossRef]
- Castellví, F.; González Dugo, M.P. A one-source model to estimate sensible heat flux in agricultural landscapes. Agric. For. Meteorol. 2021, 310, 108628. [Google Scholar] [CrossRef]
- Aubinet, M.; Vesala, T.; Papale, D.; Kb, D.P.D.F.; William, J.M.; Loescher, H.W.; Luo, H.; Rebmann, C.; Kolle, O.; Heinesch, B.; et al. Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Oliphant, A.J.; Grimmond, C.S.B.; Zutter, H.N.; Schmid, H.P.; Su, H.B.; Scott, S.L.; Offerle, B.; Randolph, J.C.; Ehman, J. Heat storage and energy balance fluxes for a temperate deciduous forest. Agric. For. Meteorol. 2004, 126, 185–201. [Google Scholar] [CrossRef]
- Barr, A.G.; Betts, A.K.; Black, T.A.; McCaughey, J.H.; Smith, C.D. Intercomparison of BOREAS northern and southern study area surface fluxes in 1994. J. Geophys. Res. Atmos. 2001, 106, 33543–33550. [Google Scholar] [CrossRef]
- Panofsky, H.A.; Dutton, J.A. Atmospheric turbulence. Models and methods for engineering aplications. In Atmospheric Turbulence: Models and Methods for Engineering Aplications; Wiley: Hoboken, NJ, USA, 1984. [Google Scholar]
- Pahlow, M.; Parlange, M.B.; Porté-Agel, F. On Monin-Obukhov similarity in the stable atmospheric boundary layer. Bound. Layer Meteorol. 2001, 99, 225–248. [Google Scholar] [CrossRef]
- Garratt, J.R. Review: The atmospheric boundary layer. Earth Sci. Rev. 1994, 37, 89–134. [Google Scholar] [CrossRef]
- Arya, S.P.S. Comments on “Local Free Convection, Similarity, and the Budgets of Shear Stress and Heat Flux”. J. Atmos. Sci. 2002, 29, 1230–1231. [Google Scholar] [CrossRef]
- Savage, M.J.; Everson, C.S.; Odhiambo, G.O.; Mengistu, M.G.; Jarmain, C. Theory and Practice of Evaporation Measurement, with Special Focus on Surface Layer Scintillometry as an Operational Tool for the Estimation of Spatially Averaged Evaporation; Water Research Commission Report, 1335/1: Pretoria, South Africa, 2004. [Google Scholar]
- Paw, U.K.T.; Brunet, Y.; Collineau, S.; Shaw, R.H.; Maitani, T.; Qui, J.; Hipps, L. On coherent structures in turbulence above and within agricultural plant canopies. Agric. For. Meteorol. 1993, 63, 127. [Google Scholar] [CrossRef]
- Chen, W.; Novak, M.D.; Black, T.A.; Lee, X. Coherent eddies and temperature structure functions for three contrasting surfaces. Part II: Renewal model for sensible heat flux. Bound. Layer Meteorol. 1997, 84, 125–147. [Google Scholar] [CrossRef]
- Castellví, F. An Advanced Method Based on Surface Renewal Theory to Estimate the Friction Velocity and the Surface Heat Flux. Water Resour. Res. 2018, 54, 10134–10154. [Google Scholar] [CrossRef]
- Antonia, R.A.; Chambers, A.J.; Friehe, C.A.; Van Atta, C.W. Temperature Ramps in the Atmospheric Surface Layer. J. Atmos. Sci. 1979, 36, 99–108. [Google Scholar] [CrossRef]
- Blanken, P.D.; Black, T.A.; Neumann, H.H.; Den Hartog, G.; Yang, P.C.; Nesic, Z.; Lee, X. The seasonal water and energy exchange above and within a boreal aspen forest. J. Hydrol. 2001, 245, 118–136. [Google Scholar] [CrossRef]
- Harman, I.N.; Finnigan, J.J. A simple unified theory for flow in the canopy and roughness sublayer. Bound. Layer Meteorol. 2007, 123, 339–363. [Google Scholar] [CrossRef]
- Zilitinkevich, S.S.; Mammarella, I.; Baklanov, A.A.; Joffre, S.M. The effect of stratification on the aerodynamic roughness length and displacement height. Bound. Layer Meteorol. 2008, 129, 179–190. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Validation of the Vegetation Cover Method for Land Surface Emissivity Estimation. In Recent Research Developments in Thermal Remote Sensing 2005; Elsevie: Amsterdam, The Netherlands, 2005; pp. 1–20. ISBN 81-7736-164-3. [Google Scholar]
- Ogawa, K.; Schmugge, T.; Jacob, F.; French, A. Estimation of broadband land surface emissivity from multi-spectral thermal infrared remote sensing. Agronomie 2002, 22, 695–696. [Google Scholar] [CrossRef]
- Kidston, J.; Brümmer, C.; Black, T.A.; Morgenstern, K.; Nesic, Z.; McCaughey, J.H.; Barr, A.G. Energy balance closure using eddy covariance above two different land surfaces and implications for CO2 flux measurements. Bound. Layer Meteorol. 2010, 136, 193–218. [Google Scholar] [CrossRef]
- Buttar, N.A.; Yongguang, H.; Tanny, J.; Akram, M.W.; Shabbir, A. Fetch Effect on Flux-Variance Estimations of Sensible and Latent Heat Fluxes of Camellia Sinensis. Atmosphere 2019, 10, 299. [Google Scholar] [CrossRef]
- Chávez, J.L.; Howell, T.A.; Copeland, K.S. Evaluating eddy covariance cotton ET measurements in an advective environment with large weighing lysimeters. Irrig. Sci. 2009, 28, 35–50. [Google Scholar] [CrossRef]
- Ding, R.; Kang, S.; Li, F.; Zhang, Y.; Tong, L.; Sun, Q. Evaluating eddy covariance method by large-scale weighing lysimeter in a maize field of northwest China. Agric. Water Manag. 2010, 98, 87–95. [Google Scholar] [CrossRef]
- Buttar, N.A.; Yongguang, H.; Chuan, Z.; Tanny, J.; Ullah, I.; Aleem, M. Height effect of air temperature measurement on sensible heat flux estimation using flux variance method. Pak. J. Agric. Sci. 2019, 56, 793–800. [Google Scholar]
- Wang, X.; Huo, Z.; Shukla, M.K.; Wang, X.; Guo, P.; Xu, X.; Huang, G. Energy fluxes and evapotranspiration over irrigated maize field in an arid area with shallow groundwater. Agric. Water Manag. 2020, 228, 105922. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Blanken, P.D.; Black, T.A.; Yang, P.C.; Neumann, H.H.; Nesic, Z.; Staebler, R.; Den Hartog, G.; Novak, M.D.; Lee, X. Energy balance and canopy conductance of a boreal aspen forest: Partitioning overstory and understory components. J. Geophys. Res. Atmos. 1997, 102, 28915–28927. [Google Scholar] [CrossRef]
- Simpson, I.J.; Edwards, G.C.; Thurtell, G.W.; Den Hartog, G.; Neumann, H.H.; Staebler, R.M. Micrometeorological measurements of methane and nitrous oxide exchange above a boreal aspen forest. J. Geophys. Res. Atmos. 1997, 102, 29331–29341. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Caselles, V.; Niclòs, R.; Coll, C.; Kustas, W.P. Estimating energy balance fluxes above a boreal forest from radiometric temperature observations. Agric. For. Meteorol. 2009, 149, 1037–1049. [Google Scholar] [CrossRef]
- Jackson, P.S. On The Displacement Height in The Logarithmic Velocity Profile. J. Fluid Mech. 1981, 111, 15–25. [Google Scholar] [CrossRef]
- Cellier, P.; Brunet, Y. Flux-gradient relationships above tall plant canopies. Agric. For. Meteorol. 1992, 58, 93–117. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. Bound. Layer Meteorol. 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Harman, I.N.; Finnigan, J.J. Scalar concentration profiles in the canopy and roughness sublayer. Bound. Layer Meteorol. 2008, 129, 323–351. [Google Scholar] [CrossRef]
- Shaw, R.H.; Den Hartog, G.; Neumann, H.H. Influence of foliar density and thermal stability on profiles of Reynolds stress and turbulence intensity in a deciduous forest. Bound. Layer Meteorol. 1988, 45, 391–409. [Google Scholar] [CrossRef]
- Mahrt, L. Surface heterogeneity and vertical structure of the boundary layer. Bound. Layer Meteorol. 2000, 96, 33–62. [Google Scholar] [CrossRef]
- Dyer, A.J. A review of flux-profile relationships. Bound. Layer Meteorol. 1974, 7, 363–372. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).