Evaluating the Impact of Planetary Boundary Layer, Land Surface Model, and Microphysics Parameterization Schemes on Simulated GOES-16 Water Vapor Brightness Temperatures
Abstract
1. Introduction
2. Data
2.1. Model Configurations
2.2. Water Vapor Brightness Temperatures
2.3. Pressure-Level Data
3. Methodology
3.1. Grid Point Metrics
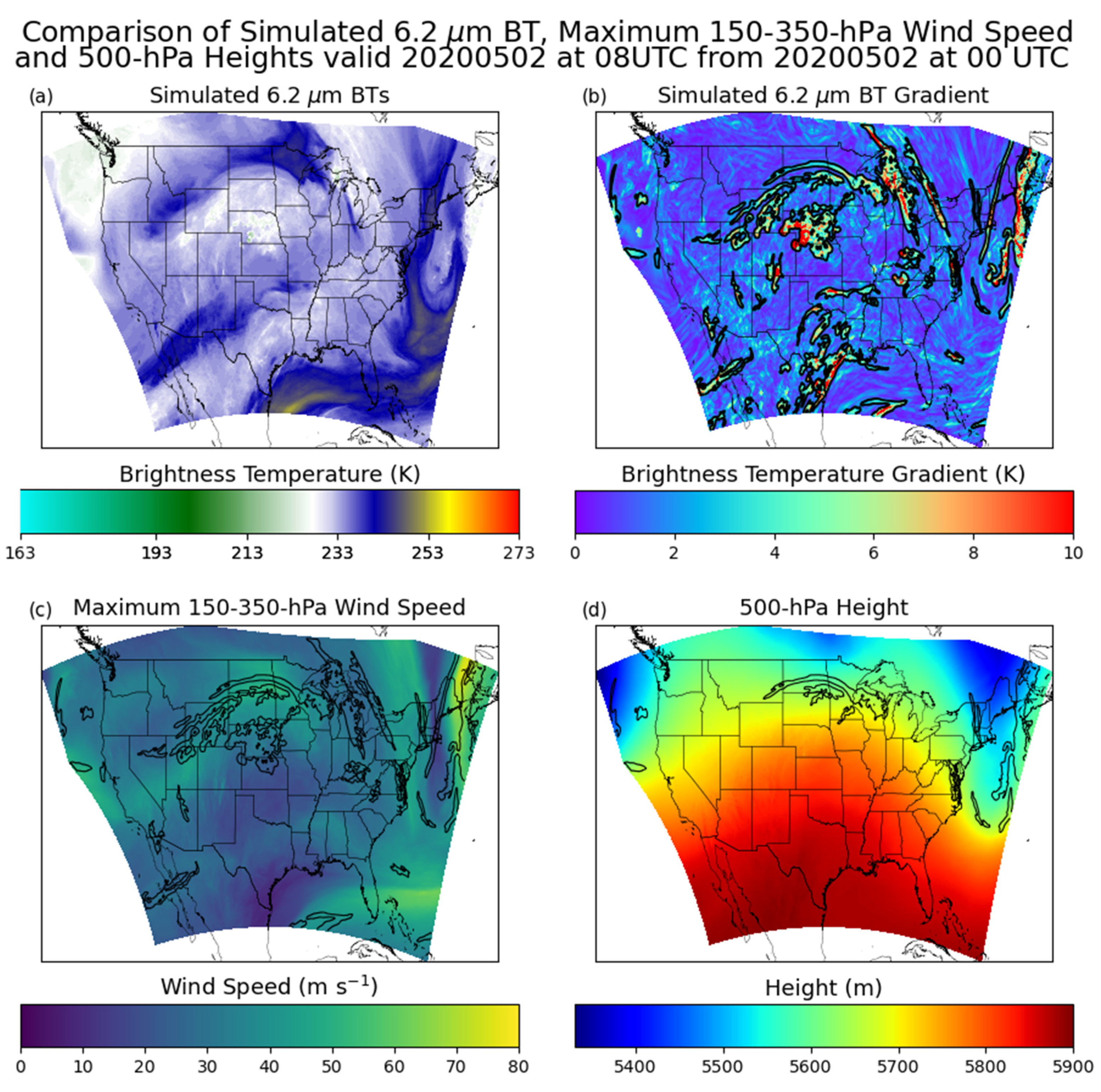
3.2. Identifying Upper-Level Jet Streams and Troughs
3.3. Mean Error Distance
4. Results
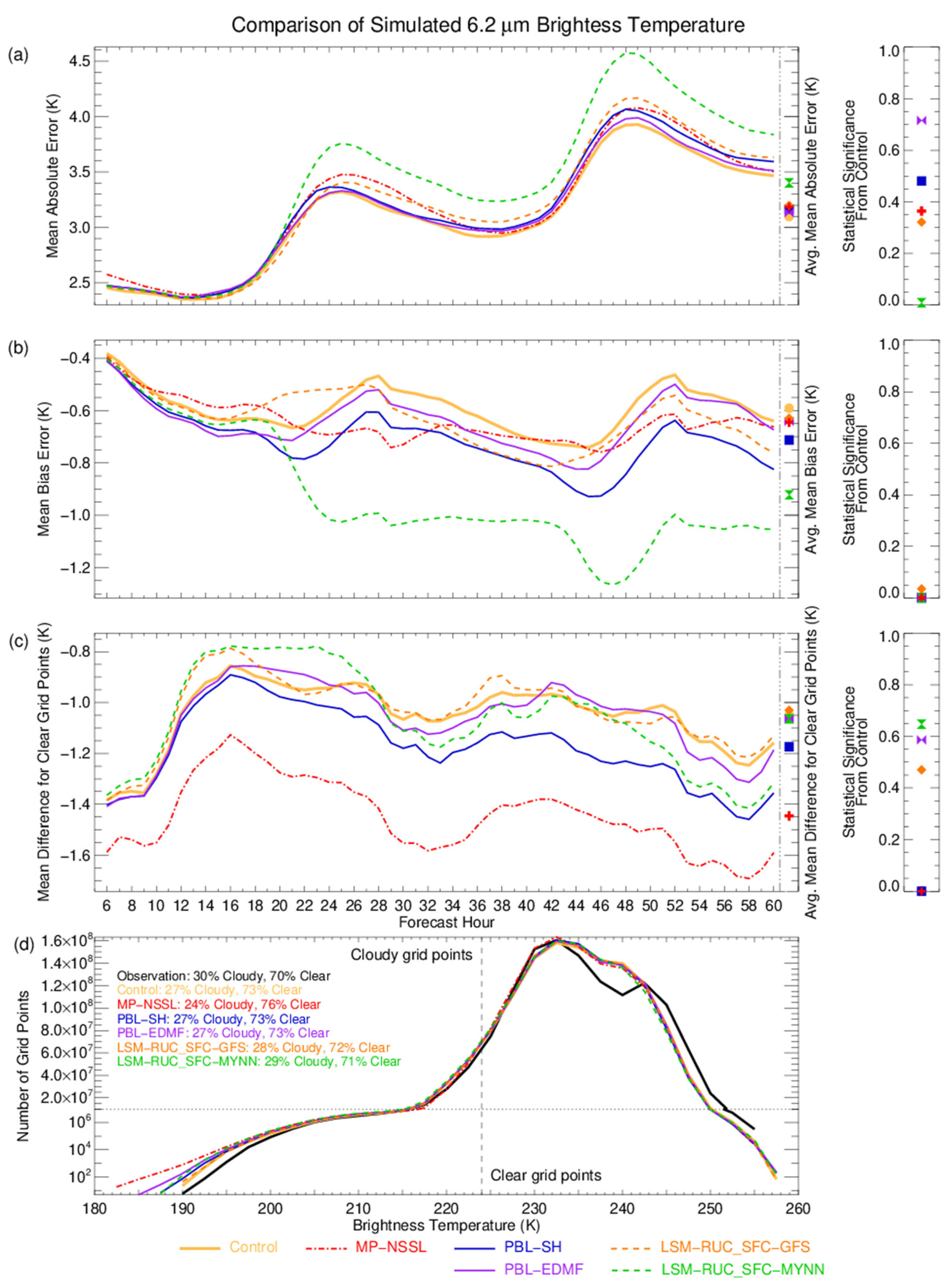
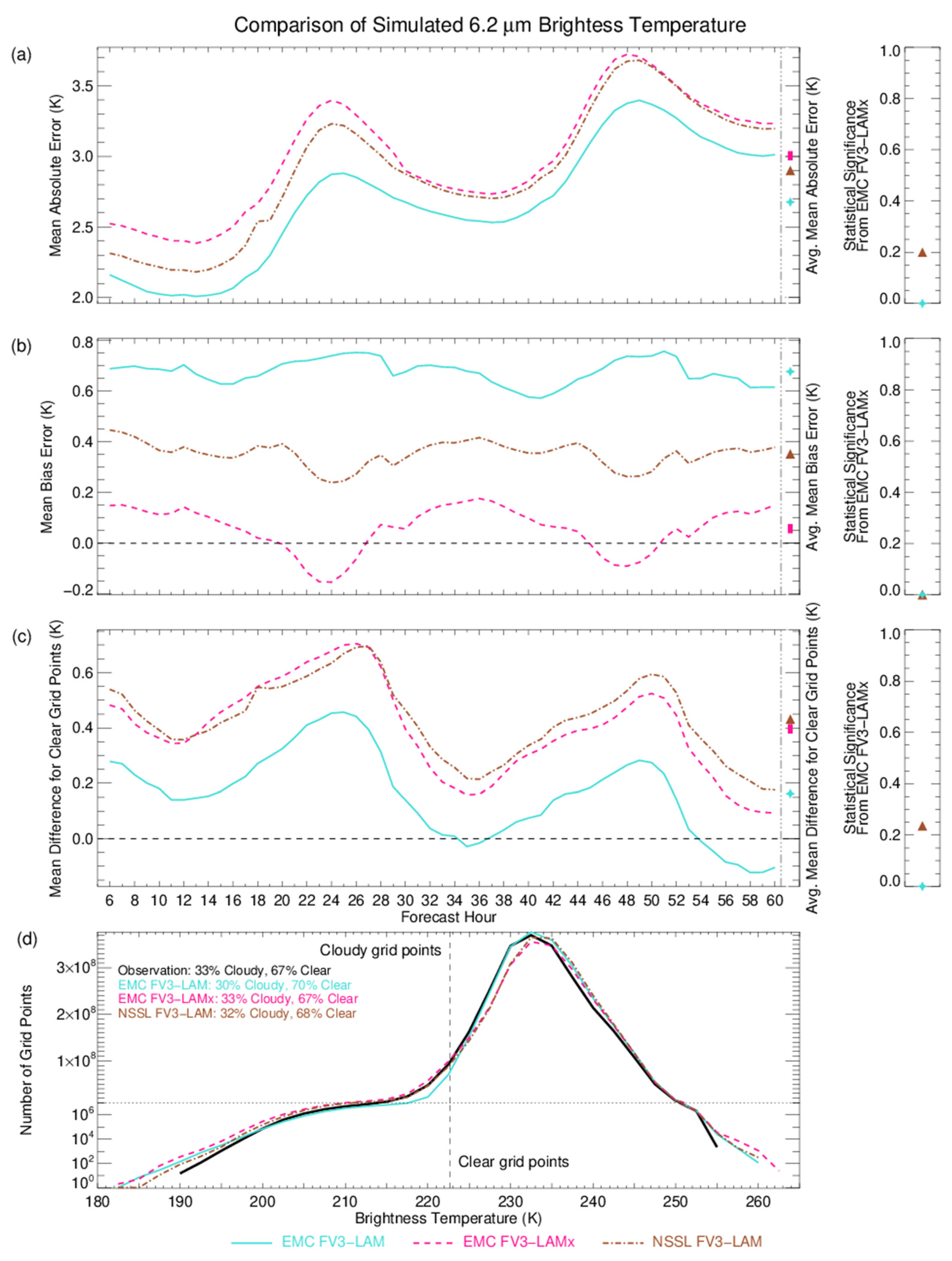
4.1. Grid Point Metrics
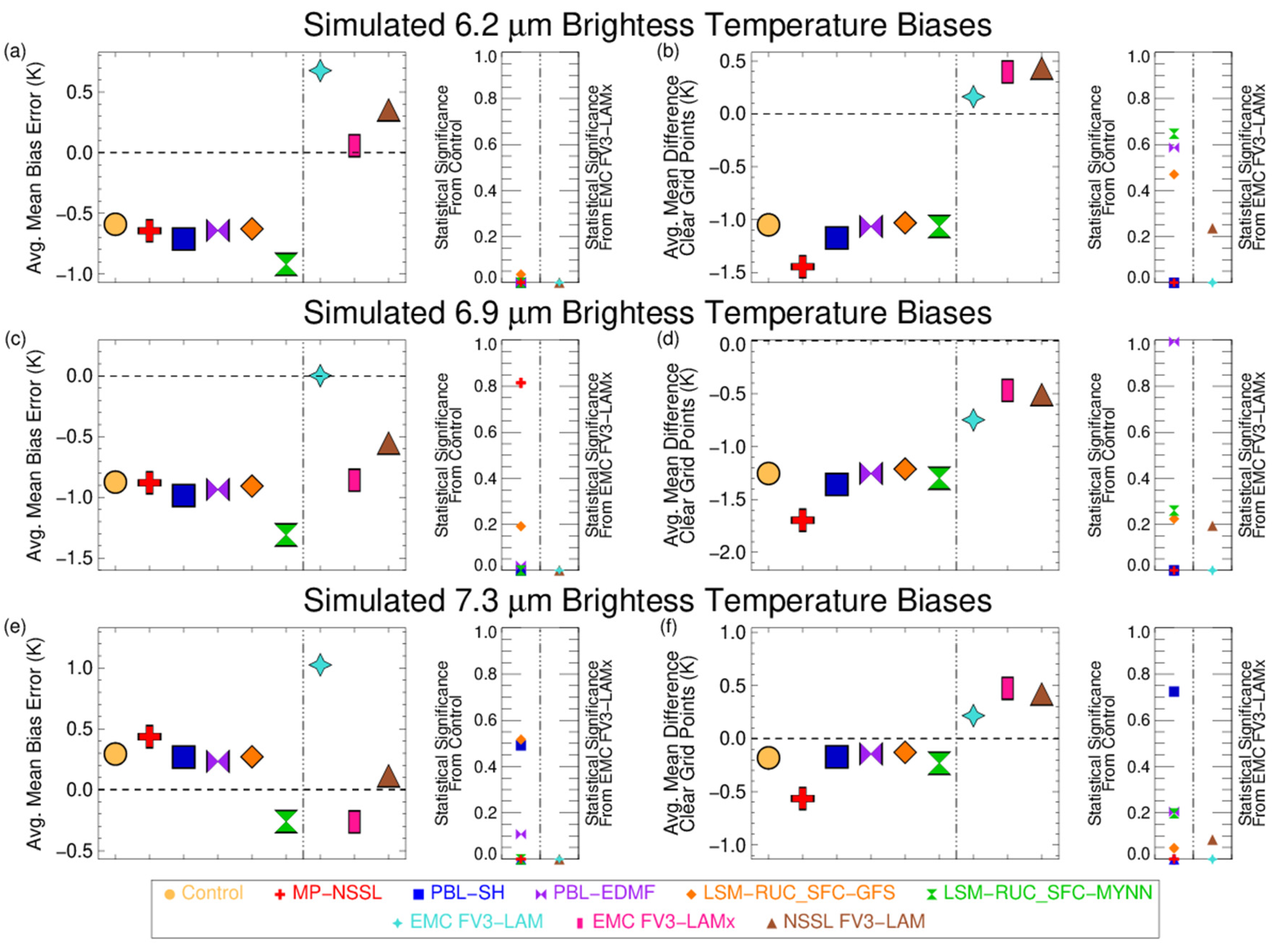
4.2. Brightness Temperature Differences
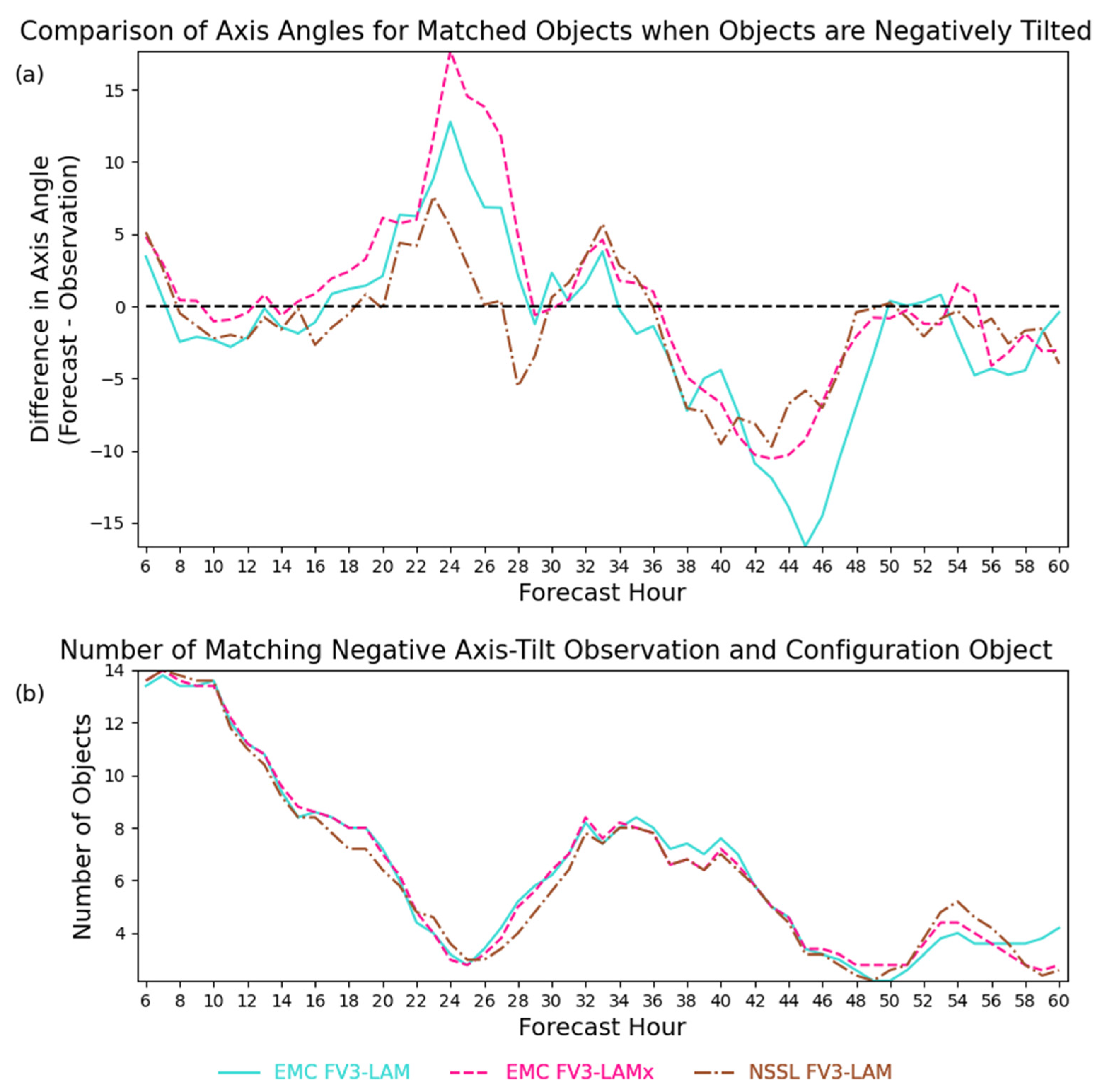
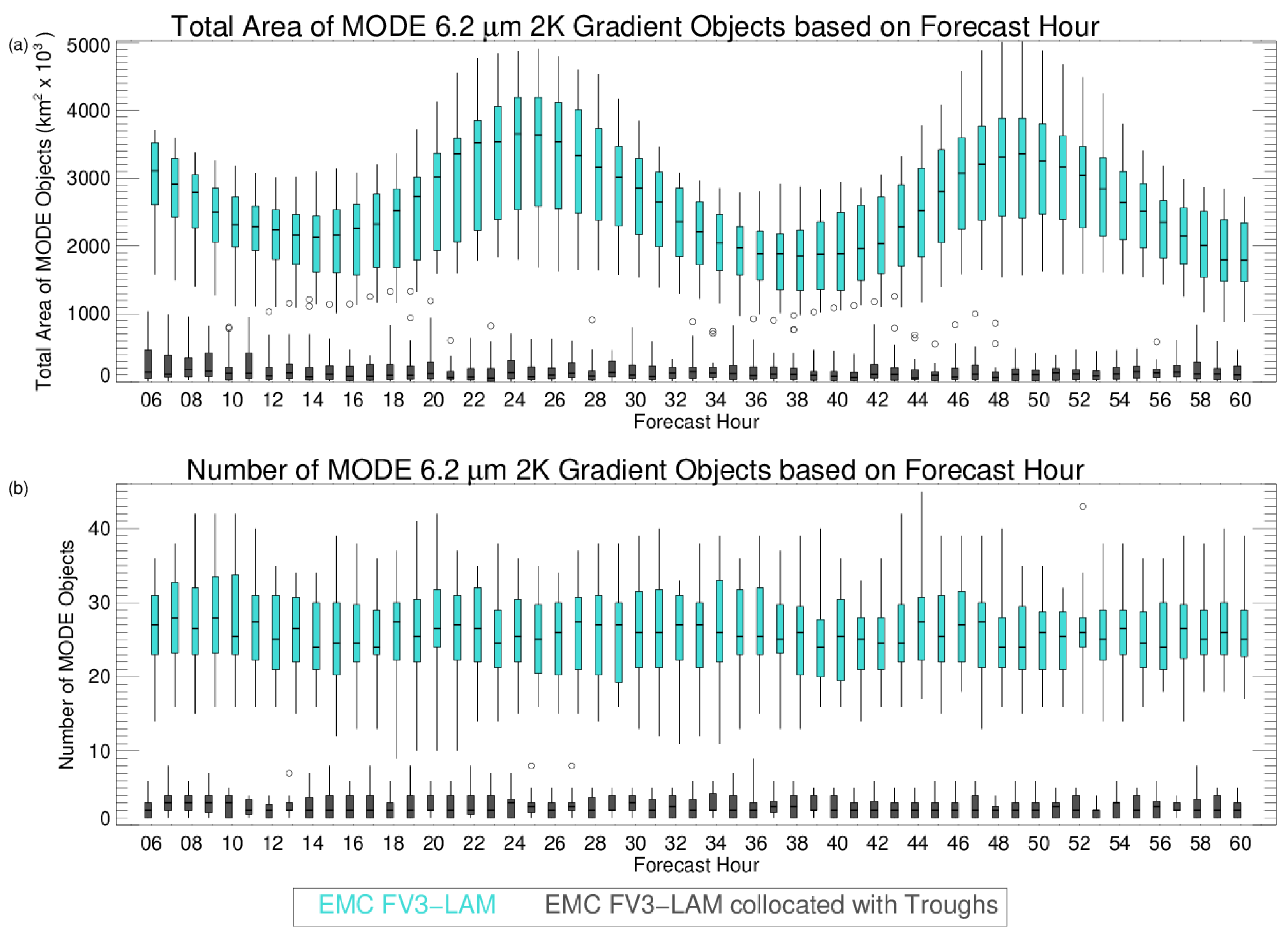
4.3. Upper-Level Jet Streams and Troughs
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, W.L., Jr.; Minnis, P.; Young, D.F. An icing product derived from operational satellite data. In Proceedings of the Ninth Conference on Aviation, Range and Aerospace Meteorology, Orlando, FL, USA, 13 September 2000; pp. 256–259. [Google Scholar]
- Ellrod, G.; Bailey, A.P. Assessment of aircraft icing potential and maximum icing altitude from geostationary meteorological satellite data. Weather Forecast. 2007, 22, 160–174. [Google Scholar] [CrossRef]
- Scofield, R.; Vicente, G.; Hodges, M. The Use of Water Vapor for Detecting Environments That Lead to Convectively Produced Heavy Precipitation and Flash Floods; NOAA Technical Reports NESDIS 99; US Department of Commerce: Washington, DC, USA, 2000; 64p. [Google Scholar]
- Velden, C.S.; Hayden, C.M.; Nieman, S.; Menzel, W.P.; Wanzong, S.; Goerss, J. Upper-tropospheric winds derived from geostationary satellite water vapor observations. Bull. Am. Meteorol. Soc. 1997, 78, 173–195. [Google Scholar] [CrossRef][Green Version]
- Laurent, H. Wind extraction from Meteosat water vapor channel image data. J. Appl. Meteorol. Climatol. 1993, 32, 1124–1133. [Google Scholar] [CrossRef][Green Version]
- Oyama, R. Relationship between Tropical Cyclone Intensification and Cloud-Top Outflow Revealed by Upper-Tropospheric Atmospheric Motion Vectors. J. Appl. Meteorol. Climatol. 2017, 56, 2801–2819. [Google Scholar] [CrossRef]
- Ramond, D.; Corbin, H.; Desbois, M.; Szejwach, G.; Waldteufel, P. The Dynamics of Polar Jet Streams as Depicted by the METEOSAT WV Channel Radiance Field. Mon. Weather Rev. 1981, 109, 2164–2176. [Google Scholar] [CrossRef][Green Version]
- Velden, C.S. Satellite observations of Hurricane Elena (1985) using the VAS 6.7 μm “water vapor” channel. Bull. Am. Meteorol. Soc. 1987, 68, 210–215. [Google Scholar] [CrossRef][Green Version]
- Muller, B.M.; Fuelberg, H.E. A Simulation and Diagnostic Study of Water Vapor Image Dry Bands. Mon. Weather Rev. 1990, 118, 705–722. [Google Scholar] [CrossRef][Green Version]
- Sharman, R.D.; Trier, S.B.; Lane, T.P.; Doyle, J.D. Sources and dynamics of turbulence in the upper troposphere and lower stratosphere: A review. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Rose, S.F.; Hobbs, P.V.; Locatelli, J.D.; Stoelinga, M.T. A 10-Yr Climatology Relating the Locations of Reported Tornadoes to the Quadrants of Upper-Level Jet Streaks. Weather Forecast. 2004, 19, 301–309. [Google Scholar] [CrossRef]
- Hurlbut, M.M.; Cohen, A.E. Environments of Northeast U.S. Severe Thunderstorm Events from 1999 to 2009. Mon. Weather Rev. 2014, 29, 3–22. [Google Scholar] [CrossRef][Green Version]
- Macdonald, N.J. On the Apparent Relationship between Convective Activity and the Shape of 500 mb Troughs. Mon. Weather Rev. 1976, 104, 1618–1622. [Google Scholar] [CrossRef][Green Version]
- Cutraro, F.; Galligani, V.S.; García Skabar, Y. Evaluation of synthetic satellite images computed from radiative transfer models over a region of South America using WRF and GOES-13/16 observations. Q. J. R. Meteorol. Soc. 2021, 147, 2988–3003. [Google Scholar] [CrossRef]
- Feltz, W.F.; Bedka, K.M.; Otkin, J.A.; Greenwald, T.; Ackerman, S.A. Understanding satellite-observed mountain wave signatures using high-resolution numerical model data. Weather Forecast. 2009, 24, 76–86. [Google Scholar] [CrossRef]
- Geiss, S.; Scheck, L.; de Lozar, A.; Weissmann, M. Understanding the model representation of clouds based on visible and infrared satellite observations. Atmos. Chem. Phys. 2021, 21, 12273–12290. [Google Scholar] [CrossRef]
- Grasso, L.D.; Greenwald, T. Analysis of 10.7-µm brightness temperatures of a simulated thunderstorm with two-moment microphysics. Mon. Weather Rev. 2004, 132, 815–825. [Google Scholar] [CrossRef][Green Version]
- Grasso, L.D.; Sengupta, M.; Dostalek, J.F.; Brummer, R.; DeMaria, M. Synthetic satellite imagery for current and future environmental satellites. Int. J. Remote Sens. 2008, 29, 4373–4384. [Google Scholar] [CrossRef]
- Grasso, L.D.; Lindsey, D.T.; Sunny Lim, K.-S.; Clark, A.J.; Bikos, D.; Dembek, S.R. Evaluation of and suggested improvements to the WSM6 microphysics in WRF-ARW using synthetic and observed GOES-13 imagery. Mon. Weather Rev. 2004, 142, 3635–3650. [Google Scholar] [CrossRef]
- Griffin, S.M.; Otkin, J.A.; Rozoff, C.M.; Sieglaff, J.M.; Cronce, L.M.; Alexander, C.R. Methods for comparing simulated and observed satellite infrared brightness temperatures and what do they tell us? Weather Forecast. 2017, 32, 5–25. [Google Scholar] [CrossRef]
- Griffin, S.M.; Otkin, J.A.; Rozoff, C.M.; Sieglaff, J.M.; Cronce, L.M.; Alexander, C.R.; Jensen, T.R.; Wolff, J.K. Seasonal analysis of cloud objects in the High-Resolution Rapid Refresh (HRRR) model using object-based verification. J. Appl. Meteorol. Climatol. 2017, 56, 2317–2334. [Google Scholar] [CrossRef]
- Griffin, S.M.; Otkin, J.A.; Thompson, G.; Frediani, M.; Berner, J.; Kong, F. Assessing the Impact of Stochastic Perturbations in Cloud Microphysics using GOES-16 Infrared Brightness Temperatures. Mon. Weather Rev. 2020, 148, 3111–3137. [Google Scholar] [CrossRef]
- Griffin, S.M.; Otkin, J.A.; Nebude, S.E.; Jensen, T.L.; Skinner, P.S.; Gilleland, E.; Supinie, T.A.; Xu, M. Evaluating the impact of planetary boundary layer, land surface model, and microphysics parameterization schemes on cold cloud objects in simulated GOES-16 brightness temperatures. J. Geophys. Res. Atmos. 2021, 126, e2021JD034709. [Google Scholar] [CrossRef]
- Henderson, D.S.; Otkin, J.A.; Mecikalski, J.R. Evaluating Convective Initiation in High-Resolution Numerical Weather Prediction Models Using GOES-16 Infrared Brightness Temperatures. Mon. Weather Rev. 2021, 149, 1153–1172. [Google Scholar] [CrossRef]
- Jones, T.A.; Skinner, P.; Knopfmeier, K.; Mansell, E.; Minnis, P.; Palikonda, R.; Smith, W., Jr. Comparison of Cloud Microphysics Schemes in a Warn-on-Forecast System Using Synthetic Satellite Objects. Weather Forecast. 2018, 33, 1681–1708. [Google Scholar] [CrossRef]
- Otkin, J.A.; Greenwald, T.J. Comparison of WRF model-simulated and MODIS-derived cloud data. Mon. Weather Rev. 2008, 136, 1957–1970. [Google Scholar] [CrossRef]
- Otkin, J.A.; Greenwald, T.J.; Sieglaff, J.; Huang, H.-L. Validation of a large-scale simulated brightness temperature dataset using SEVIRI satellite observations. J. Appl. Meteorol. Climatol. 2009, 48, 1613–1626. [Google Scholar] [CrossRef]
- Thompson, G.; Tewari, M.; Ikeda, K.; Tessendorf, S.; Weeks, C.; Otkin, J.A.; Kong, F. Explicitly-coupled cloud physics and radiation parameterizations and subsequent evaluation in WRF high-resolution convective forecasts. Atmos. Res. 2016, 168, 92–104. [Google Scholar] [CrossRef]
- Cintineo, R.; Otkin, J.A.; Kong, F.; Xue, M. Evaluating the accuracy of planetary boundary layer and cloud microphysical parameterization schemes in a convection-permitting ensemble using synthetic GOES-13 satellite observations. Mon. Weather Rev. 2014, 142, 107–124. [Google Scholar] [CrossRef]
- Soden, B.J.; Bretherton, F.P. Evaluation of water vapor distribution in general circulation models using satellite observations. J. Geophys. Res. Atmos. 1994, 99, 1187–1210. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.K.; Lang, S.; Hou, A.Y.; Zhang, M.; Simpson, J. On the sensitivity of atmospheric ensemble states to cloud microphysics in long-term cloud-resolving model simulations. J. Meteorol. Soc. Jpn. 2008, 86A, 45–65. [Google Scholar] [CrossRef]
- Chung, K.-S.; Chiu, H.-J.; Liu, C.-Y.; Lin, M.-Y. Satellite Observation for Evaluating Cloud Properties of the Microphysical Schemes in Weather Research and Forecasting Simulation: A Case Study of the Mei-Yu Front Precipitation System. Remote Sens. 2020, 12, 3060. [Google Scholar] [CrossRef]
- Schmit, T.J.; Griffith, P.; Gunshor, M.M.; Daniels, J.M.; Goodman, S.J.; Lebair, W.J. A closer look at the ABI on the GOES-R series. Bull. Am. Meteorol. Soc. 2017, 98, 681–698. [Google Scholar] [CrossRef]
- Krishnamurti, T.N.; Rajendran, K.; Kumar, T.S.V.; Lord, S.; Toth, Z.; Zou, X.; Cocke, S.; Ahlquist, J.E.; Navon, I.M. Improved Skill for the Anomaly Correlation of Geopotential Heights at 500 hPa. Mon. Weather Rev. 2003, 131, 1082–1102. [Google Scholar] [CrossRef]
- Elmore, K.L.; Baldwin, M.E.; Schultz, D.M. Field Significance Revisited: Spatial Bias Errors in Forecasts as Applied to the Eta Model. Mon. Weather Rev. 2006, 134, 519–531. [Google Scholar] [CrossRef]
- Bikos, D.; Lindsey, D.T.; Otkin, J.; Sieglaff, J.; Grasso, L.; Siewert, C.; Correia, J., Jr.; Coniglio, M.; Rabin, R.; Kain, J.S.; et al. Synthetic satellite imagery for real-time high-resolution model evaluation. Weather Forecast. 2012, 27, 784–795. [Google Scholar] [CrossRef]
- Ellrod, G.P. A water vapor image feature related to severe thunderstorms. Natl. Weather Dig. 1990, 15, 21–29. [Google Scholar]
- Santurette, P.; Georgiev, C.G. Water vapour imagery analysis in 7. In 3 µ/6.2 µ for diagnosing thermo-dynamic context of intense convection. In Proceedings of the Joint 2007 EUMETSAT Meteorological Satellite Conference and the 15th AMS Satellite Meteorology & Oceanography Conference, Amsterdam, The Netherlands, 24–28 September 2007. [Google Scholar]
- Mohan, P.M.; Srinivas, C.V.; Yesubabu, V.; Baskaran, R.; Venkatraman, B. Simulation of a heavy rainfall event over Chennai in Southeast India using WRF: Sensitivity to microphysics parameterization. Atmos. Res. 2018, 210, 83–99. [Google Scholar] [CrossRef]
- Lin, S. A “Vertically Lagrangian” Finite-Volume Dynamical Core for Global Models. Mon. Weather Rev. 2004, 132, 2293–2307. [Google Scholar] [CrossRef]
- Putman, W.M.; Lin, S.-J. Finite-volume transport on various cubed-sphere grids. J. Comput. Phys. 2007, 227, 55–78. [Google Scholar] [CrossRef]
- Gallo, B.T.; Clark, A.J.; Jirak, I.; Kain, J.S.; Weiss, S.J.; Coniglio, M.; Knopfmeier, K.; Correia, J.; Melick, C.J., Jr.; Karstens, C.D.; et al. Breaking new ground in severe weather prediction: The 2015 NOAA/Hazardous Weather Testbed Spring Forecasting Experiment. Weather Forecast. 2017, 32, 1541–1568. [Google Scholar] [CrossRef]
- Clark, A.J.; Jirak, I.L.; Gallo, B.T.; Roberts, B.; Knopfmeier, K.H.; Clark, R.A.; Vancil, J.; Dean, A.R.; Hoogewind, K.A.; Heinselman, P.L.; et al. A real-time, simulated forecasting experiment for advancing the prediction of hazardous convective weather. Bull. Am. Meteorol. Soc. 2020, 101, E2022–E2024. [Google Scholar]
- Thompson, G.; Rasmussen, R.M.; Manning, K. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part I: Description and Sensitivity Analysis. Mon. Weather Rev. 2004, 132, 519–542. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor-Yamada level-3 model with condensation physics: Its design and verification. Bound. -Layer Meteorol. 2004, 112, 1–31. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an improved turbulence closure model for the atmospheric boundary layer. J. Meteorol. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Mitchell, K. The Community Noah Land-Surface Model. User’s Guide Public Release Version 2.7.1; NOAA/NCEP; Environmental Modeling Center: College Park, MD, USA, 2005; 26p. [Google Scholar]
- Niu, G.-Y.; Yang, Z.-L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Mansell, E.R.; Ziegler, C.L.; Bruning, E.C. Simulated electrification of a small thunderstorm with two-moment bulk microphysics. J. Atmos. Sci. 2010, 67, 171–194. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.-Y. Analysis of resolved and parameterized vertical transports in convective boundary layers at gray-zone resolutions. J. Atmos. Sci. 2013, 70, 3248–3261. [Google Scholar] [CrossRef]
- Han, J.; Witek, M.L.; Teixeira, J.; Sun, R.; Pan, H.; Fletcher, J.K.; Bretherton, C.S. Implementation in the NCEP GFS of a Hybrid Eddy-Diffusivity Mass-Flux (EDMF) Boundary Layer Parameterization with Dissipative Heating and Modified Stable Boundary Layer Mixing. Weather Forecast. 2016, 31, 341–352. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Brown, J.M.; Benjamin, S.G.; Kenyon, J.S. Modifications to the Rapid Update Cycle Land Surface Model (RUC LSM) Available in the Weather Research and Forecasting (WRF) Model. Mon. Weather Rev. 2016, 144, 1851–1865. [Google Scholar] [CrossRef]
- Clough, S.; Shephard, M.; Mlawer, E.; Delamere, J.; Iacono, M.; Cady-Pereira, K.; Boukabara, S.; Brown, P.D. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Zhou, L.; Lin, S.; Chen, J.; Harris, L.M.; Chen, X.; Rees, S.L. Toward Convective-Scale Prediction within the Next Generation Global Prediction System. Bull. Am. Meteorol. Soc. 2019, 100, 1225–1243. [Google Scholar] [CrossRef]
- Han, Y.; van Delst, P.; Liu, Q.; Weng, F.; Yan, B.; Treadon, R.; Derber, J. JCSDA Community Radiative Transfer Model (CRTM) Version 1; NOAA Technical Report 122; The National Environmental Satellite, Data, and Information Service (NESDIS): Silver Spring, MD, USA, 2005. [Google Scholar]
- Ding, S.; Yang, P.; Weng, F.; Liu, Q.; Han, Y.; Van Delst, P.; Li, J.; Baum, B. Validation of the community radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1050–1064. [Google Scholar] [CrossRef]
- Otkin, J.A.; Posselt, D.J.; Olson, E.R.; Huang, H.-L.; Davies, J.E.; Li, J.; Velden, C.S. Mesoscale numerical weather prediction models used in support of infrared hyperspectral measurement simulation and product algorithm development. J. Atmos. Ocean. Technol. 2007, 24, 585–601. [Google Scholar] [CrossRef]
- Willmott, C.J.; Johnson, M.L. Resolution errors associated with gridded precipitation fields. Int. J. Climatol. 2005, 25, 1957–1963. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Davis, C.A.; Brown, B.G.; Bullock, R.G. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Davis, C.A.; Brown, B.G.; Bullock, R.G. Object-based verification of precipitation forecasts. Part II: Application to convective rain systems. Mon. Weather Rev. 2006, 134, 1785–1795. [Google Scholar] [CrossRef]
- Davis, C.A.; Brown, B.G.; Bullock, R.G.; Gotway, J.H. The Method for Object-based Diagnostic Evaluation (MODE) Applied to Numerical Forecasts from the 2005 NSSL/SPC Spring Program. Weather Forecast. 2009, 24, 1252–1267. [Google Scholar] [CrossRef]
- Bullock, R.G.; Brown, B.G.; Fowler, T.L. Method for Object-Based Diagnostic Evaluation; No. NCAR/TN-532+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2016. [Google Scholar]
- Gilleland, E. A new characterization in the spatial verification framework for false alarms, misses, and overall patterns. Weather Forecast. 2017, 32, 187–198. [Google Scholar] [CrossRef]
- Otkin, J.A.; Lewis, W.E.; Lenzen, A.; McNoldy, B.; Majumdar, S. Assessing the accuracy of the cloud and water vapor fields in the Hurricane WRF (HWRF) model using satellite infrared brightness temperatures. Mon. Weather Rev. 2017, 145, 2027–2046. [Google Scholar] [CrossRef]
- Sherwood, S.C.; Roca, R.; Weckwerth, T.M.; Andronova, N.G. Tropospheric water vapor, convection, and climate. Rev. Geophys. 2010, 48, RG2001. [Google Scholar] [CrossRef]
- Lu, E.; Takle, E. Contributions of Water Vapor and Temperature to the Interannual Variability of Precipitation: An Evaluation from North American Regional Reanalysis. In Proceedings of the 20th Conference on Climate Variability and Change, New Orleans, LA, USA, 23 January 2008. [Google Scholar]
- Mecikalski, J.R.; Bedka, K.M. Forecasting convective initiation by monitoring the evolution of moving cumulus in daytime GOES imagery. Mon. Weather Rev. 2006, 134, 49–78. [Google Scholar] [CrossRef]
- Ackerman, S.A.; Smith, W.L.; Spinhirne, J.D.; Revercomb, H.E. The 27–28 October 1986 FIRE IFO Cirrus Case Study: Spectral properties of cirrus clouds in the 8–12 μm window. Mon. Weather Rev. 1990, 118, 2377–2388. [Google Scholar] [CrossRef]
- Strabala, K.I.; Ackerman, S.A.; Menzel, W.P. Cloud properties inferred from 8–12-mm data. J. Appl. Meteorol. Climatol. 1994, 33, 212–229. [Google Scholar] [CrossRef]
- Baum, B.A.; Soulen, P.F.; Strabala, K.I.; King, M.D.; Ackerman, S.A.; Menzel, W.P.; Yang, P. Remote sensing of cloud properties using MODIS Airborne Simulator imagery during SUCCESS. II. Cloud thermodynamic phase. J. Geophys. Res. Atmos. 2000, 105, 11781–11792. [Google Scholar] [CrossRef]
- Schmetz, J.; Tjemkes, S.A.; Gube, M.; van de Berg, L. Monitoring deep convection and convective overshooting with METEOSAT. Adv. Space Res. 1997, 19, 433–441. [Google Scholar] [CrossRef]
- Thompson, G.; Politovich, M.K.; Rasmussen, R.M. A numerical weather model’s ability to predict characteristics of aircraft icing environments. Weather Forecast. 2017, 32, 207–221. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Appl. Meteorol. Climatol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Huang, M.; Gao, Z.; Miao, S.; Chen, F. Sensitivity of urban boundary layer simulation to urban canopy models and PBL schemes in Beijing. Meteorol. Atmos. Phys. 2019, 131, 1235–1248. [Google Scholar] [CrossRef]
- Schwitalla, T.; Branch, O.; Wulfmeyer, V. Sensitivity study of the planetary boundary layer and microphysical schemes to the initialization of convection over the Arabian Peninsula. Q. J. R. Meteorol. Soc. 2020, 146, 846–869. [Google Scholar] [CrossRef]
- Jin, J.; Miller, N.L.; Schegel, N. Sensitivity study of four land surface schemes in the WRF model. Adv. Meteorol. 2010, 167436. [Google Scholar] [CrossRef]
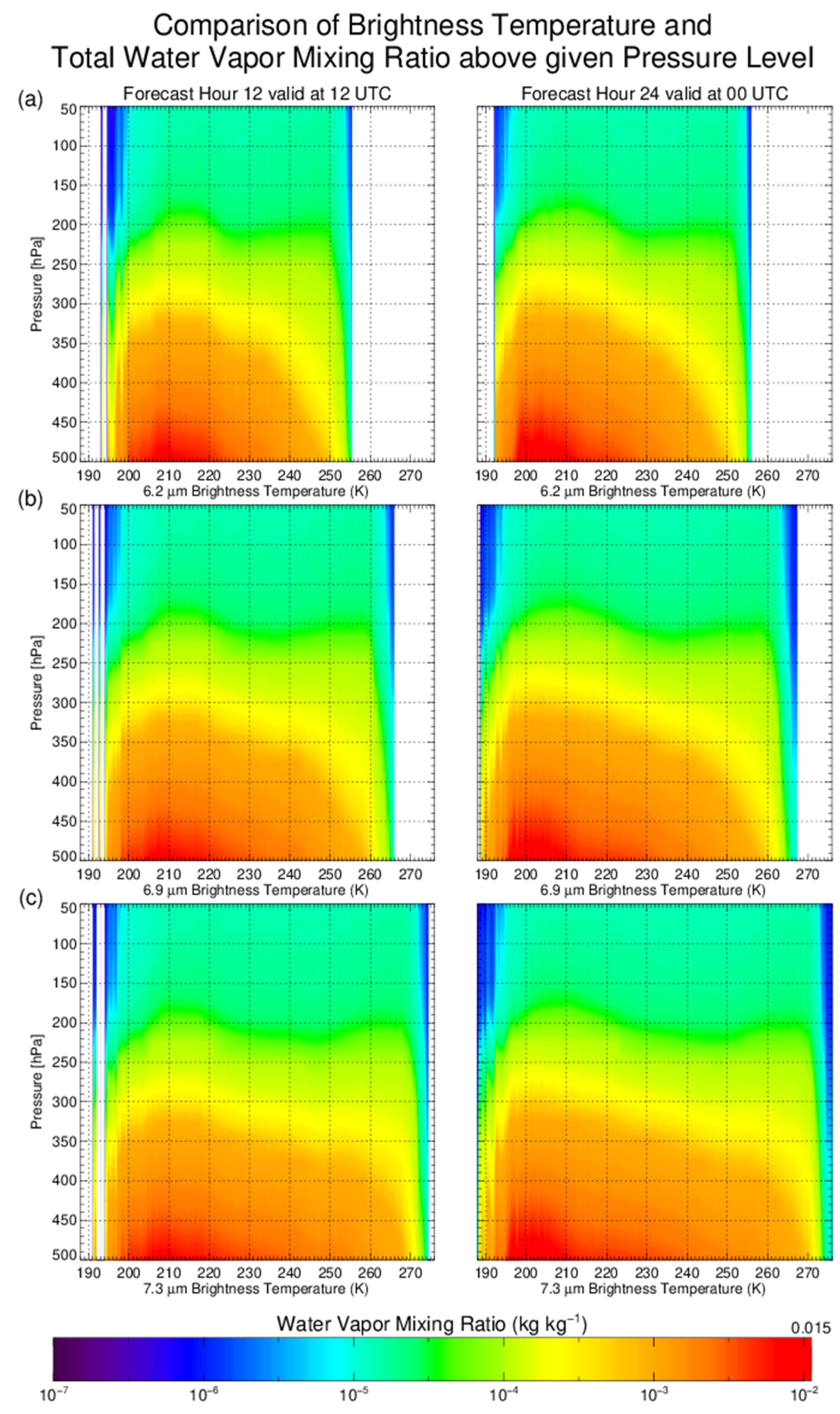
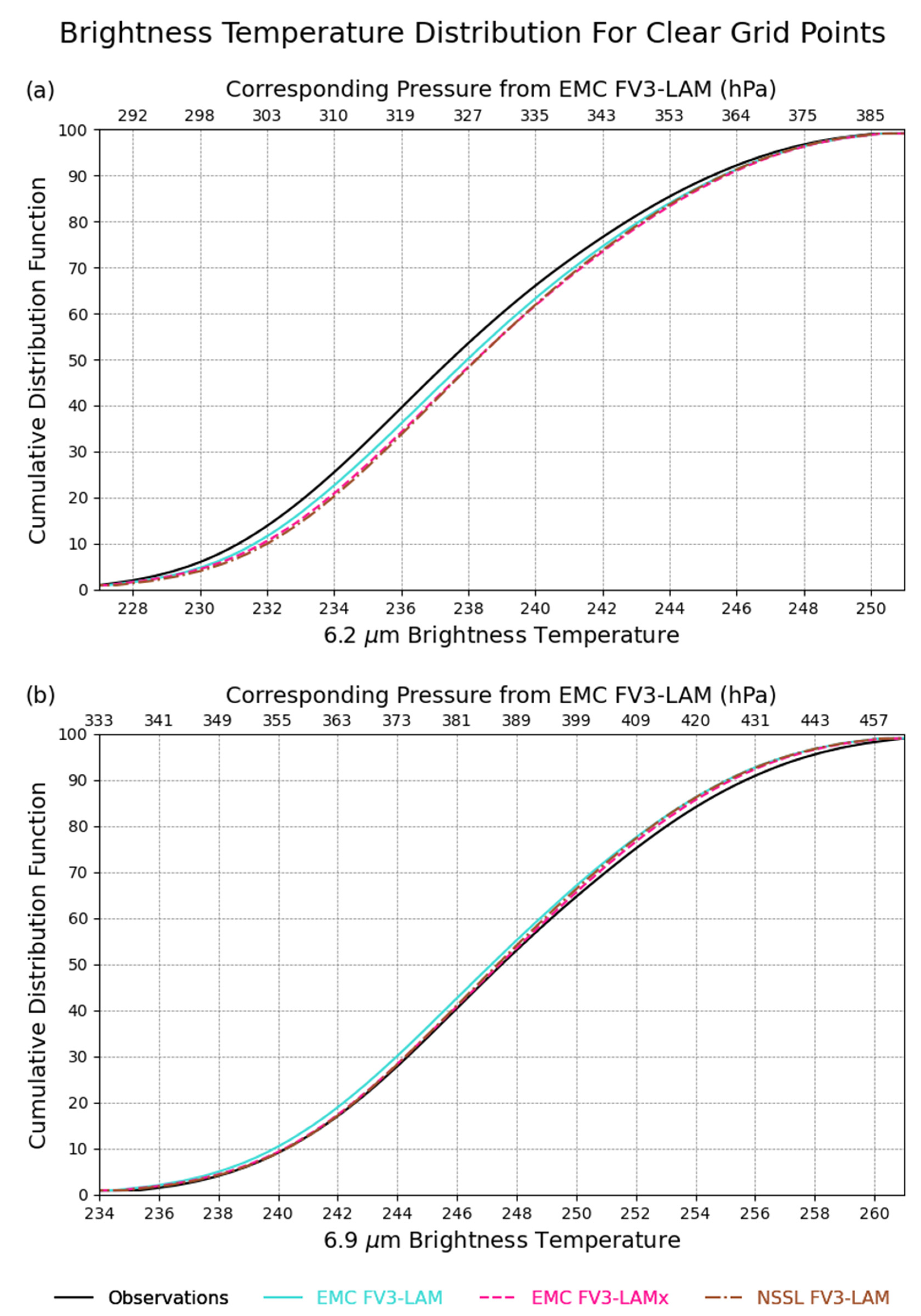

| Name | Microphysics Scheme | Planetary Boundary Layer Scheme | Surface Layer | Land Surface Model |
|---|---|---|---|---|
| Control | Thompson | MYNN | GFS | Noah |
| MP-NSSL | National Severe Storms Laboratory | MYNN | GFS | Noah |
| PBL-SH | Thompson | Shin–Hong | GFS | Noah |
| PBL-EDMF | Thompson | EDMF | GFS | Noah |
| LSM-RUC_SFC-GFS | Thompson | MYNN | GFS | RUC |
| LSM-RUC_SFC-MYNN | Thompson | MYNN | MYNN | RUC |
| Name | Microphysics Scheme | Planetary Boundary Layer Scheme | Surface Layer | Land Surface Model |
|---|---|---|---|---|
| EMC FV3-LAM | Geophysical Fluid Dynamics Laboratory | Hybrid EDMF | GFS | Noah |
| EMC FV3-LAMx | Thompson | MYNN | GFS | Noah |
| NSSL FV3-LAM | Thompson | MYNN | MYNN | Noah |
| Average MAE | NSSL | GFDL | Average MBE | NSSL | GFDL | Average MD for Clear Grid Points | NSSL | GFDL |
|---|---|---|---|---|---|---|---|---|
| 6.2 µm | 6.2 µm | 6.2 µm | ||||||
| 6.9 µm | 6.9 µm | 6.9 µm | ||||||
| 7.3 µm | 7.3 µm | 7.3 µm |
| Average MAE | Shin-Hong | EDMF | Average MBE | Shin–Hong | EDMF | Average MD for Clear Grid Points | Shin–Hong | EDMF |
|---|---|---|---|---|---|---|---|---|
| 6.2 µm | 6.2 µm | 6.2 µm | ||||||
| 6.9 µm | 6.9 µm | 6.9 µm | ||||||
| 7.3 µm | 7.3 µm | 7.3 µm |
| Average MAE | RUC GFS | RUC MYNN | Average MBE | RUC GFS | RUC MYNN | Average MD for Clear Grid Points | RUC GFS | RUC MYNN |
|---|---|---|---|---|---|---|---|---|
| 6.2 µm | 6.2 µm | 6.2 µm | ||||||
| 6.9 µm | 6.9 µm | 6.9 µm | ||||||
| 7.3 µm | 7.3 µm | 7.3 µm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Griffin, S.M.; Otkin, J.A. Evaluating the Impact of Planetary Boundary Layer, Land Surface Model, and Microphysics Parameterization Schemes on Simulated GOES-16 Water Vapor Brightness Temperatures. Atmosphere 2022, 13, 366. https://doi.org/10.3390/atmos13030366
Griffin SM, Otkin JA. Evaluating the Impact of Planetary Boundary Layer, Land Surface Model, and Microphysics Parameterization Schemes on Simulated GOES-16 Water Vapor Brightness Temperatures. Atmosphere. 2022; 13(3):366. https://doi.org/10.3390/atmos13030366
Chicago/Turabian StyleGriffin, Sarah M., and Jason A. Otkin. 2022. "Evaluating the Impact of Planetary Boundary Layer, Land Surface Model, and Microphysics Parameterization Schemes on Simulated GOES-16 Water Vapor Brightness Temperatures" Atmosphere 13, no. 3: 366. https://doi.org/10.3390/atmos13030366
APA StyleGriffin, S. M., & Otkin, J. A. (2022). Evaluating the Impact of Planetary Boundary Layer, Land Surface Model, and Microphysics Parameterization Schemes on Simulated GOES-16 Water Vapor Brightness Temperatures. Atmosphere, 13(3), 366. https://doi.org/10.3390/atmos13030366







