Projections of Future Drought by CMIP5 Multimodel Ensembles in Central Asia
Abstract
:1. Introduction
2. Data and Methods
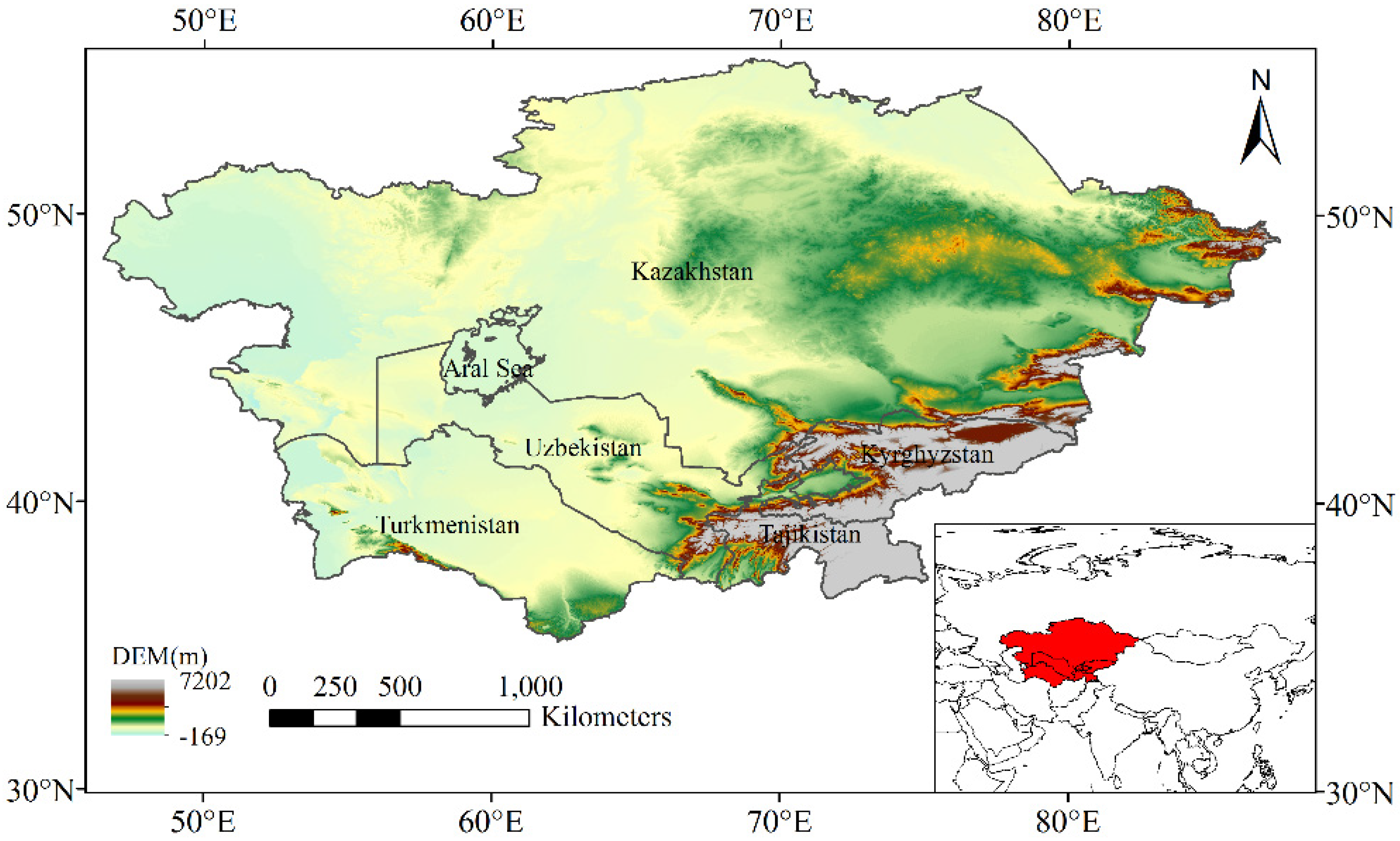
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. Quantile Mapping
2.3.2. Rotated Empirical Orthogonal Function (REOF)
2.3.3. Drought Indices
2.3.4. Frequency of Drought
2.3.5. Average Drought Duration
3. Results
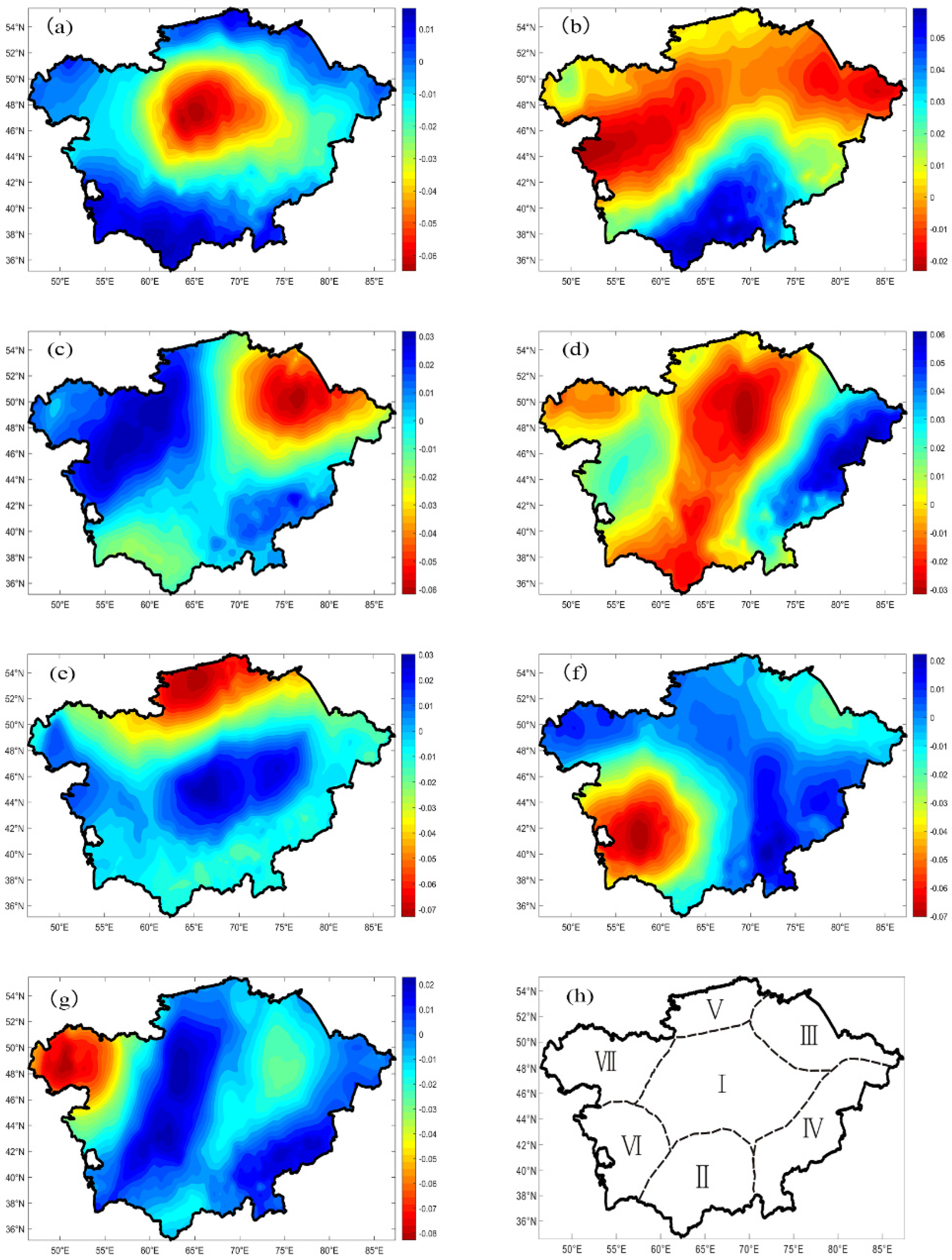
3.1. The Regional Division of Drought
3.2. Assessment of the Performance of CMIP5 Simulations and the Effect of Bias Correction
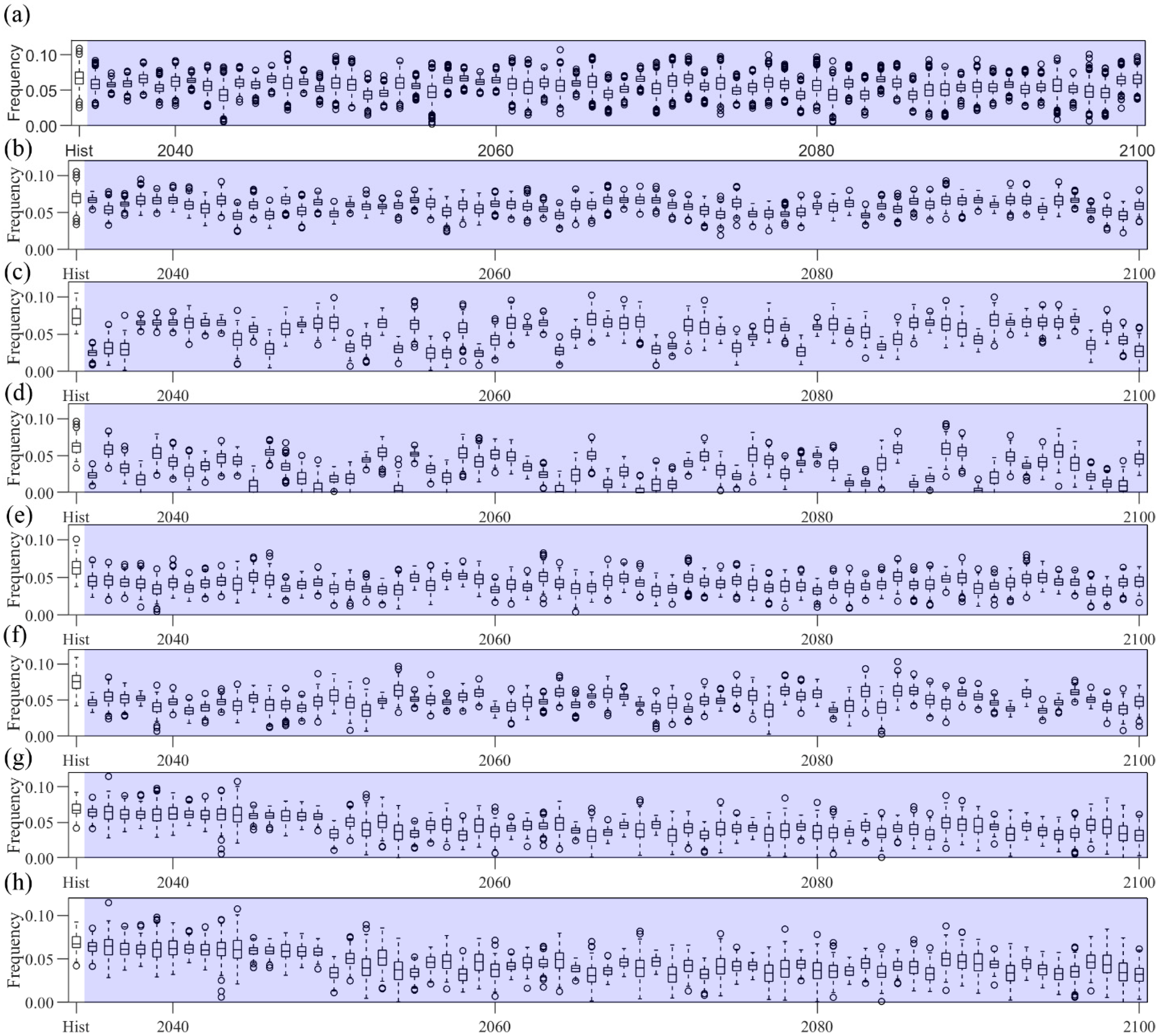
3.3. Future Drought Frequency
3.4. Future Drought Duration
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shiru, M.S.; Chung, E.S.; Shahid, S.; Alias, N. GCM selection and temperature projection of Nigeria under different RCPs of the CMIP5 GCMS. Theor. Appl. Climatol. 2020, 141, 1611–1627. [Google Scholar] [CrossRef]
- Gupta, A.; Rico-Medina, A.; Cao-Delgado, A.I. The physiology of plant responses to drought. Science 2020, 368, 266–269. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Liang, T.; Guo, J.; Xie, H.; Feng, Q.; Aimaiti, Y. Grassland dynamics in response to climate change and human activities in Xinjiang from 2000 to 2014. Entific Rep. 2018, 8, 2888. [Google Scholar] [CrossRef] [PubMed]
- Seneviratne, S. Changes in climate extremes and their impacts on the natural physical environment: An overview of the IPCC SREX report. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Burke, E.J.; Brown, S.J. Evaluating Uncertainties in the Projection of Future Drought. J. Hydrometeorol. 2008, 9, 292–299. [Google Scholar] [CrossRef]
- Botterill, L.C.; Hayes, M.J. Drought triggers and declarations: Science and policy considerations for drought risk management. Nat. Hazards 2012, 64, 139–151. [Google Scholar] [CrossRef] [Green Version]
- Svoboda, M.; Fuchs, B.A.; Poulsen, C.C.; Nothwehr, J.R. The drought risk atlas: Enhancing decision support for drought risk management in the United States. J. Hydrol. 2015, 526, 274–286. [Google Scholar] [CrossRef] [Green Version]
- Zhai, J.; Mondal, S.K.; Fischer, T.; Wang, Y.; Su, B.; Huang, J.; Tao, H.; Wang, G.; Ullah, W.; Uddin, M.J. Future drought characteristics through a multi-model ensemble from CMIP6 over South Asia. Atmos. Res. 2020, 246, 105111. [Google Scholar] [CrossRef]
- Lin, W.; Wen, C. A CMIP5 multimodel projection of future temperature, precipitation, and climatological drought in China. Int. J. Climatol. 2014, 34, 2059–2078. [Google Scholar]
- Swain, S.; Hayhoe, K. CMIP5 projected changes in spring and summer drought and wet conditions over North America. Clim. Dyn. 2015, 44, 2737–2750. [Google Scholar] [CrossRef]
- Venkataraman, K.; Tummuri, S.; Medina, A.; Perry, J. 21st century drought outlook for major climate divisions of Texas based on CMIP5 multimodel ensemble: Implications for water resource management. J. Hydrol. 2016, 534, 300–316. [Google Scholar] [CrossRef] [Green Version]
- Khan, J.U.; Islam, A.; Das, M.K.; Mohammed, K.; Islam, G. Future changes in meteorological drought characteristics over Bangladesh projected by the CMIP5 multi-model ensemble. Clim. Chang. 2020, 162, 667–685. [Google Scholar] [CrossRef]
- Erol, A.; Randhir, T.O. Climatic change impacts on the ecohydrology of Mediterranean watersheds. Clim. Chang. 2012, 114, 319–341. [Google Scholar] [CrossRef]
- Almazroui, M.; Islam, M.N. Coupled Model Inter-comparison Project Database to Calculate Drought Indices for Saudi Arabia: A Preliminary Assessment. Earth Syst. Environ. 2019, 3, 419–428. [Google Scholar] [CrossRef]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Chang. 2013, 3, 52–58. [Google Scholar] [CrossRef]
- Kai, X.; Cwa, B.; Czc, D.; Bxha, B. Uncertainty assessment of drought characteristics projections in humid subtropical basins in China based on multiple CMIP5 models and different index definitions—ScienceDirect. J. Hydrol. 2021, 600, 126502. [Google Scholar]
- Gm, A.; Vm, B.; Dn, C.; St, D.; Rao, S. Trends and variability of droughts over the Indian monsoon region. Weather Clim. Extrem. 2016, 12, 43–68. [Google Scholar]
- Ruosteenoja, K.; Markkanen, T.; Venlinen, A.; Risnen, P.; Peltola, H. Seasonal soil moisture and drought occurrence in Europe in CMIP5 projections for the 21st century. Clim. Dyn. 2018, 50, 1177–1192. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Yeh, J.F.; Chen, Y.Y.; Lv, W.; Huang, G. Copula-based risk evaluation of global meteorological drought in the 21st century based on CMIP5 multi-model ensemble projections. J. Hydrol. 2021, 126265. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Wells, N.; Goddard, S.; Hayes, M.J. A Self-Calibrating Palmer Drought Severity Index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Sheffield, J.; Andreadis, K.M.; Wood, E.F.; Lettenmaier, D.P. Global and Continental Drought in the Second Half of the Twentieth Century: Severity–Area–Duration Analysis and Temporal Variability of Large-Scale Events. J. Clim. 2009, 22, 1962–1981. [Google Scholar] [CrossRef]
- Chen, X.; Bai, J.; Li, X.; Luo, G.; Li, J.; Li, B.L. Changes in land use/land cover and ecosystem services in Central Asia during 1990–2009. Curr. Opin. Environ. Sustain. 2013, 5, 116–127. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; Vuuren, D.P.V.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engenskaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. Discuss. 2012, 9, 6185–6201. [Google Scholar] [CrossRef] [Green Version]
- Rhee, J.; Cho, J. Future Changes in Drought Characteristics: Regional Analysis for South Korea under CMIP5 Projections. J. Hydrometeorol. 2015, 17, 151016095329004. [Google Scholar] [CrossRef]
- Sunyer, M.A.; Madsen, H.; Ang, P.H. A comparison of different regional climate models and statistical downscaling methods for extreme rainfall estimation under climate change. Atmos. Res. 2012, 103, 119–128. [Google Scholar] [CrossRef]
- Moetasim, A.; Bowling, L.C.; Keith, C.; Pal, J.S.; Diffenbaugh, N.S. Influence of climate model biases and daily-scale temperature and precipitation events on hydrological impacts assessment: A case study of the United States. J. Geophys. Res. Atmos. 2010, 45, 1099–1116. [Google Scholar]
- Themeßl, M.J.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhang, Y.; Zhan, C.; Qiao, Y. Comprehensive assessment of drought risk in the arid region of Northwest China based on the global palmer drought severity index gridded data. Sci. Total Environ. 2018, 627, 951–962. [Google Scholar] [CrossRef]
- Taylor, I.H.; Burke, E.; Mccoll, L.; Falloon, P.D.; Harris, G.R.; Mcneall, D. The impact of climate mitigation on projections of future drought. Hydrol. Earth Syst. Sci. 2013, 17, 2339–2358. [Google Scholar] [CrossRef] [Green Version]
- Hayes, M.; Svoboda, M.; Wall, N.; Widhalm, M. The Lincoln Declaration on Drought Indices: Universal Meteorological Drought Index Recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef] [Green Version]
- Vicenteserrano, S.M.; Lópezmoreno, J.I. Hydrological response to different time scales of climatological drought: An evaluation of the Standardized Precipitation Index in a mountainous Mediterranean basin. Hydrol. Earth Syst. Sci. 2005, 9, 523–533. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; He, S.; Li, M.; Bao, A.; Chen, T.; Zheng, G.; Maeyer, P.D. Future changes of drought characteristics in CMIP6 SSP scenarios over Central Asia. Int. J. Climatol. 2021. [Google Scholar] [CrossRef]
- Dunnett, C.W. A Multiple Comparison Procedure for Comparing Several Treatments with a Control. Publ. Am. Stat. Assoc. 1955, 50, 1096–1121. [Google Scholar] [CrossRef]
- Miao, L.; Ye, P.; He, B.; Chen, L.; Cui, X. Future Climate Impact on the Desertification in the Dry Land Asia Using AVHRR GIMMS NDVI3g Data. Remote Sens. 2015, 7, 3863–3877. [Google Scholar] [CrossRef] [Green Version]








| Model Name | Institution and Country | Horizontal Resolution (Lat × Lon) |
|---|---|---|
| ACCESS1-0 | CSIRO-BOM, Australia | 1.25° × 1.875° |
| ACCESS1-3 | CSIRO-BOM, Australia | 1.25° × 1.875° |
| CanESM2 | CCCma, Canada | 2.784° × 2.8125° |
| CCSM4 | NCAR, USA | 0.942° × 1.25° |
| CSIRO-Mk3-6-0 | CSIRO-QCCCE, Australia | 1.861° × 1.875° |
| GFDL-ESM2G | NOAA GFDL, USA | 2.0225° × 2.5° |
| GFDL-ESM2M | NOAA GFDL, USA | 2.0225° × 2.5° |
| GISS-E2-H | NASA GISS, USA | 2.5° × 2.2° |
| GISS-E2-H-CC | NASA GISS, USA | 2.5° × 2.2° |
| GISS-E2-R | NASA GISS, USA | 2.5° × 2.2° |
| GISS-E2-R-CC | NASA GISS, USA | 2.5° × 2.2° |
| HadGEM2-CC | MOHC, UK | 1.25° × 1.875° |
| HadGEM2-ES | MOHC, UK | 1.25° × 1.875° |
| inmcm4 | INM, Russia | 1.5° × 2.0° |
| IPSL-CM5A-LR | IPSL, France | 1.895° × 3.75° |
| IPSL-CM5A-MR | IPSL, France | 1.895° × 3.75° |
| IPSL-CM5B-LR | IPSL, France | 1.895° × 3.75° |
| MIROC-ESM-CHEM | MIROC, Japan | 2.784° × 2.8125° |
| MIROC-ESM | MIROC, Japan | 2.784° × 2.8125° |
| MIROC5 | MIROC, Japan | 1.397° × 1.406° |
| NorESM1-M | NCC, Norway | 1.895° × 2.5° |
| Drought Classification | Index Value |
|---|---|
| Extreme wet (EW) | ≥2.00 |
| Very wet (VW) | From 1.50 to 1.99 |
| Moderate wet (MW) | From 1.00 to 1.49 |
| Near normal (NN) | From 0.99 to −0.99 |
| Moderate drought (MD) | From −1.00 to −1.19 |
| Severe drought (SD) | From −1.50 to −1.99 |
| Extreme drought (ED) | ≤−2.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ta, Z.; Li, K.; Yu, Y.; Yang, M. Projections of Future Drought by CMIP5 Multimodel Ensembles in Central Asia. Atmosphere 2022, 13, 232. https://doi.org/10.3390/atmos13020232
Ta Z, Li K, Yu Y, Yang M. Projections of Future Drought by CMIP5 Multimodel Ensembles in Central Asia. Atmosphere. 2022; 13(2):232. https://doi.org/10.3390/atmos13020232
Chicago/Turabian StyleTa, Zhijie, Kaiyu Li, Yang Yu, and Meilin Yang. 2022. "Projections of Future Drought by CMIP5 Multimodel Ensembles in Central Asia" Atmosphere 13, no. 2: 232. https://doi.org/10.3390/atmos13020232
APA StyleTa, Z., Li, K., Yu, Y., & Yang, M. (2022). Projections of Future Drought by CMIP5 Multimodel Ensembles in Central Asia. Atmosphere, 13(2), 232. https://doi.org/10.3390/atmos13020232









