Error Features in Predicting Typhoon Winds: A Case Study Comparing Simulated and Measured Data
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Simulation Domain
2.2. Boundary and Initial Condition
2.3. Model Configuration
2.4. Post-Processing
3. Error Statistics Report
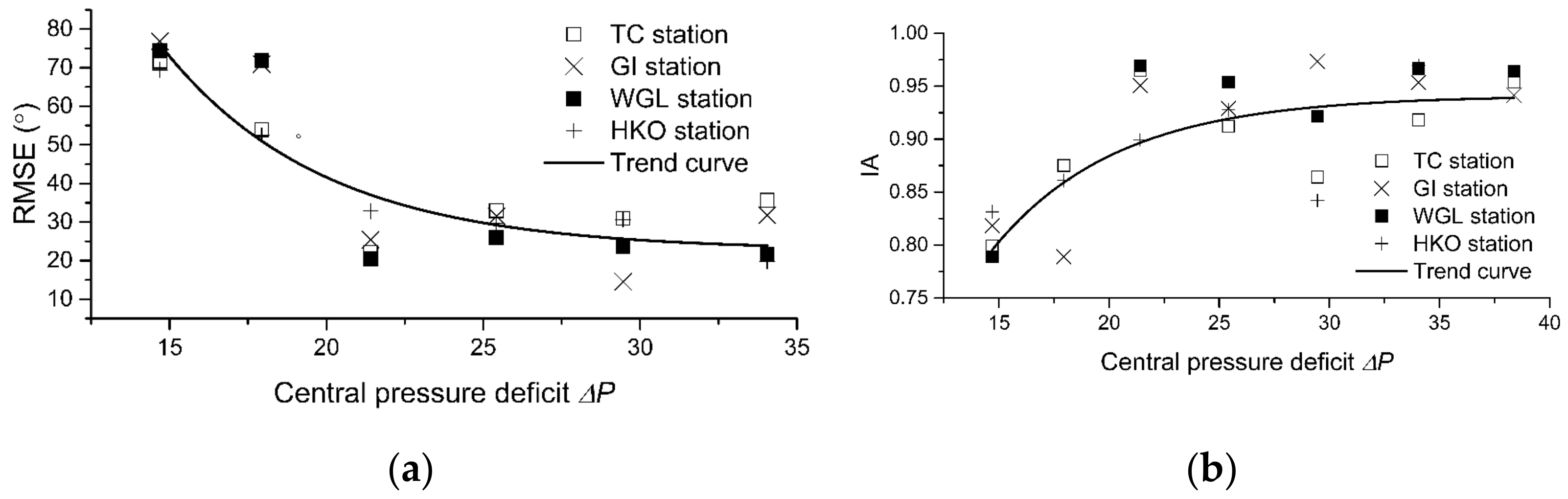
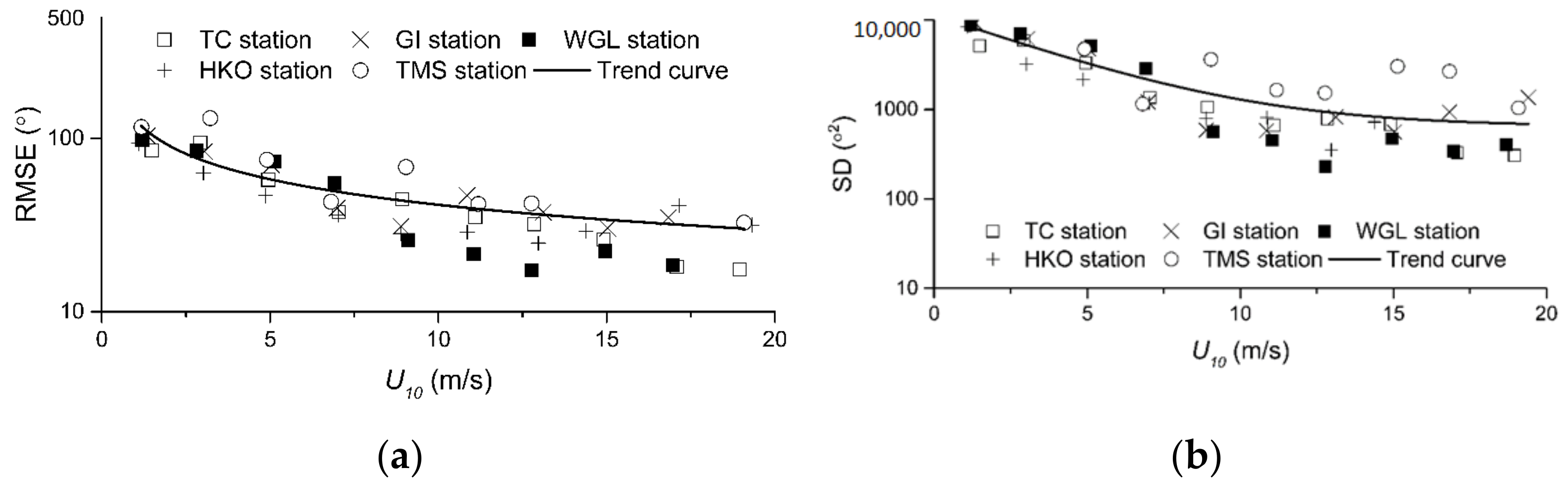
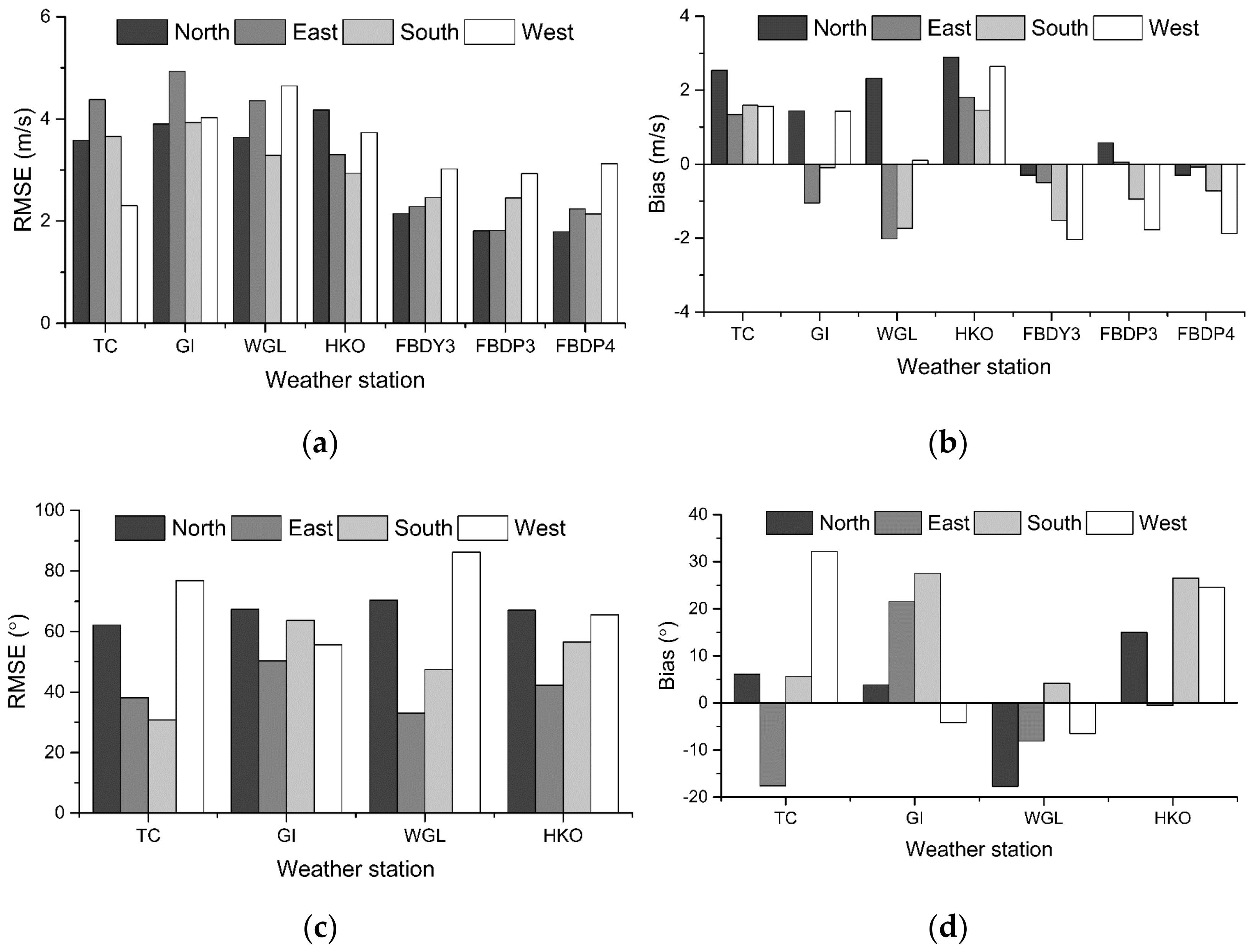
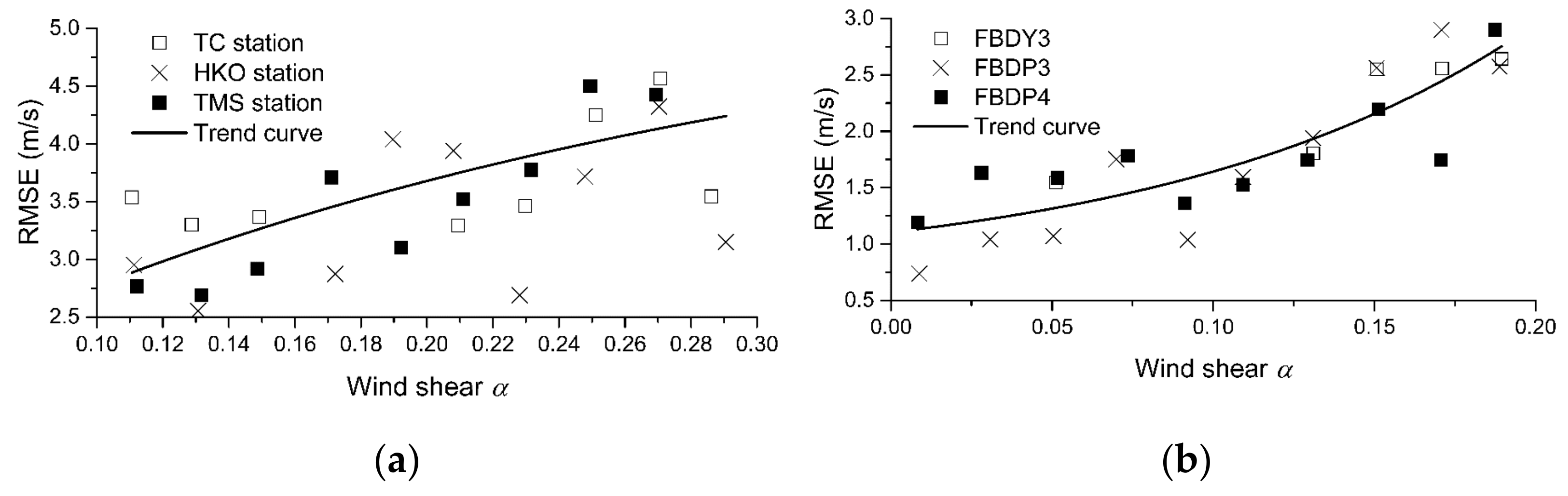
4. Discussion
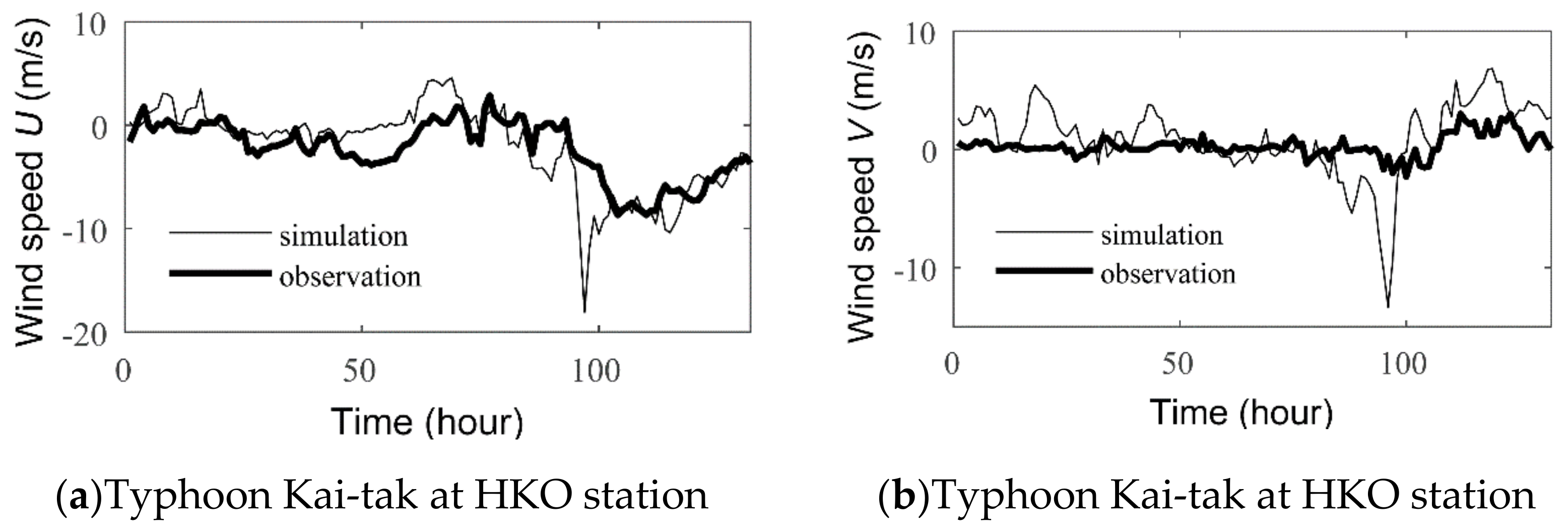
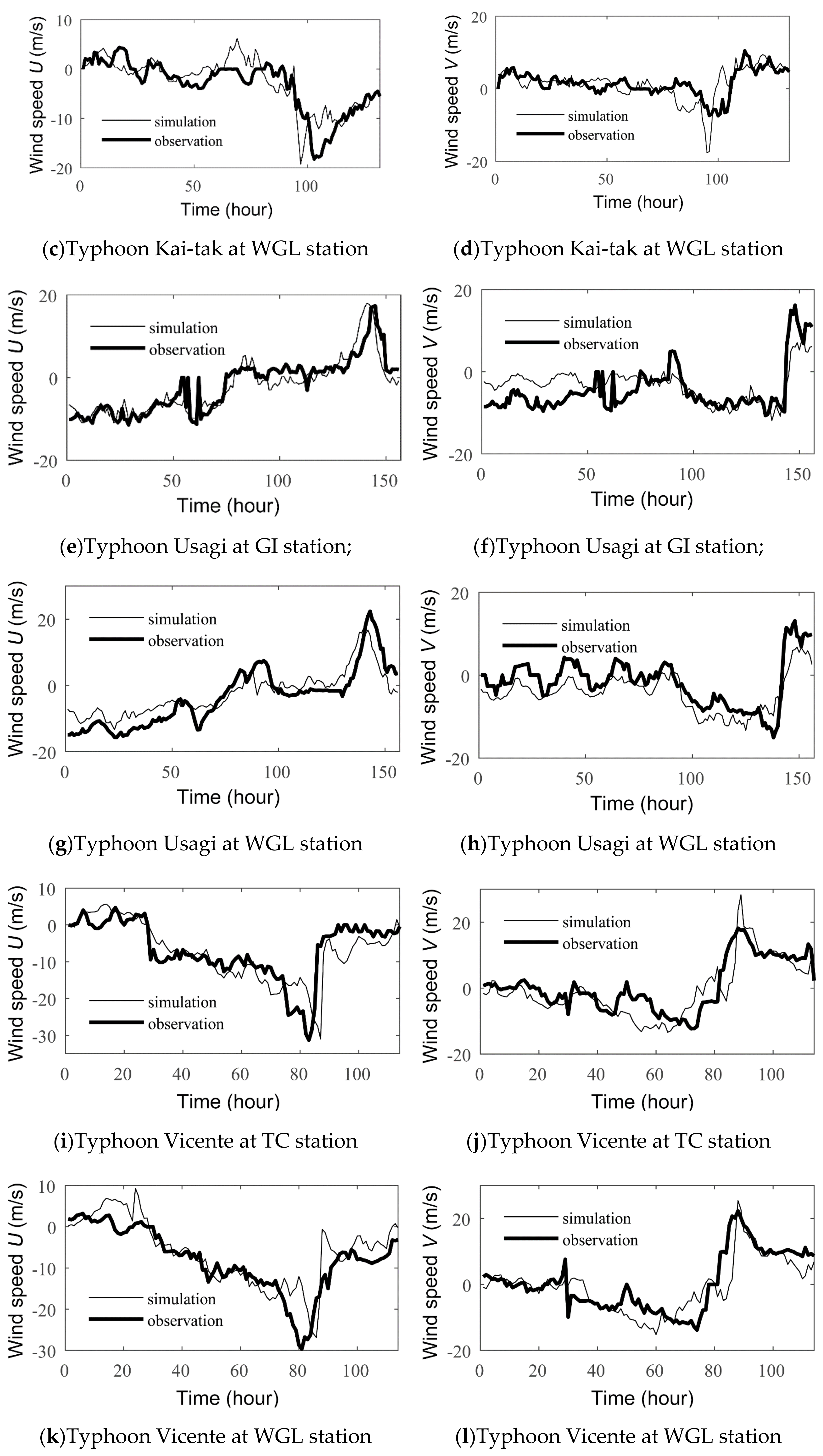
4.1. Large-Scale Feature
4.2. Localized Wind Conditions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- China Meteorological Administration. The Tropical Cyclone Yearbook; China Meteorological Press: Beijing, China, 2014. [Google Scholar]
- Liu, Y.; Chen, D.; Li, S.; Chan, P. Revised power-law model to estimate the vertical variations of extreme wind speeds in China coastal regions. J. Wind. Eng. Ind. Aerodyn. 2018, 173, 227–240. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, D.; Yi, Q.; Li, S. Wind Profiles and Wave Spectra for Potential Wind Farms in South China Sea. Part I: Wind Speed Profile Model. Energies 2017, 10, 125. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, S.; Chan, P.W.; Chen, D. Empirical Correction Ratio and Scale Factor to Project the Extreme Wind Speed Profile for Offshore Wind Energy Exploitation. IEEE Trans. Sustain. Energy 2017, 9, 1030–1040. [Google Scholar] [CrossRef]
- Sun, X.; Barros, A.P. High resolution simulation of tropical storm Ivan (2004) in the Southern Appalachians: Role of planetary boundary-layer schemes and cumulus parametrization. Q. J. R. Meteorol. Soc. 2014, 140, 1847–1865. [Google Scholar] [CrossRef]
- Kim, D.; Jin, C.-S.; Ho, C.-H.; Kim, J.; Kim, J.-H. Climatological features of WRF-simulated tropical cyclones over the western North Pacific. Clim. Dyn. 2014, 44, 3223–3235. [Google Scholar] [CrossRef]
- Grell, G.A.; Peckham, S.E.; Schmitz, R.; McKeen, S.A.; Frost, G.; Skamarock, W.C.; Eder, B. Fully coupled “online” chemistry within the WRF model. Atmos. Environ. 2005, 39, 6957–6975. [Google Scholar] [CrossRef]
- Michalakes, J.; Dudhia, J.; Gill, D.; Klemp, J.; Skamarock, W. Design of a Next-Generation Regional Weather Research and Forecast Model; Towards Teracomputing 1998; World Scientific: River Edge, NJ, USA, 1998; pp. 117–124. [Google Scholar]
- Jiménez, P.A.; Dudhia, J. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef] [Green Version]
- Papanastasiou, D.; Melas, D.; Lissaridis, I. Study of wind field under sea breeze conditions; an application of WRF model. Atmos. Res. 2010, 98, 102–117. [Google Scholar] [CrossRef]
- Tao, W.-K.; Wu, D.; Lang, S.; Chern, J.-D.; Peters-Lidard, C.; Fridlind, A.; Matsui, T. High-resolution NU-WRF simulations of a deep convective-precipitation system during MC3E: Further improvements and comparisons between Goddard microphysics schemes and observations. J. Geophys. Res. Atmos. 2016, 121, 1278–1305. [Google Scholar] [CrossRef]
- Sun, J.; He, H.; Hu, X.; Wang, D.; Gao, C.; Song, J. Numerical Simulations of Typhoon Hagupit (2008) Using WRF. Weather. Forecast. 2019, 34, 999–1015. [Google Scholar] [CrossRef]
- Banks, R.F.; Tiana-Alsina, J.; Baldasano, J.M.; Rocadenbosch, F.; Papayannis, A.; Solomos, S.; Tzanis, C.G. Sensitivity of boundary-layer variables to PBL schemes in the WRF model based on surface meteorological observations, lidar, and radiosondes during the HygrA-CD campaign. Atmos. Res. 2016, 176–177, 185–201. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. Sensitivity of the WRF model wind simulation and wind energy production estimates to planetary boundary layer parameterizations for onshore and offshore areas in the Iberian Peninsula. Appl. Energy 2014, 135, 234–246. [Google Scholar] [CrossRef]
- Lee, S.-H.; Kim, S.-W.; Angevine, W.M.; Bianco, L.; McKeen, S.A.; Senff, C.J.; Trainer, M.; Tucker, S.C.; Zamora, R.J. Evaluation of urban surface parameterizations in the WRF model using measurements during the Texas Air Quality Study 2006 field campaign. Atmos. Chem. Phys. Discuss. 2011, 11, 2127–2143. [Google Scholar] [CrossRef] [Green Version]
- Pennelly, C.; Reuter, G.; Flesch, T. Verification of the WRF model for simulating heavy precipitation in Alberta. Atmos. Res. 2014, 135–136, 172–192. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Lee, J. Assessment of the WRF model in reproducing a flash-flood heavy rainfall event over Korea. Atmos. Res. 2009, 93, 818–831. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gomez-Gesteira, M.; Santos, C.S. WRF wind simulation and wind energy production estimates forced by different reanalyses: Comparison with observed data for Portugal. Appl. Energy 2014, 117, 116–126. [Google Scholar] [CrossRef]
- Xue, L.; Li, Y.; Song, L.; Chen, W.; Wang, B. A WRF-based engineering wind field model for tropical cyclones and its applications. Nat. Hazards 2017, 87, 1735–1750. [Google Scholar] [CrossRef]
- Tse, K.; Li, S.; Fung, J.; Chan, P. An information exchange framework between physical modeling and numerical simulation to advance tropical cyclone boundary layer predictions. J. Wind. Eng. Ind. Aerodyn. 2015, 143, 78–90. [Google Scholar] [CrossRef]
- Draxl, C.; Hahmann, A.N.; Peña, A.; Giebel, G. Evaluating winds and vertical wind shear from Weather Research and Forecasting model forecasts using seven planetary boundary layer schemes. Wind. Energy 2014, 17, 39–55. [Google Scholar] [CrossRef]
- Storm, B.; Dudhia, J.; Basu, S.; Swift, A.; Giammanco, I. Evaluation of the Weather Research and Forecasting model on forecasting low-level jets: Implications for wind energy. Wind Energy 2009, 12, 81–90. [Google Scholar] [CrossRef]
- ECMWF. ERA Interim Daily Data. Available online: http://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/ (accessed on 31 December 2020).
- Wang, W.; Bruyere, C.; Duda, M.; Dudhia, J.; Gill, D.; Lin, H.; Michalakes, J.; Rizvi, S.; Zhang, X.; Beezley, J. ARW version 3 Modeling System User’s Guide; Mesoscale & Miscroscale Meteorology Division; National Center for Atmospheric Research: Boulder, CO, USA, 2010. [Google Scholar]
- Davis, C.A.; Low-Nam, S. The NCAR-AFWA Tropical Cyclone Bogussing Scheme; National Center for Atmospheric Research: Boulder, CO, USA, 2001. [Google Scholar]
- Kurihara, Y.; Bender, M.A.; Ross, R.J. An Initialization Scheme of Hurricane Models by Vortex Specification. Mon. Weather Rev. 1993, 121, 2030–2045. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, R.; Takahiro, O.; Shibayama, T.; Miguel, E.; Takagi, H. Evaluation of Storm Surge Caused by Typhoon Yolanda (2013) and Using Weather—Storm Surge—Wave—Tide Model. Procedia Eng. 2015, 116, 373–380. [Google Scholar] [CrossRef] [Green Version]
- Takagi, H.; Wu, W. Maximum wind radius estimated by the 50 kt radius: Improvement of storm surge forecasting over the western North Pacific. Nat. Hazards Earth Syst. Sci. 2016, 16, 705–717. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.M.; Fang, H.M.; Chen, Y.W.; Chuang, S.H. Discussion on the Maximum Storm Radius Equations When Calculating Typhoon Waves. J. Mar. Sci. Technol. 2015, 23, 4. [Google Scholar]
- Paulson, C.A. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. 1970, 9, 857–861. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Pan, H.-L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather. Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef] [Green Version]
- Dudhia, J. A Multi-layer Soil Temperature Model for MM5. In Proceedings of the Sixth PSU/NCAR Mesoscale Model Users’ Workshop, Boulder, CO, USA, 22–24 July 1996; pp. 49–50. [Google Scholar]
- Kain, J.S. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather. Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Miguez-Macho, G.; Stenchikov, G.L.; Robock, A. Spectral nudging to eliminate the effects of domain position and geometry in regional climate model simulations. J. Geophys. Res. Space Phys. 2004, 109, 1025–1045. [Google Scholar] [CrossRef] [Green Version]
- Mckinley, S.; Levine, M. Cubic Spline Interpolation. Numer. Math. J. Chin. Univ. 1999, 64, 44–56. [Google Scholar]
- Wang, C.; Jin, S. Error features and their possible causes in simulated low-level winds by WRF at a wind farm. Wind. Energy 2013, 17, 1315–1325. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Yi, Q.; Chen, D. Wind Profiles and Wave Spectra for Potential Wind Farms in South China Sea. Part II Wave Spectr. Model. Energ. 2017, 10, 127. [Google Scholar]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C. A sensitivity study of the WRF model in wind simulation for an area of high wind energy. Environ. Model. Softw. 2012, 33, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Charnes, A.; Frome, E.L.; Yu, P.L. The Equivalence of Generalized Least Squares and Maximum Likelihood Estimates in the Exponential Family. J. Am. Stat. Assoc. 1976, 71, 169–171. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, A.; Guo, P.; Wang, Z. Effect of surface waves on air–sea momentum flux in high wind conditions for typhoons in the South China Sea. Prog. Nat. Sci. 2008, 18, 1107–1113. [Google Scholar] [CrossRef]
- Mohan, G.M.; Srinivas, C.V.; Naidu, C.V.; Baskaran, R.; Venkatraman, B. Real-time numerical simulation of tropical cyclone nilam with wrf: Experiments with different initial conditions, 3d-var and ocean mixed layer model. Nat. Hazards 2015, 77, 597–624. [Google Scholar] [CrossRef]
- Mass, C.F. Fixing WRF’s High Speed Wind Bias: A New Subgrid Scale Drag Parameterization and the Role of Detailed Verification. In Proceedings of the 24th Conference on Weather and Forecasting/20th Conference on Numerical Weather Prediction, Seattle, WA, USA, 22–27 January 2011. [Google Scholar]
- Penabad, E.; Alvarez, I.; Balseiro, C.; DeCastro, M.; Gómez, B.; Perez-Munuzuri, V.; Gomez-Gesteira, M. Comparative analysis between operational weather prediction models and QuikSCAT wind data near the Galician coast. J. Mar. Syst. 2008, 72, 256–270. [Google Scholar] [CrossRef]
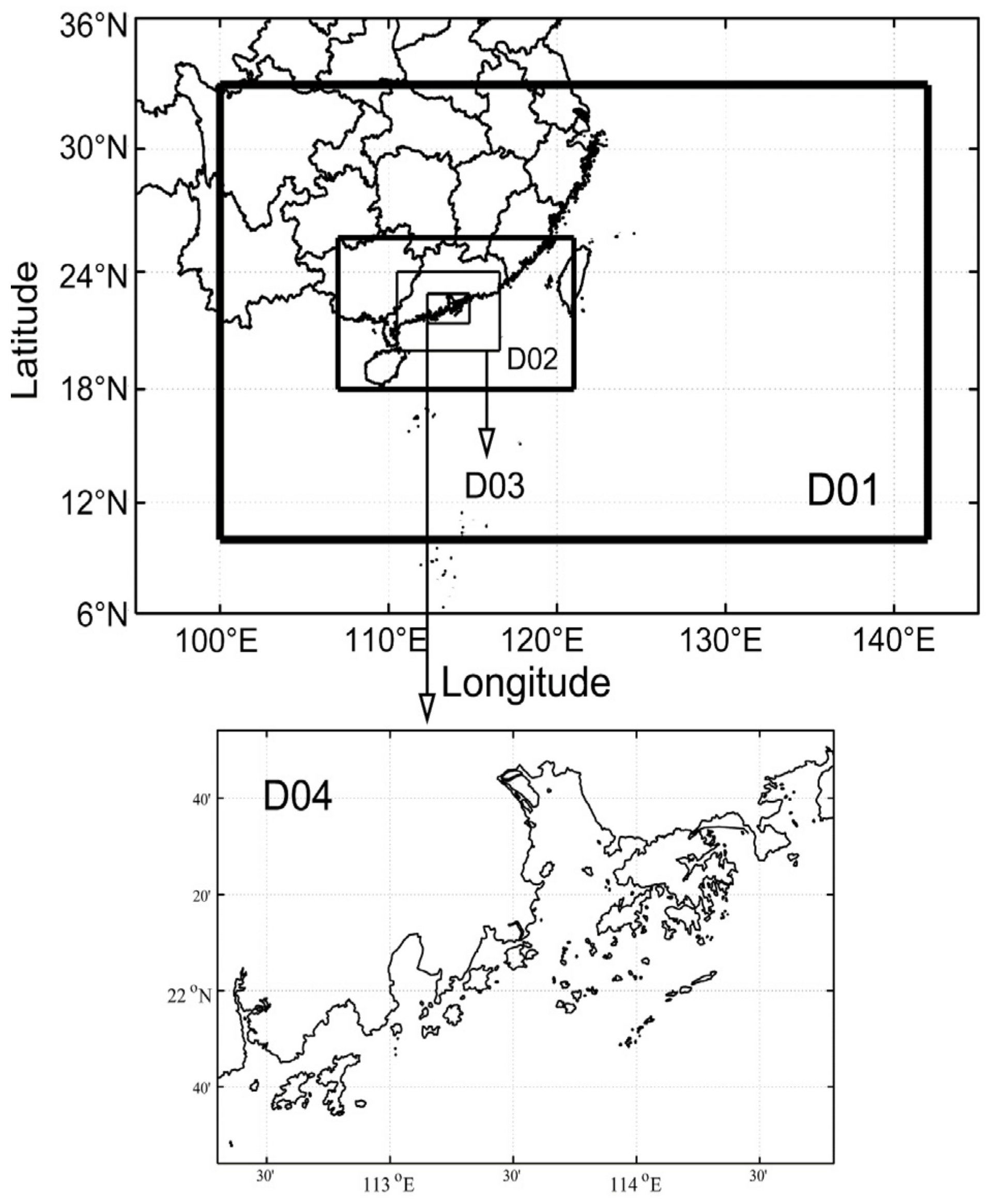








| Parameter | Content |
|---|---|
| 3D variables | U and V components of wind, temperature, relative humidity and geopotential height. |
| Pressure levels (hPa) | 10, 20, 30, 50, 70, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700, 750, 800, 850, 900, 925, 950, 975, 1000 |
| 2D variables (Surface level) | 10-m U and V components of wind, surface pressure, mean sea level pressure, skin temperature, 2-m temperature, 2-m relative humidity. |
| Areas | |
| Horizontal Resolution | |
| Temporal interval | 6 h |
| Date (UTC) | Location | Maximum Wind Speed (m/s) | Central Pressure (hPa) | |
|---|---|---|---|---|
| Typhoon Kai-tak | ||||
| Start | 08, 12 August 2012 | , | 13 | 1004 |
| End | 00, 18 August 2012 | , | 10 | 1000 |
| Typhoon Usagi | ||||
| Start | 18, 16 September 2013 | , | 13 | 1006 |
| End | 00, 23 September 2013 | , | 10 | 1002 |
| Typhoon Vicente | ||||
| Start | 06, 20 July 2012 | , | 13 | 1006 |
| End | 00, 25 July 2012 | , | 8 | 996 |
| Domain | D01 | D02 | D03 | D04 |
|---|---|---|---|---|
| Configuration | 4 nested domains, Mercator projection | |||
| Grid points | ||||
| Time step | Adaptive time step (Courant, Friedrichs, Lewy number 1.6) | |||
| Physics | Surface layer: MM5 scheme [30] | |||
| Boundary layer: YSU scheme [31] | ||||
| Land surface model: MM5 5-layer thermal diffusion [32] | ||||
| Cumulus parameterization: Kain–Fritsch scheme [33] | ||||
| Microphysics: WSM3 scheme [34] | ||||
| Radiation physics: RRTM scheme [35] | ||||
| FDDA (Four- dimensional data assimilation) | Spectral nudging [36] | |||
| Variable | Nudging coefficient () | |||
| Wind speed | ||||
| Temperature | ||||
| Geopotential height | ||||
| Wave number (x) | 4 | |||
| Wave number (y) | 2 | |||
| Station Name | Position | Elevation above the Mean Sea Level (m) |
|---|---|---|
| Land weather station | ||
| Tate’s Cairn (TC) | 587 | |
| Green Island (GI) | 107 | |
| Waglan Island (WGL) | 83 | |
| Tai Mo Shan (TMS) | 966 | |
| Hong Kong Observatory (HKO) | 74 | |
| Offshore buoy | ||
| FBDY3 | 2 | |
| FBDP3 | 2 | |
| FBDP4 | 2 |
| Station | RMSE (m/s) | Bias (m/s) | SSD () | SI (m/s) | IA |
|---|---|---|---|---|---|
| TC | 3.82 | 1.80 | 11.32 | 0.44 | 0.88 |
| GI | 4.26 | −0.07 | 18.15 | 0.55 | 0.77 |
| WGL | 3.93 | −0.67 | 15.01 | 0.44 | 0.87 |
| HKO | 3.43 | 2.05 | 7.53 | 0.93 | 0.72 |
| TMS | 4.30 | 0.64 | 18.12 | 0.42 | 0.88 |
| FBDY3 | 2.30 | −0.77 | 4.72 | 0.40 | 0.89 |
| FBDP3 | 2.01 | −0.17 | 4.00 | 0.46 | 0.84 |
| FBDP4 | 2.16 | −0.40 | 4.49 | 0.46 | 0.85 |
| Station | RMSE () | Bias () | SSD () | SI () | IA |
|---|---|---|---|---|---|
| TC | 51.35 | −5.39 | 2607.90 | 0.37 | 0.92 |
| GI | 59.25 | 17.80 | 3193.30 | 0.41 | 0.92 |
| WGL | 55.78 | −7.32 | 3057.60 | 0.43 | 0.91 |
| HKO | 55.72 | 8.68 | 3029.20 | 0.36 | 0.91 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, S.; Liu, Y.; Li, R.; Wei, Y.; Chan, P.-W.; Li, S. Error Features in Predicting Typhoon Winds: A Case Study Comparing Simulated and Measured Data. Atmosphere 2022, 13, 158. https://doi.org/10.3390/atmos13020158
Peng S, Liu Y, Li R, Wei Y, Chan P-W, Li S. Error Features in Predicting Typhoon Winds: A Case Study Comparing Simulated and Measured Data. Atmosphere. 2022; 13(2):158. https://doi.org/10.3390/atmos13020158
Chicago/Turabian StylePeng, Shaoyuan, Yichao Liu, Renge Li, Ying Wei, Pak-Wai Chan, and Sunwei Li. 2022. "Error Features in Predicting Typhoon Winds: A Case Study Comparing Simulated and Measured Data" Atmosphere 13, no. 2: 158. https://doi.org/10.3390/atmos13020158
APA StylePeng, S., Liu, Y., Li, R., Wei, Y., Chan, P.-W., & Li, S. (2022). Error Features in Predicting Typhoon Winds: A Case Study Comparing Simulated and Measured Data. Atmosphere, 13(2), 158. https://doi.org/10.3390/atmos13020158








