Abstract
The Andes mountain range divides Colombia into various climatic regions over the country, as the Andean, Caribbean, Pacific, Amazon, and Orinoco regions. Given this scenario, knowing the current change in total precipitation and their extremes values are relevant. In this study, the main goal is to assess the spatio-temporal trends of heavy and intense rainfall at a seasonal scale during the last 38 years (1981–2018) using the trend empirical orthogonal function (TEOF). An increase in maximum precipitation during five consecutive days (RX5day), Simple daily intensity index (SDII), and the number of days with precipitation above 20 mm (R20mm) and 30 mm (R30mm) during December–February and March–May was observed in most of the Colombian territory, except for the Amazon region for RX5day. A decrease in total rainfall in June–August was observed in the Andean, the Caribbean, and southern Pacific regions, while, in the northern Pacific, it increased, consistent with the trend patterns of RX5day, SDII, and R20mm. During September–November, there was a reduction in rainfall in the Amazon region and the South Pacific, and an increase in RX5day, SDII, R20mm, and R30mm in the Andean, the Caribbean, and North Pacific regions. The TEOF showed more pronounced spatial trend patterns than those obtained with the traditional Mann–Kendall test. The findings offer a better understanding of the climate extremes impacts in tropical latitudes and help planners to implement measures against the future effects of climate change.
1. Introduction
The sixth report of the Intergovernmental Panel on Climate Change (IPCC) has established that human-induced greenhouse gas emissions have led to an increased frequency and/or intensity of some weather and climate extremes [1]. Heavy precipitation follows, increasing about 7% per 1 °C temperature increase [1], and the frequency and intensity of heavy precipitation events have increased at a global scale and over a majority of land regions. The increase in the frequency, magnitude, and duration of extreme precipitation events due to climate change negatively affects the environment, ecosystems, the economy, and society’s quality of life [2,3,4,5]. In this regard, the last global risk report performed by the World Economic Forum indicates that among the highest likelihood risks of the next ten years are extreme weather with relevant negative impacts, such as loss of human life, damage to ecosystems, destruction of property, and financial loss, at a global scale [6,7].
The changes in frequency and intensity are not uniform in space and vary by region due to the different interacting drivers in extreme precipitation changes [8,9,10,11]. Tabari et al. [8] showed that the changes in floods and extreme precipitation worldwide have intensified in response to global warming. Respectively, Wahlstrom and Guha-Sapir [12] indicate that 90% of the disasters that occurred during the 1995–2015 period were generated by natural disasters, such as floods, droughts, and heatwaves, leaving 4.1 billion affected and a total of 600,000 dead. Therefore, it is necessary to understand the behavior of extreme rains to mitigate/adapt damage to society and the environment [13].
In South America, the evidence depicts an increase in total precipitation trends and extreme precipitations events, although the confidence level is low [1,14]. The changes in extreme precipitation represented by annual maxima of 1-day (RX1day) and 5-day (RX5day) registered a trend to increase in the largest proportion in South America during the 1950–2018 period [15]. Sun et al. [15] highlighted that the uncertainty in the results is high given that the data coverage in this continent is poor. Respectively, Skansi et al. [16] also reported that the trends increased in RX5day and extremely wet days (R99P) over large regions of South America during the 1950–2010 period.
In this context, the study of floods and droughts becomes significant due to the increase in the frequency and intensity of extreme hydroclimatic events in recent decades [17,18,19,20,21,22]. In the last few years, Colombia has experienced losses due to natural disasters estimated at more than 7100 million dollars [23]. The water crisis in the agricultural sector in 1997–1998, due to the El Niño–Southern Oscillation (ENSO) phenomenon during its warm phase, generated losses close to 101 million dollars for the year 2000 in Colombia. Meanwhile, the 2010–2011 La Niña phenomenon during the rainy season affected 5.2 million people (11.3% of the population) in 91% of the country, as a consequence of more than one million hectares of flooded crops, leading. to economic losses of more than 4.87 billion dollars in Colombia in that period [24]. According to Cerón et al. [25], around 90% of the disasters and natural catastrophes that have taken place in this country are associated with hydrometeorological phenomena. A total of 32,022 landslides in the period between 1900–2016 were compiled, where the precipitation showed a dominant influence on the occurrence of landslides, with 92% of landslides triggered by rainfall [26], with a greater influence of rainfall duration instead of rainfall intensity [27]. Therefore, Colombia is a country highly susceptible and vulnerable to extreme weather events due to its location, the influence by the Inter-Tropical Convergence Zone (ITCZ), the three low-level jets, the Amazon, the topography, and different processes in both the Pacific and Atlantic oceans. The ENSO in both phases, warm (El Niño) and cold (La Niña), is one of the main phenomena that has the greatest effects on the national territory of Colombia [28,29,30,31].
To identify the trends in rainfall in Colombia, authors have used several methodologies, statistical techniques, databases, and record length. Carmona and Poveda [32], for the analysis of rainfall stations with more than 25 years, used the Mann–Kendall test and Sen test to identify trends and quantify their magnitudes, respectively. They found mixed trends without a clear pattern, except for the Pacific region, where the trend increased due to the influence of moisture in the Pacific and the Chocó Jet. Following the same methodology, Cantor [33] studied 715 rainfall stations and reported that most of the rainfall series do not show a trend (76.53%), 13.56% showed an increasing trend, and 10.06% showed a decreasing trend distributed in central and northwestern Colombia. For his part, Pabon [34] evaluated the precipitation trend using the standardized method RClimDex and found that annual precipitation in the second half of the 20th century registered changes differentiated by regions. These results are consistent with Mayorga et al. [35], who used the same methodology, analyzed 310 rainfall stations during the 1970–2010 period, and reported 71% stations with increasing trend, 22% decreasing trend, and 7% without signal. For his part, Colombia, in the third national communication on climate change [36], used the extreme rainfall indices and found a positive trend of the annual precipitation in most of the Colombian territory, except the climatic regions associated with the Andean foothills, Llanero foothills, Magdalena Upper, and the southern part of the region of the Upper Cauca. It highlights that the trends were not statistically significant in all the indices analyzed. For his part, Morales-Acuña et al. [37] evaluated the trends of average monthly precipitation in the Magdalena Department based on satellite estimations and reported that the current rainfall patterns contradict previous estimates of a progressive decrease in annual averages, except for the Sierra Nevada de Santa Marta area, founding reductions between 10 mm yr−1 and 30 mm yr−1.
Considering the complexity to establish the precipitation changes in Colombia, recently, Mesa et al. [31] studied the trends of hydroclimatic intensity in Colombia using the record of all available rain gauges in Colombia and the CHIRPS (Climate Hazards Group InfraRed Precipitation) database and estimated trends in the main variables that describe the precipitation, including an index of the hydrologic cycle’s intensity. However, the results showed that neither the existing records of precipitation in the rain gauge network of Colombia nor the CHIRPS dataset shows a clear signal of statistically significant trends. Only 20% of the gauges or cells present significant trends, which depicted that the increasing trends prevail over decreasing trends. The hydrologic cycle in the Pacific and Andes regions tends to be more intense than in the Caribbean, Orinoco, and Amazon regions; moreover, the trends are opposite. With respect to frequency analysis of extreme events, Coronado-Hernández et al. [38] determined the maximum daily precipitation in the regions of Colombia, considering a return period of 100 years, where the minimum value was reached in the Andean region, with a value of 42.6 mm, and the maximum value was reported in Caribbean region, reaching an extreme precipitation of 306 mm.
Given the need to advance in the study and knowledge of the trend pattern of heavy and intense rainfall events in Colombia, in this study, a new contribution is presented analyzing the spatio-temporal trends of seasonal rainfall during the last 38 years (1981–2018) using the high-resolution gridded product CHIRPS. In this sense, this study goes beyond previous studies of precipitation trends over the region to assess the frequency and intensity indices of extreme precipitation events using an alternative technique to extract trend-robust patterns, namely the trend empirical orthogonal function (TEOF) proposed by Hannachi [39]. Hence, this article is arranged as follows: Section 2 describes the material and methods. Section 3 describes the results, and Section 4 shows the discussion and conclusions.
2. Materials and Methods
2.1. Study Area
Colombia has a continental area of 1,141,748 km2, with a total population of 50,372 million people. It is located in the northwest of South America, between the Pacific and Atlantic oceans and the Amazon rainforest, influencing its climate. It is privileged since it is the only country in South America with two coasts: the Caribbean Sea and the Pacific Ocean. In addition, this country is crossed by the Andes mountain range, which gives rise to a great variety of climates and ecosystems. Colombia has five natural regions defined by the Instituto Geográfico Agustín Codazzi [40]: Caribbean, Pacific, Andes, Orinoco, and Amazon (Figure 1).
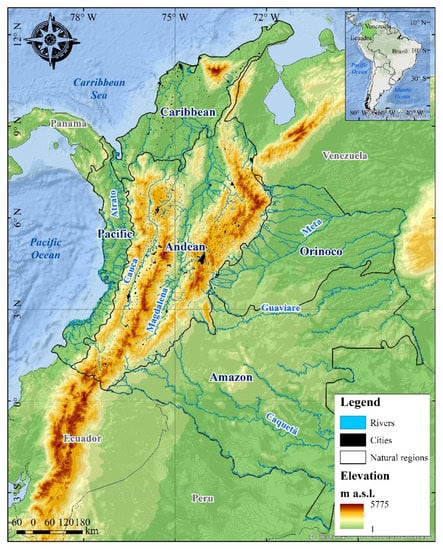
Figure 1.
Location of the study area and Colombian natural regions.
According to Urrea et al. [41], the country has four types of annual precipitation regimes: unimodal, bimodal, mixed, and aseasonal or seasonally invariant. The unimodal regime (one rainy season and one dry) is registered mainly in the Orinoco, Amazon, and Caribbean regions, probably related to the South American monsoon, whereas the bimodal regime occurs predominantly in the Andean region due to the mountainous areas and the double pass of the ITCZ. On the other hand, in transition zones between unimodal and bimodal regimes, a mixed regime is registered. Furthermore, the aseasonal regimes are evidenced in some areas of the Pacific region due to the alternation of the moisture supply by the low-level Chocó and Caribbean jets [41,42,43].
Figure 2 shows the monthly mean precipitation maps for the 1981–2018 period from the CHIRPS database; in all months, the physiographic influence of the Colombian territory is observed, mainly dominated by the three branches of the Andes mountain range. According to Estupiñan [44], the bimodality or unimodality of rainfall can be related to the ITCZ latitudinal displacement such that, in the summer of the southern hemisphere (December–January–February (DJF)), the ITCZ is located south of the equator, generating higher precipitation in latitudes southern than 2° N (Figure 2a–c). In the March–April–May (MAM) period, the ITCZ shifts northward, causing increased precipitation between latitudes 2°–7° N (Figure 2d–f), during the northern hemisphere summer (June–July–August (JJA)), the ITCZ reaches its greatest displacement towards the north of the equator, generating a reduction in rainfall, mainly in the Andean region (Figure 2g–i). In the September–November (SON) season, the ITCZ moves southward, once again generating increases in precipitation in latitudes 2°–7° North (Figure 2j–l), causing a bimodality of rainfall in the departments belonging to the Andean region, mainly in Antioquia, Caldas, Cundinamarca, Quindío, Risaralda, and Tolima [44,45].
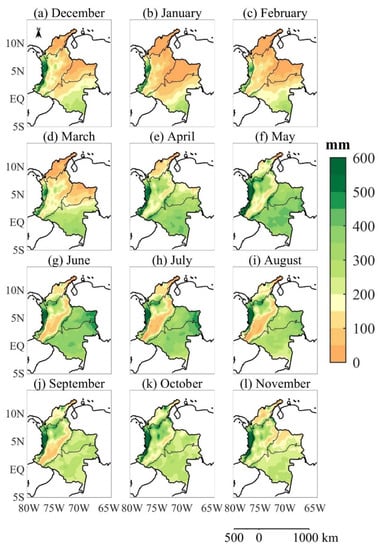
Figure 2.
Monthly rainfall climatology (mm) in Colombia for the 1981–2018 period from CHIRPS dataset for (a) December, (b) January, (c) February, (d) March, (e) April, (f) May, (g) June, (h) July, (i) August, (j) September, (k) October, and (l) November.
Thus, in the Andean region, a bimodal cycle is observed, with maxima in the April–May and October–November periods, and minima in January–February and July–August; for the Amazon region, although rainfall prevails year round, there is a minima in February and another in August–September; the Orinoco region is characterized by a rainy period during the May–July period and a dry period in the DJF season; the Caribbean region in the northern part of the Colombian territory has low rainfall between December and March, and, between April and November, rainfall tends to be above 100 mm month−1, with maxima in May, September, and October. Finally, for the Pacific region, there are variations between the north and the south; in the south, there is a cycle with maxima in the months of May and October, and less rainfall between January–February and August, while the north has the highest rainfall magnitudes in all Colombia between April and December, with precipitation greater than 500 mm month−1 (Figure 2).
2.2. The Climate Hazards Group Infrared Precipitation with Stations (CHIRPS)
CHIRPS satellite-based product [46] version v2.0, developed by the Earth Resources Observation and Science Center of the U.S. Geological Survey and the Climate Risk Group of the University of California, Santa Barbara, was selected, owing to its usefulness for trend analysis and drought monitoring [47,48]. In addition, it has been validated in Colombia by Funk et al. [48] and by Urrea et al. [49]. They showed that CHIRPS preserves important precipitation features, such as mean and seasonality, on daily, monthly, and annual time scales. This satellite dataset is freely available at the Climate Hazards Center website (https://www.chc.ucsb.edu/data, accessed 10 November 2019), with two spatial resolutions of 0.05° (≈5 km) and 0.25° *(28 km) and a 1-day temporal resolution. For the purposes of this study, it was used at 0.25° and on a daily time scale, over the entire Colombian country (Figure 1), similar to other studies over South America that assess precipitation patterns, such as Cerón et al. [22,50] and Fernandes et al. [51].
2.3. Precipitation Extremes Indices
Four precipitation indices associated with extreme rainfall patterns (Table 1), recommended by the Expert Team on Climate Detection and Change Indices (ETCCDI; http://etccdi.pacificclimate.org/, accessed 13 January 2022) [52], were selected and calculated at seasonal scales: DJF, MAM, JJA, and SON. The indices were calculated using daily precipitation from CHIRPS data for the 1981–2018 period. The seasonal approach is justified by the pronounced interannual precipitation variability in the region [28,53,54,55,56,57].

Table 1.
Extreme daily precipitation indices (http://etccdi.pacificclimate.org/list_27_indices.shtml, accessed 13 January 2022).
The selected extreme precipitation indices can be divided into three categories (Table 1): (1) intensity indices, depicting the amount of maximum precipitation accumulated in one day (RX1day), in five consecutive days (RX5day), and the simple daily intensity index (SDII) that describes the total wet-day precipitation (PRCPTOT) divided by the number of wet days (RR ≥ 1.0 mm) in a given interval (seasonal in this case); they can be used to explain flash flood risks; (2) frequency index, wherein the R1mm, R10mm, R20mm, and R30mm indices represent the count of days in which daily precipitation is greater than or equal to 1, 10, 20, and 30 mm, respectively. Noteworthy is that the R20mm and R30mm represent the number of days with the highest precipitation over tropical areas [16,17,19,58]; and (3) duration indices, representing the maximum number of consecutive dry days (CDD) and consecutive wet days (CWD). These ETCCDI indices have been demonstrated to be useful in describing climate patterns of extreme precipitation events worldwide [16,17,22,58,59,60,61,62] and, recently, characterizing flooding trends in the Colombian Andes [19], based on historical daily precipitation. Finally, the total precipitation (PRP) is also analyzed, representing the total rainfall from RR ≥ 0 mm on a seasonal scale.
2.4. Trend Empirical Orthogonal Function Analysis-TEOF
Hannachi [39] introduced an alternative technique to the traditional empirical orthogonal function (EOF) analysis to extract the trend-robust patterns from a spatio-temporal grid data set by including the concept of monotonicity. The solution is obtained by prior data transformation, thus providing a measure of monotonicity in the EOF analysis. The trend EOF (TEOF) method consists of an eigenvalue analysis of the covariance matrix, similar to the traditional EOF analysis, but with the time positions following the sequence of the ordered measurements, instead of the original ones directly. This rearrangement represents the monotonicity of the data. Maximizing the variance of a linear combination of the time positions is equivalent to maximizing the monotonicity, consequently obtaining the long-term trend hidden in the signal [39,63].
For this study, the data matrix represents the extreme precipitation indices. However, the original data are sorted in decreasing order, and then the position in a time of each data in the sorted series is taken. These ordered data positions become the new data. Thus, the newly transformed indices are made up of time series, each of which is a permutation of , i.e.,
for some permutation .
Afterwards, the maximum correlation between the time positions of the sorted data is examined to find times at which different time series increase (or decrease) together. Principal modes based on this new correlation (or covariance) answer the trends. Thus, the variance of a linear combination of two-position sequences gives a total (and common) monotonicity measure. Therefore, the greatest monotonicity and, hence, most significant trend is provided by maximizing this measure. The new data matrix of position-ordered data is now given by
and the following correlations (or covariances) are needed:
Thus, TEOF and trend principal components (TPCs) use the new covariance (or correlation) matrix obtained
where is the centering operator, is the identity matrix, and is a column vector of length containing only ones.
The singular value decomposition of the new HQ data matrix was used to obtain the new TEOFs and TPCs. The first TPC will maximize the total monotonicity, and the second TPC will also maximize the same monotonicity; nevertheless, it will not be related to the first TPC. Therefore, if is an eigenvector resulting from the above eigendecomposition, the TPCs time series in physical space is determined by , and the corresponding spatial pattern is composed of the regression coefficients between the TPC and the time series of the extreme indices of the original field [39,64]. Therefore, the method also captures local trends when they exist. For further information about the procedures, please refer to Reference [39].
This technique has the advantage of isolating from the trend of interannual scale phenomena, such as those associated with climate variability, such as ENSO, Atlantic Multidecadal Oscillation (AMO), etc. [63,65]. Barbosa and Andersen [64] further applied this technique to analyze the global Sea Surface Temperature (SST) low-frequency variability patterns and examined the sensitivity of the results to different recording lengths of data. They showed that the first trend mode reflects the low-frequency SST variability, corresponding to an increasing trend in the western Pacific and North Atlantic, mainly in the AMO index monitoring region, and a decreasing trend in the equatorial and central Pacific. The second trend mode reflects ENSO variability in the eastern Pacific.
The TEOF is a novel method tailored to systematically identify trends from spatiotemporal gridded data by decomposing it into a trend part and a non-trend part [39]. Thus, this technique is not able to distinguish between the trends due to the inherent variability and climate change. This method is used here to identify the trend patterns of extreme rainfall indices.
2.5. Mann–Kendal (MK) Test
The trends of the TPC time series for each extreme rainfall index were determined using the non-parametric Mann–Kendall statistical test to evaluate the temporal trends of each series [66,67]. The linear trend of the time series was calculated using Sen’s slope (β) estimator [68,69,70]. This test can handle abrupt discontinuities due to inhomogeneous temporal succession and is considered quite consistent [71]; moreover, it has been widely employed for rainfall trend analysis [22,71,72,73,74]. In this study, the Mann–Kendall was performed at a significance level of 0.05. The null hypothesis expressing the absence of trend is rejected for α < 0.05. This method was also employed explicitly for comparative purposes with the TEOF analysis.
3. Results
Trend Patterns
Seasonal trend patterns are derived from the extreme rainfall indices (Table 1), and total rainfall from CHIRPS through the TEOFs analysis, explained in the previous section. The data matrix of inverse ranks (time position of the ordered data) is computed from the data matrix of the extreme indices, and the TEOFs are obtained through the covariance-based eigenanalysis of the weighted data matrix of inverse ranks. The spatial patterns of the first dominant trend mode are shown in Figure 3, while the TPCs time series are in Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 for PRP, RX5day, SDII, R20mm, and R30mm. Appendix A includes the results for the other indices (Figure A1, Figure A2, Figure A3, Figure A4, Figure A5 and Figure A6). For its correct interpretation, it should be considered that a positive slope in the TPC indicates a strengthening of the TEOF spatial pattern, and vice versa for a negative slope.
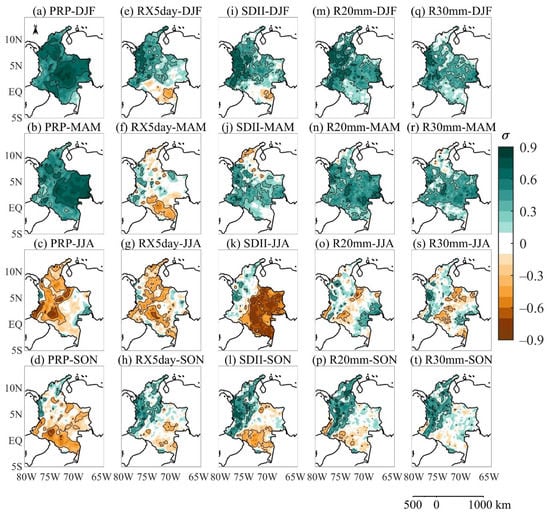
Figure 3.
(a–d) Spatial pattern of total seasonal rainfall (PRP), (e–h) Max 5-day precipitation amount (RX5day), (i–l) Simple daily intensity index (SDII), (m–p) Number of days with precipitations above R20mm (R20mm), and (q–t) Number of days with precipitations above R30mm (R30mm) for the first TEOF mode during December–February (DJF) (first row), March–May (MAM) (second row), June–August (JJA) (third row), and September–November (SON) (last row).
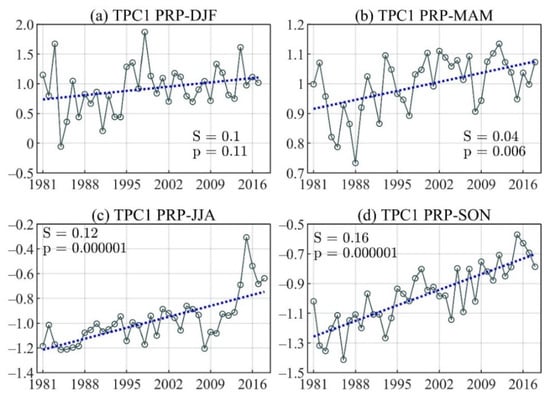
Figure 4.
The linear trend of the principal component time series for the first trend mode-EOF of total precipitation (PRP) during (a) December–February (DJF), (b) March–May (MAM), (c) June–August (JJA), and (d) September–November (SON).
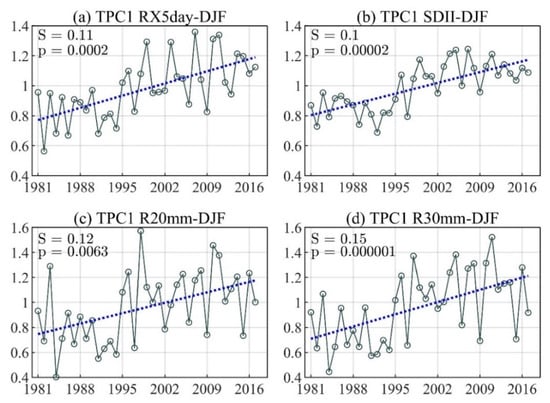
Figure 5.
The linear trend of the principal component time series for the first TEOF mode of (a) Max 5-day precipitation amount (RX5day), (b) Simple daily intensity index (SDII), (c) Number of days with precipitations above R20mm (R20mm), and (d) Number of days with precipitations above R30mm (R30mm) during December–February (DJF) season.
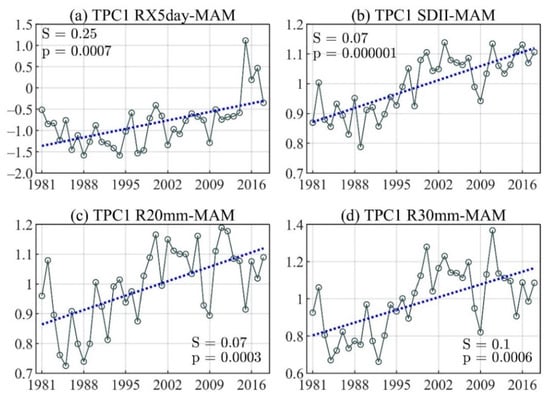
Figure 6.
The linear trend of the principal component time series for the first TEOF mode of (a) Max 5-day precipitation amount (RX5day), (b) Simple daily intensity index Number (SDII), (c) Number of days with precipitations above R20mm (R20mm), and (d) Number of days with precipitations above R30mm (R30mm) during the March–May (MAM) season.
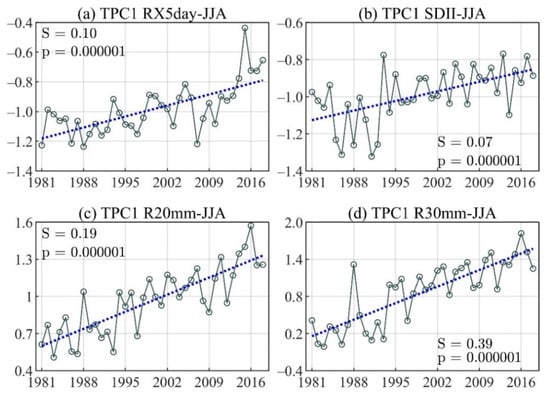
Figure 7.
The linear trend of the principal component time series for the first TEOF mode of (a) Max 5-day precipitation amount (RX5day), (b) Simple daily intensity index (SDII), (c) Number of days with precipitations above R20mm (R20mm), and (d) Number of days with precipitations above R30mm (R30mm) during the July–August (JJA) season.
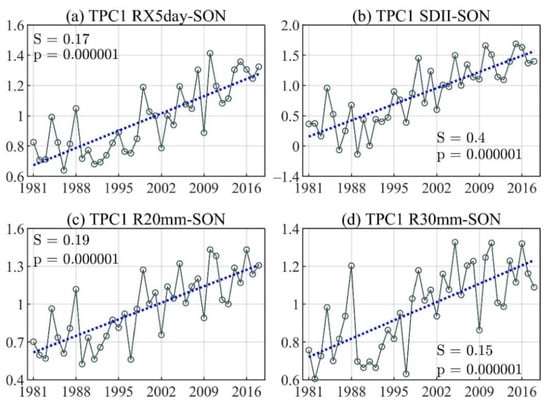
Figure 8.
The linear trend of the principal component time series for the first TEOF mode of (a) Max 5-day precipitation amount (RX5day), (b) Simple daily intensity index (SDII), (c) Number of days with precipitations above R20mm (R20mm), and (d) Number of days with precipitations above R30mm (R30mm) during the September–November (SON) season.
The TEOF spatial pattern (Figure 3a–d) and its associated TPC1 (Figure 4) for the seasonal total precipitation represent an increase in rainfall in the first half of the year throughout Colombia, especially towards the Orinoco and the Caribbean (Figure 3a,b), with an explained variance (hereafter EV) of 4.7% and 6.9% for DJF and MAM, respectively. JJA shows a decrease in precipitation in the Andes, South Pacific, Caribbean, and northern Amazon region and an increase in the north Pacific (Atrato basin) (Figure 3c), with an explained variance of 5.5%. Although there is an increase in the precipitation for SON in the northern Pacific and parts of the Caribbean, the other regions show a decrease (Figure 3d), with an explained variance of 4.1%. The corresponding TPC1 time series of the TEOF1 modes of total precipitation shows an increasing trend for all seasons (Figure 4). It is essential to highlight that the positive slope of TPC1 of JJA and SON mainly reflects an increase of drier areas in the western part during JJA, and in the south and east of Colombia for SON.
During DJF, the first trend mode of the RX5day (4.2% EV) and SDII (7.7% EV) show an increase in most of the Colombian territory, which coincides with the TEOF of total precipitation (Figure 3a), except for the Amazon region, where a decrease is observed (Figure 3e,i). At the same time, the first mode of the R20mm (16% EV) and R30mm (27% EV) frequency indices show an increase in most of the territory, with greater intensity in the north of the Pacific region (Figure 3m,q). The corresponding TPC1 time series shows an overall positive trend (Figure 5), i.e.an intensification of the intensity and frequency spatial pattern of extreme events, during DJF.
For the MAM season, an increase of the first RX5day mode is observed in the Pacific region, and a decrease in the Amazon region (Figure 3f), with an EV of 3.8%. On the other hand, the first SDII mode (EV 5.4%) indicates an increase in the Pacific, Andean, and Orinoco regions, while a decrease is observed in the Caribbean (Figure 3j). The R20mm (EV 9.2%) and R30mm (EV 13.3%) indices show an increase over most of the territory, except for some regions of the Caribbean and the Amazon (Figure 3n,r), consistent with the TEOF of total MAM precipitation (Figure 3b). In general, the significant positive trend observed in MAM TPC1 (Figure 6) indicates a strengthening of the MAM TEOF1 pattern, with the main feature being the increase in the intensity and frequency of extreme rainfall in the Pacific, Andes, and Orinoco regions, and an increase in dry areas of Amazon region (RX5day).
During JJA, the first trend mode of RX5day presents an EV of 4.0% and is consistent with the decrease of total precipitation over the Andes, South Pacific, and Caribbean (Figure 3c,g). Moreover, a more extended RX5day decrease is observed over the Amazon and an increase over the northern Pacific (Figure 3g). On the other hand, the SDII (EV 5.7%) shows a decrease in the Amazon and Orinoco regions, and an increase in the northern Pacific (Figure 3k). The R20mm and R30mm frequency indices indicate a decrease in the eastern Andean region, the Amazonian foothills, and the Orinoco. In contrast, an increase is observed in the northern Pacific, some areas of the Caribbean, and the eastern Amazon (Figure 3o,s). The positive slope of the TPC1 time series for JJA (Figure 7) indicates that the TEOF1 patterns for JJA tend to strengthen, which is reflected in an increase of dry areas, mainly in the Orinoco, Amazon, eastern flank of the Andes, and the South Pacific, and an increase of the wet areas in the North Pacific, specifically.
The first SON trend mode indicates an increase in the intensity and frequency of extreme rainfall events in the North Pacific, Andes, and Caribbean regions, and a decrease along the Amazon, mainly for SDII, with an EV of 3.7% for RX5day, 6.2% for SDII, 5.7% for R20mm, and 10% for R30mm (Figure 3h,l,p,t). These results are consistent with the general pattern of the first TEOF of total precipitation for SON (Figure 3d). The positive trend of the TPC1 SON time-series (Figure 8) indicates a strengthening of the areas with positive intense and frequent rainfall events in the Andes, North Pacific, and the Caribbean during SON, and negative events in the Amazon and South Pacific.
Note that the main trend mode of RX1day, shown in Figure A1a–d of Appendix A, is consistent with the trend EOF pattern of RX5day previously reported (Figure 3e–h), coinciding mainly with the increases observed in the Pacific, Andes, and Orinoco regions for DJF, decreases in the Amazon during MAM, and in the Andes during JJA, and increases in the Pacific during SON. The positive trend of the RX1day TPC1 time series during DJF, MAM, and JJA (Figure A2a–c) indicate a strengthening of the observed spatial pattern (Figure A1a–c), whereas the negative trend of RX1day TPC1 during SON (Figure A2d) indicates a weakening of the spatial pattern, observed in Figure A1d.
4. Discussion and Conclusions
The trend of the PRP in Colombia varies between different regions and seasons; however, it generally depicts an upward trend, consistent with previous national studies that showed mixed precipitation trends (positive and negative) over specific country areas, predominant the positive trend. In this way, in the Third Communication from Colombia to the United Nations Framework Convention on Climate Change of 2017 [36], positive (negative) precipitation trends are shown in 61% (31%) of the analyzed stations. On the other hand, the technical study of the evidence of climate change by the Institute of Hydrology, Meteorology, and Environmental Studies (IDEAM) [35] delimits the areas of the country with a tendency to increase precipitation (Caribbean region, Orinoco, middle valleys of the Magdalena and Cauca rivers) and the areas with a tendency to decrease precipitation (insular zone, northeast of the country and the eastern slope of the Eastern Cordillera). Recently, Mesa et al. [31] studied hydroclimatic trends at the national level and found positive trends in the North Pacific and the middle valley of Cauca, and negative trends in the eastern slope of the Eastern Cordillera, during 1981–2013, using rainfall stations and CHIRPS dataset. However, only 21% of the rainfall station and 25% of grids from CHIRPS showed significant trends over the country.
Meanwhile, ambiguous precipitation trend patterns are shown in regional studies. Estupiñan and Carvajal [75] reported 50% of the stations with an upward trend, and the other 50% with a negative trend, in the Aburra river basin. Similar findings were reported by García et al. [76] in the Río Grande basin. The last of which were both assessed in the northwest of Colombia. On the other hand, Carmona and Poveda [32] reported no clear pattern over Colombia because the precipitation time series show increasing trends in 41%, and decreasing trends in 44%, of the rainfall stations. Finally, Cardona et al. [77] determined that the rainfall stations located at an altitude higher (lower) than 1500 m above sea level show a trend to decrease (increase) the precipitation in the Andean basins, located in southwestern Colombia.
In general, there is no statistical significance in most of the rainfall time series of the studies mentioned above. In these research studies, trend characterization methods, such as linear regression method of ordinary least squares, Mann–Kendall test, and Sen slope technique, were used for the analysis of rainfall time series. For instance, Puertas et al. [78] showed statistical significance in 22% of the stations used in the Upper Cauca river basin (Southwestern Colombia). Furthermore, Rojas et al. [79] found statistical significance in 23% of the stations used in Boyacá and Cundinamarca departments (center of the country), and Arrieta-Castro et al. [80] in the Meta River depicted the presence of statistically significant downward trends in the upstream stations and upward trends in the downstream stations, with the latter presenting steep positive slopes. According to the Third National Communication of Colombia to the United Nations Framework Convention on Climate Change of 2017, the number of stations in Colombia with significant trends does not exceed 20%, and mixed trends are shown in precipitation climate extremes [36]. For example, 55% (45%) of the stations show a positive (negative) trend for Rx5day; 50% of the stations have a positive trend for the SDII, and 56% (44%) of the stations have a positive (negative) trend for the R20mm. A first approximation of less ambiguous results was reported by Ávila et al. [19] in a regional study of the Alto Cauca basin (Andean region). This research identified seasonal trends as positive precipitation trends in 74% of the stations during DJF, and negative trends at 59%, for MAM and JJA, and 69% for SON.
Li and Ren [81] argue that linear trend patterns exhibit less spatially coherent structures than TEOF1 patterns because a trend using simple linear regression has at least two shortcomings: one is that it assumes that trends are linear and uniform over time; and another is that linear trends are quite sensitive to the time interval over which they are calculated and can also be easily affected by some strong high-frequency signals, particularly for a short time interval. In contrast, considering the self-analysis of the covariance matrix of inverse classification, TEOF analysis separates the coherent spatio-temporal trend patterns into a single dominant mode [39,64], reducing the possible interference from high-frequency signals.
In this regard, the methodology used in this research, the TEOF analysis [39], allowed identifying the trend patterns of extreme rainfall indices (Figure 3) and the corresponding TPC time series, in which the temporal trend magnitudes and their statistical significance in most indices were shown (Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8). The linear trend patterns of the extreme rainfall indices obtained from the Mann–Kendall test are illustrated in Figure 9 and Figure A7, for visual comparisons with those obtained from TEOF technique. For most indices, the trend patterns obtained from the Mann–Kendall test do not show spatially coherent structure due to the lack of statistical significance of the trend in most analyzed stations. In contrast, the TEOF analysis provides spatially coherent trend patterns throughout the study area for most indices, and their corresponding TPCs show significant trends. Therefore, in the sense that the climate trends have spatial coherency, the TEOF technique has a better performance than the Man–Kendall test.
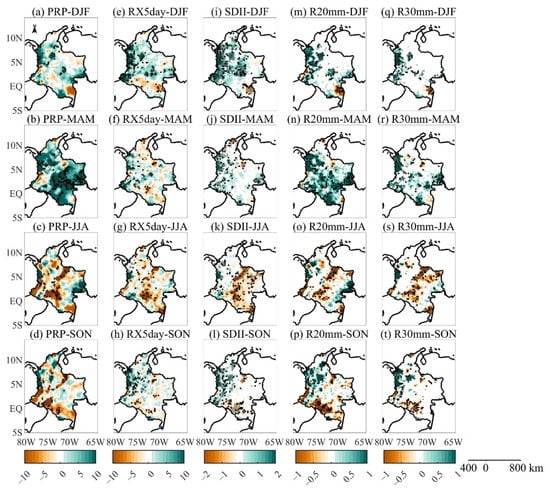
Figure 9.
Trends of seasonal time series of extreme precipitation indices during the 1981–2018 period: (a–d) rainfall (PRP), (e–h) Max 5-day precipitation amount (RX5day), (i–l) Simple daily intensity index (SDII), (m–p) Number of days with precipitations above R20mm (R20mm), and (q–t) Number of days with precipitations above R30mm (R30mm) used the time series of extreme climate indices during December–February (DJF) (first row), March–May (MAM) (second row), June–August (JJA) (third row), and September–November (SON) [(last row). Green and brown areas represent the positive and negative trends, respectively. Filled (empty) dots are significant trends at the 95% significance level.
Author Contributions
Conceptualization, W.L.C., R.V.A. and J.A.; methodology, W.L.C., R.V.A., M.T.K. and J.A.; software, W.L.C., R.V.A. and A.A.-D.; validation, W.L.C., R.V.A. and M.T.K.; formal analysis, W.L.C., R.V.A., M.T.K. and T.C.; investigation, W.L.C., R.V.A., M.T.K., T.C., C.O.-M. and J.A.; data curation, W.L.C. and A.A.-D.; writing—original draft preparation, W.L.C., R.V.A., M.T.K., T.C., C.O.-M. and A.A.-D.; writing—review and editing, W.L.C., R.V.A., M.T.K., T.C., C.O.-M., A.A.-D. and J.A.; visualization, W.L.C., T.C., C.O.-M. and A.A.-D.; supervision, W.L.C. and R.V.A. All authors have read and agreed to the published version of the manuscript.
Funding
The Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) of Brazil partially supported the second and third authors under grants 305611/2019-4 and 302322/2017-5, respectively. Seventh author was supported by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES) (Finance Code 001).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful to the Universidad del Valle, Fundación Universitaria de San Gil and Universidad de Ciencias Aplicadas y Ambientales—UDCA. The authors wish to thank the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) for the supported receiving during the research. We are thankful to the research groups TERRITORIOS of the Universidad del Valle. The authors thank the two anonymous reviewers for their helpful comments.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design, analysis, and interpretation of data, the writing manuscript, or the decision to publish the results.
Appendix A
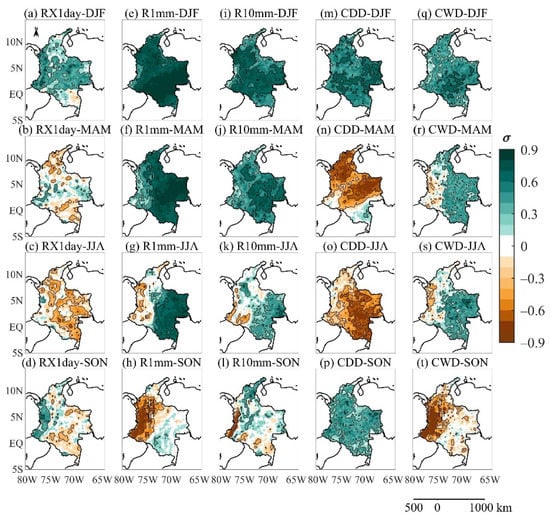
Figure A1.
(a–d) Spatial pattern of Max 1-day precipitation amount (RX1day), (e–h) Number of wet days (R1mm), (i–l) Number of days with precipitations above R10mm (R10mm), (m–p) Consecutive dry days (CDD), and (q–t) Consecutive wet days (CWD) for the first TEOF mode during December–February (DJF) (first row), March–May (MAM) (second row), June–August (JJA) (third row), and September–November (SON) (last row).
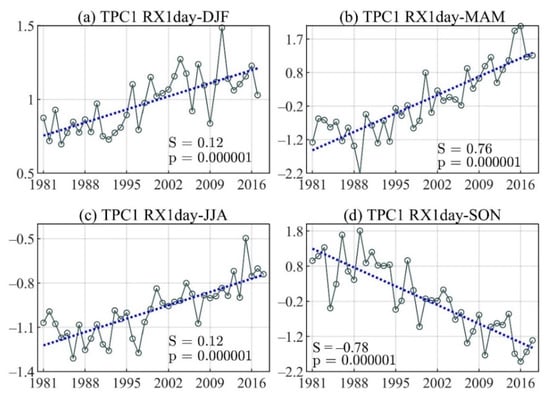
Figure A2.
The linear trend of the principal component time series for the first trend mode-EOF of Max 1-day precipitation amount (RX1day) during (a) December–February (DJF), (b) March–May (MAM), (c) June–August (JJA), and (d) September–November (SON).
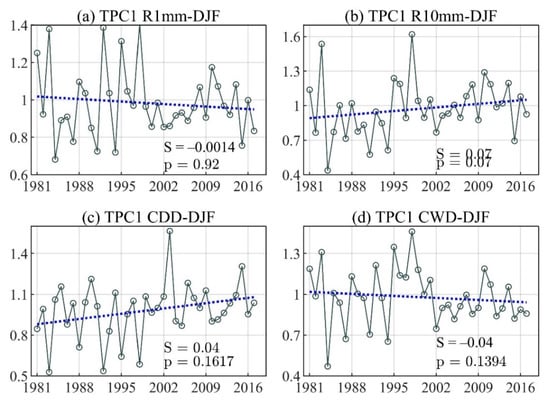
Figure A3.
The linear trend of the principal component time series for the first TEOF mode of (a) Number of wet days (R1mm), (b) Number of days with precipitations above R10mm (R10mm), (c) Consecutive dry days (CDD), and (d) Consecutive wet days (CWD) during the December–February (DJF) season.
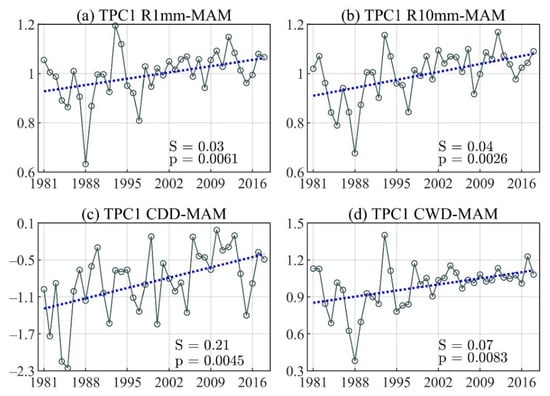
Figure A4.
The linear trend of the principal component time series for the first TEOF mode of (a) Number of wet days (R1mm), (b) Number of days with precipitations above R10mm (R10mm), (c) Consecutive dry days (CDD), and (d) Consecutive wet days (CWD) during the March–May (MAM) season.
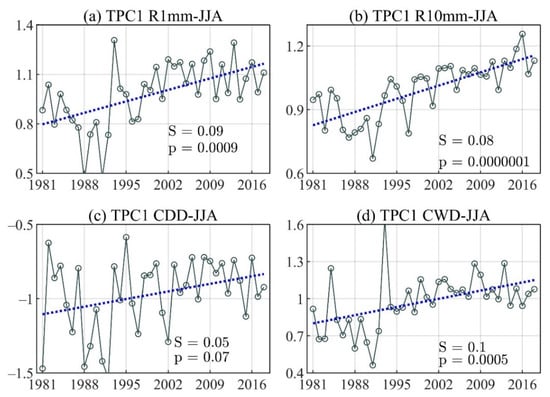
Figure A5.
The linear trend of the principal component time series for the first TEOF mode of (a) Number of wet days (R1mm), (b) Number of days with precipitations above R10mm (R10mm), (c) Consecutive dry days (CDD), and (d) Consecutive wet days (CWD) during the June–August (JJA) season.
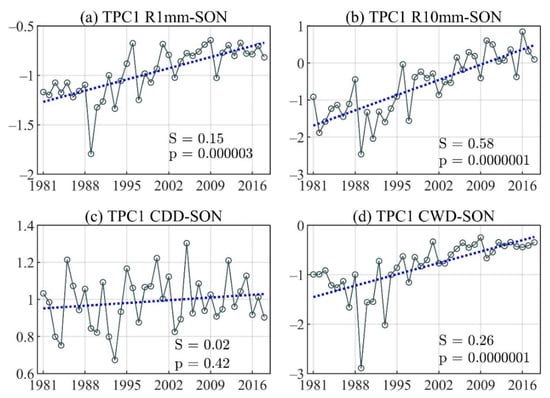
Figure A6.
The linear trend of the principal component time series for the first TEOF mode of (a) Number of wet days (R1mm), (b) Number of days with precipitations above R10mm (R10mm), (c) Consecutive dry days (CDD), and (d) Consecutive wet days (CWD) during the September–November (SON) season.
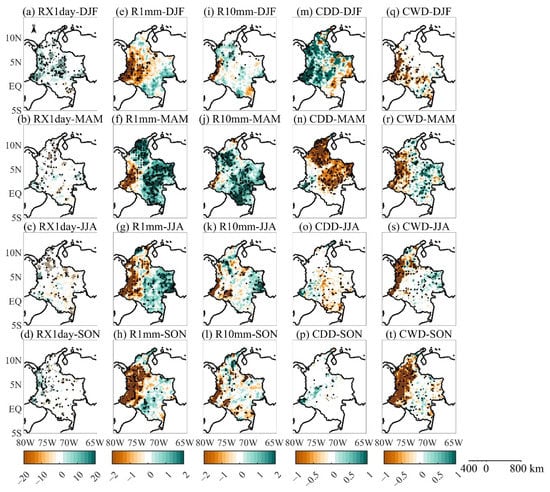
Figure A7.
Trends of seasonal time series of extreme precipitation indices during the 1981–2018 period: (a–d) Max 1-day precipitation amount (RX1day), (e–h) Number of wet days (R1mm), (i–l) Number of days with precipitations above R10mm (R10mm), (m–p) Consecutive dry days (CDD), and (q–t) Consecutive wet days (CWD) used the time series of extreme climate indices during December–February (DJF) (first row), March–May (MAM) (second row), June–August (JJA) (third row), and September–November (SON) (last row). Green and brown areas represent the positive and negative trends, respectively. Filled (empty) dots are significant trends at the 95% significance level.
References
- Seneviratne, S.I.; Zhang, X.; Adnan, M.; Badi, W.; Dereczynski, C.; Di Luca, A.; Ghosh, S.; Iskandar, I.; Kossin, J.; Lewis, S.; et al. Chapter 11: Weather and climate extreme events in a changing climate. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V.P., Zhai, A., Pirani, S.L., Connors, C., Péan, S., Berger, N., Caud, Y., Chen, L., Goldfarb, M.I., Gomis, M., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021; p. 345, in press. [Google Scholar]
- Meehl, G.A.; Zwiers, F.; Evans, J.; Knutson, T.; Mearns, L.; Whetton, P. Trends in extreme weather and climate events: Issues related to modeling extremes in projections of future climate change. Bull. Am. Meteorol. Soc. 2000, 81, 427–436. [Google Scholar] [CrossRef]
- Schneider, S.H. Abrupt Non-Linear Climate Change, Irreversibility and Surprise: OECD Workshop on the Benefits of Climate Policy: Improving Information for Policy Makers; OECD: Paris, France, 2003. [Google Scholar]
- Retana, J. Eventos hidrometeorológicos extremos lluviosos en Costa Rica desde la perspectiva de la adaptación al cambio en el clima. Rev. Ciencias Ambient. 2012, 44, 5. [Google Scholar] [CrossRef][Green Version]
- Marelle, L.; Myhre, G.; Hodnebrog, Ø.; Sillmann, J.; Samset, B.H. The Changing Seasonality of Extreme Daily Precipitation. Geophys. Res. Lett. 2018, 45, 352. [Google Scholar] [CrossRef]
- World Economic Forum. The Global Risks Report 2021, 16th ed.; World Economic Forum: Geneva, Switzerland, 2021; ISBN 9782940631247. [Google Scholar]
- AghaKouchak, A.; Chiang, F.; Huning, L.S.; Love, C.A.; Mallakpour, I.; Mazdiyasni, O.; Moftakhari, H.; Papalexiou, S.M.; Ragno, E.; Sadegh, M. Climate Extremes and Compound Hazards in a Warming World. Annu. Rev. Earth Planet. Sci. 2020, 48, 519–548. [Google Scholar] [CrossRef]
- Tabari, H. Climate change impact on flood and extreme precipitation increases with water availability. Sci. Rep. 2020, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Balmaceda-Huarte, R.; Olmo, M.E.; Bettolli, M.L.; Poggi, M.M. Evaluation of multiple reanalyses in reproducing the spatio-temporal variability of temperature and precipitation indices over southern South America. Int. J. Climatol. 2021, joc.7142. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; García-Herrera, R.; Peña-Angulo, D.; Tomas-Burguera, M.; Domínguez-Castro, F.; Noguera, I.; Calvo, N.; Murphy, C.; Nieto, R.; Gimeno, L.; et al. Do CMIP models capture long-term observed annual precipitation trends? Clim. Dyn. 2021, 1–18. [Google Scholar] [CrossRef]
- Donat, M.; Alexander, L.V.; Herold, N.; Dittus, A.J. Temperature and precipitation extremes in century-long gridded observations, reanalyses, and atmospheric model simulations. J. Geophys. Res. Atmos. 2016, 121, 11–174. [Google Scholar] [CrossRef]
- Wahlstrom, M.; Guha-Sapir, D. The Human Cost of Weather Related Disasters—1995–2015. 2016. Available online: https://www.unisdr.org/files/46796_cop21weatherdisastersreport2015.pdf (accessed on 13 January 2022).
- Chadwick, R.; Good, P.; Martin, G.; Rowell, D.P. Large rainfall changes consistently projected over substantial areas of tropical land. Nat. Clim. Chang. 2016, 6, 177–181. [Google Scholar] [CrossRef]
- Soares, D.; Lee, H.; Loikith, P.; Barkhordarian, A.; Mechoso, C. Can significant trends be detected in surface air temperature and precipitation over South America in recent decades? Int. J. Climatol. 2017, 37, 1483–1493. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.; Zwiers, F.; Westra, S.; Alexander, L.V. A global, continental, and regional analysis of changes in extreme precipitation. J. Clim. 2021, 34, 243–258. [Google Scholar] [CrossRef]
- Skansi, M.; Brunet, M.; Sigró, J.; Aguilar, E.; Arevalo, G.; Bentancur, O.; Castellón, G.; Correa, A.; Jácome, H.; Malheiros, R.; et al. Warming and wetting signals emerging from analysis of changes in climate extreme indices over South America. Glob. Planet. Change 2013, 100, 295–307. [Google Scholar] [CrossRef]
- Aguilar, E.; Peterson, T.; Obando, P.R.; Frutos, R.; Retana, J.A.; Solera, M.; Soley, J.; García, I.G.; Araujo, R.M.; Santos, A.R.; et al. Changes in precipitation and temperature extremes in Central America and northern South America, 1961-2003. J. Geophys. Res. Atmos. 2005, 110, 1–15. [Google Scholar] [CrossRef]
- Ávila, A.; Justino, F.; Wilson, A.; Bromwich, D.; Amorim, M. Recent precipitation trends, flash floods and landslides in southern Brazil. Environ. Res. Lett. 2016, 11, 114029. [Google Scholar] [CrossRef]
- Ávila, Á.; Guerrero, F.C.; Escobar, Y.C.; Justino, F. Recent precipitation trends and floods in the Colombian Andes. Water 2019, 11, 379. [Google Scholar] [CrossRef]
- Avila-Diaz, A.; Justino, F.; Lindemann, D.S.; Rodrigues, J.M.; Ferreira, G.R. Climatological aspects and changes in temperature and precipitation extremes in viçosa-Minas Gerais. An. Acad. Bras. Cienc. 2020, 92, 1–19. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Ronchail, J.; Marengo, J.A.; Segura, H. Contrasting North–South changes in Amazon wet-day and dry-day frequency and related atmospheric features (1981–2017). Clim. Dyn. 2019, 52, 5413–5430. [Google Scholar] [CrossRef]
- Cerón, W.L.; Kayano, M.T.; Andreoli, R.V.; Avila-Diaz, A.; Ayes, I.; Freitas, E.D.; Martins, J.A.; Souza, R.A.F. Recent intensification of extreme precipitation events in the La Plata Basin in Southern South America (1981–2018). Atmos. Res. 2021, 249, 105299. [Google Scholar] [CrossRef]
- Campos, G.A.; Nielsen, H.N.; Díaz, G.C.; Ubiano, V.D.M.; Costa, P.C.R.; Ramírez, C.F.; Dickson, E. Análisis de la Gestión del Riesgo de Desastres en Colombia. Un Aporte para la Construcción de Políticas Públicas; Mundial, B., Ed.; Banco Mundial: Bogotá, Columbia, 2012. [Google Scholar]
- Sedano-Cruz, K.; Carvajal-Escobar, Y.; Ávila, Á. Análisis de aspectos que incrementan el riesgo de inundaciones en Colombia. Rev. Luna Azul 2013, 37, 219–238. [Google Scholar]
- Loaiza, W.; Carvajal-Escobar, Y.; Baquero, O.L. Sequías & Adaptación: Principios Para su Evaluación en Sistemas Productivos Agrícolas del Valle del Cauca, Colombia; Universidad del Valle: Cali, Columbia, 2014. [Google Scholar]
- Sanchez, O.; Aristizábal, E. Spatial and temporal paterns and socieconomic impact of landslides in Colombia. Poster Eur. Geosci. Meet 2018, 20, 3575. [Google Scholar]
- Aristizábal, E.; García, E.F.; Marín, R.J.; Gómez, F.; Guzmán-Martínez, J. Rainfall-intensity effect on landslide hazard assessment due to climate change in north-western Colombian Andes. Rev. Fac. Ing. Univ. Antioquia 2022, 51–66. [Google Scholar] [CrossRef]
- Poveda, G.; Álvarez, D.M.; Rueda, Ó.A. Hydro-climatic variability over the Andes of Colombia associated with ENSO: A review of climatic processes and their impact on one of the Earth’s most important biodiversity hotspots. Clim. Dyn. 2011, 36, 2233–2249. [Google Scholar] [CrossRef]
- Arias, P.A.; Martínez, J.A.; Vieira, S.C. Moisture sources to the 2010–2012 anomalous wet season in northern South America. Clim. Dyn. 2015, 45, 2861–2884. [Google Scholar] [CrossRef]
- Serna, L.M.; Arias, P.A.; Vieira, S.C. Las corrientes superficiales de chorro del Chocó y el Caribe durante los eventos de El Niño y El Niño Modoki. Rev. Acad. Colomb. Cienc. Exactas Físicas Nat. 2018, 42, 410. [Google Scholar] [CrossRef]
- Mesa, O.; Urrea, V.; Ochoa, A. Trends of hydroclimatic intensity in Colombia. Climate 2021, 9, 120. [Google Scholar] [CrossRef]
- Carmona, A.M.; Poveda, G. Detection of long-term trends in monthly hydro-climatic series of Colombia through Empirical Mode Decomposition. Clim. Chang. 2014, 123, 301–313. [Google Scholar] [CrossRef]
- Cantor, D.C. Evaluación y Análisis Espacio Temporal de Tendencias de Largo Plazo en la Hidroclimatología Colombiana. Master’s Thesis, Universidad Nacional de Colombia, Medellín, Colombia, 2011. [Google Scholar]
- Pabón-Caicedo, J.D. Cambio Climático en Colombia: Tendencias en la segunda mitad del siglo XX Y escenarios posibles para el siglo XXI. Rev. Acad. Colomb. Cienc. Exactas Físicas Nat. 2012, 36, 261–278. [Google Scholar]
- Mayorga, R.; Hurtado, G.M.; Benavides, H. Evidencias de Cambio Climático en Colombia Con Base en Información Estadística. 2011. Available online: http://www.ideam.gov.co/documents/21021/21138/Evidencias+de+Cambio+Clim%C3%A1tico+en+Colombia+con+base+en+informaci%C3%B3n+estad%C3%ADstica.pdf/1170efb4-65f7-4a12-8903-b3614351423f (accessed on 13 January 2022).
- IDEAM PNUD MADS DNP CANCILLERÍA Tercera Comunicación Nacional de Colombia, Resumen Ejecutivo a la Convención Marco de las Naciones Unidas Sobre Cambio Climático; Bogotá (Colombia). 2017. Available online: http://documentacion.ideam.gov.co/openbiblio/bvirtual/023732/RESUMEN_EJECUTIVO_TCNCC_COLOMBIA.pdf (accessed on 13 January 2022).
- Morales-Acuña, E.; Linero-Cueto, J.R.; Canales, F.A. Assessment of precipitation variability and trends based on satellite estimations for a heterogeneous Colombian region. Hydrology 2021, 8, 128. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Merlano-Sabalza, E.; Díaz-Vergara, Z.; Coronado-Hernández, J.R. Selection of hydrological probability distributions for extreme rainfall events in the regions of Colombia. Water 2020, 12, 1397. [Google Scholar] [CrossRef]
- Hannachi, A. Pattern hunting in climate: A new method for finding trends in gridded climate data. Int. J. Climatol. 2007, 27, 1–15. [Google Scholar] [CrossRef]
- IGAC Instituto Geográfico Agustín Codazzi Regiones Naturales. Available online: http://www2.igac.gov.co/ninos/UserFiles/Image/Mapas/regiones%20naturales.pdf (accessed on 13 January 2022).
- Urrea, V.; Ochoa, A.; Mesa, O. Seasonality of Rainfall in Colombia. Water Resour. Res. 2019, 55, 4149–4162. [Google Scholar] [CrossRef]
- Cerón, W.L.; Andreoli, R.V.; Kayano, M.T.; Avila-Diaz, A. Role of the eastern Pacific-Caribbean Sea SST gradient in the Choco low-level jet variations from 1900–2015. Clim. Res. 2021, 83, 61–74. [Google Scholar] [CrossRef]
- Yepes, J.; Poveda, G.; Mejía, J.F.; Moreno, L.; Rueda, C. Choco-jex: A research experiment focused on the Chocó low-level jet over the far eastern Pacific and western Colombia. Bull. Am. Meteorol. Soc. 2019, 100, 779–796. [Google Scholar] [CrossRef]
- Estupiñan, A.R.C. Estudio de la Variabilidad Espacio Temporal de la Precipitación en Colombia. Doctoral Dissertation, Universidad Nacional de Colombia. 2016. Available online: http://bdigital.unal.edu.co/54014/1/1110490004.2016.pdf (accessed on 5 October 2019).
- Mejía, J.; Mesa, O.J.; Poveda, G.; Vélez, J.I.; Hoyos, C.; Ricardo, M.; Barco, J.; Cuartas, A.; Montoya, M.; Botero, B. Distribución espacial y ciclos anual y semianual de la precipitación en Colombia. Dyna 1999, 127, 7–26. [Google Scholar]
- Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) CHIRPS Data. Available online: https://www.chc.ucsb.edu/data/chirps/ (accessed on 6 June 2020).
- Funk, C.; Verdin, A.; Michaelsen, J.; Peterson, P.; Pedreros, D. A global satellite assisted precipitation climatology. Earth Syst. Dyn. Discuss. 2015, 8, 401–425. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Urrea, V.; Ochoa, A.; Mesa, O. Validación de la base de datos de precipitación CHIRPS para Colombia a escala diaria, mensual y anual en el período 1981–2014 Conference. In Proceedings of the XXVII Congreso Latinoamericano de Hidráulica, San Isidro, Peru, 26–30 September 2016; pp. 1–12. [Google Scholar]
- Cerón, W.L.; Kayano, M.T.; Andreoli, R.V.; Canchala, T.; Carvajal-Escobar, Y.; Alfonso-Morales, W. Rainfall variability in Southwestern Colombia: Changes in ENSO—Related features. Pure Appl. Geophys. 2021, 178, 1–17. [Google Scholar] [CrossRef]
- Fernandes, K.; Muñoz, A.G.; Ramirez-Villegas, J.; Agudelo, D.; Llanos-Herrera, L.; Esquivel, A.; Rodriguez-Espinoza, J.; Prager, S.D. Improving seasonal precipitation forecasts for agriculture in the orinoquía Region of Colombia. Weather Forecast. 2020, 35, 437–449. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, F.; Canada, E. RClimDex (1.0) User Manual; Climate Research Branch, Environment Canada: Downsview, ON, Canada, 2004; pp. 1–23. [Google Scholar]
- Poveda, G.; Vélez, J.I.; Mesa, O.; Hoyos, C.; Mejía, J.; Barco, O.J.; Correa, P.L. Influencia de fenómenos macroclimáticos sobre el ciclo anual de la hidrología Colombiana: Cuantificación lineal, no lineal y percentiles probabilísticos. Meteorol. Colomb. 2002, 121–130. [Google Scholar]
- Poveda, G.; Waylen, P.R.; Pulwarty, R.S. Annual and inter-annual variability of the present climate in northern South America and southern Mesoamerica. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2006, 234, 3–27. [Google Scholar] [CrossRef]
- Poveda, G. La hidroclimatología de Colombia: Una síntesis desde la escala inter-decadal hasta la escala diurna. Rev. Académica Colomb. Ciencias Tierra 2004, 28, 201–222. Available online: https://www.researchgate.net/publication/284691636_La_hidroclimatologia_de_Colombia_Una_sintesis_desde_la_escala_inter-decadal_hasta_la_escala_diurna (accessed on 13 January 2022).
- Guzmán, D.; Ruíz, J.F.; Cadena, M. Regionalización de Colombia según la Estacionalidad de la Precipitación Media Mensual, a Través Análisis de Componentes Principales (ACP); IDEAM: Bogotá, Colombia, 2014. [Google Scholar]
- Cerón, W.L.; Andreoli, R.V.; Kayano, M.T.; de Ferreria, S.R.; Canchala, N.T.; Carvajal-Escobar, Y. Comparison of spatial interpolation methods for annual and seasonal rainfall in two hotspots of biodiversity in South America. An. Acad. Bras. Ciencias 2021, 93, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Valverde, M.C.; Marengo, J.A. Extreme Rainfall Indices in the Hydrographic Basins of Brazil. Open J. Mod. Hydrol. 2014, 04, 10–26. [Google Scholar] [CrossRef]
- Cerón, W.L.; Kayano, M.T.; Andreoli, R.V.; Avila, A.; Canchala, T.; Francés, F.; Ayes Rivera, I.; Alfonso-Morales, W.; Ferreira de Souza, R.A.; Carvajal-Escobar, Y. Streamflow Intensification Driven by the Atlantic Multidecadal Oscillation (AMO) in the Atrato River Basin, Northwestern Colombia. Water 2020, 12, 216. [Google Scholar] [CrossRef]
- Espírito Santo, F.; Ramos, A.M.; de Lima, M.I.P.; Trigo, R.M. Seasonal changes in daily precipitation extremes in mainland Portugal from 1941 to 2007. Reg. Environ. Chang. 2014, 14, 1765–1788. [Google Scholar] [CrossRef]
- Wang, R.; Li, C. Spatiotemporal analysis of precipitation trends during 1961–2010 in Hubei province, central China. Theor. Appl. Climatol. 2016, 124, 385–399. [Google Scholar] [CrossRef]
- Donat, M.G.; Angélil, O.; Ukkola, A.M. Intensification of precipitation extremes in the world’s humid and water-limited regions. Environ. Res. Lett. 2019, 14, 065003. [Google Scholar] [CrossRef]
- Naciones Unidas CEPAL. Efectos del Cambio Climático en la Costa de América Latina y el Caribe Efectos del Cambio Climático en la costa de América Latina y el Caribe: Dinámicas, Tendencias y Variabilidad Climática; CEPAL: Santander, España, 2011; Volume 447. [Google Scholar]
- Barbosa, S.M.; Andersen, O.B. Trend patterns in global sea surface temperature. Int. J. Climatol. 2009, 29, 2049–2055. [Google Scholar] [CrossRef]
- Latif, M.; Syed, F.S.; Hannachi, A. Rainfall trends in the South Asian summer monsoon and its related large-scale dynamics with focus over Pakistan. Clim. Dyn. 2017, 48, 3565–3581. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Griffin: London, UK, 1975; ISBN 0852641990. [Google Scholar]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, 3; confidence regions for the parameters of polynomial regression equations. Indag. Math. 1950, 1, 467–482. [Google Scholar]
- Theil, H. A Rank-Invariant Method of Linear and Polynomial Regression Analysis. In Advanced Studies in Theoretical and Applied Econometrics; Raj, B., Koerts, J., Eds.; Henri Theil’s Contributions to Economics and Econometrics; Springer: Dordrecht, The Netherlands, 1992; Volume 23. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Jonah, K.; Wen, W.; Shahid, S.; Ali, M.A.; Bilal, M.; Habtemicheal, B.A.; Iyakaremye, V.; Qiu, Z.; Almazroui, M.; Wang, Y.; et al. Spatiotemporal variability of rainfall trends and influencing factors in Rwanda. J. Atmos. Sol.-Terr. Phys. 2021, 219, 105631. [Google Scholar] [CrossRef]
- Endo, N.; Ailikun, B.; Yasunari, T. Trends in precipitation amounts and the number of rainy days and heavy rainfall events during summer in China from 1961 to 2000. J. Meteorol. Soc. Japan 2005, 83, 621–631. [Google Scholar] [CrossRef]
- Rajeevan, M.; Bhate, J.; Jaswal, A.K. Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar]
- Doyle, M.E.; Saurral, I.; Barros, V.R. Trends in the distributions of aggregated monthly precipitation over the La Plata Basin. Int. J. Climatol. 2012, 32, 2149–2162. [Google Scholar] [CrossRef]
- Estupiñan, A.; Carvajal-Serna, L.F. Evaluación de las tendencias de largo plazo en la cuenca del río Aburra (Medellin-Colombia) durante el período 1981–2017. In Proceedings of the XXVIII Congr. Latinoamericano Hidráulica, Buenos Aires, Argentina, 18–21 September 2018. [Google Scholar]
- García Múnera, V.; Arias Gómez, P.; Vieria Agudelo, S. Análisis de tendencias en series de precipitación y tempertura de la Cuenca del Río Grande—Antioquía. In Proceedings of the XXII Seminario Nacional de Hidraúlica e Hidrología. Sociedad Colombiana de Ingenieros, Bogotá, Colombia, 24–26 August 2016; p. 13. [Google Scholar]
- Cardona, F.; Ávila, Á.J.; Carvajal-Escobar, Y.; Jiménez, H. Tendencias en las series de precipitación en dos cuencas torrenciales andinas del Valle del Cauca (Colombia). Tecno Lógicas 2014, 17, 85–95. [Google Scholar] [CrossRef]
- Puertas, O.O.; Carvajal-Escobar, Y.; Quintero, A.M. Estudio de tendencias de la precipitación mensual en la cuenca alta-media del río Cauca, Colombia. DYNA 2011, 78, 112–120. [Google Scholar]
- Rojas, E.; Arce, B.; Peña, A.; Boshell, F.; Ayarza, M. Cuantificación e interpolación de tendencias locales de temperatura y precipitación en zonas alto andinas de Cundinamarca y Boyacá (Colombia). Corpoica Cienc. Tecnol. Agropecu. 2010, 11, 173. [Google Scholar] [CrossRef]
- Arrieta-Castro, M.; Donado-Rodríguez, A.; Acuña, G.J.; Canales, F.A.; Teegavarapu, R.S.V.; Kaźmierczak, B. Analysis of streamflow variability and trends in the meta river, Colombia. Water 2020, 12, 1451. [Google Scholar] [CrossRef]
- Li, G.; Ren, B. Evidence for strengthening of the tropical Pacific Ocean surface wind speed during 1979-2001. Theor. Appl. Climatol. 2012, 107, 59–72. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).