Analogue Ensemble Averaging Method for Bias Correction of 2-m Temperature of the Medium-Range Forecasts in China
Abstract
1. Introduction
2. Forecast and Observation Data
3. Methods and Verification Scores
3.1. Analogue Ensemble Averaging Method
3.2. Verification Scores
4. Results
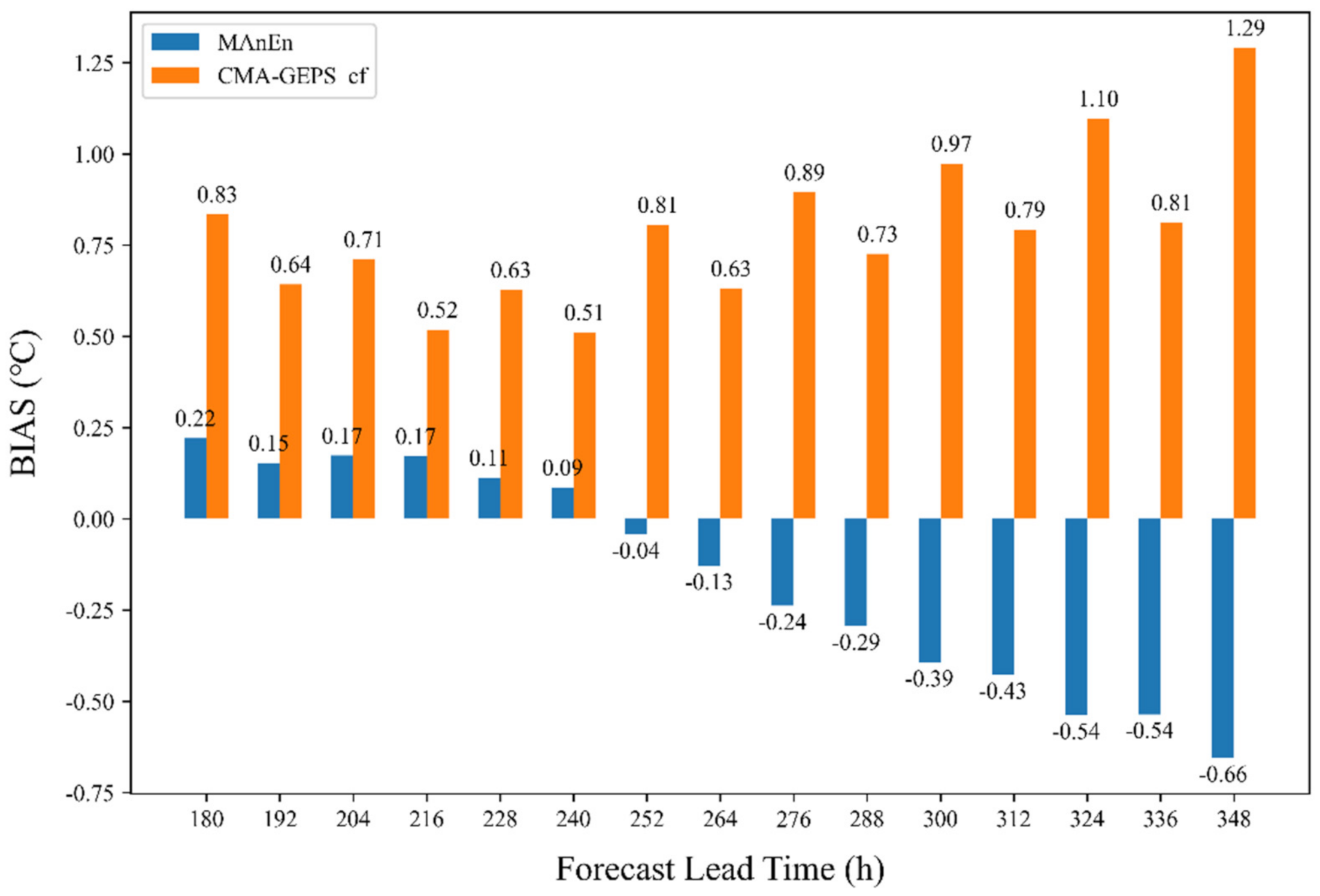
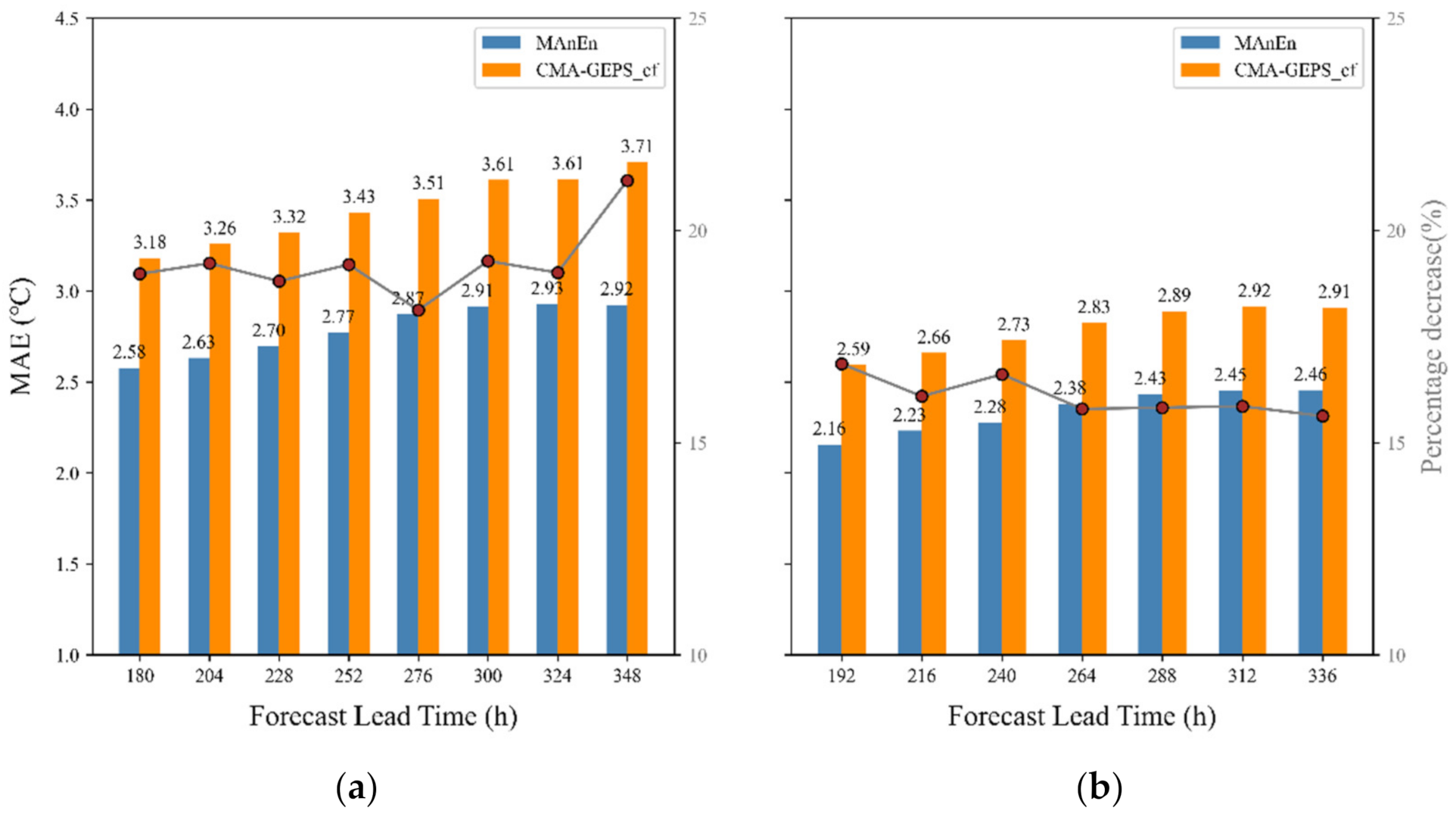
4.1. Comparisons of Different Forecast Lead Time Results between Analogue Ensemble Averaging Forecast and Numerical Weather Prediction Methods
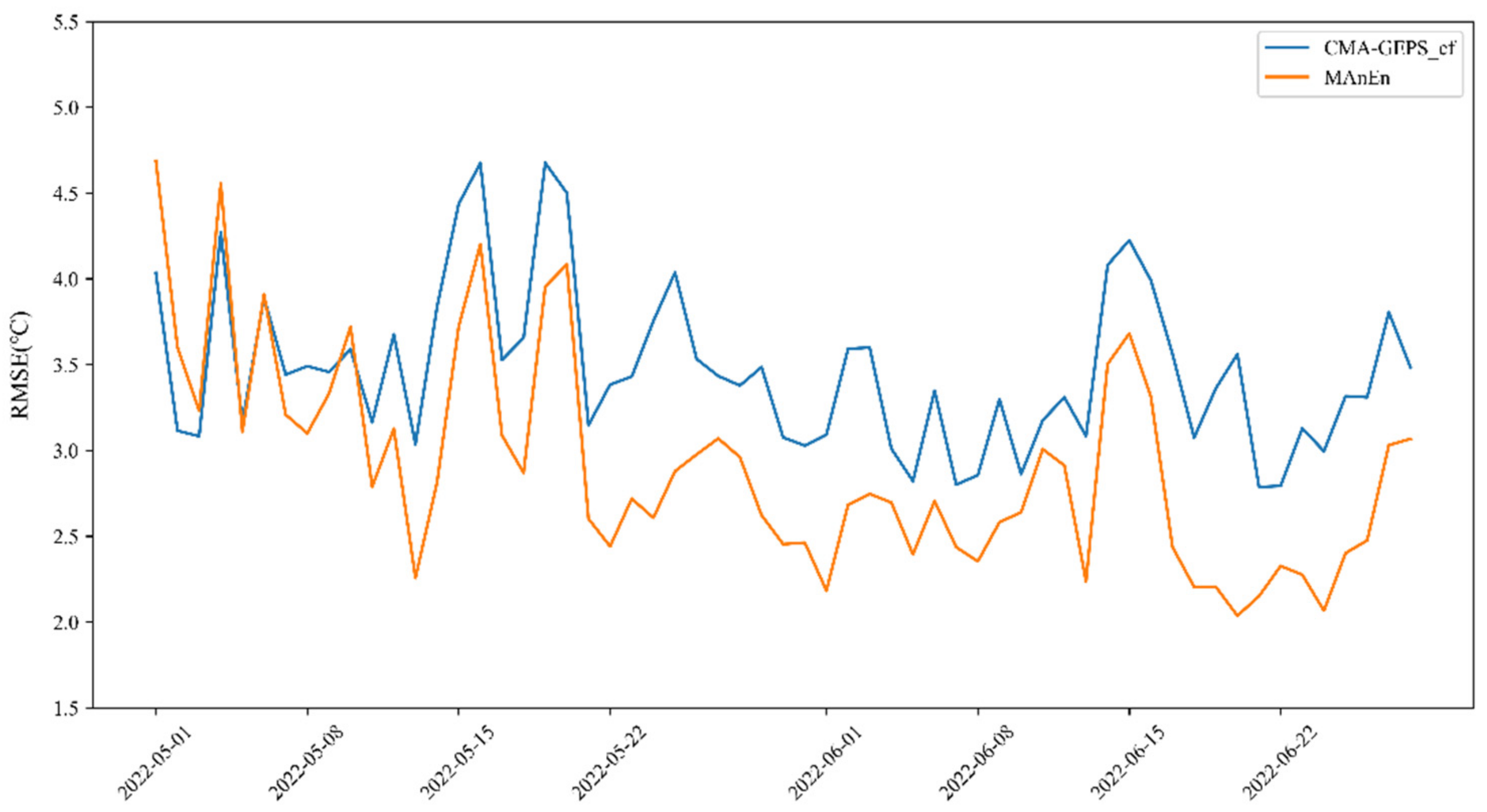
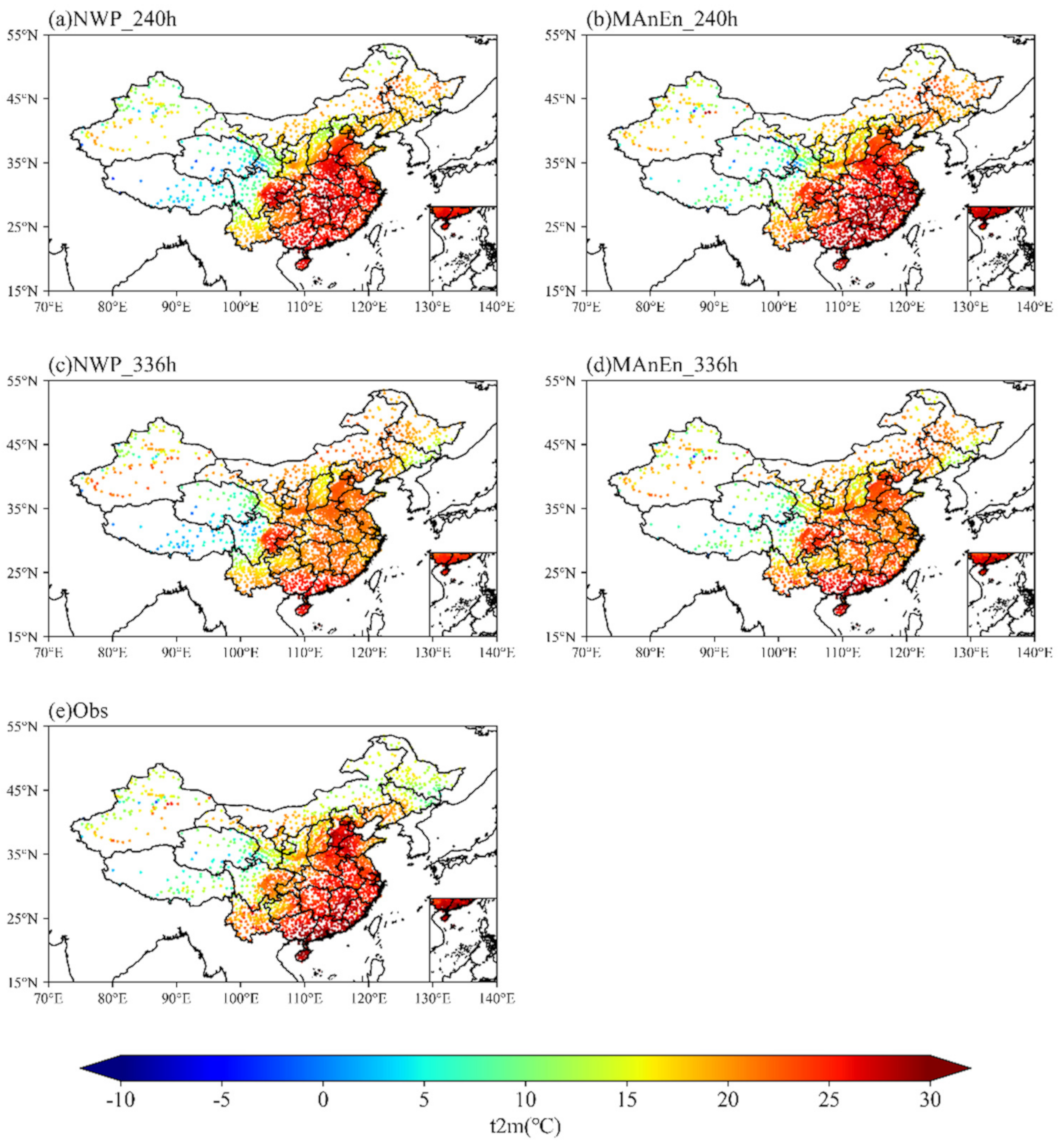
4.2. Tests of Forecast Ability at the Stations
4.3. Forecast Case
5. Conclusions and Discussion
- (1)
- The analogue ensemble averaging method has a good correction effect on the long forecast time of 180–348 h and effectively reduces the systematic error of the model forecasts of the 2-m temperature, which is higher at night and lower during the day. The forecast deviation is reduced by approximately 0.5 °C, and the MAE and RMSE are reduced by approximately 10–20%. During the test period from 1 May to 28 June 2022, the RMSE reduction rate of 240 h forecast reached 91% (the proportion of samples with reduced RMSE to all samples). Comparing the correction effect of different forecast lead times, the analogue ensemble averaging forecast method still has a better correction effect in longer forecast lead times.
- (2)
- After comparisons based on the spatial prediction results from 2405 stations, it is shown that the application of the analogue ensemble averaging forecast method effectively reduces the RMSEs of forecasts in Southwest China, Northwest China, and North China. The improvement rate of different forecast times reaches 31.4%. This method has a more obvious effect on the correction of complex terrain areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knag, Z.M.; Bao, Y.Y.; Zhou, N.F. Current Situation and Development of Medium-Range and Extended-Range Weather Forecast in China. Adv. Meteor. Sci. Technol. 2013, 3, 18–24. [Google Scholar]
- Zhang, J.J.; Ge, L. Basis of Medium-and Long-Term Weather Forecast, 1st ed.; China Meteorological Press: Beijing, China, 1983.
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.H.; Xue, J.S. An overview on recent progresses of the operational numerical weather prediction models. Acta Meteor. Sin. 2004, 62, 623–633. [Google Scholar]
- Dai, K.; Cao, Y.; Qian, Q.F.; Gao, S.; Zhao, S.G.; Chen, Y.; Qian, C.H. Situation and Tendency of Operational Technologies in Short-and Medium-Range Weather Forecast. Meteor. Mon 2016, 42, 1445–1455. [Google Scholar]
- Li, Z.C.; Bi, B.G.; Jin, R.H.; Xu, Z.F.; Xue, F. The development and application of the modern weather forecast in China for the recent 10 years. Acta Meteor. Sin. 2014, 72, 1069–1078. [Google Scholar]
- Shen, X.S.; Wang, J.J.; Li, Z.C.; Chen, D.H.; Gong, J.D. China’s independent and innovative development of numerical weather prediction. Acta Meteor. Sin. 2020, 78, 451–476. [Google Scholar]
- Sun, C.; Liang, X. Understanding and Reducing Warm and Dry Summer Biases in the Central United States: Analytical Modeling to Identify the Mechanisms for CMIP Ensemble Error Spread. J. Clim. 2022, 1–42. [Google Scholar] [CrossRef]
- Sun, C.; Liang, X. Understanding and Reducing Warm and Dry Summer Biases in the Central United States: Improving Cumulus Parameterization. J. Clim. 2022, 1–42. [Google Scholar] [CrossRef]
- Bannister, R.N. A review of operational methods of variational and ensemble-variational data assimilation. Quart. J. Roy Meteor. Soc. 2017, 143, 607–633. [Google Scholar] [CrossRef]
- Tao, Z.Y.; Zhao, C.G.; Chen, M. The Necessity of Statistical Forecasts. Adv. Meteor. Sci. Technol. 2016, 6, 6–13. [Google Scholar]
- Su, X.; Yuan, H.L. The research progress of ensemble statistical postprocessing methods. Adv. Meteor. Sci. Technol. 2020, 10, 30–41. [Google Scholar]
- Klein, W.H.; Lewis, B.M.; Enger, I. Objective prediction of five-day mean temperature during winter. J. Meteorol. 1959, 16, 672–682. [Google Scholar] [CrossRef]
- Carter, G.M.; Dallavalle, J.P.; Glahn, H.R. Statistical forecasts based on the National Meteorological Center’s numerical weather prediction system. Weather. Forecast. 1989, 4, 401–412. [Google Scholar] [CrossRef]
- Glahn, H.R.; Lowry, D.A. The use of Model Output Statistics (MOS) in objective weather forecasting. J. Appl. Meteorol. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Ding, S.S. The advance of model output statistics method in China. Acta Meteor Sin. 1985, 43, 332–338. [Google Scholar]
- Lemcke, C.; Kruizinga, S. Model output statistics forecasts: Three years of operational experience in the Netherlands. Mon. Weather. Rev. 1988, 116, 1077–1090. [Google Scholar] [CrossRef]
- Francis, P.E.; Day, A.P.; Davis, G.P. Automated temperature forecasting, an application of Model Output Statistics to the Meteorological Office numerical weather prediction model. Meteorol. Mag. 1982, 111, 73–87. [Google Scholar]
- Conte, M.; DeSimone, C.; Finizio, C. Post-processing of numerical models: Forecasting the maximum temperature at Milano Linate. Rev. Meteor. Aeronautica. 1980, 40, 247–265. [Google Scholar]
- Lu, R. The application of NWP products and progress of interpretation techniques in China. In Programme on Short- and Medium-Range Weather Prediction Research; Glahn, H.R., Murphy, A.H., Wilson, L.J., Jensenius, J.S., Jr., Eds.; World Meteorological Organization: Geneva, Switzerland, 1991; pp. 19–22. [Google Scholar]
- Azcarraga, R.; Ballester, G.A.J. Statistical system for forecasting in Spain. In Programme on Short- and Medium-Range Weather Prediction Research; Glahn, H.R., Murphy, A.H., Wilson, L.J., Jensenius, J.S., Jr., Eds.; World Meteorological Organization: Geneva, Switzerland, 1991; pp. 23–25. [Google Scholar]
- Brunet, N.; Verret, R.; Yacowar, N. An objective comparison of model output statistics and “perfect prog” systems in producing numerical weather element forecasts. Weather. Forecast. 1988, 3, 273–283. [Google Scholar] [CrossRef]
- Lu, R.H.; Xu, C.Y.; Zhang, L.; Mao, W.X. Calculation method for initial value of Kalman Filter and its application. Quart. J. Appl. Meteor. 1997, 8, 34–43. [Google Scholar]
- Homleid, M. Diurnal corrections of short-term surface temperature forecasts using Kalman filter. Wea. Forecast. 1995, 10, 689–707. [Google Scholar] [CrossRef]
- Galanis, G.; Anadranistakis, M. A one-dimensional Kalman filter for the correction of near surface temperature forecasts. Meteorol. Appl. 2002, 9, 437–441. [Google Scholar] [CrossRef]
- Liu, S.Y.; Xu, L.Q.; Li, D.L. Multi-scale prediction of water temperature using empirical mode decomposition with back-propagation neural networks. Comput. Electr. Eng. 2016, 49, 1–8. [Google Scholar] [CrossRef]
- Xiong, S.W.; Yu, L.H.; Hu, S.S.; Shen, A.Y.; Shen, Y.; Jing, Y.S. An optimized BP-MOS temperature forecast method based on the fine-mesh products of ECMWF. J. Arid. Meteorol. 2017, 35, 668–673. [Google Scholar]
- Feng, H.Z.; Chen, Y.Y. Application of support vector machine regression method in weather forecast. Meteor. Mon. 2005, 31, 41–44. [Google Scholar]
- Sun, J.; Cao, Z.; Li, H.; Qian, S.; Wang, X.; Yan, L.; Xue, W. Application of artificial intelligence technology to numerical weather prediction. J. Appl. Meteor. Sci. 2021, 32, 1–11. [Google Scholar]
- Han, L.; Chen, M.; Chen, K.; Chen, H.; Zhang, Y.; Lu, B.; Song, L.; Qin, R. A deep learning method for bias correction of ECMWF 24–240 h forecasts. Adv. Atmos. Sci. 2021, 38, 1444–1459. [Google Scholar] [CrossRef]
- Peng, T.; Zhi, X.F.; Ji, Y.; Ji, L.Y.; Ye, T. Prediction skill of extended range 2 m maximum air temperature probabilistic forecasts using machine learning Post-processing methods. Atmosphere 2020, 11, 823. [Google Scholar] [CrossRef]
- Zarei, M.; Najarchi, M.; Mastouri, R. Bias correction of global ensemble precipitation forecasts by Random Forest method. Earth Sci. Inform. 2021, 14, 677–689. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Chen, D.; Feng, D.; You, X.; Wu, W. Temperature Forecasting Correction Based on Operational GRAPES-3km Model Using Machine Learning Methods. Atmosphere 2022, 13, 362. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S. Probabilistic quantitative precipitation forecasts based on reforecast analogs: Theory and application. Mon. Weather. Rev. 2006, 134, 3209–3229. [Google Scholar] [CrossRef]
- Mayr, G.J.; Messner, J.W. Probabilistic Forecasts Using Analogs in the Idealized Lorenz96 Setting. Mon. Weather. Rev. 2011, 139, 1960–1971. [Google Scholar]
- Delle Monache, L.; Eckel, F.A.; Rife, D.L.; Nagarajan, B.; Searight, K. Probabilistic Weather Prediction with an Analog Ensemble. Mon. Weather. Rev. 2013, 141, 3498–3516. [Google Scholar] [CrossRef]
- Junk, C.; Monache, L.D.; Alessandrini, S.; Cervone, G.; Von Bremen, L. Predictor-weighting strategies for probabilistic wind power forecasting with an analog ensemble. Meteorol. Z. 2015, 24, 361–379. [Google Scholar] [CrossRef]
- Yang, J.; Astitha, M.; Monache, L.D.; Alessandrini, S. An analog technique to improve storm wind speed prediction using a dual NWP model approach. Mon. Weather. Rev. 2018, 146, 4057–4077. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Nissen, J. A novel application of an analog ensemble for short-term wind power forecasting. Renew. Energy 2015, 76, 768–781. [Google Scholar] [CrossRef]
- Monache, L.D.; Nipen, T.; Liu, Y.; Roux, G.; Stull, R.B. Kalman filter and analog schemes to postprocess numerical weather predictions. Mon. Weather. Rev. 2011, 139, 3554–3570. [Google Scholar] [CrossRef]
- Mahoney, W.P.; Parks, K.; Wiener, G.; Liu, Y.; Myers, W.L.; Sun, J.; Monache, L.D.; Hopson, T.; Johnson, D.; Haupt, S.E. A wind power forecasting system to optimize grid integration. IEEE Trans. Sustain. Energy 2012, 3, 670–682. [Google Scholar] [CrossRef]
- Eckel, F.A.; Delle Monache, L. A hybrid NWP-analog ensemble. Mon. Weather. Rev. 2016, 144, 897–911. [Google Scholar] [CrossRef]
- Hamill, T.M.; Scheuerer, M.; Bates, G.T. Analog Probabilistic Precipitation Forecasts Using GEFS Reforecasts and Climatology-Calibrated Precipitation Analyses*. Mon. Weather. Rev. 2015, 143, 3300–3309. [Google Scholar] [CrossRef]
- Panziera, L.; Germann, U.; Gabella, M.; Mandapaka, P.V. NORA–Nowcasting of orographic rainfall by means of an alogues. Quart. J. Roy. Meteor. Soc. 2011, 137, 2106–2123. [Google Scholar] [CrossRef]
- Liu, C.X. The short-term climate forecasting of tropical cyclone in Guangdong: In the phase space similarity method. J. Trop. Meteor. 2002, 18, 83–90. [Google Scholar]
- Alessandrini, S.; Monache, L.D.; Rozoff, C.M.; Lewis, W.E. Probabilistic Prediction of Tropical Cyclone Intensity with an Analog Ensemble. Mon. Weather. Rev. 2018, 146, 1723–1744. [Google Scholar] [CrossRef]
- Chen, P.; Yu, H.; Brown, B.; Chen, G.; Wan, R. A probabilistic climatology-based analogue intensity forecast scheme for tropical cyclones. Q. J. R. Meteorol. Soc. 2016, 142, 2386–2397. [Google Scholar] [CrossRef]
- Djalalova, I.; Monache, L.D.; Wilczak, J. PM2.5 analog forecast and Kalman filter post-processing for the Community Multiscale Air Quality (CMAQ) model. Atmos. Environ. 2015, 108, 76–87. [Google Scholar] [CrossRef]
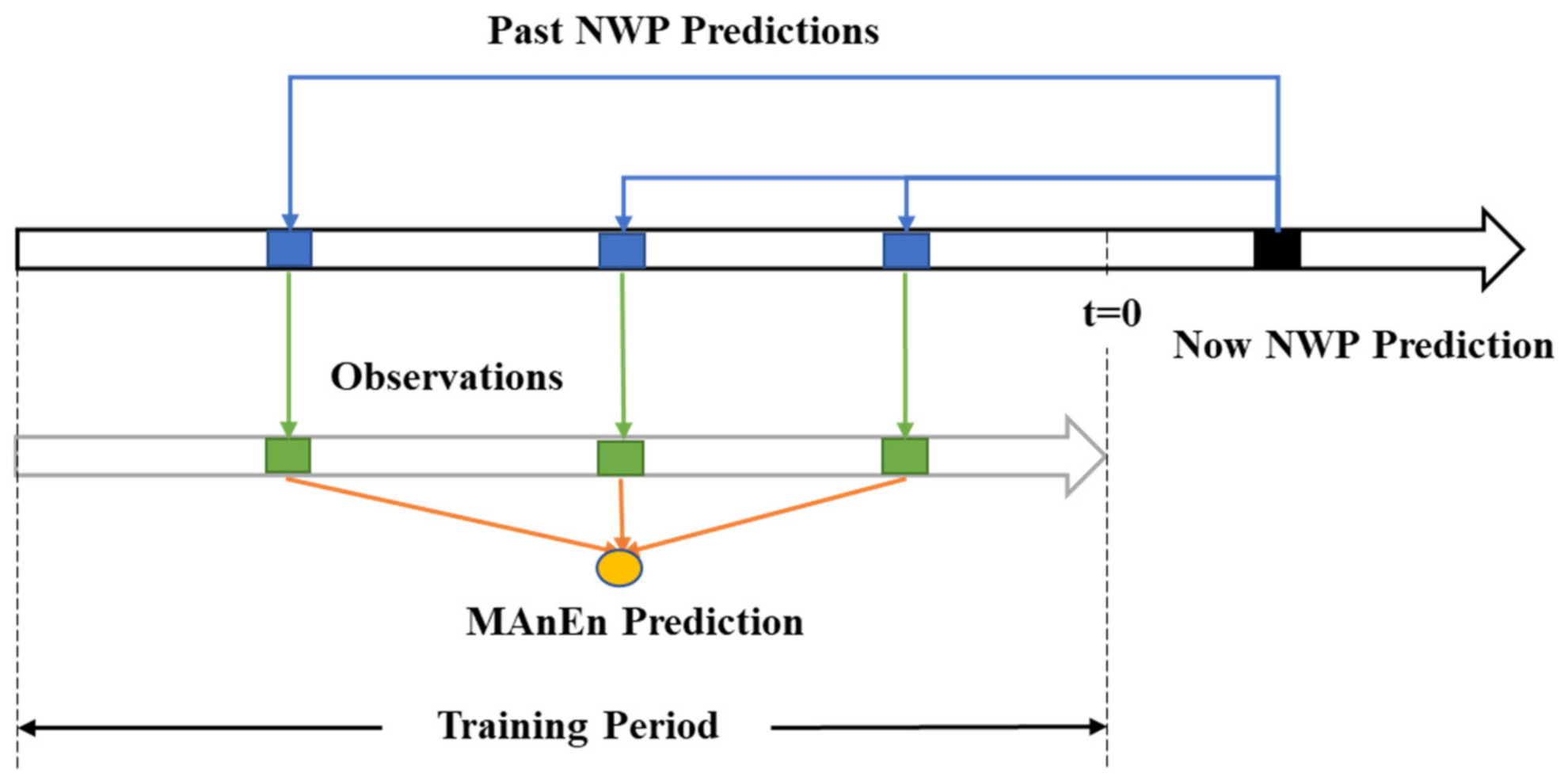



| Forecast Lead Time | Testing Period | Training Period | Selected Lead Time | Analog Ensemble Members |
|---|---|---|---|---|
| 180 h | 20220501–0628 (59 d) | 20181225–20220423 (1216 d) | 168 h, 180 h, 192 h | 30 |
| 192 h | –20220422 (1215 d) | 180 h, 192 h, 204 h | ||
| 204 h | 1215 d | 192 h, 204 h, 216 h | ||
| 216 h | –20220421 (1214 d) | 204 h, 216 h, 228 h | ||
| 228 h | 1214 d | 216 h, 228 h, 240 h | ||
| 240 h | –20220420 (1213 d) | 228 h, 240 h, 252 h | ||
| 252 h | 1213 d | 240 h, 252 h, 264 h | ||
| 264 h | –20220419 (1212 d) | 252 h, 264 h, 276 h | ||
| 276 h | 1212 d | 264 h, 276 h, 288 h | ||
| 288 h | –20220418 (1211 d) | 276 h, 288 h, 300 h | ||
| 300 h | 1211 d | 288 h, 300 h, 312 h | ||
| 312 h | –20220417 (1210 d) | 300 h, 312 h, 324 h | ||
| 324 h | 1210 d | 312 h, 324 h, 336 h | ||
| 336 h | –20220416 (1209 d) | 324 h, 336 h, 348 h | ||
| 348 h | 1209 d | 336 h, 348 h, 360 h |
| Forecast Lead Time | Decreasing Percent |
|---|---|
| 192 h | 31.4% |
| 240 h | 29.6% |
| 288 h | 23.5% |
| 336 h | 24.4% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Wang, Q.; Shen, X. Analogue Ensemble Averaging Method for Bias Correction of 2-m Temperature of the Medium-Range Forecasts in China. Atmosphere 2022, 13, 2097. https://doi.org/10.3390/atmos13122097
Hu Y, Wang Q, Shen X. Analogue Ensemble Averaging Method for Bias Correction of 2-m Temperature of the Medium-Range Forecasts in China. Atmosphere. 2022; 13(12):2097. https://doi.org/10.3390/atmos13122097
Chicago/Turabian StyleHu, Yingying, Qiguang Wang, and Xueshun Shen. 2022. "Analogue Ensemble Averaging Method for Bias Correction of 2-m Temperature of the Medium-Range Forecasts in China" Atmosphere 13, no. 12: 2097. https://doi.org/10.3390/atmos13122097
APA StyleHu, Y., Wang, Q., & Shen, X. (2022). Analogue Ensemble Averaging Method for Bias Correction of 2-m Temperature of the Medium-Range Forecasts in China. Atmosphere, 13(12), 2097. https://doi.org/10.3390/atmos13122097





