Analysis and Research on Chaotic Dynamics of Evaporation Duct Height Time Series with Multiple Time Scales
Abstract
1. Introduction
2. Methods
2.1. Statistical Tests
2.2. Rescaled Range Analysis
2.3. Phase Space Reconstruction
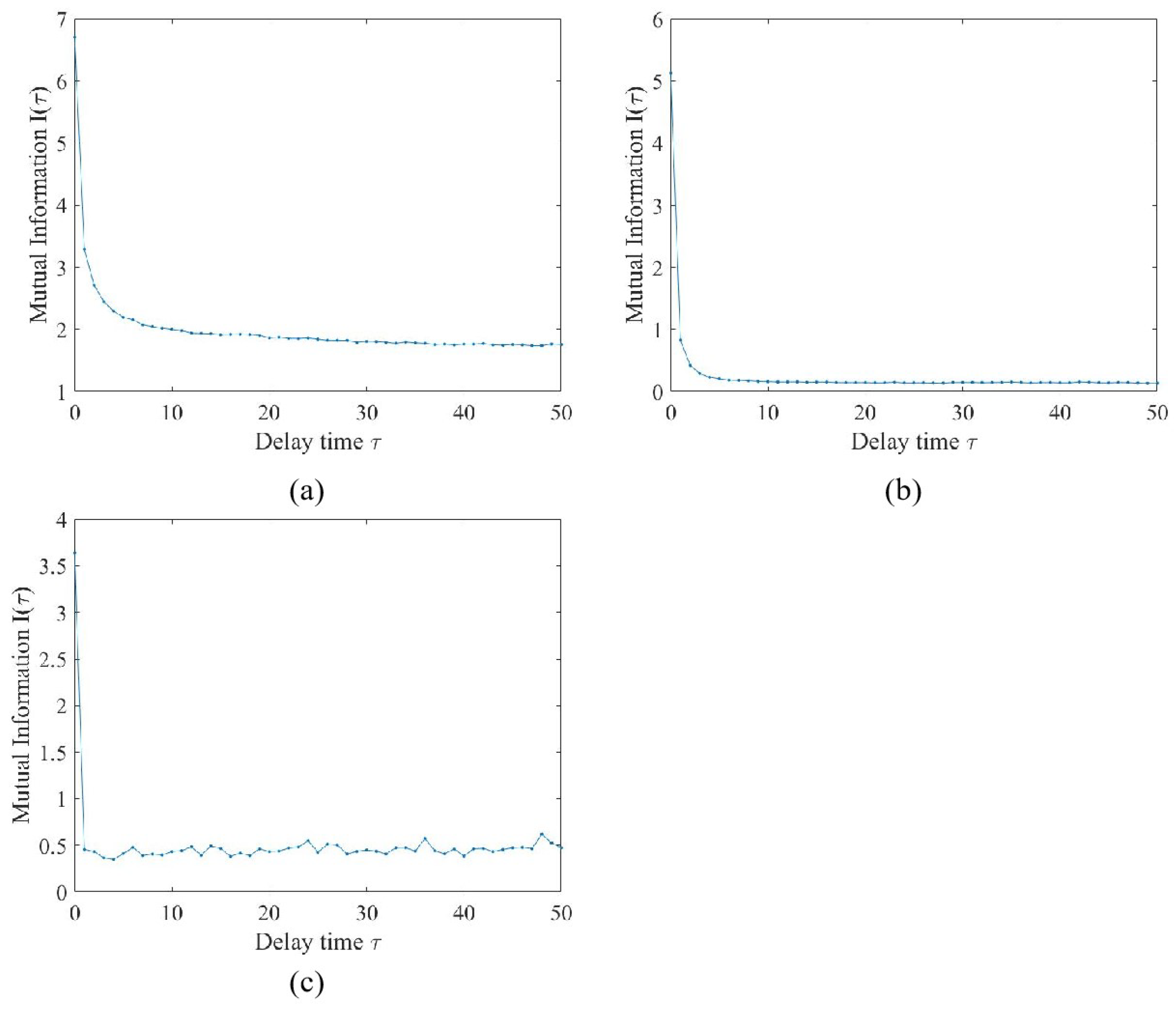
2.3.1. Delay Time
2.3.2. Embedding Dimension m
2.4. Lyapunov Exponent
3. Case Study
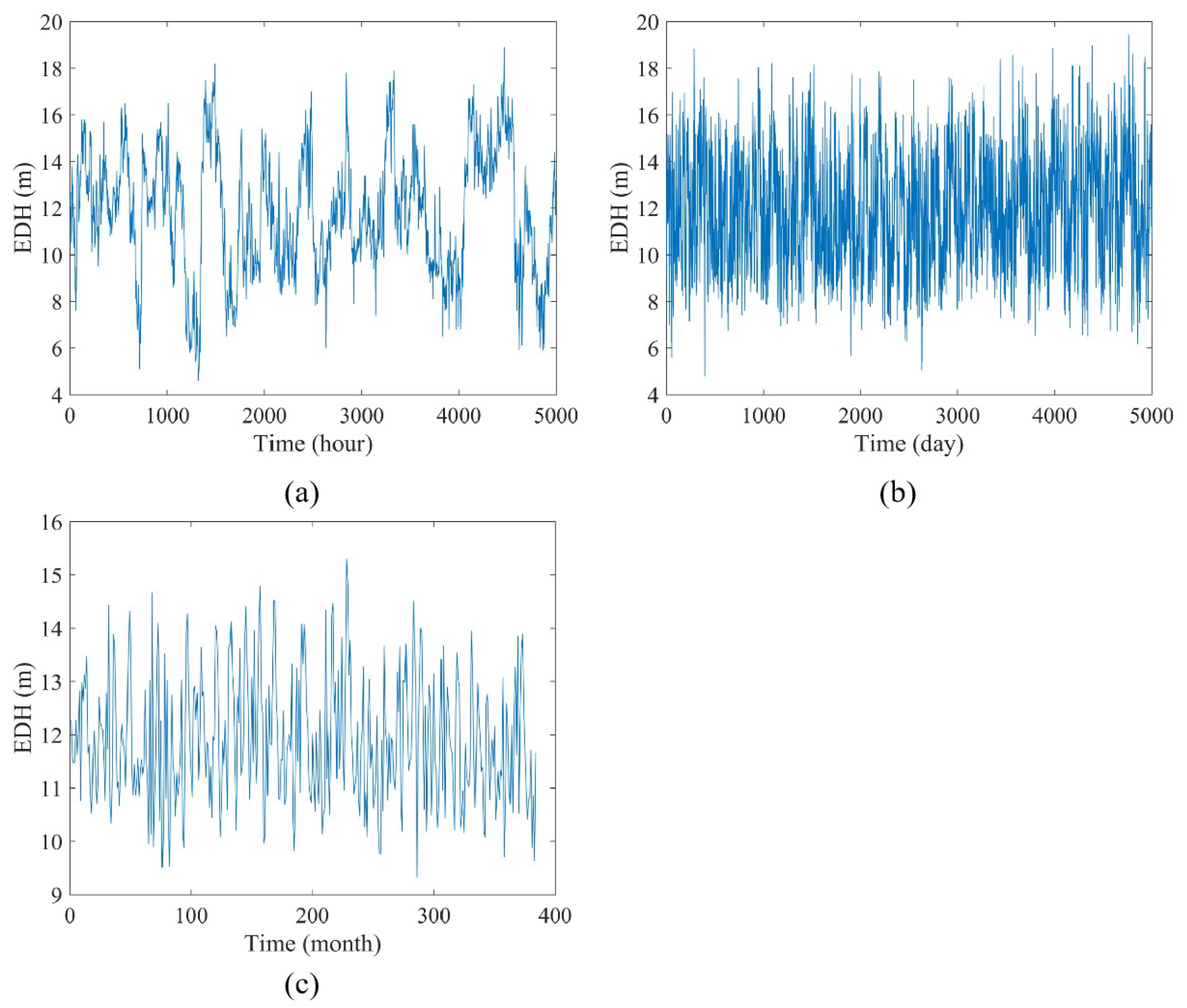
3.1. EDH Time Series at Three Time Scales
3.2. Statistical Characteristics
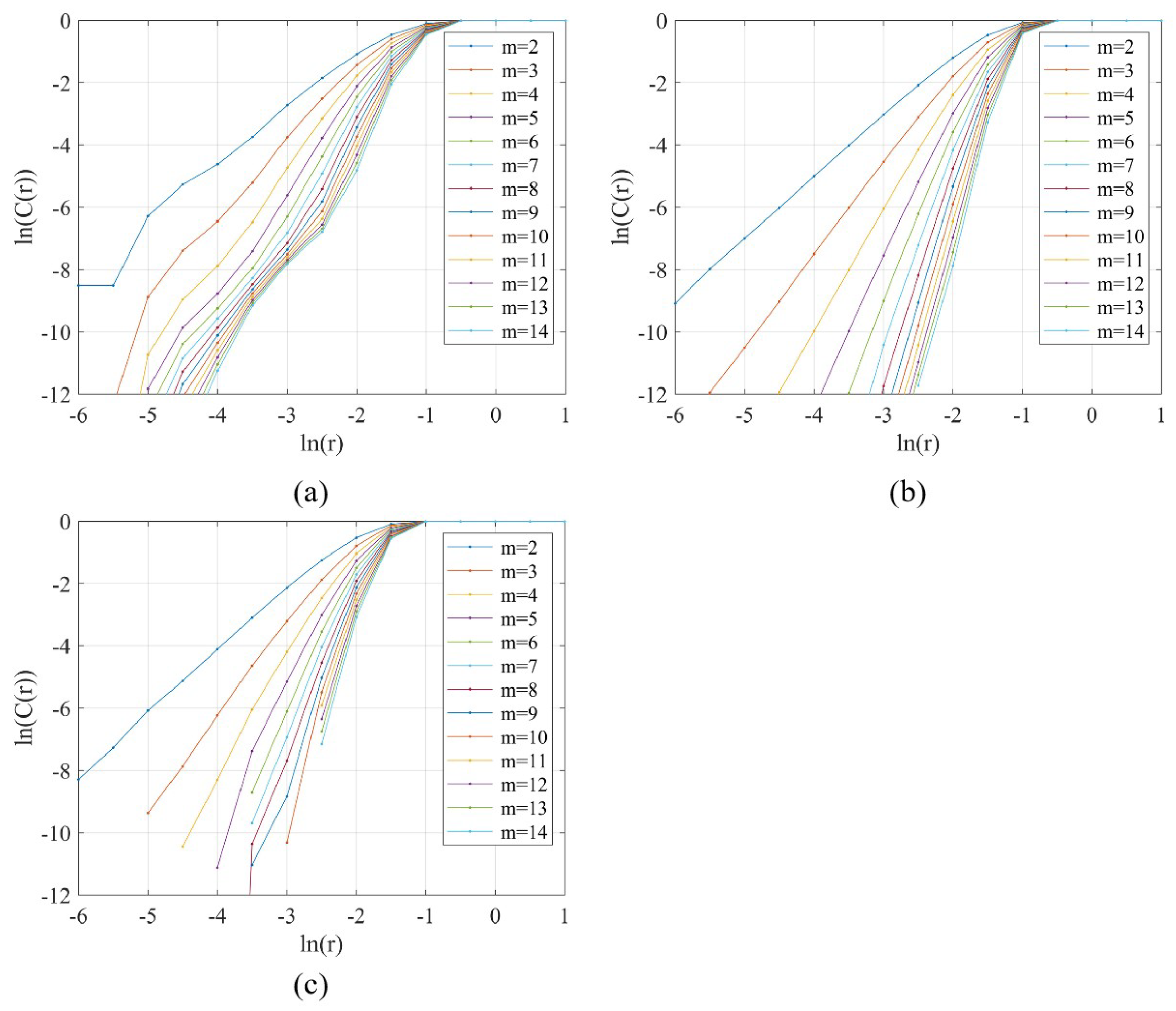
3.3. Fractal Characteristics
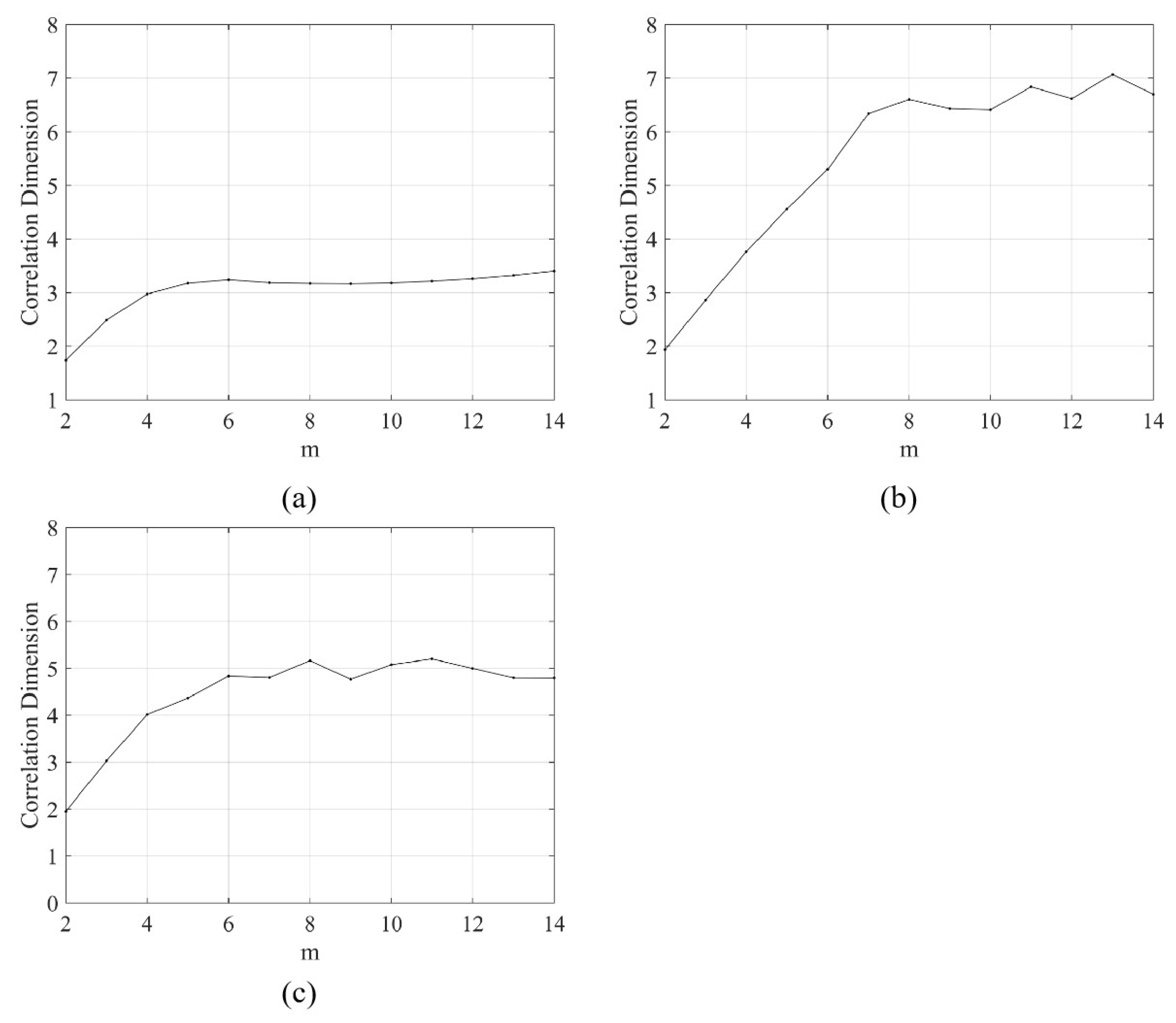
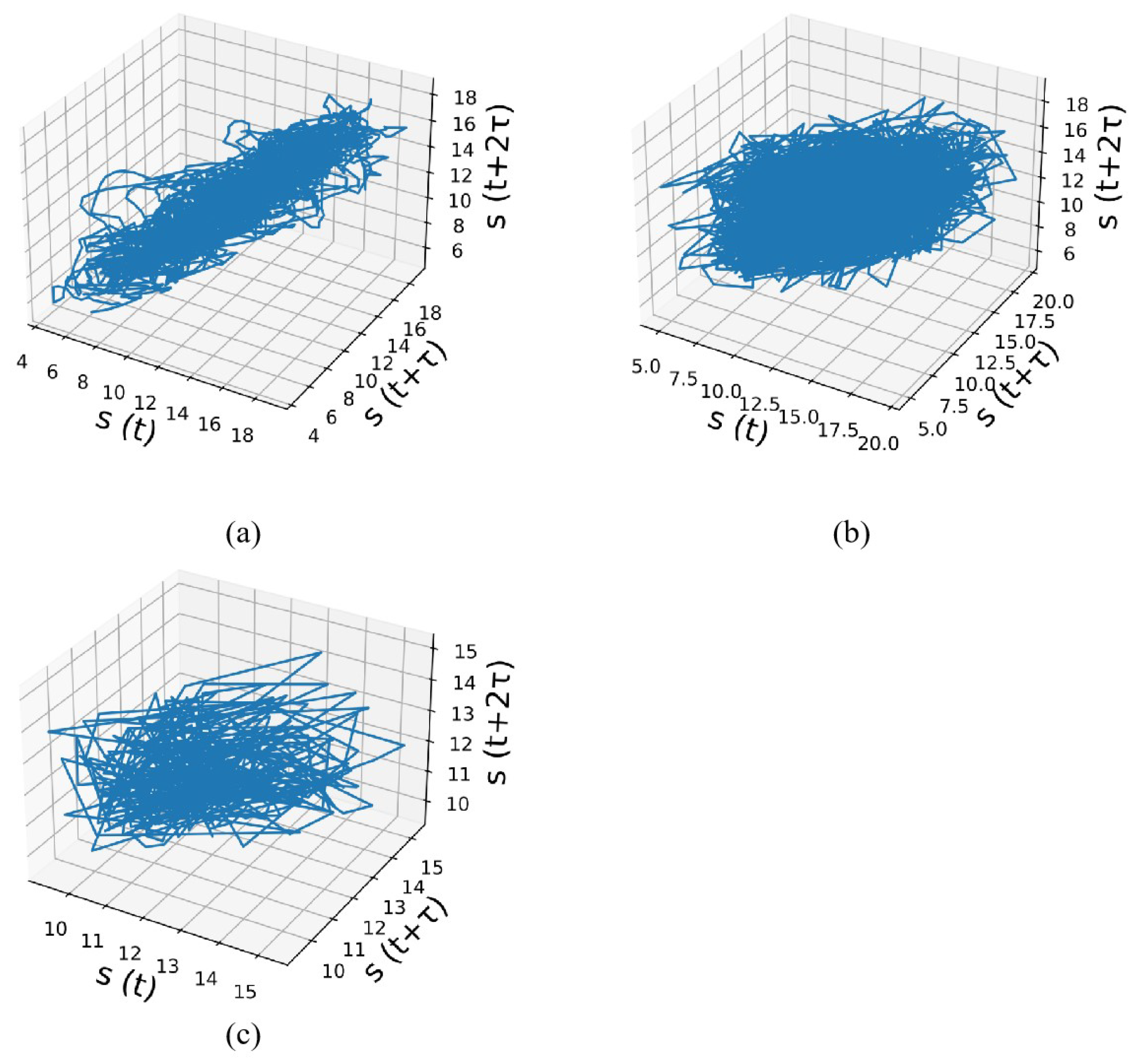
3.4. Phase Space Reconstruction
3.5. Largest Lyapunov Exponent
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Q.; Alappattu, D.P.; Billingsley, S.; Blomquist, B.; Burkholder, R.J.; Christman, A.J.; Creegan, E.D.; De Paolo, T.; Eleuterio, D.P.; Fernando, H.J.S.; et al. CASPER: Coupled air–sea processes and electromagnetic ducting research. Bull. Amer. Meteoro. Soc. 2018, 99, 1449–1471. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, K.D.; Shi, Y. Spatial and temporal variability of the evaporation duct in the Gulf of Aden. Tellus A 2016, 68, 29792. [Google Scholar] [CrossRef]
- Pozderac, J.; Johnson, J.; Yardim, C.; Merrill, C.; de Paolo, T.; Terrill, E.; Ryan, F.; Frederickson, P. X-band beacon-receiver array evaporation duct height estimation. IEEE Trans. Antennas Propag. 2018, 66, 2545–2556. [Google Scholar] [CrossRef]
- Guo, X.; Zhao, D.; Zhang, L.; Wang, H.; Kang, S.; Lin, L. C band transhorizon signal characterisations in evaporation duct propagation environment over Bohai Sea of China. IET Microw. Antennas Propaga. 2019, 13, 407–413. [Google Scholar] [CrossRef]
- Ma, J.; Wang, J.; Yang, C. Long-range microwave links guided by evaporation ducts. IEEE Commun. Mag. 2022, 60, 68–72. [Google Scholar] [CrossRef]
- Wash, C.; Davidson, K. Remote measurements and coastal atmospheric refraction. IEEE IGARSS 1994, 1, 397–401. [Google Scholar]
- Richter, J.H. Sensing of radio refractivity and aerosol extinction. IEEE IGARSS 1994, 1, 381–395. [Google Scholar]
- Pons, J.; Reising, S.C.; Padmanabhan, S.; Camps, A.; Duffo, N. Passive polarimetric remote sensing of the ocean surface during the Rough Evaporation Duct experiment (RED 2001). IEEE IGARSS 2003, 4, 2732–2734. [Google Scholar]
- Karimian, A.; Yardim, C.; Gerstoft, P.; Hodgkiss, W.S.; Barrios, A.E. Refractivity estimation from sea clutter: An invited review. Radio Sci. 2011, 46, 1–16. [Google Scholar] [CrossRef]
- Zhao, X.; Yardim, C.; Wang, D.; Howe, B.M. Estimating range-dependent evaporation duct height. J. Atmos. Ocean. Technol. 2017, 34, 1113–1123. [Google Scholar] [CrossRef]
- Ji, H.; Yin, B.; Zhang, J.; Zhang, Y. Joint inversion of evaporation duct based on radar sea clutter and target echo using deep learning. Electronics 2022, 11, 2157. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Z.S.; Zhao, Z.W.; Wang, H.G. A passive technique to monitor evaporation duct height using coastal GNSS-R. IEEE Geosci. Remote Sens. Lett. 2011, 8, 587–591. [Google Scholar] [CrossRef]
- Liao, Q.; Sheng, Z.; Shi, H.; Xiang, J.; Yu, H. Estimation of surface duct using ground-based GPS phase delay and propagation loss. Remote Sens. 2018, 10, 724. [Google Scholar] [CrossRef]
- Mai, Y.; Shi, H.; Liao, Q.; Sheng, Z.; Zhao, S.; Ni, Q.; Zhang, W. Using the decomposition-based multi-objective evolutionary algorithm with adaptive neighborhood sizes and dynamic constraint strategies to retrieve atmospheric ducts. Sensors 2020, 20, 2230. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, K.D. Study on evaporation duct estimation from point-to-point propagation measurements. IET Sci. Meas. Technol. 2018, 4, 456–460. [Google Scholar] [CrossRef]
- Karabacs, U.; Diouane, Y.; Douvenot, R. A variational adjoint approach on wide-angle parabolic equation for refractivity inversion. IEEE Trans. Antennas Propag. 2021, 69, 4861–4870. [Google Scholar] [CrossRef]
- Pastore, D.M.; Wessinger, S.E.; Greenway, D.P.; Stanek, M.J.; Burkholder, R.J.; Haack, T.; Wang, Q.; Hackett, E.E. Refractivity inversions from point-to-point X-band radar propagation measurements. Radio Sci. 2022, 57, 1–16. [Google Scholar] [CrossRef]
- Hristov, T. Study of EM Signals Propagation Through Marine Atmospheric Boundary Layer and Static Pressure Measurements in Marine Atmospheric Boundary Layer During CBLAST; Johns Hopkins University: Baltimore, MD, USA, 2005. [Google Scholar]
- Kukushkin, A. Radio Wave Propagation in the Marine Boundary Layer; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Edson, J.; Crawford, T.; Crescenti, J.; Farrar, T.; Frew, N.; Gerbi, G.; Helmis, C.; Hristov, T.; Khelif, D.; Jessup, A.; et al. The coupled boundary layers and air–sea transfer experiment in low winds. Bull. Amer. Meteoro. Soc. 2007, 88, 341–356. [Google Scholar] [CrossRef]
- Hristov, T. Wave-Driven Marine Boundary Layers: Implications for Atmospheric Electromagnetics and Ocean Acoustics; Johns Hopkins University: Baltimore, MD, USA, 2008. [Google Scholar]
- Mai, Y.; Sheng, Z.; Shi, H.; Li, C.; Liao, Q.; Bao, J. A new short-term prediction method for estimation of the evaporation duct height. IEEE Access 2020, 8, 136036–136045. [Google Scholar] [CrossRef]
- Chai, X.; Li, J.; Zhao, J.; Wang, W.; Zhao, X. LGB-PHY: An evaporation duct height prediction model based on physically constrained lightGBM algorithm. Remote Sens. 2022, 14, 3448. [Google Scholar] [CrossRef]
- Liu, W.T.; Katsaros, K.B.; Businger, J.A. Bulk parameterization of air–sea exchanges of heat and water vapor including the molecular constraints at the interface. J. Atmos. Sci. 1979, 36, 1722–1735. [Google Scholar] [CrossRef]
- Babin, S.M.; Dockery, G.D. LKB-based evaporation duct model comparison with buoy data. J. Appl. Meteor. 2002, 41, 434–446. [Google Scholar] [CrossRef]
- Liu, W.T.; Blanc, T.V. The Liu, Katsaros, and Businger (1979) Bulk Atmospheric Flux Computational Iteration Program in FORTRAN and BASIC; Naval Research Lab.: Washington, DC, USA, 1984. [Google Scholar]
- Cook, J. A Sensitivity Study of Weather Data Inaccuracies on Evaporation Duct Height Algorithms. Radio Sci. 1991, 26, 731–746. [Google Scholar] [CrossRef]
- Cook, J.; Burk, S. Potential Refractivity as a Similarity Variable. Bound.-Layer Meteorol. 1992, 58, 151–159. [Google Scholar] [CrossRef][Green Version]
- Babin, S.M.; Young, G.S.; Carton, J.A. A New Model of the Oceanic Evaporation Duct. J. Appl. Meteor. 1997, 36, 193–204. [Google Scholar] [CrossRef]
- Frederickson, P.A.; Davidson, K.L.; Goroch, A.K. Operational Bulk Evaporation Duct Model for MORIAH; Version 12; Naval Postgraduate School: Monterey, CA, USA, 2000; pp. 93943–95114. [Google Scholar]
- Karimian, A.; Yardim, C.; Haack, T.; Gerstoft, P.; Hodgkiss, W.S.; Rogers, T. Toward the Assimilation of the Atmospheric Surface Layer Using Numerical Weather Prediction and Radar Clutter Observations. J. Appl. Meteor. Climatol. 2013, 52, 2345–2355. [Google Scholar] [CrossRef]
- Jiao, L.; Zhang, Y. An Evaporation Duct Prediction Model Coupled with the MM5. Acta Oceanol. Sin. 2015, 34, 46–50. [Google Scholar] [CrossRef]
- Frederickson, P.A.; Murphree, J.T.; Twigg, K.L.; Barrios, A. A modern global evaporation duct climatology. In Proceedings of the IEEE International Conference Radar, Adelaide, SA, Australia, 10–12 September 2008; pp. 292–296. [Google Scholar]
- Yang, K.D.; Zhang, Q.; Shi, Y.; He, Z.Y.; Lei, B.; Han, Y.N. On Analyzing Space-time Distribution of Evaporation Duct Height over the Global Ocean. Acta Oceanol. Sin. 2016, 7, 20–29. [Google Scholar] [CrossRef]
- Twigg, K.L. A Smart Climatology of Evaporation Duct Height and Surface Radar Propagation in the Indian Ocean. Master’s Thesis, Naval Postgrad School, Monterey, CA, USA, 2007. [Google Scholar]
- Ramsaur, D. Climate Analysis and Long Range Forecasting of Radar Performance in the Western North Pacific. Master’s Thesis, Naval Postgrad School, Monterey, CA, USA, 2009. [Google Scholar]
- McKeon, B.D. Climate Analysis of Evaporation Ducts in the South China Sea. Master’s Thesis, Naval Postgrad School, Monterey, CA, USA, 2013. [Google Scholar]
- Gurbuz, S.C. Assessing Evaporation Duct Variability in the Eastern Mediterranean Sea in Support of Radar and Radio Communications. Master’s Thesis, Naval Postgrad School, Monterey, CA, USA, 2016. [Google Scholar]
- Javeed, S.; Alimgeer, K.S.; Javed, W.; Atif, M.; Uddin, M. A modified artificial neural network based prediction technique for tropospheric radio refractivity. PLoS ONE 2018, 13, e0192069. [Google Scholar] [CrossRef]
- Mai, Y.; Sheng, Z.; Shi, H.; Li, C.; Liu, L.; Liao, Q.; Zhang, W.; Zhou, S. A new diagnostic model and improved prediction algorithm for the heights of evaporation ducts. Front. Earth Sci. 2020, 8, 102. [Google Scholar] [CrossRef]
- Zhao, W.; Li, J.; Zhao, J.; Jiang, T.; Zhu, J.; Zhao, D. Research on evaporation duct height prediction based on back propagation neural network. IET Microw. Antennas Propaga. 2020, 14, 1547–1554. [Google Scholar] [CrossRef]
- Hong, F.; Zhang, Q. Time series analysis of evaporation duct height over South China Sea: A stochastic modeling approach. Atmosphere 2021, 12, 1663. [Google Scholar] [CrossRef]
- Yanez, J.F. Machine Learning Approach for Evaporation Duct Nowcast. Master’s Thesis, Naval Postgrad School, Monterey, CA, USA, 2021. [Google Scholar]
- Zhao, W.; Zhao, J.; Li, J.; Zhao, D.; Huang, L.; Zhu, J.; Lu, J.; Wang, X. An evaporation duct height prediction model based on a long short-term memory neural network. IEEE Trans. Antennas Propaga. 2021, 69, 7795–7804. [Google Scholar] [CrossRef]
- Han, J.; Wu, J.-J.; Zhu, Q.-L.; Wang, H.-G.; Zhou, Y.-F.; Jiang, M.-B.; Zhang, S.-B.; Wang, B. Evaporation duct height nowcasting in China’s Yellow Sea based on deep learning. Remote Sens. 2021, 13, 1577. [Google Scholar] [CrossRef]
- Ma, Y.; He, X.; Wu, R.; Shen, C. Spatial Distribution of Multi-Fractal Scaling Behaviours of Atmospheric XCO2 Concentration Time Series during 2010–2018 over China. Entropy 2022, 24, 817. [Google Scholar] [CrossRef]
- Kalamaras, N.; Tzanis, C.; Deligiorgi, D.; Philippopoulos, K.; Koutsogiannis, I. Distribution of Air Temperature Multifractal Characteristics Over Greece. Atmosphere 2019, 10, 45. [Google Scholar] [CrossRef]
- Gómez-Gómez, J.; Carmona-Cabezas, R.; Sánchez-López, E.; Gutiérrez de Ravé, E.; Jiménez-Hornero, F.J. Multifractal Fluctuations of the Precipitation in Spain (1960–2019). Chaos Solitons Fractals 2022, 157, 111909. [Google Scholar] [CrossRef]
- Gil-Alana, L.A.; Yaya, O.S.; Awolaja, O.G.; Cristofaro, L. Long Memory and Time Trends in Particulate Matter Pollution (PM2.5 and PM10) in the 50 U.S. States. J. Appl. Meteo. Climatol. 2020, 59, 1351–1367. [Google Scholar] [CrossRef]
- Senyange, B.; Manda, B.M.; Skokos, C. Characteristics of chaos evolution in one-dimensional disordered nonlinear lattices. Phys. Rev. E 2018, 98, 052229. [Google Scholar] [CrossRef]
- Safari, N.; Chung, C.; Price, G. Novel multi-step short-term wind power prediction framework based on chaotic time series analysis and singular spectrum analysis. IEEE Trans. Power Syst. 2017, 33, 590–601. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Amer. Stat. Assoc. 1979, 74, 427–431. [Google Scholar]
- Said, S.E.; Dickey, D.A. Testing for unit roots in autoregressive-moving average models of unknown order. Biometrika 1984, 71, 599–607. [Google Scholar] [CrossRef]
- Ljung, G.M.; Box, G.E. On a measure of lack of fit in time series models. Biometrika 1978, 65, 297–303. [Google Scholar] [CrossRef]
- Hurst, H.E. Long-term storage capacity of reservoirs. Trans. Ameri. Soc. Civil Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Granero, M.S.; Segovia, J.T.; Perez, J.G. Some comments on Hurst exponent and the long memory processes on capital markets. Phys. A 2008, 387, 5543–5551. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence. Dyn. Syst. Turb. 1981, 366–381. [Google Scholar]
- Hu, Z.; Zhang, C.; Luo, G.; Teng, Z.; Jia, C. Characterizing cross-scale chaotic behaviors of the runoff time series in an inland river of central Asia. Quatern. Int. 2013, 311, 132–139. [Google Scholar] [CrossRef]
- Dhanya, C.; Kumar, D.N. Multivariate nonlinear ensemble prediction of daily chaotic rainfall with climate inputs. J. Hydro. 2011, 403, 292–306. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef]
- Barna, G.; Tsuda, I. A new method for computing lyapunov exponents. Phys. Lett. A 1993, 175, 421–427. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest lyapunov exponents from small datasets. Phys. D 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, L.; Jie, J.; Liu, X. A multi-scale prediction model based on empirical mode decomposition and chaos theory for industrial melt index prediction. Chemometr. Intell. Lab. Syst. 2019, 186, 23–32. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Amer. Meteoro. Soc. 2010, 8, 1015–1058. [Google Scholar] [CrossRef]
- Frederickson, P.A. Further improvements and validation for the navy atmospheric vertical surface layer model (NAVSLaM). In Proceedings of the IEEE 2015 USNC-URSI Radio Science Meeting (Joint with AP-S Symposium), Piscataway, NJ, USA, 19–24 July 2015; p. 242. [Google Scholar]
- Frederickson, P.; Alappattu, D.; Wang, Q.; Yardim, C.; Xu, L.; Christman, A.; Fernando, H.J.S.; Blomquist, B. Evaluating the use of different flux-gradient functions in NAVSLaM during two experiments. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting (IEEE), Boston, MA, USA, 8–13 July 2018; pp. 885–886. [Google Scholar]
- Zhang, Q.; Yang, K.D.; Yang, Q.L. Statistical analysis of the quantified relationship between evaporation duct and oceanic evaporation for unstable conditions. J. Atmos. Ocean. Technol. 2017, 11, 2489–2497. [Google Scholar] [CrossRef]
- Yang, K.D.; Zhang, Q.; Shi, Y. Interannual variability of the evaporation duct over the South China Sea and its relations with regional evaporation. J. Geophys. Res.-Oceans 2017, 8, 6698–6713. [Google Scholar] [CrossRef]
- Yang, S.; Li, X.; Wu, C.; He, X.; Zhong, Y. Application of the PJ and NPS evaporation duct models over the South China Sea (SCS) in winter. PLoS ONE 2017, 12, e0172284. [Google Scholar] [CrossRef]
- Yang, C.; Wang, J.; Ma, J. Exploration of X-band communication for maritime applications in the South China Sea. IEEE Antennas Wire. Propag. Lett. 2021, 21, 481–485. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, K.; Shi, Y.; Yan, X. Oceanic Propagation Measurement in the Northern Part of the South China Sea. In Proceedings of the OCEANS 2016, Shanghai, China, 10–13 April 2016; IEEE: Shanghai, China, 2016; pp. 1–4. [Google Scholar]
- Tian, Z. Chaotic characteristic analysis of network traffic time series at different timescales. Chaos Soliton. Fract. 2020, 130, 109412. [Google Scholar] [CrossRef]
- Jiang, F.; Deng, M.; Long, Y.; Sun, H. Spatial pattern and dynamic change of vegetation greenness from 2001 to 2020 in Tibet, China. Front. Plant Sci. 2022, 1292. [Google Scholar] [CrossRef] [PubMed]
- Rahmani, F.; Fattahi, M.H. Multi-temporal-scale analysis of the underlying association between temperature and river flow using a cross-correlation and nonlinear dynamic approach. IJST Trans. Civil Eng. 2022, 46, 2511–2529. [Google Scholar] [CrossRef]
- Foken, T. 50 Years of the Monin–Obukhov similarity theory. Bound.-Lay. Meteorol. 2006, 119, 431–447. [Google Scholar] [CrossRef]
- Alappattu, D.P.; Wang, Q.; Kalogiros, J. Anomalous propagation conditions over Eastern Pacific Ocean derived from MAGIC data. Radio Sci. 2016, 51, 1142–1156. [Google Scholar] [CrossRef]
- Østenstad, P.; Meltzer, M.M. Evaporation duct height climatology for Norwegian waters using hindcast data. In Proceedings of the Meet Procedings of the SET-244 Symposium “Bridging the Gap between the Development and Operational Deployment of Naval Tactical Decision Aids”, Den Helder, The Netherlands, 31 October–2 November 2017; pp. 10A1–10A10. [Google Scholar]
- Ansorge, C. Scale Dependence of atmosphere–surface coupling through similarity theory. Bound.-Lay. Meteorol. 2019, 170, 1–27. [Google Scholar] [CrossRef]
- Jiang, Q. Influence of swell on marine surface-layer structure. J. Atmos. Sci. 2020, 77, 1865–1885. [Google Scholar] [CrossRef]
| Time Scale | t-Values of ADF | p-Values of Ljung–Box |
|---|---|---|
| Hourly | −32.67 | 0 |
| Daily | −24.84 | 0 |
| Monthly | −4.71 | 0 |
| Time Scale | Hurst Index | Fractal Dimension |
|---|---|---|
| Hourly | 0.851 | 1.149 |
| Daily | 0.944 | 1.056 |
| Monthly | 0.961 | 1.039 |
| Time Scale | Delay Time | Embedding Dimension m |
|---|---|---|
| Hourly | 15 | 7 |
| Daily | 11 | 15 |
| Monthly | 4 | 11 |
| Time Scale | Maximum Lyapunov Exponent |
|---|---|
| Hourly | 0.0393 |
| Daily | 0.1876 |
| Monthly | 0.2872 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Chen, X.; Yin, F.; Hong, F. Analysis and Research on Chaotic Dynamics of Evaporation Duct Height Time Series with Multiple Time Scales. Atmosphere 2022, 13, 2072. https://doi.org/10.3390/atmos13122072
Zhang Q, Chen X, Yin F, Hong F. Analysis and Research on Chaotic Dynamics of Evaporation Duct Height Time Series with Multiple Time Scales. Atmosphere. 2022; 13(12):2072. https://doi.org/10.3390/atmos13122072
Chicago/Turabian StyleZhang, Qi, Xi Chen, Fuyu Yin, and Fei Hong. 2022. "Analysis and Research on Chaotic Dynamics of Evaporation Duct Height Time Series with Multiple Time Scales" Atmosphere 13, no. 12: 2072. https://doi.org/10.3390/atmos13122072
APA StyleZhang, Q., Chen, X., Yin, F., & Hong, F. (2022). Analysis and Research on Chaotic Dynamics of Evaporation Duct Height Time Series with Multiple Time Scales. Atmosphere, 13(12), 2072. https://doi.org/10.3390/atmos13122072






