Abstract
Synoptic eddies (with a period of two to eight days) are active in the South China Sea-Philippine Sea (SCS-PS) and control weather variations. In addition, the intensity and frequency of synoptic eddies may change along with variations in sea surface temperatures (SST). This paper presented the influence of SST in the northwest Indian Ocean on synoptic eddies in the lower troposphere over the SCS-PS in June. Our statistical analysis showed a significant negative correlation between the SST in the northwest Indian Ocean and the synoptic scale eddy kinetic energy (EKE) in the SCS-PS. By analyzing the EKE budget of synoptic eddies, we found that the variation in the synoptic scale EKE over the SCS-PS is mainly due to the change in the monthly zonal wind gradient, which affects the barotropic energy conversion between the monthly mean flow and the synoptic eddies. Additionally, the northwest Indian Ocean SST modulates the monthly flow over the SCS-PS by alternating the strength of the Walker circulation in the west Pacific and Indian Ocean. Finally, the influence of SST in the northwest Indian Ocean on EKE in the SCS-PS was reproduced using the simplified atmospheric general circulation model, SPEEDY.
1. Introduction
In the South China Sea-Philippine Sea, synoptic eddies regularly propagate in a northwestern direction from the western equatorial Pacific Ocean [1]. Synoptic eddies, a type of tropical disturbance, can trigger tropical cyclone genesis in the SCS-PS and its surrounding regions [2]. Li (2006) [3] used an atmospheric general circulation model to prove this evolution from tropical disturbances to tropical cyclones. Other studies have shown that around 30% of typhoons are associated with synoptic eddies [4,5]. Furthermore, Xu et al. (2014) [6], who investigated typhoon Manyi in 2001 using a sensitivity experiment, showed that a synoptic wave train was crucial for the generation of the typhoon. Additionally, Zhou et al. (2018) [7] showed that the phases of quasi-biweekly oscillation can affect the development of synoptic disturbances, which leads to the intraseasonal variation in the intensity of tropical cyclones over the western North Pacific Ocean.
In addition to tropical cyclone genesis and intensity, Liu et al. (2022) [8] pointed out that the multiscale interaction between synoptic eddies and low-frequency disturbances also causes extreme pre-summer precipitation over South China. The work of Hu et al. (2022) [9] also showed that the early and late onset of the South China Sea summer monsoon may alter synoptic eddy activity, which affects the frequency of extreme precipitation events in the Indochina Peninsula, Hainan Island, and the Philippines. In addition, synoptic weather patterns also modulate extreme temperature and the range of temperature on diurnal and synoptic timescales in southeast China [10,11,12]. Hence, synoptic eddies also play a role in controlling precipitation and temperature fluctuations in China.
The synoptic eddies in the lower troposphere over the South China Sea are subject to sea surface temperature variations in the equatorial eastern Pacific. Hsu et al. (2009) [13] showed that the El Niño/Southern Oscillation is associated with the southeastward extension of the monsoon trough and the intensification of the westerly jet over the tropical western Pacific, which is favorable for the baroclinic energy conversion of synoptic eddies. Additionally, Zeng et al. (2012) [14] proved the relation between the El Niño/Southern Oscillation and synoptic eddies in the South China Sea, based on mooring observations.
Previous studies have demonstrated that the SST in the Indian Ocean can influence atmospheric circulation in the South China Sea and its surrounding regions. Yuan et al. (2008) [15] found that SST anomalies in the tropical Indian Ocean influenced the onset of the South China Sea summer monsoon by affecting the Walker circulation and regulating convection in the western Pacific. A recent study pointed out that the increase in June precipitation in the South China Sea and decrease in June precipitation in the Indochina Peninsula are caused by warming in the tropical western Indian Ocean [16]. Hence, previous studies have reported the impact of the western Indian Ocean on atmospheric circulation in the South China Sea, on monthly and seasonal timescales. However, its impact on a synoptic timescale has still not been well investigated.
Lorenz proposed an energy cycle theory including the potential and kinetic energies of the mean flow and eddy components on a global scale [17]. In the energy cycle, energy is converted from the available potential energy of mean flow to eddy potential energy and then to eddy kinetic energy. Subsequently, Ulbrich and Speth (1991) [18] divided the eddy component into stationary and transient parts. The energy cycle has been utilized in past studies on atmospheric dynamics, including multiscale eddy interaction, eddy–mean flow interaction, and the influence of SST on synoptic eddies [7,19,20,21,22]. For instance, Hu et al. (2020) [20] demonstrated that synoptic eddies will be stronger (weaker) during the years with late (early) withdrawal date.
Furthermore, it has also been noted that the SST in the central equatorial Pacific is positively correlated with synoptic scale eddy kinetic energy over the northwest Pacific during boreal summer [21]. In short, the energy cycle has been widely utilized in the study of synoptic eddies. In this study, the energy cycle was applied to investigate the potential influence of the SST in the Indian Ocean on synoptic eddies in the SCS-PS, which remains unclear.
The main purpose of this paper was to explore and discuss the influence of the SST in the northwest Indian Ocean on synoptic eddies in the South China Sea-Philippine Sea using statistical analysis and numerical simulation. This paper is divided into four sections. Section 2 introduces the data, methods and numerical models employed in this study; Section 3 describes the underlying process and SST forcing, leading to anomalous synoptic eddies in the SCS-PS. Finally, the results are summarized in Section 4.
2. Data and Methods
Daily atmosphere parameters were obtained from the National Centers for Environmental Prediction (NCEP2; Kanamitsu et al., 2002 [23]), including geopotential height, air temperature, horizontal wind, and vertical velocity. The NCEP2 reanalysis contained 17 vertical levels extending from 1000 to 10 hPa, where each level had a horizontal resolution of 2.5° × 2.5°. The NOAA Extended Reconstruction Sea Surface Temperature version 5 (ERSSTv5; Huang et al., 2017 [24]) dataset, with a horizontal resolution of 2° × 2°, was employed to determine SST. The study period was from 1979 to 2020 (42 years).
Previous studies have isolated the synoptic signal by using 2–10-day [20,21], 3–8-day [1,25] or 2–8 day [26,27] bandpass filters. In this study, the synoptic signal (2–8 days) was obtained using the Lanczos bandpass filter [28]. There are several variables, such as wind speed, geopotential height, relative vorticity, air temperature, etc., that can demonstrate synoptic variation at different levels of troposphere [1,29]. In this study, the signal of horizontal wind and geopotential height were primarily considered to represent the intensity of synoptic eddies.
To calculate the synoptic scale EKE and diagnose its variation, two equations described by Hsu et al. (2009) [13] were employed, as shown below:
where overbar and prime represent the June mean and 2–8-day bandpass filtered values, respectively; is the horizontal velocity with zonal and meridional components and , respectively; denotes a three-dimensional gradient; is the time; is the air temperature; is the pressure; is the geopotential; is the gas constant of dry air; is the vertical velocity; and denotes the dissipation of EKE by frictional effects.
EKE is calculated using Equation (1). Equation (2) is the budget equation of EKE. On the right-hand side of Equation (2), CK represents barotropic energy conversion, BG is the boundary flux of geopotential, BK indicates the boundary contribution of EKE, and CE denotes baroclinic energy conversion. In addition, the term CK in Equation (2) is divided into six terms, as presented in Equation (3), which can be used to quantify the contributions of different eddy-mean flow components to the variation in barotropic energy conversion.
In this study, we further divide CK1 and CK3 to Equations (4) and (5) for figuring out the contribution of perturbation anomaly and mean flow anomaly, respectively. “[]” represents climatological mean and “{}” represents anomaly.
In addition, several statistical analysis methods were used in this study. The dominant mode of EKE in the SCS-PS (0–35° N, 100–150° E) was identified using the empirical orthogonal function (EOF) analysis. In addition, spectral analysis was employed to investigate the frequency geopotential height at 850 hPa in the SCS-PS [30,31]. A Student’s t-test is employed to examine the difference between two-sample means. The results of the numerical simulations are examined using a paired z-test.
For numerical simulations, this study used a simplified atmospheric general circulation model—Simplified Parameterizations, privitivE-Equation DYnamics (SPEEDY; Molteni 2003; Kucharski et al., 2006, 2013 [32,33,34])—which was developed by the International Centre for Theoretical Physics to simulate anomalous SST forcing on EKE over the SCS-PS. SPEEDY uses semi-implicit processing for gravity waves and parameterizes large-scale physical processes. Thus, it can easily simulate global climate anomalies caused by anomalies in SST or other meteorological elements in a local area. As a global model, SPEEDY’s boundary conditions are mainly the boundary of the underlying surface, including SST, sea ice fraction, soil temperature in the deep soil layer (about 1 m), moisture in the top soil layer and the root-zone layer, snow depth, bare-surface albedo (in the absence of snow or sea ice), and the fraction of land-surface covered by vegetation. In this study, only the boundary condition of SST was modified, and the other conditions were set to default. In addition, the horizontal and vertical resolution were set to T30, and 8 levels, respectively.
Previous studies have shown that this model can reasonably simulate the atmospheric response to anomalous SST forcings [35,36,37,38,39]. In this study, the model was firstly driven with the climatological mean of global monthly SST for 165 years. Subsequently, each of the last 160 years was used as an initial condition for sensitive simulations.
3. Results
3.1. Link between Synoptic Eddies in the SCS-PS and Northwest Indian Ocean SST
The climatological mean of the monthly synoptic scale EKE at 850 hPa is presented in Figure 1a–c, which demonstrates an active region of synoptic eddies in the SCS-PS in June and July. It was noted that synoptic eddies were substantially weaker in May. In addition, as illustrated in Figure 1d, the EOF1 of May EKE showed weak signals in the SCS-PS. For the EOF1s of June and July EKE, a negative center was located in the SCS-PS, which implied a suppression of synoptic eddies (Figure 1e,f). The three EOF1s accounted for 37.6% to 46.9% of EKE variance and passed the 0.05 significance level of the North test [40]. The corresponding time series of the EOF1s are presented in Figure 1g–i.

Figure 1.
Variation in monthly EKE in the SCS-PS. Climatological mean (1979−2020) of EKE at 850 hPa in: (a) May; (b) June; and (c) July; (d–f) EOF1s of monthly EKE at 850 hPa in the SCS-PS; (g–i) time series of EOF1s.
The relation between the SST in the Indian Ocean and EKE in the SCS-PS was examined using the correlation coefficient between monthly SST and the time series of EOF1. For SCS-PS, a significant correlation was found, as shown in Figure 2a,b, which led to a result similar to that reported by Huangfu et al. (2022) [21]: local SST is connected to the intensity of synoptic eddies. In this study, we were more interested in the modulation of the Indian Ocean. In June (Figure 2a), a significant positive correlation was found in the northwest Indian Ocean, with a maximum center in the eastern Arabian Sea. In addition, the correlation of detrended values is shown in Figure 2b, which is similar to Figure 2a. This implies that the relation between the SST in the northwest Indian Ocean and EKE is significant in June, even when the trends are removed. On the other hand, for the correlation in July, no significant signal was noted in the northwest Indian Ocean (figure not shown). This suggests that the linkage between the SST in the northwest Indian Ocean and synoptic EKE in the SCS-PS occurs on a monthly timescale. Hereafter, we will focus solely on the linkage in June.
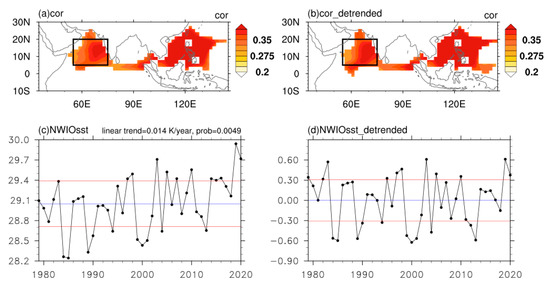
Figure 2.
Relation between June EKE and SST: (a) correlation between time series of EOF1 and SST in June; only values significant at the 0.05 significance level or better are presented; (b) similar to (a), showing the detrended signal; and (c,d) northwest Indian Ocean SST and its detrended values, respectively; blue line indicates the average and red lines indicate ±0.82 (standard deviation).
The northwest Indian Ocean SST index (NWIO) was used to measure the temporal variation in SST, which was obtained by standardizing and averaging SST over 5°–20° N and 55°–75° E (black box in Figure 2a,b). As shown in Figure 2c, a significant increasing trend was found in the NWIO. Thus, detrended variables were used for subsequent analyses. The detrended NWIO is shown in Figure 2d. Subsequently, a standard deviation of 0.82 standard deviation was chosen as the threshold to identify the 11 warmest and coldest Junes in the northwest Indian Ocean (Figure 2d), which were termed as Pos_year and Neg_year groups. The two groups were used to study anomalous atmospheric circulation in association with SST anomalies in the northwest Indian Ocean.
The difference in geopotential height between Pos_year and Neg_year (Pos_year–Neg_year) is presented in Figure 3a; a significant positive difference was found in the West Pacific. This implies a southwestward extension of the western north Pacific subtropical high. On the other hand, as presented in Figure 3b, the difference in the standard deviation of synoptic geopotential height at 850 hPa between Pos_year and Neg_year manifested a negative center in the SCS-PS. This suggests that synoptic eddies in the SCS-PS are suppressed along with warm northwest Indian Ocean SST. In addition, spectral analysis was applied to the daily geopotential height at 850 hPa over 2°–15° N,115°–140° E (black box in Figure 3a,b), for Pos_year and Neg_year. As shown in Figure 3c,d, the magnitude of the 5-day variation was notably weaker in Pos_year than in Neg_year.
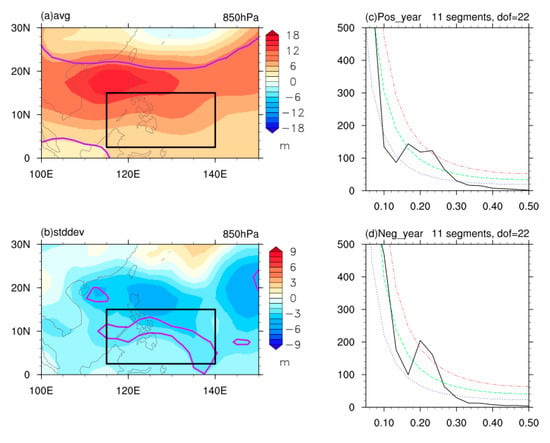
Figure 3.
Difference in geopotential height at 850 hPa between Pos_year and Neg_year: (a) June mean geopotential height at 850 hPa; (b) standard deviation of synoptic geopotential height at 850 hPa; purple counters indicate p-value of 0.05; and (c,d) spectral analysis of geopotential height at 850 hPa for the black box in (a,b) for Pos_year and Neg_year, respectively. Green, blue and red dashed lines represent the red noise spectra, and its 0.95 and 0.05 confidence intervals, respectively.
3.2. Change in the Energy Conversion of EKE over the SCS-PS in Response to Anomalous Northwest Indian Ocean SST
According to Equation (2), we calculated the difference in the terms , , , and between Pos_year and Neg_year, as illustrated in Figure 4. demonstrated a spatial pattern that was consistent with EOF1, with a negative difference in synoptic scale eddy kinetic energy in the SCS-PS. In contrast, BK showed a positive difference in the SCS-PS. For and , the difference in synoptic kinetic energy was not significant in the SCS-PS. Therefore, EOF1 is likely to be controlled by the barotropic energy conversion (term ). In addition, this also suggests a that a warm northwest Indian Ocean SST (Pos_year) is concurrent with the suppression of barotropic energy conversion.
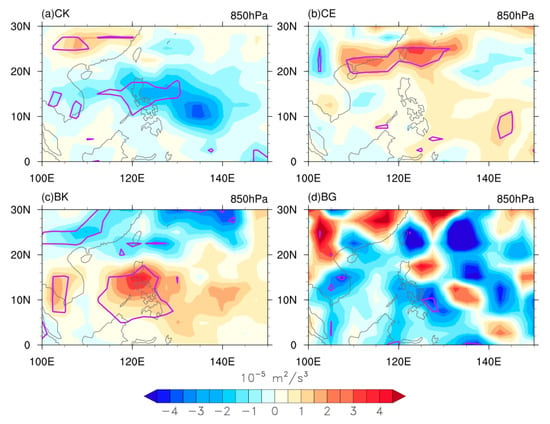
Figure 4.
Difference in terms: (a) CK; (b) CE; (c) BK; and (d) BG at 850 hPa, between Pos_year and Neg_year, in units of m2/s3; purple contours indicate the 0.05 significance level.
In order to clarify the cause of the difference in barotropic energy conversion between Pos_year and Neg_year, the term was divided into subterms, according to Equation (3), as shown in Figure 5. It was found that the subterms and dominated the difference in barotropic energy conversion between Pos_year and Neg_year. The contribution of the remaining subterms was negligible (not shown). In addition, as presented in Figure 5a, a significant negative difference in was noted at the upstream region (around 5° N and 145° E), which could play a role in suppressing the intensification of synoptic eddies during its development stage. This could weaken their intensification afterward, because of the smaller magnitude of and .

Figure 5.
Difference in subterms of the barotropic process: (a) ; and (b) at 850 hPa between Pos_year and Neg_year, in units of m2/s3; purple contours indicate p-value of 0.05.
In Equation (3), the subterms and are subject to the variation in the perturbation component ( and ) and June mean flow component ( and ). To quantify the importance of these two components for and , we replace each component with its climatological mean in each calculation, which can eliminate its contributions to the difference in subterms and . For instance, was calculated with the climatological mean . Therefore, four combinations were obtained (Figure 6). For (Figure 6a,b), the negative center in the upstream was mainly due to the meridional zonal wind gradient (). In contrast, the perturbation component () was more important in the SCS-PS. For (Figure 6c,d), both the perturbation and mean flow components are also essential to the difference in barotropic energy conversion between Pos_year and Neg_year.
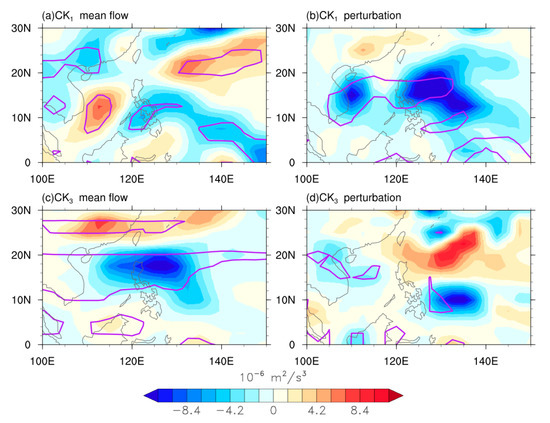
Figure 6.
Contribution of perturbation and June mean flow components to the difference in and : (a) considers the anomalous zonal gradient of June mean zonal wind only and (b) considers the turbulence flux anomaly only; (c,d) are similar to (a,b), but (c) considers the anomalous meridional gradient of June mean zonal wind only and (d) considers the turbulence flux anomaly only. Purple contours indicate p-level of 0.05.
3.3. Atmospheric Circulation Anomaly Driven by Anomalous Northwest Indian Ocean SST
As mentioned above, the change in mean flow can influence the barotropic energy conversion, which alters the intensity of synoptic eddies in the SCS-PS. The difference in horizontal wind at 850 hPa and the zonal and meridional gradients of zonal wind between Pos_year and Neg_year is presented in Figure 7. We observed an anomalous anticyclone flow over the SCS-PS along with an anomalous zonal wind gradient. At the southern part of the anomalous flow (Figure 7a), an easterly anomaly led to positive difference in the zonal gradient of zonal wind at the upstream region of the SCS-PS (around 5° N and 145° E). In addition, the anomalous anticyclone corresponded to the positive difference in the meridional gradient of the zonal wind in the SCS-PS. Thus, the variation in zonal wind affects the barotropic energy conversion between synoptic eddies and mean flow.
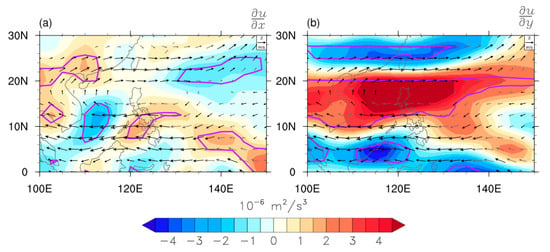
Figure 7.
Difference of horizontal wind at 850 hPa between Pos_year and Neg_year: (a,b) show the difference in the zonal and meridional gradients of zonal wind; purple contours indicate p-level of 0.05; vectors show the difference in horizontal wind at 850 hPa.
Figure 8 depicts the difference in atmospheric circulation over the tropical western Indian Ocean and the western Pacific Ocean between Pos_year and Neg_year. The difference showed upper-level divergence and a rising motion over the northwest Indian Ocean, and convergence and a sinking motion in the SCS-PS (Figure 8a,b). In addition, the easterly wind in the lower troposphere formed a closed loop of the anomalous overturning circulation (Figure 8c). Therefore, the Walker circulation was suppressed, concurrent with the warm northwest Indian Ocean SST.
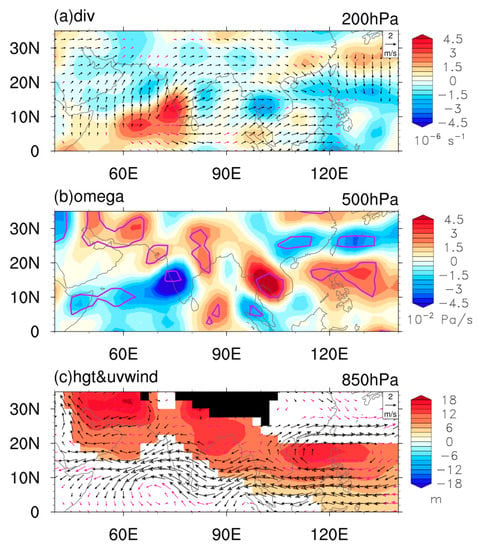
Figure 8.
Difference in atmospheric circulation between Pos_year and Neg_year. Shading indicates the difference in: (a) divergence at 200 hPa; (b) vertical motion at 500 hPa; and (c) geopotential height at 850 hPa. In (a,c), vectors show the difference in divergent wind at the corresponding levels; black vectors indicate better than the 0.05 significance level. In (b), purple contours indicate the p-value at a significance level of 0.05. In (c), only the difference in geopotential height exceeding the 0.05 significance level is presented. Values below the ground surface are shaded black.
SPEEDY was utilized to examine the forcing of a warm northwest Indian Ocean SST on Walker circulation and zonal wind in the SCS-PS. June SST anomalies over northwest Indian Ocean (black box in Figure 2c) were added to drive the warm and cold northwest Indian Ocean simulations. The difference between the two simulations (warm—cold northwest Indian Ocean simulations) demonstrated the suppression of EKE around the Philippine Sea (Figure 9a) and an anomalous anticyclonic flow in the SCS-PS (Figure 9b,c). For the difference in the zonal gradient of zonal wind (Figure 9b), a positive center was noted upstream of the SCS-PS. Additionally, for the difference in the meridional gradient of zonal wind (Figure 9c), a positive center was located in the SCS-PS. Thus, the results of the numerical simulations were generally consistent with the difference between Pos_year and Neg_year, as presented in Figure 7a,b. This implies that a warm northwest Indian Ocean SST can induce anomalous anticyclonic flow in the SCS-PS, which suppresses the barotropic energy conversion and synoptic scale EKE.
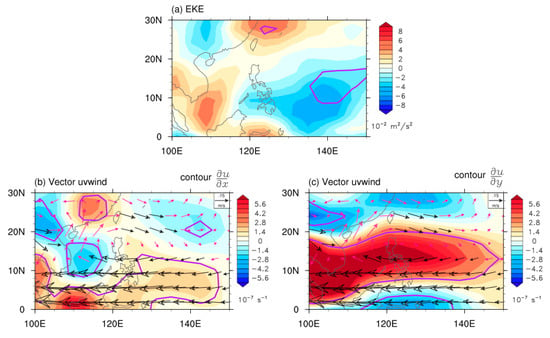
Figure 9.
Difference in: (a) EKE; and the (b) zonal and (c) meridional gradient of zonal wind between warm and cold northwest Indian Ocean SST simulations using SPEEDY. In (b,c), vectors are the difference in horizontal wind at 850 hPa; black vectors indicate better than the 0.05 significance level.
Figure 10 shows the differences in atmospheric circulation across the tropical western Indian Ocean and the western Pacific. In the upper troposphere, there was divergence and rising motion at the Arabian Sea area, while convergence and sinking motion were observed around the SCS-PS (Figure 10a,b). There was also an obvious difference in easterly wind from the Philippine Sea to the Arabian Sea, which suggests a weakened overturning circulation (Figure 10c). A positive geopotential height difference also appeared at 850 hPa over the SCS-PS, which corresponded to a center of anomalous anticyclone flow. Therefore, the numerical model was able to simulate the influence of northwest Indian Ocean SST on Walker circulation.
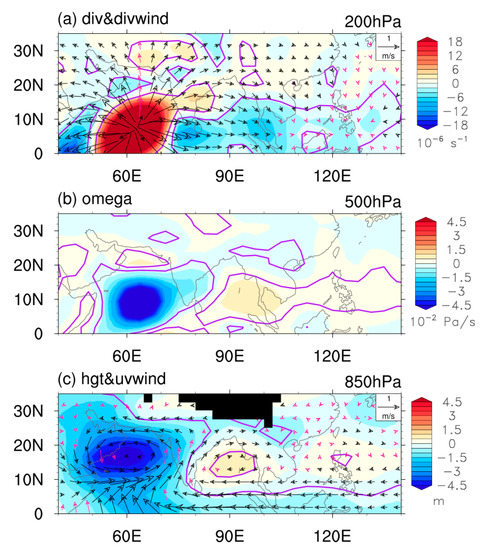
Figure 10.
Similar to Figure 8, but for the difference between warm and cold northwest Indian Ocean simulations using SPEEDY.
4. Discussion
The results of this study suggest that the SST in the northwest Indian Ocean modulates the intensity of synoptic eddies in the South China Sea-Philippine Sea (SCS-PS) in June. The possible mechanism is summarized in a schematic diagram presented in Figure 11. Northwest Indian Ocean SST warming (cooling) may induce anomalously warm (cold) near-surface temperatures and anomalous rising motion in the western Indian Ocean, which weakens (enhances) the Walker circulation in the tropical western Indian Ocean and the western Pacific. Thus, an anomalous anticyclonic (cyclonic) flow is induced in the SCS-PS. The change in June mean flow decreases (increases) the barotropic energy conversion between synoptic eddies and mean flow and subsequently weakens (intensifies) the synoptic eddies. The results of the numerical simulations also support this conclusion.
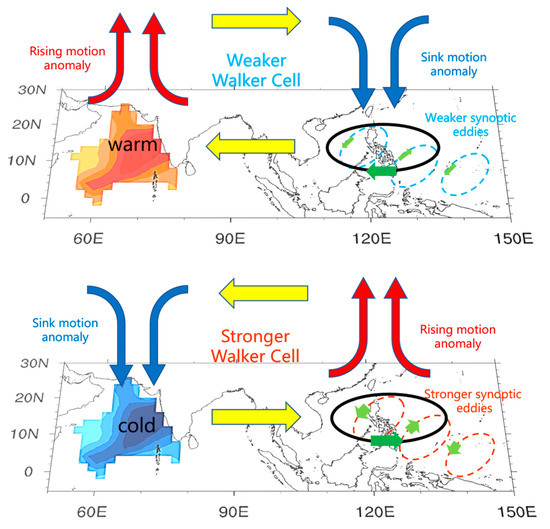
Figure 11.
Schematic diagram. The upper panel shows the impact of warmer SSTs in the northwest Indian Ocean on synoptic eddies in the SCS-PS, while the lower panel shows the effect of cooler SSTs.
In the numerical simulation, it was noted that the anomaly of EKE determined using SPEEDY was much weaker than that determined via observation. This could possibly be due to the bias of June mean flow between the model and real atmosphere. In addition, the contribution of other ocean basins, inter-ocean basin interactions, and atmospheric intraseasonal oscillation also influence June mean flow and synoptic eddies in the SCS-PS [2,10,13]. Additionally, the bias in the simulation could be also due to excluding local SST in the SCS-PS. As presented in Huangfu et al. (2022) [21] and Figure 2a,b in this study, a significant relation is found between synoptic-scale eddies and local SST in the SCS-PS. Hence, future studies are needed to clarify the relative contributions of the northwest Indian Ocean, other ocean basins and local SST to synoptic eddies in the SCS-PS.
Additionally, the trend of global warming has been shown to be reflected in the state of the ocean and atmosphere. Bader and Latif (2003) [41] pointed out that the equatorial Indian Ocean SST has shown a significant upward trend since 1950. The work of Sharma et al. (2022) [42] reported that with the gradual increase in SST in the northwest Indian Ocean, the Walker circulation in the Indian Ocean is gradually weakening and may disappear. However, long-term changes in the intensity of synoptic eddies in the SCS-PS and the contribution of SST in the northwest Indian Ocean to these future changes remain unclear.
Author Contributions
Conceptualization, M.L., M.Y.-T.L. and D.W.; methodology, M.L.; software, W.F.; writing—original draft preparation, M.L.; writing—review and editing, M.Y.-T.L. and D.W.; project administration, W.Y.; funding acquisition, W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This study was jointly supported by the National Natural Science Foundation of China (Grant 92158204); the Science and Technology Program of Guangzhou, China (grant no. 202102020939); the Fundamental Research Funds for the Central University, Sun Yat-Sen University (grant no. 22qntd2202); and the Key Laboratory of South China Sea Meteorological Disaster Prevention and Mitigation of Hainan Province (grant no SCSF202002).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Daily NCEP/DOE Reanalysis II data from 1979 to 2020 were obtained from the NOAA Physical Sciences Laboratory, Boulder, Colorado, USA, https://psl.noaa.gov (accessed on 15 August 2020; Kanamitsu et al., 2002). and Monthly ERSST (Version 5) was obtained from the NOAA National Centers for Environmental Information, https://doi.org/10.7289/V5T72FNM (Huang et al., 2017).
Conflicts of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Lau, K.; Lau, N. Observed structure and propagation characteristics of tropical summertime synoptic scale disturbances. Mon. Weather Rev. 1990, 118, 1888–1913. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Li, T.; Tsou, C.-H. Interactions between Boreal Summer Intraseasonal Oscillations and Synoptic-Scale Disturbances over the Western North Pacific. Part I: Energetics Diagnosis. J. Clim. 2011, 24, 927–994. [Google Scholar] [CrossRef]
- Li, T. Origin of the Summertime Synoptic-Scale Wave Train in the Western North Pacific. J. Atmos. Sci. 2006, 63, 1093–1102. [Google Scholar] [CrossRef]
- Fu, B.; Li, T.; Peng, M.S.; Weng, F. Analysis of tropical cyclogenesis in the western North Pacific for 2000 and 2001. Weather Forecast 2007, 22, 763–780. [Google Scholar] [CrossRef]
- Yuan, J.; Li, T.; Wang, D. Precursor synoptic-scale disturbances associated with tropical cyclogenesis in the South China Sea during 2000–2011. Int. J. Climatol. 2015, 35, 3454–3470. [Google Scholar] [CrossRef]
- Xu, Y.; Li, T.; Peng, M. Roles of the synoptic-scale wave train, the intraseasonal oscillation, and high-frequency eddies in the genesis of Typhoon Manyi (2001). J Atmos Sci. 2014, 71, 3706–3722. [Google Scholar] [CrossRef]
- Zhou, H.; Hsu, P.-C.; Qian, Y. Close linkage between quasi-biweekly oscillation and tropical cyclone intensification over the western North Pacific. Atmos. Sci. Lett. 2018, 19, e826. [Google Scholar] [CrossRef]
- Liu, H.B.; Yan, R.J.; Wang, B.; Chen, G.H.; Ling, J.; Fu, S.M. Multiscale combined action and disturbance characteristics of pre-summer extreme precipitation events over South China. Adv. Atmos. Sci. 2022, in press. [Google Scholar] [CrossRef]
- Hu, P.; Chen, W.; Li, Z.; Chen, S.; Wang, L.; Liu, Y. Close Linkage of the South China Sea Summer Monsoon Onset and Extreme Rainfall in May over Southeast Asia: Role of the Synoptic-Scale Systems. J. Clim. 2022, 35, 4347–4362. [Google Scholar] [CrossRef]
- Wang, W.; Zhou, W.; Li, X.; Wang, X.; Wang, D. Synoptic-scale characteristics and atmospheric controls of summer heat waves in China. Clim. Dyn. 2016, 46, 2923–2941. [Google Scholar] [CrossRef]
- Leung, M.Y.-T.; Zhou, W.; Cheung, K.Y.; Gong, H.N.; Zhang, Y. Enhancement of lower tropospheric winter synoptic temperature variations in Southwest China and the northern Indochina Peninsula after 2010. Clim. Dyn. 2019, 53, 2281–2294. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, M.; Wang, H.; Wang, L.; Liu, S.; Zong, L.; Zhang, Y.; Li, Y. Dual effects of synoptic weather patterns and urbanization on summer diurnal temperature range in an urban agglomeration of East China. Front. Environ. Sci. 2021, 9, 672295. [Google Scholar] [CrossRef]
- Hsu, P.-C.; Tsou, C.-H.; Hsu, H.-H.; Chen, J.-H. Eddy energy along the tropical storm track in association with ENSO. J. Meteorol. Soc. Jpn. 2009, 87, 687–704. [Google Scholar] [CrossRef]
- Zeng, L.; Li, X.; Du, Y.; Shi, R.; Yao, J.; Wang, D.; Sui, D. Synoptic-scale disturbances over the northern South China Sea and their responses to El Niño. Acta Oceanol. Sin. 2012, 31, 69–78. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhou, W.; Chan, J.C.L.; Li, C. Impacts of the basin-wide Indian Ocean SSTA on the South China Sea summer monsoon onset. Int. J. Climatol. 2008, 28, 1579–1587. [Google Scholar] [CrossRef]
- Leung, M.Y.T.; Zhou, W.; Wang, D.; Chan, P.W.; Lee, S.M.; Tong, H.W. Remote tropical Western Indian ocean forcing on changes in June precipitation in South China and the Indochina Peninsula. J. Clim. 2020, 33, 7553–7566. [Google Scholar] [CrossRef]
- Lorenz, E.N. Available Potential Energy and the Maintenance of the General Circulation. Tellus 1955, 7, 157–167. [Google Scholar] [CrossRef]
- Ulbrich, U.; Speth, P. The Global Energy Cycle of Stationary and Transient Atmospheric Waves: Results from ECMWF Analyses. Meteorol. Atmos. Phys. 1991, 45, 125–138. [Google Scholar] [CrossRef]
- Leung, M.Y.-T.; Cheung, H.H.N.; Zhou, W. Energetics and dynamics associated with two typical mobile trough pathways over East Asia in boreal winter. Clim. Dyn. 2015, 44, 1611–1626. [Google Scholar] [CrossRef]
- Hu, P.; Huangfu, J.; Chen, W.; Huang, R. South China Sea summer monsoon withdrawal and the synoptic-scale wave train over the western North Pacific. Int. J. Climatol. 2020, 40, 5599–5611. [Google Scholar] [CrossRef]
- Huangfu, J.; Cao, X.; Wu, R.; Chen, G.; Chen, W. Influences of central Pacific warming on synoptic-scale wave intensity over the northwest Pacific. Clim. Dyn. 2022, 58, 555–567. [Google Scholar] [CrossRef]
- Yang, M.; Li, C.; Li, X.; Chen, X.; Li, L. The linkage between midwinter suppression of the North Pacific storm track and atmospheric circulation features in the Northern Hemisphere. Adv. Atmos. Sci. 2022, 39, 502–518. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP-DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1643. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended Reconstructed Sea Surface Temperature, Version 5 (ERSSTv5): Upgrades, Validations, and Intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Lau, K.; Lau, N. The energetics and propagation dynamics of tropical summertime synoptic-scale disturbances. Mon. Weather Rev. 1992, 120, 2523–2539. [Google Scholar] [CrossRef]
- Fukutomi, Y.; Kodama, C.; Yamada, Y.; Noda, A.T.; Satoh, M. Tropical synoptic-scale wave disturbances over the western Pacific simulated by a global cloud-system resolving model. Theor. Appl. Climatol. 2016, 124, 737–755. [Google Scholar] [CrossRef]
- Ha, Y.; Zhong, Z.; Zhao, H.; Zhu, Y.; Hu, Y. A Climatological Perspective on Extratropical Synoptic-Scale Transient Eddy Activity Response to Western Pacific Tropical Cyclones. Adv. Atmos. Sci. 2022, 39, 333–343. [Google Scholar] [CrossRef]
- Duchon, C.E. Lanczos Filtering in One and Two Dimensions. J. Appl. Meteorol. 1979, 18, 1016–1022. [Google Scholar] [CrossRef]
- Belu, R.; Koracin, D. Statistical and Spectral Analysis of Wind Characteristics Relevant to Wind Energy Assessment Using Tower Measurements in Complex Terrain. J. Wind Energy 2013, 2013, 739162. [Google Scholar] [CrossRef]
- Kaya, E.; Barutcu, B.; Mentes, S.S. A method based on the Van der Hoven spectrum for performance evaluation in prediction of wind speed. Turk. J. Earth Sci. 2013, 22, 12. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Pavel, G.K.; Evgeniy, A.K.; Mansur, A.I.; Shuhrat, A.E.; Yusufjon, A.T. Energy Spectra of Atmospheric Turbulence for Calculating C2n Parameter. I. Maidanak and Suffa Observatories in Uzbekistan. Atmosphere 2021, 12, 1614. [Google Scholar] [CrossRef]
- Molteni, F. Atmospheric simulations using a GCM with simplified physical parametrizations. I: Model climatology and variability in multi-decadal experiments. Clim. Dyn. 2003, 20, 175–191. [Google Scholar] [CrossRef]
- Kucharski, F.; Molteni, F.; Bracco, A. Decadal interactions between the western tropical Pacific and the North Atlantic Oscillation. Clim. Dyn. 2006, 26, 79–91. [Google Scholar] [CrossRef]
- Kucharski, F.; Molteni, F.; King, M.P.; Farneti, R.; Kang, I.S.; Feudale, L. On the need of intermediate complexity general circulation models: A “SPEEDY’’ example. Bull. Am. Meteorol. Soc. 2013, 94, 25–30. [Google Scholar] [CrossRef]
- Jian, Y.; Lin, X.; Zhou, W.; Jian, M.; Leung, M.Y.-T.; Cheung, P.K.Y. Analysis of record-high temperature over southeast coastal China in winter 2018/19: The combined effect of mid- to high-latitude circulation systems and SST forcing over the North Atlantic and tropical western Pacific. J. Clim. 2020, 33, 8813–8831. [Google Scholar] [CrossRef]
- Jian, Y.; Leung, M.Y.-T.; Zhou, W.; Jian, M.; Yang, S.; Lin, X. Interdecadal shift of the relationship between ENSO and winter synoptic temperature variability over the Asian–Pacific–American region in the 1980s. J. Clim. 2021, 34, 5321–5335. [Google Scholar] [CrossRef]
- Leung, M.Y.-T.; Wang, D.; Zhou, W.; Cheung, P.K.Y.; Jian, Y.; Xiao, F. Joint effect of West Pacific warming and the Arctic Oscillation on the bidecadal variation and trend of the East Asian trough. J. Clim. 2022, 35, 2491–2501. [Google Scholar] [CrossRef]
- Leung, M.Y.-T.; Wang, D.; Zhou, W.; Zhang, Y.; Wang, L. Interdecadal variation in available potential energy of stationary eddies in the midlatitude Northern Hemisphere in response to the North Pacific Gyre Oscillation. Geophys. Res. Let. 2022, 49, e2022GL098297. [Google Scholar] [CrossRef]
- Feng, W.; Leung, M.Y.-T.; Wang, D.; Zhou, W.; Zhang, O.Y.W. An extreme drought over South China in 2020/21 concurrent with an unprecedented warm Northwest Pacific and La Niña. Adv. Atmos. Sci. 2022, 39, 1637–1649. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling Errors in the Estimation of Empirical Orthogonal Functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Bader, J.; Latif, M. The impact of decadal-scale Indian Ocean sea surface temperature anomalies on Sahelian rainfall and the North Atlantic Oscillation. Geophys. Res. Lett. 2003, 30, 2169. [Google Scholar] [CrossRef]
- Sharma, S.; Ha, K.J.; Cai, W.; Chung, E.S.; Bódai, T. Local meridional circulation changes contribute to a projected slowdown of the Indian Ocean Walker circulation. NPJ Clim. Atmos. Sci. 2022, 5, 15. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).