Reduced Sea-Surface Roughness Length at a Coastal Site

Abstract

Sea-surface roughness length is a key parameter for characterizing marine atmospheric boundary layer. Although aerodynamic roughness lengths for homogeneous land and open water surfaces have been examined extensively, the extension of relevant knowledge to the highly inhomogeneous coastal area is problematic due to the complex mechanisms controlling coastal meteorology. This study presented a lidar-based observational analysis of sea-surface roughness length at a coastal site in Hong Kong, in which the wind data recorded from March 2012 to November 2015 were considered and analyzed. The results indicated the turning of wind near the land-sea boundary, leading to a dominative wind direction parallel to the coastline and an acceleration in wind. Moreover, the roughness lengths corresponding to two representative azimuthal sectors were compared, in which the roughness lengths for the onshore wind sector (i.e., 120°–240°) appear to be larger than the constant value (z₀ = 0.2 mm) recommended in much existing literature, whereas the values for the alongshore wind sector (i.e., 60°–90°) are significantly smaller, i.e., about two orders of magnitude less than that of a typical sea surface. However, it is to be noted that the effect of atmospheric stability, which is of crucial importance in governing the marine atmospheric boundary layer, is not taken into account in this study.

1. Introduction

Proper understanding of marine atmospheric boundary layer (MABL) is meeting growing attention [1,2,3,4], taking into account the substantial increase in coastal and offshore activities, such as the construction of marine structures (e.g., oil platform) and implementation of ocean-based renewable energy technologies (e.g., offshore wind farm). On the other hand, the knowledge of MABL also reveals practical importance in a wide variety of applications, spanning from shipping and fishing, coastal management, and pollution control to prediction of coastal weather and sea states [5,6]. However, it is well recognized that the ABL characteristics at coastal regions are more complicated than those at relatively homogeneous land and open sea terrains, which is mainly attributed to the inherent heterogeneity of the coastal site [7]. Factors affecting the boundary layer characteristics in the coastal site can be multi-fold. Fuentes et al. [8] addressed that the coastal atmospheric boundary layer is influenced by complex physical processes associated with variation in terrain conditions and strong gradients in moisture, temperature, and surface roughness. Rogers [7] underscored that the understanding of coastal meteorology requires the combined knowledge of the interaction of marine and land atmospheric boundary layers, air-sea interaction, large-scale atmospheric dynamics, as well as the circulation of the coastal ocean. A more detailed interpretation and discussion on the factors affecting coastal meteorology was presented by Barthelmie et al. [9] and Barthelmie [10], which mainly consists of air-sea temperature differences, orientation of the coastline, prevailing wind speed and direction, water depth, latitude, distance from the coastal discontinuity, and fetch distance.

For the characterization of MABL, the assessment of sea-surface roughness has received much attention [4,11,12,13,14,15,16]. For example, Anctil and Donelan [2] focused on the effect of shoaling waves (i.e., wave steepness and celerity) on the aerodynamic roughness of the water surface. Essentially, sea-surface roughness is one of the key parameters for describing MABL [15]. For both large-eddy simulations and global general circulation models, air-sea turbulence fluxes are usually parametrized by means of a bulk flux formula and Monin–Obukhov similarity theory, in which the sea-surface roughness lengths for momentum, heat, and moisture are important inputs [17]. Moreover, understanding the sea-surface aerodynamic roughness in a quantitative manner is imperative with respect to diagnosing air-sea interaction, and therefore aiding the study of global energy and water cycle [18]. The surface roughness length for a given location over land is generally specified to be constant depending on the terrain condition, whereas the roughness length over the sea can be highly variant, which depends strongly on the time-dependent air-sea momentum transfer via the wind-driven surface wave field [18,19]. Moreover, it has been widely acknowledged that the effect of atmospheric stability is of crucial importance in governing the properties of MABL. Kara et al. [20] presented a quantitative assessment on the spatial and temporal variability of the impact of air-sea stratification on the difference between satellite-derived equivalent neutral wind speeds and stability-dependent in situ wind data. Sathe and Bierbooms [21] highlighted that the cooling and heating of the sea surface occurs throughout the diurnal cycle, which causes different stability conditions (i.e., stratifications) and hence affects the vertical wind profiles. Likewise, Holtslag et al. [22] found that wind shear at offshore sites depends strongly on atmospheric stability, especially for stable conditions. The shear profiles that do not consider stability deviate distinctly from the stability-dependent observations.

Johnson et al. [23] highlighted that the momentum exchange at the air-sea interface plays an important role in many processes (e.g., wind-wave growth, storm surges, and atmospheric circulation). One of the common approaches to characterize such momentum exchange is by using the aerodynamic roughness length. The aerodynamic roughness length determines the level of turbulence near the air-sea interface and thus determines the wind stress [23,24]. The sea-surface aerodynamic roughness is strongly correlated with the surface wave characteristics, such as the wavelength, the development state, and the phase speed of waves [6,16,25,26,27]. Lange et al. [4] noted that the surface roughness over water is relatively low as compared to that over land. More importantly, it is closely tied with the wave field, which in turn is determined by the wind speed, fetch distance, etc. Nevertheless, for ease of usage, a constant surface roughness length (z₀) of about 0.2 mm has been widely used in existing literature, e.g., wind resource estimation program WAsP [28] and Charnok relation [29].

On the other hand, numerous studies have indicated that the roughness length over shallow waters is likely to be larger than the corresponding values over the deep open ocean [16,26,27]. Kim et al. [6] reported that the sea-surface waves over shallow waters in coastal regions are influenced by the topographic characteristics of the seafloor, e.g., the water depth, the direction of the coastline relative to the prevailing wind, as well as the shape of the terrain. Likewise, Gao et al. [1] highlighted that the surface aerodynamic roughness for coastal shallow water surface appears to differ from those for deepwater surface, and thus the roughness length in terms of wave age or significant wave height should be treated differently. In a nutshell, sea-surface waves at the coastal region are modulated by more complicated mechanisms than those encountered in the open waters.

Previous studies on atmospheric boundary layer are mostly associated with horizontally homogeneous terrains (land or open waters), the extension of relevant knowledge to coastal site might be less accurate, given that the mechanisms governing the coastal meteorology are much more complex. The authors have carried out a comparative study with emphasis on the performance of various micrometeorological methods and direct modeling methods for characterizing marine surface roughness at coastal sites [13]. This study is a follow-up and extension of our previous work, with particular emphasis on identifying and discussing unprecedented values of marine surface roughness. The remaining contents in this paper are structured as follows: Section 2 details the information related to the observation site and instruments, Section 3 presents results and discussion of the lidar-based observation, and Section 4 summarizes the major conclusions.

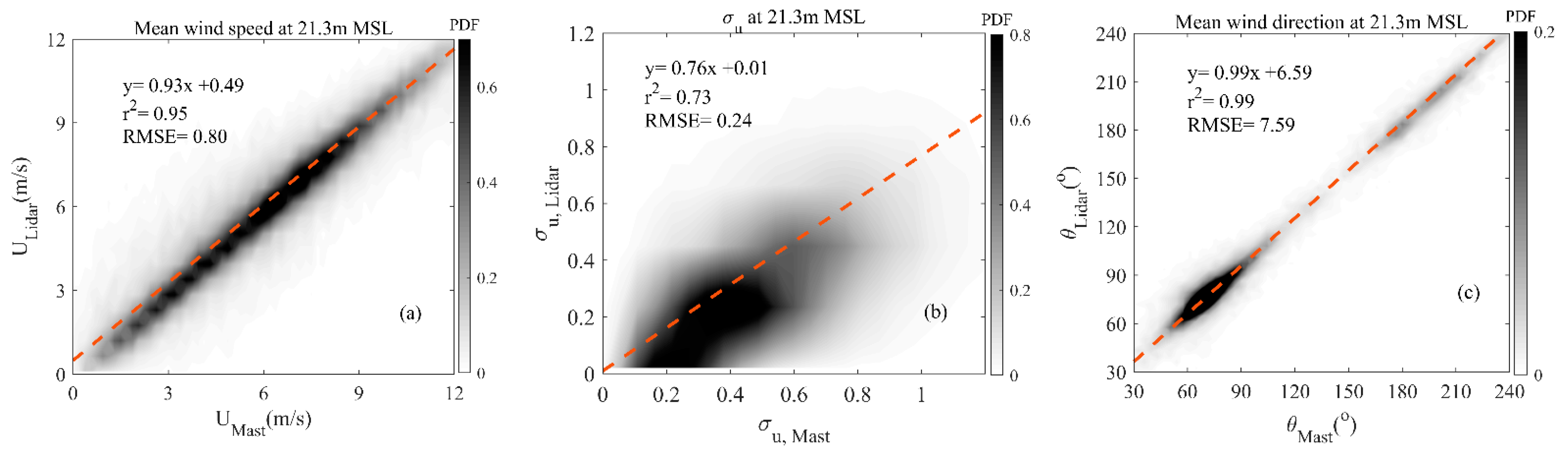
2. Site Description and Data Collection

The wind data involved in the current study were obtained at an offshore platform located in the southern waters of the Lamma Island in Hong Kong, with a nearest distance of about 3.5 km (see Figure 1). Cheung Chau Island and Lantau Island are located off the northwest of the platform, with a distance of, respectively, 9 and 15 km. As Figure 1 shows, the platform is exposed to fairly featureless terrain within the range of 60°–240° [13,30,31]. The average water depth around the platform is approximately 20 m. The offshore platform was equipped with a comprehensive wind observation system consisting of a traditional wind mast and a light detection and ranging (lidar) system. The measurement campaign was carried out continuously during the period from March 2012 to November 2015.

As can be seen in Figure 1, the wind mast on the offshore platform is of a lattice structure design, and the total height of the mast is 22 m. For wind data measurement, two side-mounted A100L2 cup anemometers (Vector Instrument) were installed in pairs at 21.3 m above mean sea level (MSL), which were oriented toward the northwest (denoted as NW anemometer, hereafter) and southeast (SE anemometer, hereafter), respectively. Measurements of wind direction were taken by a wind vane (manufactured by Vector Instrument) at 18.6 m MSL, which was oriented toward the southeast. All the cup anemometer and wind vane were mounted on horizontal cylindrical booms with a distance of 2.3 m to the center of the mast to minimize the flow distortion caused by the physical structure of the mast. The cup anemometer and wind vane were pre-configured to record instantaneous data at a sampling frequency of 1 Hz, which were further averaged and output at every 10 min using a CR3000 micro-logger system (manufactured by Campbell Scientific). In essence, the wind mast data is used for validating the fidelity of wind lidar measurement.

The offshore platform was equipped with a second-generation Galion G250 Lidar Unit (distributed by SgurrEnergy), which provides multi-level wind measurement up to 250 m. The wind lidar unit was positioned on the southwest corner of the platform, and the distance between the wind lidar and the mast is 2.3 m. The wind lidar used in the current study is a pulsed laser device. In order to capture the wind at different levels, the wind lidar emits laser pulses into the atmosphere, and these laser pulses are subsequently reflected by the aerosols in the atmosphere. In this case, the along-beam velocity can be estimated based on the frequency shift using the Doppler equation [32,33]. In this study, the wind lidar unit was configured into velocity azimuth display (VAD) mode, in which the elevation angle was fixed, whereas the azimuth angle varied over a circle at an angular speed of ≈30°/s. To enhance the fidelity of the lidar measurement, the original high-resolution lidar data were filtered by the wind field reconstruction and a carrier-to-noise (CNR) filter. For comparison purposes, the wind lidar also outputs the mean and standard deviation of horizontal wind speed and mean horizontal wind direction every 10-min.

It is to be noted that, unlike other wind lidar observation studies where the measurement height is uniformly distributed (i.e., with a constant height increment), the pre-specified measurements height in the current study are two-fold, i.e., the lower observation region (21.3 to 44.1 m) characterizes a vertical increment of 2.5 m, while in the upper region (44.1 to 178.3 m), it increases at an interval of 20 m.

The accuracy and reliability of wind lidar data were evaluated standardly via comparison with their wind mast counterparts at equivalent height, as shown in Figure 2. The agreements are overall satisfactory, particularly with respect to the comparison of mean wind speed and mean wind direction, which, respectively, yield a regression slope of 0.93 and 0.99, and a correlation coefficient above 0.95. The root mean square error (RMSE) for mean wind speed is 0.80 m/s, and that for mean wind direction is 7.59°. The comparison of the standard deviation of wind speed is somewhat less gratifying, resulting in a regression slope of 0.76 and a correlation coefficient of 0.73. The attenuation of lidar-based measurement of the standard deviation of wind speed has also been observed by Peña et al. [34], Wagner et al. [35], and Shu et al. [36]. It has been well documented that the conically scanning wind lidar has an inherent low-pass filter for wind speed spectrum when measuring wind speeds over the probe length, which may filter out turbulence structures that are of smaller length scale than the probe length. As a consequence, the turbulence characterizing a length scale smaller than the probe length cannot be accurately resolved, which could lead to attenuation. In the following analysis, the validated wind lidar data are used unless otherwise specified.

It should be mentioned that due to the lack of proper temperature measurement data, the stability condition of the atmosphere cannot be determined using traditional methods. Alternatively, Basu [37,38] proposed a simple method for the characterization of atmospheric stability, which depends purely on wind speed data. For a better interpretation of atmospheric stratification, the Obukhov length (L) can be determined step by step as follows:

(1) Calculate R based on wind speed measured at three different heights:

$$R=\frac{\Delta U_{31}}{\Delta U_{21}}=\frac{\ln \left(\frac{z_3}{z_1}\right)-{\psi }_M\left(\frac{z_3}{L}\right)+{\psi }_M\left(\frac{z_1}{L}\right)}{\ln \left(\frac{z_2}{z_1}\right)-{\psi }_M\left(\frac{z_2}{L}\right)+{\psi }_M\left(\frac{z_1}{L}\right)}$$

(1)

where ${\psi }_M$ is the stability correction term. $\Delta U_{31}$ is the wind speed difference measured at heights $z_3$ and $z_1$, and $\Delta U_{21}$ is the wind speed difference measured at heights $z_2$ and $z_1$

(2) Calculate R_N according to the given heights, assuming $z_3>z_2>z_1$:

$$R_N=\frac{\ln \left(\frac{z_3}{z_1}\right)}{\ln \left(\frac{z_2}{z_1}\right)}$$

(2)

(3) Estimate the Obukhov length (L) using the empirical ${\psi }_M$ functions [39,40,41]. If $R>R_N$, then use Equation (1) in conjunction with Equation (3). Conversely, if $R<R_N,$ then use Equation (4) instead of Equation (3).

$${\psi }_M=2 \ln \left(\frac{1+x}{2}\right)+\ln \left(\frac{1+x^2}{2}\right)-2ta{n}^{-1}x+\frac{\pi }{2}$$

(3)

$${\psi }_M=-\frac{5z}{L}$$

(4)

in which $x={\left(1-\frac{16z}{L}\right)}^{1/4}$.

Table 1. Classification of atmospheric stratification in this study.

Category	Description	L (m)	R (−)	Percentage
A	Unstable	$-200<L\le -100$	$1.684<R\le 1.686$	1.5%
B	Near-neutral unstable	$-500<L\le -200$	$1.686\le R<1.691$	2.4%
C	Neutral	$\left|L\right| \ge 500$	$1.691\le R\le 1.795$	65.7%
D	Near-neutral stable	$200 \le L<500$	$1.795<R\le 1.830$	22.1%
E	Stable	$50 \le L<200$	$1.830<R\le 1.850$	8.3%

outlines the classification of atmospheric stratification in this study based on the calculated values of R. It is to be noted that the method proposed by Basu [37,38] is valid primarily within the surface boundary layer. Therefore, the calculation of R in this study is based on wind speed data recorded at z₁ = 31.4 m, z₂ = 41.5 m, and z₃ = 63.0 m. As can been seen, the atmospheric boundary layer within the considered coastal region is mostly neutral (65.7%) or near-neutral stable (22.1%) over the measurement period. This is similar to the results presented by Sathe et al. [42]. In this case, it can be reasonably assumed that the data involved in the current study were collected under neutrally stratified conditions.

3. Results and Discussion

Prior to the assessment of sea-surface roughness length, it is imperative to obtain a general picture of the coastal atmospheric boundary layer. Figure 3 compares the distribution of wind speed and wind direction measured at the offshore platform and that at a nearby reference station (CCH, see Figure 1). The reference station is located in the southern part of Cheung Chau Island, with a distance of 9 km to the platform. Notwithstanding the relatively short distance between CCH and the offshore platform, site-to-site variability in their respective wind rose plot is apparent. Not only the wind speed measured at the offshore platform appears to be larger than its counterpart at CCH, but the dominative wind direction is also markedly different. A large fraction of wind measured at CCH comes from east and southeast directions. In contrast, the wind measured at the offshore platform is dominated by prevailing east-northeasterly (ENE) wind, which is more or less parallel to the main coastline at Lamma Island. It is anticipated that the discrepancies in terms of wind speed and prevailing wind direction are partly associated with the existence of a lateral, orographic boundary layer near the land-sea transition region near Lamma Island. Evidence has shown that such a boundary layer is likely to accelerate the wind and constrain the flow parallel to the coastline [7,43,44].

To further examine the potential effect of upstream terrain, Figure 4 depicts the vertical profiles of horizontal wind speed within two selected directional sectors. Since the winds within realistic boundary layer tend to be unsteady in nature [45,46,47,48,49,50,51,52,53] and individual wind profiles can be highly variant in terms of both shape and magnitude, composite analysis is often used as a useful tool to construct more representative wind profiles [49,54,55,56,57]. Specifically, all individual wind profiles in this study are grouped in accordance with their mean boundary layer (MBL) wind speed and wind direction, and thus the ensemble-average wind profile for each group can be determined.

As can be seen in Figure 4, the vertical distribution of wind speed follows well to the logarithmic-law model, and hence wind profile method can be applied to determine the aerodynamic roughness length. The wind profile method is a direct method to estimate aerodynamic roughness length [13], in which the variation of horizontal wind speed is described as [58,59,60]:

$$U\left(z\right)=\frac{u_{*0}}{\kappa }[\ln \left(\frac{z}{z_0}\right)-{\mathsf{\psi }}_m\left(\frac{z}{L}\right)]$$

(5)

in which $U\left(z\right)$ is the mean wind speed at height z, $u_{*0}$ is the friction velocity, $\kappa \approx 0.4$ is the von Kármán constant, $z_0$ represents the aerodynamic roughness length,${ \mathsf{\psi }}_m\left(z/L\right)$ is the empirical stability function (i.e., stability correction to wind speed), and $L$ is the Obukhov length:

$$L=-u_{*0}^{3}T/(kg\overline{{\omega }^{\prime }{\theta }_v^{\prime }})$$

(6)

where $T$ denotes the absolute temperature, ${\theta }_v$ is the virtual potential temperature, and $\overline{{\omega }^{\prime }{\theta }_v^{\prime }}$ is the virtual kinematic heat flux. Note that as the stability conditions approach neutral, the magnitude of L increases. Conversely, as the conditions become increasingly unstable or stable, the magnitude of L tends toward zero. For neutrally stratified conditions, Equation (5) can be simplified as:

$$U\left(z\right)=\frac{u_{*0}}{\kappa } \ln \left(\frac{z}{z_0}\right)$$

(7)

The aerodynamic roughness length can be therewith approximated using Charnock’s relation as follows:

$$z_0=\alpha \frac{u_{*0}^2}{G}$$

(8)

in which $\alpha =0.0144$ is the Charnock parameter, $u_{*0}$ is the surface friction velocity estimated in the log-law model, and G is the gravitational acceleration. Clearly, the aerodynamic roughness length varies as a function of mean boundary layer (MBL) wind speed. It is interesting to note that the value of surface roughness length for the sector of 120°–240° appears to decrease with increasing mean wind speed, whereas for the sector of 60°–90°, a reverse correlation is more likely to occur, where the estimated aerodynamic roughness length increases in parallel with the increasing mean wind speed. Moreover, the consequent sea-surface roughness lengths for the sector of 60°–90° are much smaller in magnitude than those for the sector of 120°–240° at equivalent mean wind speeds. For example, when the mean wind speed lies in the range between 11 and14 m/s, the aerodynamic roughness length for the sector of 60°–90° is estimated to be 0.002 mm, whereas the value for the sector of 120°–240° is about 0.23 mm.

Figure 4 shows that the roughness length for the sector of 120°–240° exhibits a negative correlation with mean wind speed, i.e., decreases in magnitude as the MBL wind speed increases. This appears to contradict that in deep water. The estimated aerodynamic roughness length for sectors of 120°–240° ranges from 0.14 to 12 mm, which are larger than the typical surface roughness length specified for deep water (i.e., z₀ = 0.2 mm [4,28,29]), particularly at low wind speeds. This is qualitatively consistent with many existing measurement results, in which wind stress at shallow waters is found to be larger than that in deep water [12,26,61,62,63]. Jiménez and Dudhia [27] highlighted that a larger roughness length is essential for Weather Research and Forecasting (WRF) model for coastal shallow water because it usually exhibits more satisfactory agreement between model simulation and measurements. MacMahan [64] and Shabani et al. [65] reported a 100% increase in wind stress in shallow water as compared to deep water at low wind speeds (5–11 m/s). Chen et al. [61] addressed that the larger wind stress obtained in coastal regions is predominantly attributed to shoaling wave effect. It has been documented that when the wind-induced waves move toward the shore from intermediate into progressively shallower water, the wave height tends to increase (i.e., steepening of the dominant wave) due to the reduction in wave phase speed and increase in wave amplitude, and thus resulting in larger surface roughness [61,66]. Unfortunately, given that the wave measurement data is not available in this study, the possible effect of wave shoaling cannot be properly diagnosed. On the other hand, previous studies [67,68] have also shown that, in addition to shoaling waves, the wind stress at coastal shallow waters can also be affected by processes, such as the development of shallow stable internal boundary layer near the coast or nonstationary sub-mesoscale motions.

By contrast, the surface roughness length for the sector of 60°–90° is about two orders of magnitude less than that of typical deepwater surfaces (z₀ = 0.2 mm), especially at lower wind speed ranges (i.e., less than 15 m/s) where the consequent value lies between 10⁻⁵ and 0.006 mm. The possible causes for such small surface roughness length are likely to be two-fold. First, the relatively short fetch distance corresponding to the sector of 60°–90° is insufficient for sea waves to develop, thus lead to lower wave height. An alternative explanation for the reduced roughness length is the occurrence of coastal upwelling. Coastal upwelling is likely to occur when the prevalent wind direction is parallel to the coastline, which generates wind-driven currents. The complex interaction between upwelled water and surface water during the upwelling process may result in a reduction in surface wind stress [67,68]. Moreover, evidence has shown that the upwelled cold water can lead to reduced sea-surface temperature by several degrees near the coast sites, and the atmosphere becomes more thermally stable. The interaction of the atmospheric boundary layer with the cold upwelled water results in the formation of an internal boundary layer, as well as a reduction in wind stress [69,70].

To further diagnose the characteristics of roughness length associated with these two sectors, the magnitudes of aerodynamic roughness length were also determined using the gust factor method using the cup anemometric data, and the results are illustrated in Figure 5 in a comparative sense.

Gust factor (GF) is a common term in the wind engineering community, which depends on a number of factors, e.g., instrument height, gust duration, averaging time, as well as the height and density of the upwind terrain elements [71]. In general, a small value is indicative of relatively aerodynamically smooth conditions, and a large value reflects the existence of large obstructions, such as buildings and trees. Ashcroft [72] once investigated the relationships between the gust factor, the terrain roughness, and the hourly mean wind speed by gust duration, in which the median gust factor was well correlated with the estimate of terrain roughness derived from the best estimate of aerodynamic roughness length. On this account, z₀ can be obtained from a known GF using established wind speed conversion techniques. More recently, a theoretical gust factor (GF) has been developed to calculate aerodynamic roughness length [71]:

$$GF\left(T, t, z,z_0\right)=1+g \left(T, t, z\right)\frac{\sigma \left(T, t, z, z_0\right)}{U \left(z,z_0\right)}$$

(9)

in which t and T are, respectively, the gust duration and mean time duration, $g \left(T, t, z\right)$ is the peak factor and $\sigma \left(T, t, z, z_0\right)$ is the standard deviation of the fluctuating component of the wind. It is worth noting that both $g \left(T, t, z\right)$ and $\sigma \left(T, t, z, z_0\right)$ are tied with t and T. The peak factor can be estimated as:

$$g(T,\tau ,z)=\sqrt{2\ln (\upsilon T)}+0.5772/\sqrt{2\ln (\upsilon T)}$$

(10)

where $\upsilon$ is the zero up-crossing rate. The spectrum of wind turbulence at the end reads $S_r(n)$ is usually represented as [71]:

$$S_r(n)=S(n)·{\chi }^2(n)$$

(11)

$${\chi }^2(n)=T_1(n)·T_{hp}(n)·T_{ra}(n)$$

(12)

$$T_1(n)={[1+{(2\pi n\lambda /U)}^2]}^{-1}$$

(13)

$$T_{hp}(n)=1-{[1+{(2\pi nT)}^2]}^{-1}$$

(14)

$$T_{ra}(n)={[\frac{\sin (\pi n{t}_0)}{\pi n{t}_0}]}^2,\hspace{0.17em}or T_{ra}(n)={[\frac{\sin (\pi n\mathsf{\Delta }N)}{N\sin (\pi n\mathsf{\Delta })}]}^2$$

(15)

where $S(n)$ is the unfiltered power spectrum, $T_1$ accounts for low-pass filtering effect due to the inertia of anemometer’s rotating components, $T_{hp}$ represents high-pass filter associated with the measurement period $T$, $T_{ra}$ represents the running average filtering effects for the analog (first) or discrete (second) signals, $\lambda$ is the distance constant of the anemometer, $n$ is the frequency (unit: Hz), $t_0$ is the analog running-average duration, and $\mathsf{\Delta }$ and $N$ are the sampling interval and sample number of instantaneous readings involved in the discrete average. In this case, the measured $\upsilon$ and ${\sigma }_u$ can be represented as:

$${\upsilon }^2=\frac{{\displaystyle {\mathsf{\int }}_0^{\infty }{n}^2{S}_u(n,z,z_0){\chi }^2(n)dn}}{{\displaystyle {\mathsf{\int }}_0^{\infty }{S}_u(n,z,z_0){\chi }^2(n)dn}}$$

(16)

$${\sigma }_u{}^2(T,\tau ,z,z_0)={\displaystyle {\mathsf{\int }}_0^{\infty }{S}_u(n,z,z_0){\chi }^2(n)dn}$$

(17)

Masters et al. [71] used the von Kármán wind spectrum to estimate the filtered wind speed variance ${\sigma }_u(T,\tau ,z,z_0)$:

$$\frac{n·S_u(n)}{{\sigma }_u^2}=\frac{4n{L}_u^x/U}{{[1+70.8{(n{L}_u^x/U)}^2]}^{5/6}}$$

(18)

where the turbulence integral length $L_u^x$ can be calculated by the combined usage of Taylor’s hypothesis, i.e., $L_u^x=U{T}_u$, and an empirical estimator of the integral time scale recommended in Engineering Sciences Data Unit [73], i.e., $T_u=3.13z^{0.2}$, and the ${\sigma }_u^2$ is the unfiltered wind variance formulated by the Harris variance model:

$${\sigma }_u(z)=\frac{u_{*}7.5\eta {[0.538+0.09\ln (z/z_0)]}^{{\eta }^{16}}}{1+0.156\ln [u_{*}/|f{z}_0|]}, \eta =1-6|f|z/u_{*}$$

(19)

In this case, the roughness length can be calculated effectively using an iterative method based on the above equations. Nevertheless, it should be emphasized that the methodology used by Masters et al. [71] aims to estimate effective surface roughness length based on neutrally stratified mean gust factors, and data associated with stable or unstable conditions were discharged.

As illustrated in Figure 5, the estimated roughness lengths for the sector of 60°–90° are generally smaller than those of 120°–240°, regardless of the method used. This is in line with Sethuraman and Raynor [74], who also found that the wind stress associated with alongshore winds is generally much less significant as compared to those for offshore and onshore winds.

Note that in existing sea-surface flux parameterization models, the sea-surface wind stress is primarily represented by aerodynamic roughness length or drag coefficient. In essence, either the aerodynamic roughness length and the drag coefficient are likely to exhibit a positive correlation with wind speed in the low-to-moderate wind speed range, i.e., increases with increasing wind speed. However, when the wind speed further increases above the hurricane force, the estimated drag coefficient appears to level off or decrease slightly [57]. Similar behavior of sea-surface wind stress can also be well observed in Figure 5. As it shows, the aerodynamic roughness length determined using different methods is somewhat divergent. The values for sector 120°–240° based on the profile method are larger than 0.2 mm, whereas those determined by the gust factor method are smaller. Even for the sector of 60°–90°, the values of roughness length estimated by the profile method tend to be smaller than those of the gust factor method. Such difference is most pronounced at low-speed ranges. As the wind speed increases, the estimated roughness lengths from different methods are found to approach the standard value of 0.2 mm. A possible reason for such difference is related to the data used in these methods. Given the availability of data in this study, the wind profile method uses wind lidar observations, whereas, for the gust factor method, measured data obtained from a cup anemometer were used. In addition, the atmospheric stability appears to influence the results of roughness length estimated by means of both profile and gust factor method, but in different manners. It is anticipated that at a relatively low-speed range, the atmosphere is more likely to be non-neutral, which may cause larger deviation than those in neutral stratification (i.e., larger wind speed).

On the other hand, the aerodynamic roughness lengths estimated for alongshore winds (i.e., 60°–90°) are consistently smaller than the standard value for deepwater surfaces, particularly at low wind speeds. Of particular note is that when using the profile method to estimate the roughness length, the consequent results for the sector of 120°–240° yield a decreasing trend with increasing wind speeds, which is contrasting as compared to other results. This highlights the potential limitation of using the traditional profile method for determining sea-surface roughness length, which needs to be further investigated.

4. Concluding Remarks

Given the substantial importance of sea-surface roughness length for describing marine atmospheric boundary layer, this study examines and discusses the observations of coastal-site roughness length based on wind lidar measurement at an offshore platform in Hong Kong. The major conclusions in this study are summarized as follows:

• Comparison of wind roses shows that the wind direction at the offshore platform is turned parallel to the coastline. Meanwhile, a slight acceleration in wind speed is also observed. This can be related to the formation of a land-sea boundary;
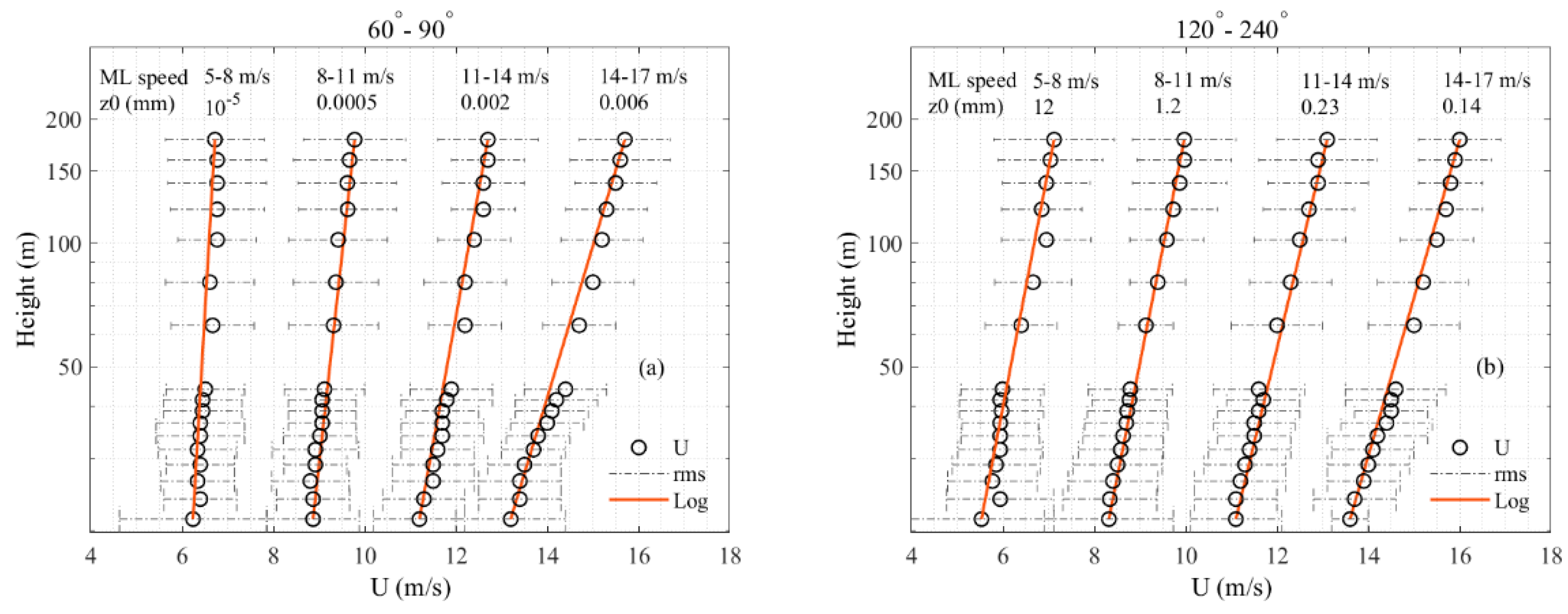
• Based on the log-law profile fit, the estimated roughness lengths for the sector of 120°–240° (perpendicular to the shore) are larger than the constant value widely used for deepwater surface (z₀ = 0.2 mm);
• In contrast, the roughness lengths for alongshore winds (i.e., sector of 60°–90°) are about two orders of magnitude less than that of typical deep-water surface, particularly at lower wind speed ranges.

The results obtained in this study are expected to be useful in a wide range of applications. For example, the unprecedented aerodynamic roughness length is of great concern with respect to the calculation of energy flux at the air-sea interface, given that roughness-based parameters have several uses in modeling energy flux [75,76,77]. Moreover, to take into account the importance of wind, wave, and wind-driven sea circulation in coastal regions, the results provide valuable insights to advance our understanding of coastal meteorology and thus aid coastal vulnerability assessment [78]. Moreover, the outputs of this study can also be used in the numerical algorithms in some other contexts, such as the modeling and canvas detection with a “blended” approach or in the numerical assimilation phase [79].

However, this study is also subjected to several limitations. First, the data involved in this study are site-specific, and the results are somewhat robust. The environmental condition is unique. Uncertainties may also arise due to the selected data processing method. Our previous study [13] has shown that the use of various methods may lead to different results. Secondly, the lack of other oceanographic data, e.g., wave period, peak wavelength, and significant wave height, makes it difficult to diagnose the results in a comprehensive sense. For example, the effect of the wave field on sea-surface roughness cannot be properly investigated. Moreover, due to the lack of temperature measurement data, the atmospheric stability effect has not been fully taken into account, and a neutral stratification condition is assumed. The importance of stability has been highlighted in previous studies. Barthelmie [10] addressed that atmospheric stability is of essential importance in local and mesoscale atmospheric circulation. For coastal areas, in particular, the change in surface roughness and the availability of heat and moisture might influence stability and hence affect turbulent mixing and momentum transfer. Floors et al. [80] noted that when the atmospheric stability condition is misdiagnosed, the heat fluxes can be affected such that the shape of the upstream wind profile can be wrongly characterized, which could lead to erroneous roughness description of the sea surface. Van Wijk et al. [81] also found that the diabatic method tends to provide a better description of wind profile than the logarithmic method. It is shown that stability correction in stable stratification indicates a pronounced effect on the logarithmic wind profile, whereas such effect is not significant in unstable stratification. Ro and Hunt [82] reported that the log-fits of wind speed under stable stratification are more likely to yield overestimates of aerodynamic roughness length, whereas wind speed data under unstable stratification may yield slightly underestimates of z₀. On the other hand, as have been highlighted hereinabove, the gust factor method adopted in this study is mainly based on neutrally stratified gust factors, which may be another source of uncertainty as the atmospheric stability effect is neglected in the current study

On this account, it is highly recommended to include more extensive data, e.g., air/sea temperature and wave field data, in future studies. This could lead to a much more detailed and comprehensive investigation of coastal meteorological characteristics.