Observation and Inversion of Aerosol Particle Size Distribution over Yinchuan Area
Abstract
:1. Introduction
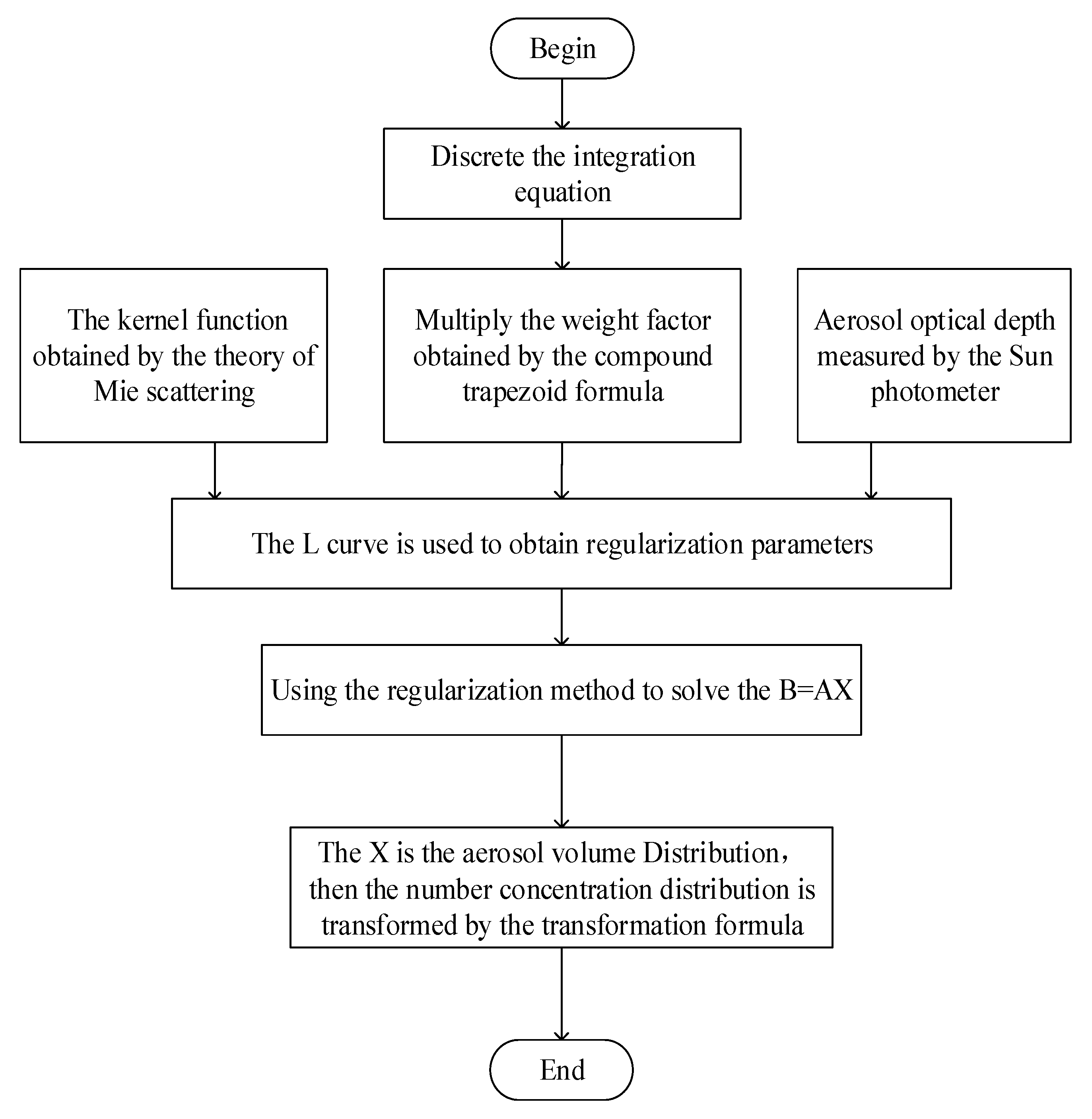
2. Inversion of PSD
2.1. Discretization
2.2. Regularization
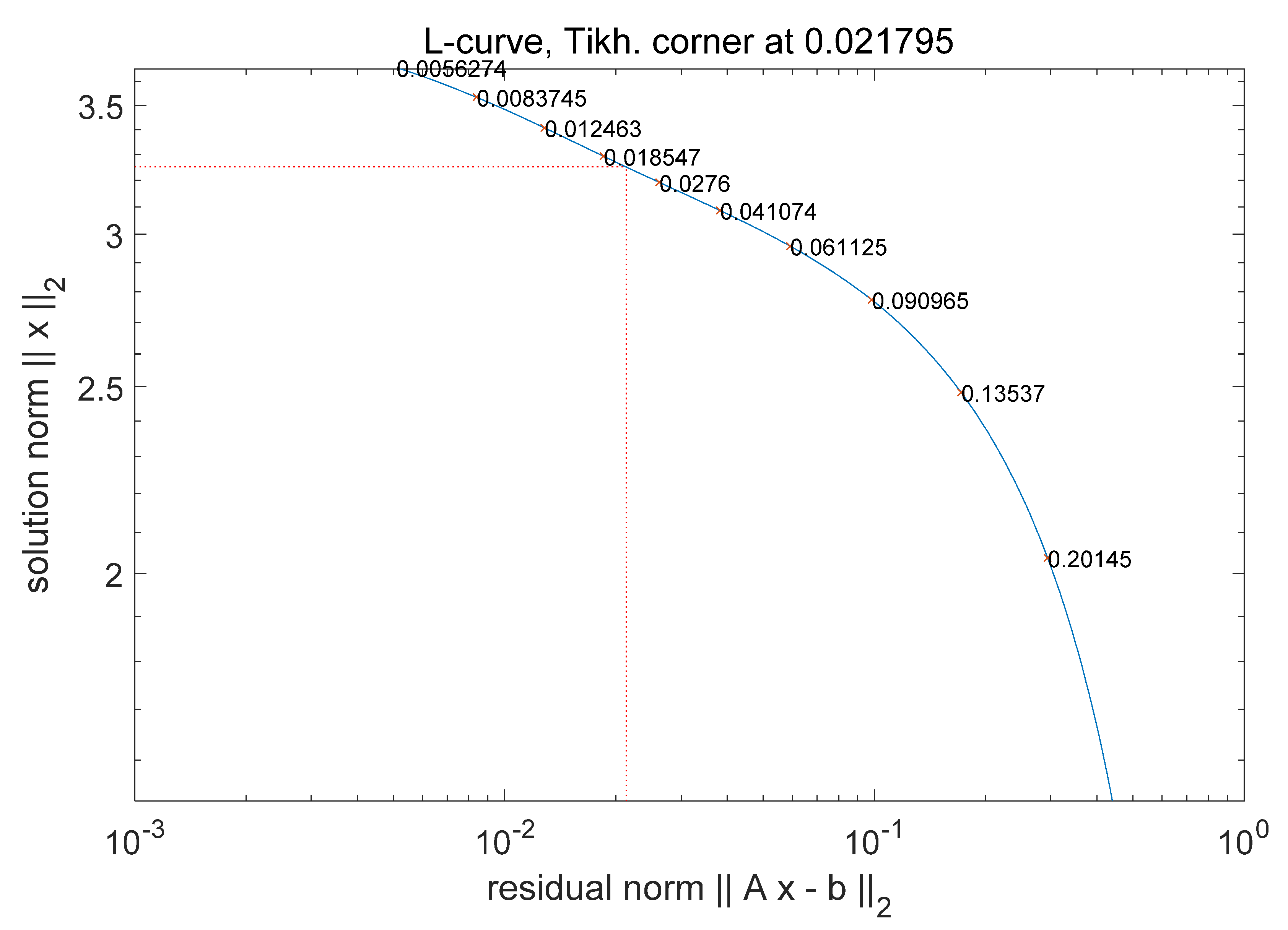
2.2.1. Selection of Regularization Parameters
2.2.2. TSVD Regularization
2.2.3. Tikhonov Regularization
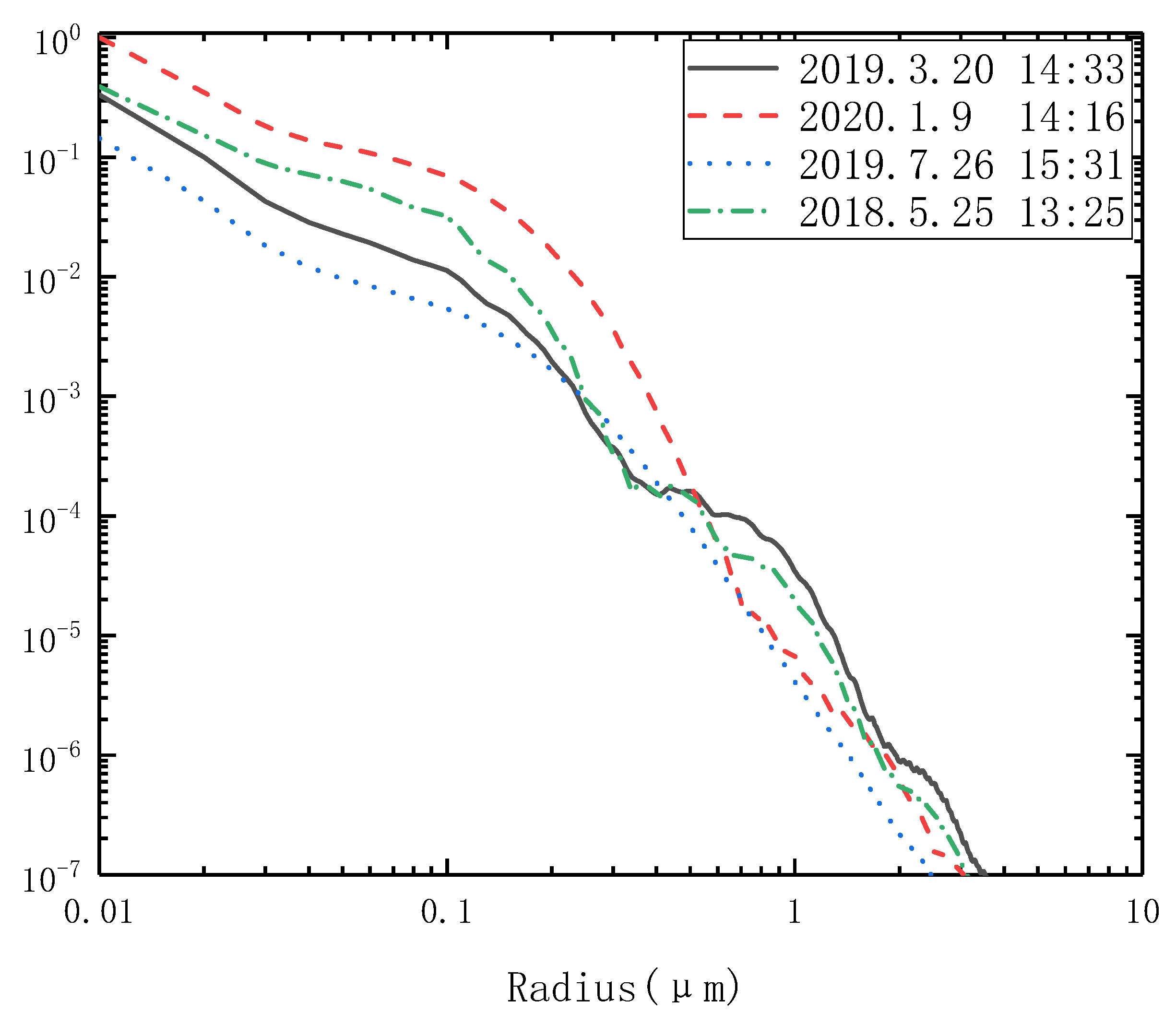
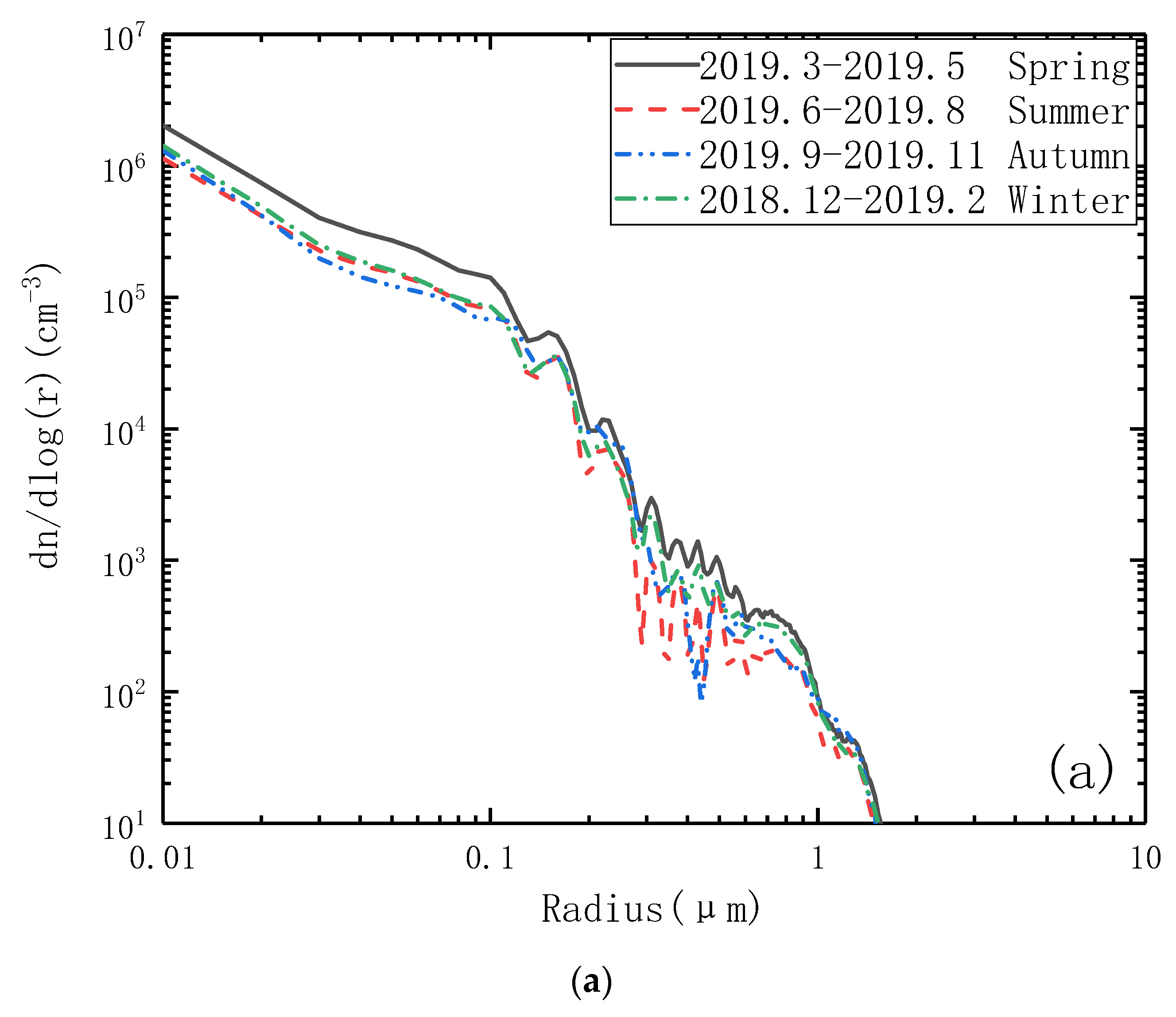
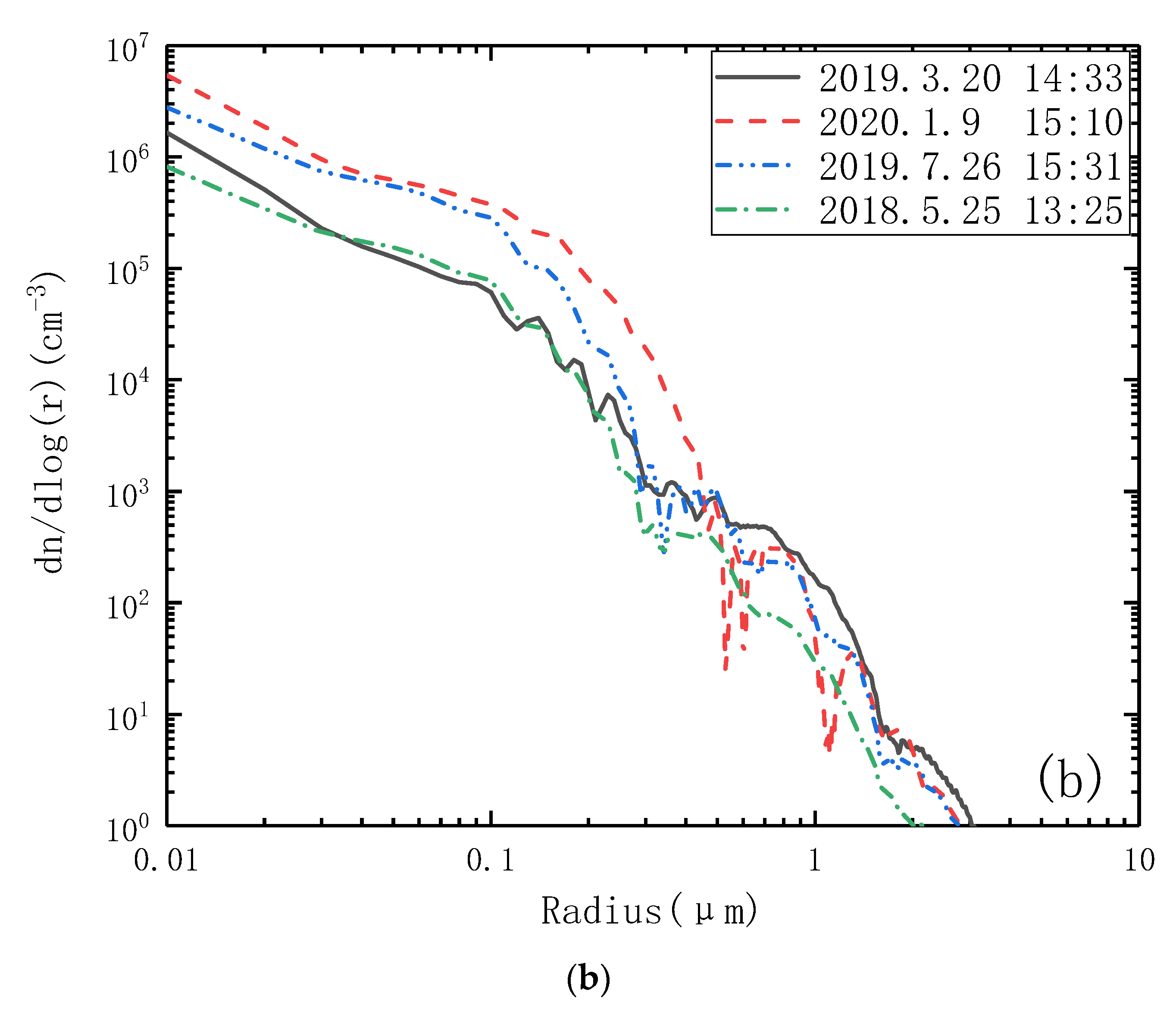
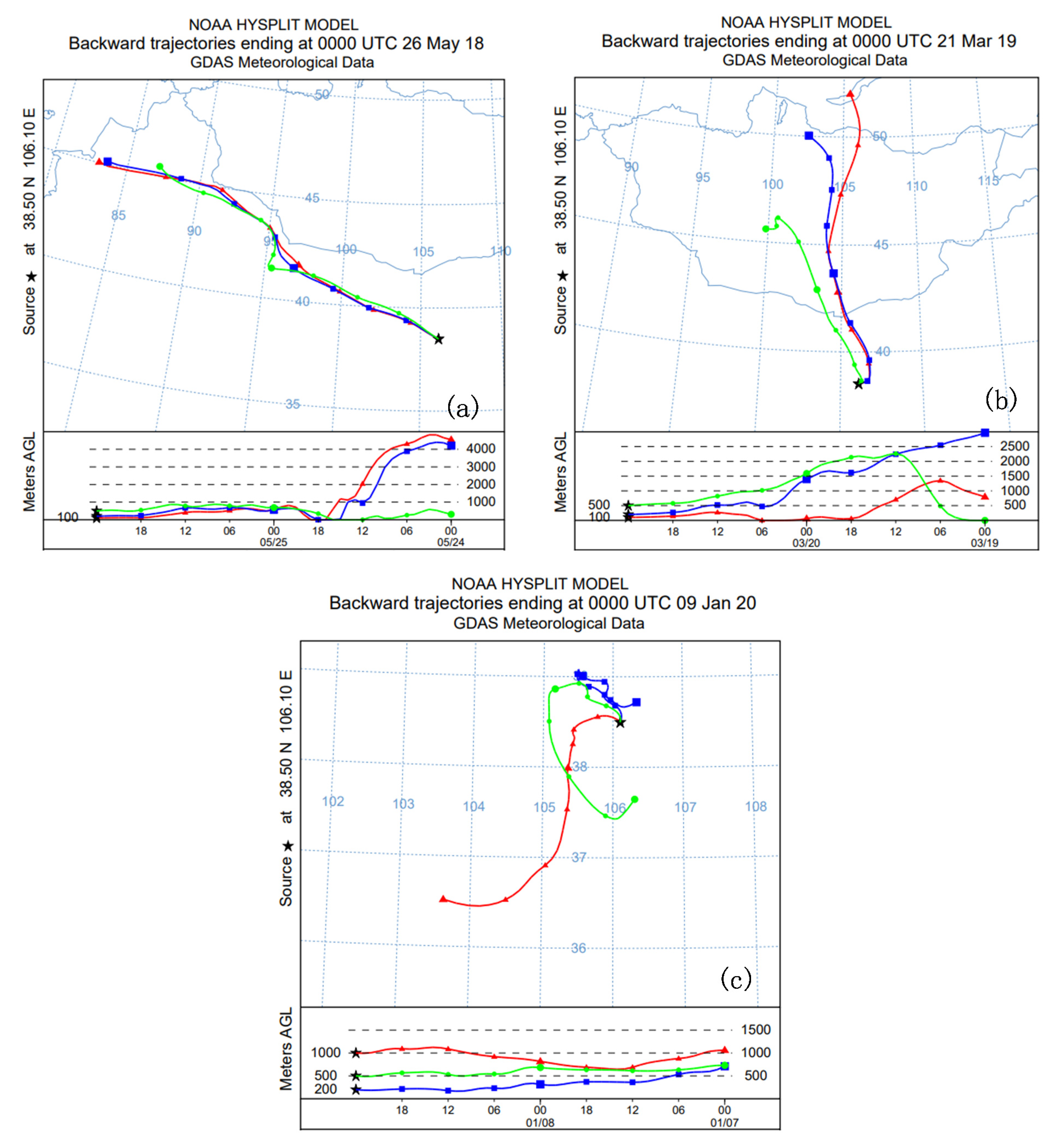
3. Experiment Results and Analysis
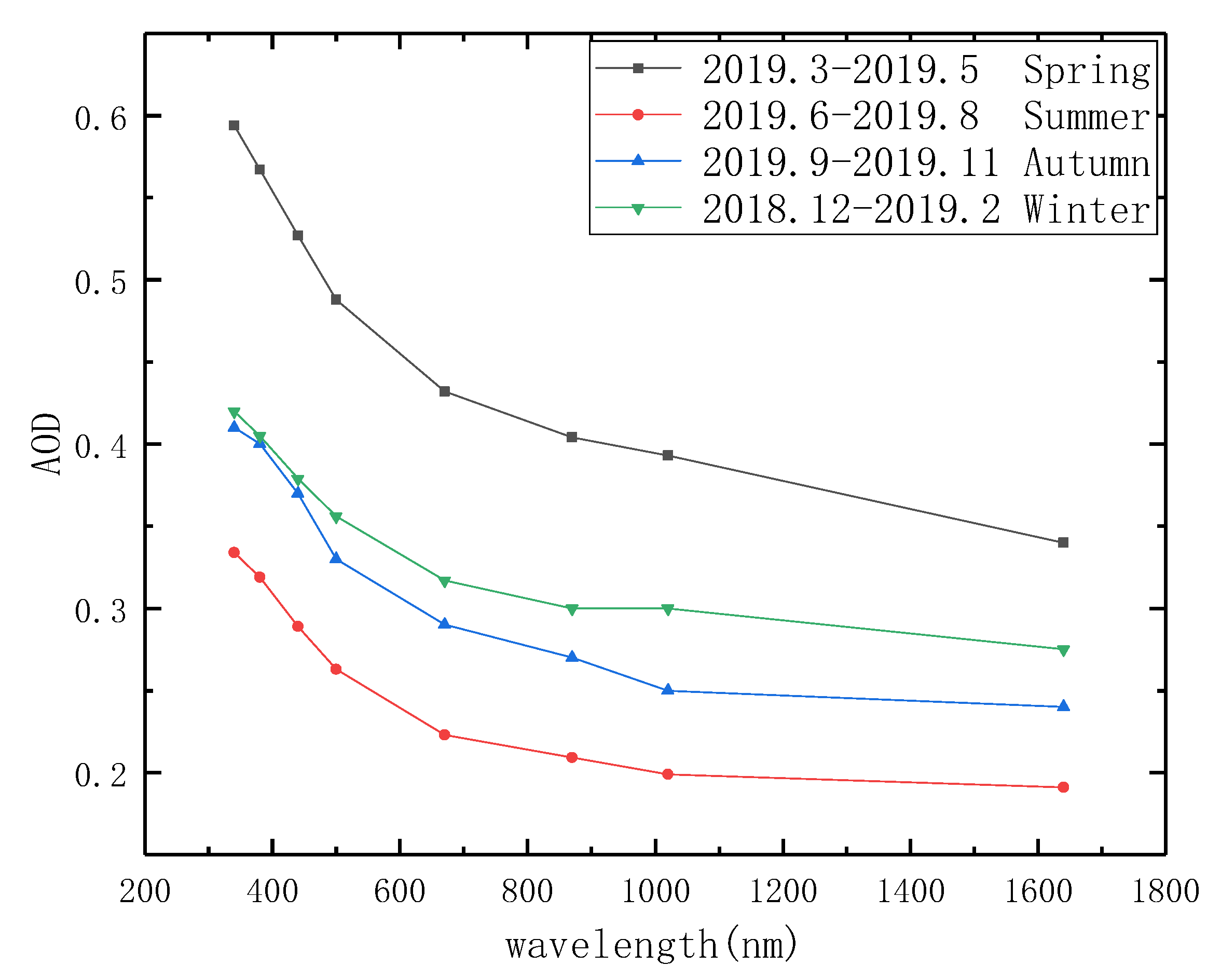
3.1. Analysis of AODs in Different Seasons and Different Weathers
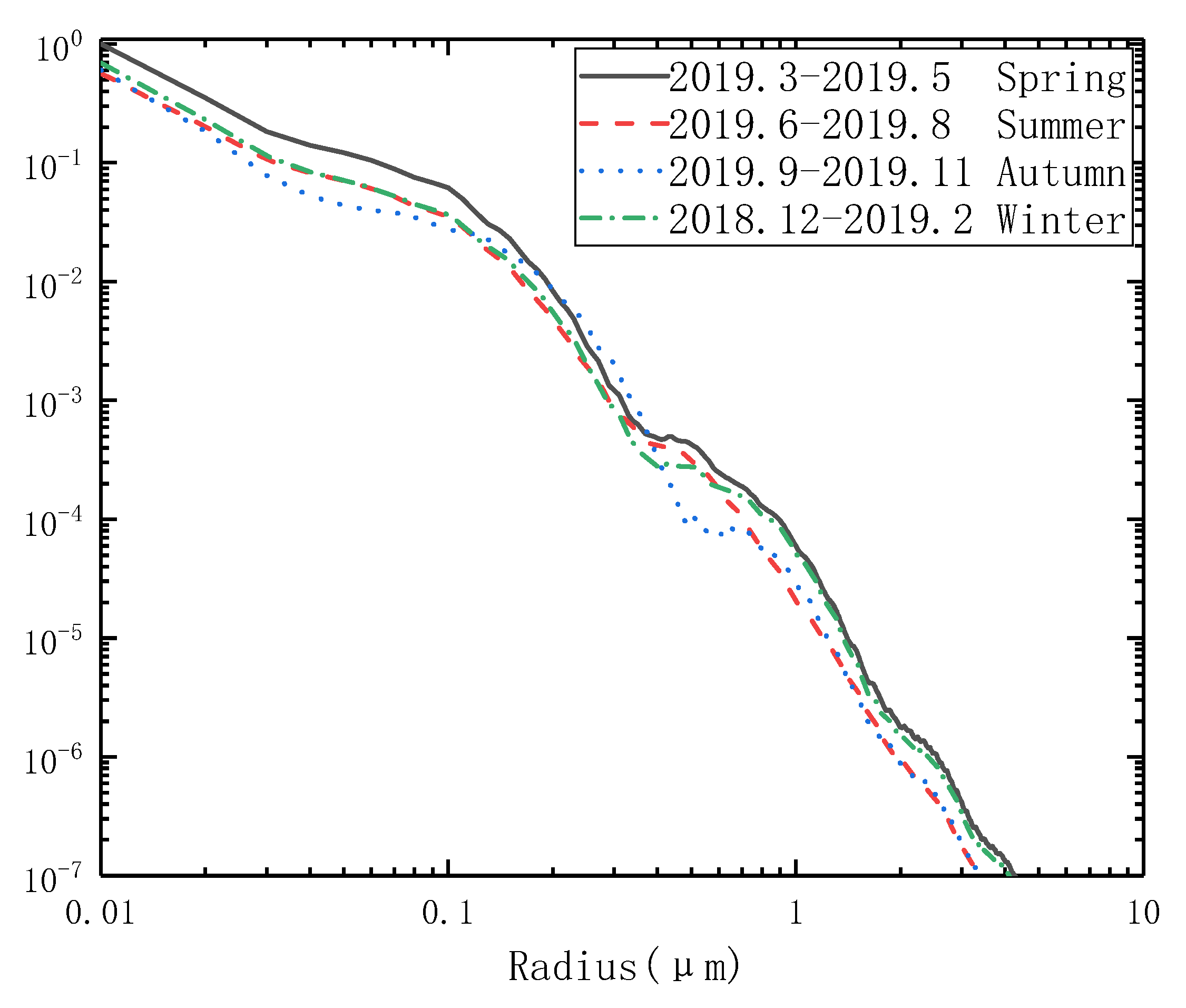
3.2. Inversion of Aerosol PSD in Different Seasons and Different Weathers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Yin, Y.; Li, P.; Xu, F. Advances in research on mechanism and observation of impacts of aerosol on cloud and precipitation. J. Meteorol. Sci. 2014, 34, 581–590. [Google Scholar]
- Graham, E.L.; Zieger, P.; Mohr, C.; Wideqvist, U.; Hennig, T.; Ekman, A.M.L.; Krejci, R.; Ström, J.; Riipinen, I. Physical and chemical properties of aerosol particles and cloud residuals on Mt. Åreskutan in Central Sweden during summer 2014. Tellus B Chem. Phys. Meteorol. 2020, 72, 1–16. [Google Scholar]
- Hussein, T.; Puustinen, A.; Aalto, P.P.; Mäkelä, J.M.; Hämeri, K.; Kulmala, M. Urban aerosol number size distributions. Atmos. Chem. Phys. 2004, 28, 391–411. [Google Scholar] [CrossRef] [Green Version]
- Volckensa, J.; Peters, T.M. Counting and particle transmission efficiency of the aerodynamic particle sizer. J. Aerosol Sci. 2005, 36, 1400–1408. [Google Scholar] [CrossRef]
- Pfeifer, S.; Müller, T.; Weinhold, K.; Zikova, N.; Santos, S.M.D.; Marinoni, A.; Bischof, O.F.; Kykal, C.; Ries, L.; Meinhardt, F.; et al. Intercomparison of 15 aerodynamic particle size spectrometer (APS 3321): Uncertainties in particle sizing and number size distribution. Atmos. Meas. Tech. 2016, 9, 1545–1551. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Niu, S. Analysis and fitting of the instantaneous size distribution of sand dust aerosol particles in Helan Mountainous area. J. Nanjing Inst. Meteorol. 2006, 29, 500–506. [Google Scholar]
- Liu, Z.; Sun, Y.; Li, L.; Wang, Y. Particle mass concentrations and size distribution during and after the Beijing Olympic Games. Environ. Sci. 2011, 32, 913–923. [Google Scholar]
- Shang, Q.; Li, Z.; Yang, J.; Pu, M. Size distributions of aerosol particles and the impact on visibility in winter of Nanjing. Environ. Sci. 2011, 32, 256–266. [Google Scholar]
- Huang, A.; Deng, R.; Qin, Y.; Chen, Q.; Liang, Y. A Study on Remote-Sensing Inversion of Aerosol Particle Size Distributions over Yongxing Island. Acta Scientiarum Nat. Univ. Sunyatseni 2015, 54, 138–144. [Google Scholar]
- Goloub, P.; Li, Z.; Dubovik, O.; Blarel, L.; Podvin, T.; Jankowiak, I.; Lecoq, R.; Deroo, C.; Chatenet, B.; Morel, J.P.; et al. PHOTONS/AERONET sunphotometer network overview: Description, activities, results. In Atmospheric and Ocean Optics; SPIE: Bellingham, WA, USA, 2008. [Google Scholar] [CrossRef] [Green Version]
- Yue, G.K.; Deepak, A. Retrieval of stratospheric aerosol size distribution from atmospheric extinction of solar radiation at two wavelengths. Appl. Opt. 1983, 22, 1639. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res. Atmos. 2000, 105, 20673. [Google Scholar] [CrossRef] [Green Version]
- Veselovskii, I.; Kolgotin, A.; Griaznov, V.; Muller, D.; Wandinger, U.; Whiteman, D.N. Inversion with regularization for the retrieval of tropospheric aerosol parameters from multiwavelength lidar sounding. Appl. Opt. 2002, 41, 3685–3699. [Google Scholar] [CrossRef] [Green Version]
- Jagodnicka, A.K.; Stacewicz, T.; Posyniak, M.; Malinowski, S.; Gaussa, M. Lidar Investigation of aerosol particle size distribution in the vicinity of cloud. In Proceedings of the 15th International Conference on Clouds and Precipitation (ICCP), Cancun, Mexico, 7 July 2008. [Google Scholar]
- Granados-Muñoz, M.J.; Navas-Guzmán, F.; Bravo-Aranda, J.A.; Guerrero-Rascado, J.L.; Lyamani, H.; Valenzuela, A.; Titos, G.; Fernández-Gálvez, J.; Alados-Arboledas, L. Hygroscopic growth of atmospheric aerosol particles based on active remote sensing and radiosounding measurements: Selected cases in southeastern Spain. Atmos. Meas. Tech. 2015, 7, 10293–10326. [Google Scholar] [CrossRef] [Green Version]
- Chaikovsky, A.P.; Bril, A.I.; Fedarenka, A.S.; Peshcharankou, V.A.; Denisov, S.V.; Dick, V.P.; Asipenka, F.P.; Miatselskaya, N.S.; Balin, Y.S.; Kokhanenko, G.P.; et al. Synergy of Ground-Based and Satellite Optical Remote Measurements for Studying Atmospheric Aerosols. J. Appl. Spectrosc. 2020, 86, 1092–1099. [Google Scholar] [CrossRef]
- Gong, W.; Zhang, S.; Ma, Y. Aerosol Optical Properties and Determination of Aerosol Size Distribution in Wuhan, China. Atmosphere 2014, 5, 81–91. [Google Scholar] [CrossRef] [Green Version]
- Mao, J.; Sheng, H.; Zhao, H.; Zhou, C. Observation Study on the Size Distribution of Sand Dust Aerosol Particles over Yinchuan, China. Adv. Meteorol. 2014, 6, 1–7. [Google Scholar] [CrossRef]
- Yan, C. Optimization of Regulation Algorithm about Particle Size Distribution and Analysis of Error. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2017. [Google Scholar]
- Phillips, D.L. A technique for the numerical solution of certain integral equations of the first kind. J. ACM 1962, 9, 84–97. [Google Scholar] [CrossRef]
- Twomey, S. Comparison of constrained linear inversion and an iterative nonlinear algorithm applied to the indirect estimation of particle size distributions. J. Comput. Phys. 1975, 18, 188–200. [Google Scholar] [CrossRef]
- Shan, L.; Cao, L.X.L.; Hong, B.; Zhao, J.; Wang, D.; Kong, M. Inversion of particle size distribution based on iterative non-negative Philips-Twomey algorithm. Trans. Inst. Meas. Control 2019, 42, 014233121987373. [Google Scholar] [CrossRef]
- Dey, S.; Tripathi, S.; Singh, R.P.; Holben, B. Retrieval of black carbon and specific absorption over Kanpur city, northern India during 2001–2003 using AERONET data. Atmos. Environ. 2006, 40, 445–456. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Xie, Y.; Li, Z.; Zhang, Y.; Zhang, Y.; Li, D.; Li, K.; Xu, H.; Wang, Y.; Chen, X.; Schauer, J. Estimation of Atmospheric Aerosol Composition from Ground-Based Remote Sensing Measurements of Sun-Sky Radiometer. J. Geophys. Res. Atmos. 2017, 122, 498–518. [Google Scholar] [CrossRef]
- King, M.D.; Byrne, D.M.; Herman, B.M.; Reagan, J.A. Aerosol size distribution obtained by inversion of spectral optical depth measurement. J. Atmos. Sci. 1978, 35, 2153–2167. [Google Scholar] [CrossRef]
- Liu, J. The Normalization Method and Application of the Problem of An Unsuitable Problem; Science Press: Beijing, China, 2005; p. 9. [Google Scholar]
- Zhang, X. The Regularization for the First Kind of Fredholm Integral Equation. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2013. [Google Scholar]
- Liu, M. The error estimates of Fredholm integral equations of the first class are solved by direct discretization. J. Nat. Sci. Heilongjiang Univ. 2011, 28, 1. [Google Scholar]
- Mesgarani, H.; Azari, Y. Numerical investigation of Fredholm integral equation of the first kind with noisy data. Math. Sci. 2019, 13, 267–278. [Google Scholar] [CrossRef] [Green Version]
- Mao, H. The Tikhonov Regularization for Fredholm Equation of the First Kind with Applications. Master’s Thesis, Shanghai JiaoTong University, Shanghai, China, 2010. [Google Scholar]
- Wang, B. Study on Numerical Methods of Discrete Ill-Posed Problem in Inversion Problem. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2006. [Google Scholar]
- O’Leary, D.P. The Use of the L-Curve in the Regularization of Discrete Ill-Posed Problems. Soc. Ind. Appl. Math. 1993, 14, 1487–1503. [Google Scholar]
- Carfora, M.F.; Serio, C. Numerical Methods for Retrieving Aerosol Size Distributions from Optical Measurements of Solar Radiation. J. Aerosol Sci. 1998, 29, 1225–1236. [Google Scholar] [CrossRef]
- Bo, G.; Xu, C.; Li, A.; Wang, Y.; Chen, H.; Jiang, Y. Optical and hygroscopic properties of Asian dust particles based on a horizontal Mie lidar: Case study at Hefei, China. Chin. Opt. Lett. 2017, 15, 020102. [Google Scholar]


| Data | Weather | Wind | Maximum/Minimum Temperature (°C) | AQI |
|---|---|---|---|---|
| 20 March 2019 | floating dusty day | Northwest wind level 2 | 10/−3 | 181 Moderate |
| 9 January 2020 | haze day | Northeast wind level 1 | −2/−9 | 188 Moderate |
| 25 May 2018 | blowing dusty day | Northwest wind level 4 | 31/25 | 174 Moderate |
| 26 July 2019 | sunny day | Southeast wind level 3 | 36/21 | 50 Good |
| Spring | Summer | Autumn | Winter | Floating Dusty Days | Haze Days | Blowing Dusty Days | Sunny Days | |
|---|---|---|---|---|---|---|---|---|
| Perturbation error | 0.0133 | 0.0054 | 0.01 | 0.0104 | 0.0049 | 0.1353 | 0.0332 | 0.0591 |
| Regularization error | 5.6478 | 3.2987 | 4.0699 | 4.4690 | 6.6227 | 12.062 | 6.1585 | 3.581 |
| Spring | Summer | Autumn | Winter | Floating Dusty Days | Hazy Days | Blowing Dusty Days | Sunny Days | |
|---|---|---|---|---|---|---|---|---|
| Perturbation error | 0.0056 | 0.0052 | 0.0056 | 0.0055 | 0.0056 | 0.0811 | 0.0324 | 0.00230 |
| Regularization error | 5.7217 | 3.3567 | 4.1137 | 4.5141 | 6.6794 | 13.558 | 5.8901 | 1.8076 |
| m | Perturbation Error | Regularization Error |
|---|---|---|
| 1.55 + 0.01i | 0.1353 | 12.062 |
| 1.51612 + 0.1178i | 0.1375 | 12.5446 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mao, J.; Ren, Y.; Li, J.; Wang, Q.; Zhang, Y. Observation and Inversion of Aerosol Particle Size Distribution over Yinchuan Area. Atmosphere 2021, 12, 992. https://doi.org/10.3390/atmos12080992
Mao J, Ren Y, Li J, Wang Q, Zhang Y. Observation and Inversion of Aerosol Particle Size Distribution over Yinchuan Area. Atmosphere. 2021; 12(8):992. https://doi.org/10.3390/atmos12080992
Chicago/Turabian StyleMao, Jiandong, Yali Ren, Juan Li, Qiang Wang, and Yi Zhang. 2021. "Observation and Inversion of Aerosol Particle Size Distribution over Yinchuan Area" Atmosphere 12, no. 8: 992. https://doi.org/10.3390/atmos12080992
APA StyleMao, J., Ren, Y., Li, J., Wang, Q., & Zhang, Y. (2021). Observation and Inversion of Aerosol Particle Size Distribution over Yinchuan Area. Atmosphere, 12(8), 992. https://doi.org/10.3390/atmos12080992





