The Influence of Typhoon “MITAG” on Waves and Currents in Zhoushan Sea Area, China
Abstract
:1. Introduction
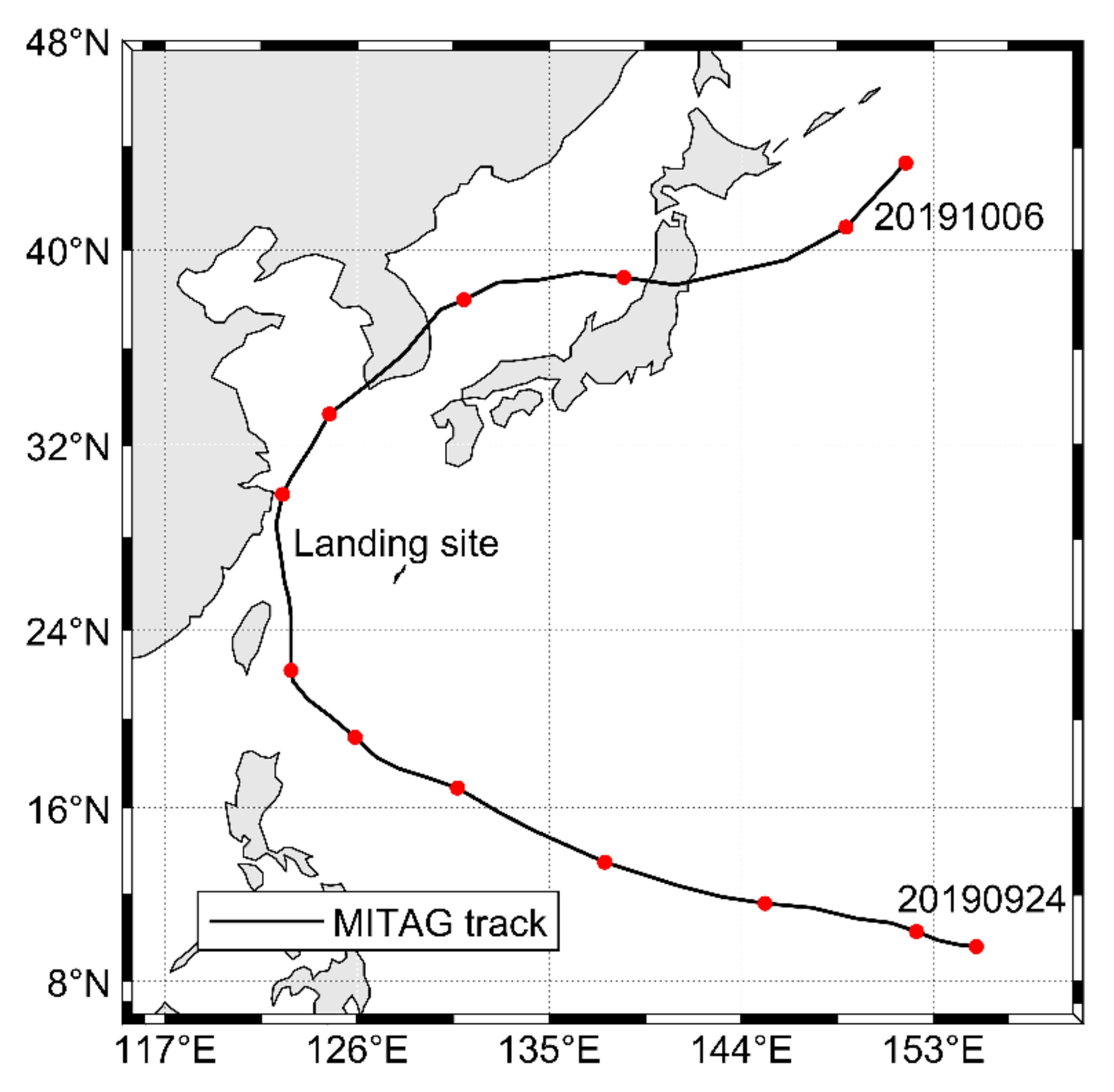
2. Typhoon “MITAG”
3. Data and Study Area
3.1. Data
- The selected typhoon path data are from the best typhoon path data obtained from RSMC (Regional Specialized Meteorological Center). Data contain the position (latitude and longitude) for each 6 h along with pressure and wind speed. (Available online: http://www.jma.go.jp/jma/jma-eng/jma-center/rsmc-hp-pub-eg/trackarchives.html (accessed on 15 February 2021).
- The wave data are from ERA5 (European Environment Agency) datum of ECMWF (European Centre for Medium Range Weather Forecast) between 6:00 on 24 September and 6:00 on 06 October. (Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=form (accessed on 15 February 2021). The temporal and spatial resolution of wave datum are hourly and 0.25° × 0.25°, including significant wave height, mean wave period, significant height of wind wave, significant height of total swell wave.
- The wind field, currents data, and SSH (Sea Surface Hight) are from NCEP (National Centers for Environmental Prediction) reanalysis datum CFSR (Climate Forecast System Reanalysis) between 6:00 on 24 September and 6:00 on 6 October. The resolution of temporal and spatial are 6 h and 0.205 degrees. (Available online: https://rda.ucar.edu/datasets/ds094.0/ (accessed on 15 February 2021).
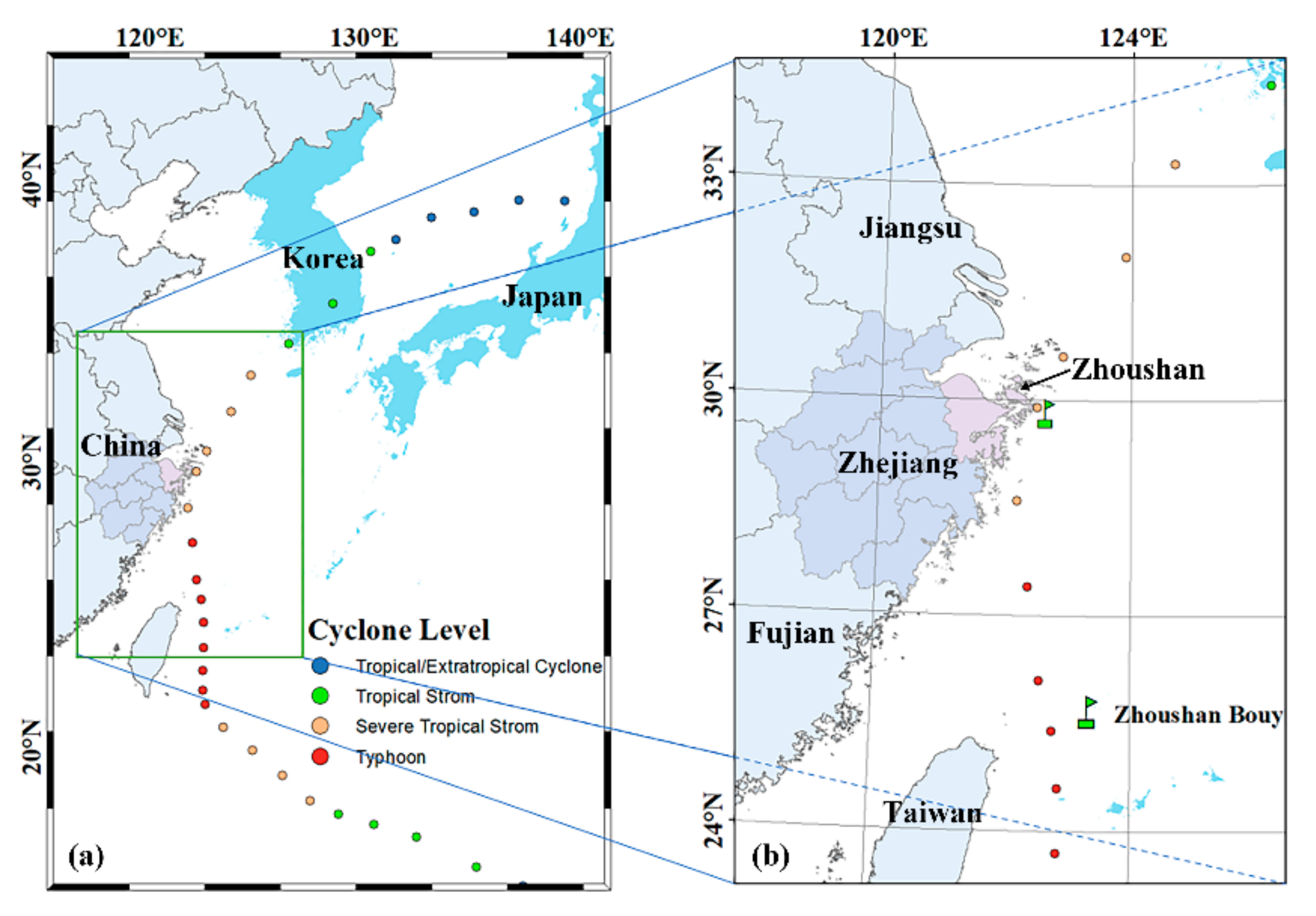
3.2. Study Area
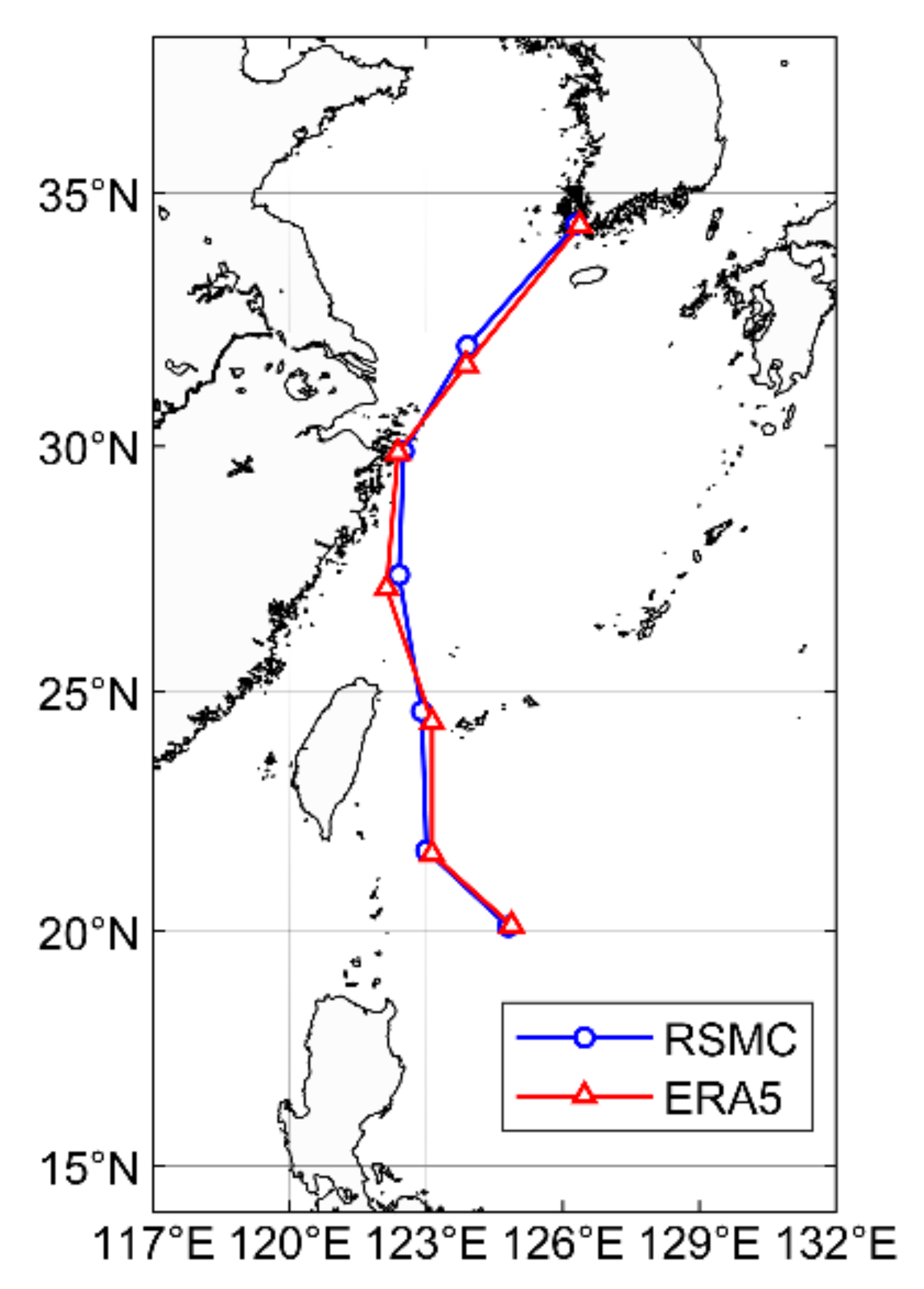
3.3. Data Feasibility
4. Methods
4.1. Wave Study Methods
4.2. Currents Study Methods
5. Result
5.1. Analysis of Wave Characteristics during “MITAG”
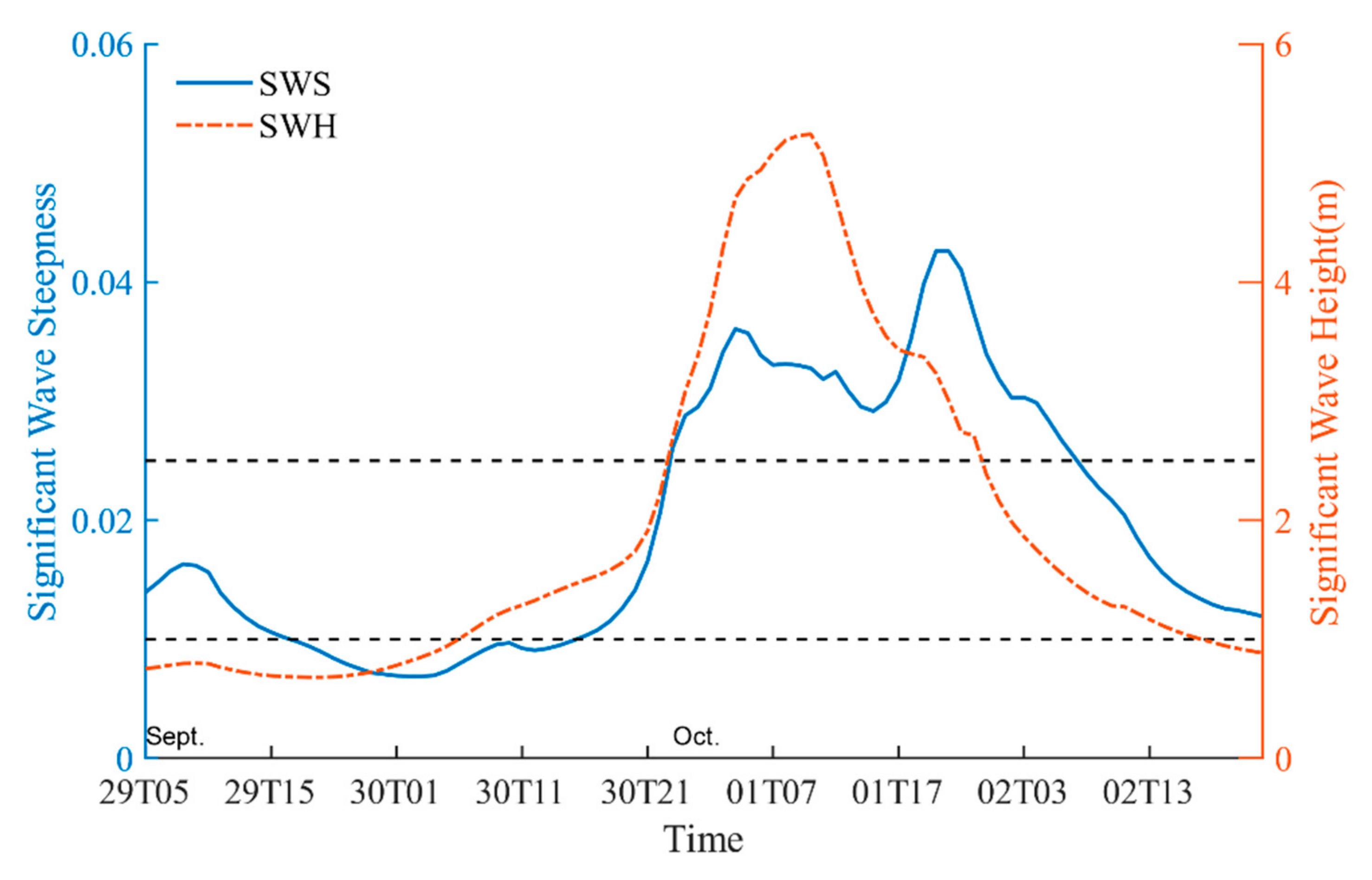
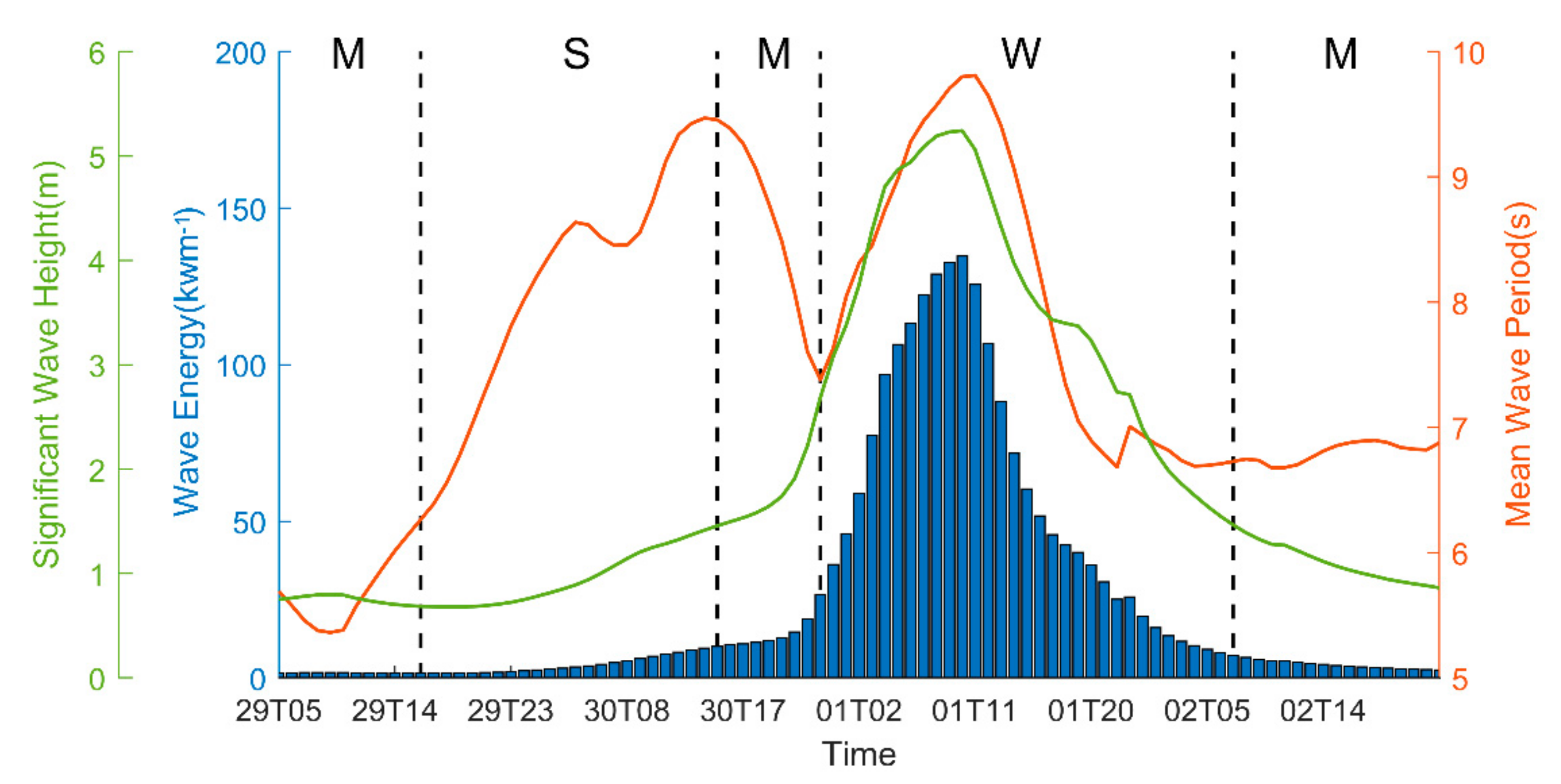
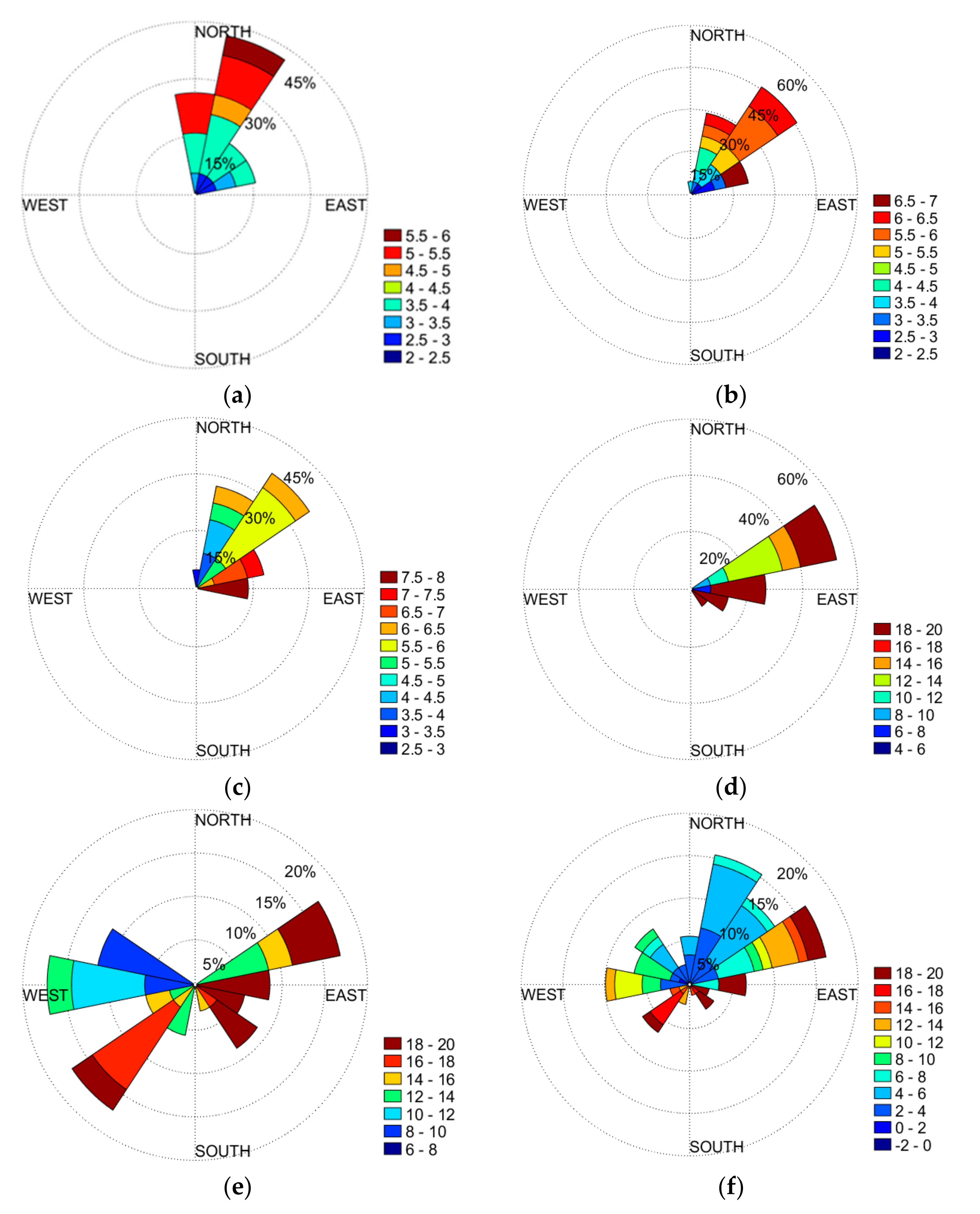
5.1.1. Waveform Evolution Characteristics
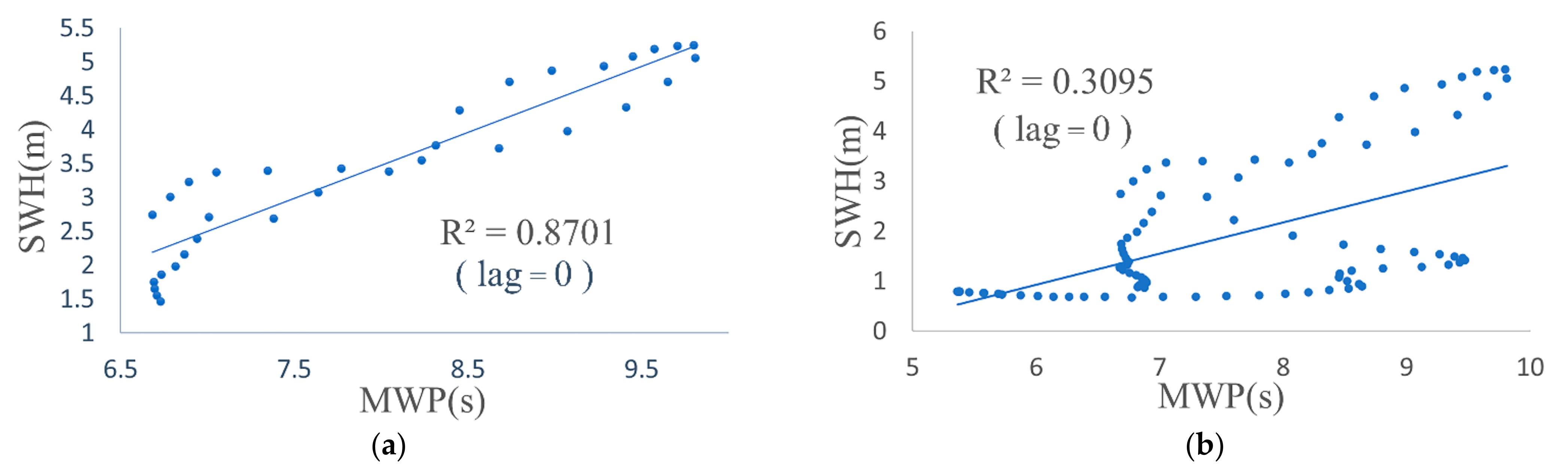
5.1.2. Wave Height and Wave Period
5.2. Analysis of Currents Characteristics during “MITAG”
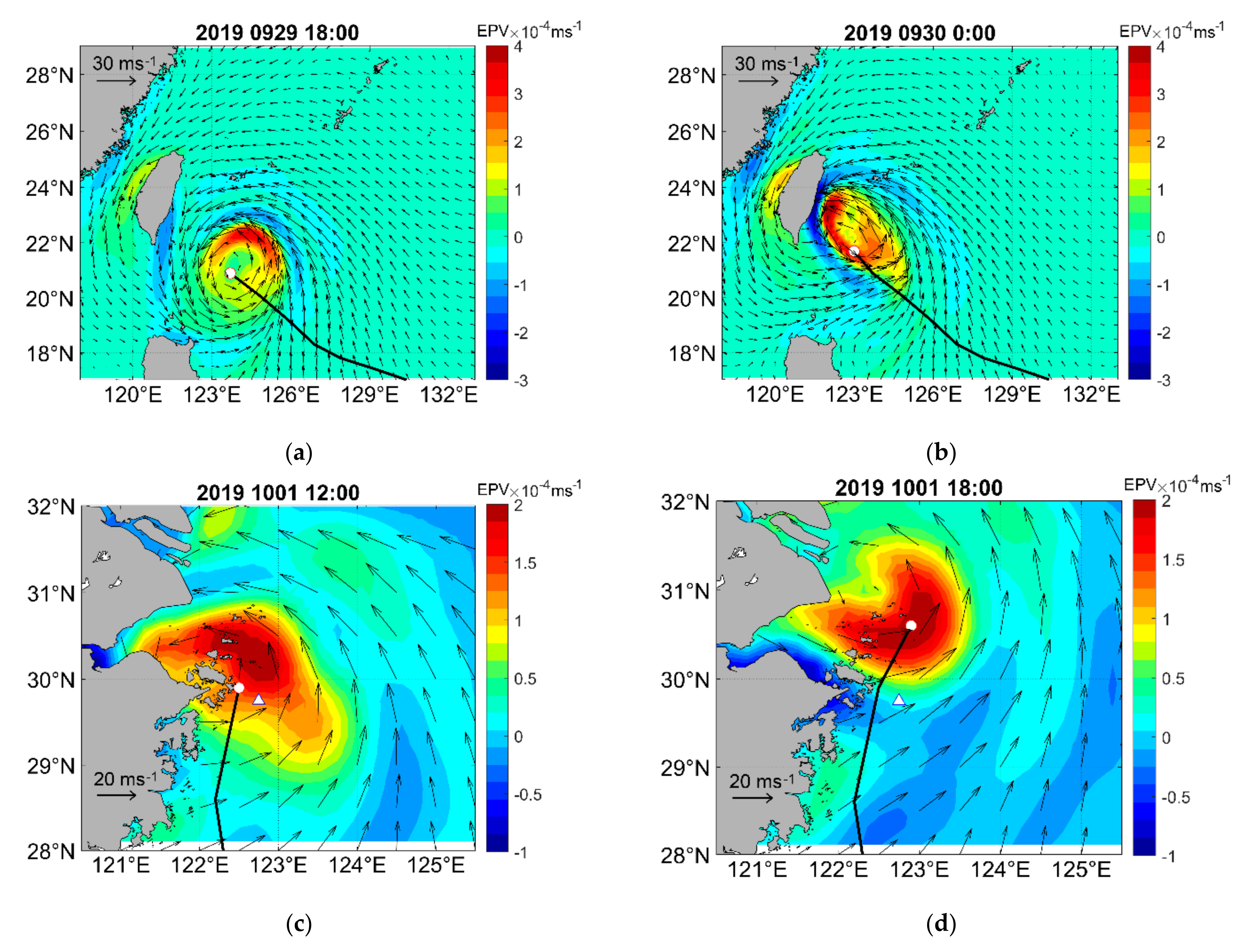
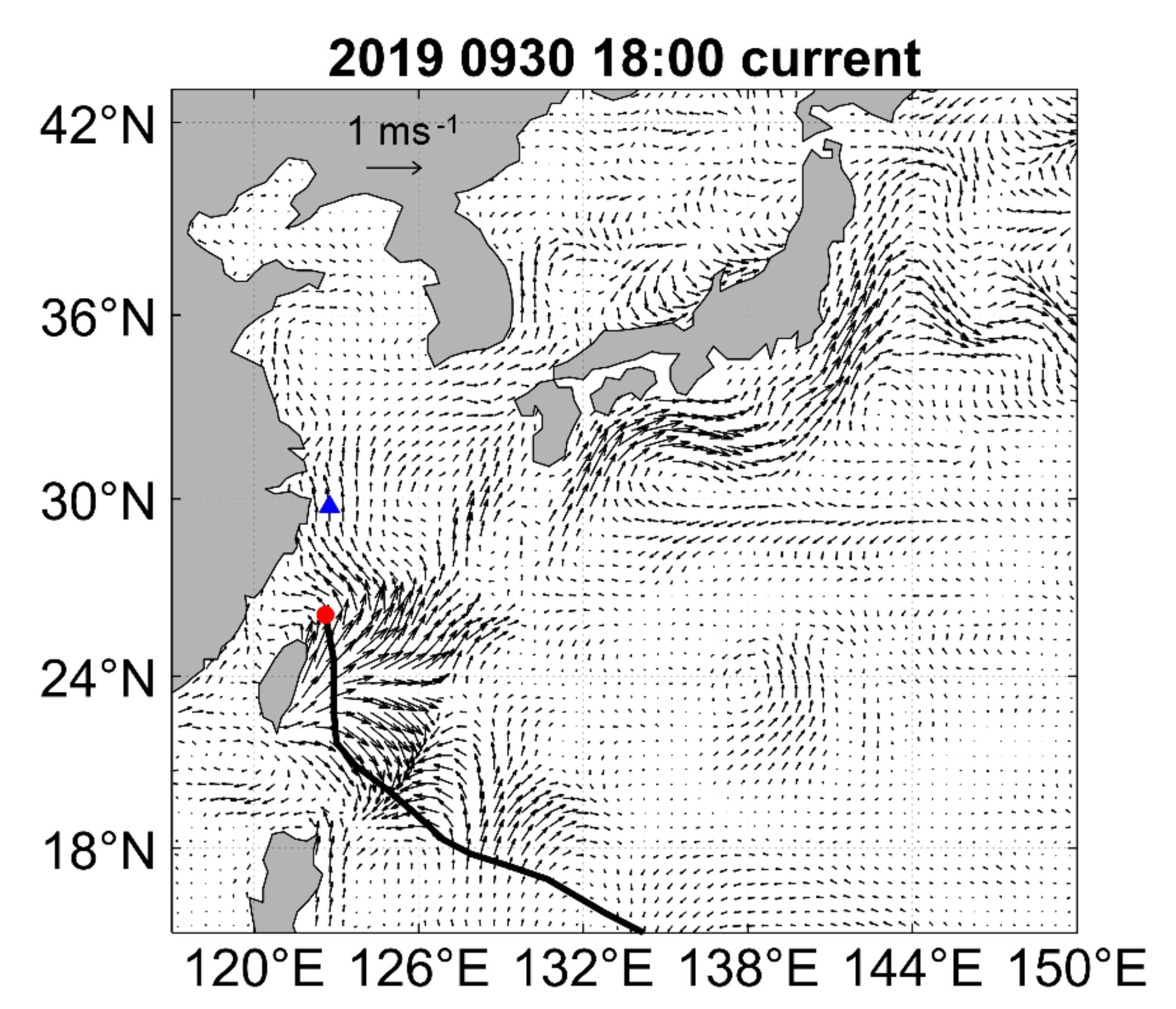
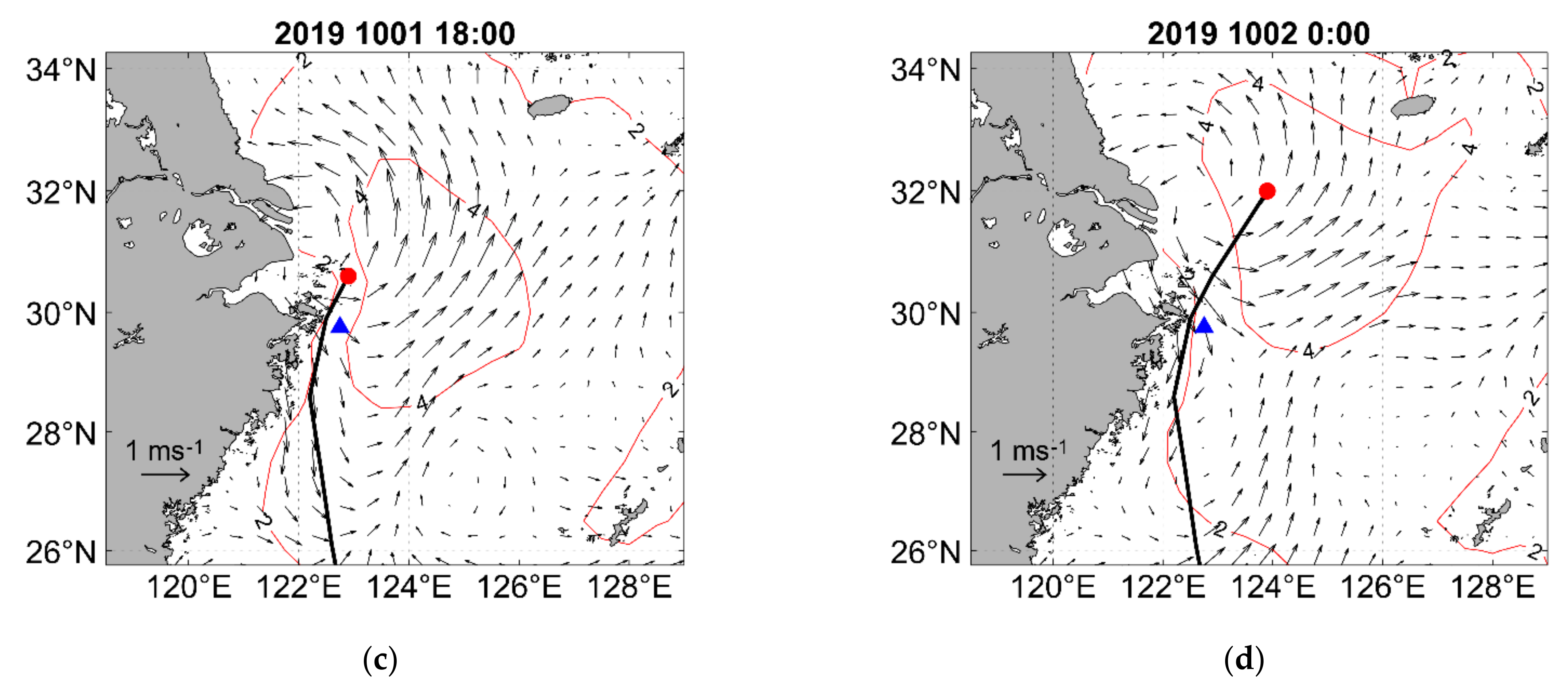
5.2.1. Characteristics of Ocean Currents near Zhoushan
5.2.2. Influence of “MITAG” on the Sea Surface Current
6. Discussion
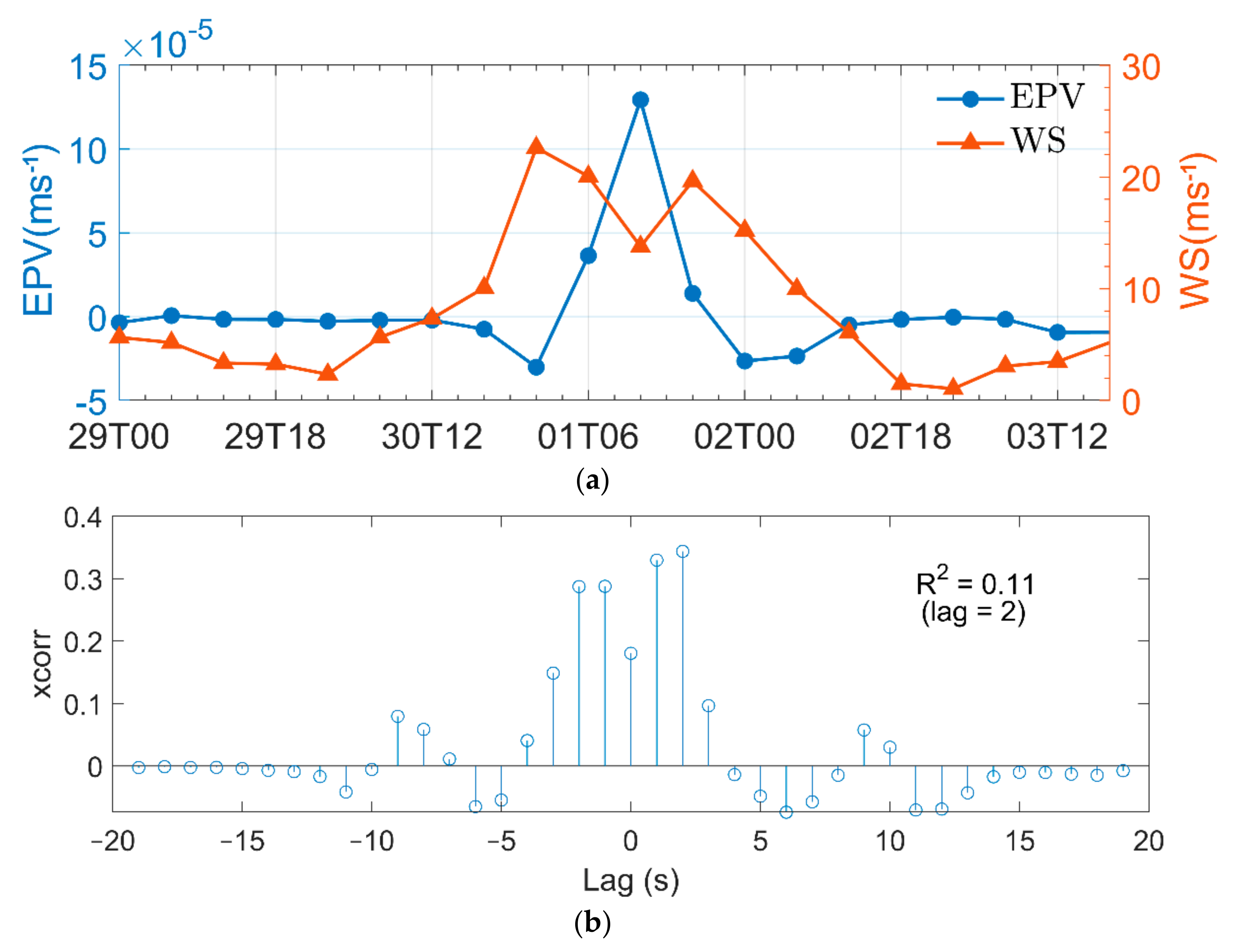
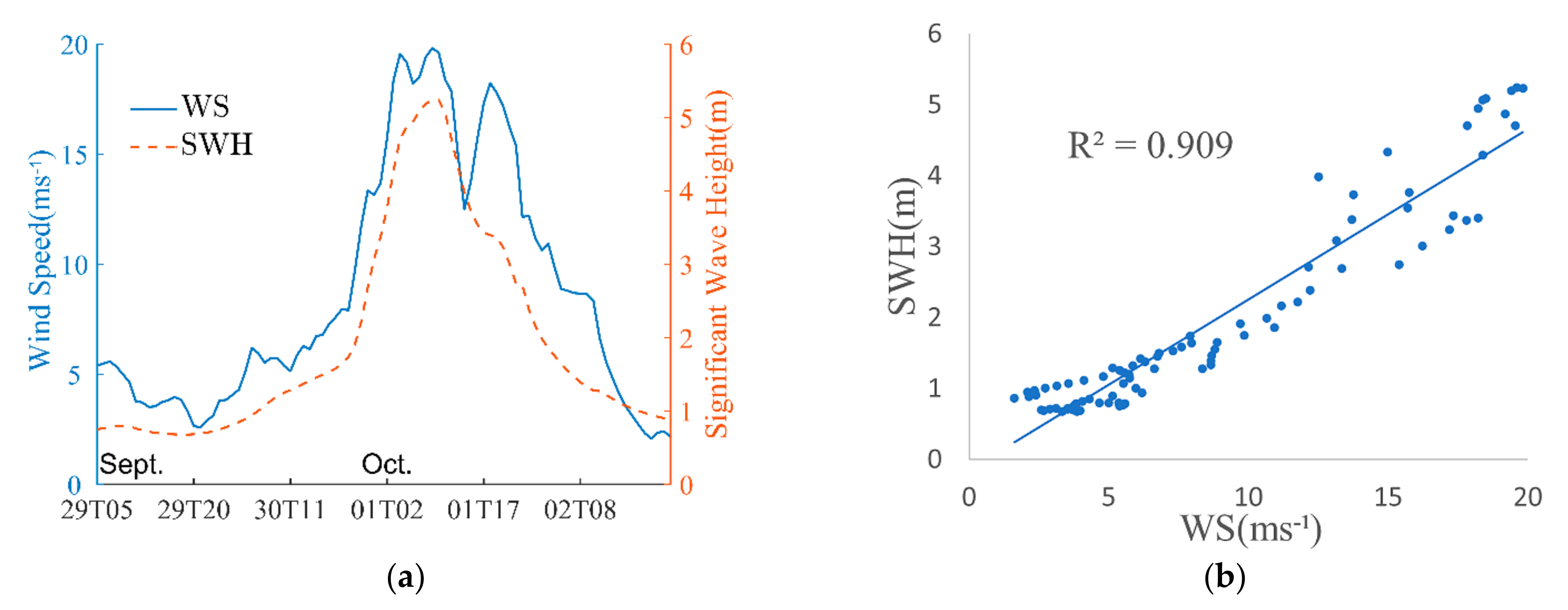
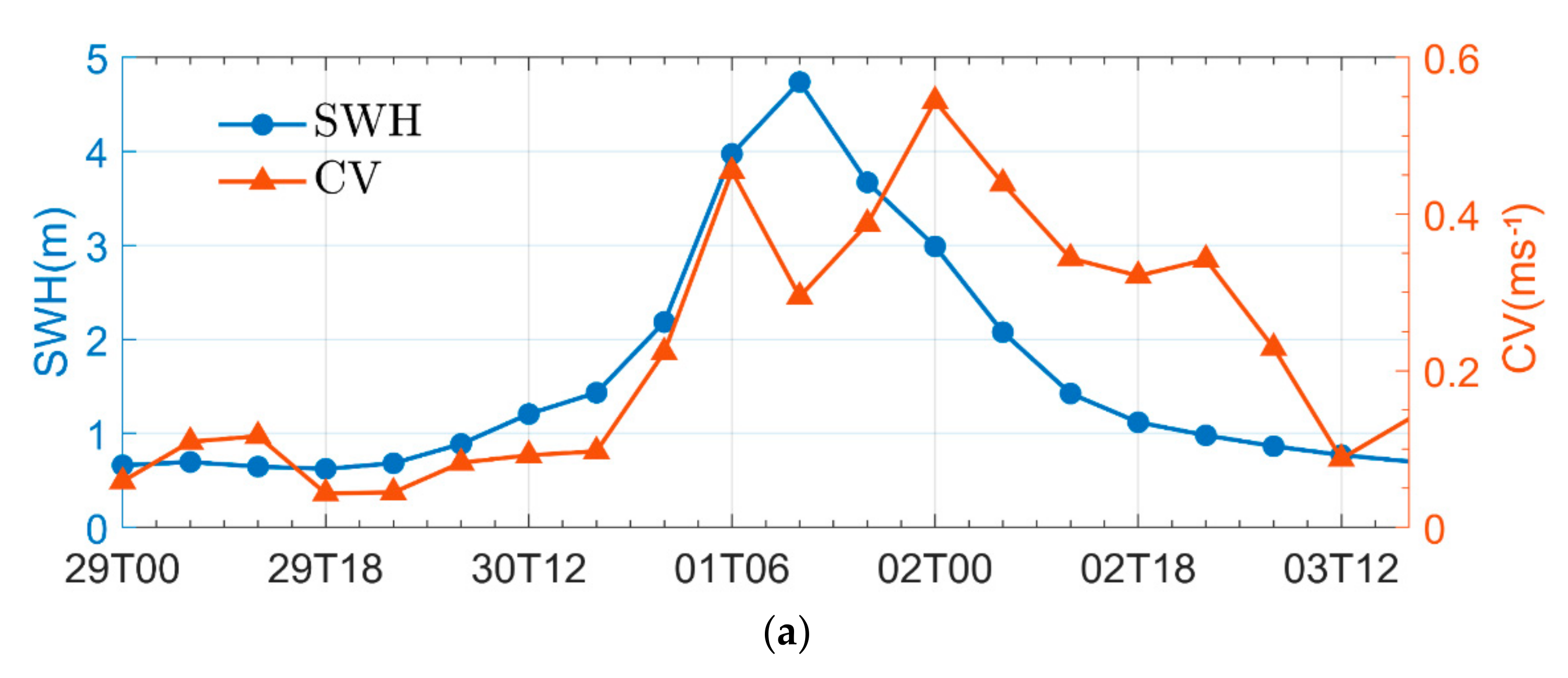
6.1. The Effect of Wind on Waves
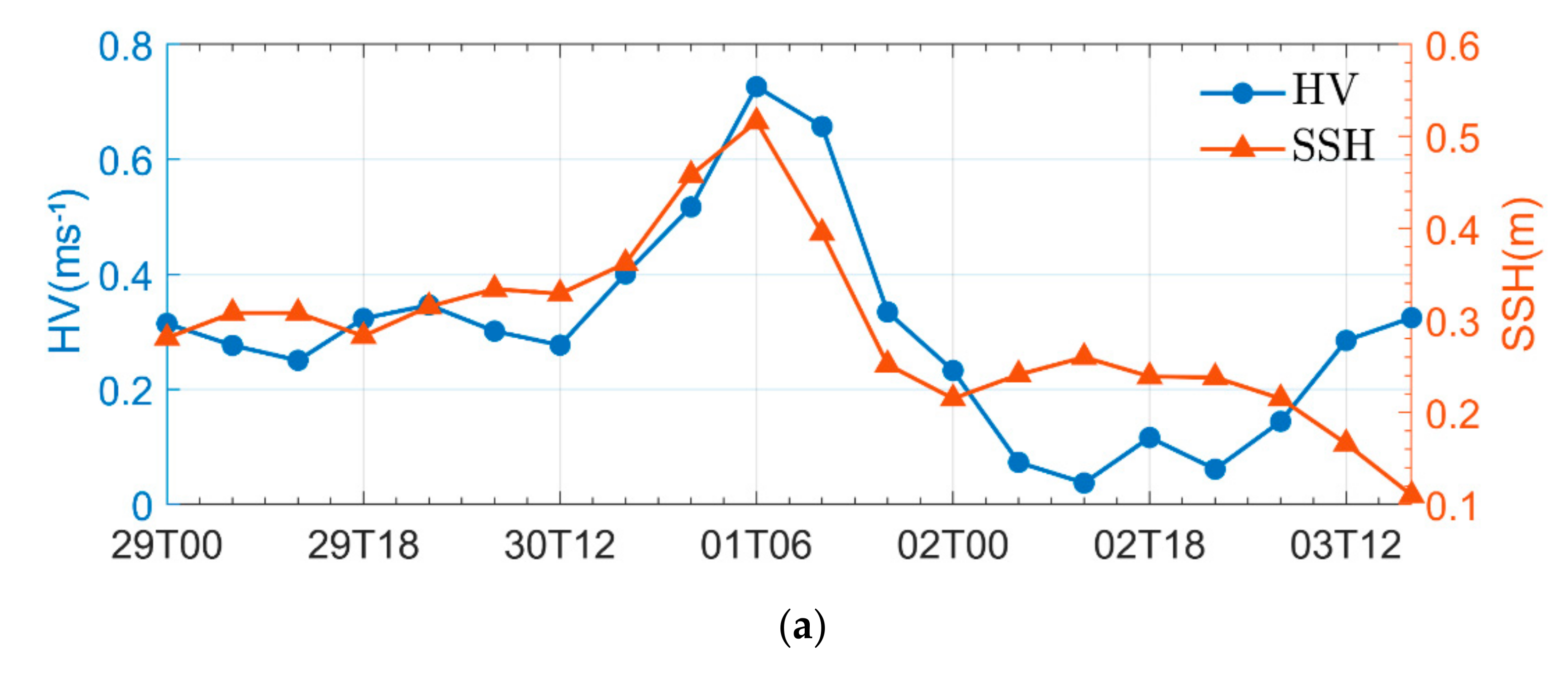
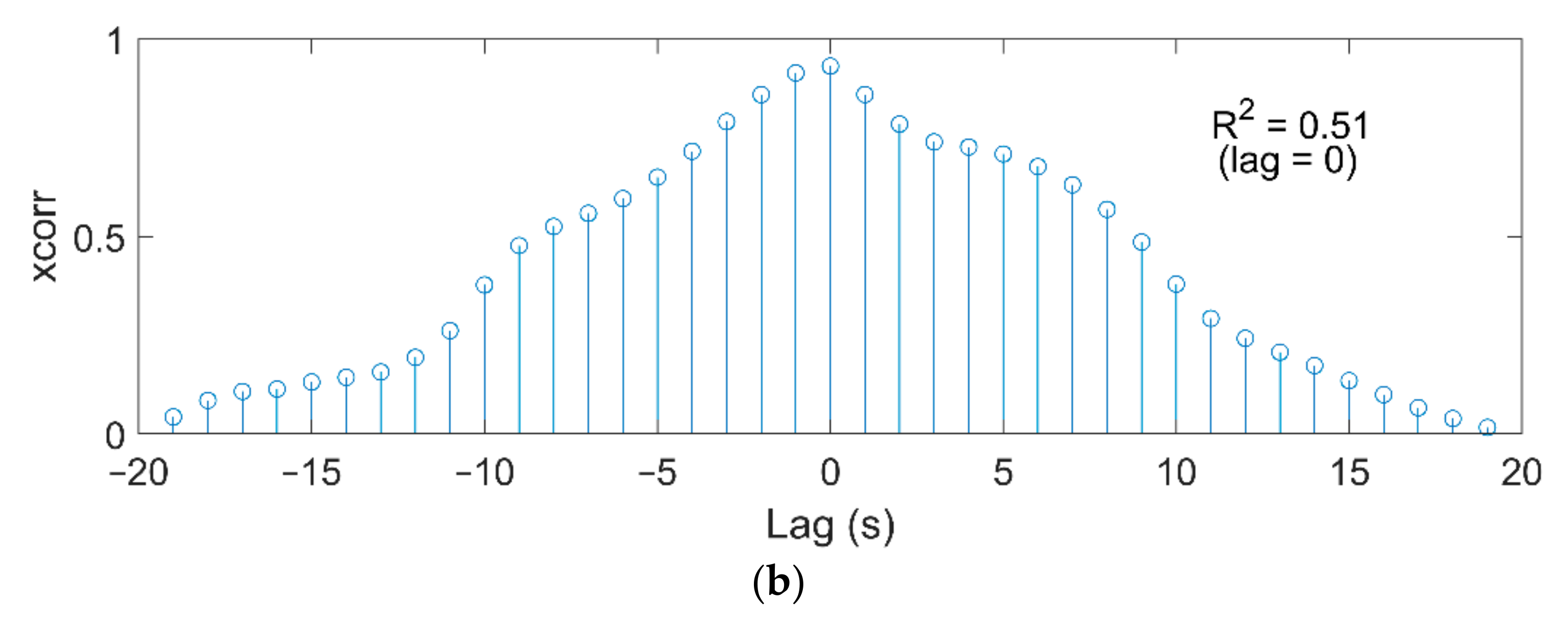
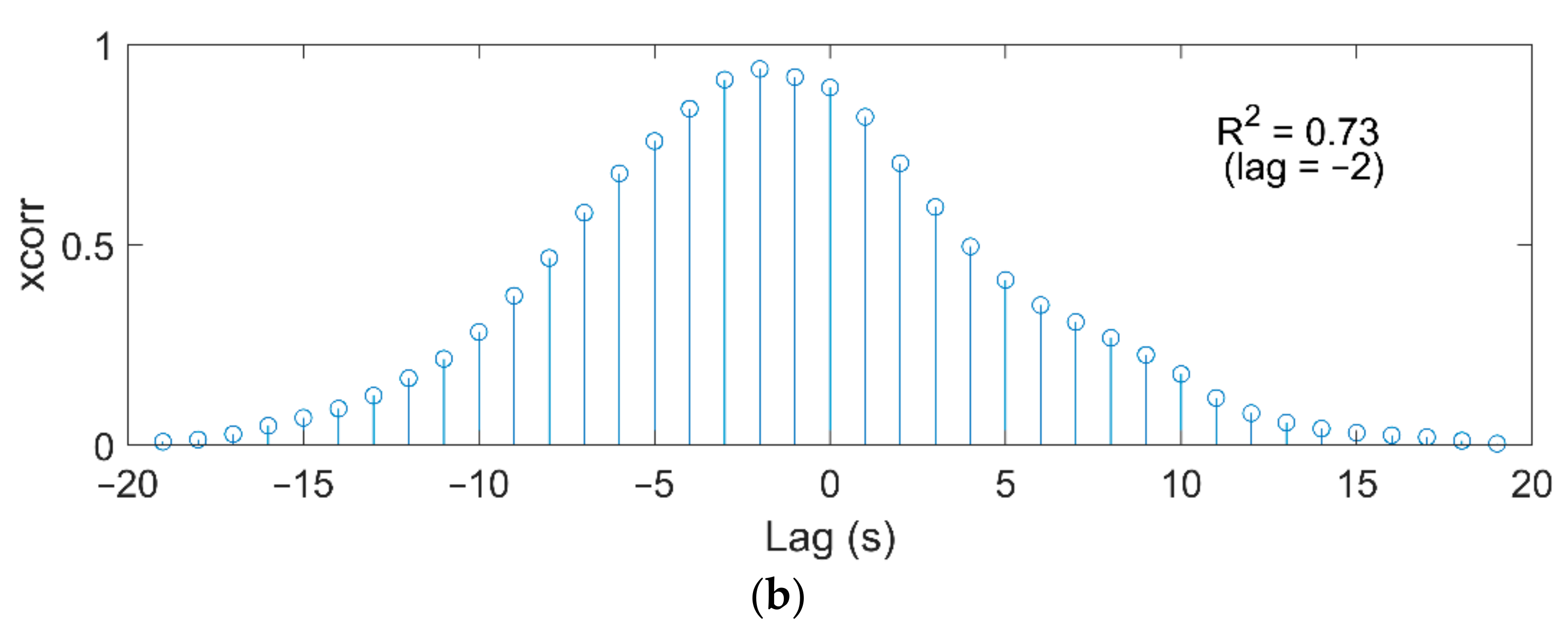
6.2. The Effect of Waves on Current
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, H.; Dong, G.; Wang, M.; Yuan, L.; Fei, X. Analysis on Main Characteristics and Causes of Landfall Typhoons in Recent 70 Years. Environ. Sci. Manag. 2020, 45, 128–131. [Google Scholar]
- Peereman, J.; Hogan, J.A.; Lin, T.C. Assessing Typhoon-Induced Canopy Damage Using Vegetation Indices in the Fushan Experimental Forest, Taiwan. Remote Sens. 2020, 12, 1654. [Google Scholar] [CrossRef]
- Beirne, J.; Renzhi, N.; Volz, U. Bracing for the Typhoon: Climate Change and Sovereign Risk in Southeast Asia; ADBI Working Papers; ADBI: Tokyo, Japan, 2021. [Google Scholar]
- Tamura, H.; Kawaguchi, K.; Iwamoto, T. Coastal destruction and unusual wave spectra induced by Typhoon Faxai in 2019. Coast. Eng. J. 2021, 63, 92–105. [Google Scholar] [CrossRef]
- Okuwaki, R.; Fan, W.; Yamada, M. Multiple Small-Scale Landslides Triggered by Typhoon Talas 2011. 2020. Available online: https://eprints.whiterose.ac.uk/173217/ (accessed on 9 August 2021).
- Cao, H.; Han, L. Drift path of green tide and the impact of typhoon “Chan-hom” in the Chinese Yellow Sea based on GOCI images in 2015. Ecol. Inform. 2020, 60, 101156. [Google Scholar] [CrossRef]
- Zhu, S.; Yin, X. Typhoon influence on ocean dynamic based on microwave remote sensing. J. Terahertz Sci. Electron. Inf. Technol. 2020, 18, 64–69. [Google Scholar]
- Zhang, C.; Wang, L.; Sun, M.; Zhang, J. Tentative analysis on multi-typhoon characteristics and atmospheric circulation background in the midsummer of 2012. Torrential Rain Disasters 2012, 31, 298–305. [Google Scholar]
- Xie, S.; Su, X.; Liang, Y. An Analysis on Precipitation Characteristics of Typhoon “Prapiroon”. Trop. Geogr. 2008, 28, 21–25. [Google Scholar]
- Wang, Y.; Tu, X.; Jiang, L.; Fang, Y.; Xu, B. Analysis of wave characteristics along Zhejiang coast during typhoon “Lekima”. J. Meteorol. Sci. 2020, 40, 97–105. [Google Scholar]
- Qiu, S.; Liang, C.; Dong, C.; Liu, Z. Analysis of the temporal and spatial variation in the wind and wave over the South China Sea. J. Mar. Sci. 2013, 31, 1–9. [Google Scholar]
- Xiao, L.; Shi, J.; Jiang, G.; Liu, Z. The influence of ocean waves on sea surface current field and sea surface temperature under the typhoon background. Mar. Sci. Bull. 2018, 37, 396–403. [Google Scholar]
- Hormann, V.; Centurioni, L.R.; Rainville, L.; Lee, C.M.; Braasch, L.J. Braasch. Response of ocean currents to Typhoon Fanapi. Geophys. Res. Lett. 2014, 41, 3995–4003. [Google Scholar] [CrossRef]
- Ginis, I. Ocean Response to Tropical Cyclone. Chapter 5 of Global Perspectives on Tropical Cyclones; WMO/TD-No. 693; World Meteorological Organization: Geneva, Switzerland, 1995; pp. 198–260. [Google Scholar]
- Li, M. A Study on Reginal Characteristics and Influence Mechanism of Typhoon-Induced Ocean Eddies in the Eastern Chinese Seas. Ph.D. Thesis, Nanjing University of Information Science and Technology, Nanjing, China, 2017. [Google Scholar]
- Ling, C.; Liu, L.; He, W. Impact of a typhoon process on the source region of Northwest Pacific western boundary current system. Mar. Forecast. 2015, 32, 24–34. [Google Scholar]
- Lai, Q.; Wu, L. SHIE Chung-lin. Sea surface temperature response to typhoon MORAKOT (2009) and the influence on its activity. J. Trop. Meteorol. 2013, 29, 221–234. [Google Scholar]
- Chan, C.L.; Duan, Y.; Shay, L.K. Tropical cyclone intensity change from a simple ocean atmosphere coupled model. J. Atmos Sci. 2001, 58, 154–172. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stress and mass transport in gravity waves, with application to ‘surf beats’. J. Fluid Mech. 1962, 13, 481–504. [Google Scholar] [CrossRef]
- Donelan, M.A.; Dobson, F.W.; Smith, S.D. On the Dependence of Sea Surface Roughness on Wave Development. J. Phys. Oceanogr. 1993, 23, 2143–2149. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Liu, H.; Peng, M. The effect of wave–Current interactions on the storm surge and inundation in Charleston Harbor during Hurricane Hugo 1989. Ocean. Model. 2008, 20, 252–269. [Google Scholar] [CrossRef]
- Xia, B.; Zhang, Q.; Jiang, C. A coupled wave—Current numerical model on unstructured grids. Oceanol. Limnol. Sin. 2013, 44, 1451–1456. [Google Scholar]
- Liu, L.; Fei, J.; Zhang, L. New parameterization of wave-current interaction used in a two-way coupled model under typhoon conditions. Acta Phys. Sin. 2012, 61, 59201. [Google Scholar]
- Zheng, J.; Yan, Y. Research and Application of Wave-Induced Radiation Stress Theory. Adv. Sci. Technol. Water Resour. 1999, 20, 5–7. [Google Scholar]
- Hasselmann, K. Wave-driven inertial oscillations. Geophys. Astrophys. Fluid Dyn. 1970, 1, 463–502. [Google Scholar] [CrossRef]
- Xie, L.; Wu, K.; Pietrafesa, L. A numerical study of wave-current interaction through surface and bottom stresses Wind-driven circulation in the South Atlantic Bight under uniform winds. J. Geophys. Res. Atmos. 2001, 106, 16841–16856. [Google Scholar] [CrossRef] [Green Version]
- Lin, X.; Yin, B. Influence of interaction of waves in tide-surge on surface wind stress coefficient. J. Hohai Univ. (Nat. Sci.) 2007, 35, 714–717. [Google Scholar]
- Xu, H.; Du, H.; Xiang, J.; Cao, J. The characteristics of ocean wave induced by typhoon “Megi” (2010) and its influence on the ocean and atmosphere. Mar. Forecast. 2020, 37, 6–16. [Google Scholar]
- Emanuel, K. Thermodynamic control of hurricane intensity. Nature 1999, 401, 665–669. [Google Scholar] [CrossRef]
- He, L.; Wang, Y.; Ma, X. Matching Relation among TC Initiating Locations of High Frequency, SST Warm-Water Region and ITCZ Measured by GMS-5 in the North-West Pacific Ocean. J. Nanjing Inst. Meteorol. 2006, 29, 440–447. [Google Scholar]
- Kumar, P.; Kaur, S.; Weller, E.; Young, I.R. Influence of Natural Climate Variability on Extreme Wave Power over Indo-Pacific Ocean Assessed Using ERA5. 2021. Available online: https://www.researchsquare.com/article/rs-372607/v1 (accessed on 9 August 2021).
- Patra, A.; Min, S.; Seong, M. Climate Variability Impacts on Global Extreme Wave Heights: Seasonal Assessment Using Satellite Data and ERA5 Reanalysis. J. Geophys. Res. Ocean. 2020, 125, e2020JC016754. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, Q.; Hang, R.; Liu, G. Predicting Tropical Cyclogenesis Using a Deep Learning Method from Gridded Satellite and ERA5 Reanalysis Data in the Western North Pacific Basin. IEEE Trans. Geosci. Remote. Sens. 2021, 99, 1–10. [Google Scholar]
- Yitian, Q.; Qibang, X. Early onset of the typhoon season over the western North Pacific in 2015: Influence of the 2015/2016 super El Ni(n)o event. Trans. Atmos. Sci. 2016, 039, 788–800. [Google Scholar]
- Xue, L.; Li, Y.; Wang, B.; Zhou, R. Characteristics of tropical cyclone-induced low-level wind fields over Hainan. Clim. Environ. Res. 2018, 23, 299–310. (In Chinese) [Google Scholar]
- Feng, J.; Wang, X. Impact of Increasing Horizontal and Vertical Resolution during the HWRF Hybrid EnVar Data Assimilation on the Analysis and Prediction of Hurricane Patricia (2015). Mon. Weather. Rev. 2020, 149, 419–444. [Google Scholar] [CrossRef]
- Biswas, M.K. Hurricane Weather Research and Forecasting (HWRF) Model: 2018 Scientific Documentation. 2018. Available online: https://dtcenter.org/HurrWRF/users/docs/index.php (accessed on 11 May 2021).
- Wen, S.; Yu, Z. Wave Theory and Computational Principles; Science Press: Beijing, China, 1994; pp. 110–112. [Google Scholar]
- Sun, L.; Huang, C.; Cai, W. Statistical analysis of wave characteristics in the Guanghai Bay. J. Trop. Oceanogr. 2014, 33, 17–23. [Google Scholar]
- Thompson, W.C.; Nelson, A.R.; Sedivy, D.G. Wave group anatomy of ocean wave spectra. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984; pp. 661–677. [Google Scholar]
- Wang, T.; Zhang, S.; Chen, F. Upper Ocean Response to Sequential Typhoons in Northwest Pacific Ocean. J. Guangdong Ocean. Univ. 2019, 39, 62–74. [Google Scholar]
- Zhang, Z. A case study of the response of northwest Pacific upper ocean to typhoon. Mar. Sci. Bull. 2019, 38, 562–568. [Google Scholar]
- Kong, Y.; Ding, P.; Zhou, G. Characteristic Analyses of Storm Waves in the Changjiang Estuary. J. East China Norm. Univ. (Nat. Sci.) 2001, 3, 85–90. [Google Scholar]
- Li, J.; Zheng, C.; Liu, K. Numerical analysis of wave energy propagation regulation. J. Harbin Eng. Univ. 2021, 42, 49–54. [Google Scholar]
- Tian, Z. Parameters optimization research of Ekman wind current model. Trans. Oceanol. Limnol. 2018, 1–9. [Google Scholar] [CrossRef]
- Chen, Q.; Huang, D. Characteristics of the tidal current and residual current in the seas adjacent to Zhejiang. Donghai Mar. Sci. 2003, 21, 7–13. [Google Scholar]
- Basco, D.R. Surf zone currents. Coast. Eng. 1983, 7, 331–355. [Google Scholar] [CrossRef]
- Phillips, O.M. The Dynamics of the Upper Ocean. Science 1967, 157, 1029. [Google Scholar]
- Deng, Z. A Study of Influences of Coriolis-Stocks Forcing on the Numerical Ocean Modeling. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2009. [Google Scholar]



| Wave Level | Significant Height/m | Wave Level | Significant Height/m |
|---|---|---|---|
| 0 (calm—glassy) | 0 | 5 (rough) | 2.5–4 |
| 1 (clam—rippled) | 0–0.1 | 6 (very rough) | 4–6 |
| 2 (smooth wavelet) | 0.1–0.5 | 7 (high) | 6–9 |
| 3 (light) | 0.5–1.25 | 8 (very high) | 9–14 |
| 4 (moderate) | 1.25–2.5 | 9 (phenomenal) | >14 |
| Period(t)/Wave Level | Slight | Moderate | Rough | Very Rough |
|---|---|---|---|---|
| T < 6 s | 11 | 0 | 0 | 0 |
| 6 s < T < 8 s | 22 | 16 | 10 | 0 |
| 8 s < T | 13 | 6 | 4 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, Y.; Guo, B.; Subrahmanyam, M.V.; Xue, B.; Ye, Y. The Influence of Typhoon “MITAG” on Waves and Currents in Zhoushan Sea Area, China. Atmosphere 2021, 12, 1027. https://doi.org/10.3390/atmos12081027
Niu Y, Guo B, Subrahmanyam MV, Xue B, Ye Y. The Influence of Typhoon “MITAG” on Waves and Currents in Zhoushan Sea Area, China. Atmosphere. 2021; 12(8):1027. https://doi.org/10.3390/atmos12081027
Chicago/Turabian StyleNiu, Yuqian, Biyun Guo, Mantravadi Venkata Subrahmanyam, Bin Xue, and Yun Ye. 2021. "The Influence of Typhoon “MITAG” on Waves and Currents in Zhoushan Sea Area, China" Atmosphere 12, no. 8: 1027. https://doi.org/10.3390/atmos12081027
APA StyleNiu, Y., Guo, B., Subrahmanyam, M. V., Xue, B., & Ye, Y. (2021). The Influence of Typhoon “MITAG” on Waves and Currents in Zhoushan Sea Area, China. Atmosphere, 12(8), 1027. https://doi.org/10.3390/atmos12081027







