Abstract
The main aim of this paper is to propose a statistical indicator for wind shear prediction from Light Detection and Ranging (LIDAR) observational data. Accurate warning signal of wind shear is particularly important for aviation safety. The main challenges are that wind shear may result from a sustained change of the headwind and the possible velocity of wind shear may have a wide range. Traditionally, aviation models based on terrain-induced setting are used to detect wind shear phenomena. Different from traditional methods, we study a statistical indicator which is used to measure the variation of headwinds from multiple headwind profiles. Because the indicator value is nonnegative, a decision rule based on one-side normal distribution is employed to distinguish wind shear cases and non-wind shear cases. Experimental results based on real data sets obtained at Hong Kong International Airport runway are presented to demonstrate that the proposed indicator is quite effective. The prediction performance of the proposed method is better than that by the supervised learning methods (LDA, KNN, SVM, and logistic regression). This model would also provide more accurate warnings of wind shear for pilots and improve the performance of Wind shear and Turbulence Warning System.
1. Introduction
Wind shear is a kind of microscale meteorological phenomenon which refers to a sustained change in the wind direction and/or speed, resulting in a change in the headwind or tailwind encountered by an aircraft, see, for instance, [1,2]. Accurate wind shear detection is crucial for aviation safety in approach and landing. Typically, a sustained change of the headwind or tailwind of 15 knots (7.72 m/s) or more for more than a few seconds is significant wind shear. A significant wind shear occurring at low levels on approach and departure zones at airport might result in the difficulty in control for aircrafts. This losing of altitude could become very dangerous during an aircraft’s landing and takeoff phases. Pilots require timely and appropriate corrective actions to ensure the safety of aircrafts when they encounter wind shear.
There were models and hardware launched at various airports to detect wind shear. Boilley and Mahfouf [3] studied a wind shear event using both observational and numerical data and demonstrated that a numerical model (Meso-NH) could be used to detect wind shear over the Nice airport. Weipert et al. [4] researched on low-level wind shear detection systems consisting of an Xband polarimetric scanning radar and an infrared scanning LIDAR (Light Detection and Ranging) to detect wind shear at the German international airports of Frankfurt and Munich. Since 2017, Airport Low-level Wind Information (ALWIN) system was operated at Tokyo International Airport (Haneda) and Narita International Airport to detect low-level wind shear, see [5].
Research on the low-level wind shear algorithm has begun using anemometers since 1970s and Doppler radars since 1980s. They are dedicated to some special weather phenomena such as gust front and microbursts/mesocyclones. The detailed information of Low-Level Windshear Alert System can be found in [6]. It is still used at some airports such as those in the United States and Taiwan, to deal with wind shear issues. The siting of the anemometers at critical locations is important for the success of the algorithm in capturing low level wind shear due to microburst. Currently, it is also effective in the detection and warning of low-level wind shear in rainy weather. However, there are limitations of the use of anemometer-based algorithms and Doppler weather radars in capturing wind shear due to dry microburst.
A method to capture low level wind shear in clear air situations is the use of wind profilers, such as the system used at Juneau, United States [7]. It is claimed to be capable of capturing wind shear due to terrain effects. However, wind profiler data consists of 10-min averages and its wind alerts may not be fast enough (i.e., not so frequently updated) to detect rapidly changing wind shear due to terrain effects, which may occur in a time interval of a few minutes or even within one minute. The detection of wind shear due to dry microburst and terrain effect points to the use of new remote sensing instrumentation for wind shear detection, namely, the Doppler weather LIDAR system. Recent advances in LIDAR techniques have spurred the development of several methods (see for instance [8,9,10,11,12]), for predicting wind shear from the LIDAR data. Some researchers have developed methods by using Doppler weather LIDAR to detect microburst wind shear, see [11]. In contrast, much fewer methods have been developed on the detection of terrain-induced wind shear by using Doppler weather LIDAR.
Wind shear at Hong Kong International Airport (HKIA) is terrain induced. HKIA lies to the north of the mountainous Lantau Island with highest peaks above 900 m and valleys as low as 300 m, see Figure 1. Sometimes, the flow of air across this hilly terrain could be disrupted to form mountain waves, gap outflow, etc., over the flight paths of HKIA, inducing wind shear. Most of the wind shear episodes at HKIA are related to airflow disturbances by the complex terrain near HKIA, see [1]. In addition, forecasters [8,9] in Hong Kong Observatory can issue warnings for imminent wind shear based on the broad prevailing meteorological conditions and the real time data from the Wind shear and Turbulence Warning System [2]. Currently, this warning system can generate “up-to-the-minute” alerts after wind shear is measured. The LIDAR alarm rate is about 0.76, see the results reported in [1]. In 2016, a high-resolution numerical aviation model was employed to forecast the terrain-induced wind shear at HKIA, see [12]. In 2018, a synthesized scheme based on the combination of improved signal smoothing and wind shear detection was proposed to detect wind shear. The scheme could capture 80.6% of wind shear according to pilot reports from HKIA, see [10]. The performance of this warning system should be further improved to issue timely warmings of wind shear for pilots. Therefore, further research is ongoing to explore the use of LIDAR data in detection of wind shear at HKIA.
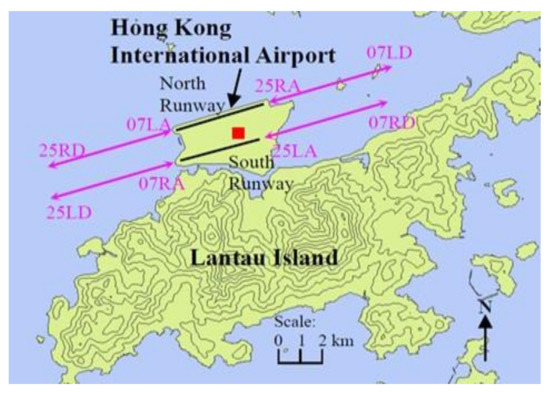
Figure 1.
Map of Hong Kong International Airport and Lantau Island (height contours: 100 m) [1], with the location of the LIDAR (red square). Runway corridors are shown as pink arrows with the names marked alongside.
Modern data mining techniques can be applied to various datasets used in many meteorological applications for prediction purposes. The main aim of this paper is to propose an indicator for wind shear prediction from Light Detection and Ranging (LIDAR) observational data. In the literature, the research on machine learning methods for wind shear detection with LIDAR data has received some attention. In 2012, a chaotic oscillatory-based neural network with a new learning algorithm was proposed to identify the wind shear occurrence, see [13]. Li et al. [14] designed a new method that employs a neural network as the position amendment module and exponential smoothing as the fluctuation compensation module. This method was applied to HKIA Doppler LIDAR data and a reasonable wind shear forecasting precision was obtained, see for example [15].
Different from the above traditional hardware-based and aviation methods, we propose in this paper to use supervised learning methods for wind shear detection. We will present a statistical indicator which is used to measure the variation of headwinds from multiple headwind profiles. The indicator is based on the maximum spread of measured velocities along the range of the measurement beam with respect to different azimuth ranges. Because the indicator value is a nonnegative number, we employ a decision rule based on one-side normal distribution to distinguish a wind shear case and a non-wind shear case. Experimental results based on real data sets on two different periods obtained at Hong Kong International Airport runway are presented to demonstrate the proposed indicator is quite effective. In particular, the prediction accuracies of the proposed model are 98.0% for training data collected at 2015 and 92.0% for testing data collected at 2018, which are better than the other methods like LDA, KNN, SVM and logistic regression.
The outline of this paper is given as follows. In Section 2, we study the LIDAR observational data from HKIA. In Section 3, we present the proposed method. In Section 4, results are presented to demonstrate the effectiveness of the proposed method for wind shear prediction. Finally, some concluding remarks are given in Section 5.
2. LIDAR Observational Data
To measure the variable wind profile to be encountered by the aircraft at HKIA, Hong Kong Observatory developed Glide Path Scan (GPScan) strategy for the LIDAR [2]. A diagram of a glide path scan is given in Figure 2. For arrival corridors, three-degree glide paths originating from the touchdown points of the runways are considered. The laser beam of the LIDAR is used to slide along the glide paths and measure the winds. The azimuth and elevation motions of the LIDAR scanner must be configured so that the laser beam can slide smoothly. The radial wind measurements along a glide path are considered together to construct a headwind profile. During the scanning process, the wind velocities are measured at the locations represented by slant ranges (or range gates), azimuth angles, and elevation angles in three-dimensional space.
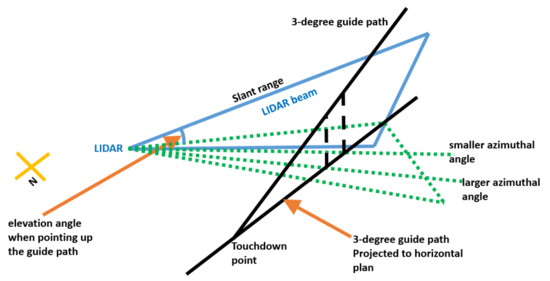
Figure 2.
Diagram illustrating a LIDAR glide path scan along the 3-degree glide path for the western approach towards the north runway.
Since the aircraft on approach closely follows the three-degree glide slope in the final three nautical miles prior to touchdown on the runway, we only analyze the LIDAR of three-degree elevation angle. On the other hand, the glide path area in HKIA is measured by around 250-degree azimuth angle. Here we focus on the azimuth angles in between 220 degrees and 280 degrees. The slant ranges of the LIDAR data are from 350 to 10,000 m. However, the LIDAR data points with slant ranges over 4500 m are neglected since there are many missing Doppler velocities. In this paper, we focus on the LIDAR data at three-degree elevation angle, the azimuth angles in between 220 and 280 degrees, and the slant ranges in between 350 and 4500 m. At HKIA, the LIDAR scanner takes about four seconds to obtain velocities at 1560 locations which refer to the combination of 39 azimuth angles and 40 slant ranges in the above setting.
In Table 1, we show an example of the collected LIDAR data on 2 March 2015. The LIDAR cannot return actual locations in elevation angles, azimuth angles and slant ranges of measured velocities, and it only provides their minimum and maximum values. In Table 1, the differences between the maximum and minimum values in azimuth angles are about one-degree. However, the differences between the maximum and minimum values in slant ranges are from 10 to 105 m.

Table 1.
An example of the collected LIDAR data at HKIA.
3. The Detection Method
In this section, we show developed data mining techniques for wind shear prediction from Light Detection and Ranging (LIDAR) observational data. We aimed to convert the raw LIDAR dataset into headwind profiles as wind shear results from a sustained change of the headwind. Since the exact location and range of wind shear are unknown, considering LIDAR in one azimuth range from 220 to 280 degrees for each episode is not enough. For the wind shear episodes that happen within a narrow range, such as from 245 to 255 degrees, there would be a large noise by considering all LIDAR data ranging from 220 to 280 degrees. Moreover, we may lose information about wind shear if we consider a narrow azimuth range for wind shear occurring in a wide azimuth range. Therefore, for each episode, we consider seven different azimuth ranges where one headwind profile is constructed for each azimuth range. Then there are seven different headwind profiles for each episode. The seven azimuth ranges are included as follows: az1 = 220°–280°, az2 = 230°–270°, az3 = 240°–260°, az4 = 245°–255°, az5 = 248°–252°, az6 = 249°–250°, az7 = 250°–251°. Moreover, there are 40 measurements along the slant range. Each headwind profile is a vector of size 40. For convenience, we set xi,j to be the headwind profile for the j-th azimuth range at the i-th episode, where j = 1, 2, …, 7 and i = 1, 2, …, N. Here N is the size of the training dataset.
To detect a wind shear case, we study two statistical indicators based on seven headwind profiles to measure the variation of headwind for each episode, which are given as follows:
where max(xi,j) and min(xi,j) refer to the largest and smallest magnitudes of the values in xi,j with respect to the slant range in the headwind profile (i.e., all forty values in the vector); and
where var(xi,j) refers to the variance of the forty values in xi,j. For ki,1, the maximum spread of measured velocities along the range of the measurement beam (slant range) with respect to different azimuth ranges (azj) is used. For ki,2, the maximum variance of measured velocities along the range of the measurement beam (slant range) with respect to different azimuth ranges (azj) is used. Both indicators are considered to check a change in the wind direction and/or speed across multiple headwind profiles.
ki,1 = max {max(xi,j) − min(xi,j)}
j = 1,…,7
j = 1,…,7
ki,2 = max {var(xi,j)}
j = 1,…,7
j = 1,…,7
In this paper, we propose to determine a threshold value of the indicator to identify a wind shear case or a non-wind shear case. In other words, if ki,1 (or ki,2) is larger than the threshold value, then a wind shear case is identified, otherwise a non-wind shear case is identified. In Figure 3, we report the histograms of ki,1 and ki,2 for a data set in March 2015 at Hong Kong International Airport. The detailed information of the data set will be described and used in Section 4. The values of ki,1 and ki,2 for wind shear cases and non-wind shear cases are shown in the histograms. We see from the figure that wind shear and non-wind shear cases cannot be distinguished clearly though ki,2 is one measure of the variation of wind velocity. However, there is a clear boundary to separate wind shear cases and non-wind shear cases in the histogram of ki,1. In the following discussion, we consider how to determine a decision boundary of ki,1 for wind shear and non-wind shear cases.
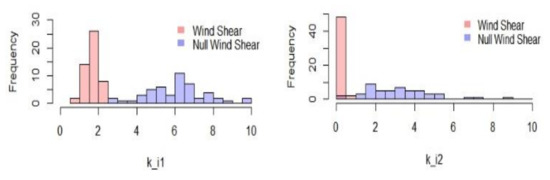
Figure 3.
Histograms of ki,1 and ki,2 for wind shear and non-wind shear cases in March 2015. (left) ki,1 for wind shear and non-wind shear cases; (right) ki,2 for wind shear and non-wind shear cases.
According to (1), we know that the value of ki,1 is nonnegative. Moreover, we use the same data set in Figure 3 to show a QQ Plot in Figure 4. We find that the values of ki,1 for wind shear and non-wind shear cases are skewed and the measurements are not normal distributed. Because of these two issues, we may not set a boundary point using classical quadratic discriminant analysis which assumes that the measurements from each class are normally distributed (see for instance [16]).
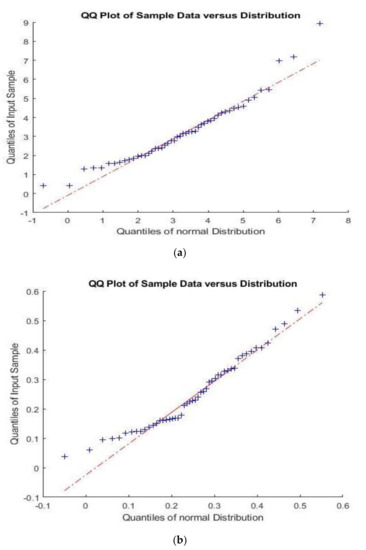
Figure 4.
QQ Plot of ki,1 for wind shear and null wind shear cases in March 2015. (a) ki,1 for wind shear; (b) ki,1 for non-wind shear cases.
In this paper, we fit one-sided normal distributions with truncation of the lower tail for ki,1 of wind shear cases and non-wind shear cases. Then we calculate the means and standard deviations of the truncated normal distributions for wind shear cases and non-wind shear cases. The means of the truncated normal distributions for non-wind shear cases and wind shear cases are denoted as mnon and mwind, respectively. The standard deviations of the truncated normal distributions for non-wind shear cases and wind shear cases are denoted as snon and swind, respectively. A decision boundary, denoted as z, is simply selected such that the number of standard deviations from the mean of non-wind shear cases and that from the mean of wind shear cases, are equal, i.e.,
(z − mnon)/snon = (mwind − z)/swind
Here the main idea is to find a threshold value for the change in the wind direction and/or speed (the unit is knot) that can distinguish wind shear cases and non-wind shear cases. In (3), the normalization is done within wind shear cases and non-wind shear cases. The threshold value is measured in terms of z-score in the standard normal distribution after normalization. In the next section, we validate the proposed method in our case study by using HKIA data sets.
4. Prediction Results and Discussion
The training and testing LIDAR datasets were collected for validation of our pro-posed method in Section 3. Both training and testing datasets were for the glide path at a specific time. Training data was collected from the LIDAR data in 2015, whereas testing data was collected from the LIDAR data in 2018. Pilot reports serve as ground truth for the occurrence of wind shear. Wind shear training data was collected according to the timestamps of wind shears from pilot reports in 2015. For each timestamp of wind shear reported, the recent timestamp from the LIDAR data was matched and their related headwind profiles were collected. Non-wind shear training data sets were collected on 2 March 2015 where there was no wind shear. Moreover, on 2 March 2015, there was no cross-mountain airflow in HKIA though the easterly winds were fresh (it was around 5 knots). Similarly, wind shear testing data was collected according to the timestamps of wind shears from pilot reports in 2018. Non-wind shear testing data was collected on the days in March 2018 when there was no wind shear under the suggestion from Hong Kong Observatory. In total, there are fifty training wind shear cases and thirty-nine testing wind shear cases. There are also fifty training non-wind shear cases and thirty-nine testing non-wind shear cases. For each case, the LIDAR scanner takes about four seconds to obtain velocities at 1560 locations (see Section 2).
In the comparison, we test supervised principal component analysis [17] that minimizes Bayes error for data classification. By applying to headwind profiles of episodes in 2015, supervised Principal Component Analysis (PCA) selects the three features [r1, r2, r3] that greatly separate a wind shear case and a non-wind shear case. Moreover, linear discriminant analysis (LDA), k-nearest neighbor (kNN), linear support vector machine (SVM), and logistic regression (see [16]) are used to classify wind shear cases and non-wind shear cases. LDA assumes that the covariance matrices of wind shear class and non-wind shear class are the same, and determines a linear combination of features (i.e., (r1), (r1, r2), or (r1, r2, r3) in our experiment) and a threshold. A wind shear case (a non-wind shear case) can be determined if the inner product between the linear combination weights and the input features of a testing example is larger than (less than or equal to) the threshold value. SVM maps input features (i.e., (r1), (r1, r2), or (r1, r2, r3) in our experiment) of wind shear examples and non-wind shear examples to points and maximizes the width of the gap between the wind shear cases and non-wind shear cases. The gap can be represented by the maximum-margin hyperplane. The class of a testing case based on its input features can be determined if the corresponding point lies on the one side of the hyperplane. Logistic regression assumes a linear relationship between the response variables (a wind shear case or a non-wind shear case) and the log-odds of the event of wind shear case. After the regression coefficients are estimated from input features of wind shear cases and non-wind shear cases, the logistic regression can be used to model the probability of a headwind profile existing such as a wind shear or a non-wind shear case based on input features (r1), (r1, r2), or (r1, r2, r3). kNN is a non-parametric classification method with the headwind profile being assigned to the wind shear case or non-wind shear case most common among its k nearest neighbors.
The proposed detection method in Section 3 is to compute a threshold about the change in the wind direction and/or speed in the boundary of two one-sided normal distributions with truncation of the lower tails for wind shear cases and non-wind shear cases. The proposed method assumes that the distributions of wind shear cases and non-wind shear cases are one-sided normal which is different from LDA. Moreover, we do not employ a linear combination of weights in LDA, a hyperplane in SVM and a linear relationship in logistic regression. Instead of using neighbors in kNN, we consider the distributions of wind shear examples and non-wind shear examples in the proposed method. The proposed method is different from the above compared classification methods.
4.1. Results for 2015
By applying to headwind profiles of episodes in 2015, supervised PCA selects the three features [r1, r2, r3] that greatly separate a wind shear case and a non-wind shear case. Then we apply the features selected by supervised PCA to wind shear cases and non-wind shear cases for classification. The three selected features are tested with LDA, kNN, SVM, and logistic regression. Here a fivefold cross validation procedure is applied to each supervised learning method. In fivefold cross-validation, the wind shear cases (or non-wind shear cases) are randomly partitioned into five equal sized subsamples. Each subsample contains 10 windshear cases and 10 non-wind shear cases. Of the five subsamples, a single subsample is retained as the validation data for testing the model, and the remaining four subsamples are used as training data. The cross-validation process is then repeated five times, with each of the five subsamples used exactly once as the validation data. The five results can then be averaged to produce cross-validation accuracy results. In Table 2, Table 3 and Table 4, we show the cross-validation results based on three different combinations of supervised PCA features ((r1), (r1, r2), (r1, r2, r3)), see Supplementary Materials.

Table 2.
Cross-validation results of wind shear cases and non-wind shear cases in March 2015 under four classification methods with supervised PCA with (r1).

Table 3.
Cross-validation results of wind shear cases and non-wind shear cases in March 2015 under four classification methods with supervised PCA with (r1, r2).

Table 4.
Cross-validation results of wind shear cases and non-wind shear cases in March 2015 under four classification methods with supervised PCA with (r1, r2, r3).
For logistic regression based on (r1, r2) or (r1, r2, r3), there are more than one group of parameters estimated not significant at the 0.05 level of significance. Therefore, logistic regression models are not significant in Table 3 and Table 4. Table 2, Table 3 and Table 4 show that four classification algorithms based on supervised PCA features could predict wind shear and non-wind shear with a cross-validation accuracy up to 0.930.
In addition, we show the fivefold cross-validation results for linear SVM, LDA, kNN, and logistic regression based on the statistical indicators ki,1 and ki,2 in (1) and (2), see Supplementary Materials. We test on two combinations of statistical indicators: (ki,1) and (ki,1, ki,2). The cross-validation results are summarized in Table 5 and Table 6. We note from Table 5 and Table 6 that kNN performs best in terms of the cross-validation accuracy for wind shear cases in March 2015, which are 0.960 based on (ki,1) and 0.940 based on (ki,1, ki,2). For the general prediction of wind shear cases and non-wind shear cases in March 2015, kNN also reaches the most satisfactory cross-validation results which are 0.950 based on (ki,1) and 0.940 based on (ki,1, ki,2). We observe in the four machine learning methods that the proposed statistical indicator ki,1 is more effective than the supervised PCA features and the statistical indicator ki,2 in terms of cross-validation accuracy for wind shear cases and non-wind shear cases.

Table 5.
Cross-validation results of wind shear cases and non-wind shear cases in March 2015 under four classification methods with supervised PCA with (ki,1).

Table 6.
Cross-validation results of wind shear cases and non-wind shear cases in March 2015 under four classification methods with supervised PCA with (ki,1, ki,2).
On the other hand, we apply the proposed data analytics algorithm in Section 3 to training datasets in 2015. Fivefold cross-validation is applied to the statistical indicator ki,1 of training datasets to set a decision boundary according to (3). The cross-validation results of wind shear and nonwind shear in March 2015 are presented in Table 7. The cross-validation accuracy is 0.980, which is better than those of other methods by at least 3.00%. In Table 8, we show the values of mnon, mwind, snon, and swind and the determined threshold value z in the five cross-validation tests. Note that the average threshold value is z = 2.290, i.e., if ki,1 (the maximum spread of measured velocities along the range of the measurement beam) is greater than or equal to 2.290, then it is a wind shear case; otherwise, it is a non-wind shear case. Correspondingly, the number (mwind − 2.290)/swind of standard deviations of the truncated normal distribution of wind shear cases and the number (2.290 − mnon)/snon of standard deviations of the truncated normal distribution of non-wind shear cases are about 2.458.

Table 7.
Cross-validation results of wind shear and non-wind shear in March 2015 under the proposed data analytics algorithm.

Table 8.
The values of mnon, mwind, snon, and swind and the determined threshold value z in the five cross-validation tests.
4.2. Results for 2018
In this subsection, we show the testing results for LIDAR in 2018 under the models trained by the LIDAR data in March 2015. There are thirty-nine wind shear cases and thirty-nine non-wind shear cases in March 2018. It is an out-of-training-sample test.
For supervised PCA with (r1), we apply five training models under each classification method respectively to test all the seventy-eight cases in March 2018. In Table 9, we calculate the wind shear prediction accuracy and non-wind shear prediction accuracy by averaging the results over five training models for each classification method. The prediction accuracy is calculated by averaging wind shear prediction accuracy and non-wind shear prediction accuracy for each classification method. Similarly, for supervised PCA with (r1, r2) and (r1, r2, r3), the prediction accuracy results are summarized in Table 10 and Table 11. Furthermore, the prediction results based on the proposed statistical indicators (ki,1) and (ki,1, ki,2) are shown in Table 12 and Table 13, respectively. Moreover, we apply the determined threshold value (z = 2.290) trained from the LIDAR data in March 2015 to the LIDAR data in March 2018 to detect wind shear cases and non-wind shear cases. The prediction accuracy results are shown in Table 14.

Table 9.
Cross-validation results of wind shear cases and non-wind shear cases in March 2018 under four classification methods with supervised PCA with (r1).

Table 10.
Cross-validation results of wind shear cases and non-wind shear cases in March 2018 under four classification methods with supervised PCA with (r1, r2).

Table 11.
Cross-validation results of wind shear cases and non-wind shear cases in March 2018 under four classification methods with supervised PCA with (r1, r2, r3).

Table 12.
Cross-validation results of wind shear cases and non-wind shear cases in March 2018 under four classification methods with supervised PCA with (ki,1).

Table 13.
Cross-validation results of wind shear cases and non-wind shear cases in March 2018 under four classification methods with supervised PCA with (ki,1, ki,2).

Table 14.
Cross-validation results of wind shear cases and non-wind shear cases in March 2018 under the proposed data analytics algorithm.
By comparing the prediction accuracy results in Table 14 with those in Table 9, Table 10, Table 11, Table 12 and Table 13, we observe that the proposed statistical indicator ki,1 is more effective than supervised PCA features and statistical indicator ki,2. The prediction accuracy of wind shear cases and non-wind shear cases in March 2018 by the proposed data analytics algorithm is 0.920, which is higher than the average prediction accuracy results of other machine learning methods based on (r1), (r1, r2), (r1, r2, r3), (ki,1) and (ki,1, ki,2). We also see from Table 9, Table 10, Table 11, Table 12 and Table 13 that the prediction accuracy of wind shear cases is very high, but the prediction accuracy of non-wind shear cases is very low. The models trained by the LIDAR data in March 2015 may be overfitting.
On the other hand, the prediction accuracy by the proposed data analytics algorithm is also higher than 0.806, the prediction accuracy of wind shear cases and non-wind shear cases by a recent synthesized scheme in [10]. Overall, our data analytics algorithm has a good performance in predictions of wind shear cases and non-wind shear cases, which could be applied to more the LIDAR data to predict wind shear.
5. Conclusions
In this paper, we construct headwind profiles from the LIDAR observations. With the unknown location and range of wind shear, seven different azimuth ranges are considered where one headwind profile is constructed for each azimuth range, which could gain a higher accuracy than one headwind profile for measuring a wind shear case. After that, a statistical indicator is proposed on the seven headwind profiles to measure the variation of headwinds for each episode. Then a decision rule is generated from the proposed statistical indicator. A wind shear case is identified when the indicator is larger than 2.290 that is obtained by using the LIDAR data in 2015, a non-wind shear case otherwise. The training and testing results in 2015 and 2018 respectively show that the proposed statistical indicator is more effective than supervised PCA features. Furthermore, the prediction accuracies of the proposed model are 98.0% for training data and 92.0% for testing data, which are better than the other methods like LDA, KNN, linear SVM and logistic regression.
In the future, the proposed model could be applied to more LIDAR datasets to predict wind shear. We plan to check the performance of the decision point to the LIDAR data in different locations and different periods. We would like to improve this model that can provide more accurate warnings of wind shear for pilots and improve the performance of Wind shear and Turbulence Warning System. On the other hand, doppler LIDARs are increasingly more commonly used for detecting airflow turbulence. The turbulence may arise from natural terrain, or even by man-made structures and buildings. The behavior of the turbulence from Terrain and buildings may be different. As a future research topic, the methods studied in the present paper may be applied to other meteorological conditions, such as tropical cyclones, thunderstorms, and other kinds of disturbed airflow, such as building effects on the low-level wind.
Supplementary Materials
The extracted features (r1, r2, r3) and (ki,1, ki,2) of LIDAR data of wind shear cases and non-wind shear cases are available online at http://hkumath.hku.hk/~mng/mng_files/supplementary-data.xlsx.
Author Contributions
Conceptualization, J.H., M.K.P.N., and P.W.C.; methodology, J.H. and M.K.P.N.; software, J.H.; validation, J.H. and P.W.C.; formal analysis, J.H., M.K.P.N., and P.W.C.; investigation, J.H.; resources, P.W.C.; data curation, J.H. and P.W.C.; writing—original draft preparation, J.H.; writing—review and editing, M.K.P.N. and P.W.C.; visualization, J.H., M.K.P.N., and P.W.C.; supervision, M.K.P.N. and P.W.C.; project administration, M.K.P.N.; funding acquisition, M.K.P.N. All authors have read and agreed to the published version of the manuscript.
Funding
M.K.P.N.’s research is funded by HKU grant number 006028001.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Hong Kong Observatory for the data used in this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chan, P.; Shun, C.; Wu, K. Operational Lidar-Based System for Automatic Windshear Alerting at the Hong Kong International Airport. Reprint 613, Hong Kong Observatory. Available online: www.hko.gov.hk/hko/publica/reprint/r613.pdf (accessed on 15 April 2021).
- Windshear and Turbulence in Hong Kong—Information for Pilots. Available online: http://www.hko.gov.hk/en/aviat/articles/files/WS-turb-booklet-eng-3rd.pdf (accessed on 15 April 2021).
- Boille, A.; Mahfouf, J. Wind shear over the Nice Cote d’Azur airport: Case studies. Nat. Hazards Earth Syst. Sci. 2013, 13, 2223–2238. [Google Scholar] [CrossRef]
- Weipert, A.; Kauczok, S.; Hannesen, R.; Ernsdorf, T.; Stiller, B. Wind shear detection using radar and lidar at Frankfurt and Munich airports. In Proceedings of the Eighth European Conference on Rader in Meteorology and Hydrology, Garmisch-Partenkirchen, Garmisch-Partenkirchen, Germany, 1 September 2014; Abstract ID 058. 2014. Available online: http://www.pa.op.dlr.de/erad2014/programme/ExtendedAbstracts/058_Weipert (accessed on 15 April 2021).
- Airport Low-Level Wind Information (ALWIN) Starts Operation at Haneda and Narita Airports. Available online: https://global.jaxa.jp/press/2017/04/20170419_alwin.html (accessed on 15 April 2021).
- Low Level Wind Shear Alert System (LLWAS). Available online: https://ral.ucar.edu/projects/low-level-wind-shear-alert-system-llwas (accessed on 15 April 2021).
- Juneau Airport Wind System (JAWS). Available online: https://ral.ucar.edu/projects/juneau-airport-wind-system-jaws (accessed on 15 April 2021).
- Shun, C.; Chan, P. Applications of an infrared doppler lidar in detection of windshear. J. Atmos. Ocean Technol. 2007, 25, 637–694. [Google Scholar] [CrossRef]
- Chan, P.; Hon, K. Observation and numerical simulation of terrain-induced windshear at the Hong Kong international airport in a planetary boundary layer without temperature inversions. Adv. Meteorol. 2016, 2016, 1–9. [Google Scholar] [CrossRef]
- Meng, L.; Xu, J.; Xiong, X.; Ma, Y.; Zhao, Y. A novel ramp method based on improved smoothing algorithm and second recognition for windshear detection using lidar. Curr. Opt. Photonics 2018, 2, 7–14. [Google Scholar]
- Keohan, C.; Keith, B.; Hannon, S. Evaluation of pulsed lidar wind hazard detection at Las Vegas international airport. In Proceedings of the 12th Conference on Aviation Range & Aerospace Meteorology, American Meteor Society, Atlanta, GA, USA, 29 January–2 February 2006; Available online: https://ams.confex.com/ams/pdfpapers/105481.pdf (accessed on 15 April 2021).
- Chan, P.; Hon, K. Performance of super high resolution numerical weather prediction model in forecasting terrain disrupted airflow at the Hong Kong international airport: Case studies. Meteor. Appl. 2016, 23, 101–114. [Google Scholar] [CrossRef]
- Liu, N.; Kwong, K.; Chan, P. Chaotic oscillatory-based neural network for wind shear and turbulence forecast with lidar data. IEEE Trans. Syst. Man Cybern. Part C 2012, 42, 1412–1423. [Google Scholar] [CrossRef]
- Li, Y.; Hu, Q.; Liu, S. Wind-shear prediction with airport lidar data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3704–3707. [Google Scholar]
- Chan, P.; Shun, C. Application of a ground-based doppler lidar to automatic windshear alerting. In Proceedings of the 1st AIAA Atmospheric and Space Environments Conference, San Antonio, TX, USA, 22–25 June 2009; AIAA 2009-3870. Available online: https://arc.aiaa.org/doi/10.2514/6.2009-3870 (accessed on 15 April 2021).
- Aggarwal, C. Data Classification: Algorithms and Applications; IBM T. J. Watson Research Center Yorktown Heights: New York, NY, USA, 2014. [Google Scholar]
- De Carvalho, T.; Sibaldo, M.; Tsang, I.; da Cunha Cavalcanti, G. Principal component analysis for supervised learning: A minimum classification error approach. J. Inf. Data Manag. 2017, 8, 131–145. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).