Improving Air Pollutant Metal Oxide Sensor Quantification Practices through: An Exploration of Sensor Signal Normalization, Multi-Sensor and Universal Calibration Model Generation, and Physical Factors Such as Co-Location Duration and Sensor Age
Abstract
1. Introduction
1.1. Previous Gas-Phase Sensor Quantification Works
1.2. Accepted Signal Normalization and Universal Calibration Methods
1.3. Relevance of Oil and Gas
1.4. Organizational Overview
2. Methods
2.1. Overview
2.2. Sensor System Deployment Overview
2.3. Generalized Calibration Models
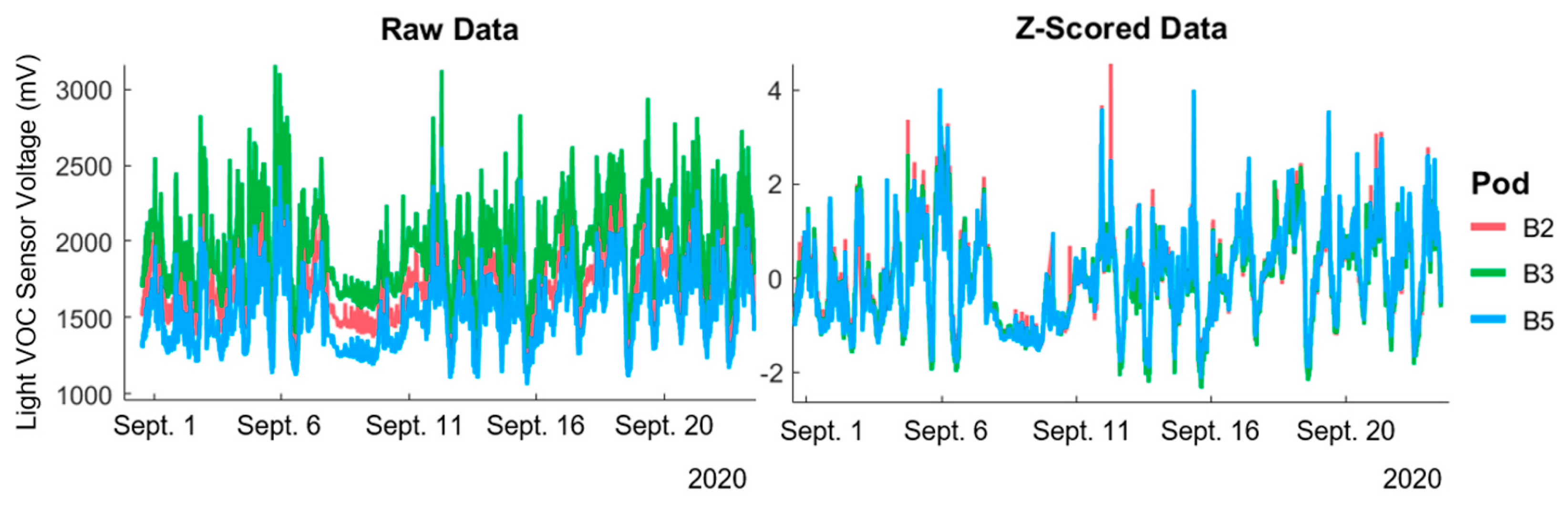
2.4. Sensor Signal Normalization Approaches
2.5. Overview of Universal Calibration Models
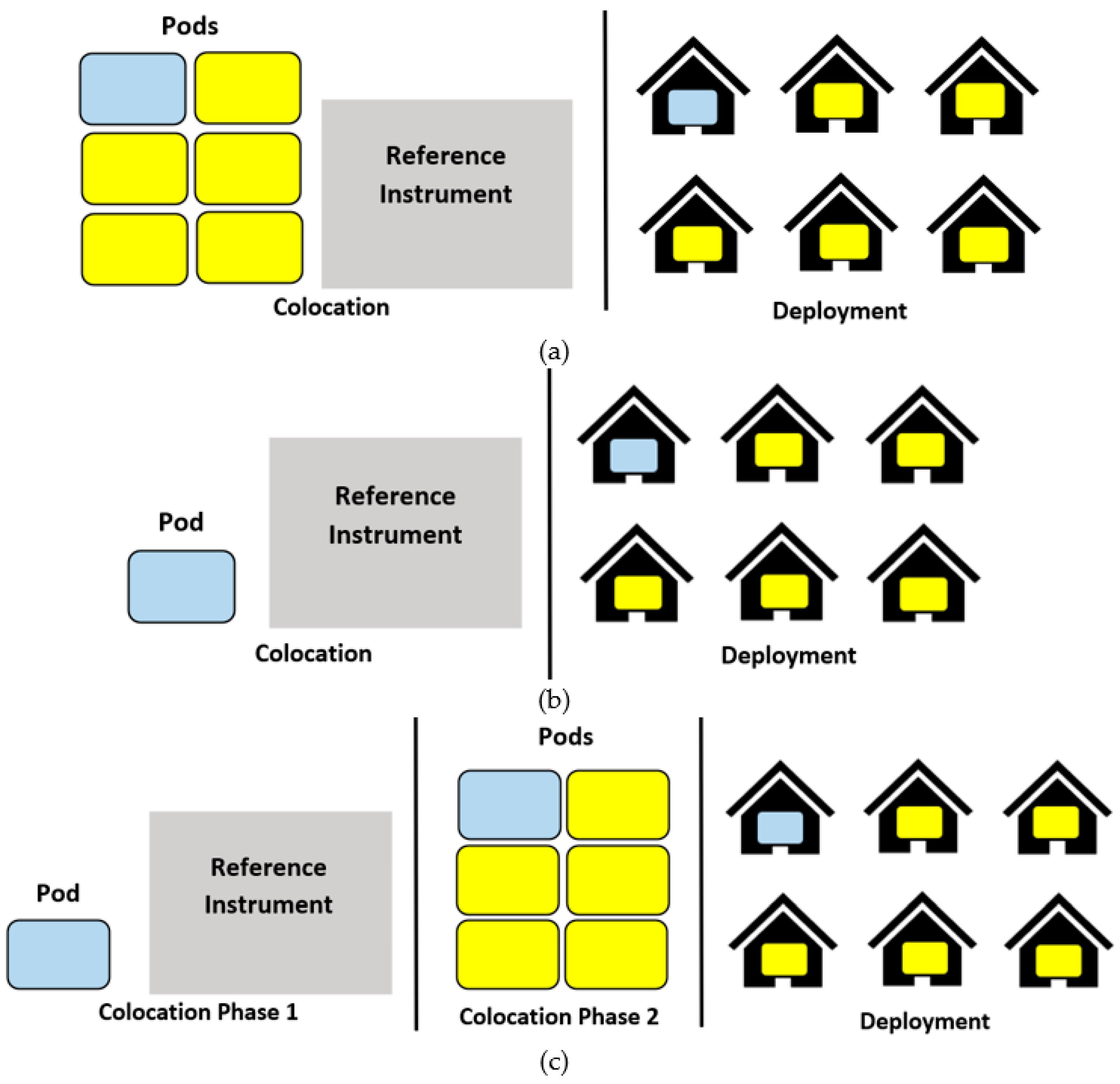
2.5.1. Calibration Models Specific to Each Pod, Requiring Individual Co-Location
2.5.2. Multi-Pod Calibration Models, Requiring One Pod to Be Co-Located with a Reference
2.6. Calibration Model Evaluation
3. Results
3.1. Applying Universal Calibration Models
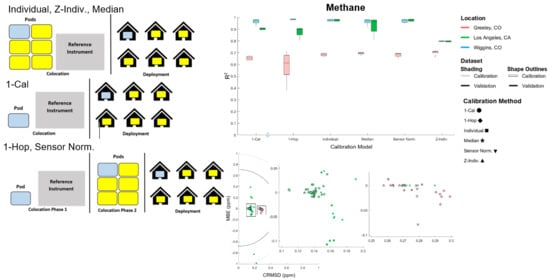
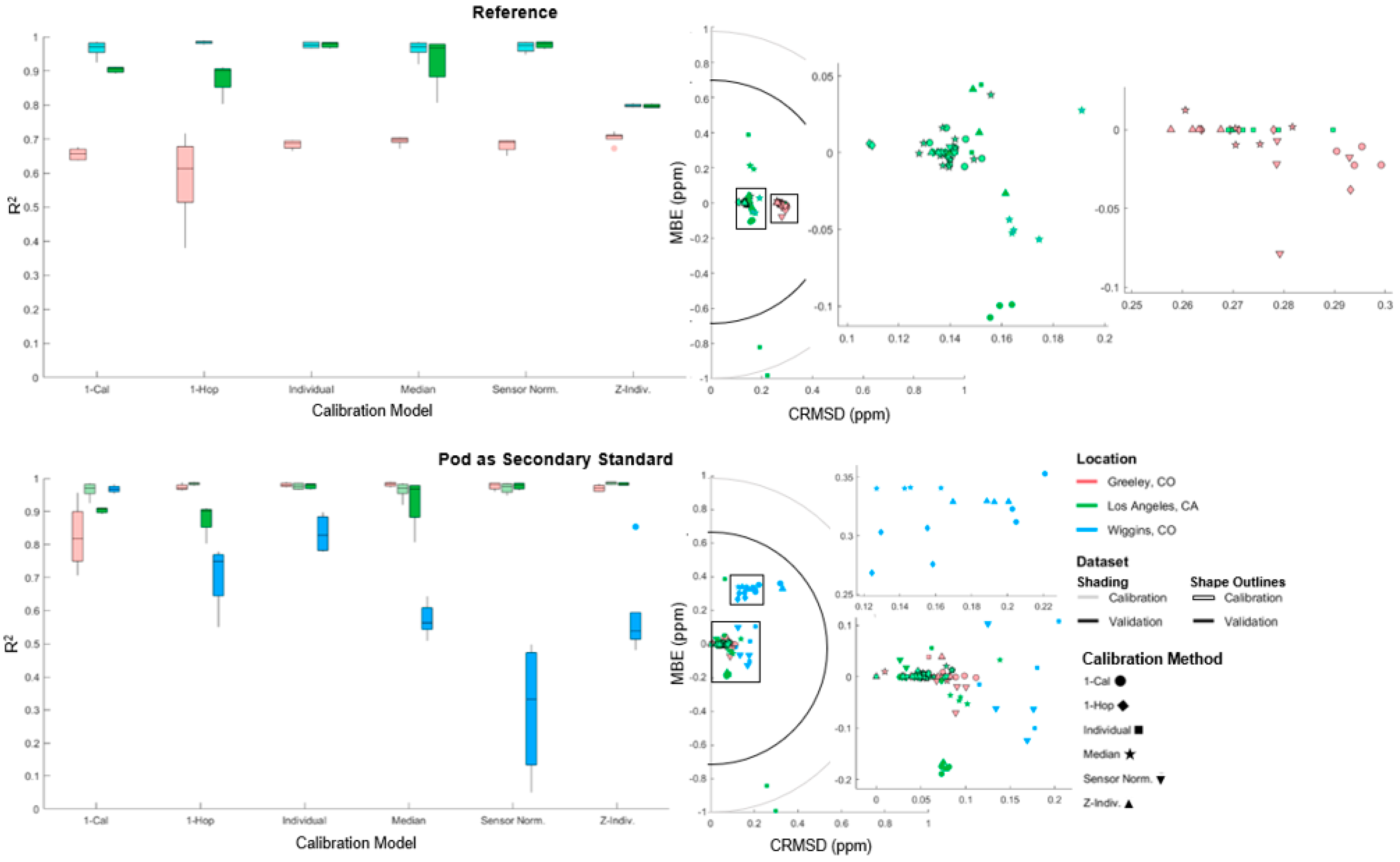
3.1.1. Methane Results
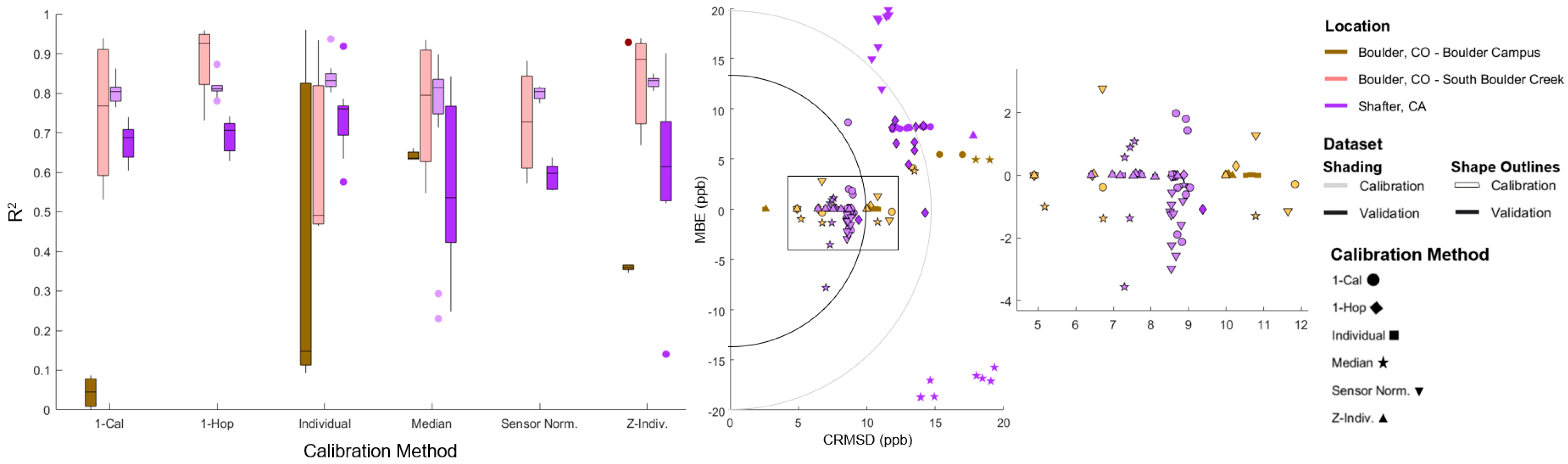
3.1.2. Ozone Results
3.2. Ability of Universal Calibration to Correct otherIissues Plaguing Low-Cost Sensors
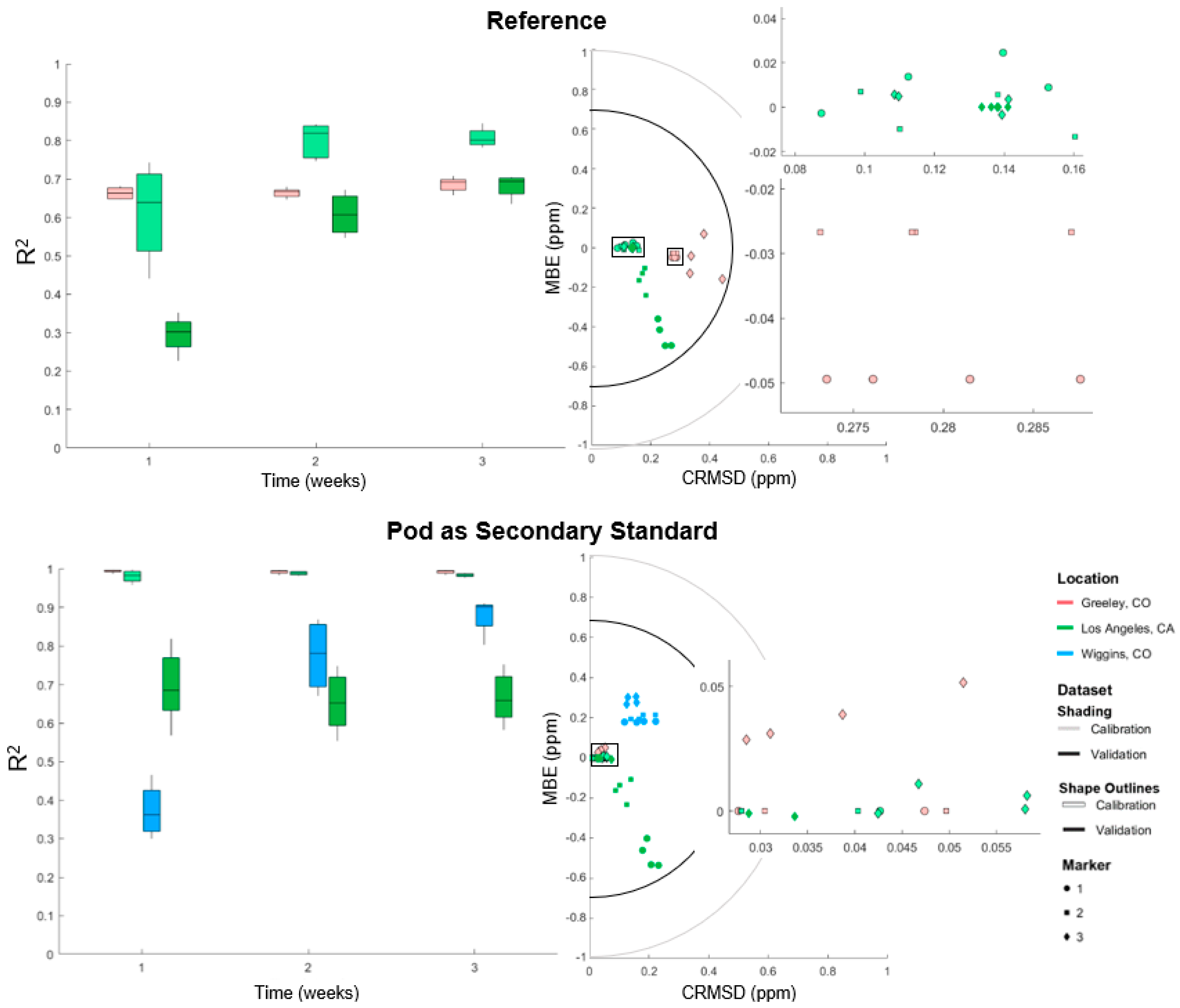
3.2.1. Co-Locating and Deploying Sensors in Different Environments
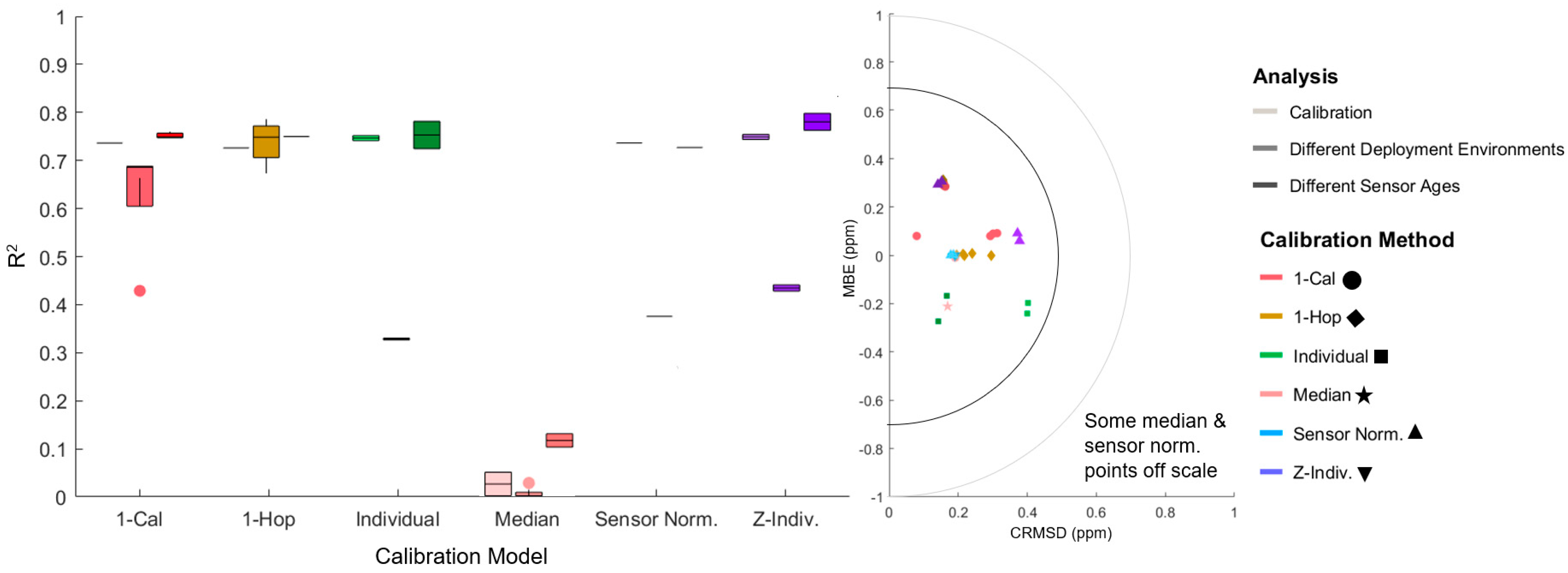
3.2.2. Age of Sensors
3.3. Factors Affecting Individual Calibration
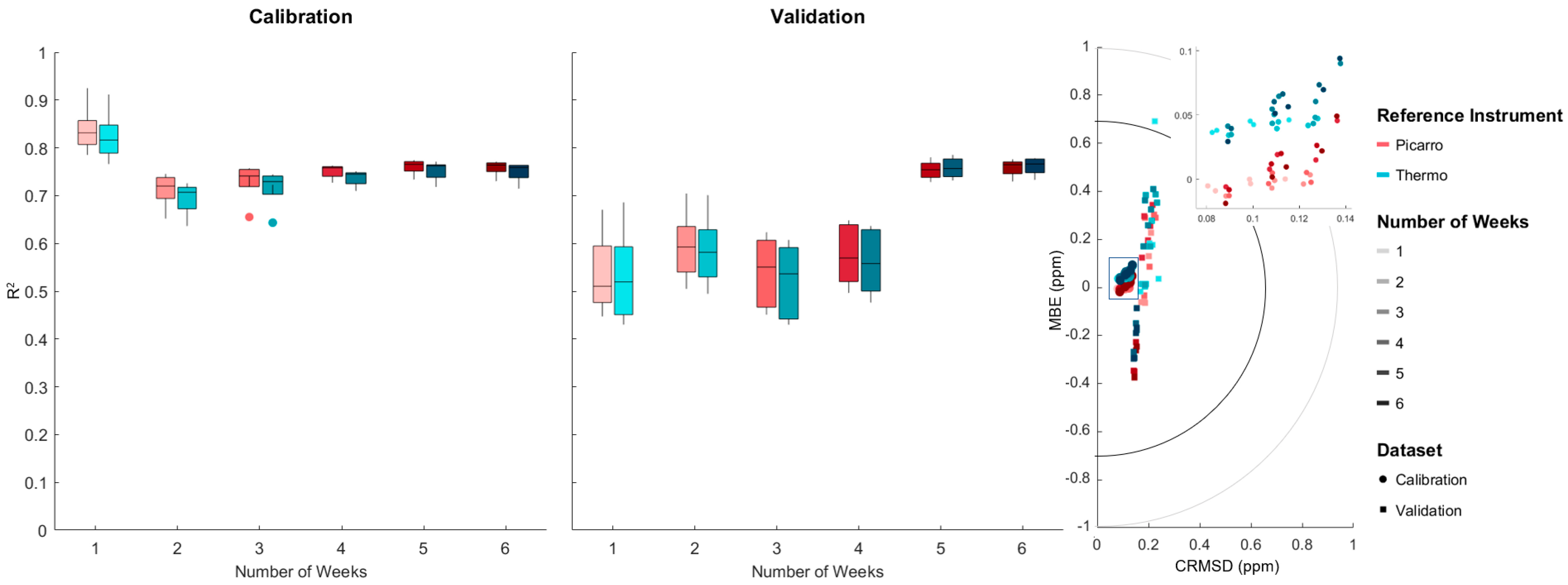
3.3.1. Duration of Co-Location
3.3.2. Reference Instrument Calibrations
3.4. Factors Affecting Universal Calibration
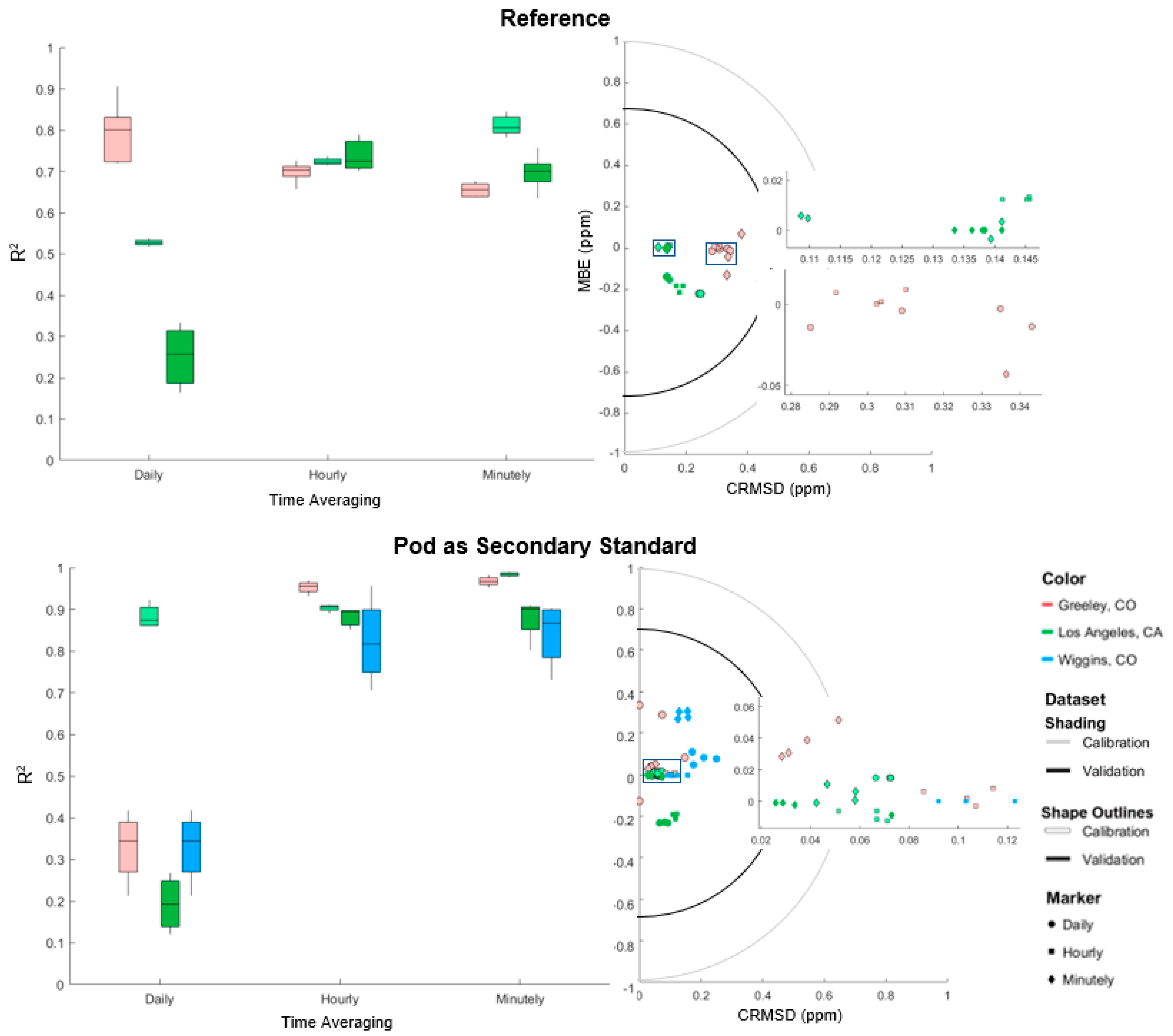
3.4.1. Duration of Co-Location
3.4.2. Time Averaging
4. Discussion
4.1. Benefits of Standardizing Sensor Data
4.2. Using a Field Normalized Pod as a Secondary Standard
4.3. Influence of Location on Pod Fits
4.4. Co-Location Recommendations
4.5. Considerations for Field Applications
4.6. Broader Implications
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Collier-Oxandale, A.; Coffey, E.; Thorson, J.; Johnston, J.; Hannigan, M. Comparing Building and Neighborhood-Scale Variability of CO2 and O3 to Inform Deployment Considerations for Low-Cost Sensor System Use. Sensors 2018, 18, 1349. [Google Scholar] [CrossRef]
- Cheadle, L.; Deanes, L.; Sadighi, K.; Gordon Casey, J.; Collier-Oxandale, A.; Hannigan, M. Quantifying Neighborhood-Scale Spatial Variations of Ozone at Open Space and Urban Sites in Boulder, Colorado Using Low-Cost Sensor Technology. Sensors 2017, 17, 2072. [Google Scholar] [CrossRef]
- Collier-Oxandale, A.; Wong, N.; Navarro, S.; Johnston, J.; Hannigan, M. Using gas-phase air quality sensors to disentangle potential sources in a Los Angeles neighborhood. Atmos. Environ. 2020, 233. [Google Scholar] [CrossRef]
- Okorn, K.; Jimenez, A.; Collier-Oxandale, A.; Johnston, J.; Hannigan, M. Characterizing methane and total non-methane hydrocarbon levels in Los Angeles communities with oil and gas facilities using air quality monitors. Sci. Total Environ. 2021, 146194. [Google Scholar] [CrossRef]
- Sadighi, K.; Coffey, E.; Polidori, A.; Feenstra, B.; Lv, Q.; Henze, D.K.; Hannigan, M. Intra-urban spatial variability of surface ozone in Riverside, CA: Viability and validation of low-cost sensors. Atmos. Meas. Tech. 2018, 11, 1777–1792. [Google Scholar] [CrossRef]
- Ripoll, A.; Viana, M.; Padrosa, M.; Querol, X.; Minutolo, A.; Hou, K.M.; Barcelo-Ordinas, J.M.; Garcia-Vidal, J. Testing the performance of sensors for ozone pollution monitoring in a citizen science approach. Sci. Total Environ. 2019, 651, 116–1179. [Google Scholar] [CrossRef]
- Spinelle, L.; Gerboles, M.; Villani, M.G.; Aleixandre, M.; Bonavitacola, F. Field calibration of a cluster of low-cost available sensors for air quality monitoring. Part A: Ozone and nitrogen dioxide. Sens. Actuators B Chem. 2015, 215, 249–257. [Google Scholar] [CrossRef]
- Suriano, D.; Cassano, G.; Penza, M. Design and Development of a Flexible, Plug-and-Play, Cost-Effective Tool for on-Field Evaluation of Gas Sensors. J. Sens. 2020, 2020. [Google Scholar] [CrossRef]
- Sayahi, T.; Garff, A.; Quah, T.; Lê, K.; Becnel, T.; Powell, K.M.; Gaillardon, P.E.; Butterfield, A.E.; Kelly, K.E. Long-term calibration models to estimate ozone concentrations with a metal oxide sensor. Environ. Pollut. 2020, 267, 115363. [Google Scholar] [CrossRef]
- Casey, J.; Collier-Oxandale, A.; Hannigan, M. Performance of artificial neural networks and linear models to quantify 4 trace gas species in an oil and gas production region with low-cost sensors. Sens. Actuators B Chem. 2019, 283, 504–514. [Google Scholar] [CrossRef]
- Honeycutt, W.T.; Ley, M.T.; Materer, N.F. Precision and Limits of Detection for Selected Commercially Available, Low-Cost Carbon Dioxide and Methane Gas Sensors. Sensors 2018, 19, 3157. [Google Scholar] [CrossRef] [PubMed]
- Zaidan, M.A.; Motlagh, N.H.; Fung, P.L.; Lu, D.; Timonen, H.; Kuula, J.; Niemi, J.V.; Tarkoma, S.; Petäjä, T.; Kulmala, M.; et al. Intelligent Calibration and Virtual Sensing for Integrated Low-Cost Air Quality Sensors. IEEE Sens. J. 2020, 20, 13638–13652. [Google Scholar] [CrossRef]
- Collier-Oxandale, A.; Casey, J.G.; Piedrahita, R.; Ortega, J.; Halliday, H.; Johnston, J.; Hannigan, M. Assessing a low-cost methane sensor quantification system for use in complex rural and urban environments. Atmos. Meas. Tech. 2018, 11, 3569–3594. [Google Scholar] [CrossRef] [PubMed]
- Piedrahita, R.; Xiang, Y.; Masson, N.; Ortega, J.; Collier, A.; Jiang, Y.; Li, K.; Dick, R.P.; Lv, Q.; Hannigan, M.; et al. The next generation of low-cost personal air quality sensors for quantitative exposure monitoring. Atmos. Meas. Tech. 2014, 7, 3325–3336. [Google Scholar] [CrossRef]
- Casey, J.G.; Hannigan, M. Testing the performance of field calibration techniques for low-cost gas sensors in new deployment locations: Across a county line and across Colorado. Atmos. Meas. Tech. 2018, 11, 6351–6378. [Google Scholar] [CrossRef]
- Maag, B.; Zhou, Z.; Thiele, L. Enhancing Multi-Hop Sensor Calibration with Uncertainty Estimates. In Proceedings of the 2019 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Leicester, UK, 19–23 August 2019; pp. 618–625. [Google Scholar] [CrossRef]
- Maag, B.; Zhou, Z.; Saukh, O.; Thiele, L. SCAN: Multi-Hop Calibration for Mobile Sensor Arrays. In Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies; 2017. Available online: https://www.bibsonomy.org/bibtex/4d5cb6a006cc5a66367420c07cffafa1 (accessed on 18 May 2021).
- Saukh, O.; Hasenfratz, D.; Thiele, L. Reducing multi-hop calibration errors in large-scale mobile sensor networks. In Proceedings of the 14th International Conference on Information Processing in Sensor Networks, Seattle, WA, USA, 14–16 April 2015; pp. 274–285. [Google Scholar] [CrossRef]
- Xi, T.; Wang, W.; Ngai, E.C.-H.; Liu, X. Spatio-Temporal Aware Collaborative Mobile Sensing with Online Multi-Hop Calibration. In Proceedings of the International Symposium on Mobile Ad Hoc Networking and Computing (MobiHoc), Los Angeles, CA, USA, 26–29 June 2018; pp. 310–311. [Google Scholar]
- Hasenfratz, D.; Saukh, O.; Thiele, L. On-the-Fly Calibration of Low-Cost Gas Sensors. In Proceedings of the 9th European Conference, Trento, Italy, 15–17 February 2012. [Google Scholar] [CrossRef]
- Zhang, X. Automatic Calibration of Methane Monitoring Based on Wireless Sensor Network. In Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing, Dalian, China, 12–14 October 2008; pp. 1–4. [Google Scholar] [CrossRef]
- Somov, A.; Baranov, A.; Savkin, A.; Spirjakin, D.; Spirjakin, A.; Passerone, R. Development of wireless sensor network for combustible gas monitoring. Sens. Actuators A Phys. 2011, 171, 398–405. [Google Scholar] [CrossRef]
- California Department of Conservation. Available online: https://www.conservation.ca.gov/calgem/Pages/WellFinder.aspx (accessed on 1 February 2021).
- Liberty Hill Foundation. Drilling Down: The Community Consequences of Expanded Oil Development in Los Angeles; Liberty Hill Foundation: Los Angeles, CA, USA, 2015. [Google Scholar]
- Mayer, A.; Malin, S.; McKenzie, M.; Peel, J.; Adgate, J. Understanding Self-Rated Health and Unconventional Oil and Gas Development in Three Colorado Communities. Soc. Nat. Resour. 2021, 34, 60–81. [Google Scholar] [CrossRef]
- Colorado Oil & Gas Conservation Commission: Interactive Map. Available online: https://cogcc.state.co.us/maps.html#/gisonline (accessed on 1 February 2021).
- Allen, D.T.; Torres, V.M.; Thomas, J.; Sullivan, D.W.; Harrison, M.; Hendler, A.; Herndon, S.C.; Kolb, C.E.; Fraser, M.P.; Hill, A.D.; et al. Methane emissions at natural gas production sites. Proc. Natl. Acad. Sci. USA 2013, 110, 17768–17773. [Google Scholar] [CrossRef]
- Alvarez, R.; Zavala-Araiza, D.; Lyon, D.; Allen, D.; Barkley, Z.; Brandt, A.; Davis, K.; Herndon, S.; Jacob, D.; Karion, A.; et al. Assessment of methane emissions from the U.S. oil and gas supply chain. Science 2018, 186–188. [Google Scholar] [CrossRef]
- Olaguer, E.P. The potential near-source ozone impacts of upstream oil and gas industry emissions. J. Air Waste Manag. Assoc. 2012, 62, 966–977. [Google Scholar] [CrossRef]
- Jolliff, J.K.; Kindle, J.C.; Shulman, I.; Penta, B.; Friedrichs, M.A.M.; Helber, R.; Arnone, R.A. Summary diagrams for coupled hydrodynamic-ecosystem model skill assessment. J. Mar. Syst. 2009, 76, 64–82. [Google Scholar] [CrossRef]
- Masson, N.; Piedrahita, R.; Hannigan, M. Approach for quantification of metal oxide type semiconductor gas sensors used for ambient air quality monitoring. Sens. Actuators B Chem. 2015, 208, 339–345. [Google Scholar] [CrossRef]
- Morel, P. Gramm: Grammar of graphics plotting in Matlab. J. Open Source Softw. 2018, 3, 568. [Google Scholar] [CrossRef]
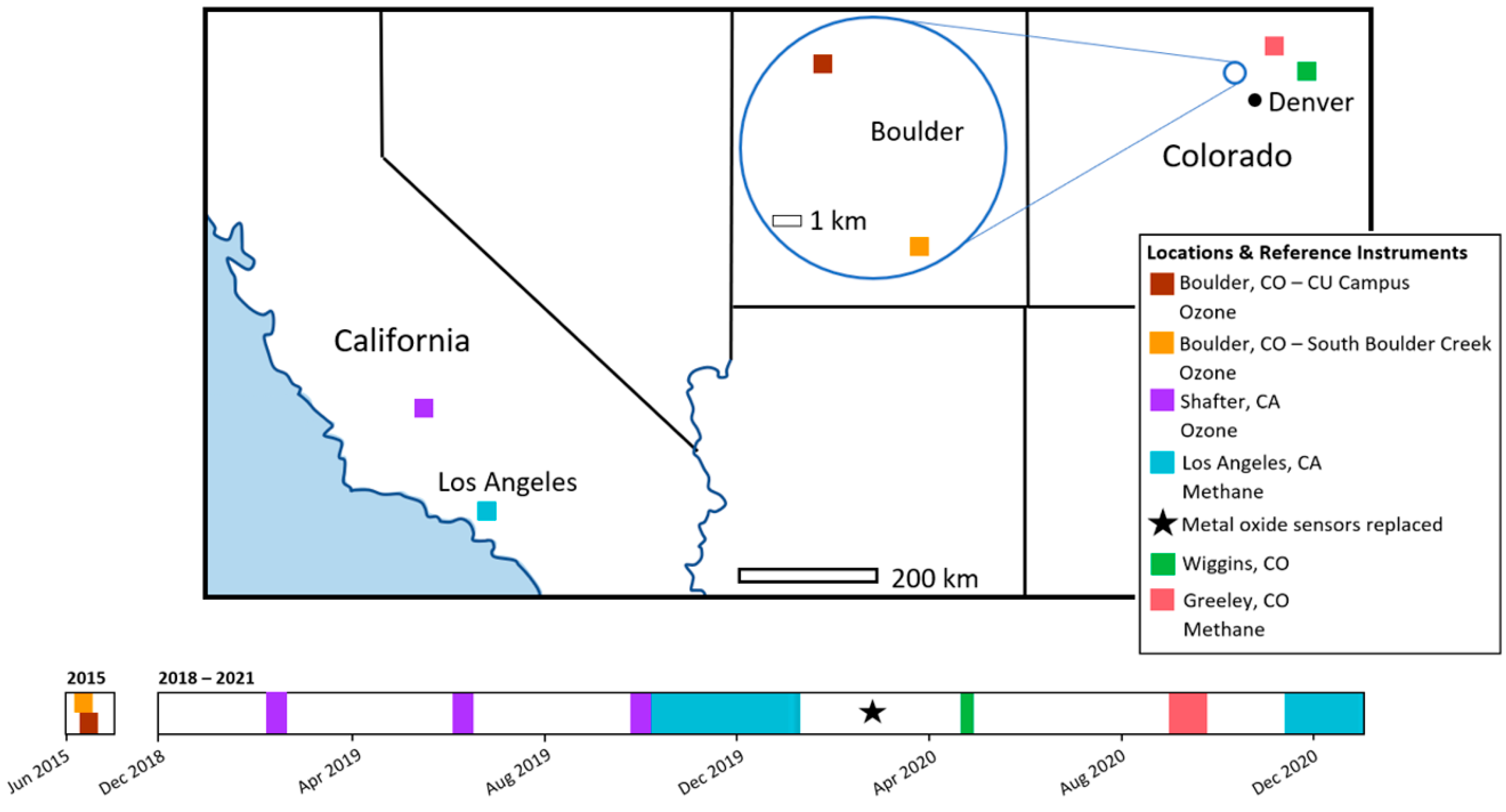

| Location | Physical Specifications | Pod Configuration |
|---|---|---|
| South Boulder Creek | Ground mounted tripods, 1.5 m high | Tripod placements ~3–4 m below reference instrument inlet |
| Boulder Campus | Roof or balcony-mounted tripods | Tripod placements ~3–4 m below reference instrument inlet |
| Shafter, CA, USA | Roof of 2-story building | Pods stacked on top of a container at the base of the inlet |
| Los Angeles, CA, USA (2019–2020) | Roof of 1-story trailer | Pods stacked on top of a container at the base of the inlet |
| Wiggins, CO, USA | Ground mounted tripods, 1.5 m high | 6 pods arranged 2 × 3 in an approximately 1 m × 0.5 m area |
| Greeley, CO, USA | Roof of 1-story trailer | Pods stacked on top of a container at the base of the inlet |
| Los Angeles, CA, USA (2020–2021) | Roof of 1-story trailer | Pods stacked directly on roof at the base of the inlet |
| Pollutant | Equation |
|---|---|
| Methane | CH4 (ppm) = p1 + p2*temperature + p3*humidity + p4*VOC1 + p5*VOC2 + p6*(VOC1/VOC2) + p7*elapsed time |
| Ozone | O3 (ppm) = p1 + p2*temperature +p3*1/temperature + p4*humidity + p5*o3 + p6*elapsed time |
| Model Attributes | Individual | Z-Scored Individual | Median | 1-Cal | 1-Hop | Sensor-Specific Normalization |
|---|---|---|---|---|---|---|
| All pods co-located at reference site | X | X | X | |||
| One pod co-located at reference site | X | X | X | |||
| Secondary co-location site | X | X | ||||
| One quantification model | X | X | X | |||
| Quantification model for each pod | X | X | X | |||
| Quantification model for each sensor | X | |||||
| Z-Score | X | X | X | X | X | |
| Linear de-trending | X |
| Statistic | Formula | Relevant Terms |
|---|---|---|
| R2 | SSE = sum of squared errors TSS = total sum of squares | |
| CRMSE | N = total number of samples n = current sample p = concentration predicted using model | |
| MBE | r = concentration from reference instrument |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okorn, K.; Hannigan, M. Improving Air Pollutant Metal Oxide Sensor Quantification Practices through: An Exploration of Sensor Signal Normalization, Multi-Sensor and Universal Calibration Model Generation, and Physical Factors Such as Co-Location Duration and Sensor Age. Atmosphere 2021, 12, 645. https://doi.org/10.3390/atmos12050645
Okorn K, Hannigan M. Improving Air Pollutant Metal Oxide Sensor Quantification Practices through: An Exploration of Sensor Signal Normalization, Multi-Sensor and Universal Calibration Model Generation, and Physical Factors Such as Co-Location Duration and Sensor Age. Atmosphere. 2021; 12(5):645. https://doi.org/10.3390/atmos12050645
Chicago/Turabian StyleOkorn, Kristen, and Michael Hannigan. 2021. "Improving Air Pollutant Metal Oxide Sensor Quantification Practices through: An Exploration of Sensor Signal Normalization, Multi-Sensor and Universal Calibration Model Generation, and Physical Factors Such as Co-Location Duration and Sensor Age" Atmosphere 12, no. 5: 645. https://doi.org/10.3390/atmos12050645
APA StyleOkorn, K., & Hannigan, M. (2021). Improving Air Pollutant Metal Oxide Sensor Quantification Practices through: An Exploration of Sensor Signal Normalization, Multi-Sensor and Universal Calibration Model Generation, and Physical Factors Such as Co-Location Duration and Sensor Age. Atmosphere, 12(5), 645. https://doi.org/10.3390/atmos12050645