Abstract
In this study; the spatial distribution of the Daily Precipitation Concentration Index (DPCI) has been analyzed inside the Greater Sydney Metropolitan Area (GSMA). Accordingly, the rainfall database from the Australian Bureau of Meteorology archive was utilized after comprehensive quality control. The compiled data contains a set of 41 rainfall stations indicating consistent daily precipitation series from 1950 to 2015. In the analysis of the DPCI across GSMA the techniques of Moran’s Spatial Autocorrelation has been applied. In addition, a cross-covariance method was applied to assess the spatial interdependency between vector-based datasets after performing an Ordinary Kriging interpolation. The results identify four well-recognized intense rainfall development zones: the south coast and topographic areas of the Illawarra district characterized by Tasman Sea coastal regions with DPCI values ranging from 0.61 to 0.63, the western highlands of the Blue Mountains, with values between 0.60 and 0.62, the inland regions, with lowest rainfall concentrations between 0.55 and 0.59, and lastly the districts located inside the GSMA with DPCI ranging 0.60 to 0.61. Such spatial distribution has revealed the rainstorm and severe thunderstorm activity in the area. This study applies the present models to identify the nature and mechanisms underlying the distribution of torrential rains over space within the metropolis of Sydney, and to monitor any changes in the spatial pattern under the warming climate.
1. Introduction
The awareness of the importance of the spatial and temporal distribution of precipitation is important not only from a meteorological viewpoint, but also for its importance in different fields such as agriculture, hydrology, water resources and flood control. Estimation of the spatial and temporal distribution of precipitation is a complex undertaking, particularly in cases where detailed information concerning the impact of topography and land−use impacts on the prevailing atmospheric circulation is not quite available, such as the situation over southeastern Australia [1].
The concentration index (CI) is one of the indices that can be applied to characterize the temporal concentration of precipitation followed by spatial analysis [2]. A CI analysis makes it possible to characterize different spatial scales, which is of interest due to its effects on geo−hydrological processes and the analysis of erosion and soil loss [3]. Applying this type of analysis, interest is not only focused on climate but also on the effect of heavy rainfall on other areas of the environment and society [4,5]. The CI method was already applied in many different parts of the world [6,7,8,9,10,11,12,13,14,15,16,17,18]. While we focus on the most commonly applied index here, there are other indices that indicate different aspects of precipitation concentration, such as the relative cumulative precipitation, inequality concentration indices and the ordered version of the n index [2].
Many of the previous studies analyzed the CI based on monthly precipitation and examined the annual and seasonal CI values, which are mostly determined by the climatological and synoptic characteristics of a particular region. On a shorter timescale, daily analysis and prediction of the intensity of precipitation would help in in water resource planning and also identifying areas of high and low flash flooding potential. Likewise, it would facilitate the regulation of the flows from high−intensity areas towards low−intensity ones [19]. For example, a high precipitation concentration, represented by large percentages of the yearly total precipitation in a few very rainy days, has the potential to cause floods and also drought phenomena. This is exactly the scenario of precipitation extremes inside the Sydney region, such as rainstorms, ex-tropical cyclone remnants, east coast lows and severe thunderstorm events occurring over a few days that account for high percentages of the annual total. These events may potentially bring more frequent disasters for human society of the Greater Sydney metropolitan area (GSMA). In the past, specific attention has been paid to patterns of such uneven spatial variation of intense rainfalls using different statistics and mathematical methods (e.g., [20]). Nevertheless, a long time-span daily precipitation series has not been analyzed by applying a CI approach. Thus, this study examines the precipitation concentration in the area based on data with daily resolution. The DPCI is also good supplementary information to other extreme precipitation indices on similar timescale, such as the highest amount of daily precipitation (RX), the maximum consecutive 5-day precipitation (RX5D), number of days with precipitation ≥ 20 mm or above 50 mm (R20/D50MM) and days with precipitation > 95 percentile (D95P) recommended by the World Climate Research Programme’s Expert Team on Climate Change Detection and Indices (ETCCDI, [21,22]).
The organization of the paper is as follows. Section 2 first introduces the climatological characteristics of the GSMA. Section 3 then depicts the methodology applied, including the daily CI and spatial correlation analysis. Results are discussed in Section 4. Finally an overall summary is given in Section 5 together with further discussion on implications and future work.
2. Climatology of the Study Area
The GSMA, which is located on the southeast coast of Australia in New South Wales and lies in the western part of the Tasman Sea (Figure 1), includes a highly populated area of approximately 3.8 million in population. The study area is bounded in the north by 33°30′ S latitude, extending to 150°30′ E longitude in the west, and to the southeast at 34°30′ latitude and 151°30′ longitude. The region is bowl-shaped with a low plain in the middle which is effectively walled in on three sides by hills. In general, the Sydney region enjoys a temperate climate and commonly the broad-scale wind pattern is westerly in the winter, and easterly in the summer. The climate of this region arises from a complex interaction of broad-scale, regional and local controls [23].
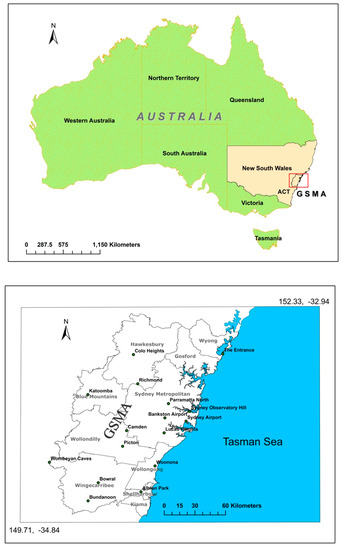
Figure 1.
The location map of the GSMA within New South Wales of Australia (upper). The lower panel shows the boundaries of the local government areas within the GSMA, with the names of some major local cities (dots).
Rainfall over the GSMA may occur throughout the year but is highest between March and June. Also, precipitation is slightly higher during the first half of the year when easterly winds dominate (February–June), and lower in the second half; mainly from July to September. Rainfall can occur throughout the year with variation concerning altitude and distance from the coast, with wetter areas being closer to the coast or in higher altitudes. Due to the low predictability of rain as well as the well-known impacts from climate drivers to the region [24], the wettest and driest months change annually. Within the study area and surrounds, annual rainfall varies from around 700 mm to 1400 mm. More climatological information of the study area can be found in [25] and [26].
On the regional scale, rainfall in the GSMA is influenced by the synoptic weather systems in the region, such as fronts originated from the Southern Ocean, east coast lows, subtropical cyclones and ex-tropical cyclone remnants migrating to the higher latitudes. More locally, the GMSA is also known as one of the hotspots for severe thunderstorms in Australia [26]. As can be seen in the following analysis, the torrential rain from severe thunderstorms contribute significantly to the spatial characteristics of CI in the area.
3. Data and Method
3.1. Data
Daily rainfall data for forty−one (41) weather stations have been extracted from the Australian Bureau of Meteorology (BoM) online archives. Recording periods varied in duration for each station, but many data are available from 1950 to 2015. Rainfall data from the BoM has already been quality controlled with confirmation of the extremes with local reports and that observations from nearby stations do not disagree with each other. We have further verified such agreement among the stations after we downloaded the data. Most of the stations have complete data series in the study period—even the station with the least recorded data over the whole period has over 90% of coverage. The provided daily rainfall data, presenting relatively uniform coverage throughout the study area, have been carefully entered in a particular GIS database. Rainfall station characteristics are shown in Table A1 (Appendix A) and their spatial distribution is mapped in Figure 2. The only series with less than 10% missing data on an annual scale were used to calculate the DPCI indexes.
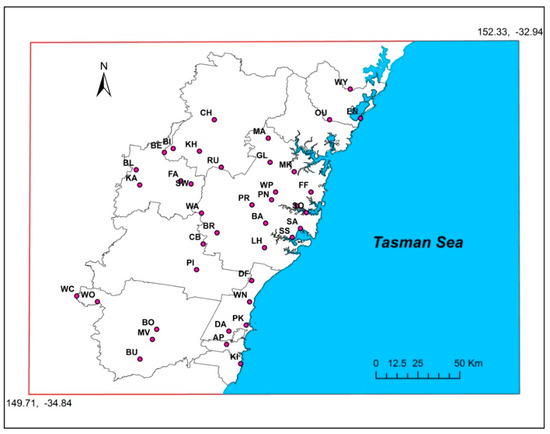
Figure 2.
Spatial distribution of the rainfall stations with abbreviated codes as in Table A1 (Appendix A). Topography in the area can refer to the DEM in Figure 4.
To reach the main aims of the study, four interconnected techniques of Concentration Index, Moran’s Spatial Autocorrelation, Ordinary Kriging interpolation, and a cross-covariance method were applied to assess the spatial dependence (covariance) between vector-based datasets. The last method was applied to reveal several of the inherent spatial inter-dependencies among dissimilar variables.
3.2. The Daily Precipitation Concentration Index (DPCI)
The DPCI, proposed by [27], is examined in this study. An example is illustrated for the Albion Park station data; this station recorded the highest rain during the 67 years from 1950 to 2015 (see Table A2 in Appendix A). In computing the DPCI, only observed daily precipitation values more than 1 mm were considered. The DPCI method was applied to the data based on the fact that the contribution of daily rainfall events to the total amount is generally well described by a negative exponential distribution [28].
The DPCI in this study consists of aggregating daily precipitation into increasing 10−mm categories and determining the relative impact of the different classes by analyzing the relative contribution (as a percentage) of the accumulated precipitation, Y, as a function of the accumulated percentage of occurrence frequency (X). Previous work such as [11] showed that such function can be based on Equation (1).
where a and b are constants that can be determined through the least−squares method.
where N is the number of classes. After determining the two constants a and b, the integral of the exponential curve (so−called Lorenz curve) between 0 and 100 shows the area S (Figure 3), which is given by:
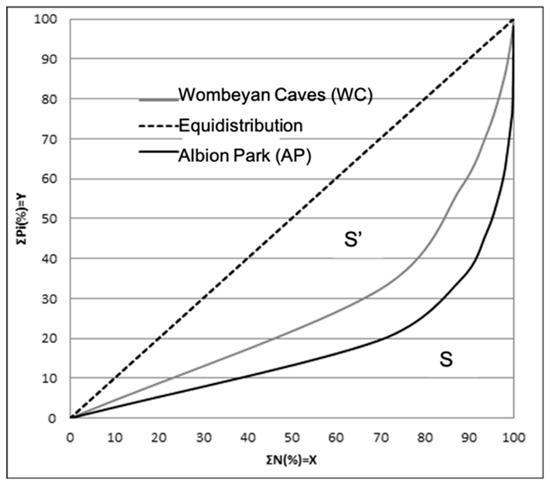
Figure 3.
The empirical concentration curves for Albion Park and Wombeyan rain stations with the dash straight line the reference equidistribution line. The area S′ is that bounded by the diagonal equidistribution line and the concentration curve, while area S is the remaining area underneath the equidistribution line.
Based on S, the area S′ compressed by the exponential curve, the equidistribution line and X = 100 is apparently the difference between 5000 (half of the total area) and the value of S:
Applying Equation (5) the DPCI value for each rainfall station is then a fraction of S′ to the lower surface of the triangle bounded by the equidistribution line.
Examples of the empirical curves or “concentration curves” of Y versus X for Albion Parks and Wombeyan stations are presented in Figure 3. The annual DPCI values for these two stations are 0.62 and 0.54, respectively (see Table 1). By definition, the value of the DPCI is always a number between 0 and 1, and geometrically it represents the percentage of the triangle area between the line Y = X and the exponential curve. The DPCI is virtually equal to 0 when the contribution of each category of precipitation to the total is the same, and equal to 1 when precipitation falls into one category only and the exponential curve becomes the straight line Y = 0. Exponential curves of this type were calculated for all meteorological stations across the GSMA. As an example, different stages of calculating the above−mentioned parameters are given in Table A1 and Table A2 (Appendix A).

Table 1.
Values of the constants “a”, “b”, DPCI, 90% percentile of rain and maximum daily rainfall (mm) at each of the 41 stations (with full names given in Table A1).
3.3. Spatial Correlation
In the second stage of data analysis, a Moran’s spatial autocorrelation technique was used to measure spatial autocorrelation based on rainfall station locations and DPCI values [29]. Given the set of 41 rainfall stations and associated DPCIs, it evaluates whether the pattern expressed is clustered, dispersed or random (Figure A1 in Appendix B). The tool calculates the Moran’s I Index value and both a z-score and p-value to evaluate the significance of that Index. The Moran’s I statistic for spatial autocorrelation is given by
where Zi is the deviation of an attribute for feature (i.e., a particular rainfall station’s DPCI) from its mean, Wi,j is the spatial weight between stations i and j (designated as the significance, i.e., the p−value, of the correlation of rain between the two stations), N is the total number of stations and S0 is the aggregate of the spatial weights by:
For the current study, the ZI score for the statistic is computed by applying the following equations.
In which E is the expectation value and V the variance. Under the case of no spatial autocorrelation, .
Subsequently, a spatial interpolation method, known as the Kriging technique, was applied to yield better results than other techniques ([30,31]). The Kriging technique assumes that the statistical surface to be interpolated has a certain degree of continuity ([32]). The technique applies moving averages and has the advantage of producing the standard error for the estimated values. Among all the Kriging methods, the ordinary mode was applied, as an advanced geostatistical procedure. This method was well fitted to all data layers to generate estimated DPCI surfaces from a re−projected set of point values [33]. The Kriging model is based on a statistical technique that includes autocorrelation; that is, the statistical relationships among the measured points. Potentially, geostatistical techniques not only have the capability to produce a prediction surface but also provide some measure of the certainty or accuracy of the predictions. Kriging tools weight the surrounding measured values to derive a prediction for each DPCI unmeasured location. There are variations of the techniques, such as the Ordinary Cokirging and those that consider topographical information, that can further improve the performance ([34,35]). The general formula for both interpolators is formed as a weighted sum of the data:
where Z (Si) is regarded as the measured DPCI values at the ith location, λi shows an unknown weight for the measured value at the ith rainfall station location, S0 specifies the prediction location and N indicates the number of stations. With the Kriging method, the weights are based not only on the distance between the measured points and the prediction location but also on the overall spatial arrangement of the measured points. To use the spatial arrangement in the weights, the spatial autocorrelation must be quantified. Thus, in ordinary Kriging, the weight, λi, depends on a fitted model to the measured points, the distance to the prediction location and the spatial relationships among the measured DPCI values around the prediction location. In the current study, an Ordinary Kriging formula is used to create maps of the prediction DPCI and “b” constant surfaces and associated accuracy models. Ordinary Kriging assumes the second−order trend removal model with no transformation type:
In the above equation, μ is an unknown constant whereas one of the main issues concerning ordinary Kriging is whether the assumption of a constant mean is reasonable. Sometimes there are good scientific reasons to reject this assumption. However, in this study, it was found that applying a second−order trend removal following an exponential Kernal Function (as a simple prediction method) gives remarkable flexibility in final interpolation method accuracy. Once again, the Kriging method was also applied to illustrate the variation and spatial distribution of the constant “b” values in the study area. This arbitrary way allows direct interstation comparison of the distribution of “b” value at each rainfall station across all districts.
To calculate the Pearson Overall Correlation Coefficient, a band collection statistic tool was furthermore computed among the DPCI and one of the other rainfall related parameters [36]. These parameters include the mean annual precipitation (AP), coefficient of variation (CV) of rainfall, the total number of rainfall days (TN), maximum rainfall observed (MxR) and the “a” and “b” constants taken from Equation (1). This tool was applied to provide statistics for the bivariate analysis of a set of raster bands by computing covariance and correlation for every event. The following equation was accordingly used to determine the covariance between layers i and j.
In the above equation, Z indicates for example DPCIs observed of a cell, i, j are layers of a stack, u is the mean of cells and N is the number of cells. The overall correlation between the rainfall datasets was then computed as:
where the σ’s are standard deviations. As usual, the correlation coefficient is between −1 and 1.
4. Results
4.1. Spatial Distribution of DPCI
By calculating the annual DPCI values it was found that they range greatly, between 0.54 and 0.63, and are spread across the study area represented by the 41 rainfall stations. This range is consistent with the global results in [2] that showed high values (>0.5) of the Gini Index (which has the same concept of the DPCI but without the assumed mathematical form of the Lorenz curve as in Equation (1), thus the Gini index is highly correlated with the DPCI) over eastern Australia. Table 1 indicates the DPCI values and the rainfall percentage contributed by 90% of the rainiest days for the 41 weather stations across GSMA from 1950 to 2015. Also values of the constants “a” and “b” (as the exponential curves are given by Equation (1)) and observed maximum daily rainfall are represented in the table. DPCI values present strongly different daily precipitation regimes, as Woonona station (0.63) is located in the southeast of the study area and precipitation there has a higher concentration and is more irregular than in Wombeyan station (0.54) which is located on the Tableland somewhere in the outlying southwest of the study area. The concentration can be considered a function of the relative separation of the equidistribution line, which is greater in Albion Park (with the highest maximum daily rainfall observed) than others (Figure 3).
Applying the Global Moran’s I statistic it is possible to test an existing spatial autocorrelation based on rainfall station locations and DPCI values. The Spatial Autocorrelation tool returns five values: the Moran’s I index, expected index, variance, z-score and p-value. Given the z-score of 3.55, there is a less than 1% likelihood that this clustered pattern could be the result of random chance, expressing the fact that there are spatially significant clusters of DPCI values among the existing dataset based on the spatial autocorrelation report.
The result of the Ordinary Kriging interpolator model is shown in Figure 4 after smoothing small errors depending on the measurement parameters overlaid with a Digital Elevation Model (DEM) of the study area. The maximum values of DPCI are crossing over the Kiama, Shellharbour and Wollongong districts located in the southeast of the study area. For example, Woonona station (34.34° S; 150.90° E) represents the highest value of 0.63, while the lowest values of DPCI could be seen in Wombeyan station (34.31° S; 140.97° E) with 0.54. The highest DPCIs were detected primarily in the Illawarra (along with the south coast) and Blue Mountains districts (Katoomba station with 0.62). Furthermore, the secondary maximum annual values of DPCI were found around the Sydney Metropolitan, mainly around the Central Business District (CBD). On the other hand, districts with the lowest values are located in the southwest Tablelands of the Wingecarribee and Hawkesbury districts. Meanwhile, the strongest gradient occurs between the west and east and between the northwest and southeast of GSMA, as coastlines meet the highest DPCI values.
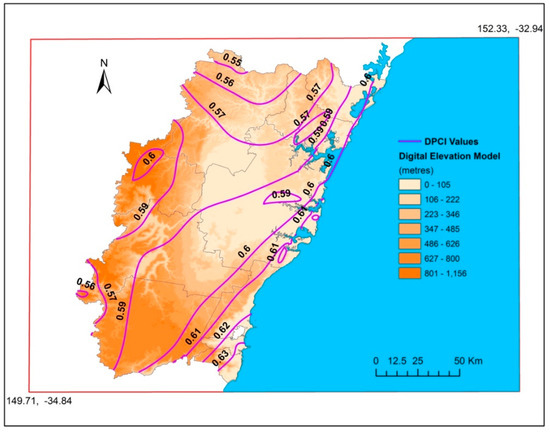
Figure 4.
Spatial distribution of DPCI (contours) overlaid on a DEM inside the GSMA.
To find more about the nature of the spatial distribution of intense rains inside of the GSMA, the geographical distribution of the “b” constant, which from Equation (1) is the parameter to control the shape of the rainfall concentration curve and thus carries important information on the rainfall distribution, has been converted to classes of intensity level of rainfall occurrence (Figure 5). Very high intense amounts can be seen near the topography southeast of the study area, just over the Illawarra Escarpment. Besides, in some parts of the Sydney Metropolitan district, for example in the west of the City, and areas located in the northwestern corner of the Parramatta River, very intense "b" values can be observed. In comparison with the lowlands of the GSMA, over the Blue Mountains (Katoomba station), intense rain events are also relatively high. In contrast, non−intense classes of "b" values can be seen over the inland parts of the GSMA.
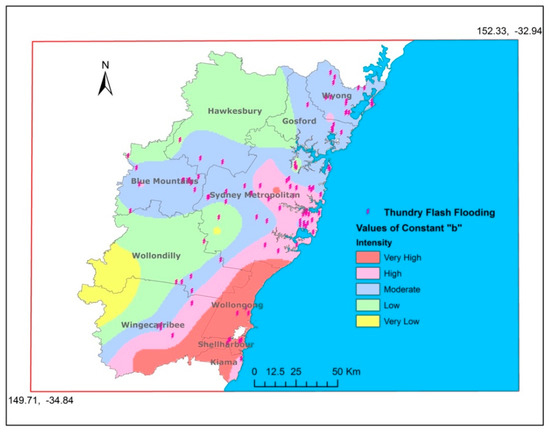
Figure 5.
Spatial distribution of the constant “b” (shaded) with classification into four groups of intensity and occurrence locations of the thundery flash flooding days during 1989–2015 (lightning symbol) based on the BoM storm archive.
For comparison, the geographic position of the flash flood events (observed during 1989−2015 with a thundery−rain more than 50 mm) is overlaid on the distribution of the “b” constant map. In the GSMA, flash flood events are mostly induced by several weather systems, such as the local thunderstorms and east coast lows over the ocean. It can be seen that most of these flash flood events occurred in the areas with the high “b” values, which determine the shape of the concentration curve. The spatial pattern of “b” also highly resembles that of the severe thunderstorms, especially those with hail occurrence [26]. These facts indicate that the storm activity in the GSMA largely determine the CI pattern on the daily timescale.
4.2. Spatial Correspondences
A cross−covariance model was presented to assess the spatial dependence (covariance) between two vector-based datasets. Here the first dataset is the DPCI, while the second is one of the important rainfall-related parameters such as mean annual rainfalls (AP), coefficient of variation (CV), the total number of rainfall days (TN), maximum rainfalls observed (MxR) and the “a” and “b” constants taken from Equation (1) that control the concentration curve. In the analysis, the attribute of one point (i.e., the DPCI) is correlated with the second attribute (i.e., one of the rain−related parameters) at another point, and this is repeated for all pairs of geographic points. The spatial distribution of the correlation (termed cross-covariance surface or cloud) can then be applied to examine the local characteristics of spatial correlation between the two attributes (datasets). The details of this cross-covariance model has been documented in Appendix C. This technique was applied to look for spatial shifts in existing correspondences between the DPCI and the other datasets throughout the GSMA.
A covariance surface with directional search capabilities was also involved in the modeling. For this reason, the values in the cross−covariance cloud were put into six bins based on the direction and distance separating a pair of locations [37]. These binned values were then averaged and smoothed to produce a cross−covariance surface (and associated correlations) for each pair of dataset throughout the study area (Figure 6). It can be seen that the DPCI possesses regions of high covariance with most of the rain parameters and also the “a” and “b” constants in the concentration curve, however, there is variability in the locations with the highest covariance. For example, the DPCI has high covariance with the climatological parameters AP and TN over the northwest. The highest covariance with the ‘magnitude’ of the concentration curve (“a”) is also on the western side. This may be due to the topographic variation. However, the pattern of covariance with the two parameters directly related to the DPCI, namely the MxR and “b”, has a southwest−northeast orientation. This is aligned with the distribution of the DPCI in Figure 4.
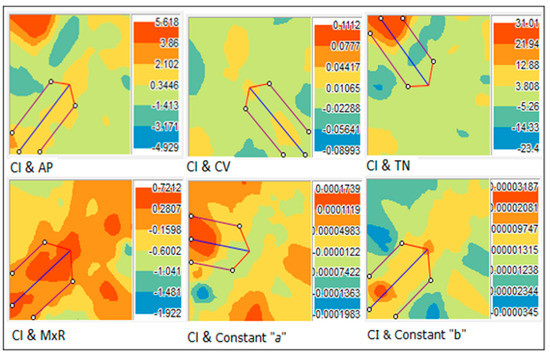
Figure 6.
The result of cross−covariance surfaces for all pairs of variables: (CI,AP); (CI,CV); (CI,TN); (CI,MxR); (CI,a); (CI,b). CI is the same as the DPCI. Six bins have been set for the categories of covariance values. The arrows (with the blue and red lines) are examples of directional searches of high covariance values over the surfaces. See Appendix C for details.
In Table 2, the values of Pearson’s correlation coefficient for the five pairs of variables are indicated. The Pearson overall correlations (r) for all rainfall related parameters, except the total number of rainy days (TN), are statistically significant at 0.95 and 0.99 levels, respectively. Correlation between TN and annual DPCI is nearly +0.24 (p < 0.5) and not significant; in other words high number of rain days is not a good indicator of high DPCI. The reason is that similar annual values could be achieved with different daily distributions.

Table 2.
Values of the Pearson’s correlation coefficient, significance level and category of cross−covariance spatial shifting for five pairs of variables: (CI,AP); (CI,CV); (CI,TN); (CI,MxR); (CI,a); (CI,b).
5. Conclusions and Discussion
5.1. Summary
In the current study, daily rainfall observations (1950–2015) from 41 rainfall stations inside the GSMA have been analyzed. According to the applied criteria and techniques used, the outcomes are summarized as follow:
- Within the GSMA, the essential features of climate in different districts are characterized by narrow rainfall zones close to the coast, under the combined influence of the Tasman Sea and the topography and land use patterns, leading to very different rainfall spatial distributions.
- The DPCI values in the Illawarra coastal elevated areas, parts of the Sydney Metropolitan area and the Blue Mountains are high, with concentration index values close to 0.60–0.63. This reflects the fact that very few rainy days could bring a high percentage of annual precipitation.
- The DPCI values obtained and distribution pattern of constant “b” are largely subject to influences from the topography and land use of the region. Generally, western and central regions inside GSMA are areas where rainfall is regular compared to eastern regions, while the southeastern districts and small parts of Metropolitan areas show the most aggressive DPCI values.
- Despite the significant variations in spatial cross−correlating models between the DPCI and 6 other rain−related parameters (AP, CV, TN, MxR, “a” and “b”), there are considerable positive relationships among data layers at 0.95 significance levels for most parts of the study area.
- The spatial patterns of the DPCI and “b” constant highlight the importance of catastrophic effects of such intense rainfall events, predominantly originating with severe thunderstorm and flash flood events.
5.2. Discussion
Inside of the Sydney Metropolitan area, daily precipitation is one of the factors in the processes of creating flash floods, and accordingly, differences in the spatial distribution of precipitation can lead to dissimilar precipitation regimes and various climatic conditions [38]. As was indicated in Table A1 (Appendix A), even if the annual total amounts are similar in many of the rainfall stations, precipitation processes may be different due to a different degree of concentrated rainfall in the time and space of the study area. Accordingly, the spatial distribution of precipitation can produce noticeably different impacts on natural and social processes across the GSMA—of particular interest for water management—flood control programs, and water availability for natural ecosystems. As the results show, the daily concentration of precipitation on an annual scale (expressed by the DPCI values in Table 1) is characterized by two different spatial gradients. One lies from the east to the west and the second is detectable from south to north, the latter characterized by the Tasman Sea coastal areas.
Overall, the spatial distribution of DPCIs follows a gradient between inland and the coastal areas, which may indicate approaching intense rainfall from different geographic directions. The results in this study have indicated that most parts inside GSMA are subject to severe rain, but with different likelihood of high DPCI (Figure 4). For example, the gigantic water resources of the Tasman Sea may influence the distribution of intense rainfall. On the other hand, a large proportion of rainfall comes from severe thunderstorms that occur over the northeast GSMA, the CBD and over the inner metropolitan area [26]. Also, the increased roughness associated with variation in topography and heat island phenomena may affect the spatial distribution of concentrated precipitation [39].
However, the pronounced dissimilar DPCI values and the subsequent cross−covariance surfaces (Figure 4 and Figure 6) support the overall picture of multi−subjected developing areas and approaching weather systems from various directions in the region, which are under dissimilar synoptic patterns causing atmospheric instability [40,41]. It was found by previous studies that at least four types of weather patterns account for most of the rainfall in the region [42,43], and logically the amount, frequency, and intensity of precipitation events vary substantially in the region, as shown in the records during a long period from 1950–2015 [44,45]. Another weather pattern occurs in summer and involves the location of the Tropical Convergence Zone bringing torrential rainfalls [46]. Occasionally, weather systems from the southeast generate storms striking the region with torrential precipitation. During the warm months (October to March) the prevailing easterly moist winds provide much of the moisture needed in the intensification of widespread and severe thunderstorm activity in the region [26]. Given the short duration of typical thunderstorm activity in terms of hours, likely it would contribute substantially to the DPCI.
Not all variations in the total precipitation and associated differences in the DPCI can be explained simply in terms of differences between dissimilar weather systems and the nature of the prevailing air masses [47]. The geographical distribution of DPCI and the “b” values illustrate that the coastal areas are subject to a high probability of intense rainfall (Figure 5). In the southwest extension of the coastal area, over the Illawarra Escarpment, topography has clear influences on the rainfall amounts. The high “b” distribution in the vicinity of elevated topography of the Illawarra Escarpment suggests an orographic enhancement of instability, particularly for sites facing the east (as indicated by Figure 4). Similarly, in the highland area west of Sydney, there appears at least two different patterns of intense rainfall events. The Blue Mountain ranges, located at the northwest of the study area, have some of the highest DPCI values, particularly in the summer months. Thus, the issue arises whether the limited number of rain stations, especially over the high mountains, can capture such topographic effect to extreme precipitation adequately. One way to improve is to extend the data sources representing rainfall distribution, which may include a radar−based estimate and gridded reanalysis dataset, the latter able to reduce the uncertainty during the spatial interpolation process. The other method is to incorporate theoretical topographic rainfall models (e.g., [48,49]) to improve the representation of extreme precipitation over high elevations.
Internationally, the values of CIs found across Europe are similar to those described in Iran by [6] and are lower than those offered by [7] in China. It has been proposed by [7] as a general explanation for differences between results from [27] in the Iberian Peninsula and China, that different climate systems and precipitation mechanisms were responsible for rainfall (such as a typhoon). Generally, it has been suggested that precipitation trends based on annual maximum daily events observed in most parts of the world have nearly the same signs. However, the trend of heavy precipitation is disproportionately larger than the trend of the total [50]. Some of the previous investigations and the more recent work of [5] demonstrated the prominence and precision of CI applications in different parts of the world. It was suggested that even without any change in total precipitation, there may be changes in the frequency of intense daily precipitation in a climate change context; a fact that would have led to meaningful variations in the precipitation concentration patterns [51,52,53].
Author Contributions
Conceptualization, K.K.W.C. and A.A.R.; methodology, K.K.W.C. and A.A.R.; software, A.A.R.; validation, K.K.W.C., A.A.R., F.J. and L.T.-C.C.; formal analysis, A.A.R.; investigation, K.K.W.C.; resources, F.J.; data curation, L.T.-C.C.; writing—original draft preparation, K.K.W.C. and A.A.R.; writing—review and editing, F.J. and L.T.-C.C.; visualization, A.A.R.; supervision, K.K.W.C. and A.A.R.; project administration, K.K.W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data applied in this study is acquired from the Bureau of Meteorology, Australia and available from the authors.
Acknowledgments
A.A.R. would like to acknowledge the honorary fellowship from Macquarie University, Australia during part of this study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The tables in this appendix document basic information of the rain stations and rainfall statistics in this study (Table A1), and parameters for computing the DPCI using Albion Park station as an example (Table A2).

Table A1.
The geographic coordinates, study period, average annual rainfall (AP), coefficient of variation (CV) and total number of rainy days (TN) for the 41 rain stations across the GSMA.
Table A1.
The geographic coordinates, study period, average annual rainfall (AP), coefficient of variation (CV) and total number of rainy days (TN) for the 41 rain stations across the GSMA.
| Station Name (With Abbreviated Map Codes) | Latitude | Longitude | Altitude (m) | Study Period (year) | AP (mm) | CV (%) | TN |
|---|---|---|---|---|---|---|---|
| Albion Park (AP) | −4.57 | 150.78 | 8 | 1950–2015 | 1186.9 | 35.1 | 4811 |
| Bankston Airport (BA) | −33.92 | 150.99 | 6.5 | 1969–2015 | 874.6 | 25.1 | 3910 |
| Berambing (BE) | −33.54 | 150.44 | 792 | 1950–2015 | 1452.1 | 27.7 | 6774 |
| Bilpin (BI) | −33.52 | 150.49 | 610 | 1950–2015 | 1363.2 | 26.2 | 7224 |
| Blackheath (BL) | −33.63 | 150.29 | 1060 | 1950–2015 | 1240.6 | 28.3 | 6395 |
| Bowral (BO) | −34.49 | 150.40 | 690 | 1962–2015 | 931.7 | 26.6 | 5041 |
| Bringelly (BR) | −33.97 | 150.73 | 122 | 1950–2015 | 803.3 | 32.9 | 4496 |
| Bundanoon (BU) | −34.65 | 150.31 | 688 | 1950–2015 | 1249.6 | 30.7 | 5894 |
| Camden (CA) | −34.03 | 150.65 | 61 | 1950–2015 | 805.6 | 32.7 | 4964 |
| Colo Heights (CH) | −33.36 | 150.71 | 320 | 1963–2015 | 1034.4 | 26.7 | 4991 |
| Dapto (DA) | −34.50 | 150.79 | 10 | 1950–2015 | 1232.0 | 35.4 | 4822 |
| Darkes Forest (DF) | −34.23 | 150.91 | 370 | 1950–2015 | 1558.4 | 31.1 | 6994 |
| Faulconbridge (FA) | −33.69 | 150.53 | 460 | 1950–2015 | 1225.3 | 34.7 | 3351 |
| Frenchs Forest (FF) | −33.75 | 151.23 | 158 | 1957–2015 | 1374.9 | 25.5 | 6012 |
| Glenorie (GL) | −33.59 | 151.01 | 170 | 1950–2015 | 1002.7 | 27.7 | 5249 |
| Katoomba (KA) | −33.71 | 150.31 | 1015 | 1950–2015 | 1449.9 | 27.8 | 7479 |
| Kiama (KI) | −34.68 | 150.85 | 10 | 1950–2011 | 1332.9 | 31.1 | 5689 |
| Kurrajong Heights (KH) | −33.53 | 150.63 | 460 | 1950–2015 | 1278.8 | 28.9 | 6347 |
| Lucas Heights (LH) | −34.05 | 150.98 | 140 | 1958–2015 | 1021.9 | 26.6 | 5090 |
| Maroota (MA) | −33.46 | 151.00 | 203 | 1950-2015 | 952.9 | 31.7 | 4062 |
| Moss Vale (MV) | −34.54 | 150.38 | 675 | 1950–2015 | 961.6 | 30.1 | 6106 |
| Mount Kuring-Gai (MK) | −33.64 | 151.14 | 215 | 1965–2015 | 1171.1 | 28.7 | 4560 |
| Ourimbah (OU) | −33.36 | 151.33 | 195 | 1954–2015 | 1406.5 | 25.3 | 6183 |
| Parramatta North (PN) | −33.79 | 151.02 | 55 | 1966–2015 | 970.6 | 26.9 | 4554 |
| Picton (PI) | −34.17 | 150.61 | 165 | 1950–2015 | 886.5 | 32.8 | 4224 |
| Port Kembla (PK) | −34.47 | 150.88 | 9 | 1964–2015 | 1119.9 | 30.4 | 4440 |
| Prospect Reservoir (PR) | −33.82 | 150.91 | 61 | 1950–2015 | 936.4 | 28.6 | 5692 |
| Richmond (RI) | −33.62 | 150.75 | 20 | 1950–2015 | 868.8 | 29.5 | 5287 |
| Riverview Observatory (RO) | −33.83 | 151.16 | 40 | 1950–2015 | 1204.2 | 26.6 | 4946 |
| Sans Souci (SS) | −33.99 | 151.13 | 9 | 1950–2015 | 1153.5 | 28.3 | 6728 |
| Springwood (SW) | −33.71 | 150.58 | 320 | 1950–2015 | 1166.5 | 30.0 | 5727 |
| Sydney Airport (SA) | −33.95 | 151.17 | 6 | 1950–2015 | 1123.0 | 27.5 | 6384 |
| Sydney Observatory Hill (SO) | −33.86 | 151.21 | 39 | 1950–2015 | 1264.7 | 26.8 | 6607 |
| The Entrance (EN) | −33.35 | 151.50 | 22 | 1950–2015 | 1176.8 | 25.6 | 5889 |
| Wallacia (WA) | −33.86 | 150.64 | 50 | 1950–2015 | 890.9 | 33.0 | 5027 |
| West Pennant Hills (WP) | −33.75 | 151.04 | 120 | 1950–2014 | 1115.2 | 30.8 | 4858 |
| Wollondilly (WO) | −34.34 | 150.08 | 270 | 1974–2015 | 692.1 | 25.8 | 2781 |
| Wombeyan Caves (WC) | −34.31 | 149.97 | 580 | 1952–2015 | 847.8 | 22.7 | 4466 |
| Woonona (WN) | −34.34 | 150.90 | 45 | 1950–2015 | 1328.3 | 32.5 | 5679 |
| Wyee (WY) | −33.20 | 151.44 | 40 | 1950–2015 | 1250.9 | 24.8 | 6293 |

Table A2.
Frequency distribution (Ni, for rain >1 mm), total precipitation (Pi), relative cumulative frequencies (X) and percentage of total precipitation (Y) for the Albion Park station.
Table A2.
Frequency distribution (Ni, for rain >1 mm), total precipitation (Pi), relative cumulative frequencies (X) and percentage of total precipitation (Y) for the Albion Park station.
| Classes | Midpoint | Ni | ΣNi | Pi | Σpi | ΣN (%) = X | Σpi (%) = Y |
|---|---|---|---|---|---|---|---|
| 1–10 | 5 | 3037 | 3037 | 15,185 | 15,185 | 63.13 | 19.43 |
| 10.1–20 | 15 | 796 | 3833 | 11,940 | 27,125 | 79.67 | 34.70 |
| 20.1–30 | 25 | 367 | 4200 | 9175 | 36,300 | 87.30 | 46.44 |
| 30.1–40 | 35 | 187 | 4387 | 6545 | 42,845 | 91.19 | 54.81 |
| 40.1–50 | 45 | 109 | 4496 | 4905 | 47,750 | 93.45 | 61.09 |
| 50.1–60 | 55 | 71 | 4567 | 3905 | 51,655 | 94.93 | 66.08 |
| 60.1–70 | 65 | 52 | 4619 | 3380 | 55,035 | 96.01 | 70.41 |
| 70.1–80 | 75 | 38 | 4657 | 2850 | 57,885 | 96.80 | 74.05 |
| 80.1–90 | 85 | 22 | 4679 | 1870 | 59,755 | 97.26 | 76.45 |
| 90.1–100 | 95 | 30 | 4709 | 2850 | 62,605 | 97.88 | 80.09 |
| 100.1–110 | 105 | 20 | 4729 | 2100 | 64,705 | 98.30 | 82.78 |
| 110.1–120 | 115 | 12 | 4741 | 1380 | 66,085 | 98.55 | 84.55 |
| 120.1–130 | 125 | 8 | 4749 | 1000 | 67,085 | 98.71 | 85.82 |
| 130.1–140 | 135 | 12 | 4761 | 1620 | 68,705 | 98.96 | 87.90 |
| 140.1–150 | 145 | 13 | 4774 | 1885 | 70,590 | 99.23 | 90.31 |
| 150.1–200 | 175 | 25 | 4799 | 4375 | 74,965 | 99.75 | 95.91 |
| 200.1–250 | 225 | 8 | 4807 | 1800 | 76,765 | 99.92 | 98.21 |
| 250.1–300 | 275 | 2 | 4809 | 550 | 77,315 | 99.96 | 98.91 |
| 300.1–350 | 325 | 1 | 4810 | 325 | 77,640 | 99.98 | 99.33 |
| 500.1–550 | 525 | 1 | 4811 | 525 | 78,165 | 100.00 | 100.00 |
| Sum | 4811 | 78,165 | 1890.96 | 1507.27 |
Appendix B
Figure A1 in this appendix illustrates the physical interpretation of the Global Moran’s I Statistic. Depending on the z-score value, the rainfall distribution changes from a dispersed pattern (negative extreme), random pattern (most of the z-score around the mean) to a clustered pattern (positive extreme). The values of the Moran’s Index (−0.001755), z-score (3.553463) and the p-value (0.000380) based on the dataset in this study are given in the upper left corner of the figure.
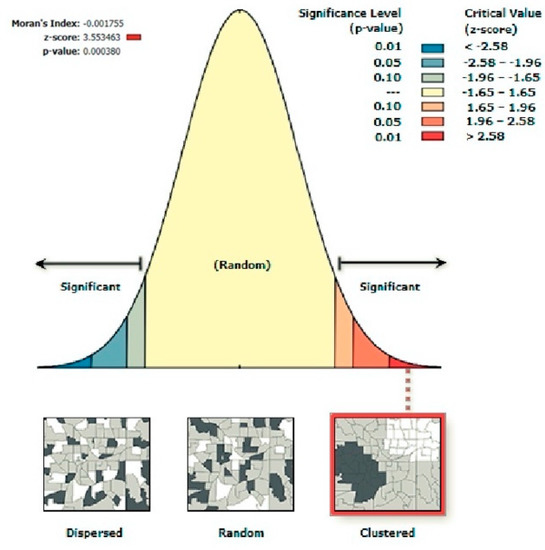
Figure A1.
Illustration of the Global Moran’s statistic and association with the dispersed, random and clustered precipitation patterns.
Appendix C
In this appendix the details in the procedure of performing spatial cross-covariance analysis between two attributes (datasets) are documented. An example of the DPCI (first attribute) and the constant “b” (second attribute) is illustrated in Figure A2. There are several steps in the analysis:
- The empirical cross-covariance for a pair of locations (NSW rainfall stations) between two datasets (DPCI and “b”) is first plotted as a function of the distance between the two locations (Figure A2 upper panel). In this illustration, each red dot shows the empirical cross-covariance between the pair of stations, with the attribute of one station taken from the first dataset and the attribute of the second station taken from the second dataset. The Cross-covariance cloud can be used to examine the local characteristics of spatial correlation between two datasets, and it can be used to look for spatial shifts in the correlation between two datasets. A cross-covariance cloud looks something like the NSW example.
- The values in the cross-covariance cloud are put into bins based on the direction and distance separating a pair of locations. These binned values are then averaged and smoothed to produce a cross-covariance surface. The legend (Figure A2 lower panel left) shows the colors and values separating classes of covariance values.
- A covariance surface with search direction capabilities is also provided in the ArcGIS tool. The extent of the cross-covariance surface is controlled by the lag size and number of lags that are specified (Figure A2 lower panel right). The search direction and width are indicated by the blue and red lines over the cross-covariance surface. One example has been shown in the figure and these options can be modified.
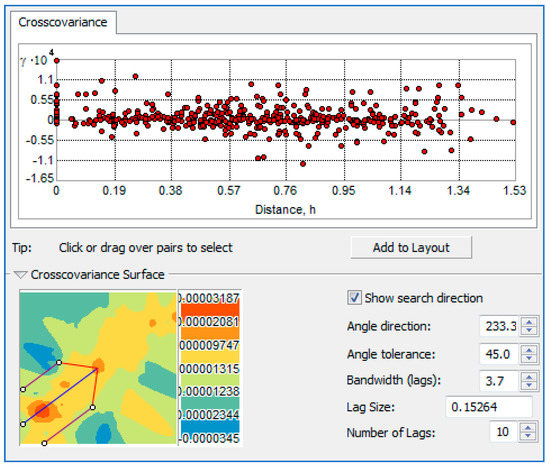
Figure A2.
Cross-covariance surface or cloud between the DPCI and the constant “b” in the concentration curve. The upper panel has all the covariance values according to the distance between the two points for computing the covariance. The lower panel has the cross-covariance map and an example of the directional search arrow. The search arrow is set based on the parameters on the right hand side (such as the direction, lag size and number of lags).
References
- Rasuly, A.A.; Cheung, K. The Spatial Distribution of Severe Thunderstorm Rainfall Events throughout the GMSTWA and Adjacent Tasman Sea. In Proceedings of the the 7th Annual CAWCR Workshop, Observing, Estimating and Forecasting Rainfall: From Science to Applications, Melbourne, Australia, 21–23 October 2013; Centre for Australian Weather and Climate Research: Melbourne, Australia, 2013. [Google Scholar]
- Monjo, R.; Martin-Vide, J. Daily precipitation concentration around the world according to several indices. Int. J. Climatol. 2016, 36, 3828–3838. [Google Scholar] [CrossRef]
- Máyer, P.; Jaén, M.V.M. Daily precipitation concentration and the rainy spells in the Canary Islands: Two risk factors. Boletín de la Assoc. de Geogr. Espaanoles 2014, 65, 463–468. [Google Scholar]
- Martin-Vide, J. Geographical factors in the pluviometry of Mediterranean Spain: Drought and torrential rainfall. In The U.S.-Spain Workshop on Natural Hazards, Iowa. Inst. Hydra Res.; The University of Iowa: Iowa City, IA, USA, 1994; pp. 9–25. [Google Scholar]
- Benhamrouche, A.; Boucherf, D.; Hamadache, R.; Bendahmane, L.; Martin-Vide, J.; Teixeira Nery, J. The spatial distribution of the daily precipitation concentration index in Algeria. Nat. Hazards Earth Syst. Sci. 2015, 15, 617–625. [Google Scholar] [CrossRef][Green Version]
- Alijani, B.; O’Brien, J.; Yarnal, B. Spatial analysis of precipitation intensity and concentration in Iran. Theor. Appl. Climatol. 2008, 94, 107–124. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, C.Y.; Gemmer, M.; Chen, Y.Q.; Liu, C.L. Changing properties of precipitation concentration in the Pearl River basin, China. Stoch. Env. Res. Risk Assess. 2009, 23, 377–385. [Google Scholar] [CrossRef]
- Suhaila, J.; Jemain, A.A. Spatial analysis of daily rainfall intensity and concentration index in Peninsular Malaysia. Theor. Appl. Climatol. 2012, 108, 235–245. [Google Scholar] [CrossRef]
- Cortesi, N.; Gonzalez-Hidalgo, J.C.; Brunetti, M.; Martin-Vide, J. Daily precipitation concentration across Europe 1971–2010. Nat. Hazards Earth Syst. Sci. 2012, 12, 2799–2810. [Google Scholar] [CrossRef]
- Coscarelli, R.; Caloiero, T. Analysis of daily and monthly rainfall concentration in Southern Italy (Calabria region). J. Hydrol. 2012, 416–417, 145–156. [Google Scholar] [CrossRef]
- Caloiero, T. Analysis of daily rainfall concentration in New Zealand. Nat. Hazards 2014, 72, 389–404. [Google Scholar] [CrossRef]
- Voskresenskaya, E. Precipitation inequality over Ukraine. J. Sci. Res. Rep. 2014, 3, 384–396. [Google Scholar]
- Sarricolea, P.; Martín-Vide, J. Spatial analysis of rainfall daily trends and concentration in Chile. Investig. Geogr. 2014, 47, 53–66. [Google Scholar] [CrossRef]
- Zubieta, R.; Saavedra, M.; Silva, Y.; Gira’Idez, L. Spatial analysis and temporal trends of daily precipitation concentration in the Mantaro River basin: Central Andes of Peru. Stoch. Env. Res. Risk Assess. 2017, 31, 1305–1318. [Google Scholar] [CrossRef]
- AL-Shamarti, H.K.A. The variation of annual precipitation and precipitation concentration index of IRAQ. IOSR J. Appl. Phys. 2016, 8, 36–44. [Google Scholar] [CrossRef]
- Ezenwaji, E.E.; Nzoiwu, C.P.; Chima, G.N. Analysis of precipitation concentration index (PCI) for Awka urban area, Nigeria. Hydrol. Current Res. 2017, 8, 4. [Google Scholar] [CrossRef]
- Nandargi, S.S.; Aman, K. Precipitation concentration changes over India during 1951 to 2015. Sci. Res. Essays 2018, 13, 14–26. [Google Scholar] [CrossRef]
- Zhang, K.; Yao, Y.; Qian, X.; Wang, J. Various characteristics of precipitation concentration index and its cause analysis in China between 1960 and 2016. Int. J. Climatol. 2019, 39, 4648–4658. [Google Scholar] [CrossRef]
- Patel, N.R.; Shete, D.T. Analyzing Precipitation Using Concentration Indices for North Gujarat Agro Climatic Zone, India. In Proceedings of the International Conference on Water Resources, Coastal and Ocean Engineering (ICWRCOE), Mangalore, Karnataka, Indian; Elsevier Procedia: Amsterdam, The Netherlands, 2015; Volume 4, pp. 917–924. [Google Scholar]
- Rasuly, A.A. The spatial variation and distribution of thunderstorm rainfall in the Greater Sydney Region. In Proceedings of the International Conference on Storms, Brisbane, Australia, 4–9 July 2004. [Google Scholar]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Klein Tank, A.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Kalyan, A.V.S.; Ghose, D.K.; Thalagapu, R.; Guntu, R.K.; Agarwal, A.; Kurths, K.; Rathinasamy, M. Multiscale spatiotemporal analysis of extreme events in the Gomati River basin, India. Atmosphere 2021, 12, 480. [Google Scholar] [CrossRef]
- Griffiths, D.J.; Colquhoun, J.R.; Batt, K.L.; Casinader, T.R. Severe thunderstorms in New South Wales: Climatology and means of assessing the impact of climate change. Clim. Chang. 1993, 25, 369–388. [Google Scholar] [CrossRef]
- Risbey, J.S.; Pook, M.J.; McIntosh, P.C.; Wheeler, M.C.; Hendon, H.H. On the remote drivers of rainfall variability in Australia. Mon. Wea. Rev. 2009, 137, 3233–3253. [Google Scholar] [CrossRef]
- Rasuly, A.; Cheung, K. Applying a climatologically oriented GIS in comparison of TRMM estimated severe thunderstorm rainfalls with ground truth in Sydney metropolitan area. J. Appl. Hydrol. 2014, 1, 1–13. [Google Scholar]
- Rasuly, A.A.; Cheung, K.; McBurney, B. Hail events across the Greater Metropolitan Severe Thunderstorm Warning Area. Nat. Haz. Earth Syst. Sci. 2015, 15, 973–984. [Google Scholar] [CrossRef]
- Martin-Vide, J. The spatial distribution of a daily precipitation concentration index in Peninsular Spain. Int. J. Climatol. 2004, 24, 959–971. [Google Scholar] [CrossRef]
- Brooks, C.E.P.; Carruthers, N. Handbook of Statistical Methods in Meteorology. Her Majesty’s Stationery Office, M.O.538.: London, UK, 1953; p. 412. [Google Scholar]
- Mitchell, A. The ESRI Guide to GIS Analysis; ESRI Press: Redlands, CA, USA, 2005; Volume 2. [Google Scholar]
- Karnieli, A. Application of Kriging technique to areal precipitation mapping in Arizona. GeoJournal 1990, 22, 391–398. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degre, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Yang, X.; Xie, X.; Liu, D.L.; Ji, F.; Wang, L. Spatial interpolation of daily rainfall data for local climate impact assessment over Greater Sydney region. Adv. Meteorol. 2015. [Google Scholar] [CrossRef]
- Cressie, N. The origins of Kriging. Math. Geol. 1990, 21, 239–252. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Usowicz, B.; Lipiec, J.; Lukowski, M.; Sloninski, J. Improvement of spatial interpolation of precipitation distribution using cokriging incorporating rain-gauge and satellite (SMOS) soil moisture data. Remote Sens. 2021, 13, 1039. [Google Scholar] [CrossRef]
- Zhang, P.; Huang, Y.; Shekhar, S.; Kumar, V. Exploiting spatial autocorrelation to efficiently process correlation-based similarity queries. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2750. [Google Scholar]
- Haining, R. Spatial Data Analysis: Theory and Practice; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Johnson, F.; White, C.J.; van Dijk, A.; Ekstrom, M.; Evans, J.P.; Jakob, D.; Kiem, A.S.; Leonard, M.; Rouillard, A.; Westra, S. Natural hazards in Australia: Floods. Clim. Chang. 2016, 139, 21–35. [Google Scholar] [CrossRef]
- Walsh, K.; White, C.J.; McInnes, K.; Holmes, J.; Schuster, S.; Richter, H.; Evans, J.P.; Luca, A.D.; Warren, R.A. Natural hazards in Australia: Storms, wind and hail. Clim. Chang. 2016, 139, 55–67. [Google Scholar] [CrossRef]
- Hopkins, L.C.; Holland, G. Australian Heavy-rain days and associated east coast cyclones: 1958–1992. J. Clim. 1997, 10, 621–635. [Google Scholar] [CrossRef]
- Pepler, A.S.; Dowdy, A.J.; Rensch, P.; Rudeva, I.; Catto, J.L.; Hope, P. The contributions of fronts, lows and thunderstorms to southern Australian rainfall. Clim. Dyn. 2020, 55, 1489–1505. [Google Scholar] [CrossRef]
- Speer, M.; Wiles, P.; Pepler, A. Low pressure systems off the New South Wales coast and associated hazardous weather: Establishment of a database. Aust. Meteorol. Oceanogr. J. 2009, 58, 29–39. [Google Scholar] [CrossRef]
- Risbey, J.S.; McIntosh, P.C.; Pook, M. Synoptic components of rainfall variability and trends in southeast Australia. Intl. J. Climatol. 2013, 33, 2459–2472. [Google Scholar] [CrossRef]
- Bureau of Meteorology. Stormy Weather, A Century of Storms, Flood and Drought in New South Wales; Australian Government: Melbourne, Australia, 2011; p. 40. [Google Scholar]
- Dare, R.A.; Davidson, N.E.; McBride, J.L. Tropical cyclone contribution to rainfall over Australia. Mon. Wea. Rev. 2012, 140, 3606–3619. [Google Scholar] [CrossRef]
- Lavender, S.L.; Abbs, D.J. Trends in Australian rainfall: Contribution of tropical cyclones and closed lows. Clim. Dyn. 2013, 40, 317–326. [Google Scholar] [CrossRef]
- Pepler, A.; Timbal, B.; Rakich, C.; Coutts-Smith, A. Indian ocean dipole overrides ENSO’s influence on cool season rainfall across the Eastern seaboard of Australian. J. Clim. 2014, 27, 3816–3826. [Google Scholar] [CrossRef]
- Chang, L.T.-C.; Cheung, K.K.W.; McAneney, J. Case Study of TRMM satellite rainfall estimation for landfalling tropical cyclones: Issues and challenges. Trop. Cycl. Res. Rev. 2013, 2, 109–123. [Google Scholar]
- Abbate, A.; Papini, M.; Longoni, L. Extreme rainfall over complex terrain: An application of the linear model of orographic precipitation to a case study in the Italian pre-alps. Geosciences 2021, 11, 18. [Google Scholar] [CrossRef]
- Easterling, D.R.; Evans, J.L.; Groisman, P.Y.; Karl, T.R.; Kunkel, K.E.; Ambenje, P. Observed variability and trends in extreme climate events: A brief review. Bull. Amer. Meteor. Soc. 2000, 81, 417–426. [Google Scholar] [CrossRef]
- Allan, R.J.; Haylock, M.R. Circulation Features Associated with the winter rainfall decrease in Southwestern Australia. J. Clim. 1993, 6, 1356–1367. [Google Scholar] [CrossRef]
- Alexander, L.V.; Wang, X.L.L.; Wan, H.; Trewin, B. Significant decline in storminess over southeast Australia since the late 19th century. Aust. Meteorol. Oceanogr. J. 2011, 61, 23–30. [Google Scholar] [CrossRef]
- Dey, R.; Lewis, S.; Abram, N.; Arblaster, J. A review of past and projected changes in Australia’s rainfall. Wiley Interdiscip. Rev. 2019, 10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).