Flight Data-Based Wind Disturbance and Air Data Estimation
Abstract
1. Introduction
2. Method
2.1. Preprocessing of Flight Data
2.2. Wind Field Modeling
2.2.1. Modeling of Horizontal Prevailing Wind
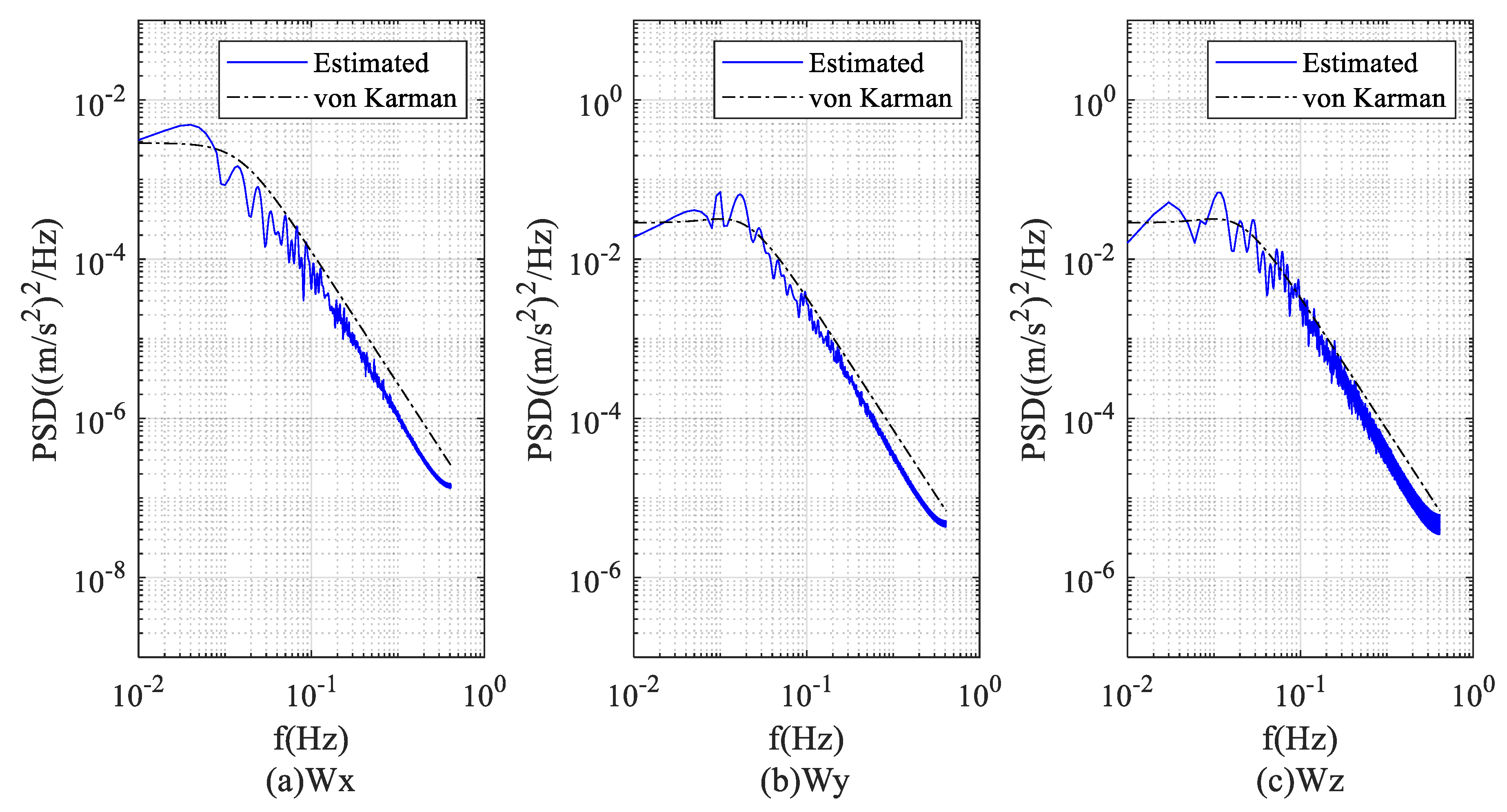
2.2.2. Turbulence Modeling
2.3. Design of Forward–Backward Filter
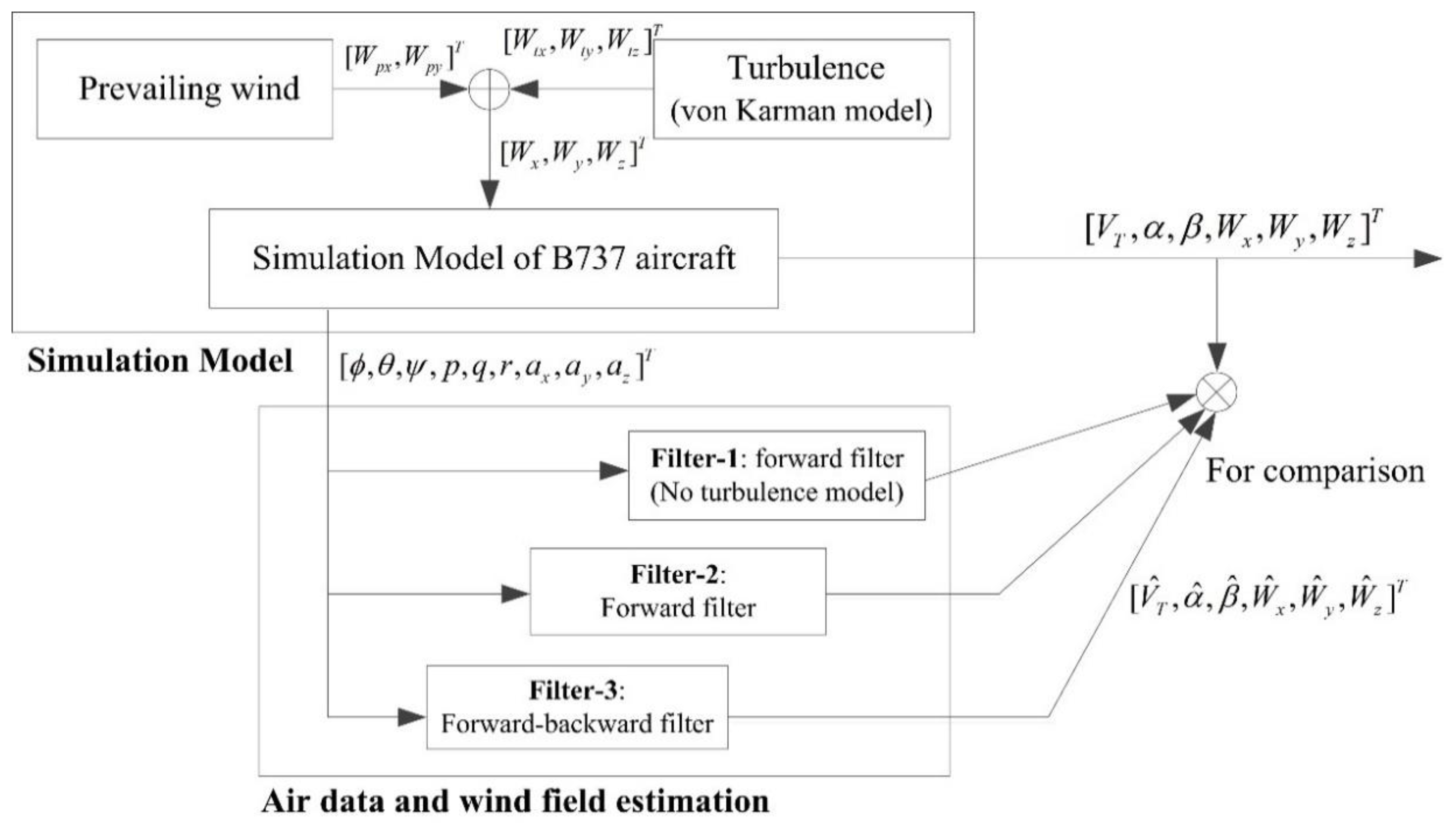
2.3.1. Building the Filtering System
2.3.2. Design of the Forward–Backward Filtering Algorithm
3. Experiments and Discussion
3.1. Simulation Analysis
3.1.1. Simulation Settings
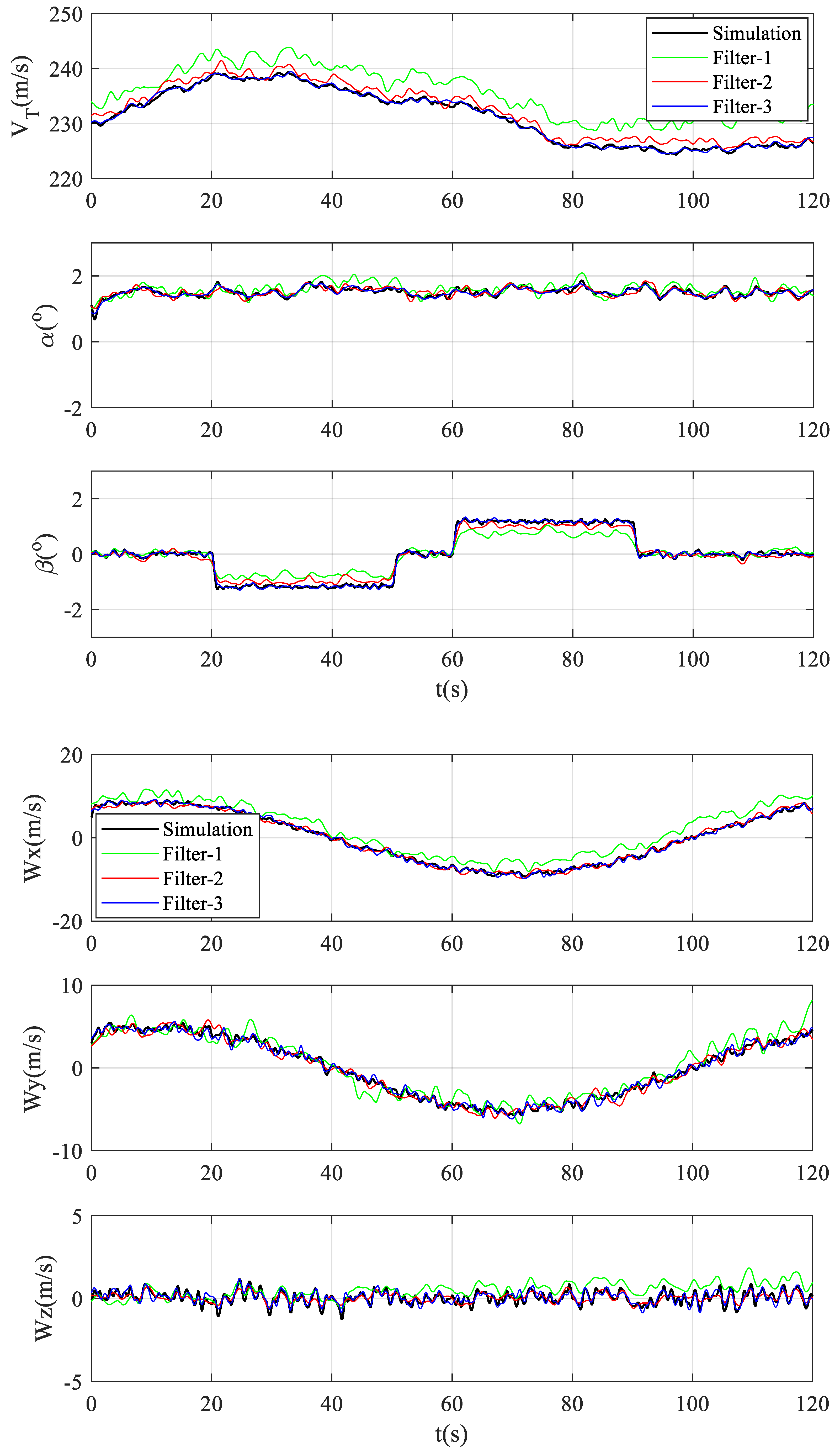
3.1.2. Performance Comparison of Three Filters
3.2. Experiments with Flight Data
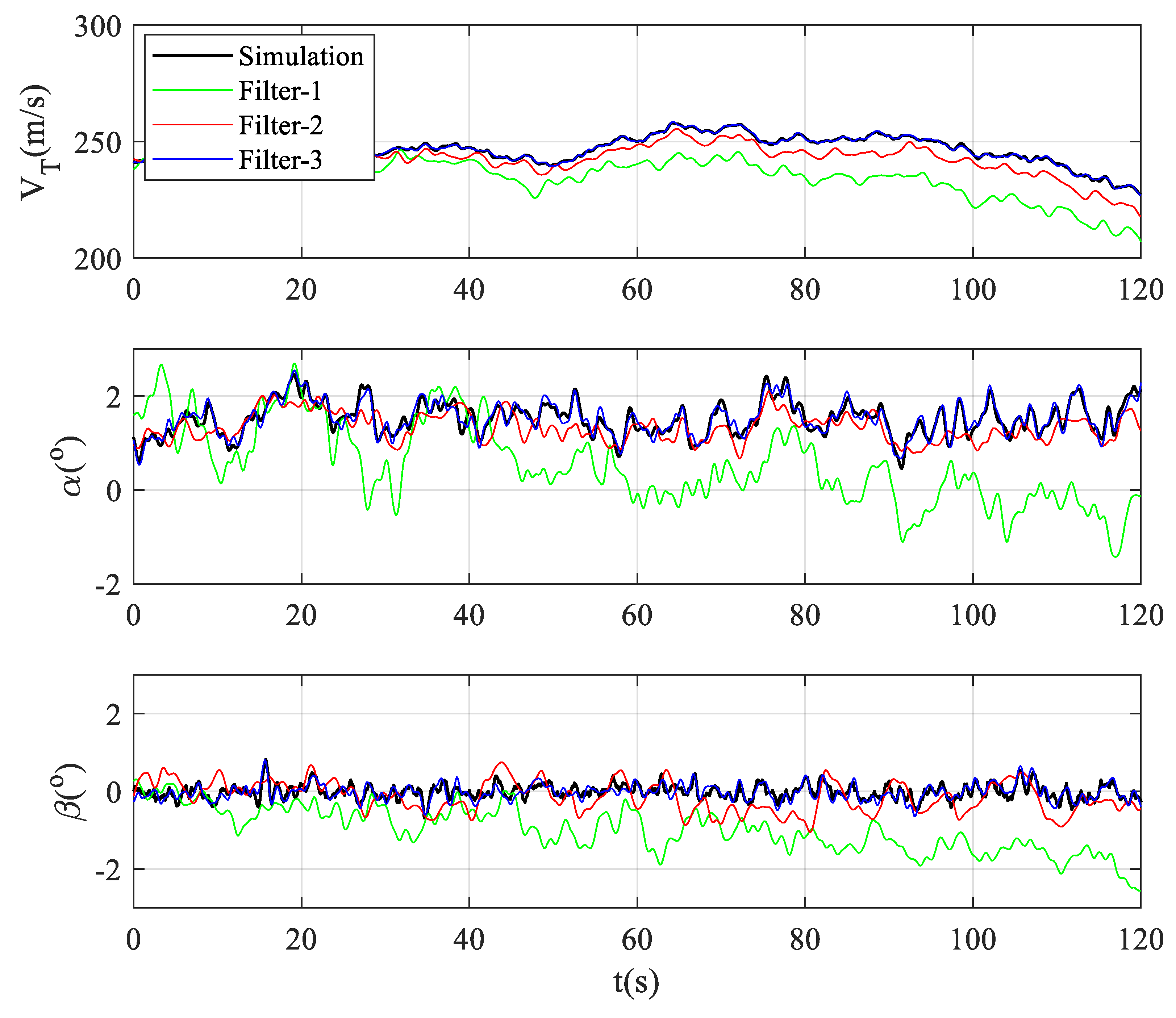
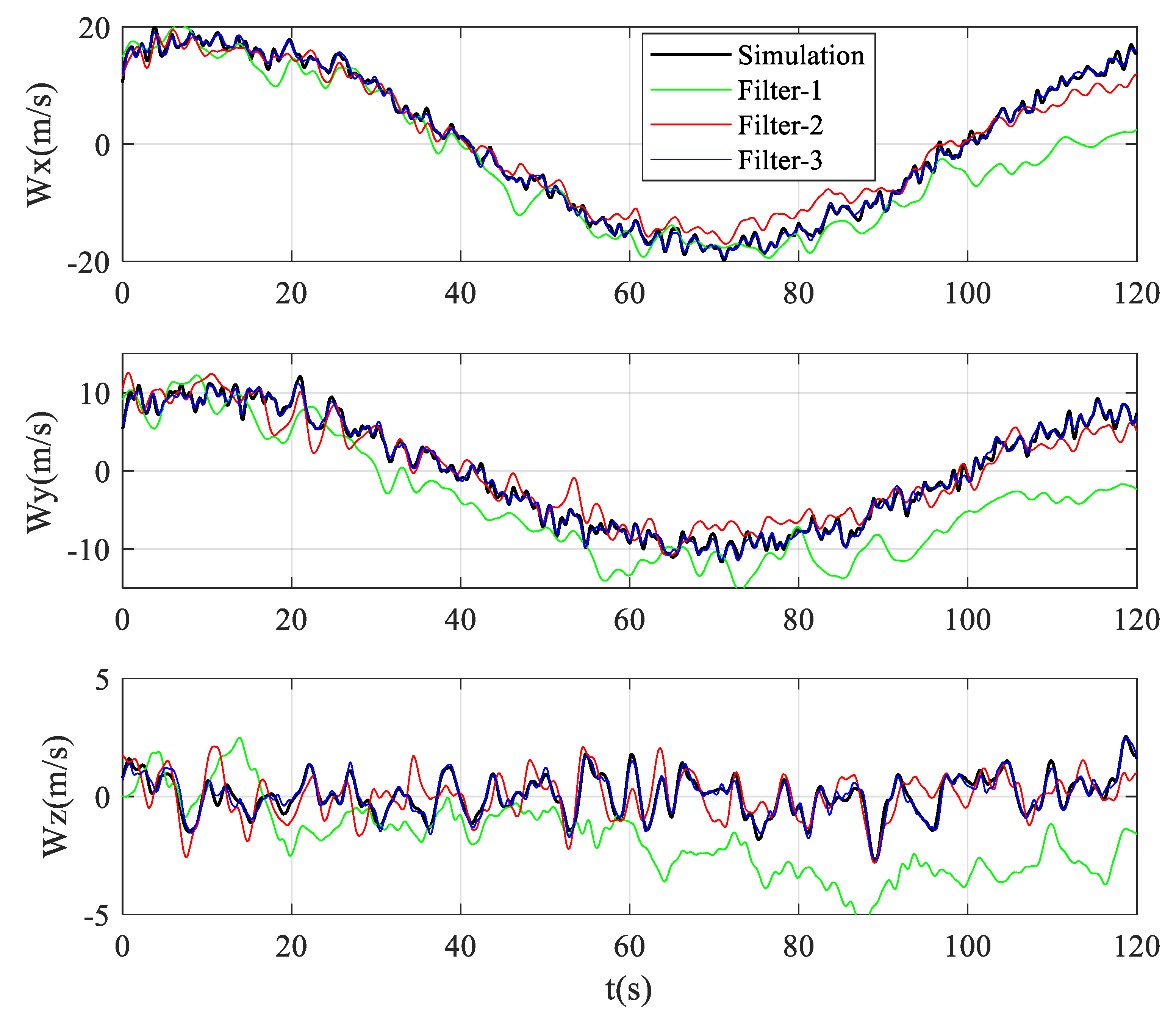
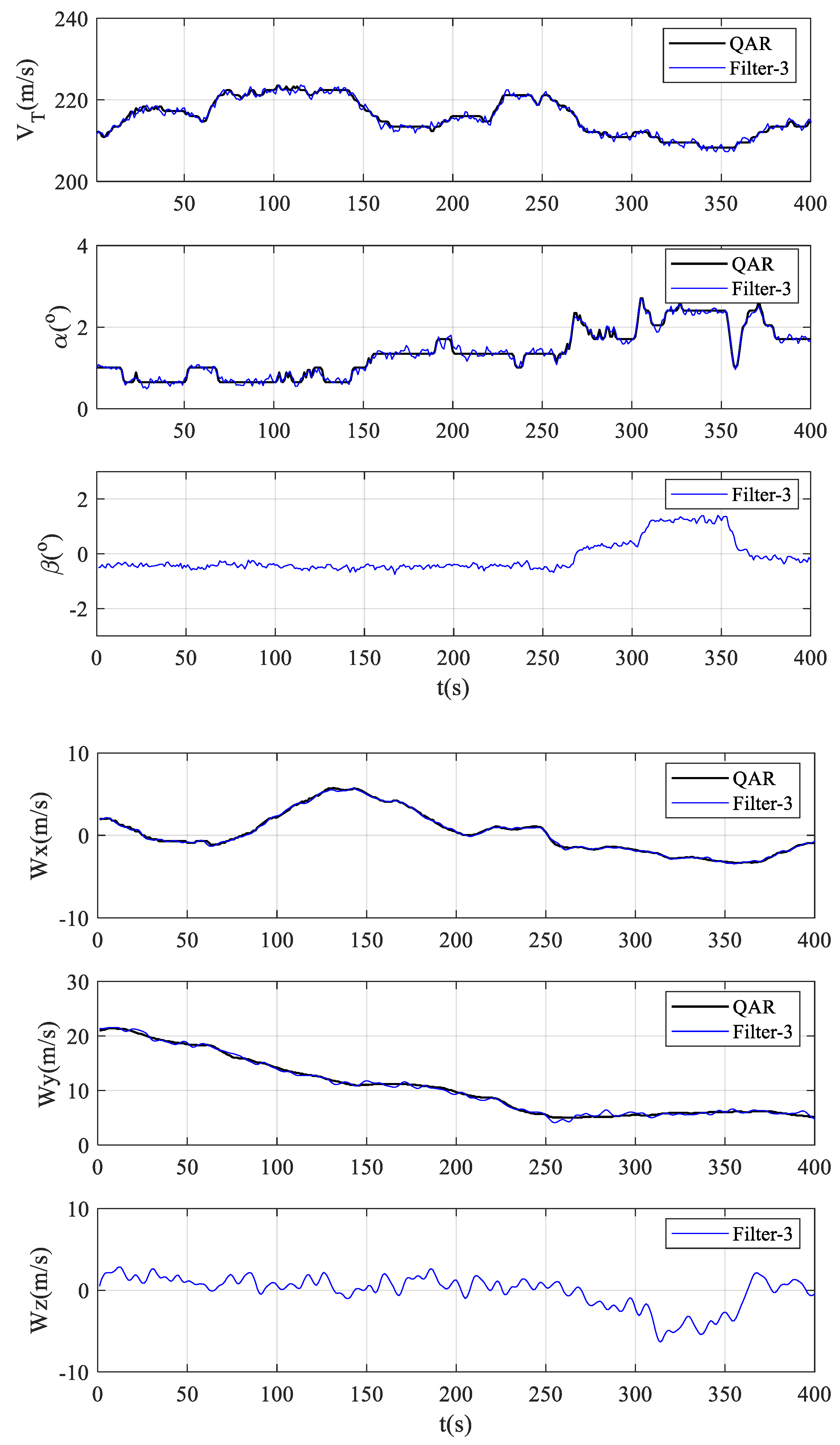
3.2.1. In-Turbulence Air Data and Wind Field Estimation
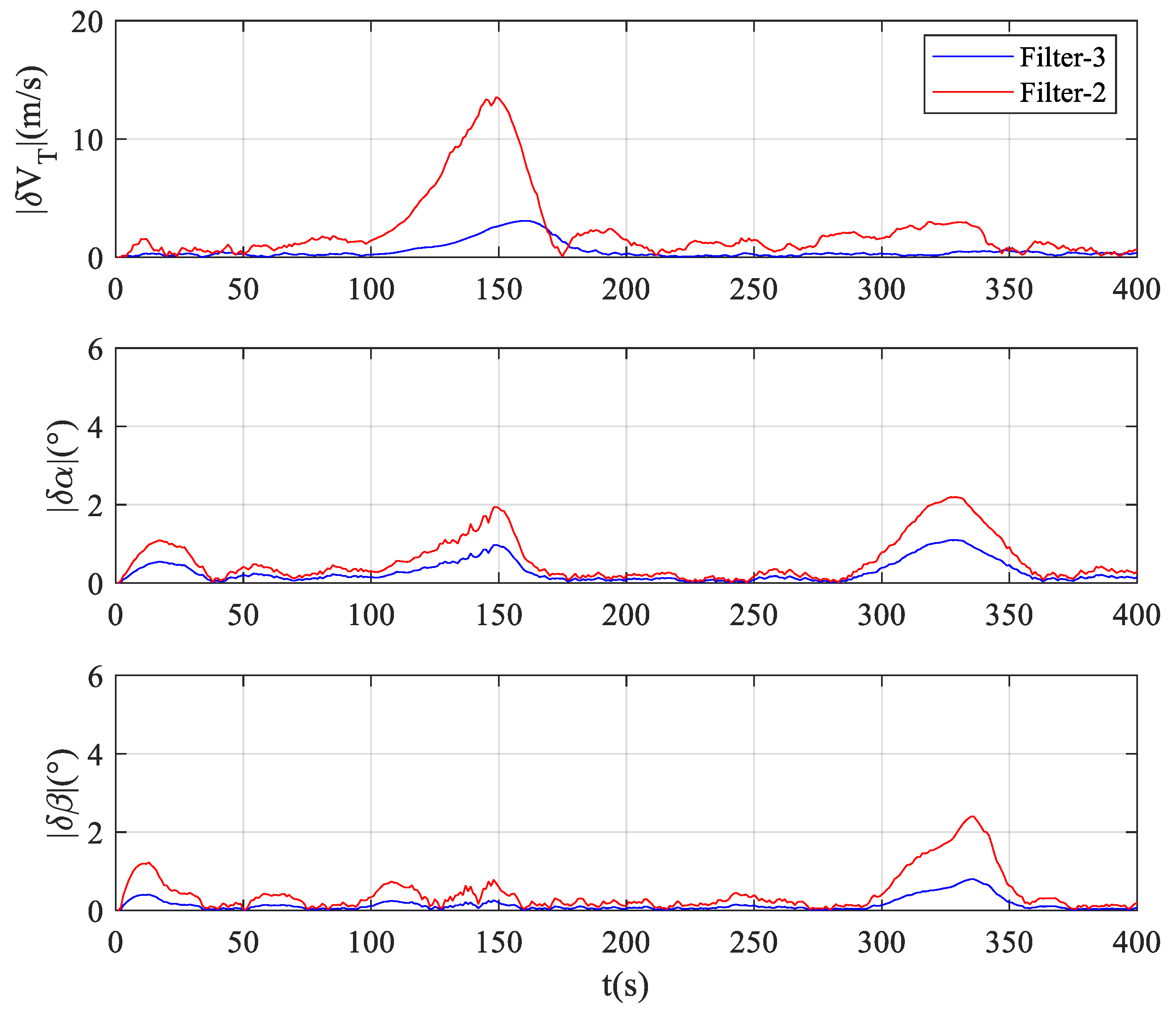
3.2.2. Effects of Uncertain Disturbance on Filtering
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter Type | Parameter Assignment | Symbol (Unit) | Sampling Rate/Hz | Out Resolution | Out Range | Accuracy |
|---|---|---|---|---|---|---|
| Inertial measurements | Longitudinal acceleration | 4 | 0.000976563 | −1~+1 | 0.01 | |
| Lateral acceleration | 4 | 0.00203649 | −1~+1 | 0.01 | ||
| Vertical acceleration | 8 | 0.001953125 | −3~6 | 0.046 | ||
| Roll angle | 4 | 0.005493164 | −90~90 | 0.05 | ||
| Pitch angle | 4 | 0.005493164 | −90~90 | 0.05 | ||
| Yaw angle | 2 | 0.005493164 | −180~180 | 0.05 | ||
| Roll angular rate | 8 | 0.00390625 | −45~45 | 0.1 | ||
| Pitch angular rate | 8 | 0.00390625 | −45~45 | 0.1 | ||
| Yaw angular rate | 8 | 0.00390625 | −45~45 | 0.1 | ||
| Ground speed | 4 | 0.1 | 0~1024 | N/A | ||
| Air data | Mach number | 1 | 0.001 | 0~1.024 | N/A | |
| Angle of attack | 1 | 0.17578125 | −90~90 | N/A | ||
| Total temperature | 1 | 0.5 | −512~512 | N/A |
References
- Burns, A.A.; Chenkovich, G.A. Digital Flight Data Acquisition Unit 737-600/-700/-700C/-800/-900 Data Frame Interface Control and Requirements Document; Report. No. D226A101-2; The Boeing Company: Seattle, WA, USA, 2003. [Google Scholar]
- Sharman, R.D.; Lane, T. Aviation Turbulence: Processes, Detection, Prediction; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Sikkel, L.N.C.; Croon, G.C.H.E.; Wagter, C.D.; Chu, Q.P. A novel online model-based wind estimation approach for quadrotor micro air vehicles using low cost MEMS IMUs. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 2141–2146. [Google Scholar]
- Li, R.; Lu, C.; Liu, J.; Lei, T. Air data estimation algorithm under unknown wind based on information fusion. J. Aerosp. Eng. 2018, 31, 040418072. [Google Scholar] [CrossRef]
- Colgren, R.D.; Frye, M.T.; Olson, W.M. A proposed system architecture for estimation of angle of attack and sideslip angle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Portland, OR, USA, 9–11 August 1999. [Google Scholar]
- Myschik, S.; Holzapfel, F.; Sachs, G. Low-cost sensor based integrated air data and navigation system for general aviation aircraft. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Wise, K.A. Flight testing of the X-45A J-UCAS computational alpha-beta system. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Cho, A.; Kim, J.; Lee, S.; Kee, C. Wind estimation and airspeed calibration using a UAV with a single-antenna GPS receiver and Pitot tube. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 109–117. [Google Scholar] [CrossRef]
- Larrabee, T.; Chao, H.; Rhudy, M.; Gu, Y.; Napolitano, M.R. Wind field estimation in UAV formation flight. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 5408–5413. [Google Scholar]
- Lie, F.A.P.; Egziabher, D.G. Synthetic air data system. J. Aircr. 2013, 50, 1234–1249. [Google Scholar] [CrossRef]
- Nebula, F.; Palumbo, R.; Morani, G. Virtual air data: A fault-tolerant approach against ADS failures. In Proceedings of the AIAA Infotech at Aerospace Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar]
- Lv, P.; Lai, J.; Liu, J.; Zhu, B.; Song, Y. Overview and progress on study of aircraft aerodynamics model aided navigation method. Control Decis. 2015, 30, 2113–2120. [Google Scholar]
- Karlgaard, C.D.; Kutty, P.; Schoenenberger, M. Coupled inertial navigation and flush air data sensing algorithm for atmosphere estimation. J. Spacecr. Rocket. 2017, 54, 128–140. [Google Scholar] [CrossRef]
- Johansen, T.A.; Cristofaro, A.; Sorensen, K.; Hansen, J.M.; Fossen, T.I. On estimation of wind velocity, angle of attack and sideslip angle of small UAVs using standard sensors. In Proceedings of the International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 23–25 November 2015; pp. 510–519. [Google Scholar]
- Lee, J.H.; Sevil, H.E.; Dogan, A.; Hullender, D. Estimation of maneuvering aircraft states and time-varying wind with turbulence. In Proceedings of the AIAA Guidance, Navigation and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Grillo, C.; Montano, F. Wind component estimation for UAS flying in turbulent air. Aerosp. Sci. Technol. 2019, 93, 1–7. [Google Scholar] [CrossRef]
- Mutlu, T.; Hajiyev, C. An integrated air data/GPS navigation system for helicopters. Positioning 2011, 2, 103–111. [Google Scholar] [CrossRef]
- Guo, D.; Zhong, M.; Zhou, D. Multi sensor data-fusion-based approach to airspeed measurement fault detection for unmanned aerial vehicles. IEEE Trans. Instrum. Meas. 2018, 67, 317–327. [Google Scholar] [CrossRef]
- Rhudy, M.B.; Gu, Y.; Gross, J.N.; Chao, H. Onboard wind velocity estimation comparison for unmanned aircraft systems. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 55–66. [Google Scholar] [CrossRef]
- Hajiyev, C.; Guler, D.C.; Hacizade, U. Two-stage Kalman filter for estimation of wind speed and UAV flight parameters based on GPS/INS and pitot tube measurements. In Proceedings of the 9th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 11–14 June 2019; pp. 875–880. [Google Scholar]
- Rhudy, M.B.; Fraolini, M.L.; Porcacchia, M.; Napolitano, M.R. Comparison of wind speed models within a Pitot-free airspeed estimation algorithm using light aviation data. Aerosp. Sci. Technol. 2019, 86, 21–29. [Google Scholar] [CrossRef]
- Sun, K.; Regan, C.D.; Egziabher, D.G. GNSS/INS based estimation of air data and wind vector using flight maneuvers. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 838–849. [Google Scholar]
- Gao, Z.; Wang, H.; Qi, K.; Xiang, Z.; Wang, D. Acceleration-based in situ eddy dissipation rate estimation with flight data. Atmosphere 2020, 11, 1247. [Google Scholar] [CrossRef]
- Wenz, A.; Johansen, T.A. Moving horizon estimation of air data parameters for UAVs. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 2101–2121. [Google Scholar] [CrossRef]
- Tian, P.; Chao, H.; Gu, Y.; Hagerott, S.G. UAV flight test evaluation of fusion algorithms for estimation of angle of attack and sideslip angle. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Tian, P.; Chao, H. Model aided estimation of angle of attack, sideslip angle, and 3D wind without flow angle measurements. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Wang, Y.; Keviczky, T. Real-time fault-tolerant moving horizon air data estimation for the reconfigure benchmark. IEEE Trans. Control Syst. Technol. 2019, 27, 997–1011. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity and Nonlinear Approaches; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wright Patterson Air Force Base. Flying Qualities of Piloted Airplanes, MIL-F-8785C; U.S. Air Force: Dayton, OH, USA, 1980.
- Duran, I.B.; Schmidli, J.; Bhattacharya, R. A budget-based turbulence length scale diagnostic. Atmosphere 2020, 11, 425. [Google Scholar] [CrossRef]
- Rabbath, C.A.; Lechevin, N. Discrete-Time Control System Design with Application; Springer: New York, NY, USA, 2014. [Google Scholar]
- Stevens, B.L. Aircraft Control and Simulation, 3rd ed.; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Ienkaran, A.; Simon, H. Cubature Kalman smoothers. Automatica 2011, 47, 2245–2250. [Google Scholar]
- Pnevmatikakis, E.A.; Rad, K.R.; Huggins, J.; Paninski, L. Fast Kalman filtering and forward–backward smoothing via a low-rank perturbative approach. J. Comput. Graph. Stat. 2014, 23, 316–339. [Google Scholar] [CrossRef]
- Ernst, D.O.; Grammens, D. CFM56-7 Propulsion System Data for the 737-600/-700/-800 Training Simulator; Report No. D611A025; The Boeing Company: Seattle, WA, USA, 2005. [Google Scholar]
- Jens, D.R.; Neville, K.W.; Draxler, J.G. Aerodynamic Data and Flight Control System Description for the 737-600/-700/-800/-900 Training Simulator; Report No. D611A001-VOL1; The Boeing Company: Seattle, WA, USA, 2003. [Google Scholar]
- Shikany, D.A.; Neville, K.W.; Harrington, T.A. Aerodynamic Data for the 737-800 Training Simulator; Report No. D611A001-VOL3; The Boeing Company: Seattle, WA, USA, 2003. [Google Scholar]
- Stoica, P.; Moses, R. Spectral Analysis of Signals; Pearson Education: Cranbury, NJ, USA, 2005. [Google Scholar]



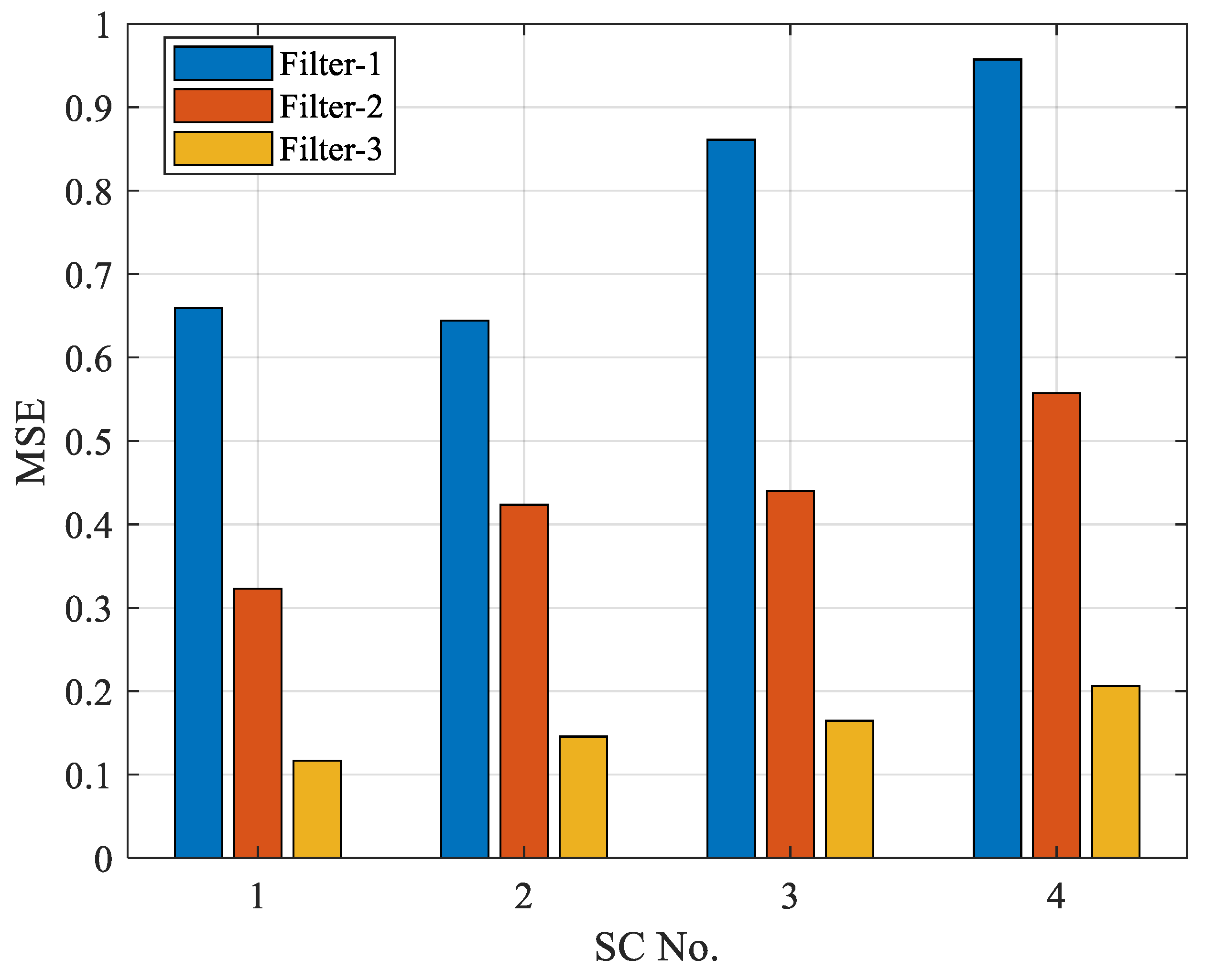
| Simulation Condition | Prevailing Wind | Turbulence Intensity | Flight State |
|---|---|---|---|
| SC-1 | , | Light, | Level flight, , |
| SC-2 | , | Moderate, | Level flight, , |
| SC-3 | , | Moderate, | Turn flight, , |
| SC-4 | , | Severe, | Level flight, , |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Wang, H.; Xiang, Z.; Wang, D. Flight Data-Based Wind Disturbance and Air Data Estimation. Atmosphere 2021, 12, 470. https://doi.org/10.3390/atmos12040470
Gao Z, Wang H, Xiang Z, Wang D. Flight Data-Based Wind Disturbance and Air Data Estimation. Atmosphere. 2021; 12(4):470. https://doi.org/10.3390/atmos12040470
Chicago/Turabian StyleGao, Zhenxing, Haofeng Wang, Zhiwei Xiang, and Debao Wang. 2021. "Flight Data-Based Wind Disturbance and Air Data Estimation" Atmosphere 12, no. 4: 470. https://doi.org/10.3390/atmos12040470
APA StyleGao, Z., Wang, H., Xiang, Z., & Wang, D. (2021). Flight Data-Based Wind Disturbance and Air Data Estimation. Atmosphere, 12(4), 470. https://doi.org/10.3390/atmos12040470






