Review on Parameterization Schemes of Visibility in Fog and Brief Discussion of Applications Performance
Abstract
:1. Introduction
2. Relationships between VIS and Extinction Coefficient
3. Relationships between VIS and RH
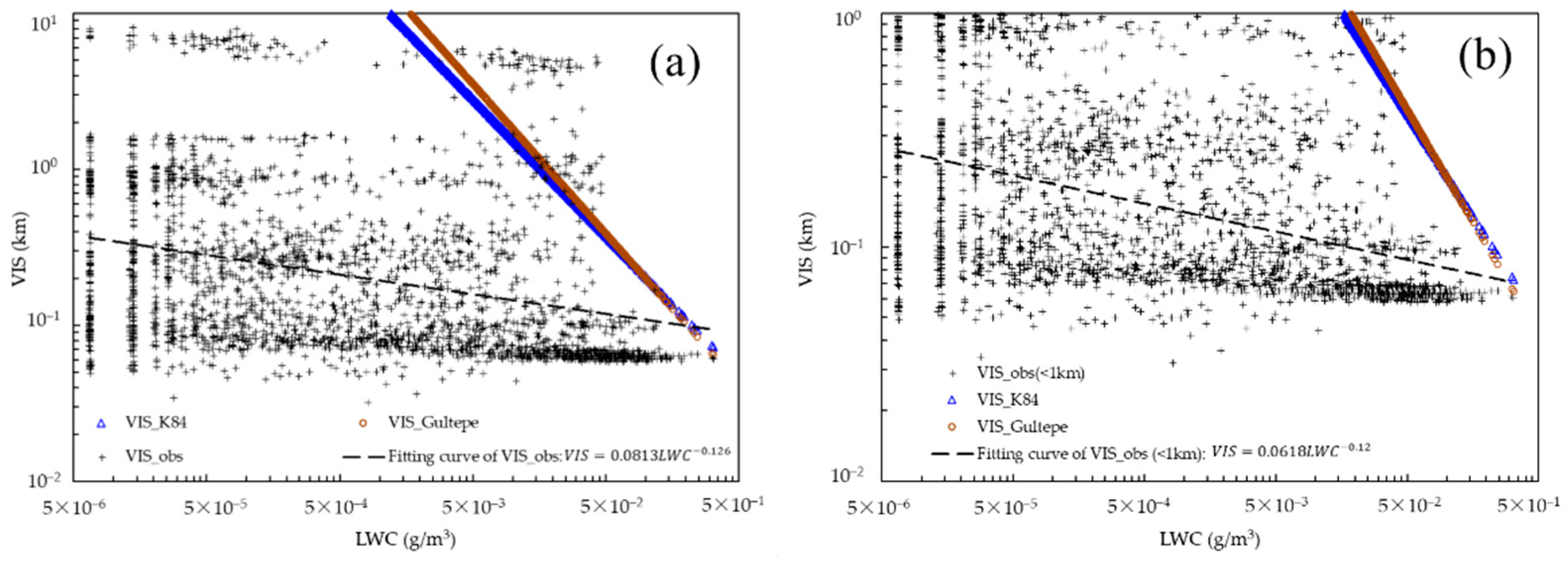
4. Relationships between VIS and LWC
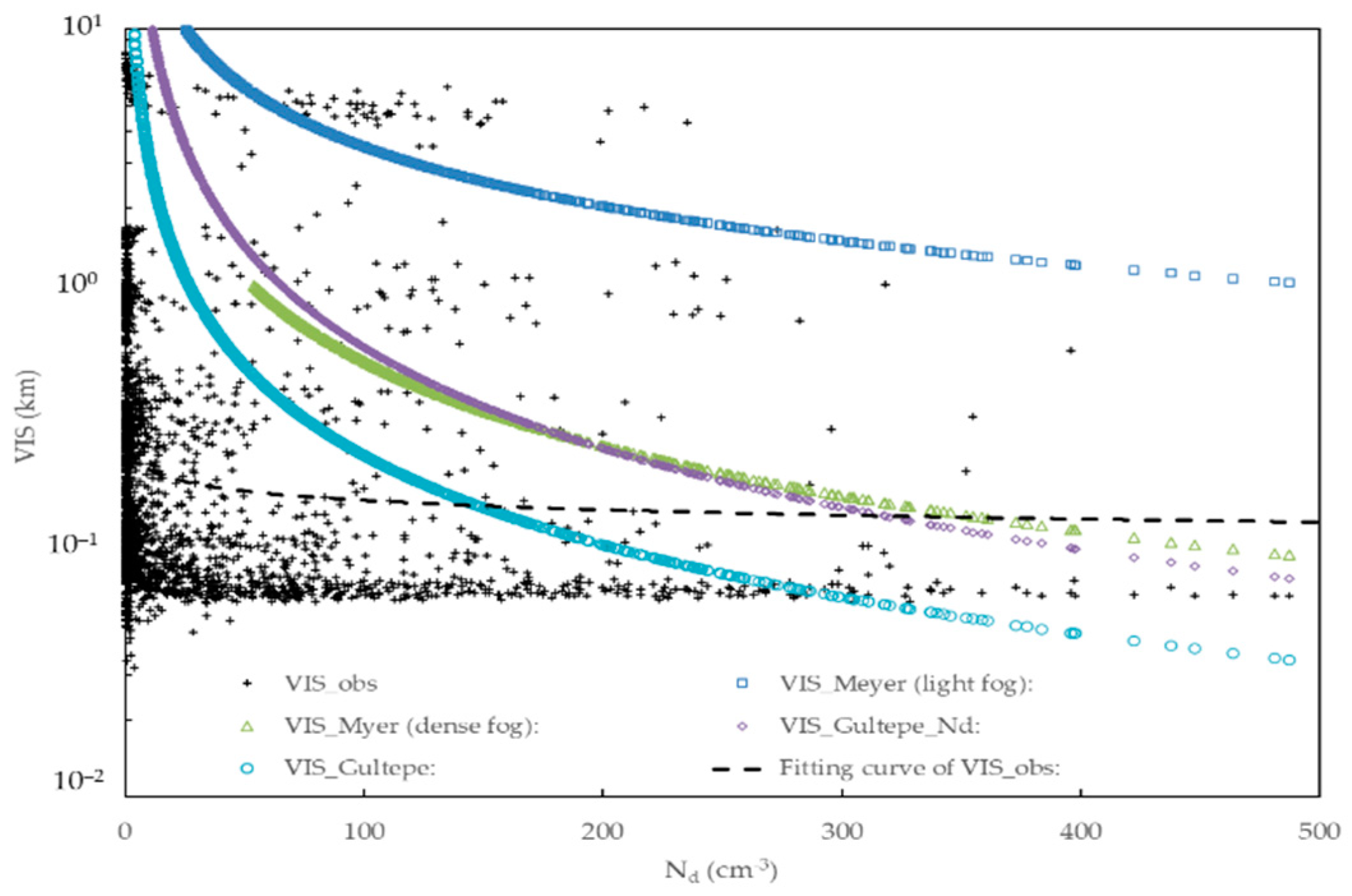
5. Relationships between VIS, Nd, and Fog Droplets Size
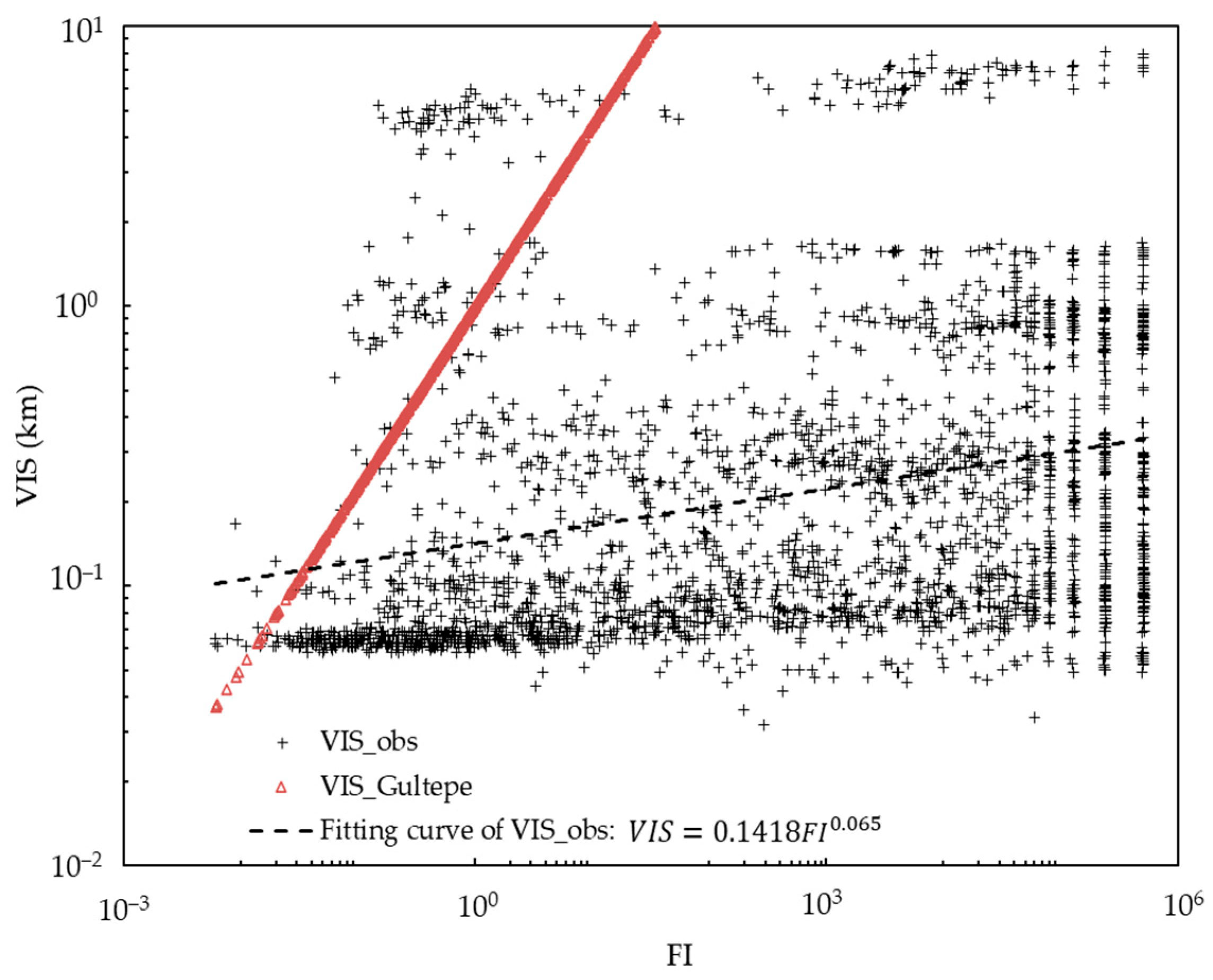
6. Relationships between VIS, LWC and Nd
7. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WMO. WMO Guide to Meteorological Instruments and Methods of Observation; Secretariat of the WMO: Geneva, Switzerland, 2006; p. 569. [Google Scholar]
- Wu, B.G.; Xie, Y.Y.; Wu, D.Z.; Wang, Y.N.; Wang, D.S. Poor visibility on Jingjintang Expressway in autumn/ winter and relevant measures. J. Nat. Disaster 2009, 18, 12–17. (In Chinese) [Google Scholar]
- Lewis, J.M.; Koracin, D.; Redmond, K.T. Sea Fog Research in the United Kingdom and United States: A Historical Essay Including Outlook. Bull. Am. Meteorol. Soc. 2004, 85, 395–408. [Google Scholar] [CrossRef] [Green Version]
- Niu, S.J.; Lu, C.S.; Lü, J.J.; Xu, F.; Zhao, L.J.; Liu, D.Y.; Yue, Y.Y.; Zhou, Y.; Yu, H.Y.; Wang, T.S. Advances in fog research in China. Adv. Meteor. Sci. Technol. 2016, 6, 6–19. [Google Scholar]
- Koračin, D.; Dorman, C.; Lewis, J.M.; Hudson, J.G.; Wilcox, E.; Torregrosa, A. Marine fog: A review. Atmos. Res. 2014, 143, 142–175. [Google Scholar] [CrossRef]
- Fu, G.; Li, X.L.; Wei, N. Review on the atmospheric visibility research. Period. Ocean. Univ. China 2009, 39, 855–862. (In Chinese) [Google Scholar]
- Niu, S.; Lu, C.; Yu, H.; Zhao, L.; Lü, J. Fog research in China: An overview. Adv. Atmos. Sci. 2010, 27, 639–662. [Google Scholar] [CrossRef]
- Gultepe, I.; Heymsfield, A.J.; Fernando, H.J.S.; Pardyjak, E.; Dorman, C.E.; Wang, Q.; Creegan, E.; Hoch, S.W.; Flagg, D.D.; Yamaguchi, R.; et al. A Review of Coastal Fog Microphysics during C-FOG. Boundary-Layer Meteorol. 2021, 181, 1–39. [Google Scholar] [CrossRef]
- Gultepe, I. Fog and Boundary Layer Clouds: Introduction. Pure Appl. Geophys. 2007, 164, 1115–1116. [Google Scholar] [CrossRef]
- Laj, P.; Fuzzi, S.; Lazzari, A. The Size Dependent Composition of Fog Droplets. Contrib. Atmos. Phys. 1998, 71, 115–130. [Google Scholar]
- Frank, G.; Martinsson, B.G.; Cederfelt, S.I. Droplet Formation and Growth in Polluted Fogs. Contrib. Atmos. Phys. 1998, 71, 65–85. [Google Scholar]
- García-García, F.; Virafuentes, U.; Montero-Martínez, G. Fine-scale measurements of fog-droplet concentrations: A preliminary assessment. Atmos. Res. 2002, 64, 179–189. [Google Scholar] [CrossRef]
- Hsieh, W.C.; Jonsson, H.; Wang, L.; Buzorius, G.; Flagan, R.C.; Seinfeld, J.H.; Nenes, A. On the representation of droplet coalescence and autoconversion: Evaluation using ambient cloud droplet size distributions. J. Geophys. Res. Atmos. 2009, 114, D07201. [Google Scholar] [CrossRef] [Green Version]
- Niu, S.; Lu, C.; Liu, Y.; Zhao, L.; Lu, J.; Yang, J. Analysis of the microphysical structure of heavy fog using a droplet spectrometer: A case study. Adv. Atmos. Sci. 2010, 27, 1259–1275. [Google Scholar] [CrossRef]
- Wang, T.; Niu, S.; Lü, J.; Zhou, Y. Observational Study on the Supercooled Fog Droplet Spectrum Distribution and Icing Accumulation Mechanism in Lushan, Southeast China. Adv. Atmos. Sci. 2019, 36, 29–40. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.-Y.; Wu, B.-G.; Liu, J.-L.; Nie, H.-H.; Chen, D.-H.; Gultepe, I. Microphysics of fog bursting in polluted urban air. Atmos. Environ. 2021, 253, 1–11. [Google Scholar] [CrossRef]
- Fuzzi, S.; Facchini, M.C.; Orsi, G.; Bonforte, G.; Martinotti, W.; Ziliani, G.; Mazzalit, P.; Rossi, P.; Natale, P.; Grosa, M.M.; et al. The NEVALPA project: A regional network for fog chemical climatology over the PO Valley basin. Atmos. Environ. 1996, 30, 201–213. [Google Scholar] [CrossRef]
- Ma, C.-J.; Kasahara, M.; Tohno, S.; Sakai, T. A replication technique for the collection of individual fog droplets and their chemical analysis using micro-PIXE. Atmos. Environ. 2003, 37, 4679–4686. [Google Scholar] [CrossRef]
- Mancinelli, V.; Decesari, S.; Emblico, L.; Tozzi, R.; Mangani, F.; Fuzzi, S.; Facchini, M.C. Extractable iron and organic matter in the suspended insoluble material of fog droplets. Water Air Soil Pollut. 2006, 174, 303–320. [Google Scholar] [CrossRef]
- Raja, S.; Raghunathan, R.; Yu, X.-Y.; Lee, T.; Chen, J.; Kommalapati, R.R.; Murugesan, K.; Shen, X.; Qingzhong, Y.; Valsaraj, K.T.; et al. Fog chemistry in the Texas–Louisiana Gulf Coast corridor. Atmos. Environ. 2008, 42, 2048–2061. [Google Scholar] [CrossRef]
- Li, Z.; Liu, D.; Yan, W.; Wang, H.; Zhu, C.; Zhu, Y.; Zu, F. Dense fog burst reinforcement over Eastern China: A review. Atmos. Res. 2019, 230, 104639. [Google Scholar] [CrossRef]
- Roach, W.T. Effective of Radiative Exchange on Growth by Consideration of a Cloud or Fog Droplet. Q. J. R. Meteorol. Soc. 1976, 102, 361–372. [Google Scholar] [CrossRef]
- Guo, L.; Guo, X.; Fang, C.; Zhu, S. Observation analysis on characteristics of formation, evolution and transition of a long-lasting severe fog and haze episode in North China. Sci. China Earth Sci. 2015, 58, 329–344. [Google Scholar] [CrossRef]
- Oliver, D.A.; Lewellen, W.S.; Williamson, G.G. The interaction between turbulent and radiative transport in the development of fog and low level stratus. J. Atmos. Sci. 1978, 35, 301–316. [Google Scholar]
- Wu, B.G.; Zhang, H.S.; Zhang, C.C.; Zhu, H.; Wang, Z.Y.; Xie, Y.Y. Characteristics of turbulent transfer and its temporal evolution during an advection fog period in North China. Chin. J. Atmos. Sci. 2010, 34, 440–448. (In Chinese) [Google Scholar]
- Ye, X.; Wu, B.; Zhang, H. The turbulent structure and transport in fog layers observed over the Tianjin area. Atmos. Res. 2015, 153, 217–234. [Google Scholar] [CrossRef]
- Wu, B.; Li, Z.; Ju, T.; Zhang, H. Characteristics of Low-level jets during 2015–2016 and the effect on fog in Tianjin. Atmos. Res. 2020, 245, 105102. [Google Scholar] [CrossRef]
- Kim, C.K.; Yum, S.S. A study on the transition mechanism of a stratus cloud into a warm sea fog using a single column model PAFOG coupled with WRF. Asia-Pacific J. Atmos. Sci. 2013, 49, 245–257. [Google Scholar] [CrossRef]
- Hu, H.; Sun, J.; Zhang, Q. Assessing the Impact of Surface and Wind Profiler Data on Fog Forecasting Using WRF 3DVAR: An OSSE Study on a Dense Fog Event over North China. J. Appl. Meteorol. Clim. 2017, 56, 1059–1081. [Google Scholar] [CrossRef] [Green Version]
- Gilson, G.F.; Jiskoot, H.; Cassano, J.J.; Gultepe, I.; James, T.D. The Thermodynamic Structure of Arctic Coastal Fog Occurring During the Melt Season over East Greenland. Boundary-Layer Meteorol. 2018, 168, 443–467. [Google Scholar] [CrossRef]
- Ju, T.; Wu, B.; Zhang, H.; Liu, J. Characteristics of turbulence and dissipation mechanism in a polluted radiation–advection fog life cycle in Tianjin. Meteorol. Atmos. Phys. 2020, 133, 515–531. [Google Scholar] [CrossRef]
- Shi, C.; Roth, M.; Zhang, H.; Li, Z. Impacts of urbanization on long-term fog variation in Anhui Province, China. Atmos. Environ. 2008, 42, 8484–8492. [Google Scholar] [CrossRef]
- Tian, M.; Wu, B.G.; Huang, H.; Wang, Z.W.; Zhang, W.Y. The synoptic condition and boundary layer characteristics of coastal fog around the Bohai Sea. Climatic Environ. Res. 2020, 25, 199–210. (In Chinese) [Google Scholar]
- Li, Q.; Wub, B.; Liu, J.; Zhang, H.; Cai, X.; Song, Y. Characteristics of the atmospheric boundary layer and its relation with PM2:5 during haze episodes in winter in the North China Plain. Atmos. Environ. 2020, 223, 1–10. [Google Scholar] [CrossRef]
- Huang, H.; Liu, H.; Huang, J.; Mao, W.; Bi, X. Atmospheric Boundary Layer Structure and Turbulence during Sea Fog on the Southern China Coast. Mon. Weather. Rev. 2015, 143, 1907–1923. [Google Scholar] [CrossRef]
- Bergot, T.; Escobar, J.; Masson, V. Effect of small-scale surface heterogeneities and buildings on radiation fog: Large-eddy simulation study at Paris-Charles de Gaulle airport. Q. J. R. Meteorol. Soc. 2015, 141, 285–298. [Google Scholar] [CrossRef]
- Gultepe, I. Fog and Boundary Layer Clouds: Fog Visibility and Forecasting; Birkhäuser Verlag AG: Basel, Switzerland, 2008. [Google Scholar]
- Roquelaure, S.; Bergot, T. A Local Ensemble Prediction System for Fog and Low Clouds: Construction, Bayesian Model Averaging Calibration, and Validation. J. Appl. Meteorol. Clim. 2008, 47, 3072–3088. [Google Scholar] [CrossRef]
- Ryerson, W.R.; Hacker, J.P. The Potential for Mesoscale Visibility Predictions with a Multimodel Ensemble. Weather. Forecast. 2014, 29, 543–562. [Google Scholar] [CrossRef]
- Lin, J.C.-H.; Tai, J.-H.; Feng, C.-H.; Lin, D.-E. Towards Improving Visibility Forecasts in Taiwan: A Statistical Approach. Terr. Atmos. Ocean. Sci. 2010, 21, 359–374. [Google Scholar] [CrossRef] [Green Version]
- Leyton, S.M.; Fritsch, J.M. Short-Term Probabilistic Forecasts of Ceiling and Visibility Utilizing High-Density Surface Weather Observations. Weather. Forecast. 2003, 18, 891–902. [Google Scholar] [CrossRef]
- Ryerson, W.R.; Hacker, J.P. A Nonparametric Ensemble Postprocessing Approach for Short-Range Visibility Predictions in Data-Sparse Areas. Weather. Forecast. 2018, 33, 835–855. [Google Scholar] [CrossRef]
- Pasini, A.; Pelino, V.; Potestà, S. A neural network model for visibility nowcasting from surface observations: Results and sensitivity to physical input variables. J. Geophys. Res. Space Phys. 2001, 106, 14951–14959. [Google Scholar] [CrossRef]
- Roquelaure, S.; Tardif, R.; Remy, S.; Bergot, T. Skill of a Ceiling and Visibility Local Ensemble Prediction System (LEPS) according to Fog-Type Prediction at Paris-Charles de Gaulle Airport. Weather. Forecast. 2009, 24, 1511–1523. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Du, J. Fog Prediction from a Multimodel Mesoscale Ensemble Prediction System. Weather. Forecast. 2010, 25, 303–322. [Google Scholar] [CrossRef]
- Hansen, B. A Fuzzy Logic–Based Analog Forecasting System for Ceiling and Visibility. Weather. Forecast. 2007, 22, 1319–1330. [Google Scholar] [CrossRef]
- Zhou, B.; Ferrier, B.S. Asymptotic Analysis of Equilibrium in Radiation Fog. J. Appl. Meteorol. Clim. 2008, 47, 1704–1722. [Google Scholar] [CrossRef]
- Sohoni, V.V.; Paranjpe, M.M. Fog and relative humidity in India. Q. J. R. Meteorol. Soc. 1934, 60, 15–22. [Google Scholar] [CrossRef]
- Francis, K.E. Study of ice fog particles in alaska. Bull. Am. Meteorol. Soc. 1962, 43, 139. [Google Scholar]
- Li, X.N.; Huang, J.A.; Shen, S.H.; Liu, S.D.; Lu, W.H. Evolution of Liquid Water Content in a Sea Fog Controlled by a High-Pressure Pattern. J. Trop. Meteorol. 2010, 16, 409–416. [Google Scholar] [CrossRef]
- Liu, D.Y.; Pu, M.J.; Yang, J.; Zhang, G.Z.; Yan, W.L.; Li, Z.H. Microphysical Structure and Evolution of a Four-Day Persistent Fog Event in Nanjing in December 2006. Acta Meteorol. Sin. 2009, 24, 104–115. [Google Scholar]
- Liu, Q.; Wu, B.; Wang, Z.; Hao, T. Fog Droplet Size Distribution and the Interaction between Fog Droplets and Fine Particles during Dense Fog in Tianjin, China. Atmosphere 2020, 11, 258. [Google Scholar] [CrossRef] [Green Version]
- Steeneveld, G.J.; Ronda, R.J.; Holtslag, A.A.M. The Challenge of Forecasting the Onset and Development of Radiation Fog Using Mesoscale Atmospheric Models. Boundary-Layer Meteorol. 2015, 154, 265–289. [Google Scholar] [CrossRef]
- Singh, A.; George, J.P.; Iyengar, G.R. Prediction of fog/visibility over India using NWP Model. J. Earth Syst. Sci. 2018, 127, 26. [Google Scholar] [CrossRef] [Green Version]
- Philip, A.; Bergot, T.; Bouteloup, Y.; Bouyssel, F. The Impact of Vertical Resolution on Fog Forecasting in the Kilometric-Scale Model AROME: A Case Study and Statistics. Weather. Forecast. 2016, 31, 1655–1671. [Google Scholar] [CrossRef]
- Tian, M.; Wu, B.; Huang, H.; Zhang, H.; Zhang, W.; Wang, Z. Impact of water vapor transfer on a Circum-Bohai-Sea heavy fog: Observation and numerical simulation. Atmos. Res. 2019, 229, 1–22. [Google Scholar] [CrossRef]
- Price, J.D.; Lane, S.; Boutle, I.; Smith, D.K.E.; Bergot, T.; Lac, C.; Duconge, L.; McGregor, J.; Kerr-Munslow, A.; Pickering, M.; et al. LANFEX: A Field and Modeling Study to Improve Our Understanding and Forecasting of Radiation Fog. Bull. Am. Meteorol. Soc. 2018, 99, 2061–2077. [Google Scholar] [CrossRef]
- Gultepe, I.; Müller, M.D.; Boybeyi, Z. A New Visibility Parameterization for Warm-Fog Applications in Numerical Weather Prediction Models. J. Appl. Meteorol. Clim. 2006, 45, 1469–1480. [Google Scholar] [CrossRef]
- Porson, A.; Price, J.; Lock, A.; Clark, P. Radiation Fog. Part II: Large-Eddy Simulations in Very Stable Conditions. Boundary-Layer Meteorol. 2011, 139, 193–224. [Google Scholar] [CrossRef]
- Kim, C.K.; Stuefer, M.; Schmitt, C.G.; Heymsfield, A.; Thompson, G. Numerical Modeling of Ice Fog in Interior Alaska Using the Weather Research and Forecasting Model. Pure Appl. Geophys. 2014, 171, 1963–1982. [Google Scholar] [CrossRef]
- Koračin, D. Modeling and Forecasting Marine Fog. In Marine Fog: Challenges and Advancements in Observations, Modeling, and Forecasting; Koračin, D., Dorman, C.E., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 425–475. [Google Scholar]
- Koschmieder, H. Theorie der horizontalen Sichtweite. Beitr. Phys. Fr. Atmos. 1924, 12, 33–53. [Google Scholar]
- Malone, T. Compendium of Meteorology; American Meteorological Society: Boston, MA, USA, 1951. [Google Scholar]
- Houghton, H.G.; Radford, W.H. On the measurement of drop size and liquid water content in fogs and clouds. Phys. Oceanogr. Meteorol. 1938, 6, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Eldridge, R.G. The Relationship Between Visibility and Liquid Water Content in Fog. Atmos. Sci. 1971, 8, 1183–1186. [Google Scholar] [CrossRef] [Green Version]
- Horvath, H. On the applicability of the koschmieder visibility formula. Atmos. Environ. 1967 1971, 5, 177–184. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S. Visibility: How applicable is the century-old Koschmieder model? J. Atmos. Sci. 2016, 73, 4573–4581. [Google Scholar] [CrossRef]
- Mie, V.G. Consideraciones sobre la óptica de los medios turbios, especialmente soluciones coloidales. Por Gustav Mie Ann. Der Phys. 1908, 25, 377–445. [Google Scholar] [CrossRef]
- Koenig, L.R. Numerical experiments pertaining to warm-fog clearing. Mon. Weather. Rev. 1971, 99, 227–241. [Google Scholar] [CrossRef] [Green Version]
- Kunkel, B.A. Parameterization of Droplet Terminal Velocity and Extinction Coefficient in Fog Models. J. Clim. Appl. Meteorol. 1984, 23, 34–41. [Google Scholar] [CrossRef] [Green Version]
- ECWMF. IFS DOCUMENTATION–Cy47r3, Operational Implementation. PART IV: PHYSICAL PROCESSES; European Centre for Medium-Range Weather Forecasts: Shinfield Park, Reading, RG2 9AX, UK. 12 October 2021. Available online: https://www.ecmwf.int/sites/default/files/elibrary/2021/20198-ifs-documentation-cy47r3-part-vi-physical-processes.pdf (accessed on 8 December 2021).
- Clark, P.A.; Harcourt, S.A.; Macpherson, B.; Mathison, C.T.; Cusack, S.; Naylor, M. Prediction of visibility and aerosol within the operational Met Office Unified Model. I: Model formulation and variational assimilation. Q. J. R. Meteorol. Soc. 2008, 134, 1801–1816. [Google Scholar] [CrossRef] [Green Version]
- Gao, S.; Lin, H.; Shen, B.; Fu, G. A heavy sea fog event over the Yellow Sea in March 2005: Analysis and numerical modeling. Adv. Atmos. Sci. 2007, 24, 65–81. [Google Scholar] [CrossRef]
- Fu, G.; Guo, J.; Pendergrass, A.; Li, P. An analysis and modeling study of a sea fog event over the Yellow and Bohai Seas. J. Ocean Univ. China 2008, 7, 27–34. [Google Scholar] [CrossRef]
- Fu, G.; Guo, J.; Xie, S.-P.; Duan, Y.; Zhang, M. Analysis and high-resolution modeling of a dense sea fog event over the Yellow Sea. Atmos. Res. 2006, 81, 293–303. [Google Scholar] [CrossRef]
- Vali, G.; Politovich, M.K.; Baumgardner, D.G. Conduct of Cloud Spectra Measurements; Air Force Geophysics Laboratory, Wright-Patterson AFB: Fairborn, OH, USA, 1979; pp. 1–61. [Google Scholar]
- Stoelinga, M.T.; Warner, T.T. Nonhydrostatic, Mesobeta-Scale Model Simulations of Cloud Ceiling and Visibility for an East Coast Winter Precipitation Event. J. Atmos. Sci. 1999, 38, 385–404. [Google Scholar] [CrossRef]
- Elias, T.; Haeffelin, M.; Drobinski, P.; Gomes, L.; Rangognio, J.; Bergot, T.; Chazette, P.; Raut, J.-C.; Colomb, M. Particulate contribution to extinction of visible radiation: Pollution, haze, and fog. Atmos. Res. 2009, 92, 443–454. [Google Scholar] [CrossRef]
- van Oldenborgh, G.J.; Yiou, P.; Vautard, R. On the roles of circulation and aerosols in the decline of mist and dense fog in Europe over the last 30 years. Atmos. Chem. Phys. Discuss. 2010, 10, 4597–4609. [Google Scholar] [CrossRef] [Green Version]
- Hänel, G. The Properties of Atmospheric Aerosol Particles as Functions of the Relative Humidity at Thermodynamic Equilibrium with the Surrounding Moist Air. Adv. Geophys. 1976, 19, 73–188. [Google Scholar] [CrossRef]
- Smirnova, T.G.; Benjamin, S.G.; Brown, J.M. Case study verification of RUC/ MAPS fog and visibility forecasts. In Preprints, 9th Conference on Aviation, Range, and Aerospace Meteorology; AMS: Orlando, FL, USA, 2000; pp. 31–36. [Google Scholar]
- Gultepe, I.; Isaac, G.A. Visibility Versus Precipitation Rate and Relative Humidity. In Proceedings of the Wisconsin: Meteor. Soc., 2006; P2.55. 12th Cloud Physics Conf. Madison, Amer. 12 July 2006. Available online: http://ams.confex.com/ams/Madison2006/techprogram/paper_113177.htm (accessed on 8 December 2021).
- Cao, X.C.; Shao, L.M.; Li, X.D. Research on parameterization scheme of visibility in Fog Model. In Proceedings of the 31st Annual Meeting of the Chinese Meteorological Society, Beijing, China, 3 November 2014; 2014; pp. 1–5. [Google Scholar]
- Gültepe, I.; Milbrandt, J.A. Probabilistic Parameterizations of Visibility Using Observations of Rain Precipitation Rate, Relative Humidity, and Visibility. J. Appl. Meteorol. 2009, 49, 36–46. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, M.S.; Lin, L.G. Numerical simulation of a winter fog in Sichuan and parameterization of visibility. J. Nanjing Univ. Inf. Sci. Technol. Nat. Sci. Ed. 2013, 5, 222–228. [Google Scholar]
- Roquelaure, S.; Bergot, T. Contributions from a Local Ensemble Prediction System (LEPS) for Improving Fog and Low Cloud Forecasts at Airports. Weather. Forecast. 2009, 24, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Yang, J.; Bao, Y.S.; Wang, Z.J.; Dai, Y.X. The numerical simulation of visibility during the fog in Shanxi province in winter. J. Nanjing Univ. Inf. Sci. Technol. Nat. Sci. Ed. 2010, 2, 436–444. [Google Scholar]
- Bari, D. A Preliminary Impact Study of Wind on Assimilation and Forecast Systems into the One-Dimensional Fog Forecasting Model COBEL-ISBA over Morocco. Atmosphere 2019, 10, 615. [Google Scholar] [CrossRef] [Green Version]
- Martinet, P.; Cimini, D.; Burnet, F.; Ménétrier, B.; Michel, Y.; Unger, V. Improvement of numerical weather prediction model analysis during fog conditions through the assimilation of ground-based microwave radiometer observations: A 1D-Var study. Atmos. Meas. Tech. 2020, 13, 6593–6611. [Google Scholar] [CrossRef]
- Eldridge, R.G. Haze and Fog Aerosol Distributions. J. Atmos. Sci. 1966, 23, 605–613. [Google Scholar] [CrossRef] [Green Version]
- Tomasi, C.; Tampieri, F. Features of the proportionality coefficient in the relationship between visibility and liquid water content in haze and fog. Atmosphere 1976, 14, 61–76. [Google Scholar] [CrossRef] [Green Version]
- Pinnick, R.G.; Hoihjelle, D.L.; Fernandez, G.; Stenmark, E.B.; Lindberg, J.D.; Hoidale, G.B.; Jennings, S.G. Vertical Structure in Atmospheric Fog and Haze and Its Effects on Visible and Infrared Extinction. J. Atmos. Sci. 1978, 35, 2020–2032. [Google Scholar] [CrossRef] [Green Version]
- Musson-Genon, L. Numerical Simulation of a Fog Event with a One-Dimensional Boundary Layer Model. Mon. Weather. Rev. 1987, 115, 592–607. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, S.-P.; Wang, Q.; Meng, Z.-X.; Koračin, D.; Gao, S.-H. A Fog Event off the Coast of the Hangzhou Bay during Meiyu Period in June 2013. Aerosol Air Qual. Res. 2018, 18, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Dey, S. Influence of aerosol composition on visibility in megacity Delhi. Atmos. Environ. 2012, 62, 367–373. [Google Scholar] [CrossRef]
- Shen, X.J.; Sun, J.Y.; Zhang, X.Y.; Zhang, Y.M.; Zhang, L.; Che, H.C.; Ma, Q.L.; Yu, X.M.; Yue, Y.; Zhang, Y.W. Characterization of submicron aerosols and effect on visibility during a severe haze-fog episode in Yangtze River Delta, China. Atmos. Environ. 2015, 120, 307–316. [Google Scholar] [CrossRef] [Green Version]
- Gonser, S.G.; Klemm, O.; Griessbaum, F.; Chang, S.-C.; Chu, H.-S.; Hsia, Y.-J. The Relation Between Humidity and Liquid Water Content in Fog: An Experimental Approach. Pure Appl. Geophys. 2011, 169, 821–833. [Google Scholar] [CrossRef]
- Meyer, M.B.; Jiusto, J.E.; Lala, G.G. Measurements of Visual Range and Radiation-Fog (Haze) Microphysics. J. Atmos. Sci. 1980, 37, 622–629. [Google Scholar] [CrossRef] [Green Version]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part I: Analysis of the Role of the Spectral Shape Parameter. J. Atmos. Sci. 2005, 62, 3051–3064. [Google Scholar] [CrossRef] [Green Version]
- Hu, B.; Du, H.L.; Hao, S.F.; Yu, L.M.; Teng, L.N. A forecast method of coastal sea fog based on the combination of statistic technique and dynamical interpretation. Marin. Forec. 2014, 31, 82–86. (In Chinese) [Google Scholar]
- Huang, H.J.; Huang, J.; Mao, W.K.; Liao, F.; Li, X.N.; Lü, W.H.; Yang, Y.Q. Characteristics of liquid water content of sea fog in Maoming area and its relationship with atmospheric horizontal visibility. Acta Oceanol. Sin. 2010, 32, 40–52. (In Chinese) [Google Scholar]
- Song, J.I.; Yum, S.S.; Gultepe, I.; Chang, K.-H.; Kim, B.-G. Development of a new visibility parameterization based on the measurement of fog microphysics at a mountain site in Korea. Atmos. Res. 2019, 229, 115–126. [Google Scholar] [CrossRef]
- Bao, Y.X.; Ding, Q.J.; Yuan, C.S.; Yan, M.L. Numerical simulations of a highly complex fog event on Shanghai-Nanjing Expressway. Chin. J. Atmos. Sci. 2013, 37, 124–136. (In Chinese) [Google Scholar]
- Long, Q.; Wang, F.; Mi, X.Y.; Wang, C.; Liu, Y. Research on the Formation Mechanism and Forecast Technology of Sea Fog on the North Coast of Bohai Bay. In Proceedings of the 2020 National Marine Ecological Environmental Protection and Monitoring Technology Symposium, Shenzhen, China, 18 December 2020; pp. 238–246. [Google Scholar]
- Haeffelin, M.; Bergot, T.; Elias, T.; Tardif, R.; Carrer, D.; Chazette, P.; Colomb, M.; Drobinski, P.; Dupont, E.; Dupont, J.-C.; et al. Parisfog Shedding New Light on Fog Physical Processes. Bull. Am. Meteorol. Soc. 2010, 91, 767–783. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.H.; Peng, Z.G. Physical and chemical characteristic of the Chongqing winter fog. Acta. Meteorol. Sin. 1994, 16, 46–54. (In Chinese) [Google Scholar]
- Sun, J.; Huang, H.; Zhang, S.; Mao, W. How Sea Fog Influences Inland Visibility on the Southern China Coast. Atmosphere 2018, 9, 344. [Google Scholar] [CrossRef] [Green Version]
- Marzban, C.; Leyton, S.; Colman, B. Ceiling and Visibility Forecasts via Neural Networks. Weather. Forecast. 2007, 22, 466–479. [Google Scholar] [CrossRef] [Green Version]
- Gilleland, E.; Fowler, T.L. Network design for verification of ceiling and visibility forecasts. Environmetrics 2006, 17, 575–589. [Google Scholar] [CrossRef]
- Fabbian, D.; de Dear, R.; Lellyett, S. Application of artificial neural network forecasts to predict fog at Canberra International Airport. Weather. Forecast. 2007, 22, 372–381. [Google Scholar] [CrossRef]
- Bari, D.; Ouagabi, A. Machine-learning regression applied to diagnose horizontal visibility from mesoscale NWP model forecasts. SN Appl. Sci. 2020, 2, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Bingui, W.; Jianchun, Z.; Yinghua, L.; Yanan, W.; Mei, X.; Jing, C.; Xuelian, W.; un, G.X.; Xiaobin, Q. Research on Numerical Interpretative Forecast for Low-Visibility at Tianjin Port in Autumn and Wint. Meteorol. Mon. 2017, 43, 8630871. [Google Scholar]
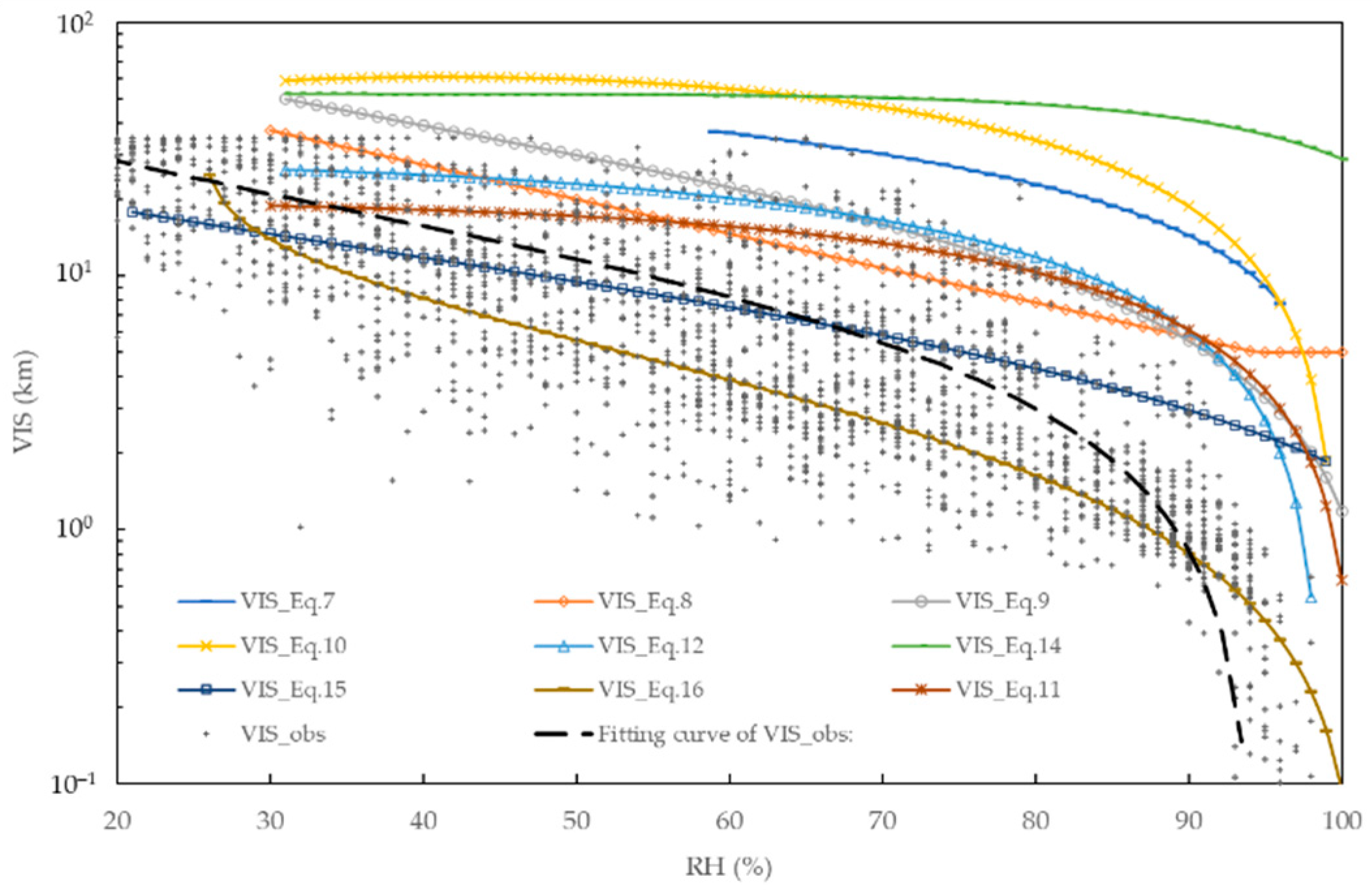
| Equation No | Relationship | Conditions | Reference |
|---|---|---|---|
| (7) | RH in decimal form For 58% < RH < 97% | Hanel [80] | |
| (8) | For 30% ≤ RH ≤ 100% Set to 5 km at RH ≥ 95% | Smirnova et al. [81] | |
| (9) | For RH > 30% | Gultepe et al. [82] | |
| (10) | For RH > 30% | Gultepe et al. [82] | |
| (11) | For 30% ≤ RH ≤ 100% | Cao et al. [83] | |
| (12) | For RH > 30% | Gultepe et al. [84] | |
| (13) | For RH > 30% | Gultepe et al. [84] | |
| (14) | For RH > 30% | Gultepe et al. [84] | |
| (15) | For 20% < RH < 100% | Lin et al. [85] | |
| (16) | For 25% < RH < 100% | Lin et al. [85] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, Q.; Wu, B.; Mi, X.; Liu, S.; Fei, X.; Ju, T. Review on Parameterization Schemes of Visibility in Fog and Brief Discussion of Applications Performance. Atmosphere 2021, 12, 1666. https://doi.org/10.3390/atmos12121666
Long Q, Wu B, Mi X, Liu S, Fei X, Ju T. Review on Parameterization Schemes of Visibility in Fog and Brief Discussion of Applications Performance. Atmosphere. 2021; 12(12):1666. https://doi.org/10.3390/atmos12121666
Chicago/Turabian StyleLong, Qiang, Bingui Wu, Xinyue Mi, Shuang Liu, Xiaochen Fei, and Tingting Ju. 2021. "Review on Parameterization Schemes of Visibility in Fog and Brief Discussion of Applications Performance" Atmosphere 12, no. 12: 1666. https://doi.org/10.3390/atmos12121666
APA StyleLong, Q., Wu, B., Mi, X., Liu, S., Fei, X., & Ju, T. (2021). Review on Parameterization Schemes of Visibility in Fog and Brief Discussion of Applications Performance. Atmosphere, 12(12), 1666. https://doi.org/10.3390/atmos12121666






