What Determines the Parameters of a Propagating Streamer: A Comparison of Outputs of the Streamer Parameter Model and of Hydrodynamic Simulations
Abstract
:1. Introduction
2. Streamer Parameter Model (SPM)
- SPM1: Electrostatic relationship between , , : the field at the streamer tip is enhanced because of available voltage due to difference in and : .
- SPM2: Current continuity at the streamer tip: the conductivity current inside the streamer becomes displacement current outside.
- SPM3: Ionization and relaxation balance: the ionization time scale in the region of the highest electric field at the streamer tip is approximately equal to the Maxwellian charge relaxation time inside the streamer.
- SPM4: Photo-ionization and impact ionization balance, which provides the relation between V and a.
3. Results
- No photoionization; presence of relatively high background free electron number density of m.
- No photoionization; presence of relatively low m.
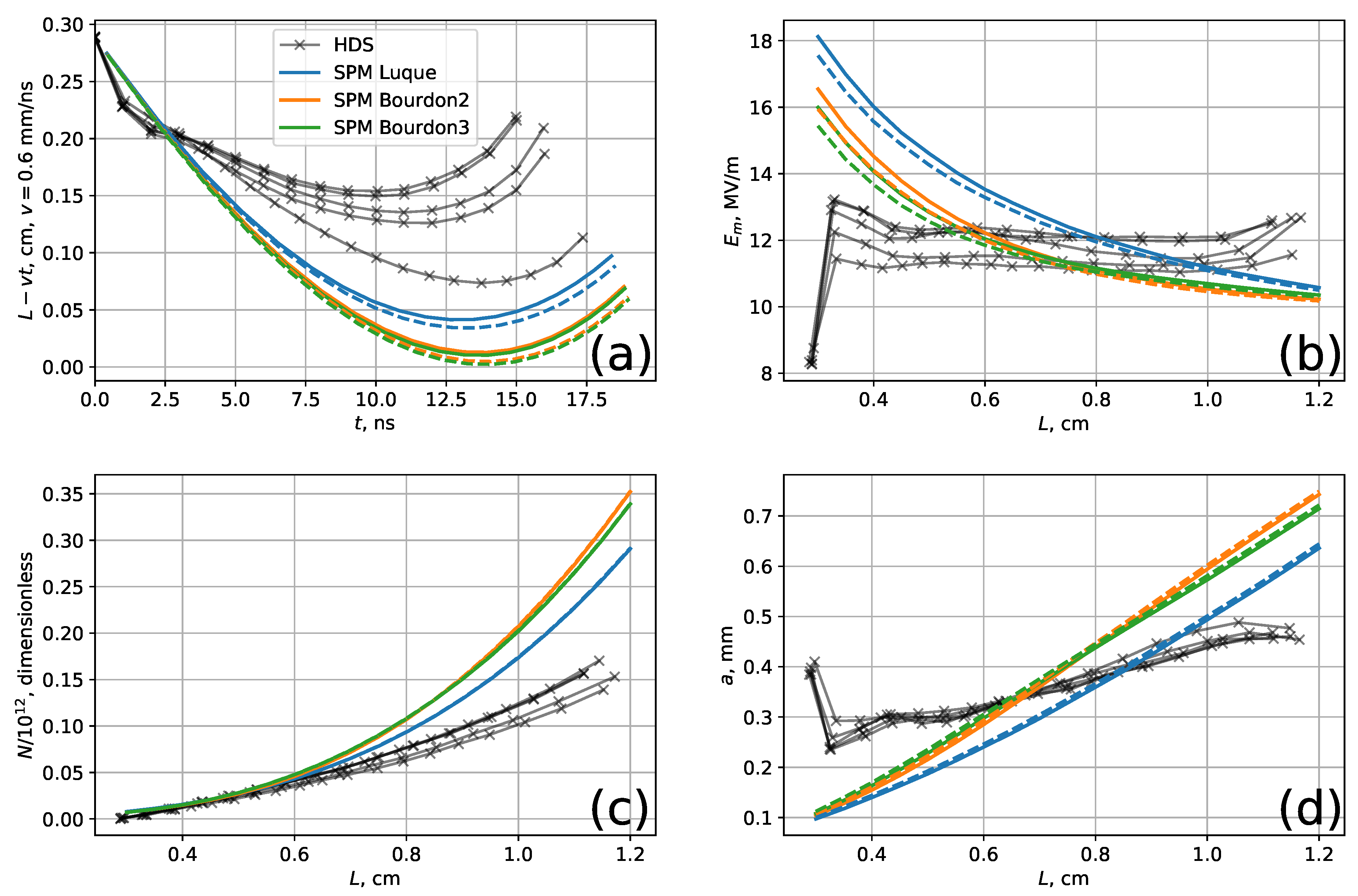
- With photoionization and m. Photoionization is treated with three different approximations to the original description by Zheleznyak et al. [20]. These approximations are described in detail in (Bagheri et al. [12] Appendix A). In this article, we label them as “Luque”, “Bourdon2”, and ”Bourdon3”, similarly to [12].
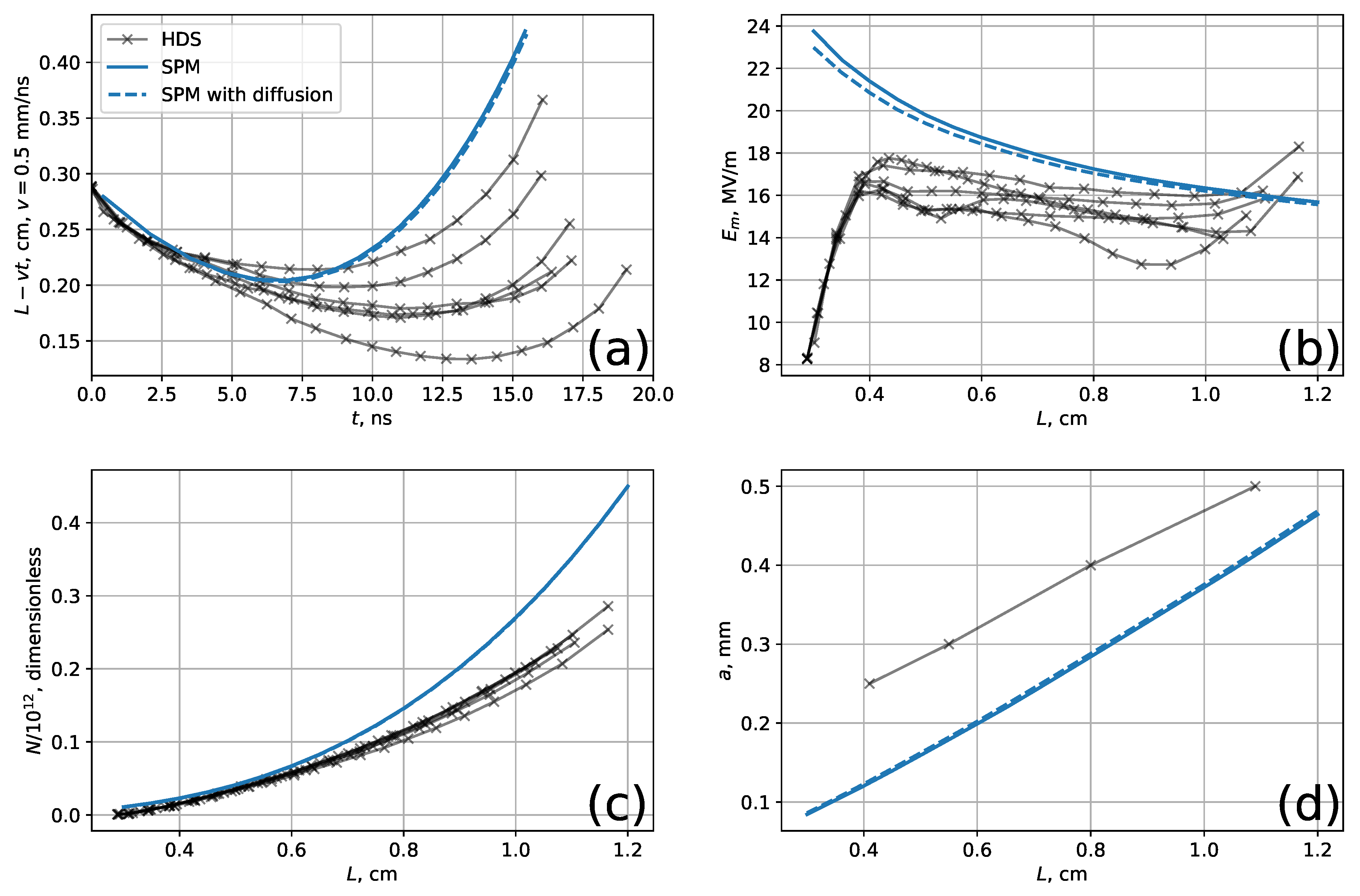
3.1. Case 1
- Velocity V in Figure 1a grows with streamer length (and with time).
- Maximum electric field decreases with streamer length L, at least for the middle values of L (the discrepancies at low and high L are discussed below).
- Number of electrons N grows with L; the rate of growth also increases with L.
- Radius a grows with length L.
- The HDS did not start at zero L, namely, it started with a small ionized region in the vicinity of the anode. This caused the field to gradually rise until the streamer was formed (see the low L values in Figure 1b). SPM, on the other hand, provided results only with the streamer already formed.
- At large L, the discrepancy is due to the proximity of the opposite electrode (cathode). The negative image charge of the streamer head, induced in the conducting cathode, enhanced the field in HDS (Figure 1b). The cathode, as we already mentioned, was not taken into account in the SPM.
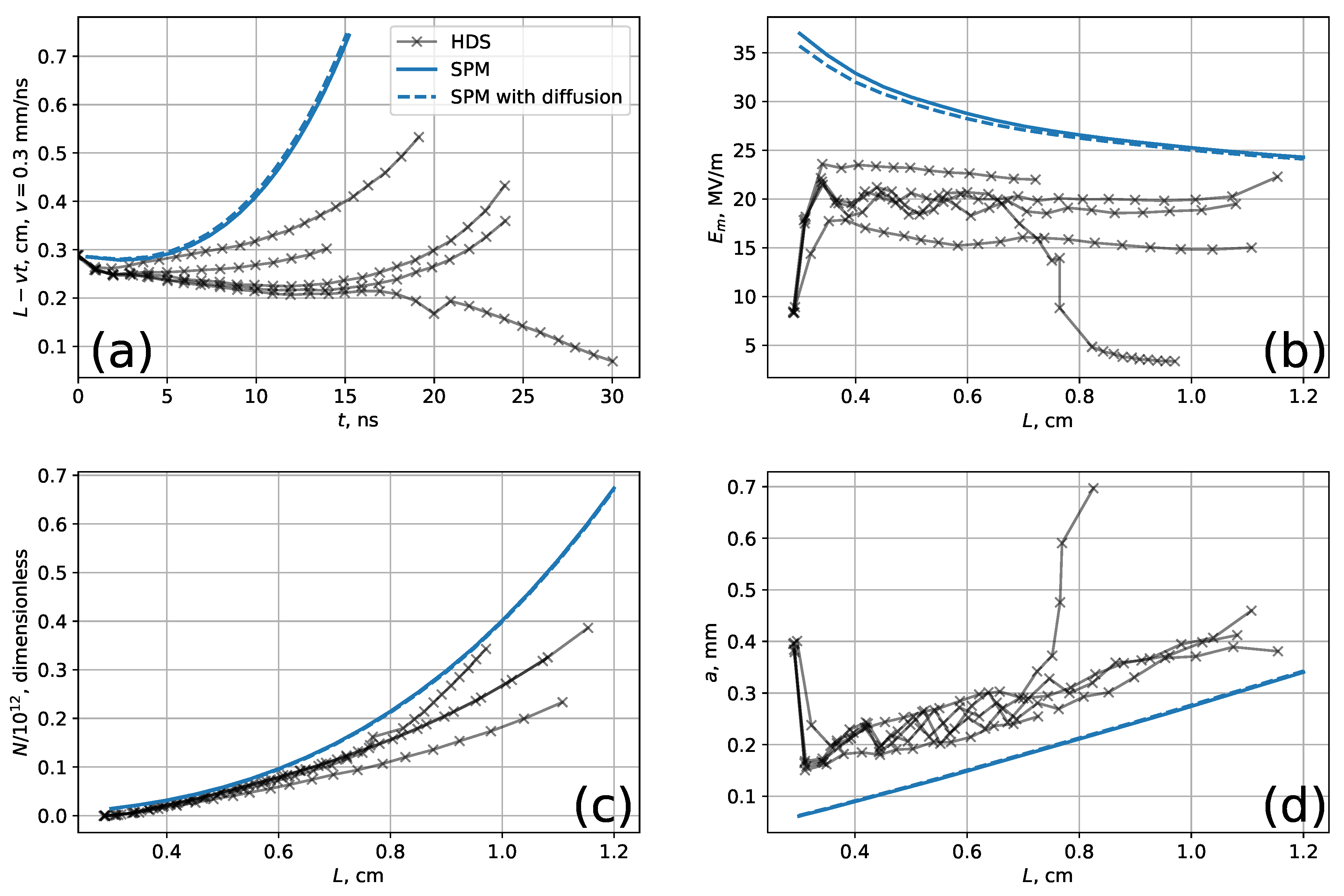
3.2. Case 2
3.3. Case 3
4. Discussion
4.1. Possible Errors Due to Approximations in SPM
- The radius, a, enters the system of SPM1–SPM4 in relations that describe processes at the tip of the streamer. Therefore, the value of a is more relevant to the tip curvature radius, than to the possibly different radius of the channel.
- We assumed that along the axis of the channel. At low external fields , especially those close to the positive streamer threshold MV/m [2] (p. 362), the number of electrons in the channel declines due to attachment. However, for the field MV/m, used in this work, attachment in the channel can be neglected, especially when using the attachment coefficient expression from Bagheri et al. [12] which gives lower values than we would get if the 3-body attachment process were included.
- Assumption of along the channel follows from taken together with the assumption of constant current, .
4.2. Shortest Spatial Scale in a Streamer and in HDS
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SPM | Streamer Parameter Model |
| HDS | Hydrodynamic simulation(s) |
| UV | Ultraviolet |
Appendix A
References
- Bazelyan, E.M.; Raizer, Y.P. Spark Discharge; CRC Press: New York, NY, USA, 1998. [Google Scholar]
- Raizer, Y.P. Gas Discharge Physics; Springer: Berlin, Germany, 1991. [Google Scholar]
- Van Deursen, A.; Kochkin, P.; de Boer, A.; Bardet, M.; Allasia, C.; Boissin, J.F.; Flourens, F. Lightning current distribution and hard radiation in aircraft, measured in-flight. In Proceedings of the 2017 International Symposium on Electromagnetic Compatibility—EMC EUROPE, Angers, France, 4–8 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Skeie, C.A.; Østgaard, N.; Lehtinen, N.G.; Sarria, D.; Kochkin, P.; de Boer, A.I.; Bardet, M.; Allasia, C.; Flourens, F. Constraints on Recoil Leader Properties Estimated from X-ray Emissions in Aircraft-Triggered Discharges. J. Geophys. Res. Atmos. 2020, 125, e2019JD032151. [Google Scholar] [CrossRef]
- Phelps, C.T.; Griffiths, R.F. Dependence of positive corona streamer propagation on air pressure and water vapor content. J. Appl. Phys. 1976, 47, 2929–2934. [Google Scholar] [CrossRef]
- Raether, H. Die Entwicklung der Elektronenlawine in den Funkenkanal. Z. Phys. 1939, 112, 464–489. [Google Scholar] [CrossRef]
- Meek, J.M. A Theory of Spark Discharge. Phys. Rev. 1940, 57, 722–728. [Google Scholar] [CrossRef]
- Loeb, L.B.; Meek, J.M. The Mechanism of the Electric Spark; Stanford University Press: Stanford, CA, USA, 1941. [Google Scholar]
- Ebert, U.; Sentman, D.D. Streamers, sprites, leaders, lightning: From micro- to macroscales. J. Phys. D Appl. Phys. 2008, 41, 230301. [Google Scholar] [CrossRef]
- Naidis, G.V. Positive and negative streamers in air: Velocity-diameter relation. Phys. Rev. E 2009, 79, 057401. [Google Scholar] [CrossRef]
- Lehtinen, N.G. Physics and mathematics of electric streamers. Radiophys. Quantum Electron. 2021, 64, 11–25. [Google Scholar] [CrossRef]
- Bagheri, B.; Teunissen, J.; Ebert, U.; Becker, M.M.; Chen, S.; Ducasse, O.; Eichwald, O.; Loffhagen, D.; Luque, A.; Mihailova, D.; et al. Comparison of six simulation codes for positive streamers in air. Plasma Sources Sci. Technol. 2018, 27, 095002. [Google Scholar] [CrossRef] [Green Version]
- Aleksandrov, N.L.; Bazelyan, E.M. Temperature and density effects on the properties of a long positive streamer in air. J. Phys. D Appl. Phys. 1996, 29, 2873–2880. [Google Scholar] [CrossRef]
- Guo, J.M.; Wu, C.H. Streamer radius model and its assessment using two-dimensional models. IEEE Trans. Plasma Sci. 1996, 24, 1348–1358. [Google Scholar] [CrossRef]
- Pavan, C.; Martinez-Sanchez, M.; Guerra-Garcia, C. Investigations of positive streamers as quasi-steady structures using reduced order models. Plasma Sources Sci. Technol. 2020, 29, 095004. [Google Scholar] [CrossRef]
- Lehtinen, N.G. Electric streamers as a nonlinear instability: The model details. arXiv 2020, arXiv:2003.09450. [Google Scholar]
- Derks, G.; Ebert, U.; Meulenbroek, B. Laplacian Instability of Planar Streamer Ionization Fronts—An Example of Pulled Front Analysis. J. Nonlinear Sci. 2008, 18, 551–590. [Google Scholar] [CrossRef] [Green Version]
- Loeb, L.B. Ionizing Waves of Potential Gradient. Science 1965, 148, 1417–1426. [Google Scholar] [CrossRef] [PubMed]
- Allen, N.L.; Mikropoulos, P.N. Dynamics of streamer propagation in air. J. Phys. D Appl. Phys. 1999, 32, 913–919. [Google Scholar] [CrossRef]
- Zheleznyak, M.B.; Mnatsakanyan, A.K.; Sizykh, S.V. Photo-ionization of nitrogen and oxygen mixtures by radiation from a gas-discharge. High Temp. (USSR) 1982, 20, 357–362. [Google Scholar]
- Francisco, H.; Bagheri, B.; Ebert, U. Electrically isolated streamer heads formed by strong electron attachment. Plasma Sources Sci. Technol. 2021, 30, 025006. [Google Scholar] [CrossRef]
- Pancheshnyi, S.V.; Starikovskii, A.Y. Stagnation dynamics of a cathode-directed streamer discharge in air. Plasma Sources Sci. Technol. 2004, 13, B1–B5. [Google Scholar] [CrossRef]
- Villa, A.; Barbieri, L.; Gondola, M.; Leon-Garzon, A.R.; Malgesini, R. Mesh dependent stability of discretization of the streamer equations for very high electric fields. Comput. Fluids 2014, 105, 1–7. [Google Scholar] [CrossRef]
- Teunissen, J.; Ebert, U. Simulating streamer discharges in 3D with the parallel adaptive Afivo framework. J. Phys. D Appl. Phys. 2017, 50, 474001. [Google Scholar] [CrossRef]
- Marskar, R. An adaptive Cartesian embedded boundary approach for fluid simulations of two- and three-dimensional low temperature plasma filaments in complex geometries. J. Comput. Phys. 2019, 388, 624–654. [Google Scholar] [CrossRef] [Green Version]
- Marskar, R. 3D fluid modeling of positive streamer discharges in air with stochastic photoionization. Plasma Sources Sci. Technol. 2020, 29, 055007. [Google Scholar] [CrossRef] [Green Version]
- Lehtinen, N.G.; Østgaard, N. X-ray emissions in a multi-scale fluid model of a streamer discharge. J. Geophys. Res. Atmos. 2018, 123, 6935–6953. [Google Scholar] [CrossRef]
- Naidis, G.V. Effects of nonlocality on the dynamics of streamers in positive corona discharges. Tech. Phys. Lett. 1997, 23, 493–494. [Google Scholar] [CrossRef]
- Pancheshnyi, S.V.; Starikovskaia, S.M.; Starikovskii, A.Y. Role of photoionization processes in propagation of cathode-directed streamer. J. Phys. D Appl. Phys. 2001, 34, 105–115. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehtinen, N.G.; Marskar, R. What Determines the Parameters of a Propagating Streamer: A Comparison of Outputs of the Streamer Parameter Model and of Hydrodynamic Simulations. Atmosphere 2021, 12, 1664. https://doi.org/10.3390/atmos12121664
Lehtinen NG, Marskar R. What Determines the Parameters of a Propagating Streamer: A Comparison of Outputs of the Streamer Parameter Model and of Hydrodynamic Simulations. Atmosphere. 2021; 12(12):1664. https://doi.org/10.3390/atmos12121664
Chicago/Turabian StyleLehtinen, Nikolai G., and Robert Marskar. 2021. "What Determines the Parameters of a Propagating Streamer: A Comparison of Outputs of the Streamer Parameter Model and of Hydrodynamic Simulations" Atmosphere 12, no. 12: 1664. https://doi.org/10.3390/atmos12121664
APA StyleLehtinen, N. G., & Marskar, R. (2021). What Determines the Parameters of a Propagating Streamer: A Comparison of Outputs of the Streamer Parameter Model and of Hydrodynamic Simulations. Atmosphere, 12(12), 1664. https://doi.org/10.3390/atmos12121664





