Abstract
Turbulent cascade transferring the free energy contained within the large scale fluctuations of the magnetic field, velocity and density into the smaller ones is probably one of the most important mechanisms responsible for heating of the solar corona and solar wind, thus the turbulent behavior of these quantities is intensively studied. The temperature is also highly fluctuating quantity but its variations are studied only rarely. There are probably two reasons, first the temperature is tensor and, second, an experimental determination of temperature variations requires knowledge of the full velocity distribution with an appropriate time resolution but such measurements are scarce. To overcome this problem, the Bright Monitor of the Solar Wind (BMSW) on board Spektr-R used the Maxwellian approximation and provided the thermal velocity with a 32 ms resolution, investigating factors influencing the temperature power spectral density shape. We discuss the question whether the temperature spectra determined from Faraday cups are real or apparent and analyze mutual relations of power spectral densities of parameters like the density, parallel and perpendicular components of the velocity and magnetic field fluctuations. Finally, we compare their spectral slopes with the slopes of the thermal velocity in both inertial and kinetic ranges and their evolution in course of solar wind expansion.
1. Introduction
As a super-Alfvénic solar wind expands into space, a particle motion in the magnetic field and their collisions as well as plasma instabilities change the shape of a velocity distribution. If the particle motion is adiabatic and collisionless, the plasma ions become anisotropic, i.e., [1] where () is the ion temperature parallel (perpendicular) to the background magnetic field. However, Coulomb collisions and pressure-anisotropy instabilities contribute to pitch-angle scattering that pushes plasma back towards isotropy [2]. According to the large statistics of Bale et al. [3], the most probable value of the ion temperature anisotropy measured by Wind is at 1 AU. The collisional age is largest around this value and it suggests that isotropy results predominantly from Coulomb collisions. The authors [3] also present histograms of the magnetic fluctuation amplitude squared in bins of collisional age because it organizes solar wind instabilities better than traditional distinction on fast and slow winds [4]. The overall magnetic fluctuation power is a function of the collisional age, with the magnetic power weaker by a factor of for more collisional plasma. This effect is a proxy for the temperature anisotropy; collisional plasma is more isotropic and farther from the instability thresholds.
Šafránková et al. [5,6] analyzed solar wind power spectra of bulk and thermal speed fluctuations computed with a time resolution of 32 ms in the frequency range of 0.001–2 Hz using the BMSW instrument (equipped with Faraday cups) on board the Spektr-R spacecraft. They reported that spectra of proton thermal speed and proton bulk speed variations exhibit similar values and follow the same trends in the inertial range whereas the bulk speed spectra are in a systematic manner steeper in the kinetic range of frequencies. Since the authors compared the results of both bulk and thermal velocity fluctuations with a similar analysis of density fluctuations [7] that are compressive, they applied the bulk velocity magnitude as a comparable quantity.
Based on theoretical considerations, Gogoberidze et al. [8] studied Alfvénic turbulent fluctuations and their spectral properties from MHD to kinetic scales and discussed the results of Šafránková et al. [6] in view of these considerations. The authors [8] argue that the authentic thermal velocity spectra should be similar to the density spectra. However, the temperature in the solar wind is usually anisotropic and the temperature determined in a particular direction is somewhere between and . Consequently, the fluctuations derived from these measurements are pseudo-temperature fluctuations and not the true temperature fluctuations. They assume that these pseudo-temperature fluctuations are driven by the high-amplitude magnetic fluctuations in Alfvén waves rather than the fluctuations of temperature or thermal velocity itself. Therefore, the frequency spectrum of the thermal speed reported by Šafránková et al. [6] would be mainly produced by an incompressible part of magnetic field perturbations which explains its similarity with the proton velocity spectrum.
As noted, an anisotropic magnetized plasma has different thermal speeds parallel and perpendicular to the local magnetic field and because an Faraday cup (FC) usually measures the reduced velocity distribution function (VDF) due to a very uniform angular response, the FC instrument reports an effective thermal speed that is a function of the orientation between the FC looking window direction and ambient magnetic field [9,10]. Kasper et al. [10] analyzed measurements of FC onboard Wind and presented the first uncertainty estimations for both and with a technique that is independent of the method used to extract an estimate of the anisotropy from the raw data. They found that maximum uncertainty occurs predominantly when the magnetic field is out of the ecliptic plane or perpendicular to the Sun–Earth line and is poorly constrained when the magnetic field is radial.
Stansby et al. [11] performed a novel fitting of bi-Maxwellian VDF to the raw Helios data and extracted the proton core number density, velocity, and and . Since their and are not a function the magnetic field direction, we can believe that their parameters are good estimates of real and of the proton core. Furthermore, also Durovcova et al. [12] reprocessed the VDFs measured by Helios and discussed evolutions of relative drifts between three dominant components—the proton core, proton beam, and -particle core at different distances from the Sun. The processing is based on assumptions that partial VDFs of all these components can be approximated by a bi-Maxwellian distribution. The authors compared their newly processed dataset with a previous study of the proton core population from Helios [11] and found a good agreement between them.
D’Amicis et al. [13] focused on a relation observed between angular displacements of the local magnetic field orientation from the radial direction and values of the proton temperature. They reported observations by Helios and Wind with a positive correlation between proton temperature and magnetic field orientation, also within Alfvénic wind characterized by large-amplitude fluctuations of the background field direction. In Wind, they found a dependence of on the magnetic field angular displacement and interpreted this signature as due to a physical mechanism related to the proton cyclotron resonance. Finally, they simulated the sampling procedure of the VDF measured by an electrostatic analyzer (EA) and showed that the observed temperature anisotropy is not due to instrumental effects.
De Marco et al. [14] performed a numerical test to understand the origin of the enhanced spectral flattening of proton density and proton temperature spectra observed by Helios in fast and Alfvénic solar winds. This spectral feature has been interpreted as a signature of sound-like perturbations generated locally by the parametric decay of large-amplitude Alfvénic fluctuations [15]. However, it has recently been shown [16,17,18] that large-amplitude Alfvénic fluctuations are able to move around the particle VDF in phase space, and this phenomenon can be important for an EA with sampling time comparable to the period of the fluctuations. They have shown that the motion of the VDF has an unpredictable influence on the moment computations as a result of the Alfvénic fluctuations.
Roberts et al. [19] discussed anisotropy of the spectral indexes in ion-scale compressible turbulence using MMS observations in the magnetosheath. They investigated the typical 1D Fourier spectra for the magnetic field, ion velocity density and ion and . They also reduced the 3D spectra to spectra along one direction to investigate how the spectral index in the dissipation/dispersion range varies with the angle from the magnetic field.
Huang et al. [20] presented a technique for deriving the temperature anisotropy of solar wind protons observed by the Parker Solar Probe (PSP) mission in the near-Sun solar wind. The radial proton temperature from combined instruments is compared with the orientation of local magnetic field, and proton and are extracted. Their results suggest that they see stronger anisotropic heating as PSP moves closer to the Sun, but they note that a careful treatment of the shape of a VDF is needed to correctly describe the temperature.
This short and incomplete survey reveals possible instrumental effects on the solar wind proton temperature determination and on clear interpretation of measured data. For this reason, we briefly discuss the problem of temperature(s) in solar wind plasma and methods of their determination from the experimental data with an emphasis on the measuring technique used in Šafránková et al. [6]. Questions to be answered in this part are: (i) what the temperature actually is, (ii) variations of temperature(s) in multi-component plasma, and (iii) could we determine the temperature spectrum from the FC experimental data? Then, the core part of the paper deals with a comparison of the spectral slopes of fluctuations of plasma parameters and magnetic field in the inertial and kinetic ranges and with their dependence on different characteristic plasma quantities.
The manuscript is organized as follows. In Section 2, the methods of determination of the temperature using Faraday cups or electrostatic analyzers and peculiarities of such estimations are discussed. Section 3 describes a fast determination of the temperature in the BMSW (Bright Monitor of the Solar Wind) instrument. The spectral indices of fluctuations of the proton density, N, both perpendicular and parallel components of the proton velocity , and magnetic field, , and trace thermal velocity, at frequencies covering the transition from the inertial to kinetic range are introduced in Section 4. In a large statistical study, we address spectral slopes in relation to the properties of the solar wind represented by proton , collisional age, temperature anisotropy, and a standard deviation of fluctuations of the magnetic field perpendicular component. The results of their mutual comparison are discussed in Section 5.
2. Temperature Determination
The problem of a temperature determination from the experimental data is not new, this topic has been discussed from different point of view in various papers. Space missions use Faraday cups (FCs) or electrostatic analyzers (EAs) to measure solar wind particles and to determine their bulk parameters but each of them has its advantages and drawbacks. EAs are designed to measure the full 3D VDF of the plasma particles with remarkably high-energy and angular resolutions and with time resolution that can be sufficient for study of fluctuations in the inertial range but they suffer with a limited geometrical factor and short exposition time at particular energy resulting in a large statistical noise. EAs are usually counting individual particles passing through the analyzer using detectors based on secondary emission (channeltrons, microchannel plates) and their detection efficiency depends on many factors like the particle type and energy, count rate, time of operation, etc. and all these effects should be taken into account in the data processing. Moreover, EA designers should undergo a complex game between the number of parallel channels, energy, angular and time resolution, and statistical noise (e.g., Helios 1, 2 [21]; ACE [22]; THEMIS [23]; MMS [24]). The last points are of a great importance because the solar wind is a highly turbulent medium in which the most energy is carried by Alfvénic fluctuations that exhibit a wide range of scales.
The second type of detectors is based on Faraday cups that directly measure the current of incoming charged particles falling onto their collector. FCs are relatively simple, reliable, and steady devices and their geometrical factor is large because they integrate ion flux over large spatial angles to reach a measurable collector current. To achieve an angular resolution, collectors divided into several segments or cups oriented in different directions (or combination of both) are used. The energy distribution is measured by application of the sweeping voltage on a control grid. This voltage can be either DC or DC with an AC component. The integral energy distribution is thus measured in the first case and its derivative in the second case (e.g., Voyager 1, 2 [25]; Wind [26]; INTERBALL-1 [27]; Parker Solar Probe [28]).
In general, the temperature is a scaling parameter of the Maxwellian VDF. It is a scalar quantity and the thermal speed can be determined as a second order moment of the distribution and it can be interpreted as a measure of the internal energy of the medium. If the distribution of the particle velocities is non-Maxwellian but isotropic, the second order moment remains scalar and can be still used as a measure of the internal energy.
The second order moment of the non-isotropic distribution is a tensor, scalar temperature is usually defined as the mean of the elements on the diagonal of tensor matrix. If there is a preferred (magnetic field) direction and the distribution is symmetric around it, and can be determined. If the medium is composed of a set of weakly interacting species, each of them has its own VDF, velocity(ies) and temperature(s). Figure 1 shows an example of the cut of ion energy distribution that demonstrates difficulties in estimations of different ion populations and their parameters. EAs as well as FCs differentiate particles according to their energy per unit charge and thus the horizontal axis is in these units. The crosses are measured data and the colored curves show the energy distribution achieved by the fit to full 3D distribution. One can see that it is not easy to separate three basic populations––proton core (red), proton beam (orange) and alpha particles (blue)––due to their overlap.
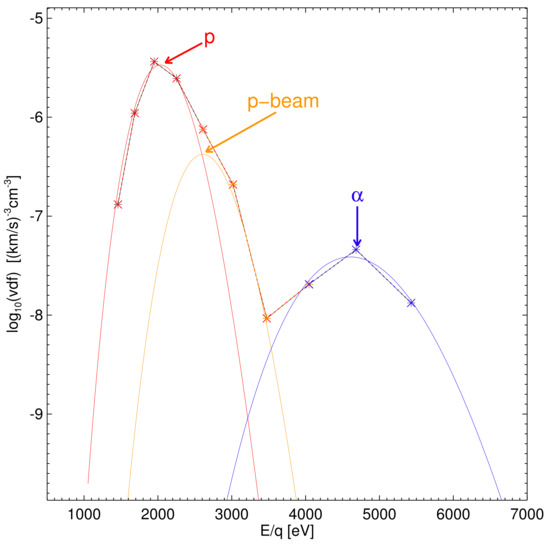
Figure 1.
An example of the cut along the magnetic field direction through 3D Helios ion energy distribution. Data measured on 11 March 1976 at 0302 UT are shown by crosses, the fitted distributions of different species (proton core—red, proton beam—orange and particles—blue) by full lines. Note that the whole 3D distribution was fitted. The parameters of fits are: The proton core— cm; km/s, km/s, km/s; proton beam— cm; km/s, km/s, km/s; and particles— cm; km/s, km/s, km/s.
Figure 2 demonstrates the proton beam effect on the temperature determination. The left-hand panel shows 2D cut through the fit of Helios measurements [12] on 11 March 1976 at 0302 UT. The velocities of the proton core (615 km/s) and beam (665 km/s) are distinguished by a small diamond and a large rectangle, respectively. The plot is made under an assumption that all particles are protons and, by design, particles exhibit an artificially high velocity due to their mass-per-charge ratio (M/Q); their real velocity (656 km/s) is shown by the asterisk. The left-hand panel shows that fitting of the proton core and beam as bi-Maxwellian distributions leads to larger than ; the values of thermal velocities (parallel, and perpendicular, are 30–48 km/s for the core and 26–56 km/s for the beam. On the other hand, particles were fitted as one population and they exhibit larger than thermal velocity (39 vs. 33 km/s). However, if the beam-core structure of the VDF is not considered and all protons are fitted as one population, the bulk speed increases to 638 km/s and becomes larger than (56 vs. 54 km/s) as the right-hand panel illustrates. It is important to note that application of this fitting leads to increase of the trace temperature of protons by a factor of two with respect to the proton core-beam fit. The reason is that the energy connected with a relatively large relative drift velocity of the beam with respect to the core is considered as thermal energy. As a result, the condition with only one proton population would lead to an apparent increase of the trace temperature and to a prevalence of that can be seen for example in [4].
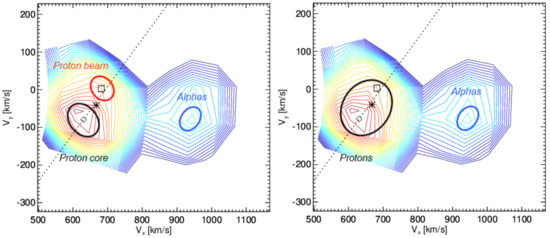
Figure 2.
A demonstration of the proton beam effect on the temperature determination. The background isocontours are fit to ion energy distribution from Figure 1, the magnetic field direction is shown by the dotted line, the ellipses distinguish identified ion populations and their temperature anisotropy. The left-hand panel reflects proton core-beam structure, the right-hand panel treats all protons as one population. The parameters of the fit under one proton population are: cm; km/s, km/s, km/s.
To quantify the effect of the proton beam in a statistical way, Figure 3 presents a comparison of the results of two ways of Wind data processing. Wind FC data was fitted by: (1) the proton-alpha (PA) code using a bi-Maxwellian VDF to a single proton and a single particle population [9,29] and (2) the proton-proton-alpha (PPA) code with a bi-Maxwellian VDF to the proton core and a Maxwellian VDF to each of the proton beam and particles [30]. This new fitting algorithm expects fifteen parameters for three solar wind ion populations: alpha particles (), proton core (p1), and proton beam (p2). Six parameters describe proton population p1 (number density, vector velocity, and and ) and p2 is described by three parameters (number density, differential flow, and isotropic thermal speed).
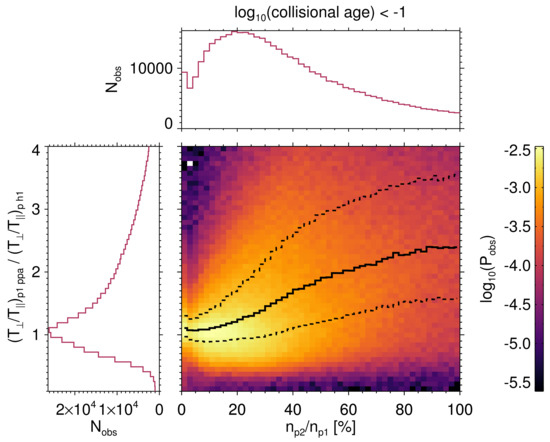
Figure 3.
A comparison of results of two ways of Wind data processing. The 2D probability distribution of the ratio of determined by the PPA procedure and determined by the PA (procedure 1) as a function of the ratio of proton beam and proton core densities, determined by the PPA is shown by a color scale. The probability of observations of mentioned ratios are shown by 1D histograms. See text for a detailed description.
The algorithms developed by Kasper et al. [9] and Alterman et al. [30] utilize magnetic field measurements [31,32] to determine each VDF orientation relative to the local magnetic field and it assumes that the extracted parameters are approximately constant over the measurement time. Figure 3 plots the ratio of anisotropy of the PPA (procedure 2) to anisotropy of the proton fit PA (procedure 1) as a function of the ratio of beam/core densities, . We use only measurements in the young solar wind (collisional age ) where the beam effect would be more pronounced. The figure shows that the anisotropy can be underestimated by a factor of 2 if the beam-core structure is not considered. Moreover, 1D histogram at the top reveals that the most probable relative beam density is 0.2 and the ratio of anisotropies corresponding to this abundance varies in a broad range with the median value of 1.2 (see black full line in 2D histogram).
The most important message following from the discussion above is that each evaluation of experimental results should always take into account peculiarities of the measuring methods and data processing. For this reason, we discuss the determination of the plasma parameters and namely the temperature using BMSW in the next section.
3. Fast Determination of the Temperature Using FCs in BMSW
A determination of the ion moments with high-temporal resolution measured by BMSW onboard Spektr-R is based on simultaneous readouts of collector currents of 6 FCs and two grid voltages. The complete procedure of the data processing can be found in Šafránková et al. [33], here we concentrate predominantly on the temperature determination.
Figure 4 shows the computer model of the normalized FC response to the change of the voltage U applied on the control grid under assumptions that the solar wind bulk velocity is oriented along the FC axis, the energy, E of incoming particles corresponds to the bulk speed, V and the thermal speed, is expressed as a fraction of the bulk speed, V. Note that the FC response depends only on this ratio [34]. The model of particle trajectories inside the cup takes into account problems discussed in [33] like real FC dimensions as well as the diameters of the grid wires and their spacing.
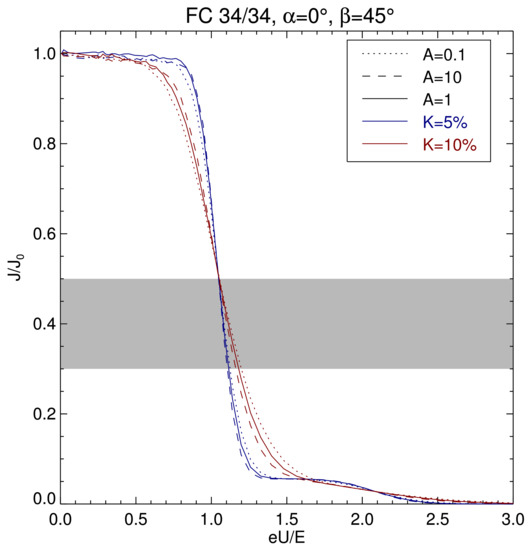
Figure 4.
FC energetic characteristics–normalized FC current, as a function of the normalized grid potential, for the incidence angle, and the angle between the IMF and z-axis, .
The velocity distributions of protons falling into the FC were gyrotropic and bi-Maxwellian with the symmetry axis (magnetic field direction) inclined by to the FC axis. This configuration approximates the solar wind with IMF directed along the Parker spiral. We kept constant the value of the trace temperature, , where and are parallel and perpendicular components of , V is the solar wind speed and K is the thermal to bulk speed ratio that was put 0.05 or 0.1 (blue and red colors in the figure). The anisotropy, was chosen as 0.1, 1 and 10 (dotted, full and dashed lines in the figure). In simulations, the input ions were protons with an addition of of alpha particles with a thermal speed equal to the trace speed of protons. The characteristics were computed using the ion trajectory tracing within a FC by the SIMION software package.
The measurements of a temperature use three identical FCs oriented toward the Sun. First of them is without a control grid voltage and measures the current , the grid voltages of other two FC are set by the feed-back loops to decrease the collector current approximately to 0.5 and 0.3 . The data transmitted to the ground are exact values of three currents and two voltages. is determined as a derivative from two points in plots like those in Figure 4.
The difference between currents used for temperature determination seems to be rather small (see shadowed area in Figure 4) but there are several reasons for our choice. First, the voltage corresponding to 0.5 does not depend on the temperature or its anisotropy and it is given by the bulk speed only, second, it takes into account the influence of low-energy plasma and effects of grid imprecisions that affect the current at low voltages and, third, the sum of currents caused by the proton beam and particles could exceptionally exceed 0.25 [12].
As it can be seen from the figure, the influence of the input temperature anisotropy on the determined thermal speed is rather weak. The red and blue curves differ by a factor of 4 in the temperature whereas the difference between dashed and dotted lines represents a change of anisotropy by two orders of magnitude. By contrast, the difference between dashed and dotted lines of the same color is much smaller than that between red and blue lines. Consequently, we can conclude that the temperature determined from FC data is a good approximation of the trace temperature of a proton core and is only slightly modified by the magnetic field rotations called pseudo-temperature effects by Gogoberidze et al. [8].
This conclusion is supported in Figure 5 that presents 20-min averages of measured by BMSW as a function of the IMF cone angle (dots). Note that we computed the cone angle as the angle between bulk velocity and magnetic field vectors. The top left panel shows all events that will be used later in the statistical study. The rest of panels shows subsets selected according to the anisotropy determined from the Wind data. The red bars stand for medians of , red dots are first and third quartiles. Looking at the medians, we can conclude that the median temperature does not depend on the magnetic field direction in the cone angle range of 60–120 (17 km/s) and it is slightly larger at lower (higher) angles. The median value of for isotropic cases and for cases with (right panels) is nearly constant and also equal to about 17 km/s, thus the dependence on the cone angle is dominantly caused by events with . The reasons can be twofold–first, the effects of the pseudo-temperature and, second, intensive proton and/or alpha particle beams that can exceed of the proton core current. The analysis of effects of temperature anisotropy determined from measurements of the FC onboard Wind spacecraft [35] shows a slight enhancement of for cone angles around . This trend is consistent with our observations but applicability of their results to our measurements is limited because the Wind FC uses different principle for a temperature determination and, as they show, the uncertainty of determination is as large as 30–40% under this condition. Nevertheless, the number of such cases in our data-set is relatively small and thus it cannot spoil large statistics presented in the next section.
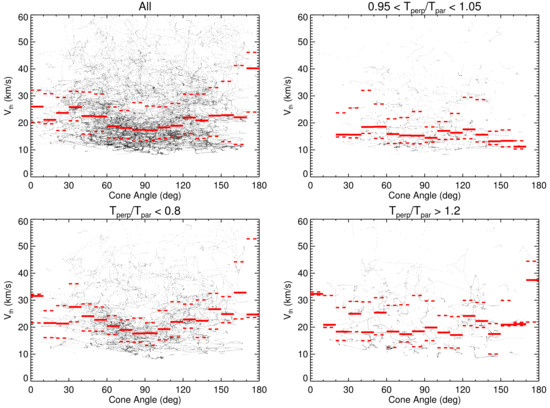
Figure 5.
The dependence of the thermal speed, as a function of the cone angle in different ranges of temperature anisotropy: all analyzed events (top left); 0.95 < < 1.05 (top right); < 0.8 (bottom left); and > 1.2 (bottom right).
4. Statistical Analysis of Spectral Slopes
The analysis focuses on solar wind (proton density, N, both perpendicular and parallel components ( and ) of the proton velocity and trace thermal velocity, ) fluctuations at frequencies covering the transition from the inertial range to the kinetic range. We have selected high cadency Spektr-R observations in the solar wind, divided them into 35,937 20-min basic subintervals with the overlapping duration 19 min and the fast Fourier transform (FFT) is computed on each subinterval [7]. Although the time resolution of measurements is 32 ms, we have limited our analysis to 2 Hz to guarantee that the power spectral densities (PSDs) are well above a noise level in the high-frequency part of the spectra, and even during intervals of low velocity variations [6].
These data were complemented with Wind measurements of the high-time resolution magnetic field [31] and plasma parameters (SWE [26]) propagated to the Spektr-R location. Since Wind and Spektr-R are not necessarily in the same solar wind stream, we analyze only the intervals when the difference between both solar wind speeds is lower than (more details in [36]). The average magnetic field direction was used for a determination of the field-aligned coordinate system and the Spektr-R plasma velocity was transformed into this system in order to determine , and .
The magnetic field and plasma parameters vary in broad ranges and the same do characteristic plasma frequencies. In order to facilitate a statistical processing of the spectra calculated in the spacecraft frame frequency, we apply the Taylor hypothesis and normalize the spacecraft frame frequency f to the frequency that corresponds to typical dimensions of solar wind structures, defined in [6] using the solar wind speed, V, proton thermal gyroradius, ( where is proton cyclotron frequency) and proton inertial length, L as
Such a normalization allows us to calculate average (median) spectrum of each quantity. Although the original spectra are calculated at identical frequencies determined by the length of an interval, the normalization shifts each of them along the frequency axis. We divided the whole range of into several hundreds of subintervals and calculated medians of all PSD values falling into this subinterval. As an example of this procedure, Figure 6 shows median spectra of analyzed quantities computed for the full set of intervals. The median spectra were fitted with two (three for the density and parallel magnetic field component) straight lines in the range of 0.05–3. The fits are shown in the figure by straight lines of a corresponding color and one can note that the slopes of spectra are well defined because the fits can be distinguished from the spectrum itself only around the spectral breaks that are defined as their intersection.
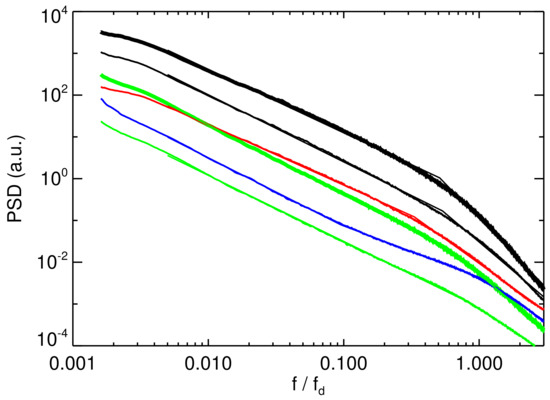
Figure 6.
Median spectra of (thick black), (thin black), (thick green), (thin green), N (blue) and (red) fluctuations. The straight thin lines of corresponding colors show the fits (note that they are distinguishable only around the spectral break). The slopes of linear fits in both inertial and kinetic ranges are given in the last row of Table 1.
A full set of spectra was sorted according to different characteristic quantities, namely proton (the ratio of proton kinetic and magnetic pressures), collisional age, , temperature anisotropy, A and a standard deviation of fluctuations of the magnetic field perpendicular component normalized to mean magnetic field, . We computed the collisional age according to Kasper et al. [4] as where is the time scale for energy exchange due to small-angle Coulomb scattering, V is the solar wind speed and R is the distance from the Sun to Spektr-R. The spectral parameters in the subsets were determined as described above. It should be noted that we use temperature anisotropy determined from Wind SWE energy spectra under an assumption of one proton population. The results of our analysis are summarized in Table 1.

Table 1.
Overview of median spectral slopes of different parameters in inertial and kinetic ranges for four groups of quantities.
As noted, the table shows both inertial and kinetic slopes of median spectra in all analyzed subsets. A quick look to numbers reveals that exhibits shallowest spectrum in the inertial range. On the other hand, there is a clear similarity between and N in the kinetic range. Since this presentation is complex but not too illustrative, we show the results in a series of panels in Figure 7.
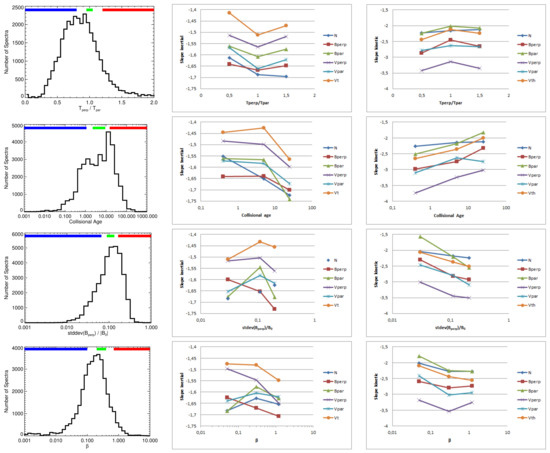
Figure 7.
The slopes of fluctuation spectra in inertial (middle panels) and kinetic (right-hand panels) ranges of frequencies as a function of temperature anisotropy (top row), collisional age (second row), level of magnetic field fluctuations (third row) and ion beta (last row). The distributions of particular parameters in the analyzed set are in the first column, the ranges used for averaging are indicated by color bars in each histogram and are also introduced in Table 1. Color and symbol codings in all panels of spectral slopes are: N—blue ⋄; —red □; —light green Δ; —violet ×; —light blue ★; and —orange •.
From the point of view of the discussion on the temperature/pseudo-temperature, the analysis presented in the top row of the panels would be probably the most interesting because it shows the dependence on the temperature anisotropy, A. The color bars indicate the anisotropy ranges used for calculations of median spectra. The slopes of the median spectra of different parameters are depicted as color dots in the middle panel for the inertial range, the analysis of kinetic range slopes is shown in the right-hand panel. However, the slopes of analyzed quantities change with the temperature anisotropy roughly in the same way. The steepest slopes are observed for the isotropic temperature in the inertial range but they are shallowest in the kinetic range. Note that differences between groups with and and are small.
The second row of panels confirms the conclusions following from the top row because one would expect the isotropic temperature at largest collisional ages (e.g., [3]) and the middle panel indeed shows steepest slopes of the quantities in the inertial range at such collisional ages. A similar conclusion follows from the right-hand panel because we observe shallowest slopes for largest collisional age.
A selection of intervals according to the standard deviation of the magnetic field is shown in the third row. The results are surprising because one would expect steepening of slopes with increasing fluctuation level but it is observed only in the kinetic range, about the same steepness of slopes in the inertial range was found for small () and large () fluctuations, moderate fluctuations with exhibit shallowest slopes. The only exception is the slope of . The shallow slopes in the kinetic range observed for all quantities (and especially for ) when the level of fluctuations is small are probably affected by the instrumental and data processing noise. The noise effect is comprehensively studied in Pitňa et al. [37] and the authors suggest that the slope can be reliably determined if the signal-to-noise ratio exceeds 30. Since the topic of this study is a comparison of a behavior of temperature fluctuations with other quantities and noise effects would be similar for all of them, we will return to this problem in a follow-up study.
The bottom panels present three proton subsets, the boundaries are marked in the first panel. The histogram in this panel shows that there are no really large or small events in the analyzed set. Concentrating on the changes of the slopes, we can note a similar behavior as slopes of and , all these slopes exhibit steepening with increasing in the inertial range. On the other hand, the slopes of the density and parallel components of the magnetic field and velocity are shallowest in the intermediate beta range and the same effect can be seen in the thermal velocity spectra. The kinetic fluctuations of quantities exhibit a slight steepening with increasing beta.
Figure 7 shows that trends of changes of spectral slopes of all quantities are similar but not identical. To quantify the degree of similarities, we made the plots like those shown in Figure 8 and computed the Spearmann correlation coefficients. The plot compares trends of median slopes of in the inertial (left column) and kinetic (right-hand column) ranges with the slopes of N (top panels) and (bottom panels); the correlation coefficients are given at the top of each panel. Larger correlations and a better organization of the bottom plots would suggest that the fluctuations of and are probably driven by the same processes. However, the spread of the points is rather large for an ultimate conclusion. For this reason, we present correlations of spectral slopes of analyzed parameters with the slopes of in Table 2.
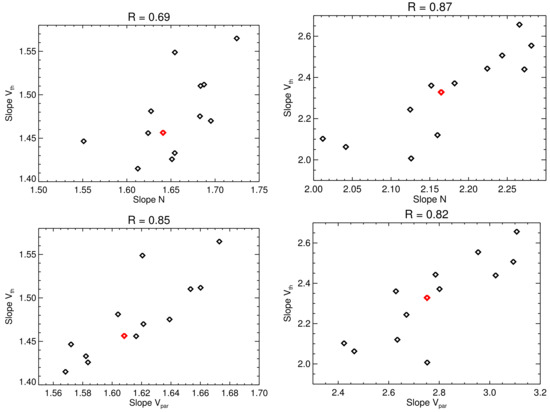
Figure 8.
A comparison of median slopes of and N (top panels) and and (bottom panels), respectively in inertial (left panels) and kinetic (right panels) ranges. Red points in particular panels mark values of slopes for the full set of events.

Table 2.
Correlations between the median slopes of and the slopes of other solar wind parameters and magnetic field determined for different subsets in inertial and kinetic ranges. The greatest correlation in each range is bolded.
The table shows that the best correlation with in the inertial range exhibits fluctuations. Since the fluctuations would be compressive in nature and the same is true for , this result is consistent with expectations and it is further supported by the fact that the second largest correlation coefficient exhibits . Moreover, the fluctuations of parallel components are often replaced with the fluctuations of magnitudes for the sake of compressibility determination (e.g., [36] and references therein) and thus, this conclusion is consistent with Šafránková et al. [6]. A lower correlation of slopes with the slope of density spectra can be caused by their flattening at the end of the inertial range that is often observed [7] but its origin is still under debate [38]. In the kinetic range, variations of median slopes of studied parameters with the temperature spectra are well correlated, the largest coefficient was found for fluctuations and this is again consistent with the compressive nature of these fluctuations.
5. Discussion and Conclusions
Although the original aim of this study is to check a suggestion of Gogoberidze et al. [8] that the spectra of the thermal speed would be similar to spectra of the density, it brings a lot of new information. Our discussion of measuring methods used for a determination of solar wind parameters illustrates effects that are often neglected and emphasizes the fact that measurement methods and spatial, energetic and temporal resolutions of a particular instrument should be taken into account in processing and presentation of the experimental data as discussed also by many authors (see Section 1). When reading an article, we often do not know how the plasma parameters were determined and thus what they mean. For example, the density or velocity can be related to the proton core, the proton core plus proton beam or it can include also somehow weighted contribution of heavier ions. As we illustrate in Figure 2 and Figure 3, the tensor nature of the temperature in anisotropic multicomponent plasma complicates a situation even more.
Our deeper analysis of measurements of the BMSW instrument that are used for an estimation of the plasma parameters in the present contribution (Figure 4 and Figure 5) revealed that the present study deals with the velocity and the trace temperature of the proton core and this conclusion should be considered in the interpretation of analyzed results.
We started with a simple check of the pseudo-temperature effect. In order to avoid problems with the anisotropy of the ion distribution, we selected intervals with (1) a large collisional age and (2) with a negligible temperature anisotropy and checked slopes of spectra of , , , , , and N in the inertial and kinetic ranges and found that exhibits shallowest slopes in both ranges (see corresponding rows in Table 1). Under these conditions, the temperature would be scalar and a contribution of pseudo-temperature can be neglected but even in these cases, we did not find similarity of the density and temperature spectra; the density spectra were always steeper. We think that it is connected with the influence of kinetic Alfvén waves/fluctuations that form the density spectrum and cause its flattening [7]. Since the flattened part is excluded in the slope determination, the resulting density slope is steeper. Note that any trend to such flattening was not observed in the spectra of the thermal speed. However, the differences between slopes were small and thus the results were not too conclusive. For this reason, we carried out a deeper analysis and sorted more than 30,000 of analyzed time intervals into groups according to the collisional age, temperature anisotropy, ion beta and a level of magnetic field fluctuations and determined median spectral slopes for each of these subsets.
The result of the presented analysis can be summarized as it follows:
- Modeling of the response of the Faraday cup has shown that the temperature determined from the fast measurements of BMSW [33] can be considered as the proton core trace temperature and the effect of the pseudo-temperature discussed in [8] exists but it is very small (Figure 4 and Figure 5) in the BMSW case.
- The values of slopes of in subsets differing by the collisional age, temperature anisotropy, proton beta, and a level of the magnetic field fluctuations vary from −1.42 to −1.56 in the inertial range and from −2.01 to −2.66 in the kinetic range.
- We did not find a clear similarity between spectra of N and fluctuations in the inertial range of frequencies, the N spectra are always steeper.
- Spectral slopes of all analyzed parameters (N, , and , components of the magnetic field and velocity, and ) depend on background parameters in a similar way; the correlation coefficients are in a range of 0.7 to 0.95. However, the quantities used for bining of our set are not fully independent. For example, larger magnetic field fluctuation level is typical for collisionally younger plasma (e.g., [3]).
- The largest correlation coefficients were found between slopes of and , , in agreement with a compressive nature of these fluctuations.
- The values of slopes of all parameters in the kinetic range are similar and well correlated.
We should note that our study combines all solar wind types regardless of their origin. The turbulent spectra are formed close to the Sun and their spectral shapes probably differ in streams emanating from various sources but mutual interactions of particular streams in course of its expansion excite waves of different kinds and form interplanetary shocks [39] that further shape the spectra of all parameters. We think that these interactions lead to the observed similarities of power spectral densities of analyzed fluctuations at 1 AU. A deeper study of power spectra measured closer to the Sun or a careful separation of scarce intervals that are not affected by stream interactions can further elucidate the problem of similarities of spectral shapes of different quantities. Another way can be also applications of advanced techniques of the data analysis like the cross-wavelet transform technique [40] that can provide instantaneous frequency information along with phase differences in the time–frequency domain.
Author Contributions
The manuscript is a result of works of all authors and their particular contributions are: Data processing—Wind, B.L.A., M.L.S. and T.Ď.; data processing—Spektr-R, F.N.; methodology, J.Š. and F.N.; data analysis and interpretation, Z.N. and J.Š.; software, manuscript preparation, visualization, J.P.; original draft preparation, Z.N.; a contribution to data interpretation and discussion, A.P., Y.M.V., B.L.A. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Czech Science Foundation under Contract 19-18993S and Charles University Grant Agency under No. 264220.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The authors acknowledge the Wind team for the magnetic field and SWE plasma data available via http://cdaweb.gsfc.nasa.gov/ accessed on 29 September 2021; the BMSW data (Spektr-R project) are available via http://aurora.troja.mff.cuni.cz/spektr-r/project/ accessed on 29 September 2021.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MMS | Magnetospheric Multiscale (MMS) mission |
| PSP | Parker Solar Probe (PSP) mission |
| BMSW | Bright Monitor of the Solar Wind (BMSW) on board the Spektr-R spacecraft |
| ACE | Advanced Composition Explorer (ACE) mission |
| THEMIS | The Time History of Events and Macroscale Interactions during |
| Substorms (THEMIS) mission | |
| AU | Astronomical Unit |
| FCs | Faraday Cups |
| EAs | Electrostatic Analyzers |
| VDF | Velocity Distribution Function |
| FFT | Fast Fourier Transform |
| PSD | Power Spectral Densities |
References
- Chew, G.F.; Goldberger, M.L.; Low, F.E. The Boltzmann equation and the one-fluid hydromagnetic equations in the absence of particle collisions. Proc. R. Soc. Math. Phys. Eng. Sci. 1956, 236, 112–118. [Google Scholar]
- Eviatar, A.; Schulz, M. Ion-temperature anisotropies and the structure of the solar wind. Planet. Space Sci. 1970, 18, 321. [Google Scholar] [CrossRef]
- Bale, S.D.; Kasper, J.C.; Howes, G.G.; Quataert, E.; Salem, C.; Sundkvist, D. Magnetic fluctuation power near proton temperature anisotropy instability thresholds in the solar wind. Phys. Rev. Lett. 2009, 103, 211101. [Google Scholar] [CrossRef] [PubMed]
- Kasper, J.C.; Lazarus, A.J.; Gary, S.P. Hot solar-wind helium: Direct evidence for local heating by Alfvén-cyclotron dissipation. Phys. Rev. Lett. 2008, 101, 261103. [Google Scholar] [CrossRef]
- Šafránková, J.; Němeček, Z.; Přech, L.; Zastenker, G.N. Ion Kinetic Scale in the Solar Wind Observed. Phys. Rev. Lett. 2013, 110, 025004. [Google Scholar] [CrossRef]
- Šafránková, J.; Němeček, Z.; Němec, F.; Přech, L.; Chen, C.H.K.; Zastenker, G.N. Power spectral density of fluctuations of bulk and thermal speeds in the solar wind. Astrophys. J. 2016, 825, 121. [Google Scholar] [CrossRef]
- Šafránková, J.; Němeček, Z.; Němec, F.; Přech, L.; Pitňa, A.; Chen, C.H.K.; Zastenker, G.N. Solar wind density spectra around the ion spectral break. Astrophys. J. 2015, 803, 107. [Google Scholar] [CrossRef][Green Version]
- Gogoberidze, G.; Voitenko, Y.M.; Machabeli, G. Temperature spectra in the solar wind turbulence. Mon. Notices R. Astron. Soc. 2018, 480, 1864–1869. [Google Scholar] [CrossRef]
- Kasper, J.C.; Lazarus, A.J.; Gary, S.P. Wind/SWE observations of firehose constraint on solar wind proton temperature anisotropy. Geophys. Res. Lett. 2002, 29, 1839. [Google Scholar] [CrossRef]
- Kasper, J.C.; Lazarus, A.J.; Steinberg, J.T.; Ogilvie, K.W.; Szabo, A. Physics-based tests to identify the accuracy of solar wind ion measurements: A case study with the Wind Faraday Cups. J. Geophys. Res. Space Phys. 2006, 111, A03105. [Google Scholar] [CrossRef]
- Stansby, D.; Salem, C.; Matteini, L.; Horbury, T. A new inner heliosphere proton parameter dataset from the Helios mission. Sol. Phys. 2018, 293, 155. [Google Scholar] [CrossRef] [PubMed]
- Ďurovcová, T.; Šafránková, J.; Němeček, Z. Evolution of relative drifts in the expanding solar wind: Helios observations. Sol. Phys. 2019, 294, 97. [Google Scholar] [CrossRef]
- D’Amicis, R.; De Marco, R.; Bruno, R.; Perrone, D. Investigating the nature of the link between magnetic field orientation and proton temperature in the solar wind. Astron. Astrophys. 2019, 632, 8. [Google Scholar] [CrossRef]
- De Marco, R.; Bruno, R.; D’Amicis, R.; Telloni, D.; Perrone, D. Possible instrumental effects on moments computation of the solar wind proton velocity distribution function: Helios observations. Astron. Astrophys. 2020, 639, 7. [Google Scholar] [CrossRef]
- Marsch, E.; Tu, C.Y. Spectral and spatial evolution of compressible turbulence in the inner solar-wind. J. Geophys. Res. Space Phys. 1990, 95, 11945–11956. [Google Scholar] [CrossRef]
- Verscharen, D.; Marsch, E. Apparent temperature anisotropies due to wave activity in the solar wind. Ann. Geophys. 2011, 29, 909–917. [Google Scholar] [CrossRef]
- Perrone, D.; Bourouaine, S.; Valentini, F.; Marsch, E.; Veltri, P. Generation of temperature anisotropy for alpha particle velocity distributions in solar wind at 0.3 AU: Vlasov simulations and Helios observations. J. Geophys. Res. Space Phys. 2014, 119, 2400. [Google Scholar] [CrossRef]
- Nicolaou, G.; Verscharen, D.; Wicks, R.T.; Owen, C.J. The impact of turbulent solar wind fluctuations on Solar Orbiter plasma proton measurements. Astrophys. J. 2019, 886, 101. [Google Scholar] [CrossRef]
- Roberts, O.W.; Narita, Y.; Nakamura, R.; Voros, Z.; Gershman, D. Anisotropy of the spectral index in ion scale compressible turbulence: MMS observations in the magnetosheath. Front. Phys. 2019, 7, 184. [Google Scholar] [CrossRef]
- Huang, J.; Kasper, J.C.; Vech, D.; Klein, K.G.; Stevens, M.; Martinović, M.M.; Alterman, B.L.; Ďurovcová, T.; Paulson, K.; Maruca, B.A.; et al. Proton temperature anisotropy variations in inner heliosphere estimated with the first Parker Solar Probe observations. Astrophys. J. Suppl. Ser. 2020, 246, 70. [Google Scholar] [CrossRef]
- Rosenbauer, H.; Schwenn, R.; Marsch, E.; Meyer, B.; Miggenrieder, H.; Montgomery, M.D.; Mühlhäuser, K.H.; Pilipp, W.; Voges, W.; Zink, S.M. Survey on initial results of Helios plasma experiment. J. Geophys.-Zeit. Geophys. 1977, 42, 561–580. [Google Scholar]
- McComas, D.J.; Bame, S.J.; Barker, P.; Feldman, W.C.; Phillips, J.L.; Riley, P.; Griffee, J.W. Solar Wind Electron Proton Alpha Monitor (SWEPAM) for the Advanced Composition Explorer. Space Sci. Rev. 1998, 86, 563. [Google Scholar] [CrossRef]
- McFadden, J.P.; Carlson, C.W.; Larson, D.; Ludlam, M.; Abiad, R.; Elliott, B.; Angelopoulos, V. The THEMIS ESA plasma instrument and in-flight calibration. Space Sci. Rev. 2008, 141, 277. [Google Scholar] [CrossRef]
- Pollock, C.; Moore, T.; Jacques, A.; Burch, J.; Gliese, U.; Saito, Y.; Omoto, T.; Avanov, L.; Barrie, A.; Coffey, V.; et al. Fast Plasma Investigation for Magnetospheric Multiscale. Space Sci. Rev. 2016, 199, 331–406. [Google Scholar] [CrossRef]
- Bridge, H.S.; Belcher, J.W.; Butler, R.J.; Lazarus, A.J.; Mavretic, A.M.; Sullivan, J.D.; Siscoe, G.L.; Vasyliunas, V.M. The plasma experiment on the 1977 Voyager Mission. Space Sci. Rev. 1977, 21, 259–287. [Google Scholar] [CrossRef]
- Ogilvie, K.W.; Chornay, D.J.; Fritzenreiter, R.J.; Hunsaker, F.; Keller, J.; Lobell, J.; Miller, G.; Scudder, J.D.; Sittler, E.C.; Torbert, R.B.; et al. SWE, A comprehensive plasma instrument for the Wind spacecraft. Space Sci. Rev. 1995, 71, 55–77. [Google Scholar] [CrossRef]
- Šafránková, J.; Zastenker, G.; Němeček, Z.; Fedorov, A.; Simerský, M.; Přech, L. Small scale observation of magnetopause motion: Preliminary results of the INTERBALL project. Ann. Geophys. 1997, 15, 562–569. [Google Scholar] [CrossRef][Green Version]
- Case, A.W.; Kasper, J.C.; Stevens, M.L.; Korreck, K.E.; Paulson, K.; Daigneau, P.; Caldwell, D.; Freeman, M.; Henry, T.; Klingensmith, B.; et al. The Solar Probe Cup on the Parker Solar Probe. Astrophys. J. Suppl. Ser. 2020, 246, 43. [Google Scholar] [CrossRef]
- Aellig, M.R.; Lazarus, A.J.; Steinberg, J.T. The solar wind helium abundance: Variation with wind speed and the solar cycle. Geophys. Res. Lett. 2001, 28, 2767. [Google Scholar] [CrossRef]
- Alterman, B.L.; Kasper, J.C.; Stevens, M.L.; Koval, A. A comparison of alpha particle and proton beam differential flows in collisionally young solar wind. Astrophys. J. 2018, 864, 112. [Google Scholar] [CrossRef]
- Lepping, R.P.; Acũna, M.H.; Burlaga, L.F.; Farrell, W.M.; Slavin, J.A.; Schatten, K.H.; Mariani, F.; Ness, N.F.; Neubauer, F.M.; Whang, Y.C.; et al. The Wind magnetic-field investigation. Space Sci. Rev. 1995, 71, 207–229. [Google Scholar] [CrossRef]
- Koval, A.; Szabo, A. Magnetic field turbulence spectra observed by the Wind spacecraft. AIP Conf. Proc. 2013, 1539, 211. [Google Scholar]
- Šafránková, J.; Němeček, Z.; Přech, L.; Zastenker, G.; Chesalin, L.; Čermák, I.; Komárek, A.; Vaverka, J.; Beránek, M.; Pavlů, J.; et al. Fast solar wind monitor (BMSW): Description and first results. Space Sci. Rev. 2013, 175, 165–182. [Google Scholar] [CrossRef]
- Šafránková, J.; Němeček, Z.; Přech, L.; Koval, A.; Čermák, I.; Beránek, M.; Zastenker, G.; Shevyrev, N.; Chesalin, L. A new approach to solar wind monitoring. Adv. Space Res. 2008, 41, 153–159. [Google Scholar] [CrossRef]
- Woodham, L.D.; Wicks, R.T.; Verscharen, D.; TenBarge, J.M.; Howes, G.G. Dependence of solar wind proton temperature on the polarization properties of Alfvénic fluctuations at ion-kinetic scales. Astrophys. J. 2021, 912, 101. [Google Scholar] [CrossRef]
- Šafránková, J.; Němeček, Z.; Němec, F.; Verscharen, D.; Chen, C.H.K.; Ďurovcová, T.; Riazantseva, M.O. Scale-dependent polarization of solar wind velocity fluctuations at the inertial and kinetic scales. Astrophys. J. 2019, 870, 40. [Google Scholar] [CrossRef]
- Pitňa, A.; Šafránková, J.; Němeček, Z.; Franci, L.; Pi, G. A novel method for estimating the intrinsic magnetic field spectrum of kinetic range turbulence. Atmosphere 2021. [Google Scholar]
- Montagud-Camps, V.; Němec, F.; Šafránková, J.; Němeček, Z.; Verdini, A.; Grappin, R.; Papini, E.; Franci, L. Flattening of the density spectrum in compressible Hall-MHD simulations. Atmosphere 2021, 12, 1162. [Google Scholar] [CrossRef]
- Pitňa, A.; Šafránková, J.; Němeček, Z.; Franci, L. Decay of solar wind turbulence behind interplanetary shocks. Astrophys. J. 2017, 844, 51. [Google Scholar] [CrossRef]
- Ghaderpour, E. Least-squares wavelet and cross-wavelet analyses of VLBI baseline length and temperature time series: Fortaleza–Hartebeesthoek–Westford–Wettzell. Publ. Astron. Soc. Pac. 2021, 133, 014502. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).